1 INTRODUCTION

The atmosphere, based on the known scheme of zonal mean circulation, consists of cells with various meridional and zonal flows: Hadley, Ferrell, and polar (Lorenz, 1970; Matveev, 2000; Mohanakumar, 2011). Such an axisymmetric circulation pattern is the main (basic state) for the application of various numerical and analytical methods for studying baroclinic or barotropic (shear) instabilities developing in the corresponding hydrodynamic flows, which lead to the formation of nonaxisymmetric flows (the Rossby regime) (Antar and Fowlis, 1981). It is important, however, that the violation of the axial symmetry of the mentioned cells is largely due to the distribution of surface and thermal contrasts over the continents (Cook, 2003).

It is interesting to consider the effect of longitudinal anomalies on the generation and distribution of Rossby waves in the case of asymmetric distribution of velocity fields in the Hadley and Ferrel cells. We use the results of both laboratory and numerical experiments with shallow water equations.

Rossby waves are known to be an important contribution to the general circulation of the atmosphere. In extratropical zones, the propagation velocity of these waves to the west \(\frac{\beta }{{k_{x}^{2} + k_{y}^{2} + \frac{1}{{L_{0}^{2}}}}}\) (\({{k}_{x}}\) and \({{k}_{y}}\) are zonal (azimuth) and meridional wave numbers, and \({{L}_{0}}\) is the Rossby deformation radius) with respect to the mean transport decreases along with the latitudinal \(\varphi \) variation in the Coriolis parameter \(f = 2\Omega \sin \varphi \) (\(\beta = {{2\Omega } \mathord{\left/ {\vphantom {{2\Omega } {R\cos \varphi }}} \right. \kern-0em} {R\cos \varphi }},\) \(R\) is the radius of the planet). One important source of Rossby wave generation is the shear instability of hydrodynamic flows in the extratropical zone (eastward polar transport and westward flow at midlatitudes). Among the large number of approaches and solutions for shear hydrodynamic instability with the \(\beta \) effect, the simplest are the explicit formulas describing the solutions of the Charney–Obukhov equations (Obukhov, 1949; Dolzhansky, 2011) for stream function \(\psi \) with time-dependent meridional wavenumber \({{k}_{y}} = {{k}_{y}}(t)\) (transient instability) (Chagelishvili and Chkhetiani, 1995; Chkhetiani et al., 2015; Chkhetiani and Kalashnik, 2018):

$$\begin{gathered} \psi = a(t){{e}^{{i\left( {{{k}_{x}}x + {{k}_{y}}(t)y} \right)}}} + {{\psi }_{0}},\,\,\,\,{{\psi }_{0}} = - Uy - s\frac{{{{y}^{2}}}}{2}, \\ \frac{\partial }{{\partial t}}\left( {\Delta \psi - \frac{1}{{L_{0}^{2}}}\psi } \right) + \left[ {\psi ,\Delta \psi } \right] + \beta \frac{{\partial \psi }}{{\partial x}} = 0,\,\,\,\,u = - \frac{{\partial \psi }}{{\partial y}}, \\ v = \frac{{\partial \psi }}{{\partial x}}, \\ \end{gathered} $$
(1)
$$\begin{gathered} \left( {{{k}^{2}} + \frac{1}{{L_{0}^{2}}}} \right)\frac{{d{{k}_{y}}(t)}}{{dt}} + s{{k}^{2}}{{k}_{x}} = 0,\,\,\,\,{{k}^{2}}(t) = k_{x}^{2} + k_{y}^{2}(t), \\ \frac{d}{{dt}}\left[ {\left( {{{k}^{2}} + \frac{1}{{L_{0}^{2}}}} \right)a} \right] - i{{k}_{x}}\left( {\beta - {{k}^{2}}U} \right)a = 0, \\ \end{gathered} $$
(2)

where \(U\) and \(s\) are the background velocity and horizontal shear of velocity, respectively, with initial conditions \({{k}_{{0y}}} \gg {{k}_{x}}\) (the condition of instability of long waves for the Kolmogorov flow (Meshalkin and Sinai, 1961; Gledzer et al., 1981)); \(a\left( {t = 0} \right) = {{a}_{0}}.\)

Formulas with wavenumber versus time dependence were used to find unstable solutions in the flows with elliptical streamlines (Gledzer and Ponomarev, 1992), in dynamical systems (Shukhman, 2005), or for the Hadley circulation with a horizontally inhomogeneous temperature distribution (Gledzer, 2008).

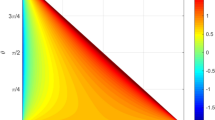
Solutions of Eqs. (2) show (Chkhetiani and Kalashnik, 2018) that, under the condition of long waves \({{L}_{v}} \gg {{L}_{0}},\) \({{k}_{x}} = \frac{{2\pi }}{{{{L}_{v}}}}\), there are comparatively long time intervals \(\Delta t\), during which meridional wavenumber \({{k}_{y}}(t),\) depending only on shear \(s\) (at fixed \({{k}_{x}},\) \({{L}_{0}}\)), changes only slightly (step) and \(\left| {{{k}_{y}}(t)} \right| \ll {{k}_{x}}\) (see Fig. 1а). The wave energy proportional to \({{\left| {a(t)} \right|}^{2}}\) increases from small initial values and remains quasisttionary during the same time interval \(\Delta t\) (intermediate (transient) velocity maximum). This case is shown in Fig. 1a for \({{k}_{x}} = \frac{\varepsilon }{{{{L}_{0}}}}\) at \(\varepsilon = 0.5.\) If \(\varepsilon = 1\) (Fig. 1а), i.e., \({{L}_{v}} = 2\pi {{L}_{0}},\) then \({{k}_{y}}(t)\) decreases monotonously; however, for \(\left| {{{k}_{y}}} \right| \leqslant {{k}_{x}}\), the amplitude of \(\left| a \right|\) also strongly increases (Fig. 1b).

Fig. 1.
figure 1

(a) Dependence of meridional wave number \({{k}_{y}}{{L}_{0}}\) on \(\tau \) for values \(\varepsilon = 0.5,\) \(\varepsilon = 1.0,\) and \(\varepsilon = {{k}_{x}}{{L}_{0}}.\) (b) Dependence of amplitude \(a(t)\) on \(\tau \) for values \(\varepsilon = 0.5\) (solid curves) and \(\varepsilon = 1.0\) (dashed line).

Full size image

2 RESONANT INTERACTION OF TRANSIENT MODES

We will consider Eqs. (1) and (2) as a mechanism for generating Rossby waves with a meridional wave number \({{k}_{y}} \ne 0,\) formed in the previously indicated interval \(\Delta t,\) with an amplitude in the vicinity of its maximum values

$$\left| a \right| = {{a}_{0}}\frac{{k_{x}^{2} + k_{{0y}}^{2} + \frac{1}{{L_{0}^{2}}}}}{{k_{x}^{2} + k_{y}^{2} + \frac{1}{{L_{0}^{2}}}}} \gg \left| {{{a}_{0}}} \right|$$

at \(k_{y}^{2} \ll k_{{0y}}^{2},\) \(k_{y}^{2} \ll k_{x}^{2}.\)

If there are two waves with zonal wave numbers \({{k}_{x}}\) and \(2{{k}_{x}}\) and the same meridional number \({{k}_{y}},\) then there is the same frequency for them \(\omega \) calculated from the Rossby formula,

$$\omega = - \frac{{\beta {{k}_{x}}}}{{k_{x}^{2} + k_{y}^{2} + \frac{1}{{L_{0}^{2}}}}} = - \frac{{\beta 2{{k}_{x}}}}{{{{{\left( {2{{k}_{x}}} \right)}}^{2}} + k_{y}^{2} + \frac{1}{{L_{0}^{2}}}}},$$

under condition

$$2k_{x}^{2} = k_{y}^{2} + \frac{1}{{L_{0}^{2}}}.$$
(3)

Relation (3), which is necessary for the search for a stationary wave, includes the Rossby deformation radius \({{L}_{0}}.\) Another condition that determines the relationship between \({{k}_{x}}\) and \({{k}_{y}},\) can be setting the relief as a natural factor that determines the scale of the Rossby waves. In particular, taking into account the shape of the relief, which is similar to the horizontal velocity shear \(s\) in Eqs. (2), gives the second relationship between \({{k}_{x}}\) and \({{k}_{y}},\) as a result of which these wave numbers can be specified.

During the resonant interaction of these two waves, formation of quasi-stationary wave \({{e}^{{i{{k}_{x}}x}}},\) independent of coordinate \(y,\) with wavenumber \({{k}_{x}}\) is possible:

$$\begin{gathered} \psi = A(t){{e}^{{i{{k}_{x}}x}}} + B(t){{e}^{{i\left( {{{k}_{x}}x + {{k}_{y}}y - \omega t} \right)}}} \\ + \,\,C(t){{e}^{{i\left( {2{{k}_{x}}x + {{k}_{y}}y - \omega t} \right)}}} + c.c. \\ \end{gathered} $$
(4)

We use the standard procedure with complex coefficients А, В, and \(C\) with averaging over oscillations with frequencies multiple to \(\omega ,\), and obtain the following equations:

$$\begin{gathered} \left( {k_{x}^{2} + \frac{1}{{L_{0}^{2}}}} \right)\dot {A} = 3k_{x}^{3}{{k}_{y}}B{\text{*}}C + i{{k}_{x}}\beta A, \\ \left( {k_{x}^{2} + k_{y}^{2} + \frac{1}{{L_{0}^{2}}}} \right)\dot {B} = - \left( {3k_{x}^{2} + k_{y}^{2}} \right){{k}_{x}}{{k}_{y}}A{\text{*}}C, \\ \left( {4k_{x}^{2} + k_{y}^{2} + \frac{1}{{L_{0}^{2}}}} \right)\dot {C} = k_{y}^{3}{{k}_{x}}AB \\ \end{gathered} $$
(5)

with energy integrals \(E = F(1)\) and squarred vorticity \({{\Omega }^{2}} = F(2)\):

$$\begin{gathered} F(n) = {{\left( {k_{x}^{2} + \frac{1}{{L_{0}^{2}}}} \right)}^{n}}{{\left| A \right|}^{2}} + {{\left( {k_{x}^{2} + k_{y}^{2} + \frac{1}{{L_{0}^{2}}}} \right)}^{n}}{{\left| B \right|}^{2}} \\ + \,\,{{\left( {4k_{x}^{2} + k_{y}^{2} + \frac{1}{{L_{0}^{2}}}} \right)}^{n}}{{\left| C \right|}^{2}}. \\ \end{gathered} $$

Equations (5) are a particular case of the triplet interaction of waves, in which the time frequency of one of the waves is equal to zero. However, waves with amplitudes \(B\) and \(C\) in (4) form three-mode blocks of interactions with waves \({{e}^{{ \pm i\left( {3{{k}_{x}}x + 2{{k}_{y}}y - 2\omega t} \right)}}},\) \({{e}^{{ \pm i\left( {4{{k}_{x}}x + 2{{k}_{y}}y - 2\omega t} \right)}}}\) with amplitudes \( \sim {\kern 1pt} \left| {BC} \right|,\) \({{\left| C \right|}^{2}},\) which contain only time-oscillating modes. These blocks, according to the ideas of resonant interaction, give corrections of the following orders, which disappear for stationary waves in the framework of the three-mode theory due to time averaging.

It is worth noting that, during interaction, the modes \({{e}^{{ \pm i\left( {3{{k}_{x}}x + 2{{k}_{y}}y - 2\omega t} \right)}}},\) \({{e}^{{ \pm i\left( {4{{k}_{x}}x + 2{{k}_{y}}y - 2\omega t} \right)}}}\) with amplitudes \( \sim {\kern 1pt} \left| {BC} \right|,\) \({{\left| C \right|}^{2}}\) can give fourth-order corrections \( \sim {\kern 1pt} \left| {BC} \right|{{\left| C \right|}^{2}}\) for stationary state \( \sim {\kern 1pt} {{e}^{{i{{k}_{x}}x}}}.\) They can be considered small under conditions of relatively small amplitudes \(B,\) \(C.\) This condition is used below to solve Eqs. (5). In any case, if we take into account a large number of three-mode interactions, the main, initial (the topmost in the hierarchy of triplets) ones are Eqs. (5).

The term with coefficient \(\beta \) (\(\beta \) effect) in the first equation (5) and the finite amplitude \(B,\) \(C\) of the Rossby waves leads to the solution of Eqs. (5) with a stationary amplitude \(A(t) = {{A}_{0}} = {\text{const}}\) of the zonal component of the stream function \(\psi .\)

We assume that such a value \(A(t) = {{A}_{0}}\) exists, i.e., in the second and third equations (5)\(A{\text{*}}(t) = A_{0}^{ * },\) \(A(t) = {{A}_{0}}.\) From these equations we get a solution for \(B\) and \(C\):

$$\begin{gathered} B(t) = {{B}_{s}}\sin \left( {\nu t} \right) + {{B}_{c}}\cos \left( {\nu t} \right), \\ C(t) = - \frac{{\left( {k_{x}^{2} + k_{y}^{2} + \frac{1}{{L_{0}^{2}}}} \right)}}{{\left( {3k_{x}^{2} + k_{y}^{2}} \right){{k}_{x}}{{k}_{y}}}}\frac{\nu }{{A_{0}^{ * }}}\left( {{{B}_{s}}\cos \left( {\nu t} \right) - {{B}_{c}}\sin \left( {\nu t} \right)} \right), \\ \end{gathered} $$
(6)
$$\begin{gathered} \nu = k_{y}^{2}\left| {{{A}_{0}}} \right|\mu ,\, \\ \mu = \sqrt {\frac{{k_{x}^{2}\left( {3k_{x}^{2} + k_{y}^{2}} \right)}}{{\left( {k_{x}^{2} + k_{y}^{2} + \frac{1}{{L_{0}^{2}}}} \right)\left( {4k_{x}^{2} + k_{y}^{2} + \frac{1}{{L_{0}^{2}}}} \right)}}} . \\ \end{gathered} $$
(7)

Then, using \(B{\text{*}}C\) (without oscillation terms ∼\( \sim {\kern 1pt} \sin \left( {2\nu t} \right),\) \(\cos \left( {2\nu t} \right)\)) in the first equation (5), we obtain \({{A}_{0}} = A_{0}^{ * }\) as a zero approximation and

$$\begin{gathered} {{A}_{0}} = \frac{3}{2}\frac{{{{k}_{x}}k_{y}^{2}}}{\beta }{{\mu }_{0}}e{{B}^{2}},\,\,\,\,e{{B}^{2}} = {\text{Im}}\left( {B_{c}^{ * }{{B}_{s}} - {{B}_{c}}B_{s}^{ * }} \right), \\ e = \pm 1,\,\,\,\,{{\mu }_{0}} = \mu \frac{{k_{x}^{2} + k_{y}^{2} + \frac{1}{{L_{0}^{2}}}}}{{3k_{x}^{2} + k_{y}^{2}}}. \\ \end{gathered} $$
(8)

Taking into account that \({{A}_{0}}\) is a real value, the formula for \(C\) in (6) will be written as

$$\begin{gathered} C(t) = - {{\mu }_{c}}\left( {{{B}_{s}}\cos \left( {\nu t} \right) - {{B}_{c}}\sin \left( {\nu t} \right)} \right), \\ {{\mu }_{c}} = {{{{k}_{y}}{{\mu }_{0}}} \mathord{\left/ {\vphantom {{{{k}_{y}}{{\mu }_{0}}} {{{k}_{x}}}}} \right. \kern-0em} {{{k}_{x}}}}. \\ \end{gathered} $$
(9)

At \(t = 0\), we get initial conditions from (6) and (9): \({{B}_{c}} = B(0),\) \({{B}_{s}} = - \frac{1}{{{{\mu }_{c}}}}\) С(0).

Wave \({{\psi }_{0}} = {{A}_{0}}\left( {{{e}^{{i{{k}_{x}}x}}} + {{e}^{{ - i{{k}_{x}}x}}}} \right) = 2{{A}_{0}}\cos \left( {{{k}_{x}}x} \right)\) corresponds to the stationary (background) distribution pattern of the stream function over zones with vorticity of different signs \(\Delta {{\psi }_{0}} = - 2k_{x}^{2}{{A}_{0}}\cos \left( {{{k}_{x}}x} \right).\) However, this background distribution exactly produces the nonstationary part as the next approximation (which is obtained if we take into account the oscillation terms discarded above under the condition that \({{A}_{1}}\) and \({{A}_{2}}\) are relatively small compared to \({{A}_{0}}\)):

$$\begin{gathered} A(t) = {{A}_{0}} + {{A}_{1}}(t) + i{{A}_{2}}(t), \\ {{A}_{1}} = \frac{1}{2}N\left( {{{d}_{s}}\cos \left( {2\nu t} \right) - {{d}_{c}}\sin \left( {2\nu t} \right)} \right), \\ {{A}_{2}} = \frac{1}{2}\frac{{{{N}^{2}}}}{{{{A}_{0}}}}\left( {{{d}_{s}}\sin \left( {2\nu t} \right) + {{d}_{c}}\cos \left( {2\nu t} \right)} \right), \\ \end{gathered} $$
(10)
$$\begin{gathered} N = \beta \frac{1}{{{{k}_{x}}k_{y}^{2}}}\frac{1}{\mu }\frac{{k_{x}^{2}}}{{k_{x}^{2} + \frac{1}{{L_{0}^{2}}}}},\,\,\,\,{{d}_{s}} = \frac{{{{{\left| {{{B}_{s}}} \right|}}^{2}} - {{{\left| {{{B}_{c}}} \right|}}^{2}}}}{{e{{B}^{2}}}}, \\ {{d}_{c}} = \frac{{B_{c}^{ * }{{B}_{s}} + {{B}_{c}}B_{s}^{ * }}}{{e{{B}^{2}}}}. \\ \end{gathered} $$
(11)

It follows from (8) that the backgrond component of \({{\psi }_{0}}\) exists if \({{B}^{2}} = \left| {{\text{Im}}\left( {B_{c}^{ * }{{B}_{s}} - {{B}_{c}}B_{s}^{ * }} \right)} \right| \ne 0,\) i.e., not under all initial conditions for the Rossby wave amplitudes \(B(0),\) \(C(0).\) In addition, solutions (10) are obtained under the conditions \(N\left| {{{d}_{s}}} \right| \ll \left| {{{A}_{0}}} \right|,\) \(N\left| {{{d}_{c}}} \right| \ll \left| {{{A}_{0}}} \right|,\) which also imposes a number of conditions on the parameters in (11).

Formulas (10) show that periodic oscillations with frequency \(2\nu = 2k_{y}^{2}{{A}_{0}}\mu \) equal to the spatial period of the stationary wave L= 2π/kx are superimposed on the background stationary circulation L= 2π/kx. In addition, Rossby waves \(B(t){{e}^{{i\left( {{{k}_{x}}x + {{k}_{y}}y - \omega t} \right)}}},\) \(C(t){{e}^{{i\left( {2{{k}_{x}}x + {{k}_{y}}y - \omega t} \right)}}}\) are also modified by time oscillations according to (6), (10) with frequency \(\nu ,\) which leads to oscillations with frequencies \(\omega \pm \nu \) or zonal transport with velocities \(\frac{{\omega \pm \nu }}{{{{k}_{x}}}}\) depending on the amplitude \(\left| {{{A}_{0}}} \right|\) of the stationary component of the flow.

The appearance of parameter \(\beta \) in the denominator of the expression for amplitude \({{A}_{0}}\) (8) is a feature of the background stationary field \({{\psi }_{0}} = 2{{A}_{0}}\cos {{k}_{x}}x\). The well-known Sverdrup relation for the stream function of the surface current in the ocean basin in the study of the western boundary intensification of currents (\(R\) is the radius of the Earth, φ is the latitude, \(\lambda \) is the longitude, and \(H\) is the characteristic depth) has the same dependence on \(\beta \) (Sverdrup, 1947; Okeanologiya, 1978).

$$\begin{array}{*{20}{l}} {\frac{1}{{R\cos \varphi }}\frac{{\partial \psi }}{{\partial \lambda }} = \frac{{{{{\text{ro}}{{{\text{t}}}_{z}}\vec {\tau }} \mathord{\left/ {\vphantom {{{\text{ro}}{{{\text{t}}}_{z}}\vec {\tau }} H}} \right. \kern-0em} H}}}{\beta }.} \end{array}$$
(12)

In this relation, the vertical component of the rotor of friction stress caused by surface waves of wind circulation over the ocean (for example, the Atlantic) is the coefficient at \(\frac{1}{\beta }\): \({{\tau }_{\lambda }} = \left\langle {u{\kern 1pt} 'w{\kern 1pt} '} \right\rangle ;\) \({{\tau }_{\varphi }} = \left\langle {v{\kern 1pt} 'w{\kern 1pt} '} \right\rangle \) is the quadratic form, where \(u{\kern 1pt} ',\) \(v{\kern 1pt} ',\) and \(w{\kern 1pt} '\) are the velocity fluctuations of surface waves generated by the wind (the dimension of the function of total fluxes \(\varphi \) in (12) is m3/s). In case (8), the coefficient at \(\frac{1}{\beta }\) includes a quadratic form associated with Rossby waves.

The dimension of \({{A}_{0}},\) \({{A}_{1}},\) \({{A}_{2}},\) \(N,\) \({{B}_{s}},\) \({{B}_{c}},\) \(B,\) as well as stream functions \(\psi ,\) \({{\psi }_{0}}\), is m2/s. Let us estimate the orders of magnitude assuming \({{k}_{y}} \sim {{k}_{x}} \sim \frac{1}{{{{L}_{0}}}}\) (this corresponds to Eq. (3)). We assume for the amplitude of the velocity of the background stationary flow \({{\psi }_{0}}\) that \({{V}_{a}} \equiv 2\left| {{{A}_{0}}} \right|{{k}_{x}};\) the amplitude of the velocity of the background stationary flow in (5) is \({{V}_{R}} = \left| B \right|{{k}_{x}}.\) We get from (3) that \(\left| {{{A}_{0}}} \right| = \frac{3}{2}\frac{{{{k}_{x}}k_{y}^{2}}}{\beta }{{\mu }_{0}}\)\({{B}^{2}} = \frac{3}{2}\frac{{{{k}_{x}}k_{y}^{2}}}{\beta }{{\mu }_{0}}\frac{{V_{R}^{2}}}{{k_{x}^{2}}}.\) Hence, \({{V}_{a}} = 3\frac{{k_{y}^{2}}}{\beta }{{\mu }_{0}}V_{R}^{2},\) or at \({{V}_{a}} = {{V}_{R}}\), \({{V}_{R}} = \frac{\beta }{{3k_{y}^{2}{{\mu }_{0}}}} \sim \) \(L_{0}^{2}\beta \sim 10\) m/s at \({{L}_{0}} \sim {{10}^{6}}\) m, \(\beta \sim {{10}^{{ - 11}}}\) (m–1 s–1).

As was previously noted, wave \({{\psi }_{0}} = 2{{A}_{0}}\cos \left( {{{k}_{x}}x} \right)\) forms vorticity anomalies with a scale of \({{L}_{x}} = \frac{{2\pi }}{{{{k}_{x}}}}\) along coordinate \(x\) (longitude). In laboratory and numerical experiments simulating surface air flows in the tropical and polar Hadley and Farrell cells at midlatitudes, such anomalies can be reproduced if the symmetry of the currents in the analogues of the mentioned cells is broken—Eqs. (5) are invariant under substitutions \(A \to A{{e}^{{i{{\varphi }_{a}}}}},\) \(B \to B{{e}^{{i{{\varphi }_{b}}}}},\) \(C \to C{{e}^{{i{{\varphi }_{c}}}}},\) \({{\varphi }_{c}} = {{\varphi }_{a}} + {{\varphi }_{b}}\).

3 NUMERICAL EXPERIMENTS

Numerical experiments were performed for the flows in thin layers of fluid in an annular rotating (counterclockwise rotation: North Pole) channel based on shallow water equations; the \(\beta \) effect was modeled by an inclined bottom (Dolzhansky, 2011). The equations and calculation methods were presented in detail in a number of works (Gledzer, 2014, 2015; Gledzer et al., 2018, 2021).

The source–sink method was used for the purposes of this work to generate eddy motions in a rotating channel. To simulate subtropical and polar easterly winds and western transport at midlatitudes (three-flow configuration), sources–sinks of fluid were used in thin annular layers on the inner (1) and outer (4) boundaries of the channel and two layers (2) and (3) in its middle. These source–sink layers are shown in Figs. 2a–2d by circles: 1 and 3 are sources and 2 and 4 are sinks. In arbitrary units (Gledzer et al., 2021), the power of sources (1 and 3) is \(E = 0.8,\) and the power of sinks (2 and 4) is \(E = - 0.8.\) The sources of layer 1 induce a directional flow towards the sink in layer 2. This flow is deflected by the Coriolis force to the right of it (clockwise between layers 1 and 2). This corresponds to the eastern winds. It is similar for the flow from source 3 to sink 4. The flow from source 3 to sink 2 forms a counterclockwise Coriolis motion in the ring between 2 and 3. This is analogous to the westward transport at midlatitudes.

Fig. 2.
figure 2

(a–d) Velocity field vectors for the numerical experiment with sources (\(E = 0.8\)) and sinks (\(E = - 0.8\)), T = 6 s, C is a cyclone, and A is an anticyclone; (e) schematic of the superposition of Rossby waves with wavenumbers differing by a factor of two.

Full size image

This configuration of flows forms velocity shears in the channel, which, as a result of instability, lead to the appearance of cyclonic (C) (Fig. 2) with counterclockwise rotation and anticyclonic (A) eddies (in Figs. 2a, 2b, 2c, and 2d, the angular velocity of rotation channel is \(\Omega = \frac{{2\pi }}{T},\) \(T = 6\) s). This entire system of eddies moves clockwise, i.e., propagates westward in accordance with the concept of Rossby waves (in the Northern Hemisphere).

However, the system of eddies that appears is not symmetrical: three closely located cyclones exist almost in half of the channel (Figs. 2a, 2b), and the other half is occupied by an anomaly, which contains an extensive anticyclone (Figs. 2a, 2b) (or two, Fig. 2c) and sometimes a cyclone (Figs. 2b, 2c).

The schematic pattern of the velocity field in Fig. 2 can be roughly represented as a superposition of two Rossby waves with wavenumbers (\(m = 2,\) \(m = 4\)) in longitude (Fig. 2e) that differ by a factor of two. In this case, wave \(m = 2\) intensifies the cyclonic circulation of wave \(m = 4\) in one half of the channel and the anticyclonic circulation in the other. The angular velocities of these two waves probably differ, since the motion to the west is not quite uniform (the time interval between the patterns in Figs. 2a–2d is the same, \(\Delta \tau = 200,\) \(\tau = \Omega t\)).

Figure 3 shows the dependences of the azimuthal (longitude) \(0 \leqslant \lambda \leqslant 2\pi \) coordinates of the centers of cyclones (Fig. 3a) and anticyclones (Fig. 3b) for moving eddies (Fig. 2). The centers are determined by the velocity field as a point in the nearest neighborhood of which the azimuthal and meridional velocity components change sign. Since cyclonic eddies are more intense, anticyclones moving at a different angular velocity (the mean slopes of the lines in Fig. 3b for anticyclones are smaller than in Fig. 3a for cyclones) sometimes change their position or completely disappear; as a result, the lines of anticyclone centers become discontinuous. However, in general, the angle λ for almost all anticyclones in Fig. 3b decreases, like for cyclones (clockwise motion).

Fig. 3.
figure 3

Time evolution of \(\tau = {t \mathord{\left/ {\vphantom {t T}} \right. \kern-0em} T}\) (period \(T = 6\) s) of the azimuthal angular coordinates \(\lambda \) of the centers of cyclones (a) and anticyclones (b) in numerical experiments with sources (\(E = 0.8\)) and sinks (\(E = - 0.8\)) in a three-flow configuration. The slope to the right (decrease in \(\lambda \)) corresponds to the clockwise motion of the eddies (Fig. 2).

Full size image

In the case shown in Fig. 2, anomalies appear as a result of the dynamics of the eddy system. It is interesting to consider the influence of an externally introduced anomaly on the distribution of western and eastern flows in the channel. We assume that, in the lower quarter of the channel \(\frac{{3\pi }}{2} - \frac{\pi }{4} < \lambda < \frac{{3\pi }}{2} + \frac{\pi }{4}\) (Fig. 4a), the sources–sinks in the annular layers decreased their intensity by half: instead of \(E = \pm 0.8\), there is an inflow–outflow \(E = \pm 0.4.\) Due to the inflows–outflows in other parts of the layers, the velocity field in this quarter of the channel does not necessarily decrease by half, although it may lose the original symmetry of the main flow.

Fig. 4.
figure 4

(a) Velocity field vectors in a numerical experiment in a three-flow configuration with sources–sinks (\(E = \pm 0.8\)) in the upper three quarters of the channel \(2\pi - \frac{\pi }{4} < \lambda < 2\pi ,\) \(0 < \lambda < \pi + \frac{\pi }{4}\) and sources–sinks (\(E = \pm 0.4\)) in the lower quarter of the channel \(\frac{{3\pi }}{2} - \frac{\pi }{4} < \lambda < \frac{{3\pi }}{2} + \frac{\pi }{4}\) (b, c) time evolution of \(\tau = {t \mathord{\left/ {\vphantom {t T}} \right. \kern-0em} T}\) (period T = 6 s) of the azimuthal angular coordinates \(\lambda \) of the centers of cyclones (b) and anticyclones (c) in numerical experiments with sources and sinks \(E = \pm 0.8,\) \(E = \pm 0.4.\)

Full size image

This anomaly can be interpreted as a decrease in the intensity of the subtropical Hadley cell, which is accompanied by a weakening of the trade winds in some sector of the equatorial atmospheric circulation and a decrease in the westerly transport at midlatitudes.

Velocity fields for the indicated inflows–outflows \(E = \pm 0.8,\) \(E = \pm 0.4\), which only slightly differ from Fig. 2, are shown in Fig. 4a for some time moments when there was no external anomaly in the distribution of sources–sinks. It is possible that, only at some moments of time, four cyclones (instead of three) of high intensity appeared more clearly, as in the second of Fig. 4a. The lines of cyclone centers shown in Figs. 4b do not strongly differ compared to Fig. 3a.

However, the lines of the centers of anticyclones (Fig. 4c), while retaining the same broken structure as in Fig. 3b, has almost lost the average slope to the right; i.e., angle \(\lambda \) does not decrease on average. Actually, this is stationaring, and the external anomaly at \(\frac{{3\pi }}{2} - \frac{\pi }{4} < \lambda < \frac{{3\pi }}{2} + \frac{\pi }{4}\) slows down only the anticyclones—only some lines of those anticyclone centers shown in Fig. 4c have a significant mean slope to the right: at some moments of time they move clockwise together with cyclones (Fig. 4b).

It is worth noting that, with an increase in the externally induced circulation anomaly, cyclones can also stop, forming correlated structures with anticyclones. In particular, this was observed in a numerical experiment with the absence of inflow–outflow (\(E = 0\)) in the lower quarter of the channel \(\frac{{3\pi }}{2} - \frac{\pi }{4} < \lambda < \frac{{3\pi }}{2} + \frac{\pi }{4}\) with the previous value \(E = \pm 0.8\) for the other angles \(\lambda \). The patterns of the lines of the centers of cyclones and anticyclones turned out to be on average horizontal and qualitatively similar (differing only in the values of the angles \(\lambda \)).

The same decelerating effect for anticyclones is shown in a numerical experiment in a different configuration, when only the western transport at midlatitudes and the eastern one at southern latitudes are simulated (two-flow configuration). To do this, instead of the source sink in the annular layers 2, 3 (Fig. 2a), a source was placed in a circle between them. The power of sinks in the inner annular layer 1 was \({{E}_{1}} = 0.2,\) on the outer layer 3 it was \({{E}_{3}} = 0.5,\) and the power of the source was calculated from the mass conservation condition.

Figures 5a and 5b show the lines of centers of cyclones and anticyclones without a source–sink anomaly in sector \(\frac{{3\pi }}{2} - \frac{\pi }{4} < \lambda < \frac{{3\pi }}{2} + \frac{\pi }{4}.\) In this case, the lines of cyclones and anticyclones do not differ much; on average they are inclined to the right and describe the clockwise motion along the channel. One peculiarity of the dynamics shown in Figs. 5a and 5b is a two-mode motion: until some time \({{t}_{{cr}}} \sim T \times 30\), there was one mode of motion of the centers, which was, after \({{t}_{{cr}}}\), replaced by a slower motion of cyclones and anticyclones. The work (Gledzer et al., 2021) was devoted to the multimode regime in numerical and laboratory experiments. The difference of the dynamics shown in Figs. 5a and 5b from that in (Gledzer et al., 2021) is the invariance of the external parameters in the numerical experiment.

Fig. 5.
figure 5

Time evolution of \(\tau = {t \mathord{\left/ {\vphantom {t T}} \right. \kern-0em} T}\) of the azimuthal angular coordinates \(\lambda \) of the centers of cyclones (a, c) and anticyclones (b, d) in numerical experiments with two-flow configuration: (a, b) \({{E}_{1}} = 0.2,\) \({{E}_{2}} = 0.5;\) (c, d) \({{E}_{1}} = 0,\) \({{E}_{2}} = 0.\)

Full size image

The differences between the lines of the centers of cyclones and anticyclones are observed if the power of sources–sinks in the anomaly sector \(\frac{{3\pi }}{2} - \frac{\pi }{4} < \lambda < \) \(\frac{{3\pi }}{2} + \frac{\pi }{4}\) is zero \({{E}_{1}} = {{E}_{3}} = 0\) (Figs. 5c, 5d). In this case, the broken structure of the lines is enhanced, but, like in Fig. 4c, most of the anticyclone lines are generally horizontal; anticyclones, on average, do not change their azimuthal position. Cyclones (Fig. 5c) mostly continue moving along the channel, although their lifetime has decreased in comparison with the nonanomalous case in Fig. 5a due to uncoordinated motion with anticyclones.

Numerical experiments show that sectoral anomalies can affect the mean characteristics of the vorticity field in the channel. Figure 6 shows the vorticity differences \(\Delta \Omega \) between the anomalous and nonanomalous cases (for a three-flow configuration) averaged over the rings between the sources–sinks on circles 2 and 3 (Fig. 6a) and 3 and 4 (Fig. 6b). In the ring between layers 2 and 3, the presence of an anomaly slightly increased the positive vorticity (Fig. 6a), which means an increase in the cyclonic component. In the ring between layers 3 and 4 (Fig. 6b), on the contrary, the change in vorticity became mostly negative. This corresponds to the strengthening of anticyclonic tendencies in this part of the stream.

Fig. 6.
figure 6

Differences in the vorticity between the anomalous and nonanomalous cases (for a three-flow configuration) averaged over the rings between the sources–sinks on circles 2 and 3 (a) and 3 and 4 (b) (see Fig. 2a).

Full size image

4 LABORATORY EXPERIMENTS

Laboratory experiments were carried out using the Magnetohydrodynamic (MHD) method for generating flows in a rotating annular channel filled with a conducting liquid. The experimental setup and experimental technique have been presented in detail in a number of works (Gledzer et al., 2013, 2018, 2021). The experiments simulate the situation in the Southern Hemisphere with the channel rotating clockwise.

In the MHD approach, the flows are generated by the interaction of the magnetic field of permanent magnets (neodymium, 0.36 T and ferrite, 0.175 T) placed along three (or two) circles (Fig. 7) under a bottom inclined from the center to the periphery in the channel, and a radially directed current between electrodes 1 and 2 on the outer and inner boundaries with radii of 5 cm and 36 cm. A number of the magnets on the outer circle were replaced with ferrite magnets or removed altogether (hereinafter, experiment 1, Figs. 11a–11f). In experiments with the results shown in Figs. 11aa and 11bb, on the contrary, a line of magnets was removed from the middle circle (experiment 2).

Fig. 7.
figure 7

Scheme of layout of electrodes 2, 1, and 3; permanent magnets; and division into sectors I–IV in Figs. 9 and 10 in the channel of the laboratory setup.

Full size image

Radially directed current \(\vec {j}\) and vertically directed field \(\vec {H}\) form the Ampère force in a direction normal to them \( \sim {\kern 1pt} \left[ {\vec {j},\vec {H}} \right],\) acting on a conductive liquid (10% solution of \({\text{CuS}}{{{\text{o}}}_{4}}\)) above an inclined bottom. The directions of the magnetic field (with different poles along the circles) and the electric current between electrodes 1 and 2 are chosen to induce a flow directed to the east in the middle of the channel (western transport at midlatitudes), while in the inner and outer parts of the channel they induce flows directed to west (trade winds at the outer border of the channel and the eastern polar wind).

In experiment 2, when the middle line of magnets was removed, only the western transport at midlatitudes and the eastern equatorial transport (trade winds) were modeled.

The difference between the source–sink method, which was used in numerical experiments (and laboratory experiments in (Gledzer et al., 2014)), and the MHD method is that sinks–sources induce currents due to the Coriolis force in a rotating channel, while in the MHD method the western and eastern transports are generated directly by the Ampère force.

Velocity anomalies in these flows in the experiments are formed by breaking the outer circular electrode 1 and electrode 3 isolated over a quarter of the circumference, to which a different current can be supplied than to electrode 1 (sector I in Fig. 7).

The velocity shear between the indicated multidirectional flows and the sloping bottom simulating the \(\beta \) effect form Rossby waves in the channel. Figures 8a (\(T\) = 42.1 s) and 8b (\(T\) = 30.8 s) show a sequence of images of flows in the channel (eddies and jets) at regular intervals \(\left( {\Delta \tau = \frac{{10}}{{24}}T} \right)\). In the case shown in Fig. 8a, the currents at electrodes 1 and 3 were the same \(400\) mA, which is equivalent to solid electrode 1, and in Fig. 8b the current at electrode 3 was zero. The images closer to the center show three cyclonic eddies with a jet stream enveloping them. This entire triangular structure rotates counterclockwise, which indicates, similarly to the numerical experiments (Fig. 2), the westward motion of eddies, which is typical for Rossby waves (counterclockwise in the Southern Hemisphere).

Fig. 8.
figure 8

Particle trajectories in the channel (images at regular time intervals \(\Delta \tau = \frac{{10}}{{24}}T\)) in the experiment: (a) at setup rotation period \(T = 42.1\) s and current \(j = 400\) mA at electrodes 1 and 3 (see Fig. 7); (b) at setup rotation period \(T = 30.8\) s at current \(j = 0\) at electrode 3 and current \(j = 400\) mA at electrode 1. (a, b) Experiments with neodymium magnets on three circles.

Full size image

A number of anticyclonic eddies formed near the outer boundary of the channel (equator), which slowly drifted to the western side (it can be seen from the four eddies in the upper part of the images in Fig. 8b or two clearly pronounced eddies on the left in Fig. 8a). At the bottom of the channel in Fig. 8b or on the right side in Fig. 8a, similarly to the numerical experiments in Fig. 2, the flow structure is not very regular: some anticyclones periodically disappear.

The results presented in Fig. 9 were obtained with an electric field anomaly in sector I: the current was switched off at electrode 3 (Fig. 7) (\(j = 0\)). At the same time, in sector I, the electric field was not equal to zero, since the current passes from electrode 1 to 2, occupying the entire space of sector I.

Fig. 9.
figure 9

Mean vorticities over sectors I–IV in the experiments: (a) with an anomalous effect of electric current and (b) without anomalous effect (\(\tau = {t \mathord{\left/ {\vphantom {t T}} \right. \kern-0em} T},\) \(T = 30.8\) s).

Full size image

Figure 9a shows the mean vorticity over sectors I–IV (Fig. 7) (rotation period \(T = 30.8\) s) at current \(j = 400\) mA at electrode 1 and current \(j = 0\) at electrode 3 (anomalous effect). For comparison, Fig. 9b shows the vorticity in sectors I–IV if the current at electrode 3 is \(j = 400\) mA, i.e., in an unanomalous external influence. In addition to the strong dispersion of oscillations in the anomalous case, there is a clearly pronounced formation of time-averaged vorticities of opposite signs in sectors II and III following sector I. In sectors I (where an external anomaly of the electric field is introduced) and IV, in addition to the previously mentioned dispersion, the vorticity fluctuations are generally similar to the vorticity of anomalous circulation. In fact, due to the external anomaly in sector I, the circulation in sector II becomes, on average, more anticyclonic, and in sector III, cyclonic.

Periodic oscillations shown in Fig. 9 with the characteristic time 60–80 s are reflected in the graphs in Fig. 9 showing the propagation of large eddies through sectors I–IV, similar to the eddies in the images of Fig. 8. It should be noted that the effect of the appearance of a nonzero mean vorticity in Figs. 9 in sectors II and III depends on the channel rotation period. In experiments with a long period \(T = 42.4\) s, this effect becomes weakly pronounced.

Experiments were carried out with a different method of introducing an external anomaly into the flows in sector I. To do this, electrode 1 at the outer boundary of the channel remained solid, so the current j was supplied to the entire circular electrode at the boundary. However, the magnets in sector I were weaker than in the other parts in the remaining sectors (ferrite magnets). In this case, vertical component of the field was weaker in sector I, which led to a decrease in the Ampère force \( \sim {\kern 1pt} [\vec {j},\vec {H}].\)

Figure 10 shows vorticity in sectors I–IV in the experiments in the described configuration at a current of 500 mA between electrodes 1 and 2 and a rotation period of \(T = 21.2\) s. Here, vorticities in sectors I and IV generally behave synchronously, forming anticyclonic vorticity that propagates in sectors II and III: cyclonic average vorticity is generated, which also occupies a “hemisphere.” It corresponds to the above-mentioned Rossby standing wave pattern with a wave number m = 2 (Fig. 2e).

Fig. 10.
figure 10

Mean vorticities over sectors I–IV in an experiment with an anomalous arrangement of permanent magnets (\(\tau = {t \mathord{\left/ {\vphantom {t T}} \right. \kern-0em} T},\) \(T = 21.2\) s).

Full size image

Figure 11 shows time dependences of the angular coordinates of the centers of cyclones and anticyclones in the experiments with the same current \(j = 400\) mA at electrodes 1 and 3 (a, b) and the anomalous action of the current (c, d and e, f), respectively; the \(j = 300\) mA current at electrode 3 with current \(j = 400\) mA at electrode 1, current \(j = 100\) mA at electrode 3, and \(j = 400\) mA at electrode 1 (experiment 1). In the experiments, the results of which are shown in Fig. 11, the outer circle of magnets was removed; i.e., like in the numerical experiment in Fig. 5, a two-flow configuration has been implemented.

Fig. 11.
figure 11

Time evolution of \(\tau = {t \mathord{\left/ {\vphantom {t T}} \right. \kern-0em} T}\) (\(T = 29.2\) s) of the azimuthal angular coordinates \(\lambda \) of the centers of cyclones (a, c, e) and anticyclones (b, d, f) in laboratory experiment 1: (a, b) with currents \(j = 400\) mA at electrodes 1 and \(j = 400\) mA on 3; (c, d) with currents \(j = 400\) mA at electrode 1 and \(j = 300\)mA at electrode 3; (e, f) with currents \(j = 400\) mA at electrode 1 and \(j = 100\) mA at electrode 3. Variations in centers of cyclones in experiment 2 (\(T = 29.6\) s): (aa) with currents \(j = 400\) mA at electrode 1 and \(j = 400\) mA at electrode 3; (bb) with currents \(j = 400\) mA at electrode 1 and \(j = 300\) mA at electrode 3.

Full size image

Figures 11a, 11c, and 11e show coordinates \((\tau ,\lambda ),\) \(\tau = {t \mathord{\left/ {\vphantom {t T}} \right. \kern-0em} T},\) \(T = 29.2\) s of the cyclone centers in all previously described cases. At each moment there were three cyclones, which are seen in Fig. 8 in a triangular structure with an enveloping jet stream.

Four to five anticyclones are seen in the nonanomalous case (Fig. 11b) that move counterclockwise (increasing angle \(\lambda \)); this is a westward motion in the South Pole laboratory configuration. They move westward with almost the same speed along with the cyclones associated with them (Fig. 11a). Short-living anticyclones (marked by thin straight lines) are also seen in Fig. 11b, which almost do not move or slowly move eastward.

In the case of a weakly anomalous current distribution (Fig. 11d) at a current of \(j = 300\) mA at electrode 3, westward moving anticyclones became less notable, but the number of short-living quasi-stationary anticyclones increased significantly (thin lines in Fig. 11d).

Under a strong anomaly in the current distribution (\(j = 100\) mA at electrode 3) (Figs. 11e, 11f), the distribution of cyclones (Fig. 11e) in the plane \((\tau ,\lambda )\) became more diffuse, but qualitatively close to the distributions in Figs. 11a and 11c.

A long-living (almost a week according to laboratory time) slowly moving eastward structure appeared in the distribution of anticyclones in the lower half of sector II (which in Fig. 11f corresponds to the angles \({{3\pi } \mathord{\left/ {\vphantom {{3\pi } 2}} \right. \kern-0em} 2} < \lambda < 2\pi \)).

The appearance of such structures was confirmed in experiment 2 (the middle line of magnets (Fig. 7) was removed). Figures 11aa and 11bb show the coordinates of the lines of anticyclone centers in the nonanomalous case (Fig. 11aa, \(j = 400\) mA current at electrode 3) and in the case of a weak anomaly (Fig. 11bb) at a \(j = 300\) mA current at electrode 3. In this case at 3π 2 < λ < 2π, several anticyclones developed at the bottom of sector II, which slowly drifted to the east.

It is interesting to compare the results of numerical and laboratory experiments on studying the dynamics of centers of cyclones and anticyclones with the corresponding data on atmospheric velocity fields. Figures 12a and 12b show the time dependences (months, from May (5) to October (10)) of the longitude of the centers (from 0° to 120° E) of cyclones (Fig. 12a) and anticyclones (Fig. 12b), which were located in latitude band from 35° to 65° N. The centers were determined by the previously described method based on the data on the velocity field at a level of 500 mb in 2010.

Fig. 12.
figure 12

Time dependence (months, from May (5) to October (10)) of the longitude of the centers (from 0˚ to 120˚ East longitude) of cyclones and anticyclones, which were located in the latitude band from 35˚ to 65˚ N: (a, b) in 2010; (c, d) in 2013.

Full size image

A region is notable in the cyclonic pattern in Fig. 12a (highlighted by an oval) between 40° and 60° E in the period from June (6) to September (9), in which there are almost no cyclones, which indicates a dry period in these months in the European part of the Russian Federation.

On the contrary, the lines of anticyclone centers condense during the same period of three months at longitudes from 80° to 100° E (anticyclones in Siberia, Kazakhstan, and Mongolia) and for almost a month (from August (8) to September (9)) at longitudes from 30° to 50° E. The center lines are almost horizontal, which corresponds to the quasi-stationary state of these anticyclones.

In other areas of the diagrams in Figs. 12a and 12b, cyclones and anticyclones show correlated motions to the east (tilts to the right of the vertical) under conditions of the westward transport of the general circulation of the atmosphere at midlatitudes. At the same time, there are no long periods of time during which the cyclones stop. In general, the diagrams in Figs. 12a and 12b are similar to Figs. 5c and 5d obtained numerically: the lifetime of cyclones and anticyclones in both cases is relatively short (up to a week in the atmosphere), which forms a discontinuous (broken) structure of center lines.

Diagrams in Figs. 12a and 12b, which show the anomalous 2010 for European Russia, can be compared with the same period in 2013. In this case, the cyclone lines almost uniformly fill the area of the diagram in Fig. 12c (from May (5) to October (10) and from 0° to 120° E), demonstrating the motion to the east. The diagram for anticyclones (Fig. 12d) shows a traditional region of almost not moving anticyclones between 80° and 100° E in the same months as in 2010. The region between 60° and 80° E, where the centers of anticyclones are absent, is distinguished; this region of the territory of the Russian Federation is occupied with propagating cyclones.

5 CONCLUSIONS

As was previously noted, symmetry breaking with respect to zonal spatial shears is necessary to reproduce stationary anomalies in the resonant interaction of transient modes in laboratory and numerical experiments. Such a violation can be compared with changes in the intensity of the subtropical Hadley cell, which, due to the rotation of the Earth, is associated with the cells of middle and polar latitudes.

Westward midlatitude transport in the troposphere is due to the Coriolis forcing when air moves from the tropics to the north (to the south in the Southern Hemisphere). This is the mean motion in the corresponding Farrel cell of the general atmospheric circulation. However, if the flow from the equatorial zone to high latitudes is disturbed (increased or weakened), the zonal western transport can change with a corresponding change in the cyclonic or anticyclonic activity at midlatitudes and in the polar cell with variations in the eastern transport in it.

In the numerical and laboratory experiments, anomalies in the flow were introduced by changing the intensity of sources–sinks or the Ampère force impact on the conducting fluid. At the same time, there were no notable changes in the visible pattern of eddy propagation in the channel in the sector in which external intervention was introduced (compare Fig. 8a (T = 42.1 s) and Fig. 8b (T = 30.8 s)). However, the results shown in Figs. 9 and 10 provide evidence that changes are notable in the mean characteristics of the eddy field when an anomaly is introduced; they are seen over the entire channel or its individual parts that do not belong to the sector with an external anomaly associated with an increase in the anticyclonic eddy component (dry periods) or cyclonic vorticity (wet periods).

The strongest influence of external force anomalies in numerical and laboratory experiments turned out to be the influence on the dynamics of anticyclones. A comparison of lines of anticyclone centers in Figs. 3b and 4c, 5b and 5d, and 11b and 11f shows that these anomalies have a decelerating effect on the velocity of propagation of anticyclones in the channel without almost affecting the dynamics of cyclones (Figs. 3a, 4b, 11a, 11c, 11e). At the same time, a significant part of moving anticyclones either disappears or almost stops (Figs. 11d, 11f), or new, quasi-stationary anticyclones appear (Fig. 11bb). However, they are not the source of blocking of the transport; they can be called “blocked” rather than “blocking” anticyclones.

Figures 3b, 4c, 11d, and 11f show that in numerical and laboratory experiments the angular velocity of anticyclones, if they move along the channel, is close to the angular velocity of the cyclones; i.e., together with cyclones, they form coupled structures of the dipole type. Quasi-stationary anticyclones form centers of action that prevent the free motion of such dipole formations.

Such a mixture of standing and moving eddies in a flow is similar to the background and transport circulation of waves in the resonant interaction of transient modes considered above, where, in addition to the stationary wave \({{\psi }_{0}} = {{A}_{0}}\cos \left( {{{k}_{x}}x} \right)\), there were waves transported with velocity \({{u}_{ \pm }} = \frac{{\omega \pm \nu }}{{{{k}_{x}}}}\) with the same zonal wave number \({{k}_{x}}.\)