1 INTRODUCTION

Numerous studies [1–6] of spatiotemporal variations in atmospheric and ionospheric parameters indicate a relationship between the disturbances in upper layers of the atmosphere and the vertical propagation of acoustic-gravity waves (AGW) from the lower atmosphere. Atmospheric waves generated by various sources in the troposphere, by reaching the thermosphere altitudes, gives up their momentum and energy and affect the general circulation in the atmosphere and the gas temperature distribution with height [7, 8]. The dissipating waves may be a source of various unstable processes, create jet streams, and change the heat balance in the upper layers of atmosphere [1, 9–11], as well as affect the plasma motion and, as a consequence, the propagation of radio waves [12, 13].

The physical mechanisms of AGW generation at tropospheric altitudes are different [3, 14–17]. One powerful energy source of AGWs is the processes of heat release/absorption in phase transitions of the atmosphere water during the creation and evolution of clouds [18, 19] and the formation of other meteorological phenomena. Heating the atmosphere by this heat release can set the atmospheric gas in motion and may cause various consequences, including a violation of the static stability of atmosphere with the subsequent development of unstable processes. This causes a great variety; complex evolution; and, as a consequence, the difficulty of describing the detailed structure of these phenomena.

In the numerical study of the AGW propagation from meteorological phenomena, the problem of specifying realistic wave sources often arises, which is associated with a significant lack of detailed experimental information about them due to the complex three-dimensional structure of many meteorological phenomena and their wide variety. The wave generation in the course of proceeding of metrological processes leads to a change in the surface pressure. In [20–22], it was proposed for the first time to use experimental data on pressure fluctuations on the Earth’s surface, recorded in a network of microbarographs, to calculate waves propagating from meteorological phenomena into the upper atmosphere. Since the problem of the propagation of waves from the pressure fluctuation at the boundary is unusual for hydrodynamics, the mathematical statement of a hydrodynamic problem of wave propagation from pressure oscillations at the boundary was formulated in [23, 24]. The correctness of the proposed problem formulation was proved, and a numerical method for solving this problem was offered and tested. In [20, 21], the problem of wave propagation from experimentally observed pressure fluctuations on the Earth’s surface during the arrival of the atmospheric front was solved for the first time.

This work is devoted to a mathematical study of the question of a relationship between the problem of wave generation by tropospheric meteorological sources and the problem of wave generation by wavelike pressure changes near the Earth’s surface. At first, the general problem of AGW generation in an isothermal atmosphere by a local heat source at tropospheric altitudes is considered analytically, and the types of waves are investigated which can be generated by this tropospheric heat source. It is shown theoretically that the generation of internal gravity waves by a heat source cannot occur without the generation of infrasonic waves by the same source, and vice versa. Partial sources of infrasonic waves and internal gravity waves for a heat source are calculated. It is shown that powers of these partial sources are approximately equal to each other.

In this work, the propagation of infrasonic and internal gravity waves generated by a model local tropospheric heat source of a relatively small size is numerically investigated. Small dimensions of the model any source are associated with the fact that an almost arbitrary heat source of complex shape can be represented as a sum of local small sources. Thus, a rather arbitrary problem of heating by a heat source is mathematically reduced to the problem under study about heating by a small source. Pressure fluctuations on the Earth’s surface from the model source under consideration are recorded for further use. Next, they are applied in calculating the propagation of waves from pressure fluctuations at the lower boundary and are analogous to the experimentally observed wavelike pressure variations on the Earth’s surface. The results of calculations of waves directly from the tropospheric source and from the recorded pressure fluctuations on the Earth’s surface will be compared. Next, it will be suggested how the surface source of pressure should be corrected in order that it more accurately describe the waves arising from the tropospheric source.

2 ANALYTICAL STUDY OF THE PROBLEM OF WAVE PROPAGATION FROM A TROPOSPHERIC HEAT SOURCE

Tropospheric meteorological events are diverse in the morphology, lifetime, and altitude of localization [25, 26]. The tropospheric heat source is located in a narrow surface layer 12 km thick near the Earth’s surface. Let us consider a two-dimensional problem of wave propagation from a tropospheric heat source. Simplification of the problem to a two-dimensional one does not introduce fundamental changes in the analysis, but greatly facilitates studying the problem. Near the Earth surface, the wave amplitude is usually small due to the high density of the gas, and the wind near the surface of the Earth is usually weak. Therefore, in the theoretical analysis of wave generation by a tropospheric source, it is possible to use the equations of linear wave theory [27] and ignore the wind:

$$\begin{gathered} {{\left( {{{\rho }_{0}}\Psi } \right)}_{t}} + {{\left( {{{\rho }_{0}}U} \right)}_{x}} + {{\left( {{{\rho }_{0}}W} \right)}_{z}} = 0, \\ {{\left( {{{\rho }_{0}}U} \right)}_{t}} + {{\rho }_{0}}gH{{\left( {\Psi + \Phi } \right)}_{x}} = 0, \\ {{\left( {{{\rho }_{0}}W} \right)}_{t}} + {{({{\rho }_{0}}gH\left( {\Psi + \Phi } \right))}_{z}} + {{\rho }_{0}}g\Psi = 0, \\ {{\left( {{{\rho }_{0}}\Phi } \right)}_{t}} + \left( {\gamma - 1} \right)\left( {{{{\left( {{{\rho }_{0}}U} \right)}}_{x}} + {{{\left( {{{\rho }_{0}}W} \right)}}_{z}}} \right) \\ + \,\,\frac{\alpha }{H}{{\rho }_{0}}W = {{\rho }_{0}}f\left( {x,z,t} \right). \\ \end{gathered} $$
(1)

Here \(\Psi = \frac{{\rho \left( {x,z,t} \right) - {{\rho }_{0}}\left( z \right)~}}{{{{\rho }_{0}}\left( z \right)}}\) is the wave addition to the background temperature, \(\Phi = \frac{{T\left( {x,z,t} \right) - {{T}_{0}}\left( z \right){{\;}}}}{{{{T}_{0}}\left( z \right)}}\) is the wave addition to the background distribution of the atmospheric gas density \({{\rho }_{0}}\left( z \right)\), \(H\left( z \right)\) is the altitude of the homogeneous atmosphere, \(\alpha = \left( {\gamma - 1~ + \gamma \frac{{dH\left( z \right)}}{{dz}}} \right)\), \(\gamma \) is the adiabatic exponent, g is the acceleration of gravity, and \(U\,\,{\text{and}}\,\,W\) are the components of the gas mass velocity along the horizontal axis \(x\) and the vertical axis\(z\). The rest of the designations are traditional. The heat source \(f\left( {x,z,t} \right)\) is written on the right-hand side of the system of equations. We assume that the source takes into account the heating/cooling of the gas during phase transitions of water in the atmosphere. Obviously, a change in the gas temperature sets the gas in the complex motion.

Let us supplement equation system (1) with the natural lower boundary condition

$$W\left( {x,z = 0,t} \right) = 0.$$
(2)

The case is considered when the atmosphere is isothermal: the background distribution of gas temperature with an altitude \({{T}_{0}}\left( z \right){{\;}}\) does not depend on altitude \(z\) and the background density changes exponentially with altitude: \({{\rho }_{0}}\left( z \right) = {{\rho }_{{00}}}{\text{exp}}\left( { - \frac{z}{H}} \right)\). The general solution of the problem under consideration can be written as an expansion in terms of the system of basis eigenfunctions of the problem. For convenience, we write equation system (1) as a single matrix equation:

$${{\rho }_{0}}\frac{{\partial \lambda }}{{\partial t}} + \hat {L}\lambda = {{\rho }_{0}}\left( z \right)F\left( {x,z,t} \right).$$
(3)

Here

$$\hat {L}\lambda = \left( {\begin{array}{*{20}{c}} {{{{\left( {{{\rho }_{0}}U} \right)}}_{x}} + {{{\left( {{{\rho }_{0}}W} \right)}}_{z}}} \\ {{{\rho }_{0}}gH{{{\left( {\Psi + \Phi } \right)}}_{x}}} \\ {{{{({{\rho }_{0}}gH\left( {\Psi + \Phi } \right))}}_{z}} + {{\rho }_{0}}g\Psi } \\ {\left( {\gamma - 1} \right)\left( {{{{\left( {{{\rho }_{0}}U} \right)}}_{x}} + {{{\left( {{{\rho }_{0}}W} \right)}}_{z}}} \right) + \frac{\alpha }{H}{{\rho }_{0}}W} \end{array}} \right),$$
(4)
$$F\left( {x,z,t} \right) = \left( {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} 0 \\ 0 \\ 0 \end{array}} \\ {f\left( {x,z,t} \right)} \end{array}} \right),\,\,\,\,~\lambda \left( {x,z,t} \right) = \left( {\begin{array}{*{20}{c}} {\Psi \left( {x,z,t} \right)} \\ {U\left( {x,z,t} \right)} \\ {W\left( {x,z,t} \right)} \\ {\Phi \left( {x,z,t} \right)} \end{array}} \right).$$
(5)

When the heat source does not work and \(F\left( {x,z,t} \right) = 0\), equation system (1) with lower boundary condition (2) has a system of particular eigensolutions of the form

$$\chi \left( {x,z,t,k,m,\omega } \right) = \tilde {\chi }\left( {x,z,t,k,m,\omega } \right)\frac{1}{{\sqrt {2\pi } }}{{e}^{{ - i\omega t}}},$$
(6)

where

$$\begin{gathered} \tilde {\chi }\left( {x,z,t,k,m,\omega } \right) = \left( {\begin{array}{*{20}{c}} {\tilde {\Psi }} \\ {\tilde {U}} \\ {\tilde {W}} \\ {\tilde {\Phi }} \end{array}} \right) = \varepsilon \frac{1}{{\sqrt {2\pi } }}{{e}^{{\frac{z}{{2H}}}}}{{e}^{{ikx}}} \\ \times \,\,\left( {\begin{array}{*{20}{c}} {\left( {A\sin ~\left( {mz} \right) + B\cos ~\left( {mz} \right)} \right)} \\ {\frac{{gHk}}{\omega }\left( {\left( {A + C} \right)\sin \left( {mz} \right) + \left( {B + D} \right)\cos \left( {mz} \right)} \right)} \\ {\sin \left( {mz} \right)} \\ {\left( {C\sin ~\left( {mz} \right) + D\cos ~\left( {mz} \right)} \right)} \end{array}} \right), \\ \end{gathered} $$
(7)
$$\begin{gathered} A = - \frac{1}{2}i\left( {\frac{{2\gamma gH{{k}^{2}} - 2gH{{k}^{2}} - {{\omega }^{2}}}}{{\omega h\left( { - {{\omega }^{2}} + \gamma ~gH{{k}^{2}}} \right)}}} \right),~ \\ B = \frac{{i\omega m}}{{ - {{\omega }^{2}} + ~gH{{k}^{2}}}}, \\ C = - \frac{1}{2}i\frac{{\left( { - {{\omega }^{2}} + ~2gH{{k}^{2}}} \right)\left( {\gamma - 1} \right)}}{{\omega h\left( { - {{\omega }^{2}} + \gamma ~gH{{k}^{2}}} \right)}},~ \\ D = \frac{{i\omega m\left( {\gamma - 1} \right)}}{{ - {{\omega }^{2}} + ~\gamma gH{{k}^{2}}}}.~ \\ \end{gathered} $$
(8)

The normalization factor \(\varepsilon \) in (7) will be determined later. Frequency \(\omega \) is determined by the dispersion relation:

$$\begin{array}{*{20}{c}} {\omega _{{A,G}}^{2} = \frac{{\gamma gH}}{2}\left( {{{k}^{2}} + {{m}^{2}} + \frac{1}{{4{{H}^{2}}}}} \right)} \\ { \times \,\,\left( {1 \pm \sqrt {1 - \frac{{4\left( {\gamma - 1} \right){{k}^{2}}}}{{{{\gamma }^{2}}{{H}^{2}}{{{\left( {{{k}^{2}} + {{m}^{2}} + {1 \mathord{\left/ {\vphantom {1 {(4{{H}^{2}})}}} \right. \kern-0em} {(4{{H}^{2}})}}} \right)}}^{2}}}}} } \right).} \end{array}$$
(9)

The dispersion relation has four branches, two of which correspond to acoustic waves and other two branches conform with internal gravity waves. In other words, with fixed components \(k\) and \(m\) of the wavevector, there are four particular solutions, two of which correspond to acoustic waves and other two correspond to internal gravity waves propagating in opposite directions.

The columns–functions \(\tilde {\chi }\left( {z,k,m,\omega } \right)~\) form a basis, and the solution to problem (1) can be written as an expansion in this basis:

$$\begin{gathered} \lambda ~\left( {x,z,t} \right) = \int\limits_{ - \infty }^\infty {\int\limits_0^\infty {\left[ {{{A}^{ + }}\left( {k,m,t} \right)\tilde {\chi }\left( {z,k,m,{{\omega }_{A}}\left( {k,m} \right)} \right)} \right.} } \\ + \,\,{{A}^{ - }}\left( {k,m,t} \right)\tilde {\chi }\left( {z,k,m, - {{\omega }_{A}}\left( {k,m} \right)} \right) \\ + \,\,{{G}^{ + }}\left( {k,m,t} \right)\tilde {\chi }\left( {z,k,m,{{\omega }_{G}}\left( {k,m} \right)} \right) \\ + \,\,{{G}^{ - }}\left( {k,m,t} \right)\tilde {\chi }\left. {\left( {z,k,m, - {{\omega }_{G}}\left( {k,m} \right)} \right)} \right]dkdm, \\ \end{gathered} $$
(10)

where the functions \({{A}^{ + }}\left( {k,m,t} \right)\), \({{A}^{ - }}\left( {k,m,t} \right)\), \({{G}^{ + }}\left( {k,m,t} \right)\), and \({{G}^{ - }}\left( {k,m,t} \right)\) satisfy the system of nonlinking ordinary differential equations, which, taking into account the wave source (\(F\left( {x,z,t} \right)~\, \ne ~\,0)\), are written as follows:

$$\begin{gathered} \frac{{d{{A}^{ \pm }}\left( {k,m,t} \right)}}{{dt}} \pm i{{\omega }_{A}}{{A}^{ \pm }}\left( {k,m,t} \right) = F_{A}^{ \pm }\left( {k,m,t} \right), \\ \frac{{d{{G}^{ \pm }}\left( {k,m,t} \right)}}{{dt}} \pm i{{\omega }_{G}}{{G}^{ \pm }}\left( {k,m,t} \right) = F_{G}^{ \pm }\left( {k,m,t} \right). \\ \end{gathered} $$
(11)

Equations (11) describe the generation and propagation of acoustic and internal gravity waves in the spectral representation. For sources of these waves \(F_{A}^{ \pm }\left( {k,m,t} \right)\) and \(F_{G}^{ \pm }\left( {k,m,t} \right)\), the following expressions are deduced:

$$\begin{gathered} F_{A}^{ \pm }\left( {k,m,t} \right) = \tilde {\chi }\left( {x,z,t,k,m, \pm {{\omega }_{A}}\left( {k,m} \right)} \right),F\left( {x,z,t} \right), \hfill \\ F_{G}^{ \pm }\left( {k,m,t} \right) = \tilde {\chi }\left( {x,z,t,k,m, \pm {{\omega }_{G}}\left( {k,m} \right)} \right),F\left( {x,z,t} \right). \hfill \\ \end{gathered} $$
(12)

The scalar product of two arbitrary columns different, representing two solutions of system (3), is defined by the formula

$$\begin{gathered} \left\langle {{{\lambda }_{1}},~{{\lambda }_{2}}} \right\rangle = \mathop \smallint \limits_{ - \infty }^\infty \mathop \smallint \limits_0^\infty {{\rho }_{0}}\left( z \right) \\ \times \,\,\left( {{{U}_{1}}{{U}_{2}} + {{W}_{1}}{{W}_{2}} + gH\left( z \right)\frac{{\left( {{{\Psi }_{1}} + {{\Phi }_{1}}} \right)\left( {{{\Psi }_{2}} + {{\Phi }_{2}}} \right)}}{\gamma }} \right. \\ \left. { + \,\,gH\left( z \right)\frac{{\left( {{{\Phi }_{1}} - \left( {\gamma - 1} \right){{\Psi }_{1}}} \right)\left( {{{\Phi }_{2}} - \left( {\gamma - 1} \right){{\Psi }_{2}}} \right)}}{{\gamma \alpha \left( z \right)}}} \right)dzdx. \\ \end{gathered} $$
(13)

The normalization factor (7) is

$$\varepsilon = \sqrt {\frac{1}{{{{\rho }_{{00}}}\tilde {\chi }\left( {x,z,t,k,m,\omega } \right),\tilde {\chi }\left( {x,z,t,k,m,\omega } \right)}}} .$$

Solutions to Eqs. (11) have the form

$$\begin{gathered} {{A}^{ \pm }}\left( {k,m,t} \right) \\ = \exp \left( { \mp i{{\omega }_{A}}t} \right)\mathop \smallint \limits_0^t \exp \left( { \pm i{{\omega }_{A}}t{\kern 1pt} '} \right)F_{A}^{ \pm }\left( {k,m,t{\kern 1pt} '} \right)dt{\kern 1pt} ', \\ {{G}^{ \pm }}\left( {k,m,t} \right) \\ = \exp \left( { \mp i{{\omega }_{G}}t} \right)\mathop \smallint \limits_0^t \exp \left( { \pm i{{\omega }_{G}}t{\kern 1pt} '} \right)F_{G}^{ \pm }\left( {k,m,t{\kern 1pt} '} \right)dt{\kern 1pt} '. \\ \end{gathered} $$
(14)

It can be seen from the presented formulas that the basis functions change with altitude for the acoustic and gravity waves almost in the same way. Therefore, the powers of sources \({{F}_{A}}\) and \({{F}_{G}}\) always are almost the same, regardless of source frequency \(F\). However, this important observation does not mean that the amplitudes of the generated acoustic and gravity waves are the same. If a heat source is associated with meteorological processes, then it has a characteristic time of change greater than the inverse Vääsälä-Brent frequency \(N~\,\, = ~\sqrt {\frac{{\gamma - 1}}{\gamma }gH} ~\) [28]. In this case, a value of the integral in (14) for acoustic waves is clipped off by a rapidly oscillating exponent \(\exp \left( { \pm i{{\omega }_{A}}t{\kern 1pt} '} \right)\) in the integrand. The clipping is not strong, so the amplitude of the generated acoustic waves can be estimated as an amplitude of the source \(F_{A}^{ \pm }\left( {k,m,t{\kern 1pt} '} \right)\), multiplied by \(\left| {\frac{1}{{{{\omega }_{A}} - \sigma }}} \right|\), where \(\sigma \) is the characteristic frequency of the source: \(\frac{{\max \left| {F_{A}^{ \pm }\left( {k,m,t{\kern 1pt} '} \right)} \right|~}}{{{{\omega }_{A}} - \sigma }}\).

If the source frequency falls within the frequency spectrum of internal gravity waves, then an amplitude of the internal gravity waves can increase linearly with time, while the source is operating. In reality, meteorological sources are usually nonperiodic and the amplitude of gravity waves is estimated as a product of the source amplitude by the operating time of the source.

Thus, meteorological heat sources, operating at frequencies lower than the Väisälä–Brent frequency, generate mainly internal gravity waves. In this case, infrasonic waves also are necessarily generated. They have an amplitude smaller than the amplitude of gravity waves, but sufficient for these waves not to be ignored.

The excitation of infrasonic waves by a low-frequency heat source occurs because the temperature and density fluctuations of gravity waves are coordinated, which is determined by polarization relations (7). The heat source changes locally only the temperature. For a gravity wave to arise, it is necessary to provide a consistent density fluctuation. The generation of accompanying acoustic waves during the occurrence of gravity waves allows the coordination of the temperature and density fluctuations to be achieved. The generation of internal gravity waves by a heat source is always accompanied by the generation of acoustic waves, and vice versa.

If a heat source operates at frequencies of acoustic waves, then this source, in addition to acoustic waves, also generates internal gravity waves. The amplitude of these additionally generated gravity waves is smaller than the amplitude of acoustic waves, but sufficient that this generation of gravity waves be not ignored.

3 FORMULATION OF THE PROBLEM OF WAVE PROPAGATION FROM A LOCAL TROPOSPHERIC HEAT SOURCE

The analytical study of a spectrum of waves generated by a local tropospheric heat source is performed for the isothermal atmosphere. To study waves in the nonisothermal atmosphere, the numerical model AtmoSym [27, 29] will be used, which allows solving the problems of wave propagation from various initial disturbances and wave sources within an altitude range of 0–500 km over a territory with a horizontal scale of up to several thousand kilometers.

A general idea of the proposed numerical experiments is illustrated in Fig. 1. Figure 1 schematically shows the propagation of waves from a tropospheric heat source. The wave amplitude at these altitudes is usually small due to the high gas density at tropospheric altitudes. Therefore, to analyze the generated waves, the concepts of the linear wave theory can be used. The source emits a wave \(\Delta {{P}_{{downward}}}~(x,~z,~t)\) downward with the same amplitude as an amplitude of the wave \(\Delta {{P}_{{upward}}}~\left( {x,~z,~t} \right)\) that travels upward. The wave \(\Delta {{P}_{{downward}}}~(x,~z,~t)\)propagating downward from a tropospheric source reaches the Earth’s surface and is reflected from it. The amplitude of the reflected wave \(\Delta {{P}_{{reflected}}}~\left( {x,~z,~t} \right)\) is equal to the amplitude of the incident wave, so the wavelike pressure fluctuation \(\Delta P~\left( {x,~z\,~ = ~\,0,~t} \right)\) recorded on the Earth’s surface is equal to the pressure fluctuation with doubled amplitude created by the incident wave:

$$\begin{gathered} \Delta P~\left( {x,~z~\,\, = 0,~t} \right) = \Delta {{P}_{{downward}}}~\left( {x,~z = 0,t} \right) \\ + \,\,\Delta {{P}_{{reflected}}}~\left( {x,~z = 0,~t} \right), \\ \Delta {{P}_{{downward}}}~\left( {x,~z = 0,t} \right) = \Delta {{P}_{{reflected}}}~\left( {x,~z = 0,~t} \right) \\ = \frac{1}{2}\Delta P~\left( {x,~z\,~ = ~\,0,~t} \right). \\ \end{gathered} $$
(15)
Fig. 1.
figure 1

Schematic picture of wave propagation from a tropospheric heat source.

Full size image

The upper atmosphere is reached by a sum of the waves, which is the result of the interference of a wave \(\Delta {{P}_{{upward}}}~\left( {x,~z,~t} \right)\) propagating directly from the source and a wave \(\Delta {{P}_{{reflected}}}~\left( {x,~z,~t} \right)\) reflected from the Earth’s surface. When the waves from variations in pressure on the Earth’s surface \(\Delta P~\left( {x,~z\,~ = ~\,0,~t} \right)\) are calculated, the wave \(\Delta {{P}_{{upward}}}~\left( {x,~z,~t} \right)\) coming directly from the tropospheric source is replaced with one more reflected wave \(\Delta {{P}_{{reflected}}}~\left( {x,~z,~t} \right)\). In this case, obviously, an error is introduced which requires investigation.

The waves \(\Delta {{P}_{{upward}}}~\left( {x,~z,~t} \right)\) and \(\Delta {{P}_{{reflected}}}~\left( {x,~z,~t} \right)\) travel different paths to the upper atmosphere. Therefore, it can be assumed that the main difference between the wave \(\Delta {{P}_{{upward}}}~\left( {x,~z,~t} \right)\) and \(\Delta {{P}_{{reflected}}}~\left( {x,~z,~t} \right)\) is reduced to the fact that these waves have different phases. This phase difference, if it is significant, can be taken into account. Then the function \({{\varphi }_{p}}\left( {x,~t} \right)\) describing pressure variations in the introduced boundary source is not equal to \(\Delta P~\left( {x,~z~\, = \,~0,~t} \right)\), but at the same time it does not differ much from it and is constructed according to \(\Delta P~\left( {x,~z~\, = \,~0,~t} \right)\) in order to take into account the phase difference of the interfering waves.

The model tropospheric heat source proposed above, which simulates the heating/cooling of atmospheric gas during phase transitions of water in the atmosphere, can be written as

$$f\left( {x,~z,~t} \right) = \left\{ {\begin{array}{*{20}{c}} {S\exp \left( { - {{{\left( {\frac{{x - {{x}_{0}}}}{{{{D}_{x}}}}} \right)}}^{2}} - {{{\left( {\frac{{z - {{z}_{0}}}}{{{{D}_{z}}}}} \right)}}^{2}}} \right)(1 - {{e}^{{ - \frac{t}{\tau }}}})} \\ 0 \end{array}} \right.\sin \left( {\omega t} \right)\,\,\,\,\,\,\begin{array}{*{20}{c}} \begin{gathered} \hfill \\ 0 \leqslant t \leqslant 1~\,\,{\text{h}} \hfill \\ \end{gathered} \\ {t > 1\,\,~{\text{h}}} \end{array}.$$
(16)

Here, parameter \({{x}_{0}}\) determines the source location in the computational domain, \({{z}_{0}}\) = 6 km, \({{D}_{x}}\) = 2 km, \({{D}_{z}}\) = 1.5 km, and \(\tau \) = 300 s. Parameters \({{z}_{0}}\), \({{D}_{x}}\), and \({{D}_{z}}\) specify the location and dimensions of the model heat source. It is assumed that these parameters roughly correspond to the size and location of a typical small cloud, since the condensation of water vapors not only implies a heat release, but is also accompanied by the formation of clouds. Parameter \(\tau \) = 300 s is introduced for the slow turning-on of the source to suppress possible transients. Parameter \(S\) is an amplitude of the source.

The action of heat sources having a complex configuration or large dimensions can be understood as the simultaneous action of several heat sources of the form of (16). Therefore, studying the solution to the problem of waves from one simple source of the form of (16) seems adequate for understanding the general case.

In studying the infrasound generation and propagation, a model source operating at the frequency \(\omega = \frac{{2\pi }}{{3~{\text{min}}}}\) will be used. In the study of the generation and propagation of internal gravity waves, a source of the form of (16) with a frequency \(\omega = \frac{{2\pi }}{{30~{\text{min}}}}\) will be specified. These frequencies are taken from the assumption that the other possible sources, operating at different frequencies and potentially interesting for this study, are qualitatively the same. In addition, the small dimensions of the source make it possible to record the other, more complex, sources as a superposition of the sources discussed above. Thus, the problem of waves from a complex source is reduced to the problem of waves from the simple sources under consideration.

3.1 NUMERICAL MODEL EQUATIONS AND INITIAL AND BOUNDARY CONDITIONS

The numerical atmosphere model of high resolution AtmoSym is based on solving a system of nonlinear two-dimensional hydrodynamic equations for atmospheric gas in a gravity field and is described in detail in [24].

The dependence of the medium parameters (viscosity, thermal conductivity, background density, and background temperature) on the vertical coordinate \(z\) in the numerical model is taken from the empirical atmosphere model [30]. The optimal computational grid is vertically nonuniform and is automatically constructed by the program on the basis of the real stratification of the medium.

The upper boundary conditions are typical for thermosphere models and are specified at an altitude of h = 500 km:

$${{\left. {\frac{{\partial T}}{{\partial z}}} \right|}_{{z = h}}} = 0,\,\,~{{\left. {\frac{{\partial U}}{{\partial z}}} \right|}_{{z = h}}} = 0,\,\,{{\left. {\frac{{\partial V}}{{\partial z}}} \right|}_{{z = h}}} = 0,\,\,{{\left. W \right|}_{{z = h}}} = 0.$$
(17)

The horizontal boundary conditions in the numerical model are set in the following form:

$$\begin{gathered} T~\left( {x\,\,~ = \,\,~0,~z,~t} \right) = ~\,\,T~\left( {x\,\,~ = \,\,~L,~z,~t} \right),~ \\ \rho \left( {x~\,\, = \,\,~0,~z,~t} \right) = \,\,~\rho \left( {x\,\,~ = \,\,~0,~z,~t} \right), \\ ~W\left( {x\,\,~ = \,\,~0,~z,~t} \right) = \,\,~W\left( {x~\,\, = \,\,~L,~z,~t} \right),~ \\ U\left( {x~\,\, = \,\,~0,~z,~t} \right) = \,\,~ - U\left( {x\,\,~ = \,\,~L,~z,~t} \right). \\ \end{gathered} $$
(18)

These boundary conditions are proposed in [22]. The conditions make it possible to simulate the runaway of waves beyond the horizontal boundaries of the region in the case of symmetry of the problem. In any case, width \(L\) of the computational domain is chosen large enough so that boundary conditions (18) horizontally did not affect solving the problem.

With the numerical simulation of wave propagation from a local heat source, two closely related problems will be solved. In the first problem, a model tropospheric heat source \(f\left( {x,~z,~t} \right)\), approximated by (16), will be specified in numerical calculations. The lower boundary conditions for the problem of wave propagation from a tropospheric source \(f\left( {x,~z,~t} \right)\) are standard for problems of the dissipative model of the atmosphere and have the form

$$\begin{gathered} U\left( {x,~z~\,\, = \,\,~0,~t} \right) = \,\,~0,~~\,\,\,\,W\left( {x,~z~\,\, = \,\,~0,~t} \right) = ~\,\,0,~ \\ ~T\left( {x,~z~\,\, = \,\,~0,~t} \right)~\,\, = ~\,\,{{T}_{0}}\left( 0 \right). \\ \end{gathered} $$
(19)

Since the propagation of waves from a tropospheric heat source is being investigated, then initial conditions correspond to the wave absence at the initial moment of time:

$$\begin{gathered} U~\left( {x,~y,~z,~t~\,\, = \,\,~0} \right) = 0,~\,\,\,\,~W~\left( {x,~y,~z,~t~\,\, = \,\,~0} \right) = 0,{{\;}} \\ \rho ~\left( {x,~y,~z,~t~\,\, = \,\,~0} \right) = {{\rho }_{0}}\left( z \right),~\,\,\,\,~T~\left( {x,~y,~z,~t~\,\, = \,\,~0} \right) = {{T}_{0}}\left( z \right). \\ \end{gathered} $$
(20)

The second problem uses data on pressure fluctuations on the Earth’s surface, which are obtained from solving the first problem and have the meaning of an analogue of experimental observations. Next, the results of solving both problems will be compared.

In the second formulation of the problem, the tropospheric heat source is absent and \(f\left( {x,~y,~t} \right) = 0\). However instead of it, there is a boundary source \({{\varphi }_{p}}\left( {x,t} \right)\) that determines the pressure variations on the Earth’s surface. Thus, the lower boundary conditions for the second problem are as follows:

$$U\left( {x,~z~\,\, = ~\,\,0,~t} \right)~\,\, = \,\,~0,~\,\,\,~\frac{{\partial W\left( {x,~z~\,\, = \,\,~0,~t} \right)~}}{{\partial z}}\,\,~ = \,\,~0,$$
$$\begin{gathered} T~\left( {x,~z~\,\, = \,\,~0,~t} \right) = \,\,~{{T}_{0}}\left( 0 \right), \\ P\,\left( {x,~z\,\,~ = \,\,~0,~t} \right) = ~\,\,{{P}_{0}}\left( 0 \right) + {{\varphi }_{p}}\left( {x,t} \right). \\ \end{gathered} $$
(21)

Here, \({{\varphi }_{p}}\left( {x,t} \right)\) is the function describing wavelike pressure fluctuations at the lower boundary and \({{P}_{0}}\left( 0 \right)\) is the background pressure on the Earth’s surface. The proof of the correctness of this problem formulation is given in [23, 24]. The problem of wave propagation from pressure variations experimentally observed on a network of microbarographs was solved in [21, 22].

The proposed problems are related through the function \({{\varphi }_{p}}\left( {x,t} \right)\) in (21). In the simplest case, \({{\varphi }_{p}}\left( {x,t} \right)\) are the recorded pressure variations \(\Delta P\left( {x,~z~\,\, = \,\,~0,~t} \right)\) at the lower boundary obtained from solving the first problem, where \(f\left( {x,~y,~t} \right) \ne 0\). This problem formulation makes it possible to find out whether it is possible by using the recorded pressure variations \(\Delta P\left( {x,~z~\,\, = \,\,~0,~t} \right)\) to calculate the same waves that propagate from a tropospheric source \(f\left( {x,~y,~t} \right)\). In a more complex case, function \({{\varphi }_{p}}\left( {x,t} \right)\) does not coincide with the recorded pressure variations \(\Delta P\left( {x,~z\,\,~ = \,\,~0,~t} \right)\), but is calculated from these pressure variations and takes phase corrections into account.

4 WAVES FROM A TROPOSPHERIC HEAT SOURCE AT FREQUENCIES OF INFRASONIC WAVES

Theoretical research has shown that any heat source generates infrasonic waves. Therefore, first and foremost, we will consider the generation of waves by a tropospheric heat source operating at frequencies of infrasonic waves.

Figures 2a and 2c show the temperature-field perturbation arising due to the operation of a tropospheric heat source \(f\left( {x,z,t} \right)~\) (16) with a period of \(T\,\,~ = ~\,\,3\) min for time moments t = 0.25 h and t = 1 h. The source with this period emits mainly infrasonic waves. In the bottom row in Figs. 2b and 2d, the results of similar calculations performed with\(f\left( {x,z,t} \right) = 0\) are shown, where the boundary source of wave oscillations \({{\varphi }_{p}}\left( {x,t} \right)\) in (19) is taken as \({{\varphi }_{p}}\left( {x,t} \right) = \Delta P\left( {x,z~\,\, = 0,t} \right).\) The function \(\Delta P\left( {x,z = 0,t} \right)\) will be obtained in the course of solving the problem with a tropospheric source \(f\left( {x,~z,~t} \right)\) and is an analogue of the experimentally observed pressure variations on the Earth’s surface. In this case, these variations in the surface pressure are calculated by numerically solving the problem of wave propagation from a tropospheric heat source.

Fig. 2.
figure 2

Temperature perturbation fields for (a, b) t = 0.5 h and (c, d) for t = 1 h. (a, c) Wave pattern from a source\(f\left( {x,z,t} \right)\); the source oscillation period T = 3 min. (b, d) Wave pattern from recorded pressure variations at the lower boundary.

Full size image

It can be seen that the wave pattern arising from the boundary source \({{\varphi }_{p}}\left( {x,t} \right) = \Delta P\left( {x,z{{\;}} = 0,t} \right)\) is similar to the wave pattern from the tropospheric source. At short time moments, an amplitude of waves from the tropospheric source exceeds the amplitude of waves from the surface source; at time moments of about 1 h, the ratio of the amplitudes is opposite. The difference in the amplitudes of the waves from the tropospheric and surface sources during the source operation sometimes reaches 30%. After switching off the source, the amplitude of waves falls off rather quickly and the amplitude from the surface source falls off faster.

The main difference between wave patterns from tropospheric and surface sources is probably explained in the same way as in the case of the generation of internal gravity waves. Wave generation by a source operating at frequencies of internal gravity waves is discussed below.

The significant amplitude of the generated infrasonic waves in Figs. 2b and 2d calls attention to itself. This amplitude is explained by the fact that the operating time of the source is much longer than the oscillation period of the source. This allows the resonant properties of the atmosphere to be fully manifested. In the case of wave generation at frequencies of internal gravity waves discussed below, the ratio of the oscillation frequency of the source to the time of its operation is much greater, which, accordingly, leads to a smaller resulting amplitude.

A good coincidence of wave patterns from tropospheric and boundary sources shows that the problem of waves from a tropospheric source above the Earth’s surface, operating at frequencies of infrasonic waves, can be successfully replaced with the problem of wave propagation from a surface source, in which the experimentally observed wave motion of the pressure is specified at the boundary.

Tropospheric heat sources are usually located at an altitude of several kilometers above the Earth’s surface and have a complex spatiotemporal structure. This makes it difficult to obtain detailed experimental information about these sources. Using a boundary wave source instead of specifying directly a tropospheric source has an advantage in numerical studies of generated waves. The pressure on the Earth’s surface is experimentally recorded by networks of microbarographs or it can be obtained in other ways. This makes it possible, when performing numerical studies of waves generated by meteorological sources, to use experimental observational information on pressure fluctuations on the Earth’s surface.

5 GENERATION AND PROPAGATION OF WAVES FROM A TROPOSPHERIC LOW-FREQUENCY HEAT SOURCE

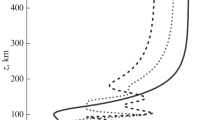
Let us consider wave generation by a tropospheric heat source, operating at frequencies of internal gravity waves, with subsequent propagation into the upper atmosphere. Figure 3 shows the result of a numerical calculation of the occurrence and propagation of a wave temperature perturbation in the altitude region of \(0 \leqslant z < 100\) km, obtained due to the operation of a tropospheric heat source (16) with a period of T = 30 min for time moments: t = 0.23 h, t = 0.5 h, t = 1 h, t = 1.6 h.

Fig. 3.
figure 3

Temperature perturbation field in the altitude interval 0 ≤ z <100 km, created by a tropospheric low-frequency heat source f(x, z, t) with a period of T = 30 min at time moments (a) t = 0.23 h, (b) t = 0.5 h, (c) t = 1 h, and (d) t = 1.6 h.

Full size image

The period of the model source under study is greater than the Väisälä–Brent frequency; i.e., the source operates at frequencies of internal gravity waves. It is known that a speed of vertical propagation of internal gravitational waves is much lower than the speed of sound. However, in Fig. 3, a rather rapid appearance of internal gravity waves at high altitudes is observed. The mechanism of this phenomenon is discussed below.

This effect is achieved due to the paired production of acoustic and internal gravity waves during the operation of a monochromatic source of internal gravity waves, which is shown below. Let us consider Eqs. (11) describing the generation of acoustic and internal gravity waves. These equations are written for the coefficients at the wave harmonics, which determine the spatial structure of the waves: the wave harmonics are determined at \(0 \leqslant z < \infty \). The wave harmonics are a solution to a system of equations in the form of functions \(\tilde {\Psi },~\,\tilde {U},\,~\tilde {W},\,~\tilde {\Phi }\) that depend on spatial coordinates according to Eqs. (7) and (8). Equations (11) show that a wave can be generated by a source \(f\left( {x,z,t} \right)\) not only strictly within the region of the source, but also outside it.

Equations (11) contain sources of acoustic and gravity waves \(F_{A}^{ \pm }~(k,~m,~t)\) and \(F_{G}^{ \pm }~\left( {k,~m,~t} \right)\), written in the k-representation as an expansion in wave modes \(\tilde {\chi }\left( {z,k,m,\omega \left( {k,m} \right)} \right)\), which depend on coordinates and are columns of components \(\tilde {\Psi },~\tilde {U},~\tilde {W},~\tilde {\Phi }\). If we go to the usual coordinate representation, then we get the same sources in the form of \(F_{A}^{ \pm }~(x,~z,~t\)) and \(F_{G}^{ \pm }~(x,~z,~t\)), depending on the coordinates. These sources are defined for all four functions appearing in the problem; i.e., they are columns. Obviously, for the column components, the following is true:

$$\begin{gathered} F_{{A,\Psi }}^{ + }~\left( {x,~z,~t} \right) + F_{{A,\Psi }}^{ - }\left( {x,~z,~t} \right) \\ + \,\,F_{{G,\Psi }}^{ + }~\left( {x,~z,~t} \right) + F_{{G,\Psi }}^{ + }\left( {x,~z,~t} \right)~\,\, = \,\,~0,~ \\ F_{{A,U}}^{ + }~\left( {x,~z,~t} \right) + F_{{A,U}}^{ - }\left( {x,~z,~t} \right) \\ + \,\,F_{{G,U}}^{ + }~\left( {x,~z,~t} \right) + F_{{G,U}}^{ + }\left( {x,~z,~t} \right)~\,\, = \,\,~0,~ \\ F_{{A,W}}^{ + }~\left( {x,~z,~t} \right) + F_{{A,W}}^{ - }\left( {x,~z,~t} \right) + F_{{G,W}}^{ + }~\left( {x,~z,~t} \right) \\ + \,\,F_{{G,W}}^{ + }\left( {x,~z,~t} \right) = \,\,~0, \\ F_{{A,\Phi }}^{ + }~\left( {x,~z,~t} \right) + F_{{A,\Phi }}^{ - }\left( {x,~z,~t} \right) + F_{{G,\Phi }}^{ + }~\left( {x,~z,~t} \right) \\ + \,\,F_{{G,\Phi }}^{ + }\left( {x,~z,~t} \right)~\,\, = ~f\left( {x,~z,~t} \right). \\ \end{gathered} $$
(22)

Here, the components of the columns \(F_{A}^{ \pm }~(x,~z,~t)\) and \(F_{G}^{ \pm }~\left( {x,~z,~t} \right)\) are written on the left-hand side of Eqs. (20). The equations for velocities in (22) satisfy \(~F_{{A,U}}^{ \pm }~\left( {x,~z,~t} \right)\) = \(~F_{{G,U}}^{ \pm }~\left( {x,~z,~t} \right)\) = \(F_{{A,W}}^{ \pm }~\left( {x,~z,~t} \right)\) = \(F_{{G,W}}^{ \pm }~\left( {x,~z,~t} \right)\) = 0.

The source functions \(F_{{A,\Psi }}^{ \pm }~\left( {x,~z,~t} \right),~\) \(F_{{G,\Psi }}^{ \pm }~\left( {x,~z,~t} \right),~\) \(F_{{A,\Phi }}^{ \pm }~\left( {x,~z,~t} \right),\) and \(F_{{G,\Phi }}^{ \pm }~\left( {x,~z,~t} \right)\)are expressed in terms of a heat source \(f\left( {x,z,t} \right)\) by rather complex integral formulas, but in some cases these expressions are simplified. For illustration, consider the case when these expressions are quite simple. Namely, in the longwave approximation, when \({{k}^{2}} \ll {{m}^{2}} + \frac{1}{{4{{H}^{2}}}}\), we have

$$\begin{gathered} F_{{A,\Phi }}^{ + }~\left( {x,~z,~t} \right) = F_{{A,\Phi }}^{ - }\left( {x,~z,~t} \right) = \frac{{\gamma - 1}}{{2\gamma }}f\left( {x,z,t} \right), \\ F_{{G,\Phi }}^{ + }~\left( {x,~z,~t} \right) = F_{{G,\Phi }}^{ - }\left( {x,~z,~t} \right) = \frac{1}{{2\gamma }}f\left( {x,z,t} \right), \\ F_{{A,\Psi }}^{ \pm }~\left( {x,~z,~t} \right) = - F_{{G,\Psi }}^{ \pm }\left( {x,~z,~t} \right) \\ = \frac{1}{2}\left( {f\left( {x,z,t} \right) - \mathop \smallint \limits_{ - \infty }^z f\left( {x,z{\kern 1pt} ',t} \right)dz{\kern 1pt} '\frac{1}{H}} \right). \\ \end{gathered} $$
(23)

Relations (23) are presented in [31, 32]. These equations were deduced for solving a problem with the initial temperature perturbation, but the problem with the initial perturbation and the problem with the source are mathematically related [31, 32]. Relations (23) are written in the same form as they were derived for an infinite atmosphere. For this problem, it is natural to assume that \(f\left( {x,z,t} \right) = 0\) at \(z < 0\), and then relations (23) are also valid for a semi-infinite atmosphere.

Formulas (23) show that waves are generated not only in the region of the heat source, but also above the heat source. It is important that the sources of density \(F_{{A,\Psi }}^{ \pm }~\left( {x,~z,~t} \right)\) and \(F_{{G,\Psi }}^{ \pm }\left( {x,~z,~t} \right)\) have opposite signs for acoustic and internal gravity waves. This is explained by the fact that there is no total source of mass.

An acoustic wave and a gravity wave from a heat source are always generated in pairs. This effect of paired formation of waves is associated with the fact that the temperature and density of a gravity wave are linked by polarization relations, which is analytically shown above. The tropospheric heat source only changes the temperature of the gas. Therefore, for a gravity wave to arise, an acoustic wave must simultaneously appear, which compensates for the change in the medium density produced by the gravity wave. Moreover, this change in density, as is shown by Eq. (23), takes place not only in the region of the source localization, but also above it. This is what causes the effect of a rather rapid penetration of internal gravity waves from the heat source into the high altitudes.

Figure 4 shows the wave temperature perturbations created by a tropospheric heat source \(f\left( {x,~z,~t} \right)~\) with a period of \(T~\,\, = ~\,\,30\) min at time moments t = 0.5 h, t = 1 h, t = 1.5 h, and t = 2.16 h. The slopes of the phase front indicate that gravity waves predominate in the figures, except for the first two (Figs. 4a, 4b), where, in the central parts of the figures, a noticeable contribution is also made by infrasonic waves.

Fig. 4.
figure 4

Field of wave perturbations of the atmospheric temperature created by a tropospheric low-frequency heat source \(f\left( {x,z,t} \right)\) with a period of T = 30 min at time moments (a) t = 0.5 h, (b) t = 1 h, (c) t = 1.5 h, and (d) t = 2.16 h.

Full size image

Figure 5a shows the time dependence of temperature perturbation oscillations at the lower boundary. Fluctuations in density at the lower boundary behave in a similar way over time. The temperature oscillations and density fluctuations create together pressure fluctuations at the lower boundary, which will be used further as a boundary condition in solving the problem of wave propagation from pressure fluctuations at the lower boundary.

Fig. 5.
figure 5

Dependence of the temperature perturbation (a) at the lower boundary on time and (b) at the lower boundary near the source.

Full size image

From Fig. 5a, it can be seen that the disturbance at the boundary consists of two diverging wavelike disturbances, excluding the central part of the region. The horizontal propagation speed of these wavelike disturbances is about 250 m/s. In about 1.6 h, these diverging wavelike disturbances reach the horizontal boundaries of the computational domain.

The constant horizontal speed and the unchanged shape of two diverging waves indicate the possible manifestations of the waveguide properties of the atmosphere at the Earth’s surface. Indeed, in [33], atmospheric quasi-waveguides were studied, where the wave is captured by stratification and propagates horizontally, where a quasi-waveguide with similar parameters was found near the Earth’s surface. The propagation velocity of the first quasi-waveguide mode calculated in [33] was approximately 271 m/s, which is close to 250 m/s. The differences can be explained by discrepancies in the stratification details between this work and [32]. Figure 5b shows the central part of the graph in Fig. 5a. The wave in Fig. 5b is a sum of the incident and reflected waves, which are equal in amplitude.

5.1 PROPAGATION OF INTERNAL GRAVITY WAVES FROM SURFACE PRESSURE VARIATIONS

A comparison of the infrasonic wave propagation from the tropospheric and boundary sources showed a good coincidence of the wave patterns. It is known that only infrasonic waves, propagating at small angles to the vertical, reach a nonisothermal atmosphere with a realistic stratification of the upper atmosphere altitudes. These waves travel quickly. Infrasonic waves, emitted at large angles to the vertical, gradually change the direction of propagation due to an increase in temperature with an altitude above 100 km, or are even reflected to the Earth’s surface [34]. The propagation of internal gravity waves is much more strongly influenced by the specific features of stratification, which makes the wave pattern more complicated.

Figure 6 sequentially shows wave perturbations of the temperature field, obtained by calculating the waves from the field of pressure variations on the Earth’s surface. The pressure variations on the Earth’s surface used as a boundary source were calculated when solving the previous problem of wave propagation from a tropospheric low-frequency heat source with a period T = 30 min.

Fig. 6.
figure 6

Field of wave perturbations in the atmospheric temperature created by low-frequency variations of the pressure field at times (a) t = 0.5 h, (b) t = 1 h, (c) t = 1.5 h, and (d) t = 2.16 h.

Full size image

It is clearly seen that the waves calculated from the variations in the pressure field on the Earth’s surface differ by about a twofold overestimated amplitude. Many authors [11, 35–37] have noted that it is difficult to determine the order of the amplitude of waves reaching the upper atmosphere when simulating the wave propagation from tropospheric sources into the upper atmosphere. At the same time, many other wave parameters (frequency, propagation velocity, and scales) are confidently determined from information on tropospheric sources. Therefore, the twofold error in the amplitude of the waves is acceptable, it can be estimated, and the result can be improved. It is important that experimental data on pressure variations near the Earth’s surface can be used to calculate the parameters of waves generated by meteorological sources.

5.1.1 DESIGNING AN IMPROVED SURFACE SOURCE ACCORDING TO THE DATA ON PRESSURE VARIATIONS ON THE EARTH’S SURFACE AND CALCULATION OF WAVES FROM THE SOURCE

Let us consider the possible reasons for the obtained discrepancy between the results of calculating waves from a low-frequency tropospheric source and from pressure variations on the Earth’s surface. The schematic in Fig. 1 shows that the waves both directly from the source and reflected from the Earth’s surface reach the upper atmosphere. These waves interfere. In the process of interference, the amplitude of the resulting wave is usually approximately equal to the maximum amplitude of the interfering waves, except for the case when the interfering waves are coherent. In the presented calculations of waves from pressure variations, a wave propagating upward directly from the source is replaced with another wave reflected from the Earth’s surface. This is a special case when the interfering waves are coherent, and in this exceptional case the amplitude of the resulting wave is doubled in relation to the amplitude of the interfering waves. Therefore, in order to correct the amplitude of the waves, it is necessary, first and foremost, to try to take into account a difference in the phases of the interfering waves that reach the upper atmosphere. This phase difference is approximately equal to twice the time of propagation of waves from the source to the Earth’s surface.

Let us try to estimate the phase shift \(\Delta {{\phi }_{G}}\) between the gravity wave propagating upward directly from the source and the reflected wave. It is obvious that \(\Delta {{\phi }_{G}} = \frac{{2H}}{{{{c}_{{vert}}}}}\), where \(H\) is the height of the center of the source and \({{c}_{{vert}}}\) is the velocity of vertical propagation of waves. Speed \({{c}_{{vert}}}\) can be roughly defined as \({{c}_{{vert}}}\)\( \approx {\text{\;}}20\) m/s, so the function φp(x,t) can be written in this case as

$$\begin{gathered} {{\varphi }_{p}}\left( {x,~t} \right) = 0.5~\Delta P\left( {x,~z = 0,~t} \right) \\ + \,\,0.5~\eta ~\left( {x,~t + \Delta {{\phi }_{G}}\left( {1 - \exp \left( { - \frac{t}{\tau }} \right)} \right)} \right) \\ + \,\,0.5\left( {\Delta P\left( {x,~z = 0,~t + ~\Delta {{\phi }_{A}}} \right) - \eta ~\left( {x,~t + \Delta {{\phi }_{A}}} \right)} \right), \\ \eta ~\left( {x,~t} \right) = \frac{1}{{2{{T}_{A}}}}\mathop \smallint \limits_{t - {{T}_{A}}}^{t + {{T}_{A}}} \Delta P\left( {x,~z = 0,~t{\kern 1pt} '} \right)dt{\kern 1pt} '. \\ \end{gathered} $$
(24)

In Eq. (24), the contribution of internal gravity waves and the contribution of acoustic waves are approximately separated into the second of the interfering waves. The introduced function \(\eta {{\;}}\left( {x,{{\;}}t} \right)\) represents the gravitational component of the wave, which is obtained using local time averaging of the function \(\Delta P\left( {x,z = 0,t} \right)\). Averaging interval \(2{{T}_{A}}\) = 300 s, which roughly corresponds to the maximum period of acoustic waves. The multiplier \(\left( {1 - \exp \left( { - \frac{t}{\tau }} \right)} \right)\)in (24) is introduced in the phase shift of the gravity wave \(\eta {{\;}}\left( {x,{{\;}}t} \right)\) to suppress possible transients, \(\tau = 300\) s. The function \(\left( {\Delta P\left( {x,{{\;}}z = 0,{{\;}}t} \right) - \eta {{\;}}\left( {x,{{\;}}t} \right)} \right)\) represents the contribution of the acoustic wave to the second of the interfering waves. By analogy with gravity waves, a phase shift of \(\Delta {{\phi }_{A}} = \frac{{2H}}{{{{c}_{{vert}}}}}\) ≈ 36 s is also introduced into this function, which takes into account that the real tropospheric source is located above the Earth’s surface at a height of \(H\,~ = ~\,6\) km.

Figure 7 shows the wave variations in pressure corresponding to this surface source (24). A comparison of Fig. 4 and Fig. 7 shows that the coincidence of the wave patterns is not bad. One exception is the first results in Fig. 4 and Fig. 7, plotted for time moments not exceeding two wave periods. Despite this, in these figures, the difference in amplitudes does not exceed 25% and the shape of the waves is similar. In Fig. 7a, the wave amplitude is still small; the wave in the upper atmosphere is just being formed. Obviously, the errors affect the wave of small amplitude more noticeably. The time shift \(\Delta {{\phi }_{G}} = 10~\) min, introduced in numerical calculations of wave propagation from a boundary source, is justified at long times and takes into account the phase shift between waves that interfere in the upper atmosphere, but at short times it can lead to the fact that one of the waves arrives at high altitudes somewhat prematurely. At short times, acoustic waves, which are also present in the spectrum, make a significant contribution.

Fig. 7.
figure 7

Field of wave perturbations of the atmospheric temperature created by low-frequency modified variations of the pressure field (22) at time moments (a) t = 0.5 h, (b) t = 1 h, (c) t = 1.5 h, and (d) t = 2.16 h.

Full size image

The analysis of the wave pattern showed that even a rough allowance for the phase shift between the interfering waves significantly improved the coincidence of the results of calculations of waves from pressure fluctuations at the boundary with direct calculations of waves from a tropospheric source. Obviously, it is possible to take into account more accurately the phase shift between the interfering waves. The velocity of vertical propagation of waves depends on the wavenumbers and, accordingly, the phase shift actually also depends on them. This is not taken into account in the proposed simple model of a boundary source. It is also possible to take into account more accurately a structure of the tropospheric source, and not be confined only to entering height \(H\)of the source. However, the complication of the boundary source model should be justified by some specific considerations. To estimate the amplitude of waves, which are generated by meteorological events and reach the upper atmosphere, the use of a simple boundary source model is justified. It is important that an estimate of the parameters of waves reaching the upper atmosphere can be obtained on the basis of experimental data on pressure variations on the Earth’s surface.

6 CONCLUSIONS

The practical interest in the issue of wave generation by a boundary source is due to the importance of studying the propagation of atmospheric waves from realistic tropospheric sources into the upper atmosphere. Often, experimental information about tropospheric sources is insufficient to determine the parameters of the generated waves, especially for calculating the amplitude of the generated waves. Experimental information on pressure fluctuations on the Earth’s surface is often available, or can be obtained, and it can be used to analyze waves from meteorological sources. Therefore, the question of the possibility of replacing one problem with another seems practically justified.

The general problem of AGW generation in an isothermal atmosphere by a local heat source at tropospheric altitudes is considered analytically. The source simulates the heating of the atmosphere by phase transitions of water. The spectrum of the waves generated by the source has been studied. It is shown that the generation of internal gravity waves by this source cannot occur without the generation of infrasonic waves, and vice versa. Estimates of the amplitudes of the generated waves are obtained.

Numerical simulation of the propagation of infrasonic and internal gravity waves from a local heat source in a nonisothermal atmosphere has been carried out. Numerically solving the problem of waves from a tropospheric heat source provided data on pressure fluctuations on the Earth’s surface. The recorded pressure fluctuations are used as boundary sources in the problem of wave generation by pressure variations on the Earth’s surface. A comparison of solutions of both solved problems is carried out.

Results from the numerical study of the propagation of infrasonic and internal gravity waves from a local tropospheric heat source and from a boundary source have shown the following:

(i) if a tropospheric source operates at frequencies of infrasonic waves, then the solutions to the problems of waves from the tropospheric source and from recorded fluctuations of surface pressure coincide with a sufficient accuracy for many practical applications;

(ii) if a source operates at frequencies of internal gravity waves, then the amplitude of the waves from the surface source usually exceeds the amplitude of the waves from the tropospheric source. If the source is located high, then the amplitude may be doubled. The amplitude discrepancy is less if the tropospheric source is located near the Earth’s surface. The wave shapes in the solutions to both problems are similar in any case.

This discrepancy between the wave amplitudes in the compared problems is explained by the fact that, in the case of a tropospheric source, both waves propagating directly from the source and waves reflected from the Earth’s surface reach the upper atmosphere. These waves interfere and the amplitude of the resulting wave is determined by this interference. Waves reflected from the Earth’s surface have an amplitude equal to half of the experimentally measured pressure. Replacing the problem of waves from a tropospheric source with the problem of waves from recorded pressure fluctuations is equivalent to the fact that one of the interfering waves (propagating upward from a tropospheric source) is replaced with a wave reflected from the Earth’s surface. In this case, both interfering waves have the same phases, the interfering waves are coherent, and the amplitude of the resulting wave is twice the amplitude of the interfering waves. In the case of a real tropospheric source, wave interference can give an amplitude approximately equal to the amplitude of the interfering waves, since the phases of the interfering waves are different. The phase difference of interfering waves depends on the altitude at which the tropospheric source is located. The higher the source, the more apparent the difference in the tasks under consideration.

This analysis made it possible to construct a corrected boundary source based on the data of pressure fluctuations on the Earth’s surface which approximately takes into account the phase shift between the interfering waves. The phase shift is estimated from the tropospheric source altitude. This modification of the formula for the specified surface pressure significantly improves the wave pattern accuracy and the accuracy of calculating the wave amplitude.

The accuracy is sufficient to estimate the transfer of energy and momentum of waves into the upper atmosphere and to parameterize the effect of acoustic-gravity waves in models of the general circulation of the atmosphere. This approach makes it possible to use experimental data on pressure variations on the Earth’s surface to perform calculations of waves from meteorological sources.