1 NOTATION

\(A\)

the entrainment coefficient, \(A = - \frac{{{{B}_{h}}}}{{{{B}_{s}}}}\)

\({{A}_{1}}\)

the constant of mechanical to buoyancy TKE generation ratio, \({{A}_{1}} = \frac{{{{C}_{s}}}}{{{{C}_{1}}}}\)

\({{A}_{5}}\)

the constant of the integral of dissipation of mechanical generation of sheared convection, \({{A}_{5}}=\frac{V_{\text{*}}^{3}}{2}\left( 1-{{h}^{-1}}\underset{0}{\overset{h}{\mathop \int }}\,\text{}\varepsilon dz \right)\)

\(b\)

buoyancy

\({\Delta }b\)

buoyancy jump in the CBL entrainment layer

\(B\)

buoyancy flux

\({{C}_{1}}\)

constant of free-convection dissipation integral, \({{C}_{1}} = 1 - 2W_{*}^{{ - 3}}\mathop \smallint \limits_0^h \varepsilon dz\)

\({{c}_{2}}\)

constant of proportionality between average TKE in the CBL and the generation scale for free convection, \({{c}_{2}}=\frac{\int\limits_{0}^{h}{{{E}_{k}}dz}\text{}}{hW_{\text{*}}^{2}}\)

 

\({{C}_{{TZ}}} = \frac{{10}}{3}{{c}_{2}}\)

\({{C}_{3}},\) \({{C}_{4}}\)

proportionality constants of the turbulent TKE flux from the entrainment layer to the free atmosphere for free convection and sheared convection, respectively

\({{c}_{6}}\)

constant of proportionality between average TKE in the CBL and the mechanical generation scale \({{c}_{2}}=\frac{\int\limits_{0}^{h}{{{E}_{k}}dz-{{c}_{2}}W_{\text{*}}^{2}}\text{}}{hV_{\text{*}}^{2}}\)

\({{C}_{D}}\)

drag coefficient

\({{E}_{k}}\)

turbulence kinetic energy (TKE)

\({\Delta }f\)

LES model filter width

\(f\)

Coriolis parameter

\(F\)

turbulent TKE flux, \(F = \overline {{{u}_{i}}{{'}}{{u}_{i}}{{'}}w{{'}}} + \frac{1}{\rho }\overline {p{{'}}w{{'}}} \)

\(h\)

CBL height

\(l\)

half-depth of the entrainment layer in zero-order bulk CBL models

\(N\)

Brunt–Väisälä frequency

\(S\)

mechanical TKE generation, \(S = {\mathbf{\tau }} \cdot \frac{{\partial {\mathbf{u}}}}{{\partial z}}\)

\({{u}_{{\text{*}}}}\)

friction velocity, \(u_{{\text{*}}}^{2} = {{\tau }_{s}}{{\rho }^{{ - 1}}}\)

\({{U}_{m}}\)

modulus of wind speed in the CBL mixed sublayer

\({{U}_{g}}\)

modulus of geostrophic wind velocity

\({\Delta }U\)

wind velocity jump in the entrainment layer

\({{V}_{{\text{*}}}}\)

velocity scale determined by mechanical TKE generation, \(V_{{\text{*}}}^{3} = 2{{u}_{{\text{*}}}}{{U}_{m}}\)

\({{W}_{{\text{*}}}}\)

Deardorff convective velocity scale, \(W_{{\text{*}}}^{3} = {{B}_{s}}h\)

\({{W}_{e}}\)

combined velocity scale, \(W_{e}^{3} = W_{{\text{*}}}^{3} + {{\eta }^{3}}u_{{\text{*}}}^{3}\)

\({{W}_{{{\text{new}}}}}\)

combined velocity scale, \(W_{{{\text{new}}}}^{3} = {{\alpha }_{1}}W_{{\text{*}}}^{3} + {{\alpha }_{5}}V_{{\text{*}}}^{3}\)

\({{W}_{m}}\)

combined velocity scale, \(W_{m}^{3} = {{c}_{2}}W_{{\text{*}}}^{3} + {{c}_{6}}V_{{\text{*}}}^{3}\)

\(\delta \)

entrainment-layer thickness

\(\varepsilon \)

TKE dissipation rate

\(\zeta \)

dimensionless CBL height, \(\zeta = \frac{z}{h}\)

\({\mathbf{\tau }}\)

vertical momentum flux vector

\({\Phi }\)

universal dimensionless function of dimensionless CBL height

2 INTRODUCTION

State-of-the-art general circulation models of the atmosphere and ocean, suitable for weather forecasting as well as for climate modeling, still have an insufficient space resolution to resolve turbulent convection explicitly. Convection parameterizations are therefore used [1–5]. For this parameterizations, the height of the convective boundary layer is often used as a diagnostic variable. The correctness of convection modeling significantly influences the model-derived cloudiness and, consequently, radiative transport. On coarse-resolution grids used in climate models, large gradients of meteorological quantities in the entrainment zone of the convective boundary layer (CBL) are strongly smoothed, leading to errors in calculating the fluxes of these quantities and the dynamics of the CBL on the whole.

Observations and laboratory experiments show that the evolution of the CBL height as a whole is well described by integral (bulk) relationships [6–8], so refining the existing parametrizations of convection on their basis is reasonable. The integral CBL models are based on a set of equations whose unknown variables are the CBL height \(h\), jumps of meteorolgical quantities in the entrainment layer, and the entrainment coefficient. The entrainment coefficient is defined as the ratio of the minimum buoyancy flux in the entrainment layer to the surface buoyancy flux: \(A = \frac{{ - {{B}_{h}}}}{{{{B}_{s}}}}\).

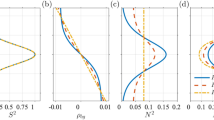
Two types of bulk CBL models—zero-order models [9] and first-order models [10]—have received wide recognition over the last decades. They differ in how the buoyancy and the velocity jump is represented at the CBL boundary in the corresponding idealized profiles. These profiles for buoyancy and horizontal velocity in zero-order models are shown in Fig. 1. In these models the gradients of buoyancy and velocity in the entrainment layer are approximated by jumps of these quantities at a height \(h\).

Fig. 1.
figure 1

Profiles of (a) buoyancy, (b) buoyancy flux, (c) horizontal wind velocity, and vertical momentum flux in the CBL developing in a stably stratified free atmosphere with a background wind. The thick solid line indicates schematic profiles used in the bulk CBL models, and the dashed line represents time-averaged profiles from the LES data of this paper (see Sections 4 and 5).

Full size image

The first-order models assume that the buoyancy and velocity vary linearly within the entrainment layer, with the entrainment-layer thickness \(\delta \) becoming a new independent variable and requiring an additional relationship needed for closure of the set of model equations. However, finding physically justified relations of \(\delta \) to other entrainment parameters is a complicated problem involving parametrizations of turbulent, wave, and thermodynamic processes in the entrainment layer. The physics of these processes reamains poorly understood (see, e.g., [11]).

Overall, the accuracy of the zero-order models is nearly the same as the accuracy of the first-order models for free and sheared convection under strong stable stratification of the free atmosphere [12, 13], worsening only when the free atmosphere is weakly stratified or when the geostrophic velocity gradient is large [14]. Models of both types also produce large errors in defining the CBL height \(h\) and the entrainment-layer velocity jump \(\Delta U\) over a very rough surface [15].

In the zero-order models proposed so far, there is no connection between the surface friction velocity \({{u}_{{\text{*}}}}\) and the entrainment-layer velocity jump \(\Delta U\), which, in particular, leads to a low accuracy of simulations over a rough surface. The first-order models account for this dependence, but parametrization uncertainties introduced by the new variable \(\delta \) and additional computational difficulties in solving the resulting set of equations mainly offset this advantage. The approach suggested in [16, 17] in which the relation of \({{u}_{{\text{*}}}}\) to \(\Delta U\) is implementd in a zero-order model is therefore a promising one (described in detail in Section 3.3).

In connection with the foregoing, the goal of this work is to test the integral model of sheared penetrative convection [16, 17] against data from numerical experiments with a large-eddy simulation (LES) model developed at the Institute of Numerical Mathematics (INM), Russian Academy of Sciences (RAS), in which the energy-dominant part of turbulent eddies is reproduced explicitly; this problem implies, among other things, the definition of the empirical constants of the integral model.

3 ANALYTICAL BULK CBL MODELS

3.1 Heat Flux Equation

The basis for the bulk CBL models is the heat flux equation integrated over the depth of the CBL in the approximation of horizontal homogeneity and under the assumption that the buoyancy flux varies linearly with height, while the Brunt–Väisälä frequency \(N\) above the CBL is constant with height. The resulting equation is

$$\frac{{d\left( {\frac{1}{2}{{N}^{2}}{{h}^{2}}} \right)}}{{dt}} = {{B}_{s}} - {{B}_{h}} = \left( {1 + A} \right){{B}_{s}},$$
((1))

where \(t\) is time, \(h\) is the CBL height, \({{B}_{s}}\) is the surface buoyancy flux (assumed for simplicity to be constant with time), and \({{B}_{h}}\) is the buoyancy flux at the CBL boundary. Because buoyancy within the CBL is constant, the buoyancy flux at the upper boundary is expressed through a buoyancy jump \(\Delta b\) by the formula \({{B}_{h}} = - \Delta b\frac{{dh}}{{dt}}\) [18], where \(\Delta b\frac{{dh}}{{dt}}\) is the CBL growth rate or the entrainment rate. The difference \({{B}_{s}} - {{B}_{h}}\) on the right-hand side of (1) is expressed through the entrainment coefficient

$$A = \frac{{ - {{B}_{h}}}}{{{{B}_{s}}}} = \frac{l}{{h - l}}.$$
((2))

If this coefficient is assumed constant and known from observations and the discussion is resticted to a free-convection regime, the CBL depth is fully described by Eq. (1). This approach was used in the early stage of development of the bulk CBL models (see [19, 18, 20]). With no entrainment \(A\left( t \right) = 0\), the solution to Eq. (1) reduces to Zubov’s classical formula \(h = \sqrt {\frac{{2{{B}_{s}}t}}{{{{N}^{2}}}}} \) [19]. When \(A = {\text{const}} > 0\), Eq. (1) becomes

$$\frac{{dh}}{{dt}} = \left( {1 + A} \right)\frac{{{{B}_{s}}}}{{{{N}^{2}}h}}.$$
((3))

The values of the entrainment coefficient measured in the atmosphere and in laboratory experiments lie in an approximate range of \(0 \leqslant A \leqslant 1\) (see Table 1 in [21]), i.e., in the nearly whole interval between the limiting regimes \({{B}_{h}} = 0\) [18] and \({{B}_{h}} = - {{B}_{s}}\) [22]. Naturally, with scatter like this, Eq. (3) involving the constant \(A\) is generally unsatisfactory, although the observed \(A\) values in atmospheric CBLs are usually close to \(0.2\) [6, 8, 21, 23]. It will be shown below that \(A \simeq 0.2\) results from the analysis of the turbulence kinetic energy balance for a well-developed CBL in free convection under the assumption that the CBL integral buoyancy generation of turbulent kinetic energy (TKE) is completely compensated by dissipation. Thus, simple bulk CBL models such as (3) reproduce the CBL height quite well in many cases.

Table 1.   Values of constants from LES data and estimates from the literature
Full size table

3.2 Integral TKE Balance Equation: Free-Convection Regime

In the general case, the entrainment coefficient is a time-variable quantity whose definition requires adding one more equation to the system that forms the bulk CBL model. For its derivation, the TKE balance equation is written at the interface of the mixed layer and of the entrainment zone \(z = h - l\) [24], or the TKE balance equation is integrated over height for a horizontally homogenous boundary layer [13, 16, 25]:

$$\mathop \smallint \limits_0^h \frac{{\partial {{E}_{k}}}}{{\partial t}}dz = \mathop \smallint \limits_0^h Bdz + \mathop \smallint \limits_0^h {\mathbf{\tau }} \cdot \frac{{\partial {\mathbf{u}}}}{{\partial z}}dz - \mathop \smallint \limits_0^h \frac{{\partial F}}{{\partial z}}dz - \mathop \smallint \limits_0^h \varepsilon dz,$$
((4))

where \(\varepsilon \) is the dissipation of turbulence kinetic energy, \(F = \overline {{{u}_{i}}{{'}}{{u}_{i}}{{'}}w{{'}}} + \frac{1}{\rho }\overline {p{{'}}w{{'}}} \) is the vertical turbulent transport of TKE and pressure correlation term, \(B\) is the buoyancy flux, \({\mathbf{\tau }} = \left( {\overline {u{{'}}w{{'}}} ,\overline {{v}{{'}}w{{'}}} ,\overline {w{{'}}w{{'}}} } \right)\) is the vertical momentum flux, and \({\mathbf{u}} = \left( {u,{v},w} \right)\) is the wind velocity vector. In free convection, the average shear generation of TKE is zero. Under this condition, S\( = {\mathbf{\tau }} \cdot \frac{{\partial {\mathbf{u}}}}{{\partial z}} = 0\), and, with the use of the Deardorff convective turbulence self-similarity theory [20], the TKE and dissipation profiles can be represented in terms of the universal functions of the dimensionless height \(\zeta = z/h\):

$${{E}_{k}} = W_{{\text{*}}}^{2}{{{\Phi }}_{{EK}}}\left( \zeta \right),\,\,\,\,\varepsilon = \left( {W_{{\text{*}}}^{3}/h} \right){{{\Phi }}_{{DK}}}\left( \zeta \right),$$
((5))

where \({{W}_{{\text{*}}}} = {{({{B}_{s}}h)}^{{1/3}}}\) is the Deardorff velocity scale characterizing a typical value of the vertical and horizontal velocity in the CBL self-organized thermals. The third term on the right-hand side of (4) is ususally considered small because the turbulent fluxes \(\int_0^h {\frac{{\partial F}}{{\partial z}}dz} = \left. {\left( {\overline {{{u}_{i}}{{'}}{{u}_{i}}{{'}}w{{'}}} + \frac{1}{\rho }\overline {p{{'}}w{{'}}} } \right)} \right|_{0}^{h}\) at the upper and lower CBL boundary are opposite in sign but close in magnitude. Zilitinkevich [16, 17] took into account a possible emission into the free atmosphere of gravity waves excited by thermal overshoots into a stably stratified entrainment layer and defined \({{F}_{{z = h}}}\) as the vertical energy flux induced by these waves. Then, from linear theory [26],

$${{F}_{{z = h}}} \propto {{\lambda }^{2}}{\Lambda }{{N}^{3}},$$
((6))

where \(\lambda \) is the wave length and \({\Lambda }\) is the wave amplitude. Assuming, after [27], that \({\Lambda }\sim \lambda \sim \frac{A}{{1 + A}}h\), we obtain

$$\mathop \smallint \limits_0^h \frac{{\partial F}}{{\partial z}}dz = {{F}_{h}} - {{F}_{0}} = {{F}_{h}} = {{C}_{3}}{{N}^{3}}{{h}^{3}}{{\left( {\frac{A}{{1 + A}}} \right)}^{3}}.$$
((7))

Given the linearity of the buoyancy flux profile (see Fig. 1), \(\int_0^h {Bdz} = {{B}_{s}}h\left( {\frac{{1 - A}}{2}} \right)\), we have the integral TKE balance equation for free convection

$${{C}_{{TZ}}}W_{*}^{{ - 1}}\frac{{dh}}{{dt}} = {{C}_{1}} - A - {{C}_{3}}\frac{{{{N}^{3}}}}{{B_{s}^{{3/2}}}}{{h}^{3}}{{\left( {\frac{A}{{1 + A}}} \right)}^{3}},$$
((8))

where \({{C}_{{TZ}}} = \frac{{10}}{3}\int_0^1 {{{\Phi }_{{EK}}}\left( \zeta \right)d\zeta } = \frac{{\frac{{10}}{3}}}{{{{c}_{2}}}}\) and C1 = 1 – 2α1 = \(1-2\int_{0}^{1}{{{\text{ }\!\!\Phi\!\!\text{ }}_{DK}}\left( \zeta \right)d\zeta }\text{}\) are the dimensionless energy constants. If (4) is simplified by assuming that the amount of TKE in the CBL does not vary \(\int_0^h {\frac{{\partial {{E}_{k}}}}{{\partial t}}dz} = 0\) and \(F\left( h \right) = 0\), that is, the total TKE generation by buoyancy forces and total dissipation balance each other, then \(A = {{C}_{1}} = {\text{const}}\). From the estimates in the literature (see Table 1) and from our LES experiments (Section 5), \(0.15 \leqslant {{C}_{1}} \leqslant 0.25\), which is matched by values \(0.15 \leqslant A \leqslant 0.25\), which is consistent with the entrainment estimates mentioned above.

3.3 Integral TKE Balance Equation: Sheared Convection

In presence of geostrophic forcing and thus non zero average wind velocity, \(\int_0^h {Sdz} \) is significant and hypothetical relations (5) become unsatisfactory. Over the last twenty years, various parametrizations have been proposed for the terms of the integral TKE balance equation for sheared convection. Some authors [9, 28, 29] neglect the left-hand side of (4), arguing that the amount of TKE in a well-developed CBL changes little. For the verification of such integral models, the results of LES experiments of significant duration are used, with the first 3–4 h of simulated time being excluded from the analysis. Parametrizations accounting for a TKE tendency [11, 15, 25, 30, 31] usually use, as a velocity scale, the quantity \({{W}_{e}}\) defined as \(W_{e}^{3} = W_{{\text{*}}}^{3} + {{\eta }^{3}}u_{{\text{*}}}^{3}\), where \({{u}_{{\text{*}}}} = \sqrt {\frac{{{{\tau }_{s}}}}{\rho }} \) is the friction velocity in the surface layer and \({{\eta }^{3}} = \frac{{\int_0^h {Sdz} - \mathop \smallint \nolimits_0^h {{\varepsilon }_{s}}dz}}{{u_{{\text{*}}}^{3}}}\) is the fraction of shear generation uncompensated by local dissipation. Using an additional assumption that the time derivative of \({{W}_{e}}\) behaves in the same way as the derivative of \({{W}_{{\text{*}}}}\) in the case of free convection, we obtain a relation

$$\mathop \smallint \limits_0^h \frac{{\partial {{E}_{k}}}}{{\partial t}}dz = {{C}_{T}}\frac{{W_{e}^{2}}}{h}\frac{{dh}}{{dt}}$$
((9))

that does not provide the self-similar profile \({{E}_{k}} = W_{e}^{2}{{{\Phi }}_{E}}\left( \zeta \right)\). Zilitinkevich [16, 17] suggested that the vertical TKE profile for the case of sheared convection can be represented as a sum of the terms describing the contribution of turbulence of mechanical (sheared) and convective origin

$${{E}_{k}} = W_{{\text{*}}}^{2}{{{\Phi }}_{{EK}}}\left( \zeta \right) + V_{{\text{*}}}^{2}{{{\Phi }}_{{SK}}}\left( \zeta \right),$$
((10))

where \({{V}_{{\text{*}}}} = {{\left( {2u_{{\text{*}}}^{2}{{U}_{m}}} \right)}^{{1{\text{/}}3}}}\) is the sheared velocity scale and \(~{{U}_{m}}\) is the modulus of the average velocity within the CBL. To calculate the left-hand side of (4), it was assumed in [16, 17] that \(\frac{{d{{V}_{{\text{*}}}}}}{{dt}} = 0\), which, however, disagrees with the LES data.

The existing bulk models of the sheared CBL can also be divided into two groups according to the way of approximating the dissipation integral over the CBL depth, i.e., the last term on the right-hand side of (4). In one group, the assumption is made that each component of the TKE balance in the CBL—buoyancy, shear, and turbulent transport—is assigned its own fraction of dissipation and the integral TKE dissipation is represented as a linear combination of the corresponding integrals. Thus, according to [16, 17],

$$\mathop \smallint \limits_0^h \varepsilon dz = {{\alpha }_{1}}W_{{\text{*}}}^{3} + {{\alpha }_{5}}V_{{\text{*}}}^{3},$$
((11))

where \({{\alpha }_{1}} = \frac{{1 - {{C}_{1}}}}{2}\) is the constant known from the free-convection experiments and \({{\alpha }_{5}}\) is an additional constant. In the other group of models, it is postulated that the integral dissipation in the CBL is proportional to integral production, in combination with a well-mixed CBL approximation. This postulate reduces the integral TKE equation to a balance between buoyancy and wind shear at the entrainment boundary. Using \({{W}_{{\text{*}}}}\) and \({{u}_{{\text{*}}}}\) as alternative velocity scales [32], we can write the following relation:

$$\mathop \smallint \limits_0^h Bdz + \mathop \smallint \limits_0^h Sdz - \mathop \smallint \limits_0^h \varepsilon dz = {{C}_{1}}\left( {W_{{\text{*}}}^{3} + {{A}_{1}}u_{{\text{*}}}^{3}} \right),$$
((12))

where \({{A}_{1}} = {{C}_{s}}/{{C}_{1}}\), \({{C}_{s}}\) being the fraction of shear TKE generation uncompensated by dissipation. Some authors assume here that \({{A}_{1}} = {{\eta }^{3}}\). The right-hand side of (12) can then be written as

$$\mathop \smallint \limits_0^h Bdz + \mathop \smallint \limits_0^h Sdz - \mathop \smallint \limits_0^h \varepsilon dz = {{C}_{1}}W_{e}^{3}.$$
((13))

We now proceed to a calculation of the second term on the right-hand side of (4). Dividing the CBL into three sublayers—surface, mixed, and entrainment—we obtain

$$\mathop \smallint \limits_0^h Sdz = \mathop \smallint \limits_0^{{{h}_{s}}} Sdz + \mathop \smallint \limits_{{{h}_{s}}}^{h - l} Sdz + \mathop \smallint \limits_{h - l}^h Sdz.$$
((14))

The first term on the right-hand side is proportional to the cube of the friction velocity \(\int_0^{{{h}_{s}}} {{\mathbf{\tau }} \cdot \frac{{\partial {\mathbf{u}}}}{{\partial z}}dz \propto u_{{\text{*}}}^{3}} \) [24, 33]. The second term is small or zero because there is hardly any velocity gradient in the mixed layer. In zero-order bulk CBL models, the expression for the momentum flux \(\overline {u{{'}}w{{'}}} = {\Delta }U\frac{{dh}}{{dt}}\) is used to determine shear generation in the entrainment layer and the velocity gradient is estimated as \(\frac{{\partial U}}{{\partial z}} \simeq \frac{{{\Delta }U}}{l}(l = \frac{A}{{1 + A}}h\), although some models use the CBL height as a length scale [24]). When the scale \(l = \frac{A}{{1 + A}}h\) is used, the integral of shear generation is

$$\mathop \smallint \limits_0^h {\mathbf{\tau }} \cdot \frac{{\partial {\mathbf{u}}}}{{\partial z}}dz \simeq {{C}_{S}}u_{{\text{*}}}^{3} + {{C}_{M}}\frac{{{{{(\Delta U)}}^{2}}}}{l}\frac{{dh}}{{dt}},$$
((15))

where, from the LES and laboratory data, \(\eta = \sqrt[3]{{{{C}_{s}}/{{C}_{1}}}} = 2\) and \({{C}_{M}} = 0.7\). Formula (15) has a significant drawback, because it leads to the expression \(A\sim \frac{{{{C}_{1}}}}{{1 + {{C}_{{TZ}}}\Delta b - {{C}_{M}}\Delta U}}\) (see a detailed derivation in [34]) and, with the adopted values of \({{C}_{{TZ}}}\) and \({{C}_{M}}\) and jumps \(\Delta b,\Delta U\) typical of well-developed CBLs, strongly overestimates the entrainment coefficient or even changes its sign. The first-order bulk CBL models are less subject to this effect because of the interpolation of the momentum flux profile in the entrainment layer and the appearance in (15) of the term \(\sim u_{{\text{*}}}^{2}\Delta U\), where \(\Delta U = {{U}_{g}} - {{U}_{m}}\). However, this term can also be introduced in a zero order model framework; in [16], for example, the same term results from the approximation \(\int_0^h {Sdz} \simeq 2u_{{\text{*}}}^{2}{{U}_{m}}\). The validity of this approximation will also be verified against LES data to be discussed below.

In [16] the integral TKE balance equation involves the TKE flux \({{F}_{h}}\) transported from the entrainment layer by upward propagating gravity waves. In this case, the wavelength scale is taken to be \({\Lambda }\sim h\) [27], as opposed to a free-convection regime, where \({\Lambda }\) is assumed to be proportional to the entrainment-layer thickness, \({\Lambda }\sim \frac{A}{{1 + A}}h\). Hence,

$${{F}_{h}} = {{C}_{4}}{{\lambda }^{2}}{\Lambda }{{N}^{3}} = {{C}_{4}}{{h}^{3}}{{N}^{3}}{{\left( {\frac{A}{{1 + A}}} \right)}^{2}}.$$
((16))

As a result for sheared convection, integral equation (4), according to [16], takes the form

$${{C}_{{TZ}}}W_{{\text{*}}}^{{ - 1}}\frac{{dh}}{{dt}}\, = \,{{C}_{1}}\, - \,A\, - \,{{C}_{4}}\frac{{{{N}^{3}}}}{{B_{s}^{{{\text{3}}{\text{/}}{\text{2}}}}}}{{\left( {\frac{A}{{1 + A}}} \right)}^{2}}\, + \,{{A}_{5}}{{\left( {\frac{{{{V}_{{\text{*}}}}}}{{{{W}_{{\text{*}}}}}}} \right)}^{3}},$$
((17))

where the constant \({{A}_{5}} = \frac{{1 - {{\alpha }_{5}}}}{2}\) has been introduced.

Optimal CBL Model

In this paper, a bulk CBL model for sheared penetrative convection is derived in which minimum complexity is combined with a realistic inclusion of all important mechanisms.

The integral heat balance (Section 3.1) is given by the conventional equation

$$\frac{d}{{dt}}\left[ {\frac{1}{2}{{N}^{2}}{{h}^{2}} - h{{B}_{s}}A{{{\left( {\frac{{dh}}{{dt}}} \right)}}^{{ - 1}}}} \right] = {{B}_{s}},$$
((18))

which is equivalent to (1), (2).

The integral TKE budget (Section 3.3), according to [16, 17], with a correction for refined formula (32) in Section 5, has the form

$$\begin{gathered} {{C}_{{TZ}}}W_{{\text{*}}}^{{ - 1}}\frac{{dh}}{{dt}} + {{C}_{6}}W_{{\text{*}}}^{{ - 3}}\frac{{d\left( {V_{{\text{*}}}^{2}h} \right)}}{{dt}} \\ = {{C}_{1}} - A - {{C}_{4}}\frac{{{{N}^{3}}}}{{B_{s}^{{3/2}}}}{{\left( {\frac{A}{{1 + A}}} \right)}^{2}} + {{A}_{5}}{{\left( {\frac{{{{V}_{{\text{*}}}}}}{{{{W}_{{\text{*}}}}}}} \right)}^{3}}, \\ \end{gathered} $$
((19))

where \({{W}_{{\text{*}}}} = {{\left( {{{B}_{s}}h} \right)}^{{1/3}}}\) is the Deardorff convective velocity scale [20] and \({{V}_{{\text{*}}}} = {{\left( {2u_{{\text{*}}}^{2}{{U}_{m}}} \right)}^{{1/3}}}\) is the velocity scale characterizing the mechanical (shear) generation of turbulence [16, 17]. The integral momentum budget is represented by two equations obtained by term-integrating the motion equations

$$h\frac{{d{{{v}}_{m}}}}{{dt}} - {\Delta }{v}\frac{{dh}}{{dt}} = - {{C}_{D}}{{u}_{m}}\sqrt {u_{m}^{2} + {v}_{m}^{2}} + fh\left( {{{u}_{m}} - {{u}_{g}}} \right),$$
((20))
$$h\frac{{d{{u}_{m}}}}{{dt}} - {\Delta }u\frac{{dh}}{{dt}} = - {{C}_{D}}{{{v}}_{m}}\sqrt {u_{m}^{2} + {v}_{m}^{2}} - fh\left( {{{{v}}_{m}} - {{{v}}_{g}}} \right),$$
((21))

where \({{u}_{m}}\) and \({{{v}}_{m}}\) are the mean values of the wind velocity components in the CBL, \(\Delta u\) and \(\Delta {v}\) are the velocity jumps at the upper CBL boundary, \(f\) is the Coriolis parameter, and \({{u}_{g}}\) and \({{{v}}_{g}}\) are the geostrophic wind components. In deriving Eqs. (20) and (21), the profiles of the vertical momentum flux components \({{\tau }_{x}}\) and \({{\tau }_{y}}\) are assumed linear, and surface values of these components are determined from the aerodynamic formulas

$${{\tau }_{{xs}}} = {{C}_{D}}{{u}_{m}}\sqrt {u_{m}^{2} + {v}_{m}^{2}} ,$$
((22))
$${{\tau }_{{ys}}} = {{C}_{D}}{{{v}}_{m}}\sqrt {u_{m}^{2} + {v}_{m}^{2}} ,$$
((23))

where \({{C}_{D}}\) is the drag coefficient. This model is verified and calibrated against the LES data.

4 SETUP OF THE LES MODEL EXPERIMENTS

A detailed description of the LES model developed at the Institute of Numerical Mathematics, Russian Academy of Sciences (hereafter LES INM RAS), which was used in this study, and the results of its comparison with other models for different flow types can be found in [35–37]. The system of hydrodynamic equations in the Boussinesq approximation is solved numerically by a finite-difference method; the fourth-order-accurate momentum- and energy-conservative scheme [38], on a staggered Aracawa C grid, is used for spatial approximation; and the second-order explicite Adams–Bashforth predictor–corrector scheme is used for time approximation. The model package code was implemented for distributed-memory multiprocessor computers using Message Passing Interface (MPI).

To estimate the applicability of various approximations of the integral TKE balance terms and other suggestions from [16] resulting in the set of equations of the bulk CBL model described above, a series of numerical experiments was performed in which the CBL was driven by a time- and horizontally constant positive surface heat flux \({{H}_{s}} = 0.35{\text{ K}}\,{\text{m}}\,{{{\text{s}}}^{{ - 1}}}\), which corresponds to the buoyancy flux \({{B}_{s}} = 0.02{\text{ m }}{{{\text{s}}}^{{ - 1}}}\). The heat flux at the top of the domain was set equal to zero. The lower and upper boundary conditions for velocity were specified in terms of the momentum flux calculated from the logarithmic profile between the boundary with surface roughness \({{z}_{{0{\text{BOT}}}}} = 0.1\) and the closest model level with \({{z}_{{0{\text{TOP}}}}} = {{10}^{{ - 9}}}\). Horizontally periodic boundary conditions were used in all the experiments. In the layer \({{z}_{{{\text{TOP}}}}} - 30\Delta z < z < {{z}_{{{\text{TOP}}}}}\), Rayleigh damping with a relaxation time \({{t}_{d}} = 1.3 \times 2 \times \Delta t\), where \(\Delta t\) is the time step and \(\Delta z\) is the vertical model resolution, was applied to the solution to eliminate the reflection, from the top boundary, of gravity waves propagating upward from the entrainment layer. The number of grid points was \({{N}_{x}} = 512,\,{{N}_{y}} = 512,\,{\text{and}}\,{{N}_{z}} = 394\) in the coordinates \(x,y,z\), respectively.

For a correct simulation of the entrainment-layer processes and independence of the first- and second-order statistics on the model resolution, the condition \(\frac{h}{{{{C}_{s}}\Delta f}} > 56\), where \({{C}_{s}}\) is the Smagorinsky constant and \(\Delta f\) is a filter width, must be satisfied [39]. For typical \(A = 0.2\) and \({{C}_{S}} = 1.2\) and the estimate of the entrainment-layer depth \(\delta = \frac{{Ah}}{{\left( {1 + A} \right)}}\), this condition corresponds to \(11.2{\Delta }f = \delta \). A choice of the domain’s minimal sizes \(\frac{{\left( {{{L}_{x}},{{L}_{y}},{{L}_{z}}} \right)}}{{{{h}_{0}}}} = \left( {5,5,2} \right)\), where \({{h}_{0}}\) is the initial height of the CBL, is considered sufficient to eliminate the influence of periodic boundary conditions on the CBL characteristics. The dynamic closure for subgrid-scale stresses in the LES INM RAS model, which assumes the isotropy of an implicit filter, imposed the constraint on the grid step \(\frac{{\Delta x}}{{\Delta y}} = \frac{{\Delta y}}{{\Delta z}} \simeq 1\), where \(\Delta x,\Delta y,\Delta z\) are the grid steps in the coordinates \(x,y,z\). The spatial resolution was taken to be \(\Delta x = \Delta y = \Delta z = 5{\text{ m}}.\) The sizes of the computational domain were \(\left( {{{L}_{x}},{{L}_{y}},{{L}_{z}}} \right) = \)\(\left( {2.56, 2.56, 1.92{\text{ km}}} \right)\), and the initial CBL height was \({{h}_{0}} = 250{\text{ m}}\).

For the experimental parameters above, we obtain \(\frac{h}{{{{C}_{s}}\Delta f}} \simeq 30\). Unlike the LES model used in [39], the LES INM RAS model calculates the Smagorinsky coefficient dynamically, so the constraint imposed on the vertical resolution can be somewhat relaxed. Recall that the goal of the LES experiment was to verify hypothetical relationships (10), (11), (5), (7), and (16) and to determine appropriate empirical constants \({{\alpha }_{1}},{{C}_{{TZ}}},\,{\text{and}}\,{{C}_{3}}\) for the case of free convection and \({{C}_{4}},{{A}_{5}}\) for sheared convection:

$${{\alpha }_{1}}=\frac{\int\limits_{0}^{h}{\varepsilon dz}\text{}}{W_{\text{*}}^{3}}=\frac{\left( 1-{{C}_{1}} \right)}{2},$$
((24))
$${{c}_{2}}=\frac{\int\limits_{0}^{h}{{{E}_{k}}dz}\text{}}{hW_{\text{*}}^{2}}=\frac{3}{10}{{C}_{TZ}},$$
((25))
$${{C}_{3}} = \frac{{{{F}_{h}}}}{{{{N}^{3}}{{h}^{3}}{{{\left( {\frac{A}{{1 + A}}} \right)}}^{3}}}},$$
((26))
$${{C}_{4}} = \frac{{{{F}_{h}}}}{{{{N}^{3}}{{h}^{3}}{{{\left( {\frac{A}{{1 + A}}} \right)}}^{2}}}},$$
((27))
$${{\alpha }_{5}}=\frac{\int\limits_{0}^{h}{\varepsilon dz-{{\alpha }_{1}}{{W}^{3}}}\text{}}{V_{\text{*}}^{3}}=\frac{\left( 1-{{A}_{5}} \right)}{2}.$$
((28))

These constants were determined as follows. A series of experiments was performed for free convection under free-atmosphere stratification characterized by different gradients of potential temperature above the CBL: \({{\gamma }_{0}} = 0.01,\, 0.02,\,{\text{and}}\,0.03\,{\text{K }}{{{\text{m}}}^{{ - 1}}}\) (hereafter referred to as CBL1, CBL2, and CBL3). Two experiments were conducted for sheared convection, in which the surface roughness \({{z}_{0}}\) and geostrophic velocity \({{U}_{g}}\)were varied: \({{z}_{0}} = 0.001 \,{\text{m}}\) in CBLu5, and \({{z}_{0}} = 0.1 \,{\text{m}}\) in CBLu7. The free-atmosphere stratification was taken to be same as in CBL3, and the values of \({{C}_{1}}\,{\text{and}}\,{{C}_{{TZ}}}\) obtained earlier from the experiments with free convection were used to calculate the constants \({{C}_{4}}\) and \({{A}_{5}}\) from the CBLu5 and CBLu7 data.

Defining the CBL height plays a key role in the analysis of the LES results. In our study the CBL height was defined as the height of the minimum buoyancy flux calculated by horizontally averaging within the LES model domain.

5 RESULTS

The main results of numerical experiments under windless conditions are illustrated in Figs. 1 and 2. Time series of \({{C}_{1}},{{C}_{{TZ}}},\) and \({{C}_{3}}\) calculated from (24), (25), and (26) and their values from [16] are shown in Fig. 2. The variance of the time series relative to the means is significant, but no distinct trends are observed, which supports the similarity hypotheses and gives grounds to take \({{C}_{1}},{{C}_{{TZ}}},{{C}_{3}}\) as constants. The LES values of \({{C}_{1}},{{C}_{{TZ}}},{{C}_{3}}\) are very different from the previous estimates: \({{C}_{1}}\), on average from the three experiments, is higher and \({{C}_{{TZ}}}\) is lower than the values proposed in [16, 17]. The estimate of \({{C}_{3}}\) from CBL1, CBL2, and CBL3 is an order of magnitude less than that in [16], but agrees with the results of other LES experiments [14]. The constants from CBL1, CBL2, and CBL3 and their values from the previous works are listed in Table 1.

Fig. 2.
figure 2

Time variations in the CBL height from the LES modeling of free convection (CBL1, CBL2, and CBL3 are shown by markers). The lines show solutions to the integral model equations [16] with two different sets of the constants \({{C}_{1}},{{C}_{{TZ}}},\,{\text{and}}\,{{C}_{3}}\): the subscript old denotes the set of constants from the original study [16], and the subscript new denotes estimates of the constants from the LES data by formulas (24), (25), and (26) (see Table 1 for more detail).

Full size image

The results of a calculation of the CBL height from the LES model and from the integral model of [16] are shown in Fig. 1. As can be seen, the CBL height grows with time \(t\) proportionally to \(\sqrt t \) in all three experiments, with fluctuations of \(h\) at a period of \(\sim h/{{W}_{{\text{*}}}}\sim {{10}^{2}}\) s.

Note that the following estimate of the total TKE is valid for shear-free convection:

$$\underset{0}{\overset{h}{\mathop \int }}\,\text{}{{E}_{k}}dz={{C}_{TZ}}hW_{\text{*}}^{2}.$$
((29))

It is therefore logical to expect that the difference \({{h}^{{ - 1}}}\int_0^h {{{E}_{k}}dz - {{C}_{{TZ}}}W_{{\text{*}}}^{2}} \) for sheared convection will be proportional to \(V_{{\text{*}}}^{2}\). As is shown in Fig. 3, the ratio of these quantities as a function of time from the CBLu7 data is indeed nearly constant:

$$\frac{{{{h}^{{ - 1}}}\int\limits_0^h {{{E}_{k}}dz} - {{C}_{{TZ}}}W_{{\text{*}}}^{2}}}{{V_{{\text{*}}}^{2}}} = {{C}_{6}} \approx 0.4,$$
((30))

where \({{C}_{6}}\) is the proportionality constant. Figure 3 presents the time evolution of the average TKE \({{h}^{{ - 1}}}\int_0^h {{{E}_{k}}dz} \) in the sheared CBL as the CBL grows; the Deardorff scale \(W_{{\text{*}}}^{2}\), characterizing the TKE of convective origin, and Zilitinkevich’s scale [16, 17] \({{V}_{{\text{*}}}} = {{\left( {2u_{{\text{*}}}^{2}{{U}_{m}}} \right)}^{{1/3}}}\), characterizing the shear-generated TKE, as well as their linear combination \({{W}_{ + }} = {{C}_{{TZ}}}W_{{\text{*}}}^{2} + {{C}_{6}}V_{{\text{*}}}^{2}\), are used to normalize TKE. As is evident from the figure, the first and second relations change significantly, while normalizing by a generalized scale makes the average TKE in the CBL almost constant. Hence a useful relationship follows

$$\underset{0}{\overset{h}{\mathop \int }}\,\text{}{{E}_{k}}dz=h\left( {{C}_{TZ}}W_{\text{*}}^{2}+{{C}_{6}}V_{\text{*}}^{2} \right).$$
((31))
Fig. 3.
figure 3

Time variations in \({{C}_{1}},{{C}_{{TZ}}},\,{\text{and}}\,{{C}_{3}}\) from CBL1, CBL2, and CBL3.

Full size image

According to (31), the left-hand side of the integral TKE balance equation is written as

$$\frac{d}{dt}\left( \underset{0}{\overset{h}{\mathop \int }}\,\text{}{{E}_{k}}dz \right)={{C}_{TZ}}\frac{d}{dt}\left( hW_{\text{*}}^{2} \right)+{{C}_{6}}\frac{d}{dt}\left( hV_{\text{*}}^{2} \right).$$
((32))

The results above are related to the fact that \({{W}_{{\text{*}}}}\) and \({{V}_{{\text{*}}}}\) vary with time in opposite direction. The Deardorff scale \({{W}_{{\text{*}}}}\) grows with \(h\), while \({{V}_{{\text{*}}}}\) drops because friction in the surface layer and the average velocity in the CBL decrease (not shown). A significant decrease in the shear-produced TKE scale \({{V}_{{\text{*}}}}\) with time violates the assumption from [16] of the invariability of this quantity \(\frac{{dV_{{\text{*}}}^{2}}}{{dt}} = 0\). Thus, the left-hand side of the integral TKE energy balance equation must take the form

$$\begin{gathered} \frac{d}{dt}\left( \underset{0}{\overset{h}{\mathop \int }}\, {{E}_{k}}dz \right)=\frac{d}{dt}h\left( {{c}_{2}}W_{{*}}^{2}+{{C}_{6}}V_{{*}}^{2} \right) \\ ={{C}_{TZ}}W_{{*}}^{2}\frac{dh}{dt}+{{C}_{6}}\frac{d\left( hV_{{*}}^{2} \right)}{dt}, \\ \end{gathered}$$
((33))

where on the right is the term \({{C}_{6}}\frac{{d\left( {hV_{{\text{*}}}^{2}} \right)}}{{dt}}\) missing in original equation (17). Expressing TKE in terms of the scale \({{W}_{e}}\) and taking the corresponding proportionality constant \({{C}_{T}}\) out of the sign of the time derivative, as in (10), do not reflect the universal property of the integral TKE balance, because the corresponding curve in Fig. 3 falls with time. This is most likely a consequence of the fact that the term with \(\Delta U\) is omitted from the estimate of shear generation (15) to simplify the scale \({{W}_{e}}\) in (13) and the resulting velocity scale \({{W}_{e}}\) grows faster than the average TKE in the CBL.

Consider now to what extent the scales above are suitable for an estimate of the TKE dissipation integral. For this, we examine Fig. 4, in which the curves of the ratio of the dissipation integral to the various scales are drawn in the same way as in Fig. 3, described above, with \(W_{{{\text{new}}}}^{'}{{{\text{3}}}} = W_{{\text{*}}}^{3} + {{A}_{5}}V_{{\text{*}}}^{3}\). It can be seen that only the ratio \(\left( {\int_0^h {\varepsilon dz} } \right)/\left( {\overline {{{c}_{1}}{\text{''}}} W_{e}^{3}} \right)\) has a significant trend, which can also be explained by a lack of the term with \(\Delta U\) in the definition of \({{W}_{e}}\).

Fig. 4.
figure 4

Time variations in the ratio of the TKE integral in the CBL to different integral scales from the CBLu7 data.

Full size image

Estimates of the constants \({{\alpha }_{5}},{{C}_{6}},{{C}_{4}}\), and of \(A\) from CBLu7 were found to be \(0.12,\;0.22,\,{\text{and}}\,0.005\), respectively. Since \(\frac{{{{\alpha }_{1}}}}{{{{\alpha }_{5}}}} \ne \frac{{{{c}_{2}}}}{{{{C}_{6}}}}\), Eq. (17) cannot be rewritten in the form of (8) by substituting \({{W}_{{{\text{new}}}}}\) for \({{W}_{{\text{*}}}}\). As can be seen from the value of \({{C}_{4}}\), which denotes the energy flux of gravity waves from the CBL to the overlying inversion, this flux for typical \(A = 0.2\), \({{B}_{s}} = {{10}^{{ - 2}}}\), and \(N = {{10}^{{ - 2}}}\)(the third term on the right-hand side of (17)) is \({{C}_{4}}\frac{{{{N}^{3}}}}{{B_{s}^{{3/2}}}}{{\left( {\frac{A}{{1 + A}}} \right)}^{2}} \simeq {{10}^{{ - 9}}}\); i.e., it is far less than the other components of the TKE balance in the convective layer (for example, \(A\)), so it can be neglected.

Fig. 5.
figure 5

Time variations in the ratio of the dissipation integral in the CBL to different integral scales from the CBLu7 data.

Full size image

6 CONCLUSIONS

Several numerical experiments have been run to simulate free convection and sheared convection above a homogeneous surface with the INM RAS LES model. The calculation data confirm that the TKE profiles and TKE dissipation profiles are well scaled by the CBL height and the Deardorff scale; the corresponding dimensionless constants have proved to be close to the previous estimates from laboratory experiments. The analysis of the experiments with sheared convection has shown that scaling the TKE integral and the dissipation integral over the CBL height by the linear combination of and is a justifiable assumption and makes it possible to develop bulk CBL models in a zero-order approximation—an instantaneous temperature and velocity jump at the top boundary. It is also shown that the TKE flux transported from the entrainment layer by gravity waves is small and can be neglected in the integral TKE balance equation.