Introduction

In recent years, freight markets have experienced increased development in terms of spot and derivatives contracts, and academics and practitioners are focusing on the valuation and hedging of the price of the different freight routes.

Many previous articles have analyzed the characteristics of freight rate dynamics. For example, in Adland et al (2006), Franses and Veenstra (1997), or Huang et al (2013) or Tvedt (2003), we can find unit root analysis. Glen et al (1981) and Hale and Vanags (1989) study the relationship between spot and time charter rates. Alizadeh and Nomikos (2004) investigate the dynamics relationship between oil prices and freight rates. Huang et al (2013) study tanker chartering decision problems faced by refinery companies, whereas Chen and Wang (2004) study the correlation between return and volatility. Adland (2000), Adland and Cullinane (2006) and Adland and Koekebakker (2007) perform non-parametric studies. Adland and Strandenes (2006) conclude that these markets are efficient markets, while Adland and Cullinane (2005) conclude that the risk premium in these markets is variable instead of constant.

There are also many articles discussing the difference in freight rates as a function of freight characteristics, such as the size of the ship (Cullinane and Khanna, 1999), the subsidies received (Dikos, 2004), and whether the ship is new or second hand (Dikos and Marcus, 2003), among other characteristics.

Moreover, there are studies proposing stochastic factor modeling to characterize freight rate dynamics. Tvedt (2003) proposes a simple Ostern-Uhlenbeck model for freight rates, and Adland and Strandenes (2007) develop a stochastic model of supply and demand with which they obtain the spot price probability function. Accordingly, Adland and Koekebakker (2004) and Rygaard (2009) have proposed a more sophisticated factor model to characterize time charter prices and use it to value the options included in this type of contracts.

Alizadeh and Kavussanos (2001, 2002) study the seasonal behavior of freight rates, but they do not propose any model to characterize price dynamics. These authors found that seasonal behavior of freight rates is an important factor in the formation of transportation policy, affecting shipowners’ cash flow and charterers’ costs.

As in any other market, freight rate markets are characterized by the interaction of supply and demand for tanker shipping services. The demand for freight services is a derived demand, depending on the economics of the hydrocarbon’s markets and trade, world-economic activity and the related macroeconomic variables of major economies, such as imports and consumption of energy commodities (see, among others, Stopford, 1997). As stated in Garcia et al (2012), many hydrocarbon’s markets present stochastic seasonality, which could be transmitted into shipping freight rates. Moreover, as noted by Alizadeh and Nomikos (2004), among other authors, there is a close relationship between hydrocarbons’ prices and freight rates. Therefore, as hydrocarbon’s prices are seasonal, presenting also a stochastic seasonality, freight rates should behave in a similar way. Accordingly, the aim of the present paper is to demonstrate that freight rates present seasonality and that seasonality is stochastic and not deterministic.

In line with previous research, we propose a factor model to characterize the stochastic behavior of freight rates. The most widely used models for the stochastic behavior of commodity prices are the multi-factor models by Schwartz (1997), Schwartz and Smith (2000), Cortazar and Schwartz (2003) and Cortazar and Naranjo (2006). These models use the assumption that the spot price is the sum of short- and long-term components. Long-term factors account for the long-term dynamics of commodity prices, assumed to follow a random walk, whereas short-term factors account for the mean reverting components in commodity prices. As in Sorensen (2002), Garcia et al (2012) and Garcia et al (2013), among others, it is also possible to incorporate seasonal factors, which are trigonometric components generated by stochastic processes.

Consequently, the factor model proposed here is the four-factors model of Garcia et al (2012). This model assumes that the log-spot price is the sum of three stochastic factors: a long-term factor, a short-term factor and a seasonal factor. We apply the Kalman filter methodology to estimate the parameters of the models using TCE (Time Charter Equivalent) and the WS (World Scale) prices listed by Baltic. It is also possible to assume, like Sorensen (2002), that seasonal factors are deterministic by simply imposing that the variance of the stochastic seasonal factor is zero.

Finally, using the estimated parameters, we examine the models’ ability to fit the term structure of futures prices and volatilities. Interestingly, we find that models allowing for stochastic seasonality outperform standard models with deterministic seasonality.

This article is organized as follows. The next section presents data and preliminary findings related to evidence of stochastic seasonality in freight rates. The model allowing for stochastic seasonality is developed in the section after that. The following section presents the empirical estimation results. Finally, the last section concludes with a summary and a discussion.

Data and Preliminary Findings

Data

The data set used in this article consists of weekly observations of spot and forward TCE and WS prices for five routes defined by Baltic:Footnote 1 TC2, TC14, TC6, TD5 and TD16 during the period 1 January 2009–25 February 2014. In Table 1, we find details of these routes such as loading and unloading ports and type of ship.

Table 1 Route details
Full size table

It is well-known that the World Scale, WS, is the payment, in $/TM, of freight rate for a given route and oil tanker's cargo. This payment includes all associated costs (except insurance costs) such as bunker cost, crew cost and port cost. The Time Charter Equivalent, TCE, is instead the daily revenue performance of a vessel. TCE is calculated by taking voyage revenues, subtracting voyage expenses and then dividing the total by the round-trip voyage duration in days. Therefore, this revenue is measured in $/day.

For TCE prices, we have concrete data from 6 May 2010 to 25 February 2014 and 200 observations for three of five routes presented above (TC2, TC6 and TD5). For route TD16, we only have data from 6 May 2010 to 25 February 2014, 147 observations, and the data set consists of spot and forward prices with maturity from current month up to 5 months and from three quarters to five quarters. Therefore, in the case of TCE, the data set comprises each case spot, FCM F1, F2, F3, F4, F5, Q3, Q4 and Q5, where FCM is the current month forward, F1 is the forward contract for the first month after the closest to maturity, F2 is the contract for the second, and so on. Q3 represents the third quarter after the current one, and so on.

In the case of WS, the data set is different for each route. Specifically, for routes TC2 and TD5, we have data from 26 February 2009 to 25 February 2014, 262 observations, for spot, FCM, F1, F2, F3, F4, F5, Q3, Q4 and Q5. For route TD16, we have the same spot and forward quotations but from 1 January 2009 to 20 February 2013, 217 observations. Finally, for route TC14, we have data from 18 May 2012 to 25 February 2014, 94 observations, for the same quotations used in the case of TCE: spot, FCM F1, F2, F3, F4, F5, Q3, Q4 and Q5. The main descriptive statistics, mean and volatility, of these variables are presented in Table 2.

Table 2 Descriptive statistics
Full size table

Preliminary Findings

Previous studies, for example, Alizadeh and Kavussanos (2001, 2002), among others, have found evidence of seasonality in freight rates. To confirm this result in our data set, Table 3 shows the FCM mean price, TCE and WS, by months divided by the total mean for each route. It is easy to see that prices are higher in winter and spring seasons than in the summer and autumn ones. Therefore, this is the first evidence of seasonality in our data set. Moreover, this result confirms what is said in Alizadeh and Kavussanos (2002), p. 750: ‘These are thought to be primarily the weather conditions and calendar effects, such as the increase in heating oil consumption during the winter, and increased demand for dry bulk commodities by Japan before the change of financial year every March.’ Table 3 only includes FCM, which is the most liquid quotation in each case; however, the same results are obtained with the remainder of the series.

Table 3 Descriptive seasonality
Full size table

Another way to confirm the presence of seasonality in the series is through the Kurskal-Wallis test. To perform the test, we have computed monthly averages from the weekly estimated convenience yield series. The null hypothesis of the test is that there are no monthly seasonal effects. The test was also performed for the FCM mean price for TCE and WS of all routes, and the results of the test are shown in Table 4. The results indicate the rejection of the null hypothesis of no seasonal effects in all cases at a 99 per cent significant level.

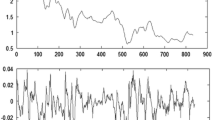
Table 4 Seasonality test – Kruscal-Wallis
Full size table

However, although the results from Table 3 and Table 4 confirm the findings from previous studies related to evidence of seasonality in freight rates, it is not possible to conclude whether this seasonality is deterministic or stochastic. We can use the spectrum to characterize the seasonality (deterministic or stochastic). From Wei (2005), it is demonstrated that deterministic seasonality appears in the spectrum as sharp peaks (or Dirac delta functions) in several frequencies, whereas stochastic seasonality shows a softer pattern. This finding implies that a sharp spike in the sample spectrum may indicate a possible deterministic cyclical component, while broad peaks often imply a non-deterministic seasonal component. Of course, the results should be taken with caution, as estimation errors and aliasing effects can confuse deterministic and ideal stochastic patterns.

The freight rates, WS and TCE of TD5 route, and their first differences spectrums are depicted in Figure 1.Footnote 2 It seems that the spectrum generally exhibits broad peaks and troughs; therefore, this preliminary result suggests that freight rates have a stochastic seasonal component.

Figure 1
figure 1

Spectrum.

Full size image

Theoretical Model

A model for stochastic seasonality

In this section, we propose and estimate two different factor models, either with or without assuming stochastic seasonality for the freight rates presented above. These comparisons demonstrate that the most suitable model in terms of both simplicity and fit is the one that assumes stochastic seasonality in all cases.

Traditionally but also currently (see for example Huang et al, 2013), freight rates have been considered non-stationary. However, there are studies which suggest that these prices seem to be stationary (see for example Tvedt, 2003), as implied by maritime economics theory, or that they sometimes present a type of mean reversion (see for example Adland and Cullinane, 2006). Therefore, to take into account long-term (non-stationary) and short-term (stationary mean reverting) effects, in addition to seasonal effects, we use the four-factor model by Garcia et al (2012) to obtain an estimation that accounts for stochastic seasonality. However, the aim of this article is not to decide which is the best model to characterize the freight rate dynamics, but rather to analyze whether freight rate seasonality is stochastic or deterministic.

In the four-factor model by Garcia et al (2012), the log-spot price (X t ) is the sum of three stochastic factors: a long-term component (ξ t ), a short-term component (χ t ) and a seasonal component (α t ).

The fourth stochastic factor is the other seasonal factor (α* t ), which complements α t .Footnote 3

The stochastic differential equations (SDEs) of these factors are:

where μ ξ , κ, ϕ, σ ξ , σ χ and σ α are constants and dW ξt , dW χt , dW αt and dW α*t are correlated Brownian-motion increments.Footnote 4

This model is ‘maximal’ as described by Dai and Singleton (2000). Moreover, this model follows the Dai-Singleton A0(4) model. We see that this model is a particular case of the canonical form given by the expressions:

where

Dai and Singleton (2000) demonstrate that this model is globally identifiable. The model of Garcia et al (2012) imposes the restrictions a=k=φ0=0 and α>0. In addition, as a restriction of a globally identifiable model imposing concrete values and intervals to the parameters, this model is also globally identifiable and maximal.

As stated above, in Garcia et al (2012), we have:Footnote 5

and

To compare the results obtained with this stochastic seasonality model, we use the model with deterministic seasonality presented in Sorensen (2002). As in the previous case, the log-spot price is assumed to be the sum of two stochastic factors (χ t and ξ t ) and a deterministic seasonal trigonometric component (α t ) (i.e., X t =ξ t +χ t +α t ). The SDEs for ξ t and χ t are the ones given before and for α t , and α* t we have:

As in the previous case, α* t is the other seasonal factor that complements α t , and ϕ is the seasonal period.

It is very easy to realize that this model with deterministic seasonality is exactly the same as that with stochastic seasonality but imposing σ α =0.

To value the derivatives contracts, we must rely on the ‘risk-neutral’ version of the stochastic models. The SDEs for the factors under the equivalent martingale measure can be expressed as:

where λ ξ , λ χ , λ α and λ α* are ‘risk premiums’ for each factor and W ξt ◊, W χt ◊, W αt ◊ and W α*t ◊ are the factor Brownian motions under the equivalent martingale measure. These Brownian motions can show any correlation structure with the restriction explained above.

In the case of deterministic seasonality, this is also a ‘risk-neutral’ version of the model whose SDEs are the same as those in the stochastic seasonality case but imposing σ α =λ α =λ α* =0.Footnote 6

Estimation Methodology

As stated in previous studies, one of the main difficulties in estimating the parameters of the model is that the factors (or state variables) are not directly observable. Instead, they must be estimated from spot and/or forward prices. To estimate the non-seasonal factors (which are short- and long-term factors), we need, as usual, short- and long-maturity forward contracts. However, to properly estimate the seasonal factors, we need to include in the dataset forward contracts maturing in many different months, thus covering seasonal cycles. Therefore, our dataset must include more forward contracts than do other studies.

The formal method for this approach is to use the Kalman-filter methodology.Footnote 7 The Kalman-filter technique is a recursive methodology that estimates the unobservable time series, the state variables or factors (Z t ), based on an observable time series (Y t ), which depend on these state variables. The measurement equation accounts for the relationship between the observable-time series and the state variables:

where , h is the number of state variables, or factors, in the model, and is a vector of serially uncorrelated Gaussian disturbances with zero mean and covariance matrix H t . To avoid dealing with a large number of parameters, we assume that H t is diagonal with main diagonal entries equal to σ η .

The transition equation accounts for the evolution of the state variables:

where is a vector of serially uncorrelated Gaussian disturbances with zero mean and covariance matrix Q t .

Let Yt|t − 1 be the conditional expectation of Y t and let Ξ t be the covariance matrix of Y t , conditional on all information available at time t−1. Then, after omitting unessential constants, the log-likelihood function can be expressed as:

Estimation Results

The four-factor model with stochastic seasonality

Here, we present the results of the estimation of the four-factor model with stochastic seasonality presented above for each freight rate, WS and TCE of the different routes. Results are shown in Table 5.

Table 5 Estimation results. Four-factor model – stochastic seasonality (Garcia et al (2012))
Full size table

One interesting result is that, in all cases, the seasonal period is typically 1 year and that the standard deviation of the seasonal factor (σ α ) is significantly different from zero. This finding implies that seasonality in freight rates is stochastic with a period of 1 year, which is consistent with the preliminary results in presented above. The speed of adjustment (k) is highly significant, implying, as in the case of hydrocarbons (see for example Schwartz, 1997, and Garcia et al, 2012), mean reversion in freight rates. It is interesting to note that this speed of adjustment is higher in the TCE than in the WS. This outcome is clear, as WS is a market price whereas TCE is a margin. The long-term trend (μ ξ ) for the WS is negative in all cases, and its significance varies from one route to another, implying slightly long-term reduction in freight rates, which is consistent with the global financial crisis. However, in the case of TCE, which is a margin, the long-term trend (μ ξ ) tends to be positive in three of four cases, which implies that, even though freight rates tend to go down, the freight rate margins tend to grow in the long term. However, as in the case of WS, in half of the cases of TCE, the long-term trend is not significantly different from zero. It is also interesting that σ ξ and σ χ are both highly significantly different from zero in all cases; therefore, to characterize freight rates, WS and TCE, both non-seasonal (long term and short term) factors are needed as stated in section 3.

The market prices of risk associated with non-seasonal factors (λ ξ and λ χ ) are significantly different from zero in some cases and not in others (it is interesting to note that in the case of TCE λ ξ is, and λ χ is not, significantly different from zero in all cases). The market prices of risk associated with seasonal factors (λ α and λα*) are not significantly different from zero in most cases; however, in some cases, they are significantly different from zero. These results suggest that the risk associated with the non-seasonal factors is more difficult to diversify than the risk associated with the seasonal factors in our data set. It is also interesting that the market price of risk associated with the seasonal factor which is included in the price (λ α ) tends to be more significantly different from zero than the other seasonal factor (λα*) in most cases. As the seasonal factor is complex, these results indicate that the risk associated with the real part (α) of the complex seasonal factor is more difficult to be diversified than the risk associated with the imaginary part (α*). It should be noted that the complex part is solely a mathematical artifact to produce the necessary cyclical behavior.

The correlation between the long-term factor (ξ) and the real part of the seasonal factor (α) is negative in almost all cases (WS and TCE for all routes), most likely because both factors are long term and are competing to capture long-term effects (see Garcia et al, 2012). However, the correlation between the long-term factor and the imaginary part of the seasonal factor (α*) is positive. The opposite phenomenon occurs with the short-term factor; the correlation between the long-term factor (ξ) and the real part of the seasonal factor (α) is positive in almost all cases, whereas the correlation between the long-term factor and the imaginary part of the seasonal factor (α*) is negative.

Deterministic versus stochastic seasonality

It is useful to compare the results obtained with the stochastic seasonality model to those obtained with the standard, deterministic seasonality model. Here we present the results of the estimation of both models for each freight rate, WS and TCE, of the different routes, presented above. Both models’ parameters have been estimated using the Kalman-filter methodology, and the results are shown in Table 5 and Table 6, respectively.

Table 6 Estimation results. Two-factors model with deterministic seasonality (Sorensen, 2002)
Full size table

First, it is interesting to compare the value of the Schwartz Information Criterion (SIC) obtained with both models. If we define the SIC as ln(L ML )−q ln(T), where q is the number of estimated parameters, T is the number of observations and L ML is the value of the likelihood function, defined in equation (12), using the q estimated parameters, then the preferred model is the one with the highest SIC. We find that the value of the SIC for the four-factor model with stochastic seasonality, shown at the bottom of Table 5, is higher than the corresponding value obtained with the deterministic seasonality model shown at the bottom of Table 6 in, almost all cases (WS and TCE for all routes). We reach the same conclusions with the Akaike Information Criterion (AIC), which is defined as ln(L ML )−2q.

A similar method of comparing the models is to compute a likelihood ratio test. As stated above, the model with stochastic seasonality nests the deterministic seasonality model (that is, Sorensen’s proposal) when σ α =0. Therefore, the restrictions imposed by the deterministic seasonality model can be tested using a likelihood ratio test. The results are shown in Table 7. The value of the LR statistic is quite large in almost all cases, indicating the rejection of the null hypothesis that the true model is the restricted one, that is, the deterministic seasonality model.

Table 7 Likelihood ratio tests
Full size table

The models can also be compared using their predictive ability. We present the in-sample predictive ability of both models for all cases in Table 8. The table presents the root mean square error as percentage of its mean (RMSE mean per.) to compare the predictive power of the two-factor model with deterministic seasonality and the four-factor model with stochastic seasonality. In general, both models have a good fit, as the predictive errors are small and, as expected, forwards with longer maturities present smaller predictive errors than the forwards with smaller maturities as these last ones have more volatility and are more exposed to market noise than the former.

Table 8 In-sample predictive ability (RMSE)
Full size table

However, the model accounting for stochastic seasonality outperforms the standard model with deterministic seasonality. Consequently, this outcome is further proof that freight rates present seasonality and that this seasonality is stochastic instead of deterministic.

The advantages of the stochastic seasonality model over the deterministic seasonality model are even clearer when we analyze the out-of-sample predictive ability (Table 9). When we perform the out-of-sample predictive ability, we divide the data sets into two panels. The first panel consists of 80 per cent of the data and is used to estimate the parameters of the model, whereas the second panel is used for out-of-sample testing purposes and consists of the remaining 20 per cent.

Table 9 Out-of-sample predictive ability (RMSE)
Full size table

As expected, out-of-sample pricing errors are slightly higher than the corresponding in-sample values. However, as in the case of in-sample predictive ability, the model accounting for stochastic seasonality outperforms the standard model with deterministic seasonality. Consequently, this outcome is further proof that freight rates present seasonality and that this seasonality is stochastic instead of deterministic.

These results imply that there is seasonality in freight rates, which implies that shipowners may be able to use the information on the seasonal movements of freight markets in order to make business decisions, such as budget planning, dry-docking of vessels when freight rates are expected to drop, adjusting vessel speeds to increase productivity and ship repositioning to loading areas during peak seasons. Charterers also can use the information derived here to optimize their transportation costs by timing, for instance, their inventory build up outside peak seasons albeit taking seasonality into account. Having said this, it should be kept in mind that seasonality is stochastic and, thus, its time period and intensity can change in time. Consequently, these seasonal movements are not perfectly predictable, and shipowners and charterers should use this information with caution.

Conclusion

This article focuses on the seasonality of freight rates and, accordingly, the seasonality of WS and TCE for different routes. Fixed costs in shipping make its supply unresponsive to seasonal variation in demand. Thus, freight rates are strongly seasonal. Moreover, analyzing the spectrum, it seems highly probable that seasonality in freight rates is a stochastic factor and not a deterministic one.

On the basis of this empirical evidence, we have proposed a model for the stochastic behavior of freight rates, considering seasonality as a stochastic factor and we have compared it with the classical ones with deterministic seasonality. These comparisons prove that the most appropriate model in terms of both simplicity and fit is the one that assumes stochastic seasonality in all cases. This conclusion is confirmed in terms of likelihood ratio test and in-sample and out-of-sample predicted ability because the model accounting for stochastic seasonality outperforms the standard model with deterministic seasonality

Consequently, these results imply that there is seasonality in freight rates and that this seasonality is stochastic instead of deterministic. Therefore, shipowners and charterers can use this information on the seasonal movements of freight markets to make business decisions. Shipowners and charterers should know that freight rates are higher in the winter and spring seasons than in the summer and autumn ones and they should try to accommodate their business strategies to this fact. Even more, as proven in this article, they should also know that these differences in freight rates between different seasons are not deterministic but stochastic. This means that it is not possible to predict the value of this difference, which can change from 1 year to the following.

Moreover, the fact that freight rate seasonality is stochastic instead of deterministic has also important consequences in derivatives valuation and hedging. Since derivatives value, especially options, tends to increase with the underlying uncertainty (volatility), the fact that seasonality is stochastic instead of deterministic should be taken into account to increase freight rate volatility and, consequently, derivatives values.