Abstract
The most general model used to describe conflict situations is the extensive form model, which specifies in detail the dynamic evolution of each situation and thus provides an exact description of ‘who knows what when’ and ‘what is the consequence of which’. The model should contain all relevant aspects of the situation; in particular, any possibility of (pre)commitment should be explicitly included. This implies that the game should be analysed by solution concepts from noncooperative game theory, that is, refinements of Nash equilibria. The term extensive form game was coined in von Neumann and Morgenstern (1944) in which a set theoretic approach was used. We will describe the graph theoretical representation proposed in Kuhn (1953) that has become the standard model. For convenience, attention will be restricted to finite games.
Access provided by CONRICYT-eBooks. Download reference work entry PDF
Similar content being viewed by others
The most general model used to describe conflict situations is the extensive form model, which specifies in detail the dynamic evolution of each situation and thus provides an exact description of ‘who knows what when’ and ‘what is the consequence of which’. The model should contain all relevant aspects of the situation; in particular, any possibility of (pre)commitment should be explicitly included. This implies that the game should be analysed by solution concepts from noncooperative game theory, that is, refinements of Nash equilibria. The term extensive form game was coined in von Neumann and Morgenstern (1944) in which a set theoretic approach was used. We will describe the graph theoretical representation proposed in Kuhn (1953) that has become the standard model. For convenience, attention will be restricted to finite games.
The basic element in the Kuhn representation of an n-person extensive form game is a rooted tree, that is, a directed acyclic graph with a distinguished vertex. The game starts at the root of the tree. The tree’s terminal nodes correspond to the endpoints of the game and associated with each of these there is an n-vector of real numbers specifying the payoff to each player (in von Neumann–Morgenstern utilities) that results from that play. The nonterminal nodes represent the decision points in the game. Each such point is labelled with an index \( i\left(i\in \left\{0,1,\dots, n\right\}\right) \) indicating which player has to move at that point.
Player O is the chance player who performs the moves of nature. A maximal set of decision points that a player cannot distinguish between is called an information set. A choice at an information set associates a unique successor to every decision point in this set, hence, a choice consists of a set of edges, exactly one edge emanating from each point in the set. Information sets of the chance player are singletons and the probability of each choice of chance is specified. Formally then, an extensive form game is a sixtuple \( \varGamma =\left(K,P,U,C,p,h\right) \) which respectively specify the underlying tree, the player labelling, the information sets, the choices, the probabilities of chance choices and the payoffs.
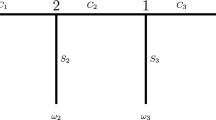
As an example, consider the 2-person game of Fig. 1a. First player 1 has to move. If he chooses A, the game terminates with both players receiving 2. If he chooses L or R, player 2 has to move and, when he is called to move, this player does not know whether L or R has been chosen. Hence, the 2 decision points of player 2 constitute an information set and this is indicated by a dashed line connecting the points. If the choices L and ℓ are taken, then player 1 receives x, while player 2 gets y. The payoff vectors at the other endpoints are listed similarly, that is, with player l’s payoff first. The game of Fig. 1b differs from that in Fig. 1a only in the fact that now player 1 has to choose between L and R only after he has decided not to choose A. In this case, the game admits a proper subgame starting at the second decision point of player 1. This subgame can also be interpreted as the players making their choices simultaneously.


Extensive Form Games, Fig. 1
A strategy is a complete specification of how a player intends to play in every contingency that might arise. It can be planned in advance and can be given to an agent (or a computing machine) who can then play on behalf of the player. A pure strategy specifies a single choice at each information set, a behaviour strategy prescribes local randomization among choices at information sets and a mixed strategy requires a player to randomize several pure strategies at the beginning of the game. The normal form of an extensive game is a table listing all pure strategy combinations and the payoff vectors resulting from them. Figure 1c displays the normal form of Fig. 1a, and, up to inessential details, this also represents the game of Fig. 1b. The normal form suppresses the dynamic structure of the extensive game and condenses all decision-making into one stage. This normalization offers a major conceptual simplification, at the expense of computational complexity: the set of strategies may be so large that normalization is not practical. Below we return to the question of whether essential information is destroyed when a game is normalized.
A game is said to be of perfect recall if each player always remembers what he has previously known or done, that is, if information is increasing over time. A game may fail to have perfect recall when a player is a team such as in bridge and in this case behaviour strategies may be inferior to mixed strategies since the latter allow for complete correlation between different agents of the team. However, by modelling different agents as different players with the same payoff function one can restore perfect recall, hence, in the literature attention is usually restricted to this class of games. In Kuhn (1953) and Aumann (1964) is has been shown that, if there is perfect recall, the restriction to behaviour strategies is justified.
A game is said to be of perfect information if all information sets are singletons, that is, if there are no simultaneous moves and if each player always is perfectly informed about anything that happened in the past. In this case, there is no need to randomize and the game can be solved by working backwards from the end (as already observed in Zermelo 1913). For generic games, this procedure yields a unique solution which is also the solution obtained by iterative elimination of dominated strategies in the normal form. The assumption of the model that there are no external commitment possibilities implies that only this dynamic programming solution is viable; however, this generally is not the unique Nash equilibrium. In the game of Fig. 2, the roll-back procedure yields (R, r), but a second equilibrium is (L, ℓ). The latter is a Nash equilibrium since player 2 does not have to execute the threat when it is believed. However, the threat is not credible: player 2 has to move only when 1 has chosen R and facing the fait accompli that R has been chosen, player 2 is better off choosing r. Note that it is essential that 2 cannot commit himself: If he could we would have a different game of which the outcome could perfectly well be (2, 2).


Extensive Form Games, Fig. 2
A major part of noncooperative game theory is concerned with how to extend the backwards induction principle to games with imperfect information, that is how to exclude intuitively unreasonable Nash equilibria in general. This research originates with Selten (1965) in which the concept of subgame perfect equilibria was introduced, that is, of strategies that constitute an equilibrium in every subgame. If y < 0, then the unique equilibrium of the subgame in Fig. 1b is (R, r) and, consequently, (BR, r) is the unique subgame perfect equilibrium in that case. If x < 2, however, then (AL, ℓ) is an equilibrium that is not subgame perfect. The game of Fig. 1a does not admit any proper subgames; hence, any equilibrium is subgame perfect, in particular (A, ℓ) is subgame perfect if x > 2. This shows that the set of subgame perfect equilibria depends on the details of the tree and that the criterion of subgame perfection does not eliminate all intuitively unreasonable equilibria.
To remedy the latter drawback, the concept of (trembling hand) perfectness was introduced in Selten (1975). The idea behind this concept is that with a small probability players make mistakes, so that each choice is taken with an infinitesimal probability and, hence, each information set can be reached. If y ≤ 0, then the unique perfect equilibrium outcome in Fig. 1a,b is (1, 3): player 2 is forced to choose r since L and R occur with positive probability.
The perfectness concept is closely related to the sequential equilibrium concept proposed in Kreps and Wilson (1982). The latter is based on the idea of ‘Bayesian’ players who construct subjective beliefs about where they are in the tree when an information set is reached unexpectedly and who maximize expected payoffs associated with such beliefs. The requirements that beliefs be shared by players and that they be consistent with the strategies being played (Bayesian updating) imply that the difference from perfection is only marginal. In Fig. 1a, only (R, r) is sequential when y < 0. When y = 0, then (A, ℓ) is sequential, but not perfect: choosing ℓ is justified if one assigns probability 1 to the mistake L, but according to perfectness R also occurs with a positive probability.
Unfortunately, the great freedom that one has in constructing beliefs implies that many intuitively unreasonable equilibria are sequential. In Fig. 1a, if y > 0, then player 2 can justify playing ℓ by assigning probability 1 to the ‘mistake’ L, hence, (A, ℓ) is a sequential equilibrium if x ≤ 2. However, if x < 0, then L is dominated by both A and R and thinking that 1 has chosen L is certainly nonsensical. (Note that, if x < 0, then (AL, ℓ) is not a sequential equilibrium of the game of Fig. 1b, hence, the set of sequential (perfect) equilibrium outcomes depends on the details of the tree.) By assuming that a player will make more costly mistakes with a much smaller probability than less costly ones (as in Myerson’s (1978) concept of proper equilibria) one can eliminate the equilibrium (A, ℓ) when x ≤ 0 (since then L is dominated by R), but this does not work if x > 0. Still, the equilibrium (A, ℓ) is nonsensical if x < 2: If player 2 is reached, he should conclude that player 1 has passed off a payoff of 2 and, hence, that he aims for the payoff of 3 and has chosen R. Consequently, player 2 should respond by r: only the equilibrium (R, r) is viable.
What distinguishes the equilibrium (R, r) in Fig. 1 is that this is the only one that is stable against all small perturbations of the equilibrium strategies, and the above discussion suggests that such equilibria might be the proper objects to study. An investigation of these stable equilibria has been performed in Kohlberg and Mertens (1984) and they have shown that whether an equilibrium outcome is stable or not can already be detected in the normal form. This brings us back to the question of whether an extensive form is adequately represented by its normal form, that is, whether two extensive games with the same normal form are equivalent. One answer is that this depends on the solution concept employed: it is affirmative for Nash equilibria, for proper equilibria (van Damme 1983, 1984) and for stable equilibria, i.e. for the strongest and the weakest concepts, but it is negative for the intermediate concepts of (subgame) perfect and sequential equilibria. A more satisfactory answer is provided by a theorem of Thompson (1952) (see Kohlberg and Mertens 1984) that completely characterizes the class of transformations that can be applied to an extensive form game without changing its (reduced) normal form: The normal form is an adequate representation if and only if these transformations are inessential. Nevertheless, the normal form should be used with care, especially in games with incomplete information (cf. Harsanyi 1967–8; Aumann and Maschler 1972), or when communication is possible (cf. Myerson 1986).
Bibliography
Aumann, R.J. 1964. Mixed and behavior strategies in infinite extensive games. In Advances in game theory, ed. M. Dresher, L.S. Shapley, and A.W. Tucker. Princeton: Princeton University Press.
Aumann, R.J., and M. Maschler. 1972. Some thoughts on the minimax principle. Management Science 18(5): 54–63.
Harsanyi, J.C. 1967–8. Games with incomplete information played by ‘Bayesian’ players. Management Science 14; Pt I, (3), November 1967, 159–182; Pt II, (5), January 1968, 320–334; Pt III, (7), March 1968, 486–502.
Kohlberg, E., and J.-F. Mertens. 1984. On the strategic stability of equilibria. Mimeo, Harvard Graduate School of Business Administration. Reprinted in Econometrica 53, 1985, 1375–1385.
Kreps, D.M., and R. Wilson. 1982. Sequential equilibria. Econometrica 50(4): 863–894.
Kuhn, H.W. 1953. Extensive games and the problem of information. Annals of Mathematics Studies 28: 193–216.
Myerson, R.B. 1978. Refinements of the Nash equilibrium concept. International Journal of Game Theory 7(2): 73–80.
Myerson, R.B. 1986. Multistage games with communication. Econometrica 54(2): 323–358.
Selten, R. 1965. Spieltheoretische Behandlung eines Oligopolmodells mit Nachfragetragheit. Zeitschrift für die gesamte Staatswissenschaft 121: 301–324; 667–689.
Selten, R. 1975. Reexamination of the perfectness concept for equilibrium points in extensive games. International Journal of Game Theory 4(1): 25–55.
Thompson, F.B. 1952. Equivalence of games in extensive form, RAND Publication RM–769. Santa Monica: Rand Corp.
Van Damme, E.E.C. 1983. Refinements of the Nash equilibrium concept, Lecture Notes in Economics and Mathematical Systems No. 219. Berlin: Springer-Verlag.
Van Damme, E.E.C. 1984. A relation between perfect equilibria in extensive form games and proper equilibria in normal form games. International Journal of Game Theory 13(1): 1–13.
Von Neumann, J., and O. Morgenstern. 1944. Theory of games and economic behavior. Princeton: Princeton University Press.
Zermelo, E. 1913. Über eine Anwendung der Mengenlehre auf die Theorie des Schachspiels. Proceedings of the Fifth International Congress of Mathematicians 2: 501–504.
Author information
Authors and Affiliations
Editor information
Copyright information
© 2018 Macmillan Publishers Ltd.
About this entry
Cite this entry
Van Damme, E. (2018). Extensive Form Games. In: The New Palgrave Dictionary of Economics. Palgrave Macmillan, London. https://doi.org/10.1057/978-1-349-95189-5_657
Download citation
DOI: https://doi.org/10.1057/978-1-349-95189-5_657
Published:
Publisher Name: Palgrave Macmillan, London
Print ISBN: 978-1-349-95188-8
Online ISBN: 978-1-349-95189-5
eBook Packages: Economics and FinanceReference Module Humanities and Social SciencesReference Module Business, Economics and Social Sciences