Keywords

JEL Classifications

Irreversible investment acknowledges that the value of capital may not be fully recoverable when resold.

This simple generalization has rich implications for investment. Beyond truncating disinvestment, irreversibility changes the dynamics of investment by creating a threshold level of returns for positive investments. Below this threshold, investment is zero – which immediately implies intermittent rather than continuous investment activity. Moreover, the threshold return that justifies investment exceeds the required return on a reversible investment.

Investment and Options

Marschak (1949) raised the potential role of irreversibility in factor accumulation by emphasizing the convertibility or liquidity of capital. Work by Arrow (1968) and Henry (1974) considered when irreversible actions in environmental applications were justified and emphasized the idea of an option value. This idea was extended by Bernanke (1983) to the role of uncertainty in delaying investment decisions.

McDonald and Siegel’s (1986) article ‘The Value of Waiting to Invest’ provides the first explicit valuation of investment allowing for irreversibility, incorporating option valuation (real options) into investment theory. McDonald and Siegel analyse a project of fixed size, so the timing of the project is the only choice to be made. They show that the value of the project includes an ‘option value of waiting’, that can be valued and interpreted using option pricing theory. The additional value of being able to choose when to invest, rather than a ‘now or never’ investment decision, can be quantitatively large, and has interesting implications for the investment decision. First, the presence of this option implies that it is optimal to delay the investment, rather than undertaking it immediately, even when immediate execution has positive value. Instead, value can be increased by waiting for additional information. Second, like most options, the value of the option to wait is increasing in uncertainty. This feature implies an effect of uncertainty on the value and timing of investments that is absent in most conventional models.

Later work by Pindyck (1988) and Bertola (1988), allows for incremental investment, so that the firm chooses both the timing and the size of its investments. They show that there is a threshold for investing with irreversibility that exceeds the return that would justify a positive reversible investment. Instead of a single investment decision, as in McDonald and Siegel, there is an infinite sequence of investment decisions, where each satisfies the threshold condition.

An Illustrative Model

Most irreversible investment models work in continuous time, so that optimal investment timing can be calculated exactly. An introduction to these techniques, as well as a broader overview, is found in Dixit and Pindyck’s (1994) Irreversible Investment. The intuition can be understood in a discrete time framework, adapted from Abel et al. (1996), specialized to the case of irreversible investment.

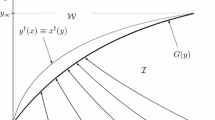
Consider the decision of a single firm to undertake a capital investment at time 1. In the first period, the return to installing capital K1 is r(K1). The total return r(K1) is strictly increasing and concave in K and satisfies the Inada conditions. The firm pays a price b per unit of capital to purchase capital. In the second period, the return to capital is uncertain and equal to R(K, ε), where ε is stochastic. The derivative of R(K, ε) with respect to K,RK (K,ε) ≥ 0, is continuous and strictly decreasing in K, continuous and strictly increasing in ε, and R(K, ε) also satisfies the Inada conditions. Define a threshold value of ε by

$$ {R}_K\left({K}_1,,,\kern0.2em ,\overline{\varepsilon}\right)=b, $$
(1)

as illustrated in Fig. 1.

Irreversible Investment, Fig. 1
figure 978figure 978

The second period marginal return to capital

Full size image

Assume that the resale price of capital is zero, or complete irreversibility. In the second period, the capital stock is optimally chosen at a level equal to K2(ε), subject to the irreversibility constraint. When \( \varepsilon >\overline{\varepsilon} \), the optimal capital stock rises to satisfy the first-order condition RK[K2(ε), ε] = b. However, when \( \varepsilon >\overline{\varepsilon} \), the marginal return to capital is less than its purchase price. If the firm could resell capital at its acquisition price b (costless reversibility) it would do so. However, the available resale price is zero, so the firm prefers to keep its capital stock, which has positive marginal return; in this case K2(ε) = K1. The optimal second-period marginal return to capital is graphed in Fig. 1 as the lower envelope of RK(K1, ε) and b.

Conditional on the optimal second-period capital stock, the firm chooses its capital stock at time 1 to maximize V(K1) − bK1, where V(K1) is the first period value of the firm equal to r(K1)) γE[R(K2,ε)] and 0 <γ< 1 is the discount factor. The first-order condition for the optimal capital choice is

$$ {V}^{\prime}\left({K}_1\right)\equiv {r}^{\prime}\left({K}_1\right)+\gamma {\int}_{-\infty}^{\overline{\varepsilon}}{R}_K\left({K}_1,\varepsilon \right)\mathrm{d}F\left(\varepsilon \right)+\gamma b\left[1-F\left(\overline{\varepsilon}\right)\right]=b, $$
(2)

where F(ε) is the cumulative distributive function (CDF) of ε.

Notice that the term V′(K1) is the marginal value of an additional unit of capital, or marginal q. The standard investment first-order condition equating marginal q to the marginal cost of capital still holds with irreversibility. The effects of irreversibility are incorporated into the value of marginal q, so when investment is non-zero the standard q-theory first-order condition equating the marginal value and the marginal cost of investment still holds.

Embedded Options

Now rewrite this first-order condition to highlight the investment options and their implications for the investment decision. Rewrite Eq. (2) as

$$ q\left({K}_1\right)\equiv {V}^{\prime}\left({K}_1\right)\equiv n\left({K}_1\right)-\gamma c\left({K}_1\right) $$
(3)

where

$$ n\left({K}_1\right)\equiv {r}^{\prime}\left({K}_1\right)+\gamma {\int}_{-\infty}^{\infty }{R}_K\left({K}_1,\varepsilon \right)\mathrm{d}F\left(\varepsilon \right)>0 $$
(4)

and

$$ c\left({K}_1\right)\equiv {\int}_{\overline{\varepsilon}}^{\infty}\left[{R}_K\left({K}_1,\varepsilon \right)-b\right]\;\mathrm{d}F\left(\varepsilon \right)>0. $$
(5)

The marginal value of an additional unit of capital is decomposed into two terms. The first term, n(K1), is equal to the present value of marginal returns to capital, evaluated at its current level, K1. The second term subtracts the discounted value of a call option, c(K1), to add more capital, as illustrated in Fig. 1, where the returns to the call option are represented by the area under RK(K1, ε) and above the line b. The call option reduces the marginal value of capital because additional capital irrevocably reduces the marginal return to capital owing to the concavity of the revenue function. If one combines these two terms, the marginal value of capital is the discounted sum of marginal revenues on the assumption that the capital stock is fixed, less the marginal value of the option to increase the capital stock. Note that the concavity of the revenue function is crucial to this mechanism. Hence, models such as Abel and Eberly, (1997) which assume constant returns to scale, do not generate these option values.

The effects of uncertainty are not transparent in the above formulation, since both terms in Eq. (3) depend on the distribution, F(ε). To better discern the effect of uncertainty, rewrite Eq. (2) instead as

$$ q\left({K}_1\right)\equiv {V}^{\prime}\left({K}_1\right)\equiv j\left({K}_1\right)-\gamma p\left({K}_1\right) $$
(6)

where

$$ j\left({K}_1\right)\equiv {r}^{\prime}\left({K}_1\right)+\gamma b>0 $$
(7)

and

$$ p\left({K}_1\right)\equiv {\int}_{-\infty}^{\overline{\varepsilon}}\left[b-{R}_K\left({K}_1,\varepsilon \right)\right]\;\mathrm{d}F\left(\varepsilon \right)>0. $$
(8)

The marginal value of an additional unit of capital is again decomposed into two terms. The first term, j(K1), is the discounted marginal return to costlessly reversible capital: the firm earns the marginal revenue in period one and can sell the capital for the same price b in period two. This is the Jorgensonian marginal return (Jorgenson, 1963); notice that it is independent of ε and risk free. The second component of q is the put option to sell capital at price b. When investment is irreversible, the put option is not available to the firm, since it cannot sell capital at any positive price. The value of the put option must be subtracted from the Jorgensonian valuation (where resale at price b would be permitted) to obtain the marginal value of irreversible capital. Marginal q can thus be written as a frictionless value less the value of the put option that is eliminated by the irreversibility constraint. This is illustrated in Fig. 1 by subtracting the returns to the put option (the area under the line b and above the function RK(K1, ε)) from the frictionless return b.

Effects of Uncertainty and Put–Call Parity

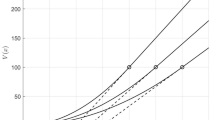
To calculate the effect of uncertainty on marginal q from Eq. (6), one need only calculate the effect of uncertainty on p(K1), since j(K1) is risk free. The effect of uncertainty on p(K1) is clear: p(K1) is an option value, and an increase in uncertainty increases the value of an option. In this case specifically, a second-order stochastic dominant shift in the distribution of ε shifts the CDF up for every value of ε. Since RK(K1, ε) is increasing in ε, the term [b − RK(K1, ε)] is decreasing in ε. Hence, greater uncertainty in ε shifts more weight of the CDF towards the large option payoffs in the left tail and unambiguously increases the value of the option, p(K1). Greater uncertainty unambiguously lowers the value of q(K1). Since q(K1) is decreasing in K1, a downward shift in q(K1) reduces the optimal value of K1 for a given value of b, as illustrated in Fig. 2. This decrease is the incremental investment counterpart to McDonald and Siegel’s finding that greater uncertainty increases the option value of waiting, lowering the value of investing immediately.

Irreversible Investment, Fig. 2
figure 979figure 979

Marginal q and the optimal capital stock under low and high uncertainty

Full size image

This formulation of q(K1) also demonstrates Bernanke’s (1983) ‘bad news principle’ of irreversible investment. The distribution of ε only appears in the expression for q in Eq. (6) via the put option p(K1). The put option only depends on the lower tail of the distribution of ε, below the threshold \( \overline{\varepsilon} \). That is, the only part of the distribution of shocks that affects the value of q(K1) is the lower tail – or the ‘bad news’. The upper tail is irrelevant, since in that region, the firm invests until the marginal product of capital equals its price. The exact realization of the shock in this region is irrelevant to the marginal return. In the lower tail, on the other hand, the firm neither invests nor disinvests, and the realization of the shock determines the marginal return to capital.

Figure 1 illustrates these arguments. The second period return to capital is the lower envelope of the price of capital, b, and the second-period marginal return, RK(K1, ε) evaluated at K1. The value of these returns depends on ε only in the lower tail of the distribution of ε (the bad news principle). The lower envelope can be expressed as either the function RK(K1, ε) less the area labelled call returns in Fig. 1; adding this difference to first-period marginal returns r′ (K1), we obtain the expression for q in Eq. (3). Equivalently, the second-period marginal return can be expressed the line b less the area labelled put returns in Fig. 1. Adding the first-period marginal return r′(K1), we obtain the expression for marginal q in Eq. (6). The fact that the second-period return can be written in two equivalent ways using options follows from put–call parity, a fundamental property of options prices. In fact, in this setting put–call parity is found simply by setting the two expressions for q in Eqs. (3) and (6) equal to each other. Equating these two expressions for q and simplifying, we find

$$ \gamma p\left({K}_1\right)+n\left({K}_1\right)=\gamma c\left({K}_1\right)+j\left({K}_1\right). $$
(9)

This expression equates the value of a portfolio containing a put option and the underlying security, n(K1), to the value of a portfolio containing a call option and a risk-free asset. For a financial security such as a stock with price S, put–call parity analogously states that P(S,τ) + S = C(S;, τ)+ X /(1+r)τ, where X is the strike price of the options and τ is the time to maturity. The terms P(S, τ) and C(S, τ) are the value of the put and call, respectively, on the underlying stock, S. X/(1 + r)τ is the present value of a risk-free payoff (a zero coupon bond) of X in τ periods.

Extensions and Applications

The above analysis assumes complete irreversibility. However, less stringent forms of the constraint deliver similar implications. Abel and Eberly (1996) examine costly reversibility, where capital can be disinvested and resold at a price less than the purchase price of capital. In this case, the gap between the investment and disinvestment thresholds opens quickly, even for small differences between the purchase and sale prices of capital. Moreover, this formulation has assumed kinked, linear adjustment costs, so that the degree of irreversibility is summarized by the ratio of the purchase and sale prices of capital. However, with more general cost formulations, such as Abel and Eberly (1994), capital may have a positive resale price and still be effectively irreversible when other costs of reselling capital exceed any potential benefits. In addition to a resale market discount, convex adjustment costs and fixed costs, for example, may induce irreversibility.

Research on irreversibility has branched out both empirically and theoretically. Initial applications included energy and natural resource markets (Brennan and Schwartz, 1985), with extensions to virtually all types of quasi-fixed capital, including durable goods, real estate and equipment investment. Modelling has been extended to include multiple types of quasi-fixed capital goods (Eberly and van Mieghem, 1997). Aggregating models with infrequent adjustment to incorporate equilibrium effects is challenging, and the results remain controversial. Except in very special cases (Caplin and Spulber, 1987) aggregating requires tracking a distribution of agents. However, it is precisely this feature that can match the observation that much of the volatility in empirical investment arises from the extensive margin (the number of agents adjusting) rather than the intensive margin (the average size of the adjustment). Much progress has been made in this direction (for example, Caballero and Engel, 1999), though the quantitative implications vary with modelling strategy (Veracierto, 2002).

See Also