Introduction

BCS–Bose-Einstein condensation (BEC) crossover has been an interesting research subject since 1980’s1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16. The experimental realization of BCS-BEC crossover in ultracold atomic Fermi gases17,18,19,20,21, with the help of Feshbach resonances, has given it a strong boost over the past decade22,23,24,25,26,27. When the pairing interaction is tuned from weak to strong in a two component Fermi gas, the superfluid behavior evolves continuously from the type of BCS to that of BEC1,2,28.

In such a fundamentally fermionic system, superfluidity mainly concerns pairing, namely, interactions in the particle-particle channel. In contrast, the particle-hole channel mainly causes a chemical potential shift and is often neglected29. For example, in a conventional superconductor, the chemical potential below and above Tc are essentially the same and thus its dependence on the temperature and the interaction strength has been completely neglected in the weak coupling BCS theory for normal metal superconductors. On the other hand, Gor’kov and Melik-Barkhudarov (GMB)30 considered the lowest order correction from the particle-hole channel, (which has been referred to as induced interaction in the literature) and found that both Tc and zero temperature gap Δ(0) are suppressed by a big factor of (4e)1/3 ≈ 2.22. Berk and Schrieffer31 also studied a similar effect in the form of ferromagnetic spin correlations in superconductors. Despite the big size of the GMB correction, the effect of the particle-hole channel has been largely overlooked in the theoretical study of BCS-BEC crossover, until it has become realistic to achieve such crossover experimentally in atomic Fermi gases. Heiselberg and coworkers32 considered the effect of the lowest order induced interaction in dilute Fermi gases and generalized it to the case of multispecies of fermions as well as the possibility of exchange of bosons. Kim et al.33 considered the lowest order induced interactions in optical lattices. Within the mean-field treatment and without including the excitation gap in the particle and hole propagators, these authors found the same effective overall interaction at zero T and at Tc and hence an unaffected mean-field ratio 2Δ(0)/kBTc ≈ 3.53. Martikainen et al.34 considered the lowest order induced interactions in a three-component Fermi gas. It has become clear that including only the perturbative lowest order induced interaction is not appropriate away from the weak coupling BCS regime. Yin and coworkers35 went beyond the lowest order and considered the induced interactions from all particle-hole ladder diagrams, i.e., the entire particle-hole T-matrix. However, in all the above works, only the bare particle-hole susceptibility was considered and it was averaged on-shell and only on the Fermi surface, with equal momenta for the particle and the hole propagators. No self-energy feedback was included. Therefore, there was necessarily no pseudogap in the fermion excitation spectrum at Tc. This is basically equivalent to replacing the particle-hole susceptibility by an essentially temperature independent constant, leading to a simple downshift in the pairing interaction.

As the gap and Tc increase with interaction strength, it can naturally be expected that the contribution from the particle-hole channel, or the induced interaction, will acquire a significant temperature dependence. More importantly, the presence of the (pseudo)gap serves to suppress the particle-hole fluctuations (which tend to break pairing). In other words, neglecting the feedback of the gap related self energy in the particle-hole susceptibility is expected to cause an over-estimate of the particle-hole channel contributions. Therefore, a proper treatment should include the gap effect in the particle-hole susceptibility. In addition, the lowest order treatment is no longer appropriate away from the weak coupling regime.

Furthermore, it has now been established that as the pairing interaction increases, pseudogap develops naturally12,28,36. Experimental evidence for its existence comes from high Tc superconductors13,28,37,38,39 as well as atomic Fermi gases40,41,42,43,44. Therefore, a theory with proper treatment of the pseudogap effect is necessary in order to arrive at results that can be quantitatively compared with experiment. For the same reason, the effect of the particle-hole channel needs also to be studied within such a theory.

There have also been various quantum Monte Carlo (QMC) simulations45,46,47,48,49,50 on atomic Fermi gases, which includes both particle-particle and particle-hole channels, with an emphasis on the unitary limit. Some recent works49,50 seem to have produced good numbers when compared with experiment51. However, due to the black-box nature of QMC for non-specialists, these approaches do not provide physical understanding which is as transparent as an analytical theory, not to mention that there are large discrepancies between these QMC results52. Therefore, it is always important to develop a proper analytical theory.

In this paper, we explore the particle-hole channel effect based on a pairing fluctuation theory10,53, originally developed for treating the pseudogap phenomena of high Tc superconductors. This theory has been successfully applied to atomic Fermi gases and has been generating results that are in good agreement with experiment12,28,40,42. Here we include the entire particle-hole T-matrix, with gap effect included in the fermion Green’s functions. Instead of a simple average of the particle-hole susceptibility χph on the Fermi surface, here we choose to average at two different levels – one on the Fermi surface, one over a narrow momentum shell around the Fermi level. We find that χph has very strong frequency and momentum as well as temperature dependencies. It is sensitive to the gap size. Therefore, self-consistently including the self-energy feedback is important. For both levels of average, we find that while in the BCS limit, the particle-hole channel effect may be approximated by a downshift in the pairing strength so that the ratio 2Δ(0)/Tc is unaffected, the situation becomes more complex as the interaction becomes stronger where the gap is no longer very small. Significant difference exists for these two levels of averaging. The particle-hole susceptibility is reduced by both a smaller Fermi surface and a big (pseudo)gap in the crossover regime. Deep in the BEC regime, the particle-hole channel contributions drop to zero. Without including the incoherent part of the self energy, we find that at unitarity, Tc/EF ≈ 0.217, in reasonable agreement with experiment.

We emphasize that our theory is not a diagrammatic approach. Instead, it is derived using equations of motion53,54,55,56 and is simply recast in the form of Feynman diagrams for easy understanding. This also explains why we have self-energy feedback included in the diagrams.

The rest of this paper is arranged as follows. In the next section, we first give a brief summary of the pairing fluctuation theory without the particle-hole channel effect. Then we derive the theory with particle-hole channel included, starting by studying the dynamic structure of the particle-hole susceptibility. Next, we present numerical results, showing the effect of the particle-hole channel on the zero T gap, transition temperature Tc and pseudogap at Tc, as well as the mean-field ratio . We also discuss and compare our value of Tc/EF with experiment and those in the literature. Finally, we conclude. More detailed results on the dynamic structure of the particle-hole susceptibility are presented in the Supplementary Info.

Pairing Fluctuation Theory with the Particle-hole Channel Effect Included

Summary of the pairing fluctuation theory without the particle-hole channel effect

To make this paper self-contained and to introduce the assumptions as well as the notations, we start by summarizing the pairing fluctuation theory10,53 without the effect of the particle-hole channel, as a foundation for adding the particle-hole channel.

We consider a Fermi gas with a short range s-wave interaction U(k, k′) = U < 0, which exists only between opposite spins. Our theory can be effectively represented by a T-matrix approximation, shown diagrammatically in Fig. 1. However, we emphasize that Fig. 1 is simply a representation of the equations derived from an equation of motion approach56. This explains why we have fully dressed Green’s functions in the diagrams, unlike a typical diagrammatic approach. The self energy Σ(K) comes from two contributions, associated with the superfluid condensate and finite momentum pairs, respectively, given by Σ(K) = Σsc(K) + Σpg(K), where

Figure 1
figure 1

Feynman diagrams for the particle-particle channel T-matrix tpg and the self energy Σ(K).

The dotted lines represent the bare pairing interaction U. The dashed line, tsc, represents the superfluid condensate.

Full size image

with Δsc being the superfluid order parameter. We use a four-vector notation, K ≡ (k, iωl), Q ≡ (q, iΩn), , etc. and ωl and Ωn are odd and even Matsubara frequencies for fermions and bosons, respectively. Here G0(K) = (iωl − ξk)−1 and are the bare and full Green’s functions, respectively, ξk = ħ2k2/2m − μ is the free fermion dispersion, measured with respect to the Fermi level. In what follows, we will set kB = ħ = 1. The pseudogap T-matrix

can be regarded as the renormalized pairing interaction with pair momentum Q, where

is the pair susceptibility. We emphasize that this asymmetric form of χ(Q) is not an ad hoc choice but rather a natural result of the equation of motion method. The bare Green’s function G0 comes from the inversion of the operator which appears on the left hand side of the equations of motion. It also appears in the particle-hole susceptibility χph, as will be shown below. Albeit not a phi-derivable theory, the equation of motion method ensures that this theory is more consistent with the Hamiltonian than a phi-derivable theory.

The gap equation is given by the pairing instability condition,

referred to as the Thouless criterion, which can also be naturally interpreted as the Bose condensation condition for the pairs, since 1 + Uχ(0) ∝ μpair. In fact, after analytical continuation iΩn → Ω + i0+, one can Taylor expand the (inverse) T-matrix as

and thus extract the pair dispersion Ωq ≈ q2/2M* to the leading order, where M* is the effective pair mass. Here Γq is the imaginary part of the pair dispersion and can be neglected when pairs become (meta)stable10,53,56. In the superfluid phase, tpg(Q) diverges at Q = 0 and a macroscopic occupation of the Q = 0 Cooper pairs, i.e., the condensate, appears. This macroscopic occupation, has to be expressed as a singular term, , (the dashed line in Fig. 1), such that , written in the same form as its pseudogap counterpart, Σpg(K).

Now we split Σpg(K) into coherent and incoherent parts:

where we have defined the pseudogap Δpg via

where b(x) is the Bose distribution function. Below Tc, the divergence of tpg(Q = 0) makes it a good mathematical approximation to neglect the incoherent term δΣ so that

Therefore, the Green’s function G(K), the quasiparticle dispersion and the gap equation, as expanded from Eq. (4), follow the same BCS form, except that the total gap Δ now contains both contributions from the order parameter Δsc and the pseudogap Δpg.

For a contact potential, we get rid of the interaction U in favor of the scattering length a via , where εk = k2/2m. Then the gap equation can be written as

where f(x) is the Fermi distribution function. In addition, we have the particle number constraint, n = 2∑KG(K), i.e.,

where is the BCS coherence factor.

Equations (9), (10) and (7) form a closed set. For given interaction 1/kFa, they can be used to solve self consistently for Tc as well as Δ and μ at Tc, or for Δ, Δsc, Δpg and μ as a function of T below Tc. Here kF is the Fermi wave vector. More details about the Taylor expansion of the inverse T matrix can be found in refs 56 and 57.

Dynamic structure of the particle-hole susceptibility χ ph(P)

Before we derive the theory with full particle-hole T-matrix tph included, we first study the dynamic structure of the particle-hole susceptibility χph(P). It is the single rung of the particle-hole scattering ladder diagrams, as shown in Fig. 2(a). Note that direct interaction exists only between fermions of opposite spins. Therefore, the particle and hole must also have opposite spins. The total particle-hole four-momentum is given by P ≡ (iνn, p). Since we are considering the effect on pairing induced by the particle-hole channel, we can twist external legs of the diagram, as shown in Fig. 2(b), so that the particle-hole contribution can be added to the original pairing interaction U directly. It is obvious that the particle-hole momentum P in Fig. 2(a) is equal to K + K′ − Q in Fig. 2(b), where Q is the pair momentum of the particle-particle channel. Therefore, we have

Figure 2
figure 2

Feynman diagrams for the particle-hole susceptibility χph in the presence of self-energy feedback effect.

Panel (b) is identical to panel (a), with twisted external legs. The total particle-hole momentum P in (a) is equal to K + K′ − Q in (b), with Q being the particle-particle pair momentum.

Full size image

Note that again we have a mixing of dressed and undressed Green’s function in χph(P), like in the expression of χ(Q). As mentioned earlier, this mixing has exactly the same origin in both cases56. For convenience, here we dress the particle propagator with self energy and leave the hole propagator undressed. This is based on the fact that the hole propagator is undressed in χ(Q). (One can equivalently dress the hole while leaving the particle undressed).

A few remarks are in order. Firstly, the induced interactions conform to the Galileo transformation. Indeed, taking ±K and ±K′ as the four momenta of the incoming and outgoing fermions in the center-of-mass (COM) reference frame, the momenta in Fig. 2(b) should be relabeled as ±K + Q/2 and ±K′ + Q/2, so that P = (K + Q/2) − (−K′ + Q/2) = K + K′, independent of Q, same as in the COM frame. Secondly, as in the Noziéres and Schmitt-Rink (NSR) theory2, one needs a fictitious separable potential Uk,k′ = Uφkφk′, such as the contact potential considered for atomic Fermi gases, in order to have a simple result in the form of Eq. (2) for the summation of the particle-particle ladder diagrams8,10,53. However, inclusion of the particle-hole channel spoils this separability for the total effective interaction Ueff(k, k′), since χph(P) only depends on the sum P = K + K′.

Upon analytical continuation, iνn → ν + i0+, we separate the retarded into real and imaginary parts, , where

It is easy to see and if or . At low T, is gapped; it is exponentially small for |ν| < Δ if μ > 0 or for otherwise. In all cases, is isotropic in p. In the BCS limit, Δ → 0, Ek → |ξk|, so that

where is the momentum on the Fermi surface.

For comparison, we analyze the undressed particle-hole pair susceptibility,

which is studied by GMB30 and others32,33,34,35 in the literature.

The imaginary part is given by

with . For ν ≠ 0, exponentially as p → 0. For small but finite p,

where the delta function can be satisfied only for . When |ν|m/p > kμ, we have ξk > 0 so that will also turn around and start to decrease exponentially. The turning points ν =  ± pkμ/m show up as two peaks in , which satisfies

and

at low T. More generally, for ν = 0 and finite p, we have

In the weak coupling limit, , since χph reduces to when the gap Δ vanishes.

It is easy to show that the hermitian conjugate . Similar relations do not hold for χph, however, due to the mixing of G0 and G in the expression of χph(P). Such symmetry relations are manifested in Supplementary Figs S1–S3, which show three- and two-dimensional plots of the real and imaginary parts of and at different T at unitarity. These plots reveal that by neglecting the feedback effect, the bare misses important interesting dynamic structures associated with the pseudogap, which leads to a low frequency gap in . This gap becomes wider at lower T. The evolution of with temperature, 1/kFa and momentum p is shown in Supplementary Figs S4 and S5,

In Fig. 3, we plot systematically the zero frequency value of the real part of the particle-hole pair susceptibility as a function of total momentum p, with and without the feedback effect. The curves are computed at a relatively low T = 0.3Tc at unitarity, where Tc is calculated in the absence of the particle-hole channel. Due to the large excitation gap Δ = 0.69EF, at p = 0, the value with the feedback is strongly suppressed from its undressed counterpart, . In other words, the neglect of the self-energy feedback in leads to serious over-estimate of the particle-hole channel contributions. At the same time, exhibits a more complex, nonmonotonic dependence on p than . In both cases, the momentum dependence is strong.

Figure 3
figure 3

Strong momentum dependence of the real part of the particle-hole susceptibility at zero frequency ν = 0 in the unitarity limit, with (black curve) and without (blue dashed curve) self-energy feedback, calculated at T = 0.3Tc, where Tc = 0.256EF.

While the undressed shows a simple monotonic behavior, the dressed susceptibility has a nonmonotonic p dependence and a substantially reduced value at p = 0. This reduction derives from the gap effect in the Green’s function G(K). Namely, seriously over-estimated particle-hole fluctuations.

Full size image

Figure 3 and Supplementary Figs S1–S5 reveal that the particle-hole susceptibility has very strong dependencies on both frequency and momentum, as well as the temperature and interaction strength.

Induced interaction – beyond the lowest order

Except for the constant factor, , in the absence of the self-energy feedback, is in fact the lowest order induced interaction, considered in GMB30 and most others32,33,34,35 in the literature:

Diagrams of the same order but between fermions of the same spin vanish.

Let us first re-plot in Fig. 4(a) the particle-particle scattering T-matrix, tpg, shown in Fig. 1 but now with external legs, referred to as t1(Q). We have

Figure 4
figure 4

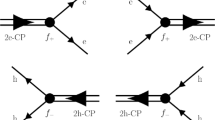
Feynman diagrams showing the particle-hole channel effect on fermion pairing, in the presence of self-energy feedback.

(a) Particle-particle T matrix t1(Q), with external four momenta labeled. (b) Particle-hole T matrix tph(P), with P = K + K′ − Q being the total particle-hole 4-momentum. (c) An effective, composite particle-particle T-matrix, t2(Q), with the contribution from the particle-hole channel included. Here different shadings represent different T matrices.

Full size image

Now we consider the contribution of an infinite particle-hole ladder series, as shown in Fig. 4(b), which should replace the bare interaction U. The summation gives rise to the T-matrix in the particle-hole channel,

At Q = 0, this gives the overall effective pairing interaction,

where ±K and ±K′ are the incoming and outgoing 4-momenta of the scattering particles in the COM reference frame. The induced interaction is thus given by

with P = K + K′. Upon Taylor expanding the denominator in powers of Uχph, the leading term, −U2χph, is the counterpart lowest-order induced interaction in our theory, except that we always consider the self energy feedback effect.

It is evident that the T matrices in the particle-particle channel and the particle-hole channel share the same lowest order term, U. Both T matrices can be regarded as a renormalized interaction, but in different channels. What we need is to replace the bare U in one of the two T matrices with the other T matrix. The results are identical, which we call t2. Shown in Fig. 4(c) is the regular particle-particle channel T matrix t1(Q) with U replaced by the particle-hole channel T matrix tph(P) (with twisted external legs), where P = K + K′ − Q. In other words, we replace U−1 with in Eq. (21) and formally obtain

Unfortunately, since Ueff(K, K′) is not a separable potential, one cannot obtain a simple summation in the form of Eq. (25). This can also be seen from the extra dependence on K and K′ on the right hand side of the equation. Certain averaging process has to be done to arrive at such a simple summation, as will be shown below.

Gap equation from the self-consistency condition in the mean-field treatment

The dependence of Ueff(P) on external momenta via P = K + K′ − Q presents a complication in the gap equation. This can be seen through the self consistency condition in the mean field treatment, even though we do not use mean field treatment in our calculations. Writing the interaction VK,K′ = Ueff(K + K′) for Q = 0, i.e., zero total pair 4-momentum, we have

where we have used the mean-field result 〈cK′c−K′〉 = G(K′)G0(−K′)ΔK′. Equivalently, this can be written as

Note that, due to the dynamic character of χph(K + K′), both the gap ΔK and the quasiparticle dispersion EK acquire a dynamical frequency dependence. The gap also develops a momentum dependence, which is originally absent for a contact potential.

We can express Ueff(P) in terms of its retarded analytical continuation, as follows:

where the second term is just the induced interaction,

Then we have

The particle-hole channel effect is contained in the 2nd term, without which this would be just the gap equation without the particle-hole channel and admit a constant gap solution. Without further approximation, the complex dynamic structure of χph(P) will inevitably render it very difficult to solve the gap equation.

Pairing instability condition in the presence of the particle-hole channel effect

In order to obtain a simple form as Eq. (25), we have to average out the dependence of Ueff(K, K′) on K and K′. Indeed, an average of χph(ν, p) has been performed in the literature on (and only on) the Fermi surface30. For the frequency part, here we follow the literature and take iνn = iωl + iωl′ = 0. From Supplementary Fig. S1, one can see that this is where the imaginary part for all p and thus the effective interaction Ueff(K, K′) is purely real. For the momentum part, we choose on-shell, elastic scattering, i.e., k = k′ and then average over scattering angles:

where θ is the angle between k and k′. It is the off-shell scattering processes which lead to imaginary part and nontrivial frequency dependence in and the order parameter. Further setting k = kμ and averaging only on the Fermi surface is the averaging process used in all papers we can find about induced interactions in the literature. We refer to this as level 1 averaging. In this paper, we also perform a level 2 average, over a range of k such that the quasiparticle energy Ek ∈ [min(Ek), min(Ek) + Δ]. Here min(Ek) = Δ if μ > 0, or if μ < 0. The basic idea is that according to the density of states of a typical s-wave superconductor, the states within the energy range Ek ∈ [Δ, 2Δ] are most strongly modified by pairing. It should be pointed out that in the BEC regime, this range can become very large.

Upon averaging of either level 1 or level 2, we drop out the complicated dynamical structure of χph(ν, p) and replace it by a constant 〈χph〉. For the purpose of comparison, we shall also perform the averaging on the undressed particle-hole susceptibility but will mostly show the result at level 1.

Shown in Fig. 5 are the angular averages of the particle-hole susceptibility at ν = 0 as a function of momentum k under the above on-shell condition, k = k′. Here we only show the unitary case at two different temperatures, T = Tc and low T = 0.1Tc ≪ Tc. For the purpose of comparison, we plot the result for both the dressed and undressed particle-hole susceptibility. The curves show strong momentum dependencies. For , it is monotonically increasing, whereas for 〈χph(0, p)〉, it exhibits nonmonotonic k dependence at low T. Both dressed and undressed particle-hole susceptibilities have a temperature dependence and this dependence is much stronger for the former. This can be attributed mainly to the temperature dependence of Δ(T) in 〈χph(0, p)〉, while depends on T only via μ(T).

Figure 5
figure 5

Angular average of the on-shell particle-hole susceptibility, 〈χph(0, p = |k + k′|)〉 at ν = 0 as a function of momentum k/kF, under the condition k = k′, calculated at unitarity for different temperatures T = 0.1Tc (black solid curve) and T = Tc (green dot-dashed curve), in units of .

Also plotted is its undressed counterpart, , which shows a serious over-estimate due to the neglect of the self-energy feedback. Here Tc = 0.256EF and associated gap and μ values are calculated without the particle-hole channel effect. The open circles on each curve denote level 1 average, i.e., k = kμ. The vertical axis readings of the horizontal short bars indicate the corresponding values of level 2 average. The thick section of each curve indicates the range of k used for level 2 averaging. Clearly, there are strong temperature and k dependencies in both 〈χph(0, p)〉 and . The (absolute) values of Level 2 average are substantially smaller than their level 1 counterpart.

Full size image

The open circles on each curve represent the level 1 average, i.e., the values at k = kμ. At the same time, the vertical axis readings of the short horizontal bars correspond to the level 2 average, while the thick segments of each curve represents the range of k used for level 2 averaging. Figure 5 shows that the (absolute) values of the level 2 average are significantly smaller than their level 1 counterpart. The level 1 average is essentially temperature independent (see the red and blue circles). In addition, it is evident that the neglect of self-energy feedback has caused to seriously over-estimate the contribution of particle-hole channel.

Similar plot for 1/kFa = 0.5 (Supplementary Fig. S6) exhibits a much stronger T dependence. In that case, μ is very close to 0 albeit still positive. As a consequence, the particle-hole susceptibility is much smaller than that shown in Fig. 5.

Now with this frequency and momentum independent χph(ν, p) ≈ 〈χph〉, we can easily carry out the simple geometric summation for t2:

Therefore, the Thouless criterion for pairing instability leads to the gap equation:

namely,

As will be shown later, 〈χph〉 is always negative. Therefore, the particle-hole channel effectively reduces the strength of the pairing interaction.

In the weak coupling limit (1/kFa = −∞), Δ → 0, , then 〈χph〉 and become equal, for either level of averaging. We have

where , , x = cos θ and N(0) = mkF/2π2ħ2 is the density of state at the Fermi level. Here we have approximated the Fermi function with its T = 0 counterpart, with a step function jump at the Fermi level.

In the weak interaction limit, the BCS result for Tc is , where γ ≈ 0.5772157 is the Euler’s constant. Equation (33) implies a replacement of 1/U by 1/U + 〈χph〉. In this way, the new transition temperature Tc is given by

and the same relation holds for zero T gap,

This result is in quantitative agreement (to the leading order) with that of GMB30 and others32 in the literature. Note that in our work, as well as in that of Yin and coworkers35, the average particle-hole susceptibility 〈χph〉 is added to 1/U or m/4πa. In other works32,33,34, only the lowest order particle-hole diagram is considered so that their induced interaction is added to U. Therefore, these works have to rely on the assumption N(0)U ≪ 1 and the validity of the BCS mean-field result in order to obtain the result of Eq. (36). Away from the weak interaction regime, a full summation of the particle-hole T matrix becomes necessary.

While the results from all different treatment seem to agree quantitatively in the weak coupling limit, we expect to see significant departures as the pairing interaction strength increases, especially in the unitary regime.

With the overall effective interaction Ueff, the self energy, as obtained from , will follow the same form as Eq. (8) although the gap values will be different. Therefore, the fermion number equation will also take the same form as Eq. (10). Furthermore, the pseudogap equation, given by , will also take the same form as Eq. (7).

Equations (10), (7) and (34) now form a new closed set and will be solved to investigate the effect of the particle-hole channel.

Note that in a very dilute Fermi gas shifting m/4πa by 〈χph〉 has no significant influence in experimental measurement of the s-wave scattering length a, because 〈χph〉 has dimension [kF]3/[EF] = [kF] and thus vanishes as kF → 0 in the zero density limit. However, a finite kF will indeed shift the resonance location except at very high T where μ < 0. In ref. 58, from which the scattering lengths are often quoted for 6Li, the actual density is comparable or even higher than that in most typical Fermi gas experiments. Therefore, the particle-hole channel may play an important role.

Here we propose that this particle-hole channel effect may be verified experimentally by precision measurement of the magnetic field B at the exact Feshbach resonance point as a function of density or kF at low T. The zero density field B0 can be obtained by extrapolation. Then one should have the field detuning δB = B−B0 ∝ kF. Because different theories predict a very different value of 〈χph〉 at unitarity, the measured field detuning can thus be used to quantify 〈χph〉 and test these theories. In principle, one may experimentally measure 〈χph〉 through the entire BCS-BEC crossover. For a Fermi gas in a trap, the trap inhomogeneity leads to a distribution of kF. Instead of a uniform shift, this inhomogeneity will spread out the unitary point at zero density into a narrow band at finite density. The band width and mean shift are both expected to be proportional to kF. Such effect deserves further investigation.

Numerical Results and Discussions

Effect of the particle-hole channel on BCS-BEC crossover

In this section, we will investigate the effect of the particle-hole channel on the BCS-BEC crossover behavior, in terms of zero temperature gap Δ(0), Tc and their ratio.

First, in Fig. 6, we show the effect on the zero T gap by comparing the calculated result with and without the particle-hole channel contributions. Shown respectively in panel (a) and (b) are plots of the zero T gap Δ and the corresponding particle-hole susceptibility (with a minus sign) as a function of 1/kFa. The black solid line in Fig. 6(a) is the result without the particle-hole channel effect, whereas the other curves are calculated with the effect at different levels of approximation. The (red) dotted curve are calculated using the undressed susceptibility at average level 1. The (green) dot-dashed and (blue) dashed curves are calculated using the dressed particle-hole susceptibility 〈χph〉 with level 1 (green dot-dashed curve) and level 2 (blue dashed line) averaging, respectively. The level 2 result shows a slightly weaker particle-hole channel effect, as can be expected from Fig. 5.

Figure 6
figure 6

Effect of the particle-hole channel contributions on the zero temperature gap in BCS-BEC crossover.

In (a), the black solid curve is the gap without the particle-hole effect. The rest curves are calculated with the particle-hole channel effect but at different levels, i.e., using undressed particle-hole susceptibility with level 1 averaging (red dotted line), dressed particle-hole susceptibility 〈χph〉 with level 1 (green dot-dashed curve) and level 2 (blue dashed line) averaging, respectively. The corresponding values of the average particle-hole susceptibility with a minus sign are plotted in (b), in units of . The particle-hole channel effect can be essentially neglected beyond 1/kFa > 1.5.

Full size image

One feature that is easy to spot is that the undressed particle-hole susceptibility has a very abrupt shut-off where the chemical potential μ changes sign. As a result, the corresponding (red dotted) curve of the gap also merges abruptly with the (black solid) gap curve calculated without particle-hole channel effect. This is not unexpected as one can see from Eq. (19) that at T = 0 for μ ≤ 0. Furthermore, Eq. (18) implies that approaches zero at μ = 0 abruptly with a finite slope as kμ does. In contrast, with the self-energy feedback included, either level 1 (green dot-dashed curves) or level 2 (blue dashed curves) average of 〈χph〉 approaches 0 smoothly as the BEC regime is reached. Consequently, in Fig. 6(a), the (green) dot-dashed and (blue) dashed curves approach the (black) solid curve very gradually. It is also worth pointing out that the difference between level 1 and level 2 average of 〈χph〉 is less dramatic than that between 〈χph〉 and the undressed . Indeed, the (green) dot-dashed and (blue) dashed curves are very close to each other. The abrupt shut-off of at μ = 0 is determined by the step function characteristic of the Fermi function at T = 0.

In the unitary regime, especially for 1/kFa ∈ [−0.5, +0.5], the particle-hole susceptibility is strongly over-estimated by the undressed in comparison with the dressed 〈χph〉. In this regime, both the gap and the underlying Fermi surface (as defined by the chemical potential) are large, so that neglecting the self-energy feedback leads to a strong over-estimate of , because the large gap serves to suppress particle-hole fluctuations.

From Fig. 6, we conclude that the particle-hole effect diminishes quickly as the Fermi gas is tuned into the BEC regime with increasing pairing interaction strength. Beyond 1/kFa > 1.5, the effect can essentially be neglected. For the level 1 average of the undressed particle-hole susceptibility, , as has been done in the literature, this effect disappears immediately once the BEC regime (defined by μ < 0) is reached, as far as the zero T gap is concerned.

As a consistency check, we notice that in the BCS limit, the average particle-hole susceptibility in all cases in Fig. 6(b) approaches the same asymptote, which is given by Eq. (35). This confirms our previous analytical analysis.

Next, we show in Fig. 7 the effect of the particle-hole channel on the behavior of Tc as well as the pseudogap at Tc. Figure 7(c) can be compared with Fig. 6(b). The curves for levels 1 and 2 average of 〈χph〉 in Fig. 7(c) are very similar to those in Fig. 6(b), with the values at 1/kFa = 0 slightly smaller. On the other hand, the curve for has a smooth thermal exponential tail in the BEC regime in Fig. 7(c). Thus, the pseudogap Δ(Tc) calculated using now merges back to the (black) solid curve smoothly.

Figure 7
figure 7

Effect of the particle-hole channel contributions on Tc and the pseudogap Δ at Tc in BCS-BEC crossover.

In (a,b), the black solid curves are calculated without the particle-hole effect. The rest curves are calculated with the particle-hole channel effect but at different levels, using undressed particle-hole susceptibility with level 1 averaging (red dotted line), dressed particle-hole susceptibility 〈χph〉 with level 1 (green dot-dashed curve) and level 2 (blue dashed line) averaging, respectively. The corresponding values of the average particle-hole susceptibility with a minus sign are plotted in (c), in units of . The particle-hole channel effect can be essentially neglected beyond 1/kFa > 1.5.

Full size image

Similar to the zero T gap case in Fig. 6, the difference in the effect on Tc and Δ(Tc) between level 1 and level 2 averaging mainly resides in the unitary regime and is less dramatic than that between undressed and dressed particle-hole susceptibility. Again, the undressed particle-hole susceptibility gives rise to an overestimate of the particle-hole channel effect.

In all cases, the particle-hole susceptibility becomes negligible in the BEC regime. The effect of the particle-hole channel shifts the Tc and Δ(Tc) curve towards larger 1/kFa, although the amount of shift clearly depends on the value of 1/kFa.

Now we study the effect of the particle-hole channel on the ratio 2Δ(0)/Tc. It suffices to consider the mean-field ratio, , since 2Δ(0)/Tc obviously will deviate from the weak coupling BCS result when pairing fluctuations are included in the crossover and BEC regimes. From Fig. 5, we see a strong T dependence of the particle-hole susceptibility. Therefore, the effect on and on zero T gap Δ(0) are different, as can be seen roughly from Figs 6 and 7.

In Fig. 8, we plot this mean-field ratio as a function of 1/kFa with (black solid curve) and without (blue dashed curve) the particle-hole channel effect. Here the particle-hole susceptibility 〈χph〉 is calculated with level 2 averaging. In the 1/kFa → −∞ limit, the ratio is unaffected by the particle-hole channel. As 1/kFa increases, the contribution of the particle-hole channel causes this ratio to increase gradually. At 1/kFa = −4, which is still a very weak pairing case, the ratio is already slightly larger. The effect is most dramatic in the unitary regime, since further into the BEC regime, 〈χph〉 will vanish gradually. It is worth noting that even without the particle-hole channel, the ratio starts to decrease from its weak coupling limit, 2πe−γ ≈ 3.53.

Figure 8
figure 8

Effect of the particle-hole channel contributions on the ratio in BCS-BEC crossover.

Shown is the mean-field ratio calculated with (black solid curve) and without (blue dashed curve) the particle-hole channel contributions. Here the particle-hole susceptibility 〈χph〉 is calculated with level 2 averaging.

Full size image

Finally, we estimate the shift in Feshbach resonance positions. From Figs 6 and 7, we find that χph does not necessarily diminish as T increases except at very high T (where μ becomes negative, so that |χph| will decrease exponentially with T.) In fact, this can be understood because Δ(T) decreases with T so that |χph| increases. We take . According to Eq. (34), the shift in 1/a is δ(1/a) = −4πħ2〈χph〉/2m = 0.08πkF. In other words, the dimensionless shift δ(1/kFa) = 0.25, which is independent of density and is no longer negligible. This is in good agreement with the actual shift 0.32 of the peak location of the Tc curve in Fig. 7(a). For a typical TF = 1 μK in 6Li, using the approximate expression a = abg[1 − W/(B − B0)], we obtain the shift in resonance position δB0 = −0.08W(kFabg) = 7.8 G. Here for the lowest two hyperfine states, the resonance position B0 = 834.15 G, the resonance width W = 300 G and the background scattering length abg = −1405a0, with a0 = 0.528 Å. Clearly, the shift δB0 is not small. In reality, one needs to solve self-consistently the equation m/(4πa) + 〈χph〉 = 0 and take care of the trap inhomogeneity. These will likely make the actual average shift smaller.

The susceptibility χph calculated with and without the self energy feedback differs by roughly a factor of 2 at unitarity. This can be used to test different theories, as mentioned earlier.

A question arises naturally as to whether the particle-hole channel effect has already been included in the experimentally measured scattering length a, since, after all, the measurements of a such as those in ref. 58 were carried out at densities comparable to typical Fermi gas experiments. This also depends on whether the temperature was high enough during the measurements.

Critical temperature Tc at unitarity

Finally, we compare our result on the critical superfluid transition temperature Tc/EF for a 3D homogeneous Fermi gas at unitarity with those reported in the literature. From Fig. 7, we read Tc/EF = 0.217 using level 2 average of 〈χph〉. And the maximum Tc ≈ 0.257 now occurs at 1/kFa ≈ 0.32, on the BEC side. The level 1 average of yields a slightly lower value, Tc/EF = 0.209. However, we emphasize that the level 2 average of 〈χph〉 is more reasonable. Note that as in the theory without particle-hole channel effect, we have dropped out the incoherent part of the self-energy from the particle-particle scattering. Inclusion of the incoherent part is necessary in order to obtain the correct value of the β factor.

Hu and coauthors59,60 have been claiming to be able to obtain the correct value of the β factor, using an NSR-based approach, without including the particle-hole channel. We note that this claim will breakdown when the particle-hole channel is included.

The value of Tc for a homogeneous Fermi gas at unitarity has been under intensive study over the past few years, both theoretically and experimentally, or using Monte Carlo simulations. The theory results for Tc/TF range from 0.1361 to 0.26462. Various experiments report a large range as well, with a recent value of 0.16751. We emphasize that, given the poor precision in experimental measurements, these measured values are far from being conclusive. More detailed comparison can be found in ref. 52.

Including the particle-hole channel contributions has reduced substantially our value of Tc, bringing it closer to the most recent experimental data. We expect that including the incoherent part of the self energy (δΣ) in Eq. (6) should lower the chemical potential and thus reduce Tc further. Indeed, if we take an constant δΣ = −0.3EF (half of the energy of a single spin down atom in a spin up Fermi sea63), Tc/EF will be suppressed down to 0.174, close to the recent experimental value. Full numerical inclusion of δΣ will be done in a future study.

Higher order corrections

In addition to non-ladder diagrams, which we have chosen not to consider, there seem to be a series of higher order corrections. For example, one can imagine repeating the T-matrix t2 in the way shown in Fig. 9 and obtaining a higher order T-matrix t3. Such t3 can then be repeated to obtain a higher order T-matrix t4 and so on. While one may argue these higher order T-matrices are indeed of higher order in bare interaction U, our experience with t2 seems to imply that detailed study needs to be carried out before we jump to a conclusion on this. Indeed, even the lowest order so-called induced interaction is one order higher in U than U itself.

Figure 9
figure 9

Higher order T-matrix, t3, obtained by repeating the T-matrix t2.

Full size image

Note added:

Our manuscript was initially posted at arXiv (arXiv:1109.2307). Since then, there have been new results from QMC on the zero temperature ground state energy of a unitary Fermi gas50. We have also learned of the QMC result from Ref. 49. Both are in good agreement with experimental results in Ref. 51.

Conclusions

In summary, we have studied the effects of the particle-hole channel on BCS-BEC crossover and compared with lower level approximations. We include the self-energy feedback in the particle-hole susceptibility χph, which leads to substantial differences than the result without self-energy feedback.

We have investigated the dynamic structure of χph and have discovered very strong temperature, momentum and frequency dependencies. Angular (as well as radial) average in the momentum space of the particle-hole susceptibility has been done in order to keep the equations manageable. We have performed the average at two different levels and also compared with the result calculated without including the self-energy feedback. We conclude that the level 2 averaging, i.e., both over angles and a range of momentum, is more reasonable. Computations of the particle-hole susceptibility without the self-energy feedback leads to an overestimate of the particle-hole channel effect.

In the weak coupling BCS limit, our result agrees, to the leading order, with that of GMB and others in the literature. Away from the weak coupling limit, Δ(0) and Tc are suppressed differently. We have also studied the ratio at the mean-field level and found that it is modified by the particle-hole fluctuations. The particle-hole channel effects diminish quickly once the system enters the BEC regime.

Since the particle-hole channel effectively renormalizes the pairing strength, therefore, it is important to have the particle-hole channel properly addressed, in order to make quantitative comparisons with experiment. This suggests that many theoretical calculations in the literature deserve to be revisited.

Without including the incoherent part of the self energy from particle-particle scattering, our present result on the critical temperature at unitarity yields Tc/EF ≈ 0.217, substantially lower than that obtained without the particle-hole effect. This value agrees reasonably well with some existing experimental measurement.

We have also made a falsifiable proposal that the particle-hole contribution can be measured by locating the Feshbach resonance positions as a function of kF and that this can be used to test different theories.

To study more accurately the quantitative consequences of the dynamic structure of the particle-hole susceptibility, full-fledged numerical calculations are needed, without taking simple angular average and setting frequency ν = 0. Further investigation is called for in order to determine whether higher order T-matrices will make a significant difference or not.

Additional Information

How to cite this article: Chen, Q. Effect of the particle-hole channel on BCS–Bose-Einstein condensation crossover in atomic Fermi gases. Sci. Rep. 6, 25772; doi: 10.1038/srep25772 (2016).