Chemical applicability and computation of K-Banhatti indices for benzenoid hydrocarbons and triazine-based covalent organic frameworks

Abstract

The novel applications in chemistry include the mathematical models of molecular structure of the compounds which has numerous findings in this area that refers to mathematical chemistry. Topological descriptors play a major role in QSAR/QSPR studies that analyses the biological and physicochemical properties of the compounds. In the recent times, a new type of topological descriptors are proposed, called K-Banhatti indices. In this study the chemical applicability of K-Banhatti indices are examined for benzenoid hydrocarbons (derivatives of benzene). These indices have shown remarkable results through the study of statistical analysis. Subsequently, triazine-based covalent organic frameworks (CoF’s) are studied for which $B_1(G)$, $B_2(G)$, $HB_1(G)$, $HB_2(G)$, ${}^mB_1(G)$, ${}^mB_2(G)$, and HB(G) of a graph G are computed.

Introduction

The structure of the molecule can be quantified by the usage of topological descriptors. There are varied applications in chemistry and these quantities are derived from their molecular structure. The chemical information obtained from the molecular descriptors vary for different algorithms proposed according to its respective definitions. Using the algorithm of a particular molecular descriptor, a detailed description of a molecule can be obtained. The selection of a molecular descriptor depends on the problem on which it is applied. The key technique is in encoding the information obtained from molecular descriptors using the structure of the molecule¹.

The modelling and forecasting of physicochemical and biological properties of molecules is aimed in the studies of Quantitative structure–property relationships (QSPR). Statistical and mathematical tools are used to extract every possible information about a compound using the help of chemometrics. The variation of physicochemical property of a molecule with respect to the topological index can be described using chemometrics through QSPR. This can replace expensive biological tests conducted in a laboratory, especially when the experiments involve hazardous and toxic materials or unstable compounds. An optimum relationship in predicting the properties of compounds is the basic strategy of QSPR. The performance of this study depends on the description of the molecular structure and their parameters².

To encode the information of a chemical structure, several topological indices were developed. These indices draw attention as they play a significant role in the contributions of QSPR studies^3,4,5,6. The molecular descriptors are used to extract most of the information of a compound using simple and quick computations.

Topological descriptors have a crucial role in QSAR/QSPR studies that analyses the biological and significant properties of the compounds. The mathematical chemistry is a combination of modelling of chemical compound to derive pivotal data through the various tools viz., topological indices, QSAR/QSPR studies and various polynomials^{7,8,9,10,11,12}.

Recently in Refs.^13,14, Kulli proposed various novel degree-based TIs such as the first K-Banhatti index $(B_1(G))$, the second K-Banhatti index $(B_2(G))$, first K hyper-Banhatti index $(HB_1(G))$, the second K hyper-Banhatti index $(HB_2(G))$, the modified first K-Banhatti index $({}^mB_1(G))$, the modified second K-Banhatti index $({}^mB_2(G))$ and the harmonic K-Banhatti index (HB(G)) of a graph G are defined as

$$\begin{aligned}{} & {} B_1(G)=\sum _{ue\in G}\left( d_u+d_e\right) ,\ \ \ B_2(G)=\sum _{ue\in G}\left( d_u\cdot d_e\right) ,\ \ \ HB_1(G)=\sum _{ue\in G} \left[ d_u+d_e \right] ^2, \\{} & {} HB_2(G)=\sum _{ue\in G}\left[ d_u\cdot d_e \right] ^2,\ {}^mB_1(G)=\sum _{ue\in G}\left( \dfrac{1}{d_u+d_e}\right) ,\ {}^mB_2(G)=\sum _{ue\in G}\left( \dfrac{1}{d_u\cdot d_e}\right) , \end{aligned}$$

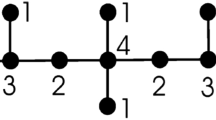
and $HB(G)=\sum _{ue\in G}\left( \dfrac{2}{d_u+d_e}\right)$ respectively. And ${ue\in G}$ or $u \sim e$ represents the vertex u, and an edge e are incident in the graph G and numerous studies have been carried out on these indices so far^{15,16,17,18,19}. But it is noticed that the chemical applicability of these indices have not been studied yet. Furthermore, the flowchart of the metodology defined above is shown in the Fig. 1. This study pinpoints in examining the chemical applicability of the K-Banhatti indices for benzenoid hydrocarbons and it is noticed that the results are truly remarkable through statistical analysis compared to existing work^20,21,22,23 . Subsequently, triazine-based covalent organic frameworks (TriCF) are studied for which the first K-Banhatti index, the second K-Banhatti index, first K-hyper Banhatti index, the second K-hyper Banhatti index, the modified first K-Banhatti index, the modified second K-Banhatti index, and the harmonic K-Banhatti index of a graph G are computed.

In this paper, consider the simple and connected graph $G=(V,E)$, and the vertex set $V=V(G)$, an edge set $E=E(G)$. The cardinality of the set V and E are known as the order, and the size of the graph G respectively. The cardinality of edges incident to a vertex $u\in V$ is called the vertex degree, represented by $d_u$, $d_e$ is the degree of an edge e denoted by, $d_e=d_u+d_v-2$ where, $e=uv$. We use $u \sim e$ for the vertex u and an edge e are adjacent in the graph G^24,25,26.

Figure 1

Flowchart to calculate the K-Banhatti indices.

Chemical applicability of K-Banhatti indices

This section concentrates on framing the linear regression model for the properties such as boiling point (BP), enthalpy (E), $\pi$- electron energy ($\pi$-ele), and molecular weight (MW) of benzene derivatives^27,28 for the considered indices using Tables 1 and 2. It is noticed from Tables 3, 4, 5, 6, 7, 8 and 9 that the regression model of statistical parameters show significant values and the coefficient of correlation R with the above four properties show high positive correlation (also see Fig. 2). It is evident from Table 10 that, $B_{1}(G)$, $B_2(G)$, $HB_1(G)$, $HB_2(G)$, ${}^mB_1(G)$, HB(G) are highly correlated with the $\pi$- electron energy, while ${}^mB_2(G)$ highly correlated with molecular weight.

• 1. The linear regression models for the first K-Banhatti index($B_1$)

  $$\begin{aligned} BP&=1.68 (\pm 0.053) B_1+ 48.68(\pm 13.68), \\ E&=0.941(\pm 0.081) B_1+ 56.91(\pm 20.84), \\ \pi -\text {ele}&=0.902(\pm 0.0021) B_1+4.734(\pm 0.5516), \\ MW&=0.772( \pm 0.0289)+52.56(\pm 7.4151). \end{aligned}$$

• 2. The linear regression models for the second K-Banhatti index($B_2$)

  $$\begin{aligned} BP&=1.083(\pm 0.0457)B_2+89.655(\pm 16.5832), \\ E&=0.5992(\pm 0.0589) B_2+82.182(\pm 21.3396), \\ \pi -ele&=0.058(\pm 0.002)B_2+6.913(\pm 0.7475), \\ MW&=0.4956(\pm 0.0244)B_2+71.747(\pm 8.8591). \end{aligned}$$

• 3. The linear regression models for the first K-hyper Banhatti index($HB_1$)

  $$\begin{aligned} BP&=0.265(\pm 0.0113)HB_1+90.885(\pm 16.6388),\\ E&=0.1469(\pm 0.145)HB_1+82.926(\pm 21.3389),\\ \pi -ele&=0.0142(\pm 0.0005)HB_1+6.979(\pm 0.7518),\\ MW&=0.1215(\pm 0.006)HB_1+72.321(\pm 8.8873). \end{aligned}$$

• 4. The linear regression models for the second K-hyper Banhatti index($HB_2$)

  $$\begin{aligned} BP&=0.1027(\pm 0.0062)HB_2+145.442(\pm 20.356),\\ E&=0.0559(\pm 0.0065)HB_2+115.865(\pm 21.6844),\\ \pi -ele&=0.0055(\pm 0.0002)HB_2+9.874(\pm 0.9758),\\ MW&=0.0468(\pm 0.0031)HB_2+97.705(\pm 10.4979). \end{aligned}$$

• 5. The linear regression models for the modified first K-Banhatti index(${}^mB_1$)

  $$\begin{aligned} BP&=60.419(\pm 1.4046){}^mB_1-68.559(\pm 12.674),\\ E&=34.893(\pm 2.0365){}^mB_1-18.295(\pm 18.2957),\\ \pi -ele&=3.2349(\pm 0.0421){}^mB_1-1.529(\pm 0.3802),\\ MW&=27.908(\pm 0.3818){}^mB_1-3.002(\pm 3.4452). \end{aligned}$$

• 6. The linear regression models for the modified second K-Banhatti index(${}^mB_2$)

  $$\begin{aligned} BP&=82.0515(\pm 3.2353){}^mB_2-131.83(\pm 23.9213),\\ E&=48.3104(\pm 2.3741){}^mB_2-61.5211(\pm 17.553),\\ \pi -ele&=4.3946(\pm 0.1485){}^mB_2-4.927(\pm 1.098),\\ MW&=38.0851(\pm 1.007){}^mB_2-33.5625(\pm 7.4502). \end{aligned}$$

• 7. The linear regression models for the harmonic K-Banhatti index(HB)

  $$\begin{aligned} BP&=30.2102(\pm 0.703)HB-68.5467(\pm 12.6876),\\ E&=17.4474(\pm 1.0182)HB-18.2934(\pm 18.3746),\\ \pi -ele&=1.6175(\pm 0.021)HB-1.5288(\pm 0.3804),\\ MW&=13.9548(\pm 0.1904)HB-3.0001(\pm 3.4359). \end{aligned}$$

Table 1 Experimental values (boiling point (BP), enthalpy (E), $\pi$-electron energy ($\pi -{\text {ele}}$) and molecular weight (MW) of benzenoid hydrocarbons.

Table 2 The values of K-Banhatti indices for benzenoid hydrocarbons.

Table 3 The regression model of statistical parameters for $B_1$.

Table 4 The regression model of statistical parameters for $B_2$.

Table 5 The regression model of statistical parameters for $HB_1$.

Table 6 The regression model of statistical parameters for $HB_2$.

Table 7 The regression model of statistical parameters for ${}^mB_1$.

Table 8 The regression model of statistical parameters for ${}^mB_2$.

Table 9 The regression model of statistical parameters for HB.

Figure 2

Correlation between (a) $\pi -ele$ with $B_1$, (b) $\pi -ele$ with $B_2$, (c) $\pi -ele$ with HB, (d) $\pi -ele$ with $HB_1$, (e) $\pi -ele$ with $HB_2$, (f) MW with $^mB_1$, (g) $\pi -ele$ with $^mB_2$.

Table 10 Correlation coefficients (R) between physicochemical properties of benzene derivatives, and K-Banhatti indices.

Triazine based covalent organic frameworks (CoF’s)

The chemical systems that possess discrete number of molecules refers to supra-molecular chemistry. The spatial arrangement of the molecules is responsible for the strength of the forces between them may be weak or strong. These forces may be due to intermolecular, hydrogen bonding, electrostatic charge, and covalent bonding. The feeble and reversible non-covalent interactions between the molecules are examined by the supramolecular chemistry while traditional chemistry examines covalent bonds. Various functions of supramolecular chemistry comprise molecular recognition, protein folding, interlocked molecular architectures, dynamic covalent chemistry, and other phenomena. Because of its interdisciplinary nature, it attracts physicists, biochemists, biologists, environmental scientists, apart from chemists.

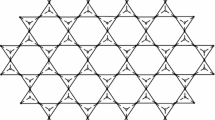
This work pinpoints on the supramolecular structure called triazine-based covalent organic frameworks (Fig. 3). To understand better about the chemical and biological properties of a chemical compound, graph theory uses a very useful tool called topological index. These indices help the chemists to derive information about the compound that may be in turn useful in drug design or drug delivery. Chemical graph theory is a combination of chemistry and mathematics in which the compound under the study will be modelled as a graph and the information about its atoms and their bonds are better understood. Chemical graph theory is the result of the strong linkages between both the subjects which have the outcomes as various significant investigations^{29,30,31,32,33}.

Biologically significant organic molecules have a new dimension as triazines act as the building blocks used in its design. Triazines and its derivatives have varied applications in antifungal, anticancer, antiviral, cardiotonic, anti-HIV, analgesic, etc., with fine tuned electronic properties. The goal of scientific researchers is to apply their theoretical research in industrial applications so that it is useful for humankind. The objective is to make the products scalable and satisfy excellent properties obtained from the experiments at a reasonable cost and long-term stability.

Covalent organic frameworks (CoF’s) have attracted various researchers across the globe because of its excellent properties such as adsorption, chemo-sensing, energy storage and production. As the CoFs and their applications are found in industries, many research achievements have come to light recently^34,35,36,37. CoF’s may be classified into boron-containing, triazine-based, imide-linked and imine-based due to swift increasing requirements in various fields. We focus on the second category of CoF’s, i.e., triazine-based in this study. In 2008, Thomas et al.³⁸, prepared triazine based CoF, by cyclotrimerization of nitrile building units at 400 $^\circ$C in the presence of ZnCl$_2$. There was destruction of ordered structure, despite the harsh conditions during the preparation which included high reaction temperature and purification in acid solution. However, few triazine-based CoF’s show crystallinity, and these building blocks were unable to adapt to harsh temperatures. Later, triazine based CoF’s (CTFs) were synthesized by the condensation reaction of aldehydes and amidines³⁹.

The distinguishing physical and chemical features of CoF’s have led to the plethora of applications in the industries. In 2011, Ding et al. reported first set of CoF’s that are useful in the field of catalysis⁴⁰. It was noted that 2-dimensional CoF’s acts as catalyst in different reactions that include nitrophenol reduction, water oxidation, in reducing CO$_2$ to CO etc. CoF’s are used tackle the problem of excessive CO$_2$ emissions as they are the principal reason for greenhouse effect. It is mainly due to the expansion of population and the development of industries. Aqueous alkanolamine is proposed to implement the CO$_2$ emissions. To control the CO$_2$ emissions, new materials are to be developed with high performance in which CoF’s play a significant role. Also, CoF plays an important role in energy storage^41,42.

Augustine et al.^43,44 theoretically examined triazine-based covalent-organic frameworks (CoF’s) using vertex and edge partition for degree-based and neighborhood degree-based topological indices. Additionally, the degree-based and neighborhood degree-based entropy measures for the results are given. The graph theoretical approach is used to compare the outcomes with obtained results. In this section, based on the previous work of Tony Augustine et al. various K-Banhatti topological indices are computed for triazine-based covalent-organic frameworks (TriCF).

Figure 3

TriCF structure.

Theorem 3.1

Let G be the the molecular graph of linear chain TriCF. Then,$B_1(G)$, $B_2(G)$, $HB_1(G)$, $HB_2(G)$, ${}^mB_1(G)$, ${}^mB_2(G)$, and HB(G) of a graph G are

$$\begin{aligned} B_1(G)= 390n+186, \ B_2(G)= 526n+242, \ HB_1(G)= 2142n+990, \ \\ HB_2(G)= 4058n+1798, \ {}^mB_1(G)= \frac{203n+109}{15}, \ {}^mB_2(G)= \frac{97n+59}{9}, \end{aligned}$$

and $HB(G)= \frac{406n+2187}{15}.$

Figure 4

Linear chain of TriCF structure.

Proof

From the Fig. 4, it is observed that, in general $\vert V(G)\vert =33n+15$ and $\vert E(G)\vert =36n+18$. Also, the edge set of linear chain of TriCF structure is classified into two edge partitions depending on the vertex degrees are given by (see⁴⁴)

$$\begin{aligned}&E_{1,3}=\lbrace uv \in E(G)|d(u)=1, d(v)=3\rbrace ,\\&E_{2,3}=\lbrace uv \in E(G)|d(u)=2, d(v)=3\rbrace , \end{aligned}$$

such that

$$\begin{aligned} E_{1,3}=2n+4, \,\,\ E_{2,3}=34n+14. \end{aligned}$$

We have by the definition of first K-Banhatti index $B_1(G)$ is given by

$$\begin{aligned} B_1(G)&=\sum _{ue}\left[ d_{G}(u)+d_{G}(e)\right] , \quad \quad where,\,\ d_e=d_u+d_v-2\\&= \sum _{ue\in E_{1,3}}\left[ (d_{G}(u)+d_{G}(e))+(d_{G}(v)+d_{G}(e))\right] \\&\quad +\sum _{ue\in E_{2,3}}\left[ (d_{G}(u)+d_{G}(e))+(d_{G}(v)+d_{G}(e))\right] \\&= (2n+4)\left[ (1+2)+(3+2)\right] +(34n+14)\left[ (2+3)+(3+3)\right] \\&=390n+186, \\ \end{aligned}$$

similarly,

$$\begin{aligned}{} & {} B_2(G)= 526n+242, \ HB_1(G)= 2142n+990, \ HB_2(G)= 4058n+1798, \\{} & {} {}^mB_1(G)= \frac{203n+109}{15}, \ {}^mB_2(G)= \frac{97n+59}{9}, \ HB(G)= \frac{406n+2187}{15}. \end{aligned}$$

$\square$

Theorem 3.2

Let G be the the molecular graph Parellelogram TriCF. Then $B_1(G)$, $B_2(G)$, $HB_1(G)$, $HB_2(G)$, ${}^mB_1(G)$, ${}^mB_2(G)$, and HB(G) of a graph G are

$$\begin{aligned}&B_1(G)= (198n+192)n+192m-6 ,\ \ B_2(G)= (270m+256)n+256m-14, \\&HB_1(G)= (1098m+1044)n+1044m-54, \ \ HB_2(G)= (2016m+1952)n+1952m-154, \\&{}^mB_1(G)= \frac{(99m+104)n+104m+5}{15}, \ \ {}^mB_2(G)= \frac{(45m+52)n+52m+7}{9}, \ \ \text {and} \\&HB(G)= \frac{(198m+208)n+208m+10}{15}. \end{aligned}$$

Figure 5

Parallelogram TriCF structure.

Proof

From the Fig. 5, it is observed that, in general $\vert V(G)\vert =(13m+20)n+3$ and $\vert E(G)\vert =(18m+18)n+18m$. Also, the edge set of parellelogram TriCF structure is classified into two edge partitions depending on the vertex degrees are given by (see⁴⁴)

$$\begin{aligned}&E_{1,3}=\lbrace uv \in E(G)|d(u)=1, d(v)=3\rbrace ,\\&E_{2,3}=\lbrace uv \in E(G)|d(u)=2, d(v)=3\rbrace , \end{aligned}$$

such that

$$\begin{aligned} E_{1,3}=2n+2m+2, \,\ E_{2,3}=(18m+16)n+16m-2. \end{aligned}$$

We have by the definition of first K-Banhatti index $B_1(G)$ is given by

$$\begin{aligned} B_1(G)&=\sum _{ue}\left[ d_{G}(u)+d_{G}(e)\right] , \quad \quad where,\,\ d_e=d_u+d_v-2\\&= \sum _{ue\in E_{1,3}}\left[ (d_{G}(u)+d_{G}(e))+(d_{G}(v)+d_{G}(e))\right] \\ {}&\quad +\sum _{ue\in E_{2,3}}\left[ (d_{G}(u)+d_{G}(e))+(d_{G}(v)+d_{G}(e))\right] \\&= (2n+2m+2)\left[ (1+2)+(3+2)\right] +((18m+16)n+16m-2)\left[ (2+3)+(3+3)\right] \\&=390n+186, \end{aligned}$$

similarly,

$$\begin{aligned}&B_2(G)= (270m+256)n+256m-14, \ \ HB_1(G)= (1098m+1044)n+1044m-54, \\&HB_2(G)= (2016m+1952)n+1952m-154, \ \ {}^mB_1(G)= \frac{(99m+104)n+104m+5}{15}, \\&{}^mB_2(G)= \frac{(45m+52)n+52m+7}{9}, \ \ HB(G)= \frac{(198m+208)n+208m+10}{15}. \end{aligned}$$

$\square$

Theorem 3.3

Let G be the the molecular graph Hexagonal TriCF. Then $B_1(G)$,$B_2(G)$, $HB_1(G)$, $HB_2(G)$, ${}^mB_1(G)$, ${}^mB_2(G)$, and HB(G) of a graph G are

$$\begin{aligned}&B_1(G)= 594n^2-18n, \ \ B_2(G)= 810n^2-42n, \ \ HB_1(G)= 3294n^2-162n, \\&HB_2(G)= 6318n^2-462n, \ \ {}^mB_1(G)= \frac{99n^2+5n}{5}, \ \ {}^mB_2(G)= \frac{45n^2+7n}{3}, \\&\text { and }\ \ HB(G)= \frac{198n^2+10n}{5}. \end{aligned}$$

Figure 6

Hexagonal TriCF structure.

Proof

From the Fig. 6, it is observed that, in general $\vert V(G)\vert =45n^2+3n$ and $\vert E(G)\vert =54n^2$. Also, the edge set of hexagonal TriCF structure is classified into two edge partitions depending on the vertex degrees are given by (see⁴⁴)

$$\begin{aligned}&E_{1,3}=\lbrace uv \in E(G)|d(u)=1, d(v)=3\rbrace ,\\&E_{2,3}=\lbrace uv \in E(G)|d(u)=2, d(v)=3\rbrace , \end{aligned}$$

such that

$$\begin{aligned} E_{1,3}=6n, \,\ E_{2,3}=54n^2-6n. \end{aligned}$$

We have by the definition of first K-Banhatti index $B_1(G)$ is given by

$$\begin{aligned} B_1(G)&=\sum _{ue}\left[ d_{G}(u)+d_{G}(e)\right] , \quad \quad where,\,\ d_e=d_u+d_v-2\\&= \sum _{ue\in E_{1,3}}\left[ (d_{G}(u)+d_{G}(e))+(d_{G}(v)+d_{G}(e))\right] \\ {}&\quad +\sum _{ue\in E_{2,3}}\left[ (d_{G}(u)+d_{G}(e))+(d_{G}(v)+d_{G}(e))\right] \\&= (6n)\left[ (1+2)+(3+2)\right] +(54n^2-6n)\left[ (2+3)+(3+3)\right] \\&=594n^2-18n, \end{aligned}$$

similarly,

$$\begin{aligned}&B_2(G)= 810n^2-42n, \ \ HB_1(G)= 3294n^2-162n, \ \ HB_2(G)= 6318n^2-462n, \\&{}^mB_1(G)= \frac{99n^2+5n}{5}, \ \ {}^mB_2(G)= \frac{45n^2+7n}{3}, \ \ HB(G)= \frac{198n^2+10n}{5}. \end{aligned}$$

$\square$

Numerical and graphical representation and discussion

Figures 4, 5 and 6 showcase the structures of linear chain, Parallelogram and Hexagonal triazine -based covalent oraganic frame works (TriCF) for which the edge and vertex partitions are determined and hence the various forms of K-Banhatti indices are computed.

Figures 7, 8 and 9 represents the graphical comparison of K-Banhatti indices for linear chain TriCF ($n\in \{1,2,3,\dots , 10\}$), Parallelogram TriCF ($n\in \{1,2,3,\dots , 10\}$) and Hexagonal TriCF ($n\in \{1,2,3,\dots , 10\}$) respectively. The figures show that the first K-Banhatti index($B_1$) has more value compared with other K-Banhatti indices while $^mB_1$ and $^mB_2$ showcase the least values and hence it is very close to the x-axis in all the graphs for all triazine-based covalent organic frame works (CoF’s).

Table  11 shows the numerical comparison of K-Banhatti indices for linear chain TriCF structure which linearly increases as n increase. Table  12 shows the variation of the indices under the study for parallelogram TriCF which increases as n, m increase. Finally, Table  13 shows the increase in the indices as n increase.

Figure 7

Graphical comparison of K-Banhatti indices for linear chain TriCF, x-axis shows the numeral values of $n\in \{1,2,3,\dots , 10\}$.

Figure 8

Graphical comparison of K-Banhatti indices for Parellelogram TriCF, x-axis shows the numeral values of $n=m\in \{1,2,3,\dots , 10\}$.

Figure 9

Graphical comparison of K-Banhatti indices for Hexagonal TriCF, x-axis shows the numeral values of $n\in \{1,2,3,\dots , 10\}$.

Table 11 The comparison of K-Banhatti indices for linear chain of TriCF structure.

Table 12 The comparison of K-Banhatti indices for parellelogram TriCF structure.

Table 13 The comparison of K-Banhatti indices for hexagonal TriCF structure.

Conclusion

The molecules are modelled, and their physicochemical and biological properties are predicted using the Quantitative structure-property relationships (QSPR) studies. Topological index is a significant tool used by QSPR studies in encoding the information of a molecule. There are a bunch of topological indices which are of significant importance in the properties of the compounds based on its algorithm defined.

In this article, chemical applicability of $B_1(G)$, $B_2(G)$, $HB_1(G)$, $HB_2(G)$, ${}^mB_1(G)$, ${}^mB_2(G)$, and HB(G) for benzenoid hydrocarbons of a graph G are examined and it is observed that the considered indices (molecular descriptors) showed good predictive potential. Benzenoid hydrocarbons have numerous applications because of its unique physical and chemical properties. Some of them include paint thinners, laminates, cement, in medicine for curing bacterial infections, mosquito repellents, cosmetics, toothpaste, detergents, and a dyeing agent.

Also the above said indices are computed for triazine-based covalent organic frameworks (CoF’s). Triazine has wide applications in industries, where one of the famous forms being melamine. It is used in kitchen appliances and carpentry. Another form of triazine is cyanuric chloride that are used in reactive dyes and herbicides. It has several applications in oil, petroleum and gas processing industries. They are used to remove harmful hydrogen sulphide gas and other species from fluid streams in infrastructure. As the chemical compound, triazine has many applications especially in industries, the work can be extended for other indices using graph operators and see the variation. Also, it has applications in medical field, attracting the pharmacists and chemists in the usage of drug design and delivery.