Main

Modern atomic clocks embody Arthur Schawlow’s motto to "never measure anything but frequency". This deceptively simple principle, fuelled by the innovative development of laser science and quantum technologies based on ultracold matter, has led to marked progress in clock performance. Recently, clock measurement precision reached the mid-nineteenth digit in 1 h (refs. 5,6), and three atomic species achieved systematic uncertainties corresponding to an error equivalent to less than 1 s over the lifetime of the Universe7,8,9,10. Central to this success in neutral atom clocks is the ability to maintain extended quantum coherence times while using large ensembles of atoms5,6,11. The pace of progress has yet to slow. Continued improvement in measurement precision and accuracy arising from the confluence of metrology and quantum information science12,13,14,15 promises discoveries in fundamental physics16,17,18,19,20.

Clocks fundamentally connect space and time, providing exquisite tests of the theory of general relativity. Hafele and Keating took caesium-beam atomic clocks aboard commercial airliners in 1971, observing differences between flight-based and ground-based clocks consistent with special and general relativity21. More recently, RIKEN researchers compared two strontium optical lattice clocks (OLCs) separated by 450 m in the Tokyo Skytree, resulting in one of the most precise terrestrial redshift measurement to date22. Proposed satellite-based measurements23,24 will provide orders of magnitude improvement to current bounds on gravitational redshifts3,4. Concurrently, clocks are anticipated to begin playing important roles for relativistic geodesy25. In 2010, Chou et al.2 demonstrated the precision of their Al+ clocks by measuring the gravitational redshift resulting from lifting one clock vertically by 30 cm in 40 h. With a decade of advancements, today’s leading clocks are poised to enable local geodetic surveys of elevation at the subcentimetre level on Earth, complementing spatial averaging techniques26.

Atomic clocks strive to simultaneously optimize measurement precision and systematic uncertainty. For traditional OLCs operated with one-dimensional (1D) optical lattices, achieving low instability has involved the use of high atom numbers at trap depths sufficiently large to suppress tunnelling between neighbouring lattice sites. Although impressive performance has been achieved, effects arising from atomic interactions and a.c. Stark shifts associated with the trapping light challenge advancements in OLCs. Here we report a new operational regime for 1D OLCs, both resolving the gravitational redshift across our atomic sample and synchronously measuring a fractional frequency uncertainty of 7.6 × 10−21 between two uncorrelated regions. Our system employs approximately 100,000 87Sr atoms at about 100 nK loaded into a shallow, large-waist optical lattice, reducing both a.c. Stark and density shifts. Motivated by our earlier work on spin–orbit-coupled lattice clocks27,28, we engineer atomic interactions by operating at a ‘magic’ trap depth, effectively removing collisional frequency shifts. These advances enable optical atomic coherence of 37 s and expected single clock stability of 3.1 × 10−18 at 1 s using macroscopic samples, paving the way towards atomic lifetime-limited OLC operation.

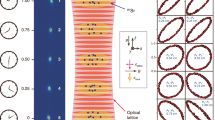
Central to our experiment is an in-vacuum optical cavity (Fig. 1a and Methods) for power enhancement of the optical lattice. The cavity (finesse 1,300) ensures wavefront homogeneity of our 1D lattice, and the large beam waist (260 μm) reduces the atomic density by an order of magnitude compared to that of our previous system10. We begin each experiment by trapping fermionic 87Sr atoms into the 1D lattice at a trap depth of 300 lattice photon recoil energies (Erec), loading a millimetre-scale atomic sample (Fig. 1a). Atoms are simultaneously cooled and polarized into a single nuclear spin before the lattice is adiabatically ramped to an operational depth of 12 Erec. Clock interrogation proceeds by probing the ultranarrow 1S0 (\(g\)) → 3P0 (\(e\)) transition with the resulting excitation fraction measured by fluorescence spectroscopy. Scattered photons are collected on a camera, enabling in situ measurement with 6 μm resolution, corresponding to about 15 lattice sites.

Fig. 1: Experimental system and quantum state control.
figure 1

a, A millimetre-length sample of about 100,000 87Sr atoms trapped within a 1D optical lattice Elattice formed in an in-vacuum cavity. The longitudinal axis of the cavity, z, is oriented along gravity. We probe atoms along the 1S0 → 3P0 transition using a clock laser Eclock locked to an ultrastable crystalline silicon cavity6,35. b, Rabi spectroscopy with a 3.1 s pulse time. Open purple circles indicate data with a corresponding Rabi fit in green. c, Neighbouring lattice sites are detuned by the gravitational potential energy difference, creating a Wannier–Stark ladder. Clock spectroscopy probes the overlap of Wannier–Stark states between lattice sites that are m sites away with Rabi frequency Ωm. d, Rabi spectroscopy probes Wannier–Stark state transitions, revealing wavefunction delocalization of up to five lattice sites. The number of lattice sites is indicated above each transition, with blue (red) denoting Wannier–Stark transitions to higher (lower) lattice sites.

Full size image

Quantum state control has been vital to recent advances in atom–atom and atom–light coherence times in 3D OLCs and tweezer clocks5,11,15. Improved quantum state control is demonstrated through precision spectroscopy of the Wannier–Stark states of the OLC29,30. The 1D lattice oriented along gravity has the degeneracy of neighbouring lattice sites lifted by the gravitational potential energy. In the limit of shallow lattice depths, this creates a set of delocalized states. By ramping the lattice depth to 6 Erec, much lower than in traditional 1D lattice operations7,8,10, clock spectroscopy probes this delocalization (Fig. 1d). The ability to engineer the extent of atomic wavefunctions through the adjustment of trap depth creates an opportunity to control the balance of on-site p-wave versus neighbouring-site s-wave atomic interactions. We utilize this tunability by operating at a ‘magic’ trap depth31, at which the frequency shifts arising from on-site and off-site atomic interactions cancel, enabling a reduction of the collisional frequency shifts by more than three orders of magnitude compared with that in our previous work10.

Extended atomic coherence times are critical for both accuracy and precision. An aspirational milestone for clock measurement precision is the ability to coherently interrogate atomic samples up to the excited state’s natural lifetime. To evaluate the limits of our clock’s atomic coherence, we perform Ramsey spectroscopy to measure the decay of fringe contrast as a function of the free-evolution time. By comparing two uncorrelated regions within our atomic sample, we determine the contrast and relative phase difference between the two sub-ensembles (Fig. 2). The contrast decays exponentially with a time constant of 37 s (quality factor of 3.6 × 1016), corresponding to an extra decoherence time of 53 s relative to the 3P0 natural lifetime (118 s)32. To our knowledge, this represents the longest optical atomic coherence time measured in any spectroscopy system to date.

Fig. 2: Atomic coherence.
figure 2

We use Ramsey spectroscopy with a randomly sampled phase for the second pulse to determine the coherence time of our system11. a, We measure the excitation fraction across the cloud, shown in purple for a single measurement, and calculate the average excitation fractions in regions p1 and p2, separated by two pixels. b, Parametric plots of the excitation fraction of p1 versus p2 in purple for 6 s, 30 s and 50 s dark time demonstrate a phase shift between the two regions and contrast decay. Using a maximum likelihood estimator, we extract the phase and contrast for each dark time with the fit, shown in green. c, Contrast decay as a function of time in green is fitted with an exponential decay in gold, giving an atomic coherence decay time of 36.5(0.7) s and a corresponding quality factor of 3.6 × 1016. After accounting for the finite radiative decay contribution, we infer an extra decoherence time constant of 52.8(1.5) s.

Full size image

We utilize Rabi spectroscopy in conjunction with in situ imaging to microscopically probe clock transition frequencies along the entire vertically oriented atomic ensemble. With a standard interleaved probing sequence using the \({{|g},{m}}_{{\rm{F}}}=\pm \frac{5}{2}\rangle \) to \({{|e},{m}}_{{\rm{F}}}=\pm \frac{3}{2}\rangle \) transitions for minimal magnetic sensitivity, we reject the first-order Zeeman shifts and vector a.c. Stark shifts. The in situ imaging of atoms in the lattice allows measurement of unprocessed frequencies across the entire atomic sample (Fig. 1a and Methods). The dominant differential perturbations arise from atom–atom interactions (residual density shift contributions after we operate at the ‘magic’ trap depth) and magnetic field gradients giving rise to pixel-specific second-order Zeeman shifts. Using the total camera counts and mF-dependent frequency splitting, we correct the density and second-order Zeeman shift at each pixel. These corrections result in the processed frequencies per pixel shown in Fig. 3a, with error bars representing the quadrature sum of statistical uncertainties from the centre frequency, the density shift correction and the second-order Zeeman shift correction. Other systematics are described in the Methods. This approach demonstrates an efficient method for rapid and accurate evaluation of various systematic effects throughout a single atomic ensemble. In contrast to traditional 1D OLCs for which systematic uncertainties are quoted as global parameters, here we microscopically characterize these effects.

Fig. 3: Evaluating frequency gradients.
figure 3

a, For each measurement, we construct a microscopic frequency map across the sample, with raw frequencies shown in green. The second-order Zeeman correction is shown as a dashed gold line. Processed frequencies shown in purple include both density shift corrections and second-order Zeeman corrections, with error bars arising from the quadrature sum of statistical, density shift correction and second-order Zeeman correction uncertainties. To this, we fit a linear function, shown in black. b, Over the course of 10 days, we completed 14 measurements. For each measurement, we create a corrected frequency map and fit a linear slope as in a. This slope is plotted for each measurement, as well as a weighted mean (black) with associated statistical uncertainty (dashed black) and total uncertainty as reported in Extended Data Table 1 (dotted black). The expected gravitational gradient is shown in red. All data are taken with Rabi spectroscopy using a 3.1 s π-pulse time except for 13 August, which used a 3.0 s pulse time. The reduced chi-square statistic is 3.0, indicating a small underestimation of error variances entirely consistent with the other systematic uncertainties in Extended Data Table 1.

Full size image

This new microscopic in situ imaging allows determination of the gravitational redshift within a single atomic sample, probing an uncharacterized fundamental clock systematic. Two identical clocks on the surface of a planet separated by a vertical distance \(h\) will differ in frequency (\(\delta f)\) as given by

$$\frac{\delta f}{f}=\frac{ah}{{c}^{2}},$$
(1)

in which \(f\) is the clock frequency, \(c\) is the speed of light, and \(a\) is the gravitational acceleration. The gravitational redshift at Earth’s surface corresponds to a fractional frequency gradient of −1.09 × 10−19 mm−1 in the coordinate system of Fig. 1a. Measurement of a vertical gradient across the atomic sample consistent with the gravitational redshift provides an exquisite verification of an individual atomic clock’s frequency control.

Our intra-cloud frequency map (Fig. 3a) allows us to evaluate gradients across the atomic sample. Over 10 days, we performed 14 measurements (ranging in duration from 1 to 17 h) to search for the gravitational redshift across our sample. For each, we fit a linear slope and offset after taking into account density shift and second-order Zeeman corrections, reporting the slope in Fig. 3b. From this measurement campaign we find the weighted mean (standard error of the weighted mean) of the frequency gradient in our system to be −1.00(12) × 10−19 mm−1. We evaluate other differential systematics (see Methods) and find a final frequency gradient of −9.8(2.3) × 10−20 mm−1, consistent with the predicted redshift.

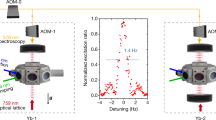
The ability to resolve the gravitational redshift within our system suggests a level of frequency control beyond previous clock demonstrations, vital for the continued advancement of clock accuracy and precision. Previous fractional frequency comparisons15 have reached uncertainties as low as 4.2 × 10−19. Similarly, we perform a synchronous comparison between two uncorrelated regions of our atomic cloud (Fig. 4a). By binning about 100 pixels per region, we substantially reduce instability caused by quantum projection noise33. Analysing the frequency difference between regions from 92 h of data, we find a fractional frequency instability of 4.4 × 10−18/\(\surd \tau \) (\(\tau \) is the averaging time in seconds), resulting in a fractional frequency uncertainty of 7.6 × 10−21 for full measurement time, nearly two orders of magnitude lower than the previous record. From this measurement we infer a single region instability of 3.1 × 10−18/\(\surd \tau \). Dividing the fractional frequency difference by the spatial separation between each region’s centre of mass gives a frequency gradient of −1.30(18) × 10−19 mm−1. Correcting for other systematics as before results in a gradient of −1.28(27) × 10−19 mm−1, again fully consistent with the predicted redshift.

Fig. 4: In situ synchronous clock comparison.
figure 4

a, The atomic cloud is separated as in Fig. 2a. The gravitational redshift leads to the higher clock (blue) ticking faster than the lower one (red). The length scale is in millimetres. b, Allan deviation of the frequency difference between the two regions in a over 92 h. Purple points show fractional frequency instability fitted by the solid green line, with the quantum projection noise limit indicated by the dashed black line. We attribute the excess instability of the measurement relative to quantum projection noise to detection noise. The expected single atomic region instability is shown in gold.

Full size image

In conclusion, we have established a new paradigm for atomic clocks. The greatly improved atomic coherence and frequency homogeneity throughout our sample allow us to resolve the gravitational redshift at the submillimetre scale, observing for the first time the frequency gradient from gravity within a single sample. We demonstrate a synchronous clock comparison between two uncorrelated regions with a fractional frequency uncertainty of 7.6 × 10−21, advancing precision by nearly two orders of magnitude. These results suggest that there are no fundamental limitations to inter-clock comparisons reaching frequency uncertainties at the 10−21 level, offering new opportunities for tests of fundamental physics.

Note added in proof: While performing the work described here, we became aware of complementary work in which high measurement precision was achieved for simultaneous differential clock comparisons between multiple atomic ensembles in vertical 1D lattices separated by centimetre-scale distances using a hertz-linewidth clock laser34.

Methods

In-vacuum cavity

Central to our system is an in-vacuum lattice buildup cavity oriented along gravity (Fig. 1a). Two mirrors with radius of curvature of 1 m are separated by around 15 cm, achieving a mode waist of 260 μm. Our over-coupled cavity has a finesse at the lattice wavelength (813 nm) of approximately 1,300 and a power buildup factor of about 700 (ratio of circulating to input intensity). This enables lattice depths in excess of 500 Erec (lattice photon recoil energy) using a diode-based laser system. The dimensional stability of the cavity combined with the simplified diode laser system enables robust operation compared with that of our previous Ti:sapphire retro-reflected design10. The cavity mirrors are anti-reflection coated at the clock wavelength of 698 nm.

One cavity mirror is mounted to a piezo for length stabilization and the other mirror is rigidly mounted for phase reference for the clock laser. Grounded copper shields between atoms and mirrors prevent d.c.-Stark-induced shifts due to charge buildup on the mirrors and piezo36,37. Each shield (5 mm thick) has a centred hole of 6 mm diameter to accommodate the optical lattice beam, with shielding performance verified through evaluation of the d.c. Stark shift systematic.

Atomic sample preparation

87Sr atoms are cooled and loaded into a 300-Erec optical lattice using standard two-stage magneto-optical trapping techniques10. Once trapped, atoms are simultaneously nuclear spin polarized, axially sideband cooled and radially Doppler cooled into a single nuclear spin state at temperatures of 800 nK. The lattice is then adiabatically ramped to the operational trap depth of 12 Erec, at which a series of pulses addressing the clock transition prepares atoms into \({{|g},{m}}_{{\rm{F}}}=\pm \frac{5}{2}\rangle \). Clock spectroscopy is performed by interrogating the \({{|g},{m}}_{{\rm{F}}}=\pm \frac{5}{2}\rangle \) to \({{|e},{m}}_{{\rm{F}}}=\pm \frac{3}{2}\rangle \) transition, the most magnetically insensitive 87Sr clock transition6.

Imaging

The clock excitation fraction is read out using standard fluorescence spectroscopy techniques6,10,38. Photons are collected on both a photomultiplier tube for global readout and an electron-multiplying charge-coupled device camera for an in situ readout of clock frequency. Camera readout is performed in full vertical binning mode, averaging the radial dimension of the lattice. This provides 1D in situ imaging for all synchronous evaluations.

We use a 25 -μs-fluorescence probe with an intensity of I/Isat ≈ 20 (Isat being the saturation intensity), ensuring uniform scattering across the atomic sample. Before imaging, the optical lattice is ramped back to 300 Erec to decrease imaging aberration resulting from the extended radial dimension at 12 Erec.

Analysis

Standard clock lock techniques and analysis are used6,11,33, with differences in excitation fraction converted to frequency differences using Rabi lineshapes. Each dataset is composed of a series of clock locks, tracking the centre-of-mass frequency of the atomic sample. A clock lock is four measurements probing alternating sides of the Rabi lineshape for opposite nuclear spin transitions. Frequency corrections based on excitation fraction become ambiguous when the excitation fraction measured is consistent with the Rabi lineshape at multiple detunings. To avoid erroneous frequency corrections, we remove clock locks with excitation fractions above (below) 0.903 × C (0.116 × C), in which C is the Rabi contrast. From each clock lock, a pixel-specific centre frequency fi and frequency splitting between opposite mF states Δi are calculated, creating an in situ frequency map of the 1D atomic sample. This allows rejection of vector shifts on a pixel-by-pixel basis and probes the magnetic-field-induced splitting of mF transitions. The atom-weighted mean frequency is subtracted from every lock cycle to reject common mode laser noise.

For each dataset, we approximate the atomic profile with a Gaussian fit, identifying a centre pixel and associated Gaussian width (σ). All analysis is performed within the central region of ±1.5σ that demonstrates the lowest frequency instability. Identifying a centre pixel for data processing ensures rejection of any day-to-day drift in the position of the cloud due to varying magnetic fields modifying magneto-optical trap operation on the narrow line transition. The density shift coefficient (see the section entitled Density shift) is derived from the average centre frequency per pixel. Using this coefficient, we correct fi and Δi for the density shift. Second-order Zeeman corrections using these updated frequencies are then applied.

Gradient analysis is based on the processed centre frequencies per pixel. A linear fit to the frequencies as a function of pixel is performed using least squares, with uncertainty per pixel arising from the quadrature sum of statistical frequency uncertainty, statistical second-order Zeeman uncertainty and density shift correction uncertainty.

For the two-clock comparison (Fig. 4b), all data from 14–22 August were taken with the same duty cycle and π-pulse time (3.1 s). Data were processed relative to a fitted centre pixel as discussed and concatenated. Two equal regions extend from the centre of the sample to a width of ±1.5σ, with two empty pixels between regions to ensure uncorrelated samples. Each region is processed for the atom-weighted mean frequency, enabling a synchronous frequency comparison between two independent clocks.

Atomic coherence

We use a Ramsey sequence to measure the atomic coherence. We prepare a sample in the \({{|g},{m}}_{{\rm{F}}}=+\frac{5}{2}\rangle \) state and apply a π/2 pulse along the \({{|g},{m}}_{{\rm{F}}}=+\frac{5}{2}\rangle \) to \({{|e},{m}}_{{\rm{F}}}=+\frac{3}{2}\rangle \) transition. After waiting for a variable dark time, we apply a second π/2 pulse with a random phase relative to the first. We then measure the excitation fraction.

Two regions, p1 and p2, are identified using the same technique as in the synchronous instability measurement. For each experimental sequence, we find the average excitation fraction in p1 and p2. A mean frequency shift across the sample primarily due to a magnetic field gradient creates a differential phase as a function of time between p1 and p2. We create a parametric plot of the average excitation in p1 and p2 for each dark time and use a maximum likelihood estimator to fit an ellipse to each dataset, calculating phase and contrast11,15. To estimate uncertainty in the contrast for each dark time, a bootstrapping technique is used11. Fitting the contrast as a function of dark time with a single exponential returns an effective atomic coherence time.

Systematics

Imaging

We calibrate our pixel size using standard time-of-flight methods, observing an atomic sample in freefall for varying times to determine an effective pixel size along the direction of gravity. Immediately after our 10-day data campaign, we measured our effective pixel size to be 6.04 μm. Owing to thermal drift of our system, the pixel size can vary by up to 0.5 μm per pixel over months, which we take as the calibration uncertainty.

Spatial correlations may limit imaging resolution. We measure these correlations by placing atoms into a superposition of clock states. Any measured spatial correlation of excitation fraction is due to the imaging procedure. In our system we find no correlations between neighbouring pixels11. The optical resolution of our imaging lens is specified at 2 μm.

Lattice tilt from gravity will modify the measured gradient. We find the lattice tilt in the imaging plane to be 0.11(0.06) degrees, providing an uncertainty orders of magnitude smaller than the pixel size uncertainty. We are insensitive to lattice tilt out of the imaging plane.

Zeeman shifts

First-order Zeeman shifts are rejected by probing opposite nuclear spin states6. The second-order Zeeman shift is given by

$$\Delta {\nu }_{{\rm{B}},2}=\xi {\left(\Delta {\nu }_{{\rm{B}},1}\right)}^{2},$$

in which \(\Delta {\nu }_{{\rm{B}},1}\) is the splitting between opposite spin states and \(\xi \) is the corresponding second-order Zeeman shift coefficient. For stretched spin state operation (\({m}_{{\rm{F}}}=\pm \frac{9}{2}\)), \(\xi \)= −2.456(3) × 10−7 Hz−1. Using known atomic coefficients39 we find the second-order Zeeman coefficient for the \({{|g},{m}}_{{\rm{F}}}=\pm \frac{5}{2}\rangle \) to \({{|e},{m}}_{{\rm{F}}}=\pm \frac{3}{2}\rangle \) transition to be \({\xi }_{{\rm{op}}}\)= −1.23(8) × 10−4 Hz, with the uncertainty arising from limited knowledge of atomic coefficients.

The second-order Zeeman corrections are made for every clock lock (analogous to the in situ density shift corrections). For a typical day (13 August), the average second-order Zeeman gradient is −7.0 × 10−20 mm−1, corresponding to a splitting between opposite nuclear spin states of 12.7 mHz mm−1 (0.291 mG mm−1). We include an error of 4 × 10−21 mm−1 in Extended Data Table 1 to account for the atomic uncertainty in the shift coefficient.

d.c. Stark

Electric fields perturb the clock frequency through the d.c. Stark effect. We evaluate gradients arising from this shift by using in-vacuum quadrant electrodes to apply bias electric fields in all three dimensions. We find a d.c. Stark gradient of 3(2) × 10−21 mm−1.

Black body radiation shift

The dominant frequency perturbation to room-temperature neutral atom clocks is black body radiation (BBR). As in our previous work10, we homogenize this shift by carefully controlling the thermal surroundings of our vacuum chamber. Attached to the vacuum chamber are further temperature control loops, with each vacuum viewport having a dedicated temperature control system. This ensures that our high-emissivity glass viewports—responsible for the largest part of the BBR contribution—are all the same temperature to within 100 mK.

To bound possible BBR gradients, we introduce a 1 K gradient between the top and bottom of the chamber along the cavity axis by raising either the top or bottom viewports by 1 K. We compare these two cases and find no statistically significant changes in the frequency gradient across the entire sample. Accounting for uncertainty in linear frequency fits for each case, we estimate an uncertainty of 3 × 10−21 mm−1. This finding is supported with a basic thermal model of the vacuum chamber.

Density shift

Atomic interactions during Rabi spectroscopy lead to clock frequency shifts as a function of atomic density40. For each gradient measurement, we evaluate the density shift coefficient \({\chi }_{{\rm{dens}}}\) by fitting the average frequency \(f\) per pixel versus average camera counts per pixel \(N\) to an equation of the form

$$f\left(N\right)={\chi }_{{\rm{dens}}}N+B.$$

Here B is an arbitrary offset. Once \({\chi }_{{\rm{dens}}}\) is known, we remove the density shift at each pixel.

Residual density shift corrections may lead to error in our linear gradient. To bound this effect, we compare the density shift coefficient and gradient from our data run with a separate dataset at 8 Erec. With the trap depth at 8 Erec we found a linear gradient of s = −1.08 × 10−18 mm−1 and a density shift coefficient of \({\chi }_{8}\) = −1.39 × 10−6 Hz per count. During our data run we had an average density shift coefficient of \({\chi }_{{\rm{op}}}\) = −2.43 × 10−8 Hz per count. We bound the uncertainty in our gradient from density shift as \({\sigma }_{{\rm{d}}{\rm{e}}{\rm{n}}{\rm{s}},{\rm{u}}{\rm{n}}{\rm{c}}}=|s\times \frac{{\chi }_{{\rm{o}}{\rm{p}}}}{{\chi }_{8}}\)| = 1.7 × 10−20 mm−1.

Lattice light shifts

Lattice light shifts arise from differential a.c. Stark shifts between the ground and excited clock states. An approximate microscopic model of the lattice light shift (\({\nu }_{{\rm{LS}}}\)) in our system is given by41

$$h{\nu }_{{\rm{LS}}}\left(u,{\delta }_{{\rm{L}}}\right)\approx \left(\frac{\delta \Delta {\alpha }^{{\rm{E}}1}}{\delta \nu }{\delta }_{{\rm{L}}}-{\Delta \alpha }_{{\rm{QM}}}\right)\frac{{u}^{\frac{1}{2}}}{2}-\left[\frac{\delta {\alpha }^{{\rm{E}}1}}{\delta \nu }{\delta }_{{\rm{L}}}\right]u,$$

in which \(u\) is the trap depth in units of Erec, \(\Delta {\alpha }^{{\rm{E}}1}\) is the differential electric dipole polarizability, \(\Delta {\alpha }^{{\rm{QM}}}\) is the differential multi-polarizability, and \({\delta }_{{\rm{L}}}=({\nu }_{{\rm{L}}}-{\nu }^{{\rm{E}}1})\) is the detuning between lattice frequency \({\nu }_{{\rm{L}}}\) and effective magic frequency \({\nu }^{{\rm{E}}1}\). Our model has no dependence on the longitudinal vibrational quanta because we are in the ground vibrational band. We neglect higher-order corrections from hyperpolarizability due to our operation at depths <60 Erec. At our temperatures, thermal averaging of the trap depth is a higher-order correction (< 5%) that is also neglected.

We model the linear differential lattice light shift across the atomic cloud as

$$\frac{\delta h{\nu }_{{\rm{LS}}}\left(u{,\delta }_{{\rm{L}}}\right)}{\delta z}\approx \left[\frac{\left(\frac{\delta {\alpha }^{{\rm{E}}1}}{\delta \nu }{\delta }_{{\rm{L}}}-{\alpha }_{{\rm{QM}}}\right)}{4{u}^{\frac{1}{2}}}-\frac{\delta {\alpha }^{{\rm{E}}1}}{\delta \nu }{\delta }_{{\rm{L}}}\right]\frac{\delta u}{\delta z},$$

in which z is the coordinate corresponding to the axis of the cavity along gravity. To evaluate our differential lattice light shift at our operational depth, we need \({\delta }_{{\rm{L}}}\) and \(\frac{\delta u}{\delta z}\). We modulate our lattice between two trap depths (u1 = 14 Erec, u2 = 56 Erec) and find our detuning from scalar magic frequency to be \({\delta }_{{\rm{L}}}\) = 7.4(0.6) MHz. To evaluate \(\frac{\delta u}{\delta z}\) at our operational depth (\({u}_{{\rm{op}}})\), we measure the linear gradient across the atomic cloud at \({\delta }_{{\rm{L}}}\) + 250 MHz and \({\delta }_{{\rm{L}}}\)− 250 MHz, the difference given by

$$\frac{\delta h{\nu }_{{\rm{LS}}}\left({u}_{{\rm{op}}},{\delta }_{{\rm{L}}+250{\rm{MHz}}}\right)}{\delta z}-\frac{\delta h{\nu }_{{\rm{LS}}}\left({u}_{{\rm{op}}},{\delta }_{{\rm{L}}-250{\rm{MHz}}}\right)}{\delta z}\approx \left[\frac{1}{4{u}_{{\rm{op}}}^{\frac{1}{2}}}-1\right]\frac{\delta {\alpha }^{{\rm{E}}1}}{\delta \nu }{\delta }_{500}\frac{\delta {u}_{{\rm{op}}}}{\delta z},$$

in which \({\delta }_{500}\) = 500 MHz. We find \(\frac{\delta {u}_{{\rm{op}}}}{\delta z}=\) 0.0383 mm−1, which when combined with \({\delta }_{{\rm{L}}}\) = 7.4 MHz, gives us a fractional frequency gradient of −5 × 10−21 mm−1. Accounting for error in our lattice detuning and linear gradient gives us an uncertainty of 1 × 10−21 mm−1.

Other systematics

For a 3.1-s π pulse, the probe a.c. Stark shift7 is −3(2) × 10−21. A frequency scan of the \({{|g},{m}}_{{\rm{F}}}=-\frac{5}{2}\rangle \) to \({{|e},{m}}_{{\rm{F}}}=-\frac{3}{2}\rangle \) transition limits the variation of excitation fraction across the atomic sample to 1% or below, bounding any possible probe a.c. Stark gradient across the sample to <1 × 10−22.

Known redshift

The gravitational acceleration (rounding to 4 digits) in our laboratory was evaluated by the United States National Geodetic Survey42 to be a = −9.796 m s−2.