Thermodynamic signatures of quantum criticality in cuprate superconductors

Abstract

The three central phenomena of cuprate (copper oxide) superconductors are linked by a common doping level p*—at which the enigmatic pseudogap phase ends and the resistivity exhibits an anomalous linear dependence on temperature, and around which the superconducting phase forms a dome-shaped area in the phase diagram¹. However, the fundamental nature of p* remains unclear, in particular regarding whether it marks a true quantum phase transition. Here we measure the specific heat C of the cuprates Eu-LSCO and Nd-LSCO at low temperature in magnetic fields large enough to suppress superconductivity, over a wide doping range² that includes p*. As a function of doping, we find that C_el/T is strongly peaked at p* (where C_el is the electronic contribution to C) and exhibits a log(1/T) dependence as temperature T tends to zero. These are the classic thermodynamic signatures of a quantum critical point^3,4,5, as observed in heavy-fermion⁶ and iron-based⁷ superconductors at the point where their antiferromagnetic phase comes to an end. We conclude that the pseudogap phase of cuprates ends at a quantum critical point, the associated fluctuations of which are probably involved in d-wave pairing and the anomalous scattering of charge carriers.

Main

In the phase diagram of several organic, heavy-fermion and iron-based superconductors, superconductivity forms a dome around the quantum critical point (QCP), where a phase of antiferromagnetic order ends. The spin fluctuations associated with that QCP are believed to cause both pairing and scattering⁴. The scattering is anomalous in that it produces a resistivity with a linear temperature dependence as T → 0, instead of the conventional T² dependence of a Fermi liquid^3,5,8. In hole-doped cuprates, the same features—a T_c dome and a T-linear resistivity—are also observed¹, but not at the critical doping where the Néel temperature T_N for the onset of long-range antiferromagnetic order vanishes. Instead, they are observed near the doping level p* where the pseudogap phase ends (Extended Data Fig. 1) and the essential nature of this phase remains unknown—it is the central enigma of cuprates.

The thermodynamic signature of a QCP is a diverging electronic mass. For an antiferromagnetic QCP in two dimensions, for example, the mass is expected to follow m* ∝ log(1/|x − x*|) and the specific heat C to follow C/T ∝ log(1/|x − x*|), as the system is moved towards its QCP at x* by varying some tuning parameter x, such as pressure or concentration³. This is what is observed in the iron-based superconductor BaFe₂(As_1−xP_x)₂ at its antiferromagnetic QCP (tuned by P concentration), both in the carrier mass m* measured via quantum oscillations and in the electronic specific heat estimated from the jump at T_c^5,7. At x = x*, we expect that C/T ∝ log(1/T), as observed in the heavy-fermion metal CeCu_6−xAu_x at its antiferromagnetic QCP (tuned by Au concentration)^3,6. This logarithmic divergence of C/T as T → 0 is the true sign of an energy scale that vanishes at x*.

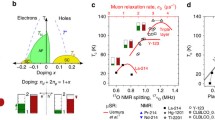
In the cuprate YBa₂Cu₃O_y (YBCO), a study of quantum oscillations⁹ has revealed an increase in m* as p approaches the pseudogap critical doping p* ≈ 0.19, suggesting that p* may be a QCP. The low value of m* at p = 0.10–0.12 is consistent with specific heat data¹⁰ (modulo a residual value attributed to CuO chains) and its increase versus p is consistent with the dramatic increase in the magnitude of the specific heat jump at T_c—that is, ΔC/T_c^11,12—which reaches its maximal value at p* (Fig. 1). However, to conclude that there is quantum criticality, what is missing is a direct measurement of the normal-state specific heat of a cuprate as T → 0, across p*. This is what we report here.

Fig. 1: Specific heat data in various cuprates.

Electronic specific heat coefficient γ (= C_el/T at T → 0) in non-superconducting Tl-2201 at p = 0.33 ± 0.02 (solid orange diamond, left axis)¹⁸ and in the field-induced normal state of YBCO at p = 0.10, 0.11 and 0.12 (solid blue circles, left axis¹⁰; a background zero-field component attributed to CuO chains is removed from these γ values). Also shown are the values of γ obtained from the effective mass m* measured by quantum oscillations in YBCO at 0.08 < p < 0.16 (open blue circles, left axis)⁹, Tl-2201 at p = 0.29 ± 0.02 (open orange diamond, left axis)¹⁹ and Hg-1201 at p ≈ 0.1 (open green square, left axis)²². The jump in specific heat at T_c, ΔC/T_c (defined in Extended Data Fig. 3), measured in Ca-doped YBCO (open blue triangles)¹² is plotted for comparison (right axis). (We note that ΔC/T_c is not a direct measurement of γ, and that it is affected by pair breaking due to disorder, more so as T_c decreases.) The doping p is taken from the original papers^{9,10,12,19,22}, except for Tl-2201 at p = 0.33, where it is estimated from the fact that the sample is non-superconducting¹⁸ and that the the T_c dome ends at p = 0.31 (ref. ¹⁹). The units are expressed per mole of planar Cu. The dashed blue line marks the pseudogap critical point p* in YBCO. The solid line is a guide to the eye. The vertical and horizontal error bars are taken from the original literature, except for the horizontal error bars on the two Tl-2201 points, which reflect the uncertainty in our estimates of the doping for those samples.

We have measured C(T) in the closely related cuprate materials La_1.8−xEu_0.2Sr_xCuO₄ (Eu-LSCO) and La_1.6−xNd_0.4Sr_xCuO₄ (Nd-LSCO). Because of their low T_c (<20 K), superconductivity can be fully suppressed with a readily accessible magnetic field (about 15 T). The two materials have the same crystal structure and phase diagram, with very similar boundaries for the pseudogap phase, T*(p) (Extended Data Fig. 1) and superconducting phase, T_c(p) (Extended Data Fig. 2). In Nd-LSCO, resistivity and Hall effect measurements yield p* = 0.23 ± 0.01 (ref. ²). At p = 0.24, ρ(T) is linear in T as T → 0, the signature of quantum criticality in electrical transport. A very similar behaviour is observed in Eu-LSCO (Extended Data Fig. 2). We deduce that p* ≈ 0.23 also in Eu-LSCO.

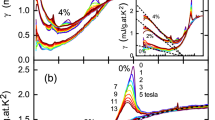
The specific heat of five crystals of Eu-LSCO and seven crystals of Nd-LSCO was measured below 10 K (Supplementary Fig. 1). The normal-state specific heat is obtained by applying a magnetic field of either H = 8 T or 18 T (Extended Data Figs. 3, 4). In Fig. 2a, c, we show normal-state data at H = 18 T in Eu-LSCO and Nd-LSCO, respectively, plotted as C/T versus T². We note that the magnetic moment on the Nd produces a Schottky anomaly in the specific heat of Nd-LSCO (C_mag), not present in Eu-LSCO (since Eu has no moment). At H = 0, this anomaly leads to a large increase of C/T at low T. However, a magnetic field moves this Schottky contribution to higher temperature, so that it becomes negligible below about 5 K at 18 T (Extended Data Fig. 5c).

Fig. 2: Specific heat of Eu-LSCO and Nd-LSCO.

a, Specific heat of Eu-LSCO measured in a field H = 18 T, plotted as C/T versus T², for four different dopings, as indicated. The dashed line is a linear fit to the data at p = 0.11 (blue) for T < 5 K; it yields γ = 2.8 mJ K⁻² mol⁻¹ and β = 0.22 mJ K⁻⁴ mol⁻¹, where C/T = γ + βT². (Data for our five crystals of Eu-LSCO are displayed in Supplementary Fig. 1.) b, Electronic specific heat of Eu-LSCO, C_el(T), obtained as described in Methods, plotted as C_el/T versus logT, from data at H = 8 T (p = 0.11 and 0.24) and at H = 18 T (p = 0.21). (The dashed line is a linear extrapolation of the p = 0.21 data.) At p = 0.11, C_el/T = γ, a constant, while at p = 0.24 ≈ p*, C_el/T ≈ log(1/T), the thermodynamic signature of a quantum critical point. c, Specific heat of Nd-LSCO measured in a field H = 18 T, plotted as C/T versus T², for four dopings, as indicated. (Data for our seven crystals of Nd-LSCO are displayed in Supplementary Fig. 1.) The dashed line is a linear fit to the data at p = 0.12, C/T = γ + βT² (below 5 K), giving γ = 3.6 mJ K⁻² mol⁻¹ and β = 0.215 mJ K⁻⁴ mol⁻¹. d, Electronic specific heat of Nd-LSCO, obtained as described in Methods, plotted as C_el/T versus logT. This is done separately for the data below (H = 8 T) and above (H = 18 T) the dashed line. At p = 0.24 ≈ p*, C_el/T ≈ log(1/T), just as in Eu-LSCO.

In Fig. 3a, we plot the raw data at T = 2 K (and H = 18 T), C/T versus p, for all 12 crystals. The 12 data points fall on the same smooth curve, demonstrating a high level of quantitative fidelity and reproducibility. Because the magnetic and nuclear Schottky contributions (C_mag and C_nuclear; see Methods) are both negligible at 2 K, we have C = C_el + C_ph, the sum of the electronic and phononic contributions. In Eu-LSCO at p = 0.11 and p = 0.16, the data obey C/T = γ + βT² below T ≈ 5 K (Fig. 2a). The residual linear term γ is electronic and the second term is due to phonons, with β ≈ 0.22 mJ K⁻⁴ mol for both dopings. The same is true in Nd-LSCO at p = 0.12 (Fig. 2c) and p = 0.15 (Supplementary Fig. 1c), again with β ≈ 0.22 mJ K⁻⁴ mol for both dopings. In Extended Data Fig. 6d, we plot β versus p for all our samples. We see that β is constant between p = 0.1 and p = 0.4, within error bars. As a result, C_ph/T is a small constant background in that range (see dashed lines in Fig. 3a).

Fig. 3: Doping dependence of the electronic specific heat.

a, Raw data for C/T in Eu-LSCO (squares) and Nd-LSCO (circles) at T = 2 K and H = 18 T (solid red symbols) and at T = 1 K and H = 8 T (solid orange squares). We also include data points for non-superconducting LSCO at H = 0 (diamonds), at T = 2 K (red) and T = 1 K (orange), at p = 0.33 (ref. ¹³). Open circles are (C – C_mag)/T at T = 2 K, obtained on polycrystalline samples of Nd-LSCO (Extended Data Figs. 7, 8). The dashed lines indicate the phonon contribution, C_ph/T = βT², to the specific heat of Nd-LSCO, at T = 2 K (red) and T = 1 K (orange) (Extended Data Fig. 6d). Error bars are explained inMethods. Horizontal error bars reflect the uncertainty in the doping p for each sample, as reported in ref. ² for the Nd-LSCO crystals and ref. ¹³ for the LSCO sample. For the Eu-LSCO crystals, the uncertainty is taken to be ±0.005; for the Nd-LSCO powders, it is ±0.01. Vertical error bars reflect the level of measurement reproducibility and the relative importance of addenda and sample contributions. For the Nd-LSCO powders, an additional uncertainty comes from having to subtract the magnetic Schottky anomaly. b, Normal-state electronic specific heat C_el of Eu-LSCO (squares) and Nd-LSCO (red circles, crystals), at T = 0.5 K, plotted as C_el/T versus p (see Extended Data Fig. 10a for details). We also include γ for Nd-LSCO (purple circles, polycrystals; see Extended Data Figs. 7, 8) and non-superconducting LSCO from published work (diamonds; p < 0.06, ref. ³²; p = 0.33, ref. ¹³), obtained by extrapolating C/T = γ + βT² to T = 0 from data below 10 K. The jump in specific heat at T_c, ΔC/T_c, measured in Eu-LSCO (blue triangles; Extended Data Fig. 3) is plotted for comparison (right axis). We see that ΔC/T_c and C_el/T scale nicely. The dashed line marks the pseudogap critical point p* in Nd-LSCO (Extended Data Fig. 1). The solid lines are a guide to the eye. The error bars are the same as in a. The vertical error bars on the blue triangles also include an uncertainty in estimating the specific heat jump ΔC relative to its background above T_c (see Extended Data Fig. 3).

To investigate what happens above p*, we measured the specific heat of three Nd-LSCO samples with p = 0.27, 0.36 and 0.40—dopings at which the material is no longer superconducting. Because it is difficult to grow single crystals at such high doping, the samples are polycrystalline powder. As a result, a field cannot be used to shift the magnetic Schottky anomaly (C_mag) up in temperature (because the effect of a field is highly anisotropic). Nevertheless, we can reliably subtract C_mag from C and obtain C_el + C_ph, as demonstrated in Extended Data Figs. 7, 8 for our five polycrystalline samples. In all cases, the zero-field data obey (C – C_mag)/T = γ + βT², with values of γ and β that are consistent with those obtained in single crystals. In Extended Data Fig. 7a, we show that polycrystalline and single-crystal samples yield exactly the same data, at the same doping (here p = 0.12). Plotting the values of (C – C_mag)/T at T = 2 K in Fig. 3a, we see that C/T drops by a factor of three in going from p* up to p = 0.4. Our values in Nd-LSCO are consistent with published data on La_2−xSr_xCuO₄ (LSCO) at p = 0.33 (ref. ¹³; Fig. 3a).

The thermodynamic signature of the pseudogap critical point in Eu-LSCO and Nd-LSCO is therefore seen to be a huge peak in C_el/T at p*, at low temperature, not just a drop below p* (Fig. 3a). There are two standard explanations for such a peak: a van Hove singularity in the band structure and a quantum critical point. Because there is indeed a van Hove singularity in Nd-LSCO at p = p_vHs ≈ p* (ref. ¹⁴), we have considered the first scenario carefully. Fortunately, the band structure of Nd-LSCO is well known and simple¹⁴, so reliable calculations can be performed. In a perfectly clean two-dimensional metal, C_el/T versus p does show a sharp cusp at p = p_vHs in the T = 0 limit (Extended Data Fig. 9). However, when the actual three-dimensional dispersion of the real Fermi surface and the actual level of disorder scattering of the real samples are included, the peak due to the van Hove singularity is much reduced and broadened (Extended Data Fig. 9). The large, sharp peak we observe is therefore clearly caused by electronic effects beyond the band structure.

We now turn to the temperature dependence of C_el. In Fig. 2a, we see that C/T at p = 0.24 deviates strongly from the γ + βT² behaviour as T → 0. To investigate this deviation in detail, measurements were carried out in a ³He refrigerator with a field of 8 T, just enough to reach the normal state at p = 0.11, 0.16 and 0.24 (Extended Data Fig. 4). The data are plotted as C/T versus T in Extended Data Fig. 5a. Below 1 K, we observe a nuclear Schottky anomaly (C_nuclear), which rises as C/T ∝ T^–3. Because C_nuclear and C_ph are both almost independent of doping, we can readily subtract them from the measured C and obtain the purely electronic contribution C_el (see Methods). The result is plotted as C_el/T versus logT in Fig. 2b. At p = 0.11, we see that C_el/T is constant, with C_el/T = γ = 2.8 mJ K⁻² mol. In contrast, at p = 0.24, we see that C_el/T grows linearly from about 10 K all the way down to 0.5 K, our lowest temperature. We arrive at the key finding that C_el/T ∝ log(1/T) at p ≈ p*.

The fact that C_el/T keeps increasing as T → 0 at p = 0.24 is confirmed directly by looking at ΔC/T_c, the jump in C/T at T_c, the two being linked by entropy balance. In Extended Data Fig. 3, we see that ΔC/T_c increases by a factor of ten in going from p = 0.11 to p = 0.24, in tandem with the increase in C_el/T at T = 0.5 K (Fig. 3b).

In Extended Data Fig. 5d (and Supplementary Fig. 1c), we show Nd-LSCO data obtained in the ³He refrigerator at H = 8 T, a field sufficient to suppress superconductivity at p = 0.12, 0.22, 0.23, 0.24 and 0.25. As described in Methods, we obtain C_el(T) as we did for Eu-LSCO. The result is displayed in Fig. 2d (and Supplementary Fig. 1d), plotted as C_el/T versus logT. The Nd-LSCO data for C_el(T) are seen to be in excellent quantitative agreement with the Eu-LSCO data (Fig. 2b). In particular, they confirm our key finding that C_el/T ∝ log(1/T) at p ≈ p*. We therefore find that the cuprates Eu-LSCO and Nd-LSCO exhibit the classic thermodynamic signature of a QCP, as observed in the antiferromagnetic heavy-fermion metals CeCu_6−xAu_x (ref. ⁶), YbRh₂Si₂ (ref. ¹⁵) and CeCoIn₅ (ref. ¹⁶).

In Fig. 3b, we plot the value of C_el/T for our 12 crystals as a function of doping, estimated at T = 0.5 K. We also plot the extrapolated γ values for our five polycrystalline samples of Nd-LSCO (p = 0.07, 0.12, 0.27, 0.36 and 0.40; Extended Data Figs. 7b, 8b) and the LSCO crystal at p = 0.33 (ref. ¹³). The huge cusp-like peak in C_el/T versus p is very similar to that seen in the iron-based superconductor BaFe₂(As_1−xP_x)₂ at its antiferromagnetic QCP, with C/T ∝ log(1/|x − x*|) (ref. ⁷). Taken together, the p and T dependence of C_el provides compelling evidence for a QCP in Eu-LSCO and Nd-LSCO.

The strong similarity of our data on Nd-LSCO and Eu-LSCO with data on other cuprates indicates that the signatures of a QCP reported here are likely to be a generic feature of hole-doped cuprates. In Extended Data Fig. 10b, we compare our values of C_el/T in Eu-LSCO and Nd-LSCO at 10 K (Extended Data Fig. 10a) with γ values in LSCO obtained from fits to C/T = γ + βT² between about 4 K and about 8 K, where C was measured on LSCO powders made non-superconducting by adding high levels of Zn impurities¹⁷. (We note that in this early work the temperature dependence of C_el/T was not investigated at very low temperature.) A clear peak in γ versus p is observed also in LSCO, similar to that found here in Nd-LSCO, although centred at a slightly lower doping—consistent with the lower p* in that material (Extended Data Fig. 1).

In no other cuprate has a direct measurement of the normal-state specific heat at low temperature been performed over a wide range including p*. To continue our survey of cuprates, we must therefore piece together different data from different materials. This is what we do in Fig. 1. Starting on the overdoped side, we have γ = 6.6 ± 1 mJ K⁻² mol⁻¹ in Tl₂Ba₂CuO_6+δ (Tl-2201) at p ≈ 0.33 (ref. ¹⁸), not far from the value of γ = 7.6 ± 0.6 mJ K⁻² mol⁻¹ obtained from the effective mass measured by quantum oscillations, m* = (5.2 ± 0.4)m_e, in Tl-2201 at p = 0.29 ± 0.02 (ref. ¹⁹). Since those are similar to the values found in Nd-LSCO and in LSCO at p ≈ 0.3 (Fig. 3b), it is reasonable to suppose that other cuprates, such as YBCO, Bi₂Sr₂CaCu₂O₈ (Bi2212) and HgBa₂CuO_4+δ (Hg-1201), would also have γ ≈ 7 mJ K⁻² mol⁻¹ at p ≈ 0.3. (In none of these three materials has m*, γ or ΔC/T_c been measured beyond p ≈ 0.23^12,20. Note that p* = 0.22 in Bi2212²¹.) On the underdoped side, γ ≈ 3 mJ K⁻² mol⁻¹ in YBCO at p ≈ 0.1 (ref. ¹⁰) and quantum oscillations in YBCO⁹ and Hg-1201²² at p ≈ 0.1 yield γ = 2.5 and 4.0 mJ K⁻² mol⁻¹, respectively (per mole of planar Cu), compared to γ = 2.8 and 3.6 mJ K⁻² mol⁻¹ in Eu-LSCO at p = 0.11 and Nd-LSCO at p = 0.12, respectively (Fig. 3b)—all in good agreement (Fig. 1).

We emphasize that γ in Tl-2201 at p ≈ 0.33 is only a factor 1.7 larger than γ in Hg-1201 at p ≈ 0.1. In other words, the opening of the pseudogap between the two has only reduced the density of states by a factor of about 1.7. This is a much smaller reduction than that observed in going from p* to p = 0.1 in any hole-doped cuprate^{11,12,17,20,23}. If we assume that the reduction below p* in Tl-2201 is comparable to that in other cuprates, then γ in Tl-2201 must first rise from p ≈ 0.33 to p* before it falls below p*. This would imply that a peak in C_el/T at p* is a generic property of cuprates. (We note, however, that the only attempt to extract the doping dependence of γ in Tl-2201, based on zero-field data, found a constant γ (ref. ¹⁸). A direct measurement of the normal-state C_el is needed to resolve this apparent contradiction.)

In Fig. 1, we also plot the specific heat jump at T_c, ΔC/T_c, as a function of p, previously measured in Ca-doped YBCO¹². We see that ΔC/T_c drops by a factor of about 10 in going from p* to p ≈ 0.1, consistent with the drop in condensation energy²³. Since ΔC/T_c ∝ γ, this implies that γ ≈ 25 mJ K⁻² mol⁻¹ at p* in YBCO (Fig. 1), comparable to our value of C_el /T = 22 mJ K⁻² mol⁻¹ at T = 0.5 K in Nd-LSCO at p* (Fig. 3b). This high value of γ in YBCO must then drop by a factor of about 3–4 above p*, if it is to reach the common value γ ≈ 7 mJ K⁻² mol⁻¹ at p ≈ 0.3 (Fig. 1). In summary, while further work is needed to establish that there is indeed a peak in C_el/T versus p for cuprates other than Nd-LSCO, Eu-LSCO and LSCO, most existing data are not incompatible with a universal peak in hole-doped cuprates.

Our finding that C_el/T peaks at p* is a change of paradigm in our understanding of cuprates—it reveals a mechanism of strong mass enhancement above p*, associated with a QCP at p*. Our observation of a continuous logarithmic increase of the electronic specific heat down to temperatures as low as 0.5 K raises the fundamental question of what energy scale, associated with most of the low-temperature entropy, might vanish at p*, and what corresponding length scale would then diverge at p*.

Given the remarkable similarity with the signatures of an antiferromagnetic QCP, as observed in heavy-fermion metals⁶ and iron-based superconductors⁷, it is tempting to attribute the quantum criticality of cuprates to antiferromagnetic spin correlations. However, unlike in electron-doped cuprates where the antiferromagnetic correlation length diverges as T → 0 (ref. ²⁴) close to the critical doping x* where the Fermi surface is reconstructed and ρ(T) is T-linear²⁵, there is no evidence of a diverging antiferromagnetic correlation length in hole-doped cuprates near p* (ref. ²⁶).

In Nd-LSCO, incommensurate spin-density-wave order is observed by neutron diffraction²⁷ to vanish with increasing p at p ≈ p*, but there is no divergent spin-density-wave correlation length or vanishing energy scale. Indeed, muon spin relaxation finds that the magnetic order in Nd-LSCO vanishes before p*, at p ≈ 0.20, which indicates that the order is not static at p = 0.20 (ref. ²⁸), or above.

It may therefore be that the quantum criticality of hole-doped cuprates is of an entirely new kind, possibly involving topological order²⁹. Alternatively, we may be dealing with two closely intertwined mechanisms: one mechanism for the pseudogap, possibly short-range antiferromagnetic correlations, and a second—separate but coupled—mechanism for the quantum criticality, possibly nematic order³⁰ or current-loop order³¹.

Methods

Samples

Eu-LSCO

Single crystals of La_2−y−xEu_ySr_xCuO₄ (Eu-LSCO) were grown at the University of Tokyo with a Eu content y = 0.2, using a travelling-float-zone technique. Five samples were cut in the shape of small rectangular platelets, of typical dimensions 1 mm × 1 mm × 0.5 mm and mass of about 1 mg, from boules with nominal Sr concentrations x = 0.08, 0.11, 0.16, 0.21 and 0.24. The hole concentration p is given by p = x, with a maximal error bar of ±0.005. The critical temperature T_c of our samples, defined as the onset of the drop in the magnetization, is plotted in Extended Data Fig. 2a.

Nd-LSCO

Single crystals of La_2−y−xNd_ySr_xCuO₄ (Nd-LSCO) were grown at the University of Texas at Austin with a Nd content y = 0.4, using a travelling-float-zone technique. Seven samples were cut in the shape of small rectangular platelets, of typical dimensions 1 mm × 1 mm × 0.5 mm and mass of about 1 mg, from boules with nominal Sr concentrations x = 0.12, 0.15, 0.20, 0.22, 0.23, 0.24 and 0.25. The hole concentration p is given by p = x, with an error bar ±0.003, except for our sample with p = 0.24, for which the error bar is ±0.005 (ref. ²). The T_c values of all samples are plotted in Extended Data Fig. 2b. The rapid decrease in T_c from p = 0.22 to p = 0.25 provides a sensitive measure of the relative doping of samples in that range.

Powder samples of Nd-LSCO were produced at McMaster University with y = 0.4 and x = 0.07, 0.12, 0.27, 0.36 and 0.40, and shaped into sintered pellets. Samples with x = 0.27, 0.36 and 0.40 are not superconducting, and so their normal-state specific heat can be measured in zero field. The uncertainty on p from x is ±0.01.

Specific heat measurements

To perform the series of specific heat measurements reported in this article, we implemented an original alternating-current modulation method that leads to an absolute accuracy of ΔC/C ≈ ±4% with a relative sensitivity ΔC/C ≈ ±0.01% on samples whose masses are of the order of 1.0 mg (down to 0.1 mg). These figures are valid for the temperature range 0.5 K < T < 20 K and for the magnetic field range 0 T < H < 18 T.

Calorimetric setup

The calorimetric chips were prepared from bare Cernox chips (1010 for T < 2 K, 1050 for T > 2 K). First, a shallow groove is made in the central part with a wire saw to obtain two independent films; one used as a heater (of resistance R_h) and the other one as a thermometer (of resistance R_t; Supplementary Fig. 2). The split chip is then attached to a small copper ring with PtW (7%) wires, 25 μm or 50 μm in diameter and 1 mm to 2 mm in length, glued with a minute amount of Ag epoxy. The choice of wires is important since it defines the external thermal conductance and the frequency range where the measurements will have their optimal accuracy (between 0.5 Hz and 20 Hz). We used PtW wires since their thermal conductivity is insensitive to magnetic fields (<1% in 18 T).

Modulation technique

In the simplest approximation, when an alternative current I_ac is applied at a frequency ω on the heater side, temperature oscillations T_ac = P_ac/(K_e + jC2ω) are induced at 2ω, where K_e is the external thermal conductance and C the total heat capacity. Introducing the phase φ of T_ac relative to the power P_ac, we obtain: C = P_acsin(−φ)/[2ω|T_ac|]where P_ac = R_h|I_ac|²/2. These oscillations can then be measured by applying a direct current I_dc across the thermometer: V_ac^t(2ω) = [(dR_t/dT)T_ac(2ω)]I_dc. The main drawback of this simple approach is that internal time corrections (due to finite thermal conductances between the different parts of the chips: thermometer, heater, substrate and sample) are not taken into account. To overcome this difficulty, especially at the lowest temperature where the thermal conductivity between the sensing layer of the Cernox and the sapphire substrate is the main limiting factor, we have also used the heater side to measure the temperature oscillations: V_ac^h(3ω) = [(dR_h/dT)T_ac(2ω)]I_ac(ω).

When all the internal conductances are larger than the external one K_e, the T_ac measured on the thermometer side (at 2ω) must be the same as that measured on the heater side (at 3ω). Any difference points to a thermal gradient within the chips, which can then be minimized by adjusting the measurement parameters. This procedure improves the absolute accuracy and enables a much better estimate of the error bars.

Thermometry

The first step is to know precisely the temperature of the main heat sink on which the measuring chip is attached. This is achieved with commercial calibrated Cernox sensors 1010 and 1050, used respectively in the ranges 0.5–5 K and 1.5–20 K. The calibration has been further improved in-house with a superconductive fixed point device and a cerium–magnesium–nitrate (CMN) thermometer to reach an accuracy of ±1% in the absolute temperature, within the temperature range considered here. All thermometers have then been thoroughly calibrated in field, from 0.2 K to 4 K against a Ge sensor placed in a compensated area of an 18 T superconducting magnet and between 2 K and 20 K against a capacitor. The output of this protocol is a quintic bivariable (T and H) spline interpolation sheet, which was used to determine and control the temperature between 0.5 K and 20 K up to 18 T with a relative accuracy ΔT/T ≈ ±0.2%.

Addenda and test

To subtract the heat capacity of the sample mount (chip + a few micrograms of Apiezon grease used to glue the sample onto the back of the chip), the empty chip (with grease) was measured before each sample measurement. This background heat capacity is of the order of C_add/T ≈ 5 nJ K⁻² at 1 K (3 K) for the 1010 (1050) chips, which represents 10% to 50% of the heat capacity of the samples.

To benchmark our measurement system and technique, we measured a piece of ultrapure copper, of mass 1 mg, whose heat capacity at low T is comparable to that of our Eu-LSCO and Nd-LSCO samples. In zero magnetic field, the reproducibility between different runs and between different chips shows an absolute accuracy of at least ΔC/C ≈ ±3% compared to the values tabulated by the National Bureau of Standards (NBS), across the range from 0.5 K to 10 K (Supplementary Fig. 3). In magnetic fields up to 18 T, the apparent change ΔC/C versus H is very smooth and does not exceed 1%.

All factors considered, the absolute accuracy of each of the specific heat runs is estimated to be ΔC/C ≈ ±4%, or better. For 0.5 K < T < 5 K, the specific heat is dominated by the electronic contribution and ΔC_el/C_el ≈ ΔC/C at T = 0.5 K and 1.0 K. But this error bar increases with temperature, owing to the rapid increase in the phonon contribution (and the Schottky term in Nd-LSCO), which makes the electronic term a smaller fraction of the total signal. The error bars plotted in Fig. 3b and Extended Data Fig. 10a show how this translates into an uncertainty on the absolute value of C_el/T for each sample separately, at each temperature.

Extracting the electronic specific heat

There are three contributions to the specific heat C of Eu-LSCO and Nd-LSCO: from electrons (C_el), phonons (C_ph) and nuclei (C_nuclear). In Nd-LSCO, there is an additional contribution from the magnetic moment on the Nd³⁺ ions (C_mag). Because Eu ions are not magnetic, this term is absent in Eu-LSCO. To extract the electronic term of interest here, we proceed as outlined in Extended Data Fig. 6, and as described in detail below.

Nuclear Schottky term, C_nuclear

The nuclear hyperfine term is a Schottky anomaly peaked at very low temperature. Above the peak, C_nuclear dies off rapidly, as C_nuclear ≈ 1/T². In Eu-LSCO and Nd-LSCO, C_nuclear is clearly visible in all samples as a rapid upturn below 1 K (Extended Data Fig. 5 and Supplementary Fig. 1). In a field of 8 T, C_nuclear becomes negligible above T ≈ 1 K (Extended Data Figs. 5b, 6a); in 18 T, above about 2 K (Extended Data Fig. 5c). By subtracting the raw data for C versus T in Eu-LSCO at p = 0.16 from the raw data C(T) at each other doping, we see that the rapid upturn below 1 K is almost entirely removed (Fig. 2b, Supplementary Fig. 1b, Extended Data Fig. 6c), at least down to 0.5 K. (Below T = 0.5 K, we do observe that the subtraction is not perfect, reflecting a small difference in the nuclear Schottky anomaly from sample to sample (within ±20% at 0.3 K), and this is why we report data only for T = 0.5 K and above.) This shows that C_nuclear is very weakly sample-dependent and doping-dependent. (The nuclear Schottky anomaly is believed to come from the Eu ions³³, and the Eu content of all our Eu-LSCO samples is kept fixed.)

In summary, to remove C_nuclear from the measured C we can work at T = 1 K (in a field of 8 T) or at T = 2 K in 18 T, and higher temperatures. Below 1 K, we can remove C_nuclear reliably down to 0.5 K by subtracting a reference curve, namely p = 0.16 in Eu-LSCO and p = 0.12 in Nd-LSCO, since C_nuclear varies from sample to sample by less than ±5% at 0.5 K. In Extended Data Fig. 6b, we see the effect of such a subtraction: (C – C_nuclear)/T is constant below 1 K at p = 0.11 and p = 0.16, while it rises monotonically as T → 0 at p = 0.24. (Note that 8 T is enough to suppress superconductivity in Eu-LSCO down to the lowest temperature for all dopings except p = 0.21, where we use 18 T and are limited to T > 2 K (Fig. 2b).)

Magnetic Schottky term, C_mag

Compared to Eu-LSCO, the specific heat of Nd-LSCO has one additional contribution, C_mag, a Schottky peak due to the magnetic moment on the Nd³⁺ ions (Extended Data Fig. 4b). A field moves this magnetic Schottky peak up in temperature, so that C_mag becomes very small below 2 K in 8 T and very small below 6 K in 18 T (Extended Data Fig. 5c). We apply the same subtraction procedure as for Eu-LSCO, using our Nd-LSCO sample with p = 0.12 as the reference. (The subtraction procedure works well to remove both C_mag and C_nuclear because the Nd content of all our Nd-LSCO samples is kept fixed.)

At high doping (p > 0.25), single crystals are difficult to grow and we have therefore resorted to powder samples of Nd-LSCO, with p = 0.27, 0.36 and 0.40. Because these samples are not superconducting, the normal state specific heat can be measured in zero field. We note, however, that the magnetic Schottky term depends on the field direction relative to the c axis of the crystal structure. As a result, we could not use a field to suppress C_mag in the powder samples, made of micro-crystallites of all orientations. In Extended Data Fig. 7a, we compare directly the raw data from our powder sample at p = 0.12 with the raw data from our single-crystal sample at p = 0.12, both at H = 0. The two sets of raw data are seen to be in excellent agreement. In the single crystal, we remove C_mag by applying a field of 18 T; a fit to C/T = γ + βT² below about 5 K yields γ = 3.6 mJ K⁻² mol⁻¹ and β = 0.215 mJ K⁻⁴ mol⁻¹ (Fig. 2c). In the powder sample, we fit the zero-field raw data to a Schottky anomaly that goes as C_mag ≈ 1/T² (in the range 3 K < T < 7 K). We subtract C_mag from the raw powder data and fit the difference to (C – C_mag)/T = γ + βT² (Extended Data Fig. 7b). The resulting values of γ (4 ± 1 mJ K⁻² mol⁻¹) and β (0.225 ± 0.015 mJ K⁻⁴ mol⁻¹) are in good agreement with those quoted above for the p = 0.12 single crystal (see Fig. 3b and Extended Data Fig. 6d).

Performing the same fit and subtraction to the zero-field raw powder data at p = 0.27, 0.36 and 0.40, reported in Extended Data Fig. 8a, yields curves that are roughly parallel when plotted as (C – C_mag)/T versus T² (Extended Data Fig. 8b). A fit to (C – C_mag)/T = γ + βT² yields the values of γ plotted in Fig. 3b (purple circles) and the values of β plotted in Extended Data Fig. 6d (orange circles). The fact that each curve in Extended Data Fig. 8b can be fitted to γ + βT² shows that the electronic term C_el/T is constant in temperature. This is illustrated in Extended Data Fig. 8c, where we subtract the phonon term C_ph = βT³.

In Extended Data Fig. 8d, we compare the three curves of Extended Data Fig. 8b to raw data on Nd-LSCO (red; from Fig. 2c) and Eu-LSCO (orange; from Fig. 2a) at p = 0.24, measured at H = 18 T, a field large enough to entirely remove superconductivity. In Eu-LSCO, there is no magnetic Schottky anomaly (C_mag = 0), and so the orange curve C/T at p = 0.24 can be compared directly to the curves (C – C_mag)/T versus T² at p = 0.27, 0.36 and 0.40. We see that the orange curve is not straight, showing a clear upward deviation from linearity at low T. Such a deviation is not seen at p = 0.36 and 0.40. At p = 0.27, there might be a slight upward deviation, which would not be inconsistent with this doping being close to p*.

In the Nd-LSCO crystal at p = 0.24 (red curve in Extended Data Fig. 8d), a field of 18 T pushes the magnetic Schottky anomaly above about 5 K. Below about 5 K, the raw curve in Nd-LSCO is essentially identical to the raw curve in Eu-LSCO, confirming that the low-T upward deviation is present in Nd-LSCO also. In conclusion, the log(1/T) behaviour seen at p = 0.24 goes away as p increases above p*.

Phonon term, C_ph

At 18 T, superconductivity is completely eliminated from all samples (Extended Data Fig. 4a). At T > 2 K, C_nuclear is negligible. In Nd-LSCO, C_mag is negligible below about 6 K. So in the range 2–6 K at 18 T, we have C = C_el + C_ph. In Eu-LSCO at p = 0.11 and 0.16, and in Nd-LSCO at p = 0.12, the raw data in that T range are well described by C/T = γ + βT² (Fig. 2a, c), with very similar values of β (Extended Data Fig. 6d). Alternatively, we can fit the 8 T data from those two samples of Eu-LSCO over the full range from T = 0.5 K to 10 K by using (C – C_nuclear)/T = γ + C_ph/T, where C_ph/T = βT² + δT⁴, as shown in Extended Data Fig. 6. The two approaches yield very similar values of γ and β (identical within error bars). Fitting single-crystal data away from p* = 0.23, namely Eu-LSCO at p = 0.08, 0.11 and 0.16 in 8 T and Nd-LSCO at p = 0.12, 0.15 and 0.20 in 18 T, to (C – C_nuclear)/T = γ + βT² + δT⁴ yields the values of β plotted in Extended Data Fig. 6d. For the five powder samples of Nd-LSCO, we fit the zero-field data to (C – C_mag)/T = γ + βT² + δT⁴ (Extended Data Figs. 7b, 8b). In Extended Data Fig. 6d, we see that the doping dependence of β is weak, and in excellent agreement with the very weak doping dependence of the phonon energy, E_ph, measured by neutron scattering (performed by Q.M., M.D., H.A.D. and B.D.G.), that is, β ≈ 1/E_ph³.

Doping dependence of the electronic term, C_el versus p

In Extended Data Fig. 6a, we see that C_nuclear in 8 T is negligible at T = 1 K (and above). In Extended Data Fig. 6b, we see that C_ph is negligible at T = 1 K (and below). Therefore the raw data at T = 1 K and H = 8 T, in Eu-LSCO, directly give the electronic specific heat at 1 K, that is, C_el = C to a very good approximation (except at p = 0.21, where 8 T is not enough to fully suppress superconductivity). The huge rise in C from p = 0.11 to p = 0.24 (Fig. 3a) is therefore entirely due to C_el.

At high doping, beyond p*, the Nd-LSCO powder data show a clear decrease in γ as p increases (Extended Data Fig. 8b). The result is therefore an unambiguous peak, at p = p*, in C_el versus p in the T = 0 limit (Fig. 3a). This is the first key signature of a QCP.

Temperature dependence of the electronic term, C_el versus T

Extended Data Fig. 6 shows that C_el/T at p = 0.16 is constant as a function of T, all T dependence being due to C_nuclear/T and C_ph/T. The same is true at p = 0.11. At p = 0.24, however, there is an additional T dependence not due to C_nuclear or C_ph, which comes from C_el(T). The simplest way to reveal this T dependence of C_el(T) is to subtract the raw curve at p = 0.16 from the raw curve at p = 0.24, as done in Fig. 2b. Or, equivalently, subtract the fit to (C – C_nuclear – C_ph)/T performed on the p = 0.16 data, as done in Extended Data Fig. 6c. Both approaches yield a clean log(1/T) dependence for C_el/T at p = 0.24, from 0.5 K to 10 K (see dotted line in Extended Data Fig. 6c).

These approaches assume that C_nuclear is the same in the two samples, which is true to better than 5%, and also that C_ph at p = 0.24 is the same as C_ph at p = 0.16, which is true to better than 4%, as established by the neutron data: E_ph changes from 14.6 meV at p = 0.12 to 14.8 meV at p = 0.24. In other words, within error bars, we find that C_el/T ≈ log(1/T) up to at least 10 K. This is the second key signature of a QCP.

In Extended Data Fig. 10a, we plot the value of C_el/T at T = 0.5 K, 2 K and 10 K, obtained using the first procedure of simply subtracting two raw curves, requiring no fitting at all. As we have just shown, the values of C_el/T obtained in this way are accurate and reliable, within the error bars.

The fact that C_el/T keeps increasing as T → 0 at p = 0.24 is confirmed directly by looking at ΔC/T_c, the jump in C_el/T at T_c, the two being linked by entropy balance. In Extended Data Fig. 3, we see that ΔC/T_c increases by a factor of ten in going from p = 0.11 to p = 0.24, in tandem with the increase in C_el/T at T = 0.5 K (Fig. 3b)—separate evidence from raw data (with no analysis or subtraction) that C_el/T at p = 0.24 must increase below 10 K.

In summary, the high level of quantitative consistency we find between the values of C_el/T obtained in our five crystals of Eu-LSCO and those obtained in our seven crystals of Nd-LSCO (Fig. 3b) is a strong validation of both the experimental technique and the data analysis. It confirms that the electronic specific heat C_el(T) we report is reproducible and accurate (within the quoted error bars). Furthermore, the excellent agreement between the values of C_el(T) plotted in Fig. 3b and the raw values of C(T) at T = 1 K and 2 K plotted in Fig. 3a confirms the fidelity of our analysis, as does the parallel growth observed in ΔC/T_c and C_el/T (Fig. 3b).

van Hove singularity

In hole-doped cuprates, the large Fermi surface in the overdoped regime undergoes a change of topology from hole-like to electron-like at some material-dependent critical doping p_vHs. According to ARPES, this change of topology occurs between p = 0.15 and p = 0.22 in LSCO³⁴ and between p = 0.20 and p = 0.24 in Nd-LSCO¹⁴, that is, close to p* in both cases (Extended Data Fig. 1; ref. ³⁵). If the Fermi surface were strictly two-dimensional, this would, in the clean limit, lead to a van Hove singularity in the density of states, producing a cusp in C_el/T versus p at p_vHs and a log(1/T) dependence of C_el/T as T → 0, analogous to the behaviour we report in Eu-LSCO and Nd-LSCO.

However, the change of Fermi-surface topology at p_vHs ≈ p* cannot in fact be responsible for that behaviour, for two reasons: because of the strong three-dimensional character of the Fermi surface in Nd-LSCO (and Eu-LSCO), and because of the high level of disorder in our samples. Each of these two mechanisms broadens the van Hove singularity, removes the cusp versus p and cuts off the log(1/T) divergence at low T.

To be quantitative, we have calculated the specific heat of Nd-LSCO associated with its known band structure, using the following one-band model³⁶:

$$\begin{array}{c}{\xi }_{{\boldsymbol{k}}}=-\mu -2t({\rm{c}}{\rm{o}}{\rm{s}}({k}_{x}a)+{\rm{c}}{\rm{o}}{\rm{s}}({k}_{y}b))-4t^{\prime} {\rm{c}}{\rm{o}}{\rm{s}}({k}_{x}a){\rm{c}}{\rm{o}}{\rm{s}}({k}_{y}b)-2t^{\prime\prime} ({\rm{c}}{\rm{o}}{\rm{s}}(2{k}_{x}a){\rm{c}}{\rm{o}}{\rm{s}}(2{k}_{y}b))\\ -2{t}_{z}{\rm{c}}{\rm{o}}{\rm{s}}({k}_{z}c/2){[{\rm{c}}{\rm{o}}{\rm{s}}({k}_{x}a)-{\rm{c}}{\rm{o}}{\rm{s}}({k}_{y}b)]}^{2}{\rm{c}}{\rm{o}}{\rm{s}}({k}_{x}a/2){\rm{c}}{\rm{o}}{\rm{s}}({k}_{y}b/2)\end{array}$$

with t = 0.189 meV, t′ = –0.17t, t′′ = 0.05t. Those parameters agree with the experimental band structure measured by ARPES³⁷, and are such that the van Hove singularity is located at p = 0.23. The three-dimensional character is controlled by the interlayer hopping parameter t_z. The doping is adjusted by tuning the chemical potential μ.

The temperature-dependent specific heat is given by³⁸:

$${C}_{{\rm{el}}}\left(T\right)=\underset{-\infty }{\overset{\infty }{\int }}{\rm{d}}\epsilon \frac{\partial f\left(\epsilon \right)}{\partial T}\epsilon N\left(\epsilon \right)$$

with

$$N(\epsilon )=\frac{1}{V}\sum _{{\boldsymbol{k}}}\frac{1}{{\rm{\pi }}}\frac{\hbar /2\tau }{{(\epsilon -{\xi }_{{\boldsymbol{k}}})}^{2}+{(\hbar /2\tau )}^{2}}$$

where f(ε) is the Fermi–Dirac function, N(ε) is the density of states, and τ is the quasiparticle lifetime.

The calculated specific heat is shown in Extended Data Fig. 9 (blue), as a function of doping (at T → 0) on the top and as a function of temperature (at p = p_vHs) on the bottom. In the left panels, we show the clean-limit two-dimensional result, with ħ/τ = 0 and t_z = 0. In the middle panels, we show the effect of disorder, with ħ/τ = t/25, the value needed to produce the measured residual resistivity of our Nd-LSCO and Eu-LSCO samples at p = 0.24, namely ρ₀ ≈ 30 μΩ cm (Extended Data Fig. 2). In the right panels, we further add the effect of three-dimensional dispersion, with t_z = 0.13t, the value needed to produce the measured resistivity anisotropy of Nd-LSCO at p = 0.24, namely ρ_c/ρ_a ≈ 250 (ref. ³⁹).

Direct comparison with our data shows that band structure effects associated with p_vHs in Nd-LSCO do produce a broad background bump in C_el versus p, but they cannot account for the large and sharp peak we observe in C_el/T at T = 0.5 K (Extended Data Fig. 9). Moreover, the fact that we see C_el/T ≈ log(1/T) persisting down to 0.5 K at p = p* completely excludes a van Hove mechanism, which yields a constant C_el/T when k_BT < ħ/τ or when k_BT < t_z, that is, below about 20 K in our samples (Extended Data Fig. 9).

Recent calculations of C_el/T versus p at T = 0 using the real three-dimensional electronic structure measured by ARPES in LSCO and Eu-LSCO⁴⁰ yield curves that are essentially identical, quantitatively, with our own curves in Extended Data Fig. 9, showing again that the van Hove singularity cannot account for the large peak observed in Nd-LSCO, Eu-LSCO or LSCO. Even when the authors of ref. ⁴⁰ assume no disorder (1/τ = 0), they find that the three-dimensional dispersion alone limits the increase in C_el/T from p = 0.40 to p = 0.24 to no more than a factor of 2, whereas our data show a fourfold increase (Fig. 3b).

We note that strong disorder does not alter the log(1/T) dependence of C_el/T coming from a QCP, as demonstrated by its persistence down to about 20 mK in samples of CeCu_5.9Au_0.1 (ref. ⁶) that have a residual resistivity ρ₀ larger than that of our own samples at p = 0.24 (Extended Data Fig. 2).

Extended data figures and tables

Extended Data Fig. 1 Temperature–doping phase diagram.

Temperature-doping phase diagram of LSCO (black), Nd-LSCO (red) and Eu-LSCO (green), showing the boundary of the phase of long-range commensurate antiferromagnetic order (T_N, brown line), the pseudogap temperature T* (blue line) and the superconducting transition temperature T_c of LSCO (grey line) and Nd-LSCO (pink line). T* is detected in two transport properties: resistivity (T_ρ, circles) and the Nernst effect (T_ν, squares). The open triangles show T* detected by ARPES as the temperature below which the anti-nodal pseudogap opens, in LSCO (black) and Nd-LSCO (red). We see that T_ν ≈ T_ρ ≈ T*, within error bars. The pseudogap phase ends at a critical doping p* = 0.18 ± 0.01 in LSCO (black diamond) and p* = 0.23 ± 0.01 in Nd-LSCO (red diamond). Figure adapted from figure 10 in ref. ³⁵ (American Physical Society) (error bars defined therein).

Extended Data Fig. 2 Characterization of our Eu-LSCO and Nd-LSCO samples.

a, T_c versus p for our Eu-LSCO samples. T_c is defined as the onset of the drop in the magnetization upon cooling. Error bars on T_c reflect the uncertainty in defining the onset of the drop in the magnetization. b, Same for our Nd-LSCO samples. c, ρ versus T in our Eu-LSCO samples with p = 0.21 (red) and p = 0.24 (blue), at H = 0 and H = 33 T (short section below 40 K). d, Same for our Nd-LSCO samples with p = 0.22 (red) and p = 0.24 (blue)². The approximately linear ρ(T) as T → 0 at p = 0.24 (blue) shows that 0.24 is close to the critical point p* ≈ 0.23 in both materials. The large upturn in ρ(T) as T → 0 at p = 0.21 and p = 0.22 (red) shows that the pseudogap has opened in both materials (at p < 0.23).

Extended Data Fig. 3 Specific heat jump at T_c in Eu-LSCO.

a, C/T versus T in our Eu-LSCO sample with p = 0.24, at H = 0 (red) and H = 8 T (blue). The inset shows the difference between the two curves in the main panel (red). This is the difference between the superconducting-state C/T and the normal-state C/T. It reveals the jump at T_c, whose peak value, ΔC/T_c, is defined as drawn. The black curve is the magnetization of that sample. At p = 0.24, the bulk T_c = 10.5 ± 0.5 K (dashed line). b, As in a, for our sample with p = 0.21, at H = 0 (red) and H = 18 T (blue). At p = 0.21, the bulk T_c = 14.5 ± 0.5 K. c, As in a, for our sample with p = 0.16, at H = 0 (red) and H = 18 T (blue). At p = 0.16, the bulk T_c = 11.5 ± 0.5 K. d, As in a, for our sample with p = 0.11, at H = 0 (red) and H = 8 T (blue). At p = 0.11, the bulk T_c = 5.0 ± 0.5 K. e, Plot of ΔC/T_c versus C_el/T at T = 0.5 K, the latter being obtained from Fig. 3b (red squares). The error bar on ΔC/T_c comes mostly from the uncertainty on defining the baseline above T_c. The dashed line is a linear fit through the first three data points. The tenfold increase in ΔC/T_c from p = 0.11 to p = 0.24 is independent evidence of a similar increase in C_el/T.

Extended Data Fig. 4 Specific heat as a function of magnetic field.

a, C/T versus H in our Eu-LSCO samples with p = 0.21 (orange) and p = 0.24 (red), at T = 2 K. The upper critical field above which there is no remaining superconductivity is H_c2 = 15 T at p = 0.21 and H_c2 = 9 T at p = 0.24. Note that for p = 0.24, C/T has reached 99% of its normal state value by 8 T. b, C/T versus H in our Nd-LSCO sample with p = 0.23, at T = 2 K, in a semi-log plot. The dashed line shows the expected field dependence of the Schottky contribution associated with Nd ions (C_mag, dashed line). The data are independent of field above H ≈ 9 T. Dotted lines are horizontal.

Extended Data Fig. 5 Specific heat of Eu-LSCO and Nd-LSCO down to base temperature.

a, Specific heat of the four Eu-LSCO samples of Fig. 2a measured in a field H = 8 T, down to 0.4 K. The rapid rise below 1 K is a nuclear Schottky anomaly (C_nuclear). b, Difference between the measured C/T of a and a constant term γ, plotted for each doping as a function of temperature, on a log–log plot (γ = 2.8 and 4.2 mJ K⁻² mol⁻¹, at p = 0.11 and 0.16, respectively). The line marked T² shows that the data at p = 0.11 and p = 0.16 obey ΔC = βT³ in the range from 1.5 K to about 5 K. The line marked T^–3 shows that the data at p = 0.11 and p = 0.16 obey ΔC ≈ T^–2 below 1 K, as expected for the upper tail of a Schottky anomaly. The ΔC curve at p = 0.16, ΔC(p = 0.16; T), therefore constitutes the non-electronic, and weakly doping-dependent, background for C(T) in Eu-LSCO, made of phonon and Schottky contributions. c, Specific heat of our Nd-LSCO crystal with p = 0.12, plotted as C/T versus T at three different fields, as indicated. At H = 0 (green), we see the large Schottky anomaly associated with Nd ions, varying as C_mag ≈ T^–2 at low T. At H = 8 T (red), it is pushed up above 2 K; at H = 18 T (blue), above 5 K. The line is a fit of the 18 T data to γ + βT² below 5 K. d, Specific heat of the four Nd-LSCO samples of Fig. 2c, plotted as C/T versus T. Below the vertical dashed line, we show low-temperature data taken at H = 8 T on three of these same samples. (See Supplementary Fig. 1 for the complete set of dopings and Extended Data Fig. 6 for further analysis and discussion.).

Extended Data Fig. 6 Analysis of specific heat data and doping dependence of β.

a, Raw data for Eu-LSCO at p = 0.11 (blue), 0.16 (green) and 0.24 (red), plotted as C/T versus logT. The width of the pale band tracking each curve is the uncertainty on the absolute measurement of C (±4%). The solid green line is a fit to C_nuclear ≈ T^–2 for the p = 0.16 data. b, Same three curves as in a, from which the same Schottky anomaly, C_nuclear/T, the green line in a, has been subtracted. The straight dotted lines show that (C – C_nuclear)/T is flat as T → 0 for p = 0.11 and 0.16, while it rises as log(1/T) for p = 0.24. The solid green line is a fit of the green curve at p = 0.16 to (C – C_nuclear)/T = γ + C_ph/T up to 10 K, where C_ph/T = βT² + δT⁴ is the phonon contribution. c, Same three curves as in b, from which the same phonon contribution C_ph/T, the green line in b, has been subtracted. We see that within error bars the resulting C_el/T is constant up to 10 K for p = 0.11 (blue) and 0.16 (green), while it varies as log(1/T) up to 10 K for p = 0.24 (red). The dotted lines are a linear fit to the data. d, Doping dependence of the phonon specific heat parameter β, in C_ph/T = βT² + δT⁴, obtained from a fit to (C – C_nuclear)/T = γ + C_ph/T up to 10 K, for Eu-LSCO crystals (dark blue squares) and Nd-LSCO crystals (red dots). For crystals, the error bars are the sum of two uncertainties: on the magnitude of the raw data, defined in the legend of Fig. 3, plus on the fitting procedure to extract β, described in a, b and c. For Nd-LSCO powders (orange dots), the values are obtained from Extended Data Figs. 7, 8; the error bars are the sum of two uncertainties: on the magnitude of the raw data, defined in the legend of Fig. 3, plus on the fitting procedure to extract β, described in the legend of Extended Data Figs. 7, 8. The black diamonds are 1/E_ph³ (right axis), where E_ph is the phonon energy (top of the acoustic branch) measured by neutron scattering on three Nd-LSCO single crystals: E_ph = 14.6, 14.7 and 14.8 meV at p = 0.12, 0.19 and 0.24, respectively (measurements performed by Q.M., M.D., H.A.D. and B.D.G.). We see that E_ph varies very little with doping, and β ≈ 1/E_ph³, justifying our assumption that C_ph(T) does not change appreciably between p = 0.11 and p = 0.25.

Extended Data Fig. 7 Specific heat of our polycrystalline samples at p = 0.07 and 0.12.

a, C/T versus T for Nd-LSCO p = 0.12, comparing raw data on crystal and powder, as indicated. The solid red line is a fit to the crystal data, consisting of the sum of three contributions, plotted below: electrons (dash-dotted), phonons (dashed) and Schottky (C_mag ≈ T^–2, dotted). b, Specific heat data for our powders with p = 0.07 and 0.12, at H = 0, from which the Schottky term (C_mag) has been subtracted, plotted as (C(H = 0) – C_mag)/T versus T². The dashed lines are linear fits to the data (γ + βT²). For p = 0.12, the fit yields γ ≈ 4.0 mJ K⁻² mol⁻¹, in reasonable agreement with the value obtained by applying 18 T to suppress the Schottky anomaly in our Nd-LSCO crystal with p = 0.12 (Fig. 2c), namely γ = 3.6 ± 0.5 mJ K⁻² mol⁻¹ (Fig. 3b). For the two powder samples, the γ values are plotted in Fig. 3b (purple dots) and the β values are plotted in Extended Data Fig. 6d (orange dots). The value of (C(H = 0) – C_mag)/T extrapolated at T = 2 K is plotted in Fig. 3a (open red circles).

Extended Data Fig. 8 Specific heat of our polycrystalline samples at p = 0.27, 0.36 and 0.40.

a, Raw specific heat data for our powders with p = 0.27, 0.36 and 0.40, at H = 0. b, The data in a from which the magnetic Schottky term (C_mag = A/T²) has been subtracted, plotted as (C – C_mag)/T versus T². The dotted lines are linear fits to the data (γ + βT²). For the three powder samples, the γ values are plotted in Fig. 3b (purple circles) and the β values are plotted in Extended Data Fig. 6d (orange circles). The value of (C(H = 0) – C_mag)/T extrapolated at T = 2 K is plotted in Fig. 3a (open red circles). c, The data in b from which the phonon term (C_ph = βT³) has been subtracted, plotted as (C – C_mag – C_ph)/T versus T². All three curves are seen to be constant. d, The data in b, compared to raw single-crystal data at p = 0.24 for Eu-LSCO (orange) and Nd-LSCO (red), taken at H = 18 T. (The two raw curves agree beautifully at T < 5 K, where C_mag in Nd-LSCO is negligible; Extended Data Fig. 5c.) The upper dotted line is a linear guide to the eye showing that the Eu-LSCO curve deviates from linearity at low temperature, unlike the curves at p = 0.27, 0.36 and 0.40.

Extended Data Fig. 9 Calculated specific heat from the Nd-LSCO band structure.

Comparison of the measured specific heat of Nd-LSCO (red; Fig. 3b, with error bars defined in the legend of Fig. 3b) and the specific heat calculated for the band structure of Nd-LSCO (blue; see Methods), with the van Hove point p_vHs set to be at p*. The calculations include the three-dimensional dispersion in the Fermi surface (along the c axis) and the disorder scattering, both consistent with the measured properties of our Nd-LSCO samples, namely their resistivity anisotropy (ρ_c/ρ_a) and their residual resistivity (see Methods). We see that while the van Hove singularity can give rise to a cusp-like peak at p_vHs (top left panel) and a log(1/T) dependence of C/T at p_vHs in a perfectly two-dimensional system with no disorder (lower left panel), these features inevitably disappear when the considerable three-dimensional dispersion of the real material and the high disorder of the real samples are included (right panels). The calculations only quantify what is naturally expected: the rise in specific heat due to the van Hove singularity is cut off when k_BT < ħΓ, where Γ is the scattering rate, or when k_BT < t_z, where t_z is the c-axis hopping parameter. The fact that we see C/T continuing to increase down to 0.5 K (lower right panel) excludes the van Hove singularity as the underlying mechanism.

Extended Data Fig. 10 Comparing with data on non-superconducting LSCO.

a, Normal-state electronic specific heat C_el of Eu-LSCO (squares; from Fig. 2b) and Nd-LSCO (circles; from Fig. 2d), at T = 0.5 K (red), 2 K (blue) and 10 K (green), plotted as C_el /T versus p. (At p = 0.08, 0.11 and 0.16, the red and green squares are split apart slightly so they can both be seen.) Open symbols are extrapolated values (dashed lines in Fig. 2b, d). Data on Nd-LSCO at p = 0.07, 0.12, 0.27, 0.36 and 0.40 (purple) are γ values obtained on polycrystalline samples, as described in Extended Data Figs. 7, 8. The black, purple and red data points are taken from Fig. 3b, with error bars defined in the legend of Fig. 3b. Error bars on the blue and green data points are defined in the same way as for the red data points (see legend of Fig. 3b). We also include γ for non-superconducting LSCO from published work (diamonds), obtained by extrapolating C/T = γ + βT² to T = 0 from data below 10 K (p < 0.06, ref. ³²; p = 0.33, ref. ¹³). The vertical dashed line marks the pseudogap critical point p* in Nd-LSCO (Extended Data Fig. 1). All solid lines are a guide to the eye. b, Comparison of C_el/T versus p in our samples of Eu-LSCO and Nd-LSCO at T = 10 K (green squares and circles in a) with published data on non-superconducting LSCO (diamonds). Open diamonds are γ measured in single crystals of LSCO at dopings where there is no superconductivity (p = 0.33, ref. ¹³; p < 0.06, ref. ³²; remainder¹⁷). Solid diamonds are data from powders made non-superconducting by Zn substitution¹⁷; γ values are obtained from fits to C/T = γ + βT² between about 4 K and about 8 K. We see that these early data on LSCO are quantitatively consistent with our data on Eu-LSCO and Nd-LSCO, apart from a downward shift in the position of the peak, consistent with a lower p* in LSCO (Extended Data Fig. 1). Lines are a guide to the eye.