Introduction

Migration of interfaces plays an important role in the final microstructure and resulting properties of crystalline materials. Decades of experiments and theory demonstrate that these processes are thermally activated and follow an Arrhenius relationship. However, in the last two decades experiments have demonstrated that structure evolution can be observed under cryogenic conditions1,2,3,4,5. A traditional thermally activated model of interface migration does not support these observations because the coarsening is more dramatic at cryogenic temperatures than at room temperature, as shown by Zhang et al.1,2. Recent molecular dynamics simulations of grain boundary migration revealed that select grain boundary types exhibit non-Arrhenius behavior, where the boundaries are mobile at cryogenic temperatures and migration rates frequently decrease with increasing temperature6,7,8,9,10,11,12,13,14,15. This inverse temperature dependence is evident in other material processes and across all classes of materials16,17,18,19,20,21,22. Processing recipes that exploit such antithermal behavior could enable new avenues for microstructure control and lead to major advances in catalysis, nanocrystalline alloys, and high efficiency engines23.

In this work we will show that while these non-Arrhenius observations are inconsistent with the traditional model used to describe grain boundary migration, they are entirely consistent with a forgotten classical model that accounts for both Arrhenius and non-Arrhenius observations of grain boundary migration. Furthermore, we will illustrate that the reason the traditional model fails in these cases is that it is a simplification of the classical model for which the assumptions are not always satisfied. We will then detail several observations from the last two decades that are now reconciled by the classical model, but which could not adequately be explained with the traditional model. Finally, the manuscript concludes with a discussion of factors to keep in mind when applying the classical model, as well as a discussion of other models that also predict non-Arrhenius behaviors but not cryogenic motion.

In the traditional model of grain boundary migration the velocity of a grain boundary v is proportional to an applied driving force p used to induce grain boundary migration according to

$$v=Mp$$
(1)

where M is the grain boundary mobility, which is the kinetic property most frequently used to describe grain boundary migration. In the traditional model, the mobility M follows an Arrhenius temperature dependence

$$M={M}_{o}\exp \left(-\frac{Q}{{k}_{B}T}\right)$$
(2)

where Mo is a pre-exponential constant and Q is an intrinsic barrier for the migration of the grain boundary. When mobility measurements follow an Arrhenius temperature dependence, estimates for Mo and Q can be obtained.

To define the classical model, we estimate the velocity of a grain boundary by considering a combination of forward and backward atomic jumps that are thermally activated24,25,26. Figure 1a illustrates the potential energy landscape for an atom that can jump from grain 1 to grain 2 to allow the boundary to migrate forward (or from grain 2 to grain 1 leading to backward migration). The two states are separated by an intrinsic barrier of magnitude Q, which can be biased by a driving force p. The activation energy barrier for the two jumps is then defined as Ea = Q ± p/2. When p is small relative to Q, Ea and Q are nearly identical, but when p is large relative to Q, one must take care in distinguishing between the activation energy Ea and the intrinsic barrier height Q.

Fig. 1: Examination of classical model.
figure 1

a Potential energy landscape with intrinsic barrier Q and driving force bias p. b Plot of Eq. (3) for values of Q equal to 0.03, 0.1, and 1 eV. c Arrhenius plot (log(v) vs. 1/T) of Eq. (3) overlaid with lines of velocity predictions based on traditional expectations following Eqs. (1) and (2). Note the large temperature range for the inset, which highlights the Arrhenius nature of curves with low values of Q at the very lowest temperature, but which obscures the non-Arrhenius nature of the same curves at high temperature, which is highlighted in the main plot. d Contour plot of Eq. (5) for different combinations of p and Q.

Full size image

In microstructure evolution, a number of different forces p can drive migration, including reduction in grain boundary area, difference in elastic energy across the boundary, stored strain energy from cold work, etc.26,27. In considering a combination of forward and backward jumps of N atoms at the grain boundary, it can be shown that the velocity is approximated by

$$v=Nb\nu \exp \left(-\frac{Q}{{k}_{B}T}\right)2\sinh \left(\frac{p}{2{k}_{B}T}\right)$$
(3)

where N is the number of atoms involved in the migration at the boundary, b is the distance of a single atom jump, \(\nu\) is the attempt frequency, kB is Boltzmann’s constant, and T is absolute temperature. Note that Eq. (3) is a variation of a form in ref. 26; a more complete description of this derivation, as well as variations thereof, is provided in the Supplementary Discussion, including Supplementary Figs. 1–3. The Supplementary Discussion also examines a similar model by Ivanov and Mishin where the forward and backward activation energies Ea are not symmetric when p/2 approaches the magnitude of Q25; however, it is shown in Supplementary Fig. 4 that the difference between these two models is less than a few percent for most cases, including those examined in this work, and decreases with increasing temperature.

It must be noted at this point that the derivation of Eq. (3) relies on the assumption that the rates at which the atoms hop are proportional to the Boltzmann probability, which can be obtained by examination of conventional transition state theory (TST)28. TST assumes equilibrium between the reactants and the activated complex (transition state). Some interpret this as a requirement of overdamped dynamics, where transitions between states are sufficiently separated in time that the system is able to sample an equilibrium ensemble of configurations. This is expected to occur when Ea ≫ kbT29.

Alternate descriptions of TST, such as variational TST, are less strict and have been applied in a broad range of scenarios, including where barrier recrossings are accounted for, when barriers are low, and the activation energy is not significantly greater than kBT28,30,31. What these examples have in common with classical TST is the requirement that the energy distribution among the reactant molecules is in accordance with the Maxwell-Boltzmann distribution28. We will later justify this approach by showing that even when Ea is comparable to kBT, atomistic simulations will follow Maxwell-Boltzmann distributions of the kinetic energy. We will also show that the form of Eq. (3) as well as its physical interpretation in terms of forward and backward atomic jumps fit the observations of the molecular dynamics simulations.

Before proceeding with the interpretation of the basic model, it is worth contrasting overdamped and underdamped dynamics. As noted above, overdamped dynamics are marked by a loss of memory from preceding jumps wherein the system is able to sample an equilibrium ensemble of configurations between jumps. In contrast, underdamped dynamics occur when the momentum from one transition is not entirely dissipated before a second transition occurs. In such cases, the transitions between subsequent states may become correlated.

Overdamped and underdamped dynamics are commonly studied by Brownian motion in tilted periodic, or washboard, potentials32,33,34,35. In these studies, particles exist in a periodic potential, which is tilted by a driving force p or bias of some kind. The result is that particles are likely to migrate in a specific direction over time depending upon the circumstances.

In the overdamped case, which occurs in two scenarios of Fig. 1a (Q ≫ kBT ≫ p/2 or Q ≫ p/2 ≫ kBT), the particles are considered to be in a ‘locked’ phase and move by thermal diffusion with hops separated by sufficient time to avoid correlated jumps.

Most measurements in the first several decades of grain boundary migration research and experiments were made in the limit of small driving force p relative to temperature T (i.e., p ≪ kBT). In this case, the sinh function is approximately linear and can be simplified using a first-order Taylor series expansion (linear term only). Using this simplification, Eq. (3) then reduces to

$$v=\frac{Nb\nu }{{k}_{B}T}\exp \left(-\frac{Q}{{k}_{B}T}\right)p$$
(4)

This form, although sometimes used36, is typically simplified to the traditional model in Eqs. (1) and (2) where a temperature dependence in the prefactor has been removed with the introduction of with the Mo constant. The linear force-velocity relation in Eq. (1) is generally referred to as the overdamped limit37.

In the underdamped case, the bias, p, is sufficiently high relative to the potential height (Q in this case) that the particles are considered to be in a ‘running’ phase, where inertia drives the particles over the barriers with the aid of the bias32. Even at low temperatures when thermal nucleation is negligible, the particles can achieve a ‘running’ phase when the bias is sufficiently high. It is also possible for a single state to transition between ‘locked’ and ‘running’ phase at intermediate values of the bias33.

This analogy has been used previously by Deng and Schuh to describe the diffusive to ballistic transition of grain boundary migration38, by Ivanov and Mishin to describe the dynamics of shear coupled grain boundary migration25, and by others to describe the migration of dislocations39.

In this work, we will show that Eq. (3) captures characteristics in both the overdamped and underdamped dynamics regimes.

Results

Analysis of the classical model

To illustrate why both Arrhenius and non-Arrhenius grain boundary migration is not only possible, but consistent with the classical model defined in Eq. (3), we examine predicted velocities for 3 different values of Q (0.03, 0.1, and 1.0 eV) at a fixed value of p = 0.01 eV. The values for \(v_0=Nb\nu\) are given as 1.71 × 103, 2.85 × 103, and 1.95 × 106 m/s, respectively, to match the values in the molecular dynamics simulations to be shown later in this work. Figure 1b plots Eq. (3) for v vs. T for the three conditions described here.

To interpret Fig. 1b, we first examine the highest intrinsic barrier height value of Q = 1.0 eV. In this case, the intrinsic barrier height is sufficiently high that the process only results in measurable grain boundary velocities at higher temperatures when sufficient thermal energy is available to enable an appreciable number of forward atomic jumps, but backward atomic jumps remain negligible.

For the intermediate intrinsic energy barrier value, Q = 0.1 eV, we see the thermally activated nature at low temperatures, but see a prolonged region where the grain boundary velocity is near a maximum value.

When the intrinsic barrier is especially low, Q = 0.03 eV, the grain boundary velocity is non-zero at cryogenic temperatures with an exponential rise expected of a thermally activated process. However, it reaches a maximum velocity before decreasing at higher temperature. The reason it is so mobile at low temperatures is because the intrinsic barrier is extremely small, Q = 0.03 eV.

For both Q = 0.1 and 0.03 eV, very little thermal energy is required to enable the forward atomic jumps, so the grain boundary is observed to migrate at low temperatures. As the thermal energy rises, it is sufficient to enable backward jumps since the intrinsic barrier is so small. The continued addition of thermal energy (increased temperature) serves to enable the backward jumps at increasing frequency. As these backward atomic jumps become more prominent, they slow the overall grain boundary velocity. The net result is a non-Arrhenius temperature dependence of the grain boundary velocity at high temperatures even though all processes are thermally activated. Furthermore, the velocity will reach a maximum and show a gradual decrease at sufficiently high temperatures. This thermal disordering and frustration of coordinated motions has been reported previously10,12,40.

Figure 1c illustrates the deviation from Arrhenius grain boundary migration in a plot of log(v) vs. 1/T where the same data from Fig. 1b are used and represented as discrete points for the three intrinsic barrier heights discussed previously. As can be seen in Fig. 1c, at higher temperatures, the lowest two intrinsic barrier heights are non-linear. However, as shown in the inset, at the lowest temperatures, all three intrinsic barrier values result in a linear temperature dependence, which is indicative of an Arrhenius process.

Also included in Fig. 1c are solid lines that conform to a single forward atomic jump with activation energy Ea = Q − p/2, which is akin to the simplified form of Eqs. (1) and (2). As can be seen, at the lowest temperatures, these lines are nearly identical to the results of Eq. (3), but at higher temperatures, the deviation becomes more apparent as the intrinsic barrier height Q decreases. As noted previously, the deviation from Arrhenius behavior occurs as intrinsic barrier height Q gets smaller and as temperature increases because the thermally activated backward jumps lower the net velocity of the grain boundary, leading to a non-Arrhenius temperature dependence.

One can calculate the critical temperature \({T}_{{v}_{max}}\) where Eq. (3) is maximum and above which the velocity will exhibit inverse temperature dependence. The critical temperature \({T}_{{v}_{max}}\) is given by

$${T}_{{v}_{max}}=\frac{p}{2{k}_{B}\,{\tanh }^{-1}\left(\frac{p}{2Q}\right)}$$
(5)

Figure 1d provides a contour plot of Eq. (5) as a function of both p and Q. As can be seen, \({T}_{{v}_{max}}\) is almost solely a function of Q and predicts values over 1000 K for intrinsic barrier heights Q over values of 0.1 eV. Thus a combination of Arrhenius and non-Arrhenius behavior is only predicted for low Q processes, which would correspond to underdamped dynamics.

Equation (3) will always predict non-Arrhenius behaviors at temperatures above \({T}_{{v}_{max}}\). But, as the intrinsic barrier height, Q, increases, the likelihood of observing non-Arrhenius behavior becomes negligible as \({T}_{{v}_{max}}\) approaches the melting temperature for a material, TM. As such, the boundary between the Arrhenius + non-Arrhenius and Arrhenius only regions, as illustrated in Fig. 1d, will be different for each material, based on its melting temperature, TM.

Thus at higher values of Q, only the thermally activated forward jumps are likely to be observed and the net result is the traditional Arrhenius temperature dependence over the temperature range of interest. This corresponds to the traditionally expected overdamped dynamics for grain boundary migration.

It is worth noting that according to Eq. (3), any driving force of p > 2Q would cause the activation energy for the forward jump to go to zero (i.e., the driving force bias p/2 would be greater than the intrinsic barrier Q). In the event that the activation energy goes to zero, the process is no longer thermally activated, rather it is a barrierless form of migration.

As we seek to use this 1-dimensional model to interpret simulated and experimental grain boundary migration, we must consider how variables in Eq. (3) might vary in a 3-dimensional solid and with grain boundaries that could exhibit different atomic structures. The number of atoms N participating in the boundary migration could change with temperature as boundary structure could change with temperature. Additionally, not all atomic jumps may be of length b or of barrier height Q. In fact, there may be a distribution of these values. As such, when using Eq. (3) to fit and interpret grain boundary migration, the parameter Q will describe the barrier height of the migration process (a representative value from the distribution of barrier heights for the constitutive atomic hops, such as its mean), rather than the barrier height of identical individual atom jumps. Nevertheless, the non-linear temperature dependence does not necessarily imply a change of mechanism nor the necessity of distinct values of Q over different temperature ranges. Rather, it is possible for the migration mechanism to remain constant, and therefore be described by a single value of Q due to the additional temperature dependence of the driving force term in Eq. (3). Finally, the prefactor Nbν represents a reference velocity vo of the process that is representative of the distributions of unit atomic processes, rather than the combination of values of N, b, and ν for single identical atomic jumps.

When applied to real grain boundaries, the individual jumps in the model of Eq. (3) can also be interpreted both literally and figuratively, depending on the unit processes involved in the migration of a particular boundary. This is important to note, because it is well-known that boundary migration can have coordinated atomic motions9,10,12,41,42 that aren’t just forward and backward relative to the placement of the boundary. A literal interpretation of forward and backward jumps applies when a boundary actually moves forward and backward as a result of the atomic jumps. We will show examples of this literal interpretation in simulations presented in this work in which such conditions hold. On the other hand, a figurative interpretation of the forward and backward jumps is more nuanced. ‘Forward jumps’ would still be those that contribute to the forward migration of the boundary, but ‘backward jumps’ could be a variety of jumps that detract from the forward migration of the boundary. In other words, in the figurative sense, any jump that simply frustrates the forward motion would be considered a backward jump, even if the boundary itself doesn’t move backward. Thus, atoms wouldn’t just have to move ‘backward’ in a literal sense to slow the migration in a manner that still gives the overall behavior described by Eq. (3). This would naturally capture thermal disordering that occurs at higher temperatures and which could frustrate atomic jumps.

Other factors that could impact the interpretation of Eq. (3), as well as other sources that could lead to non-Arrhenius temperature dependence are examined in the discussion.

Observations reconciled by the classical model

First, we note that the diverse temperature dependence of the migration behaviors illustrated in Fig. 1c are consistent with the diverse migration behaviors observed in other examinations of grain boundary migration6,7,8,9,10,11,12,13,14,15,38,43,44. This is important because the diverse behaviors in Fig. 1c come from the single equation for the classical form, Eq. (3). More importantly, when migration behaviors in these surveys did not conform to the expected Arrhenius behavior, they were often labeled under the umbrella of ‘non-thermally activated’ processes7,15. But, as has been illustrated in the examination of Eq. (3), non-Arrhenius behavior is not necessarily non-thermally activated.

Second, we reaffirm that the non-Arrhenius behaviors are observed when intrinsic barrier heights Q become small. This is illustrated in molecular dynamics simulation results of grain boundary migration new to this work. Migration is induced in 165 metastable structures of a Σ3〈11 8 5〉 Ni grain boundary. Standard energy conserving orientational force methods8,45 are used to induce migration with a driving force of 0.01 eV and 5 replicates of each simulation. Temporal subdivision methods46,47 allowed us to determine the uncertainty of the measurements. The methods used to construct, induce, and measure migration of these grain boundaries are described in the methods section.

Figure 2a displays the results for 4 representative metastable structures, with plots of the velocity distribution at each temperature. These velocity distributions are fitted with Eq. (3), which are shown over each example dataset. As can be seen, the migration behavior of these 4 structures is notably varied, from entirely antithermal (inverse temperature dependence) to entirely Arrhenius (low velocities at low temperatures that increase exponentially with increasing temperature).

Fig. 2: Metastable boundary migration.
figure 2

a Velocity distributions and corresponding fit for migration of 4 different metastable structures. b Plot of temperature at which each metastable structure has its maximum velocity as a function of the fitted intrinsic barrier height Q. Red line is a plot of Eq. (5).

Full size image

Figure 2b plots the temperature at which the velocity of each simulation is maximum Tmax(v) as a function of the fitted intrinsic barrier height Q, which is obtained from the fit of the data to Eq. (3). It can be seen that as the intrinsic barrier height Q drops, the temperature at which the velocity is a maximum moves to lower temperatures. This is overlaid with the analytical solution (Eq. (5)) in red, which captures the general trend in the data. Note that Tmax(v), as obtained from the data, only takes values corresponding to the simulation temperatures, which occur at 200 K intervals.

This data reaffirms the trend shown in Fig. 1b, in that as intrinsic barrier height Q drops, the Arrhenius behavior is observed at lower temperatures followed by non-Arrhenius behavior at high temperatures. In addition, this molecular dynamics data of grain boundary migration clearly demonstrates that the classical equation, Eq. (3), can fit a large variety of behaviors from entirely Arrhenius, to almost entirely non-Arrhenius with a single form.

To demonstrate that the atoms involved in the boundary migration process are in thermal equilibrium, Supplementary Fig. 5 plots the Maxwell-Boltzmann speed distributions for the advancing and retreating atoms in the grain boundary. These plots are for a single snapshot of the systems of the two structures examined in Fig. 2a with Q = 0.02 eV and Q = 1.05 eV, which exhibit the extremes in temperature dependence of being almost entirely non-Arrhenius (antithermal) to entirely Arrhenius over the investigated temperature range, respectively. Similar distributions are observed at different snapshots and for other structures indicating that the atoms involved in the boundary migration are in thermal equilibrium, as required by transition state theory.

Third, in atomistic simulations of grain boundary migration that exhibited non-Arrhenius (antithermal) behavior, we see evidence of both literal backward atomic jumps as well as figurative backward jumps as thermal energy is increased. The evidence of literal backward jumps is given by time periods in which a grain boundary migrates backwards. This can be seen in boundary position vs. time plots in Supplementary Fig. 6 and in Fig. 2a of ref. 12; these boundaries are generally moving quickly, but have periods of time where they are stuck and even move backwards. This is also evident in Fig. 2a where the observed velocity distributions include negative velocities.

The evidence of figurative backward jumps is provided in the scattering of very specific ordered atomic motions that result in a slower forward migration. This can be seen in plots of atomic displacements in refs. 10,12 and in Supplementary Fig. 7 for the two structures examined in Fig. 2a with Q = 0.02 eV and Q = 1.05 eV, respectively. When the barrier is low, as in the case of the Q = 0.02 eV boundary, the ordered atomic motions along the Shockley partial directions become increasingly frustrated with increased temperature, indicating that there are more figurative backward jumps that frustrate the forward jumps. This is in stark contrast to the case where the intrinsic barrier height is high, for which the addition of thermal energy promotes forward migration. For example, in the case of the Q = 1.05 eV boundary, no migration is observed at low temperatures until sufficient thermal energy at high temperatures facilitates the migration, which is does not appear to be ordered in this case. Thus, the low Q boundaries easily enter into a running state at low temperatures, but transition between locked and running states as thermal energy is increased, which is consistent with observations in underdamped systems33.

This problem can be exacerbated for some boundaries where the ordered, coordinated motion patterns don’t involve the coincidence site lattice atoms, which are coincident to both crystal lattices. The forward jumps are easily facilitated at lower temperatures and added thermal energy does little to further enable the forward jumps. But, the added thermal energy does enable backward jumps, in the form of more dramatic lattice vibrations or jumps into other positions, which only serves to frustrate the coordinated atomic motions of the surrounding atoms12.

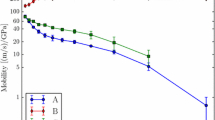
Fourth, Eq. (3) also reconciles an interesting study by Chesser and Holm where they examined how simulations of grain boundary migration are affected by interatomic potential13. Figure 3a, reproduced from their work, shows a comparison of boundary migration results for four different Ni interatomic potentials in which they observed non-Arrhenius (antithermal) migration with three of the potentials and Arrhenius migration with the fourth potential. At this point, it is not clear which of all these potentials, if any, may be representative of the expected migration behavior of real Ni with this atomic structure. Nevertheless, they determined that the observed trends correlated with the generalized interface fault energy (GIFE)48, which corresponds to the energy associated with the migration of the grain boundaries as the atoms move along the expected Shockley partial directions for this boundary. GIFE is similar to generalized stacking fault energy surfaces and twin fault energy surfaces, providing a variation of the energy between equilibrium configurations of the system during migration. As such, the GIFE can be assumed to be related to the intrinsic barrier height Q for grain boundary migration of that system. Chesser and Holm only observed antithermal behavior when GIFE values were small. Equation (3) explains why the different interatomic potentials give different answers for the same atomic shuffling process: the potentials have different intrinsic barrier heights, Q, associated with the same process, which leads to different values of Tmax(v) and, consequently, different behavior for a given temperature range (presumably Tmax(v) was below the simulation temperatures for the three simulations exhibiting antithermal behavior and above it for the Arrhenius behavior). More importantly, Eq. (3) shows that the different interatomic potentials are not necessarily predicting drastically different behaviors. Rather, they predict behaviors consistent with the intrinsic barrier heights, Q, of the potential. In examining Fig. 3a further, the Ni4 potential at its highest temperature and the Ni1 potential at its lowest temperature could both be showing signs of the Arrhenius to non-Arrhenius transition predicted by Eq. (3). This reinforces the critical need to obtain a potential that reflects the true intrinsic barrier height, Q, of this migration process; the investigated temperature range is clearly near a transition point between Arrhenius and non-Arrhenius behaviors for the interatomic potentials examined.

Fig. 3: Observations reconciled with classical model.
figure 3

a Mobility vs. temperature plot for 4 Ni interatomic potentials, reproduced with permission and adapted from ref. 13. Plots of velocity vs. b driving force and c temperature, for data reproduced from ref. 38 as individual datapoints along with a single fit over all conditions to Eq. (3) plotted as lines.

Full size image

Fifth, Eq. (3) provides a rational explanation as to why the indentation performed by Zhang et al. was more dramatic at cryogenic temperatures than it was at room temperature2. This of course assumes that the migration process would have a sufficiently low intrinsic barrier height, Q, that Eq. (3) would predict a non-Arrhenius temperature dependence with higher migration velocities at cryogenic temperatures than at room temperature. It is not yet clear that this assumption is valid, but later experimental work has indicated that the grain boundary types play an important role3,4,5 and simulations have shown that these same types of grain boundaries6,7,10,11,12 exhibit this non-Arrhenius migration. Notably, they include the same type of incoherent twin grain boundaries examined in Fig. 2, which have the low intrinsic barrier heights that facilitate migration at cryogenic temperatures.

Equation (3) would also serve to explain why as the impurity content was raised, the coarsening was reduced2; experimental measurements of migration activation enthalpies are observed to increase by several hundred percent in some cases as impurity content is increased36,49,50. Thus, increased impurity content would naturally lead to increased intrinsic barrier heights and a reduced coarsening of the microstructure as compared with the higher purity samples in ref. 2.

Sixth, while all the discussion to this point has been focused on the temperature dependence, the form of Eq. (3) also reconciles interesting observations on the driving force dependence of grain boundary migration. Of particular interest is the work by Deng and Schuh, where they used an adaptive random walk method under a driving force to study how the driving force influences the simulated migration rates of Ni grain boundaries38. In particular, they focused on the circumstances under which the migration velocity is and is not linearly dependent upon the driving force (i.e., whether or not it follows Eq. (1)). Deng and Schuh examined two different grain boundaries over a range of applied driving forces, p, and temperatures, T. Their data for the symmetric Σ5 boundary is reproduced as discrete markers in Fig. 3b, c. The data points are accompanied by a fit of Eq. (3) over all conditions. In other words, all the variation seen in both plots is fit with a single fit, giving an intrinsic barrier height of Q = 0.19 eV. As can be seen in Fig. 3b, c, the fit is not perfect but Eq. (3) describes much of the variation and has the right form to capture the non-linear dependence of velocity on driving force and temperature with a single set of parameters. This means that one is not limited to analyzing cases where velocity varies linearly with driving force. This may even account for an observed dependence of barrier heights on driving force51. Additional work will be required to better understand the role of driving force on boundary migration and Eq. (3) may be helpful in gaining this insight.

Discussion

As has been demonstrated, the classical model is critical to understanding numerous behaviors that do not always follow the expected Arrhenius behaviors predicted by the traditional model. Thus, it is important to understand when one must use the classical model (Eq. (3)) and one can reasonably use the traditional model (Eqs. (1) and (2)) with negligible error.

As noted previously in the model definitions, the traditional model (Eq. (4)) is a linearized simplification of the classical model (Eq. (3)). The linearization will only be accurate in the limit of small driving forces (p ≪ kBT). One can directly calculate the error between Eqs. (3) and (4) (plotted in Supplementary Fig. 3 as a function of p and T). In experiments this is typically not a problem since even high driving force processes, like stored deformation energy, have driving forces less than 10−3 eV/atom26. In such cases the traditional (linearized) form should not result in any significant error at non-cryogenic temperatures. In atomistic simulations, higher driving forces are frequently used6,10,38,45,52, in some cases up to 0.1 eV/atom. In these cases the use of the traditional (linearized) form could result in significant error.

This leads to an important implication of the classical form with the sinh term. At first glance it would appear that the property mobility can only be defined in the low driving force limit (p ≪ kBT). As shown earlier, Eq. (3) reduces to Eq. (4) in this limit. One could then define mobility as in Eq. (2) if the prefactor is defined as

$${M}_{o}=\frac{Nb\nu }{{k}_{B}T}$$
(6)

which preserves the additional temperature dependence in Eq. (4). Many of the temperature-dependent behaviors illustrated in this work could be captured with this temperature-dependent prefactor. In fact, the inclusion of temperature in the prefactor (e.g. Mo) is not new and a few examples include derivations in refs. 26,53,54,55 and even in recent work focused on the migration of grain boundaries through disconnections56, which shows interesting non-Arrhenius behaviors. The temperature dependence of Mo plays a bigger role as Q, and correspondingly \(\exp (-Q/{k}_{B}T)\), get smaller, which is exactly what this work shows when Q becomes small.

This leads to a more general discussion about mobility. It is always defined as a proportionality constant between velocity v and driving force p. How should we think about mobility when that proportionality constant is not linear (when the low driving force limit of p ≪ kBT is not satisfied). If the goal of defining mobility is to understand how v changes with p, one could theoretically define mobility as

$$M=\frac{\partial v}{\partial p}.$$
(7)

This form would preserve the definition in the low driving force limit (Eq. (1)), but also allow mobility to be defined for more complicated cases, such as is encountered here. It is important to note that when the mobility is calculated from Eq. (7) and retains any dependence on p, one can no longer use the mobility to calculate the velocity as in Eq. (1). But, mobility in this definition would allow one to easily determine how the velocity of a grain boundary varies as a function of p. This dependence of velocity on driving force, p, is illustrated to some effect for Eq. (3) in Supplementary Fig. 2. As the field continues to discover the mechanisms underlying grain boundary migration, it may be helpful to examine mobility in light of this revised definition. Some may argue that mobility can no longer be defined as an intrinsic property of a boundary, but perhaps this is not surprising given what we are learning about distributions of migration mechanisms that a boundary may choose from56.

It is also important to recall that in Arrhenius plots it is common to point to a change in mechanism when the slope changes over different temperature ranges. In these cases, the slope change is typically discontinuous and the slope in each range is then used to define the activation energies, or intrinsic barrier heights, of the process in the respective temperature ranges. While the classical equation defined in Eq. (3) does predict non-linearity of the Arrhenius plot when intrinsic barrier heights are small, it still has a single explanation (constant Q) for the various slopes over the whole temperature range (i.e., non-linearity of the Arrhenius plot arises from the temperature dependence of the unsimplified driving force term, rather than a change in mechanism or temperature dependent barrier height). In contrast, if a process truly has a change in mechanism, it may have a different intrinsic barrier height (or activation energy) for each mechanism, requiring a separate fit for the temperature range over which each is active. It is possible to distinguish between the two cases—(i) non-linearity arising from the driving-force term with a constant, temperature-independent barrier height, Q, vs. (ii) non-linearity arising from a temperature dependent barrier height, \(Q\left(T\right)\)—by investigating the driving force dependence. In short, one must take care when interpreting non-linearity of Arrhenius plots and what the various changes may mean.

The classical model described in this work is able to account for the non-Arrhenius temperature dependence reported in many publications. It is able to do so by reconsidering typical thermally activated models described by TST. In particular, the non-Arrhenius temperature dependence emerges when barrier heights, Q, become small and are equal to or smaller than the available thermal energy kBT. This use case is not without precedent31,57 and may be indicative that TST theory can be employed in a wider variety of scenarios than previously thought. This line of reasoning is supported by the fact that the model matches both the data and observed migration mechanisms presented in this work. However, additional work will be required to further validate or disprove that which is presented here.

As noted briefly in the introduction and the previous section, there are also other existing models that exhibit non-Arrhenius temperature dependence for various reasons that could replace or supplement the classical model described here. For example, the work of Race et al. describes the emergence of non-Arrhenius behaviors resulting from a rate limiting nucleation process that can be required for grain boundary migration58. In their work, they illustrate how a flat grain boundary would require nucleation of islands or facets, which would subsequently grow until the boundary is once again flat. The rate limiting step is the nucleation, not the subsequent growth of the new facet. They indicate that to measure accurate velocities, the system size should be above a certain threshold for multiple island nucleation to capture the effects of nucleation. The simulation cell for the grain boundary described in the methods and shown to migrate in Fig. 2, a Σ3(11 85), falls below the critical size for multiple island nucleation, but has persistent facets because it has a near (1 1 1) boundary plane with incoherent facets that separate longer coherent twin (1 1 1) facets. Thus, it migrates by step flow motion of the persistent incoherent facet. Nucleation barriers for these boundary types are significantly reduced, as shown by Hadian et al.51. Thus, the migration is not expected to be significantly limited by the need, or time required, for nucleation, although nucleation could be a factor in the variability of the migration velocities observed by the different boundary configurations examined in this work. It is worth noting that the boundaries examined by Race et al. had fast growth between nucleation events, with energy barriers of 0.1 eV, and the fastest boundary examined by Hadian et al. also had energy barriers of 0.1 eV, both of which are in the range of those shown in Fig. 2. In short, the overall migration speed was reduced by the time required to nucleate new facets, and they attribute the non-Arrhenius behavior to a roughening transition of the boundaries58. A number of other examples exist in the literature where different rate limiting factors, mechanism transitions, or a spectrum of events can impact behavior and lead to non-Arrhenius behaviors23,41,42,56,59,60,61,62,63,64.

It is also possible that one might derive alternative models that are similar in form to Eq. (3) that account for other factors. For example, in variational transition state theory barrier recrossing are typically accounted for using the transmission coefficient, κ. In the absence of any additional information, this correction factor is often set to one; however in cases with multiple crossings of the dividing surface at transition state, κ is less than one and lowers the rate of successful attempts. This type of variational approach may yield a result similar to an accounting of the ‘backward’ jumps in Eq. (3). Reaction rates can also be adjusted to account for collision cross-sections, since not all attempted collisions would initiate the correct reaction; the collision cross-sections of jumps into specific spots would naturally be reduced with increasing temperature. Again, this reduced cross-section would be similar to an increased number of ‘backward’ jumps that frustrate the forward motion in Eq. (3). Thus, there may be a variety of scenarios that have different mechanisms but similar forms to Eq. (3).

But, even when these alternative explanations may account for non-Arrhenius behaviors, it is clear that to observe boundary migration at cryogenic temperatures, low barrier height processes are required and additional thermal energy only serves to frustrate these simple, and often ordered processes. Importantly, the classical equation presented here (Eq. (3)) explains both the non-Arrhenius (antithermal) behavior, and migration at cryogenic temperatures.

In summary, non-Arrhenius does not necessarily mean non-thermally activated. For small Q (intrinsic barrier height) processes, little thermal energy is needed to initiate the forward atomic jump process, and additional thermal energy only serves to enable the backward atomic jump processes that reduce the net velocity. This leads to non-Arrhenius behavior despite the fact that both processes are thermally activated. Both driving force, p, and intrinsic barrier height, Q, play important roles in Eq. (3) that deviate from the traditional established models, Eqs. (1) and (2), when intrinsic barrier heights are low. These low barrier height processes fall into underdamped dynamics, which contrast the typical examination of boundary migration in the overdamped limit.

This explains why processes such as antithermal behavior and cryogenic grain boundary mobility have generated such confusion and interest. Most experimental measurements of grain boundary migration report activation enthalpies that are well in excess of the low Q values that Eq. (3) would suggest are required for cryogenic migration and non-Arrhenius temperature dependence. Gottstein and Schvindlerman’s review of grain boundary migration indicates that most activation enthalpy values fall in the range of 0.5–3 eV, though values as low as 0.2 eV can be found26. As such, at this time there are no known experimental studies that report activation enthalpies of sufficiently low magnitude to predict cryogenic migration or non-Arrhenius temperature dependence. Nevertheless, cryogenic coarsening has been observed in several studies1,2,3,4,5 and the coarsening in some cases has been reported to be more dramatic at cryogenic temperatures than at room temperature1,2. Equation (3) has an appropriate form to describe these phenomena, but determining the intrinsic barrier heights, or activation enthalpies, of migration for these particular cases remains an open challenge. If verified to be within the range expected to be necessary to observe such behavior based on Eq. (3), these non-Arrhenius processes could provide the key insights to enable grain boundary engineering65,66 at cryogenic temperatures.

Methods

Boundary construction

In the atomistic simulations original to this work, we examined grain boundary migration of a number of metastable grain boundary structures associated with an incoherent twin. Specifically, the grain boundary has a disorientation with a 60∘ rotation about the [111] axis, corresponding to a Σ3 coincidence site lattice. The boundary plane normals from both sides of the grain boundary are \(\left(11\,8\,5\right)/\left(8\,11\,5\right)\). The size of the simulation cell is 41.8 Å by 30.3 Å in the boundary plane and more than 85 Å in both directions normal to the boundary plane. The simulation cells are periodic in the two dimensions of the boundary plane, but not in the direction normal to the boundary plane, thus containing only a single grain boundary. Each simulation cell has 20,500 atoms. We simulated this grain boundary in Ni with the embedded atom method (EAM) potential developed by Foiles and Hoyt67. Because each grain boundary can exhibit a multiplicity of metastable atomic structures68,69,70,71, we desired to know how this variation in structure would affect the migration behavior. We followed standard construction methods to create numerous possible starting configurations before using conjugate gradient minimization to determine the minimum energy structure of each starting configuration72,73. Variables influencing the starting configurations include relative placement of the two grains, placement of the boundary, allowed proximity of atoms, and deletion of atoms from specific crystals when allowed proximity is exceeded. This resulted in 165 unique metastable grain boundary structures of the same grain boundary, whose distribution of energies can be seen in Supplementary Fig. 8. Uniqueness is simply defined here as different configurations of the atomic structures obtained in the sampling; some of these structures that are unique at 0 K may adopt similar structures at finite temperatures. Ongoing work is focused on defining uniqueness in a more complete sense since it is not a trivial process as evidenced by efforts in this area68,70,71. As such, we make no claim that these unique structures are expected to be representative of a complete ensemble of structures for this grain boundary. Rather, they represent a range of structures this grain boundary could adopt.

Boundary migration and measurement

Instead of simulating the migration of just the minimum energy grain boundary structure, as is most commonly done, we examine the migration of all 165 metastable structures. Molecular dynamics is used to simulate the grain boundary migration using LAMMPS74. Standard energy conserving orientational (ECO) force methods8,45 are used to induce migration with a driving force of 0.01 eV/atom. The ECO driving force introduces an orientation parameter that allows the method to add energy to or subtract energy from atoms in the two grains across the boundary. This difference in energy causes atoms in the high energy grain to jump onto the lattice of the low energy grain, thereby reducing the energy in the system and causing migration of the boundary. Each boundary is subjected to the ECO driving force until the boundary sweeps entirely through one crystal or for a maximum time of 400 ps. If the boundary does not travel more than 10 angstroms in the 400 ps, it is designated as immobile, with a velocity of zero.

Since molecular dynamics requires a random seed for the initial velocity distribution of the atoms, and this can lead to slightly different outcomes, we examined 5 replicates of each grain boundary migration simulation. Each simulation cell uses an NPT thermostat-barostat and is equilibrated for 50 ps to ensure adequate convergence of temperature to a desired value of 200, 400, 600, 800, 1000, 1200, or 1400 K, and a desired pressure of 0 MPa. Most temperature and pressure fluctuations about the target temperature and zero pressure are ±10 K and ±100 MPa, respectively. The NPT barostat is set to correct the system non-aggressively. In total, 5775 simulations were run (165 unique grain boundaries × 5 replicates × 7 temperatures).

Supplementary Fig. 6 plots the boundary position as a function of time for the 5 replicates of one metastable grain boundary structure. To account for the fact that not all boundary position vs time data are linear over the entire range, we employ a temporal subdivision method to fit the velocity over short times46,47, though we note that other methods to quantify boundary migration uncertainty also exist75. Thus, at any given temperature, we obtain a distribution of velocities exhibited by each metastable grain boundary structure, providing a measure of uncertainty. The 5 replicates of each simulation, together with the temporal subdivision method, allow us to determine the uncertainty of the boundary migration measurements. Velocity distributions resulting from this procedure are shown in Fig. 2a.

Supplementary Fig. 9 shows the velocity data for all 165 metastable structures with error bars that show the first and third quartiles of the measured velocity distributions at each temperature.

Bayesian regression is used to fit Eq. (3) to the velocity distributions over the full range of temperatures, as illustrated in Fig. 2a. The values and uncertainty of the fit variables, Q, and a lumped prefactor, \(Nb\nu\), are plotted in Supplementary Fig. 10. The goodness of fit for all 165 structures is given by the weighted RMSE, the average and maximum of which are 6.8 and 26 m/s, respectively.