Introduction

Phase transitions involving electronic heterogeneity are well-established in quantum materials, as evidenced by the way electron correlations lead to Mott systems with insulator-to-metal transitions1,2,3 and low carrier densities generate colossal magnetoresistance (CMR)4,5. These principles were explored in nearly Dirac materials like EuMnSb26, Mott insulating Ti-doped Ca3Ru2O77, and perovskite manganites such as La1−xSrxMnO38,9, and although there is a significant body of work revealing insulator-to-metal transitions triggered by temperature, pressure, and light10,11,12,13,14,15,16, magnetically-driven transitions are particularly attractive due to their ability to support CMR. The latter typically relies upon Jahn-Teller distortions and double-exchange mechanisms, although the recent discovery of Mn3Si2Te6 demonstrates that these interactions are not required, while also introducing a novel quantum state involving chiral orbital currents17 that merits further investigation.

Mn3Si2Te6 hosts trigonal \(P\bar{3}1c\) symmetry with two different Mn(II) sites as well as alternately stacked honeycomb and triangular layers18,19. This nodal line semiconductor displays an insulator-to-metal transition and CMR under a magnetic field for H∥c20,21. Significant magnetic anisotropy arises from strong spin-orbit coupling due to Te orbits coupled with Mn spins; this proximity effect is consistent with strong hybridization between Mn and Te orbitals and is easily perturbed by small dc currents17,20,21,22. Whether Mn3Si2Te6 hosts a spin-rotation-favored insulator-to-metal transition or chiral orbital current state-induced CMR17,21, the majority of measurements thus far involve transport techniques, making it difficult to ascertain the microscopic aspects of the electronic response—especially in the presence of a chiral orbital current that might create electronic localization in combination with spin-phonon coupling, topological nodal-line degeneracy, magnetization anisotropy, and magnetic fluctuations21,23,24,25,26,27,28. Questions have therefore arisen about how itinerary and electron correlations compete with localization and whether carriers are created homogeneously as part of the insulator-to-metal transition and CMR effect. Magneto-infrared spectroscopy is a powerful tool for addressing these issues.

In order to unravel the origin of CMR in a material that does not host Jahn-Teller or double-exchange interactions and to search for spectroscopic signatures of chiral loop currents, we measured the infrared response of Mn3Si2Te6 across the magnetic ordering and insulator-to-metal transitions. Rather than a conventional metal with a Drude response and screened phonons, the field-driven insulator-to-metal transition leads to a weakly metallic state with localized carriers. We discuss this localization in terms of the large polaron model, expectations for chiral orbital currents, and the ability of short-range spin fluctuations to give rise to Slater peaks17,29,30,31,32. The dynamics of these pinned carriers are captured by the percolation model, which emphasizes the ubiquity of electronic heterogeneity in CMR systems. In this case, a frequency-dependent threshold magnetic field accounts for the gradual formation of the weakly metallic high field phase. These findings complement the understanding of bad metal behavior in correlated oxides, reinforce the role of new quantum states in field-driven insulator-to-metal transitions and their CMR effects, and pave the way for the development of unconventional CMR materials.

Results and discussion

Classic semiconducting properties at 300 K and across the ferrimagnetic transition

Figure 1 displays the room temperature reflectance of Mn3Si2Te6 along with the optical conductivity calculated via Kramers-Kronig analysis. σ1(ω) is low and flat, characteristic of a semiconductor, punctuated by a series of sharp phonons and localized electronic excitations at higher frequencies33. Lattice dynamics calculations allow us to assign the phonons, reveal symmetries, and analyze the displacement patterns [Fig. 1b and Supplementary Table 1, Supplementary Information]. Extrapolation of σ1(ω) to zero frequency is in reasonable agreement with the dc conductivity20. The electronic properties are typical of a semiconductor with indirect and direct gaps of 0.43 and 1.73 eV, respectively [Supplementary Note 11]. The gap sizes are similar to those in CrSiTe3 due to the common [Si2Te6]6− cluster anion34,35. We assign the strong electronic features near 20,000 cm−1 shown in the inset to a combination of charge transfer and d-to-d excitations.

Fig. 1: Optical properties of Mn3Si2Te6 at room temperature.
figure 1

a Reflectance of Mn3Si2Te6 in the ab-plane at 300 K along with the crystal structure19 showing two distinct Mn sites. Inset: reflectance over a wide frequency range. b Optical conductivity calculated from a Kramers–Kronig analysis of the measured reflectance, predicted pattern of the Eu symmetry phonons from our lattice dynamics calculations (normalized for easy comparison), and dc conductivity from ref. 20. Inset: σ1(ω) over the full range of our measurements.

Full size image

To investigate how strongly these phonons interact with the Mn spin system, we measured the infrared response across the ferrimagnetic ordering transition. Figure 2 summarizes the optical conductivity of Mn3Si2Te6 as a function of temperature. Here we show six representative vibrational modes fit by Voigt functions, indicated by the red-shaded area. All of the phonons harden on approach to the magnetic ordering transition [Fig. 2b–g]—a trend that we quantify with a traditional anharmonic model36,37. Below TC = 74 K18, the frequency vs. temperature data deviates from the model curve that typifies the high-temperature phase. This perturbation is characterized by a frequency shift: Δω = λ〈Si ⋅ Sj〉, where λ is the spin-phonon coupling constant, and 〈Si ⋅ Sj〉 is the spin-spin correlation function between the (i,j) nearest neighbors. The latter approaches S2 in the low-temperature limit. The spin-phonon coupling constants that we extract for the infrared-active modes are modest—less than  ± 0.25 cm−1 [Supplementary Table 1, Supplementary Information]—similar in size to the λ’s for the Raman-active phonons23. These values are significantly smaller than those in heavy and mixed-metal oxides38 ruling out a substantial role for spin-phonon coupling of q = 0 phonons in the insulator-to-metal transition and CMR effect.

Fig. 2: Properties of Mn3Si2Te6 across the magnetic ordering transition.
figure 2

a Close-up view of the optical conductivity as a function of temperature. The red shaded area represents the fitting results. The data are offset for clarity. b–g Frequency vs. temperature for six representative phonons. Individual points are obtained from fits to σ1(ω) in a, and the dotted lines represent a fit to typical anharmonic behavior36,37. The magnetic ordering temperature is indicated by the gray vertical line at 74 K. Unless indicated, error bars are smaller than the symbol size.

Full size image

Bad metal behavior in the high-field phase

Having placed the properties of the semiconducting phase on a firm foundation, we turn our attention to the metallic phase of Mn3Si2Te6, using a magnetic field to drive the insulator-to-metal transition. Figure 3a shows the reflectance ratio as a function of magnetic field. This quantity (discussed in Supplementary Note 5) highlights the sharp phonons as well as broad changes in the electronic background. We used these data along with the absolute reflectance at base temperature and zero field to back-calculate the reflectance as a function of magnetic field [Fig. 3b]. The reflectance rises systematically between 3 and 9 T, consistent with transport results that place the insulator-to-metal transition in this range17,21. That said, the rise is nowhere near what is expected for a true metal like copper. Instead of developing a signature Drude response, we see over-damped behavior even at full field (17.5 T), characteristic of a bad metal39,40. We simulate this effect in Supplementary Note 6. At the same time, the phonons remain prominent and are not well-screened. This reveals that Mn3Si2Te6 does not behave as a conventional metal following the field-induced insulator-to-metal transition.

Fig. 3: Reflectance and optical conductivity in magnetic field.
figure 3

a Reflectance ratios of Mn3Si2Te6 as a function of magnetic field. Inset: close-up view of the reflectance ratio spectra. All data are collected at 5.5 K. As we discuss in the main text, the appearance of new features at high fields is entirely due to changes in the electronic background and is almost totally decoupled from the lattice. b Reflectance as a function of magnetic field, back-calculated from the base temperature data in Fig. 2 and the ratios in a. Inset: close-up view of the reflectance spectra. c Optical conductivity of Mn3Si2Te6 as a function of magnetic field, calculated from a Kramers–Kronig analysis of the reflectance in b. Inset: close-up view of the optical conductivity in the far infrared range.

Full size image

Figure 3c displays the optical conductivity of Mn3Si2Te6 across the insulator-to-metal transition. The most striking feature is the build-up of localized excitations with increasing magnetic field rather than the development of a free carrier (Drude) response. Electronic character is demonstrated by the broad energy range as well as the Fano lineshape of the phonons that ride on top of this band in the high field phase41. That said, the phonon positions are nearly rigid over the entire field range, excluding the lattice as the origin of these effects. Close-up views of these trends and the near-zero spin-phonon coupling constants that result from the absence of a frequency shift across the field-induced insulator-to-metal transition are given in Supplementary Fig. 6 of the Supplementary Note 7.

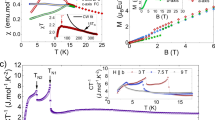
We can analyze the electronic properties in greater depth by focusing on charge localization. A sum rule analysis of the low energy localized excitation in σ1(ω) yields the oscillator strength trend shown in Fig. 4a. The spectral weight, which is proportional to the effective number of carriers, increases rapidly near 5 T and levels off above 10 T. This growth in the number of carriers aligns nicely with the field-driven insulator-to-metal transition and the associated CMR effect. To better connect charge localization, the number of carriers, and CMR, we examined several fixed-frequency cuts of σ1(ω) along with the dc conductivity from ref. 21. We note in passing that although the field enhances both ac and dc conductivities across the insulator-to-metal transition, the overall magnitude of σdc in the high field phase is not very large, consistent with our picture of Mn3Si2Te6 as a bad metal. Turning back to the analysis of electronic localization in the optical conductivity [Fig. 4b], we see that the ac conductivities at 200 and 400 cm−1 vary across the insulator-to-metal transition in a manner similar to (but broader than) the dc conductivity. This makes sense because σ1(ω → 0) is σdc. By contrast, carriers pinned at 700 cm−1 are not nearly as responsive to the transition. These findings suggest that carriers with frequencies below ≈400 cm−1 may be the primary contributors to CMR.

Fig. 4: Revealing the properties of localized carriers.
figure 4

a Spectral weight calculated by integrating σ1(ω) over an appropriate frequency window. b σ1(ω) at several different fixed frequencies ω0 (circles) vs. magnetic field. The dark orange lines are fits to the percolation model. The dc conductivity is from ref. 21. c Percolation threshold as a function of frequency, obtained from percolation model fits in b. d σ1(ω) at 17.5 T fit with a large polaron model (red area) and typical phonon oscillators (yellow area). Unless indicated, the error bars are smaller than the symbol size.

Full size image

Unraveling electronic heterogeneity and localization

Electronic heterogeneity plays a foundational role in establishing the properties of CMR manganites. One way to quantify inhomogeneity and phase separation is with the percolation model42. This model, originally developed to describe progressively increasing concentrations of metallic nanoparticles in a dielectric background like glass, has been successfully applied to correlated electron materials like VO2 across the phase transition43, WS2 nanotubes under pressure44, and rare-earth nickelates like NdNiO345. In these modern settings, the percolation model refers to “droplets” of metallicity embedded in a dielectric matrix (which represents a competing phase), as illustrated in the Supplementary Note 10. To focus on the electronic properties (and avoid the phonons), we employ a single-frequency variant of this approach.

We express the percolation model in fixed frequency form as \({\sigma }_{1}({\omega }_{0})={S}_{2}+({S}_{1}-{S}_{2})/(1+{e}^{(H-{H}_{0})/\Delta H})\)44. Here, ω0 is the fixed frequency in question, and σ1(ω0) is a fixed-frequency cut of σ1(ω). S1 and S2 are the fit values of σ1(ω0) at 0 and 17.5 T. H0 defines the percolation threshold at the fixed frequency ω0. The percolation threshold is the critical magnetic field at which the concentration of the metallic phase rises sufficiently to provide long-range connectivity. This is the parameter that gives physical significance to the model. H is magnetic field, and ΔH represents the slope of the curve (or the range over which percolation persists—from zero to full percolation). As shown in Fig. 4b, trends in σ1(ω0) vs. H are perfectly captured with fits to the model, demonstrating that the shape of the insulator-to-metal transition is a consequence of electronic heterogeneity. This means that the insulator-to-metal transition begins with a small amount of metallic phase embedded in a dielectric matrix, and with increasing magnetic field, the concentration of the metallic phase grows while that of the semiconducting phase diminishes. The fact that magnetization is not fully saturated at 17.5 T20,21,26 is consistent with our picture of an under-developed metallic phase above the insulator-to-metal transition.

Figure 4c shows the percolation threshold of Mn3Si2Te6 as a function of frequency extracted from the percolation model fits in Fig. 4b. The trend demonstrates that carriers react based on their degree of localization. Low-frequency carriers respond quickly to magnetic fields and reach their percolation threshold by 4 T, whereas the higher-frequency carriers react more slowly and require larger fields to become mobile. In fact, examination reveals that carriers with frequencies below 400 cm−1 exhibit a percolation threshold field between 3 and 4 T where dc resistance is already suppressed by >97.5%20. On the other hand, carriers above 400 cm−1 host percolation thresholds increase with frequency—a tendency that creates an uneven magnetic field response in σ1(ω) [Fig. 3c]. This distribution of percolation thresholds explains why the insulator-to-metal transition is so broad and why the conductivity is not fully developed even in fields that ought to place the material well above the transition. Mn3Si2Te6 is a clean system without mixed valencies or doping, so carriers that are less responsive to applied field are what keep the system in an electronically localized state even above the insulator-to-metal transition.

Modeling the localized excitation: large polaron, chiral loop currents, or short-range spin fluctuations

The field-driven development of the localized electronic excitation suggests that there may be important vibronic interactions or distortions of the magnetic order that pin the charge to the lattice or spin texture in the form of lattice or magnetic polarons46,47,48. A polaronic-like structure has already been observed at lower energies (~40 cm−1) under high fluences33, making it logical that additional polaronic excitations can be created in this material. Certainly, our measurements reveal strong field-induced charge localization in the optical conductivity, and electron-phonon coupling is evidenced by the Fano line shape of the in-plane Si stretching modes near 365 cm−1 [Fig. 3c]. We tested this hypothesis by fitting a large polaron model29,30,31 to the optical conductivity of Mn3Si2Te6 at 17.5 T. As shown in Fig. 4d, a single large polaron model fits the spectrum reasonably well. We extract a radius of ~6 Å, an effective mass of 1.1me, an absorption threshold of 90 cm−1, and a polaron density of np = 1.8 × 1019 cm−3. Within this picture, the presence of the polaron is attributable to the low carrier density originating from Mn-Te hybridization near the Fermi level22,49 combined with the overall charge transfer character of the material. The limited mobility of this structure is what constrains the development of a more traditional metallic response, although it is still sufficient to produce a CMR effect. We emphasize that the large polaron model is likely a major simplification and that the shape of the bound state is very sensitive to our choices of polaron size, mass, and density. The impact of these parameters is discussed in Supplementary Note 7. In any case, after revealing the behavior of Mn3Si2Te6 in a magnetic field and unveiling a competing state via a percolative process, the next challenge is to study this state further and to render it stable at zero magnetic field by chemical substitution.

The fact that phonons are rigid under a magnetic field suggests that we should consider mechanisms beyond charge or spin polaron models. An alternative framework for understanding the presence of localized carriers in the high field phase of Mn3Si2Te6 involves the presence of chiral orbital currents flowing along the edges of the MnTe6 octahedra17. The loop currents themselves are presumably in the ab-plane, and the moment is generated along c. Carriers pinned near 300 cm−1 are consistent with this picture, and based on the resonance frequency, we expect an average loop size on the order of microns. A similar phase is present in smectic metals where current flowing along specific chains displays localization induced by strong interactions50. Time-dependent bistable switching17 and the slow development of magnetization (while changes in the dc resistivity are sharp)20 are consistent with this picture.

A different approach to understanding magneto-infrared effects in Mn3Si2Te6 involves Slater peaks due to short-range spin excitations. Slater argued51 that the insulating gap can occur solely due to antiferromagnetic order rather than strong on-site Coulomb repulsion. Such a system is called a Slater insulator. Later theoretical work32 showed that short-range spin fluctuations are sufficient to produce narrow Slater peaks at the edge of the gap near the metal-insulator transition of the Hubbard model, which almost continuously closes the gap at the metal-insulator transition32,51. Such excitations come from short-range order and yield a localized excitation in the optical conductivity. One characteristic of the Slater mechanism is the relative entropy between competing states. Typically, the metallic phase has larger entropy than the insulating phase, although in our case, analysis reveals that the entropies are similar52,53. More work is obviously needed to clarify the matter, especially real space spectroscopies to unravel electronic inhomogeneities and neutron scattering to determine whether the localized excitation has a magnetic origin.

Methods

Reflectance measurements

High-quality single crystals of Mn3Si2Te6 were grown by flux techniques21 and polished to expose the ab-plane. Near-normal reflectance was measured between 22 and 55,000 cm−1 using a series of spectrometers, and a Kramers-Kronig analysis provided the optical constants54. Here, we focus on the real part of optical conductivity (σ1(ω)). Temperature was controlled with an open-flow cryostat. The magnetic field was applied using a 17.5 T superconducting magnet (H∥c) at the National High Magnetic Field Laboratory in Tallahassee, FL.

Lattice dynamic calculations

First-principles calculations were performed using density functional theory as implemented in Vienna ab initio simulation package55,56,57 with the projector-augmented wave method57,58 and the Perdew-Burke-Ernzerhof 59 exchange-correlation function. The DFT-D2 method60 provided the van der Waals correction on a Γ centered 10 × 10 × 6k-point grid with a plane-wave cutoff energy of 500 eV. The internal coordinates of the experimental structure19 were relaxed with ferrimagnetic52 constraints and the vibrational modes were obtained using the finite difference method. Details are available in Supplementary Information.