Introduction

Oscillations – rhythmic and repetitive variations in time – occur in all organisms and are essential for achieving self-organization and biological complexity1. Examples of oscillations in biology include cellular metabolic activities2,3,4, cell cycle control5,6, physiological processes such as circadian rhythms7,8, spatiotemporal pattern formation during organisms’ development9,10 and even population dynamics and in ecology11,12. Despite the ubiquitous presence of oscillations in biology, our current understanding of complex dynamic properties of oscillators – such as resonance, period-doubling and chaos – originates mainly from physics and chemistry. However, several studies indicate that these phenomena also play an important role in biological oscillators. For example, studies indirectly demonstrated the resonance phenomenon in circadian rhythm of organisms when correlating longevity or fitness to different light/dark regimes13,14. Other studies have consistently shown evidence for chaos in interactions in ecological and microbial communities15,16,17 and arrhythmic oscillations caused by non-linear phenomena seem to be linked to heart and neurological disorders18,19. The importance of understanding the emergence of these phenomena in biology is therefore evident, however the complexity of biological systems make the experimental investigation of those properties very challenging, and consequently, the research on the intricate nature of biological oscillators remains in early stages20,21.

Synthetic biology offers a complementary approach to study non-linear dynamic systems. It combines principles from engineering and biology to design and construct controllable synthetic circuits with minimal interference from the host regulatory network22. Considered a hallmark in the field, the repressilator was the first synthetic oscillator to be implemented in vivo, namely in the bacterium Escherichia coli23. This circuit is a three-node negative feedback loop, where each of the three repressors inhibits the expression of the next one in the loop (TetR⊣LacI⊣cI⊣TetR). While the first version suffered from irregular oscillations, improved molecular implementations with the same24 or different repressors25,26,27,28 led to highly robust oscillations. Since the repressilator, many other synthetic oscillatory circuits with different topologies have been established in cell-free systems, bacteria and mammalian cell cultures (reviewed in29,30), providing an improved understanding of oscillatory systems in biology. They also have a big potential for applications. Examples include oscillators for cancer treatment31, as marker of bacterial growth in the gut32, to slow down cellular aging33 and for investigating the importance of phenotypic variation in bacterial infections34. Moreover, synthetic oscillators have also been used to generate spatial patterns35. For example, growing E. coli colonies containing the improved repressilator form concentric rings of the fluorescent reporters24. This pattern is formed because only the cells at the colony edge are oscillating and growing, while cells in the interior are arrested in different phases of the oscillations. This simple method of analysing rings in colonies opens the possibility of studying patterns that are formed through oscillatory behaviors.

Most of previously built synthetic oscillators lost synchrony after few periods23 or were synchronised via cell-cell communication36,37. On the other hand, many natural oscillators, such as the circadian clock, rely on a periodic external signal to adjust their phase and stay synchronised13,14 in a process known as entrainment. An oscillator positively affected by a periodic externally applied stimulus is a forced or driven oscillator, and recent efforts have employed this approach to control oscillators. Mondragon-Palomino and colleagues showed entrainment and resonance of a 2-node synthetic oscillator in E. coli38. Later, Aufinger and colleagues21 showed period-doubling in a cell-free synthetic oscillator. In both studies, the use of a microfluidic system was essential to enable the periodic supplementation and removal of the chemical inducer in the medium. Recently, Cannarsa and colleagues39 used optogenetics to construct a repressilator that was periodically inhibited by light, which allowed for a long lasting synchronisation of individual E. coli cells and detuning from their natural frequency. Contrary to chemical inducers, using light with varying intensity and period to control oscillatory behavior confers the advantage of adjusting the level of induction in space and time with precision, without the need of refreshing the medium40,41.

Here, we build on previous studies to construct a forced synthetic optogenetic oscillator (we call it the “optoscillator”) in E. coli and investigate the emergence of complex oscillatory dynamics. We take advantage of a well-characterised light sensor40 to apply an activating external forcing to the repressilator24. Complementary to Cannarsa and colleagues39 who recently reported a light-inhibited repressilator to study synchronisation, detuning and entrainment of cells, we focus our efforts to explore the dynamical landscape of a forced synthetic oscillator. While previous research on forced synthetic oscillators21,38,39 solely relied on the analysis of temporal patterns, we explore how oscillations are translated into spatial patterns. The precise control provided by the optogenetic system allows us to test different regimes of constant or periodic forcing on growing colonies and we then analyse the ring patterns generated from oscillations in those colonies24,42,43. By combining experiments and mathematical modeling, we investigate the emergence of fundamental oscillatory dynamics and report the quantitative observation of resonance, subharmonic resonance and period-doubling (period-2 and period-\({{{\mathcal{N}}}}\)). Moreover, we provide strong evidence for chaos (see Fig. 1 for a description of the different dynamical phenomena). Our work contributes to a deeper understanding of biological oscillators and how they are translated into spatial patterns, a process for example at play during somitogenesis9,10,44. We also pave the way for manipulating oscillations within living organisms through synthetic biology, as well as the translation of these oscillations into intricate spatial patterns, a topic of high interest in engineered living materials45,46.

Fig. 1: Complex dynamics of a forced oscillator are transformed to intricate spatial patterns.
figure 1

E. coli bacteria host a synthetic optogenetic oscillator. Growing colonies form concentric rings of the fluorescent reporters. The oscillations can either be free-running (constant light) or forced (cycles of light and dark). Resonance occurs when the frequency of the external forcing matches with the frequency of the free-running oscillator. Subharmonic resonance occurs when the cells oscillate at a frequency that is a fraction of the driving frequency, whereas superharmonic resonance occurs when a system oscillates at a frequency that is a multiple of the driving frequency. Resonance phenomena are characterised by an increase in the amplitude of oscillations. Changes of the external forcing frequency can lead to bifurcation, where the period of oscillation is doubled (hence period-doubling) and a pattern of two peaks per every oscillation appears (period-2). Successive period-doubling events lead to period-\({{{\mathcal{N}}}}\), with \({{{\mathcal{N}}}}\) peaks repeating per oscillation. Further period-doubling can drive the system to chaos, where small variations between the initial parameters will lead to huge changes in the course of oscillations. The lack of repetitive pattern in the chaotic system makes it impossible to predict the trajectory of oscillations. In this scenario cells are expected to quickly desynchronise, precluding the visualisation of ring patterns. Illustration of colonies with oscillations was inspired by32.

Full size image

Results

Construction of a light-inducible repressilator

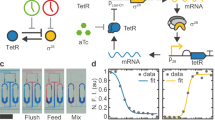
To construct an optogenetic oscillator, we decided to combine the blue light system from the red, green, and blue (RGB) color vision circuitry developed for E. coli40,47 with the improved version of the repressilator (pLPT107)24. In our design, the circuit should oscillate upon light exposure, but not display oscillations when kept in the dark. Briefly, the blue light-inducible system consists of a light sensing histidine kinase (YF1) that is active in the dark and switched off by blue light (470 nm). YF1 phosphorylates its cognate response regulator FixJ, which then activates the expression of the PhiF repressor. Thus, upon light exposure, the expression of PhiF is stopped. Without the repressor, the DNA-binding domain (called T3) of the T7 split-phage RNA polymerase (RNAP) is produced to dimerize with the constitutively expressed core of the T7 RNAP, enabling it to bind to the PT3 promoter and activate the expression of the downstream gene48(Fig. 2a).

Fig. 2: Design and characterisation of the light-inducible repressilator.
figure 2

a Schematic representation and molecular implementation of the circuit used to charaterise the PT3lacO hybrid promoter. b Colonies harboring the circuit shown in a were grown on agar plates in presence or absence of IPTG (1 mM) at different light intensities. The mCherry fluorescence (I, arbitrary units) of the colonies was quantified after 96 h of incubation. LacI tightly represses PT3lacO, as cells harboring the circuit were only responsive to light when IPTG was added. Lines connect the mean +/− SE of n = 3 or 4 biological replicates, with empty circles representing individual data points. c Schematic representation and molecular implementation of the light-inducible repressilator. d Colonies harboring the optoscillator circuit do not show ring patterns in the dark condition (left picture). However, under constant light (right picture), the circuit oscillates and generates ring patterns as the colony grows; scale bars = 1 mm. Source data are provided as a Source Data file.

Full size image

To couple the light-inducible system to the repressilator, we opted to modify the TetR node of the repressilator to make it light-inducible. We designed a hybrid promoter (PT3lacO) which is repressed by LacI and (indirectly) activated by blue light in the presence of the blue light activation system. We first characterised the functionality of this promoter in a reporter construct by controlling the expression of mCherry with light and isopropyl β-d-1-thiogalactopyranoside (IPTG) – an inhibitor of LacI (Fig. 2a). We grew colonies on agar plates in the presence of different intensities of light, controlled by a LED illumination tool (LITOS)49. After 96 h of incubation, we imaged the colonies with a fluorescence microscope and quantified the red fluorescence. We found that in absence of IPTG, there was no significant change in expression of the reporter, even with increasing light intensity. Conversely, when IPTG (1 mM) was added to the medium, mCherry expression increased proportionally with light intensity. This data shows that our hybrid promoter is (indirectly) induced by light and tightly repressed by LacI (Fig. 2b).

Once characterised, we took the improved version of the repressilator24 and exchanged the promoter controlling TetR (PLlacO1) with our hybrid promoter (PT3lacO) (Fig. 2c). Note that the corresponding CFP reporter still has the original PLlacO1 promoter. Thus, CFP is not induced by light. In this manuscript, we always report the fluorescence of the cI/mVenus node downstream of TetR and we display it as green. We first checked whether E. coli cells harboring the optoscillator would oscillate when exposed to blue light, but not oscillate in the dark. Indeed, when the plate was covered with aluminum foil for the whole duration of the experiment, the colonies did not display any fluorescent rings, while when exposed to blue light, rings appeared (Fig. 2d). To avoid excessive photo-bleaching or toxicity of the blue light, we chose to use the lowest intensity that showed robust ring formation (Supplementary Fig. 1), which was at 30% of our light device49, corresponding to 0.13 W/m2 (Supplementary Fig. 2). The observed ring patterns were similar to the patterns formed by the regular repressilator24, with the exception of a fluorescent centre in our experiments. This can be explained by our experimental setup, where we incubated the colonies the first 20 h in the dark, leading to low TetR and high cI/mVenus expression, before we started the light exposure.

Synchronization

With continuous light exposure, we noticed that ring patterns were irregular. The irregularity arose from small differences in the period of the individual cells caused by stochastic effects24. Over generations these differences increased, meaning that synchronization between the cells decreased with time39. As a consequence of this increasing phase difference, the variation in time and position of the next peak increased as the colony grew, resulting in deviations from the initially circular ring pattern. This desynchronisation decreased the average fluorescence amplitude of the rings (Fig. 3b).

Fig. 3: Synchronisation through periodic forcing.
figure 3

a Representation of the experimental setup for constant light or light pulses with colonies growing on agar plates. b Fluorescence microscopy pictures of colonies harboring the optoscillator after incubating the colonies for 20 h in the dark and 4 days under constant light (left) or light pulses (right). mVenus fluorescence is shown in green. Better defined rings appear with higher synchronisation of cells under light pulses condition (Tlight = 18 h), compared to constant light (30%); scale bars = 1 mm. c Quantification of the ring patterns from 3 colonies. The fluorescence was measured from the center to the border of the colonies and the spatial localization was converted to time scale through a mathematical projection and baseline correction (details in supplementary information section 3). The green shade represents the collection of every fluorescence intensity measured from all of the 3 replicates. The average fluorescence intensity (I, arbitrary units, left y axis) measured for each of the 3 colonies is shown in gray. The colored dots show the maxima and minima of oscillations from the averaged fluorescence of individual colonies. Light intensity (Ilight (%), right y axis) was constant or in a sinusoidal wave shape (dashed blue line). Source data are provided as a Source Data file.

Full size image

A simple way to synchronise autonomous self-sustained oscillators is to apply periodic forcing. The individual oscillating cells should re-adjust their phase to the external forcing at each cycle and thus overcome the stochastic effects. To test if our synthetic oscillator could be synchronised by light, we performed experiments with light pulses. Here, the light pulse period is defined as the duration (in hours) required for a complete cycle where the light intensity varies between 0 to 100% in a sinusoidal wave shape. We set the time period of light pulses (Tlight) to 18 h. After 4 days of growth, colonies showed rings that were sharper and stronger in fluorescence compared to the colonies grown under constant light (Fig. 3c). Thus, the synchronisation of the oscillations of the individual cells by the light prevented the amplitude from decreasing and led to sharper and more circular rings in the colonies.

Resonance

Next, we wondered what would happen if we changed the frequency of light pulses. We expected to find the resonance phenomenon, which occurs when the natural frequency of the driven oscillator (Tosc) matches with the frequency of the external forcing. We predicted that this would result in rings with higher fluorescence intensity compared to colonies exposed to different frequencies of periodic forcing. The result from the synchronization experiment already showed strong fluorescent rings, meaning that Tlight = 18 h was close to the resonance frequency. Therefore, we repeated the experiment with more Tlight conditions, ranging from 12 h to 36 h. We observed the rings with the highest fluorescence intensity – thus resonance – at Tlight = 20 h (Fig. 4a, b). In this condition, the rings had the opposite phase with respect to the light pulses. This makes sense as cI and mVenus are inhibited by the light-inducible expression of TetR. Thus, mVenus had the highest expression when the light intensity was the lowest. A more quantitative way to look for resonance is by averaging the amplitude of all rings in a colony and plotting this average fluorescence against the period of the external light pulses. The resonance can be found where the average amplitude is the highest, characterised by a peak in the graph (Fig. 4d). As expected, we found a resonance peak at 20 h, which agrees with the natural period of oscillation acquired from experiments with constant light (Fig. 3c). We also observed another phenomenon typical of forced oscillators: the bacterial oscillations were entrained according to the external light signal. Entrainment was found between Tlight = 16 h and Tlight = 24 h (Fig. 4c). In this interval, the oscillation period increased proportionally with Tlight by advancing or delaying the formation of the rings. For the data points above 24 h, the oscillation period is half the period of the light source and we can observe that the oscillator follows the external forcing with every other peak.

Fig. 4: Resonance through periodic forcing.
figure 4

a Fluorescence microscopy picture of a colony harboring the optoscillator shows strong and sharp rings, after incubating the colony for 4 days under light pulses at Tlight = 20 h. mVenus fluorescence is shown in green, scale bar = 1 mm. b Quantification of the ring patterns from 3 colonies. The fluorescence was measured from the center to the border of the colonies (details in supplementary information section 3). The green shade represents the collection of every fluorescence intensity measured from the 3 replicates. The average fluorescence intensity (I, arbitrary units, left y axis) measured for each of the 3 colonies is shown in gray. The colored dots show the maxima and minima of oscillations from the averaged fluorescence of individual colonies. Light intensity (Ilight (%), right y axis) varied in a sinusoidal wave shape with Tlight = 20 h (dashed blue line). c Evidence of entrainment: the average time period of the forced oscillator (T (h)) increases proportionally with the time period of the external forcing Tlight between 16 h and 24 h (dashed red). Above Tlight = 24 h, every other oscillation synchronises with the light pulses. We can better visualise this by multiplying the oscillator period by 2 (cyan dots) and see that it falls again in the entrainment region. The period T (h) was obtained by measuring the time intervals between consecutive maxima and consecutive minima of the oscillation, and data show mean +/− SE from n=3 biological replicates for each periodic forcing condition. d Average amplitude (A) of fluorescence signal as a function of the forcing light period (Tlight). The amplitude was obtained by subtracting the maximum from the minimum value of fluorescence for each ring. The values in the graph are the mean amplitudes +/− SE of all rings from n=3 colonies (blue). The fitted curve from the model is indicated in orange. A peak and thus resonance is observed when the period of the driving force matches the natural period of the oscillator (20 h). Source data are provided as a Source Data file.

Full size image

Bifurcation diagram

These interesting observations encouraged us to develop a mathematical model of our genetic circuit to explore whether we might be able to observe other phenomena commonly found in forced oscillators, such as regimes of period doubling or chaos50. To do so, we adapted the original mathematical model of the repressilator23 to represent our optoscillator. Briefly, the system was described with three mRNA species (corresponding to each node) and their respective protein transcription factors. The inhibition of the transcription factors and the light activation was taken into account with Langmuir–Hill functions. The details of the model and the simulation methods can be found in the SI section 2.

We parameterised the model by fitting the data from our hybrid promoter characterisation (Fig. 2b) and the data obtained from the resonance experiment (Fig. 4d, SI section 2.2). Next, we calculated the bifurcation diagram (Fig. 5a) as a function of the period of the light pulses to examine whether our optoscillator would show any other interesting dynamical behavior. The experimental relevant frequency range of the external forcing is limited: if the light source frequency is too high, the cells will not be able to follow it, resulting in the same effect as a constant light regime. Contrarily, if the frequency of the external forcing is too low, we would not get enough rings in a colony to confirm any phenomenon. We therefore limited the bifurcation diagram from 10 h to 50 h. The calculated bifurcation diagram predicted that in addition to resonance, we might be able to observe subharmonic resonance, period doubling and even chaos (Fig. 5a). Our model predicted that we should find another maximum in amplitude at half of the frequency (i.e. at the double period) of the optoscillator. Another interesting phenomenon predicted by our model is the period–doubling bifurcation. In a period-2 oscillation the same peak is repeated every second oscillation, so we can observe bigger and smaller peaks alternately. After two period–doubling bifurcations we can get period-4 (every fourth peak will be repeated) and with an infinitely period–doubling cascade we can also observe chaos. In a chaotic regime the system is deterministic, however, the oscillations are irregular, i.e. the amplitude and the time period are changing and the system is unpredictable51.

Fig. 5: Resonance, subharmonic resonance, period-2, period-\({{{\mathcal{N}}}}\) and chaos in ring patterns.
figure 5

a The bifurcation diagram (fluorescence ymax versus forcing light period (Tlight)) from the model predicts regions of chaos (vertical orange lines, 1), resonance (2), period-\({{{\mathcal{N}}}}\) region (purple box, 3), period-2 region (purple box, 4) and subharmonic resonance (5). b Experimentally measured average amplitude (A) of fluorescence signal as a function of Tlight. Amplitude was obtained by subtracting the maximum from the minimum fluorescence value for each ring. The values in the graph are the mean amplitudes +/- SE of all rings from n=3 biological replicates (blue). Apart from the resonance peak, it also shows the subharmonic resonance peak. c–g) The different regimes: c fast desynchronisation with constant light (30%), d resonance at Tlight = 24 h, e period-2 at Tlight = 44 h, f period-\({{{\mathcal{N}}}}\) at Tlight = 28 h and g chaos at Tlight = 16 h. I Fluorescence microscopy pictures of colonies harboring the optoscillator after incubating the colony for 4 days under the indicated light exposure. mVenus fluorescence is shown in green. Scale bars = 1 mm. II Two-dimensional reaction--diffusion simulations. III Quantification of the ring patterns from 3 colonies. The fluorescence was measured from the center to the border of the colonies (details in supplementary information section 3). The green shade represents the collection of every fluorescence intensity measured from all of the 3 replicates. The average fluorescence intensity (I, arbitrary units, left y axis) measured for each of the 3 colonies is shown in gray. The colored dots show the maxima and minima of oscillations from the averaged fluorescence of individual colonies. Light intensity (Ilight (%), right y axis) with period Tlight corresponding to the regime (dashed blue line). IV deterministic (blue) and stochastic (red) reaction kinetics simulations and V simulated trajectories in the phase space of the oscillator. Further simulation details and results (e.g. Fourier spectra, maxima return map and stroboscopic map) can be found in Supplementary Fig. 6. Source data are provided as a Source Data file.

Full size image

Subharmonic resonance, period-2, period-\({{{\mathcal{N}}}}\) and chaos

We thus set out to determine whether we could also observe those additional non-linear phenomena with our optogenetic oscillator. Our model predicted that the amplitude should have a second peak (subharmonic resonance) located at half of the natural frequency of the oscillator. We therefore repeated the light pulse experiment and extended the maximum time period range of the light induction from 36 h (Fig. 4d) to 56 h. Indeed, we observed a second peak in the amplitude at Tlight = 44 h (Fig. 5b). At first glance, there is a noticeable difference between the measured and the calculated second peak. In the measurements, this peak is lower than the peak at the resonance frequency, whereas in the simulations, the opposite is observed. However, this discrepancy can be explained by the way the data is presented. In the measurements, we show the average amplitude (in period-2 oscillations, this is the average of strong and faint rings), while in the bifurcation diagram, the representation of both strong and faint rings are plotted separately. If we calculate the average of these rings in the simulations (Supplementary Fig. 7), the average amplitude at the subharmonic resonance is smaller than at the natural frequency, which agrees well with the experimental results.

We then used the model to investigate the dynamics of our forced oscillatory system. The deterministic reaction kinetics model showed that – at the resonance frequency – the amplitude of oscillations is significantly larger than in the constant light regime (Fig. 5cd). However, the deterministic model cannot describe the details of the desynchronisation, which is an important property in our experiments. Therefore, we performed stochastic reaction kinetics simulations (see the details in SI section 2.2.3) to capture this phenomenon. In Fig. 5cIV the red curve shows the average of 1000 independent stochastic simulations. The phase differences between the oscillations of the individual cells increased over time leading to desynchronisation. Due to this stochastic effect, the average amplitude decreased, closely matching our experimental results. On the other hand, in the resonating condition, 1000 independent oscillators remained synchronized and the amplitude did not decrease with time (Fig. 5dIV).

To be able to even better compare the simulations to the experimentally observed colonies with rings, we also simulated how the oscillations led to the formation of rings in growing colonies. We carried out two-dimensional reaction–diffusion simulations. The growth of the colony was described with the Fisher–KPP (Kolmogorov–Petrovsky–Piskunov) equation52, while the cells contained the same stochastic reaction kinetics system that we have described before. The details for the spatial simulations can be found in SI section 2.3. The ring patterns generated from simulations (Fig. 5c–gII) were in good agreement with the experiments (Fig. 5c–gI), supporting the validity of our numerical model. We also used the model to examine the effect of the noise in the system (Supplementary Fig. 5 and Supplementary Movies). Consistent with the experiment, noise contributes to the irregular shape of the ring patterns under constant light (Fig. 5c), while the resonance regime (Fig. 5d) led to sharper and more circular rings.

The bifurcation diagram also implied that around double of the natural period of the oscillator (36 h to 48 h) we should be able to observe period-2 oscillations. In good agreement with the model, we found that colonies grown at a light induction of 44 h showed period-2 oscillations: We observed rings alternating between high and low fluorescence intensities (Fig. 5e). The strong rings had the opposite phase to the light pulse, while the weaker rings always occurred in the same phase as the light period. This clearly demonstrated the destructive interference that light imposed on the cI/mVenus node of the oscillator.

In the model, between the resonance and the subharmonic resonance, we could observe further period doubling (period-\({{{\mathcal{N}}}}\)). However, while other regions in the simulations were robust (i.e., small changes in the parameter set did not cause qualitative changes in the bifurcation diagram), the region of the period-\({{{\mathcal{N}}}}\) oscillation exhibited high parameter sensitivity. Depending on the parameters, we observed higher period oscillations and even chaos. For this reason, we called it ”period-\({{{\mathcal{N}}}}\)”, indicating the uncertainty of the model and the presence of higher period oscillations. With the given fitted parameter set, the simulation shows period-4 oscillation. On the maxima return map (Supplementary Fig. 6G,d), we clearly see four separated dots corresponding to the four different peaks in the period-4 oscillation. Unfortunately the amplitude of the four peaks is similar, which makes it difficult to observe a period-4 oscillation experimentally, especially with a limited number of peaks in the colonies. Nevertheless, we were able to observe atypical patterns in this region (Tlight = 28 h). In every set of experiments (Fig. 5f), we detected many rings of low intensity or even a lack of signal in certain regions of the colonies. In the experiments, the low amplitude and high frequency peaks might have merged together due to the stochasticity, resulting in either weak or partially disappearing rings. Furthermore, in an experiment on an agar plate the system changes gradually, as the amount of nutrient decreases and byproducts accumulate over time. Due to the high parameter sensitivity in the period-\({{{\mathcal{N}}}}\) oscillation region, it is possible that the system does not remain in the period-4 oscillation state and that it shifts towards higher period oscillations or even chaos, potentially explaining the observed blurred rings.

Finally, our model also predicted a region – occurring before the first resonance peak – where chaotic oscillations might occur (Fig. 5a). In a chaotic system, the Laypunov exponent is positive, meaning, that the distance between close trajectories will increase exponentially in time, which makes the system sensitive for initial conditions and the long term behavior of the trajectories becomes unpredictable. In our simulations we showed that in certain regimes of periodic forcing the system has a positive Laypunov exponent (Fig. 5a), the trajectories never repeat themselves in the phase space (Fig. 5gV), and the Fourier spectrum is continuous, i.e. it does not contain only discrete peaks. Furthermore the maxima return map and the stroboscopic map are continuous curves (Supplementary Fig. 6e), suggesting that our system acts as a chaotic oscillator in this region.

Due to the stochastic nature of the system, there are some variances in the initial state of the cells and, in a chaotic oscillator, these differences will increase in time, resulting in desynchronisation and resembling the case of oscillations in constant light regime. In the simulations this resulted in irregular and blurred rings (Fig. 5gII), while the average amplitude decreased (Fig. 5gIV). Some rings were partially disappearing and merging together as the system became progressively more stochastic (from top to bottom in Supplementary Fig. 5 A  → B). Indeed in the experiments, colonies grown at Tlight = 16 h (Fig. 5gI) also displayed irregular and very blurred rings, even more than in the constant light regime. An experimental verification of chaos in a biological system is generally challenging due to the low number of oscillations that can be observed, and the difficulty to distinguish variations due to chaotic behavior from those resulting from biological noise. Indeed, in our case, the colonies substantially decreased the growth rate after 4 days, and therefore the number of rings that we can observe is limited. Nevertheless, we made a number of experimental and theoretical observations suggesting that the system is in a chaotic regime: i) Due to the applied light pulses, oscillations in the individual cells should become synchronized and the peaks should be sharp, as observed in Fig. 3b. However, in the presumable chaotic region, we detected a fast desynchronization and the peaks disappeared. ii) This is an observation of the Lyapunov time, which is the predictability limit for a chaotic system. The first ring is still sharp indicating that the cells were synchronized in their oscillations. However, as time progressed they lost synchronization and reached the predictability limit, manifested in blurred rings. iii) This rapid loss of synchronization is not due to the inability of cells to follow such high frequencies of the external forcing, as we used light pulses with square wave shape at an even higher frequency (e.g. Tlight = 12 h) and we still could observe well-defined ring patterns in this experiment (Supplementary Fig. 3). The oscillators were synchronized, and the peaks were sharp, indicating that increasing noise caused by the higher frequency could not be the reason for the disappearing rings. iv) Based on the Poincare maps, Lyapunov exponents, trajectories in the phase space, and the Fourier spectra (Fig. 5g, Supplementary Fig. 6g) in the simulations, we can prove the existence of a chaotic regime. Our model was parameterized based on the resonance peak and accurately predicted the location and intensity of the second peak (subharmonic resonance) and the period-2 oscillations – supporting the validity of our model. Furthermore, we observed a pattern consistent with the simulations of chaotic oscillations (Fig. 5g) at the frequencies predicted by the bifurcation diagram to produce chaos (Fig. 5a). In conclusion, we provide evidence from simulations and experimental data that is consistent with oscillations in a chaotic regime.

Discussion

Oscillators have been thoroughly studied in every field of natural sciences, but still little is known about their non-linear dynamical properties in biological systems. A well-known example – for dumped and forced nonlinear oscillators – is the Duffing equation. In spite of its simplicity, this model can show resonance, and many other interesting dynamical phenomena, such as period doubling bifurcations, chaos and hysteresis53,54. In this work, we were inspired by this approach and constructed a forced synthetic repressilator in E. coli. Using a light-inducible system to connect the external forcing to the oscillator, we overcame the need for microfluidics and were able to transform dynamic phenomena into complex spatial patterns. Through a combination of analysing ring patterns in colonies and mathematical modeling, we have shown that this simple oscillatory circuit can generate complex dynamics depending on the external periodic forcing. In particular, we observed synchronisation, resonance, period doubling (period-2 and period-\({{{\mathcal{N}}}}\)) and even chaos.

Our optoscillator resonated when light was shone in sinusoidal waves with Tlight between 20 h and 24 h. As the driving period equaled the natural period, bacteria displayed higher synchronisation, higher fluorescence and better defined ring patterns compared to other light regimes. Cells also showed higher synchronisation rate at half of the resonance frequency (subharmonic resonance), at Tlight of 44 h. In fact, these parameter regions where synchronisation is enhanced are called Arnold’s tongues. Apart from resonance, this region allows entrainment of the oscillator to the driving force, a phenomenon observed both in our experiments (Fig. 4c) and in prior studies involving synthetic oscillators38,39. It is therefore not surprising to find that many biological oscillators are influenced by periodic environmental cues to keep their physiology and behavior synchronised55,56.

Our experimental data also showed robust period-doubling (period-2 and period-\({{{\mathcal{N}}}}\)). To best of our knowledge, no other study presented a synthetic oscillator capable of transforming such dynamic phenomena into spatial patterns. Interestingly, spatial period-doublings have been used to describe wrinkle formation57,58,59 occurring in skin folding60, mucous membranes61, the convoluted shape of the brain62,63 and biofilm formation64,65. Our circuit could thus be used to generate differential stress conditions in a cell layer in order to reproduce and control wrinkle patterns. This approach could also be interesting to create engineered living materials with desired properties. In fact, controlling wrinkle structure generates surfaces with enhanced properties in soft materials66,67.

The combination of our experiments and the mathematical model provides evidence for chaotic oscillations. As far as we are aware, this is the first experimental evidence of a synthetic oscillator producing chaos. In our current setup, the colonies typically only grow to a diameter of 6 mm. The limited number of rings in the colony hinders detailed analysis of regimes with successive period-doublings. For future work, it would be interesting to observe more oscillations and characterise these regimes better. This might be achieved by optimising growth conditions to obtain colonies of a bigger diameter with more rings68. Alternatively, if one is not interested in the spatial pattern, the oscillations could be observed in liquid culture. As oscillations are lost when cells enter stationary phase23, liquid culture experiments require frequent dilutions over several days. This is most easily achieved in turbidostat69 or microfluidic setups26,27,36,37,38,39,70. Particularly, experiments in microfluidic devices combined with single-cell image analysis should allow us to acquire data with higher number of oscillations to observe and determine the period-\({{{\mathcal{N}}}}\) regime, and give stronger evidences for chaotic oscillations. While previous studies observed synthetic oscillators in microfluidic devices26,27,36,37,39,70 and showed resonance and superharmonic resonance38, it remains to be tested if we will be able to reproduce all the regimes of the optoscillator observed on the agar plates also in a microfluidic setup.

Our finding of a chaotic regime aligns well with a growing body of literature that points to the importance of chaos in biology11,15,16,71. For example, it has been reported that chaos can increase the heterogeneity within a population of genetically identical cells. According to a mathematical model describing the expression of Nuclear Factor-κB (NF-κB), an important transcription factor for the eukaryotic immune response, chaotic oscillations lead to a broader range of expression levels across genes that are regulated by this transcription factor72. This heterogeneous gene expression could be beneficial in multi-toxic environments.

As we moved further away from the optoscillator’s natural frequency, synchronisation decreased to the point where cells became unable to produce well-defined rings. In the chaotic and period-\({{{\mathcal{N}}}}\) regimes, this desynchonisation effect developed even faster than with constant light. It is therefore a remarkable property of the optogenetic repressilator that depending on the external forcing frequency, the light can either synchronise or desynchronise the oscillations of the individual bacteria. In our simulations at extremely high noise levels in the chaotic regime, the rings became regular again, suggesting an interesting way for stochasticity to control chaos and pattern formation (Supplementary Fig. 5Ee). This stochastic effect on the switch from chaotic to non-chaotic regimes and vice-versa has been previously reported, for example in epidemiological models73,74,75.

Our synthetic optoscillator can mimic oscillatory phenomena found in natural systems and help us to distil their underlying design principles. The same optogenetic approach could also be extended to other synthetic oscillators25,26,36,37, helping us to understand how different topologies respond to external forces. Furthermore, multiple aspects of biological systems are responsive to a varying concentration of inducers in dynamic environments76,77. Consequently, there is a need to explore the behavior of oscillatory circuits within such scenarios in future research. For example, investigating how different light intensities would affect the frequency and amplitude of oscillations, or applying gradients of light intensity across space to expand our capacity to manipulate and generate more complex patterns. The ability to control oscillations in gene expression and pattern formation is interesting for a wide range of applications in fields as diverse as biotechnology, medicine, biological sensors, engineered living materials and biocomputing78,79,80. We thus hope our work paves the way for synthetic biology to exploit the rich non-linear dynamics accessible through the optoscillator.

Methods

Strains and construction of plasmids

Restriction enzymes were purchased from NEB. DNA fragments were PCR amplified using a high-fidelity DNA polymerase (2x Phanta Max Master Mix, Vazyme). Desalted primers were purchased from Sigma-Aldrich. The DNA fragments were purified using the Monarch PCR & DNA Cleanup Kit (NEB). We assembled the plasmids through Gibson Assembly using the NEBuilder HiFi DNA Assembly Master Mix (NEB) and followed the manufacturer’s protocol. Electrocompetent cells were transformed using electroporation cuvette (2mm gap, Bio-rad) and an electroporator set to 2500 V (Eporator, Eppendorf). The plasmids used in this study are described in Table 1 and primers for PCRs are listed in Table 2.

Table 1 Plasmids
Full size table
Table 2 Primers list
Full size table

To generate the bacterial chassis, we deleted the clxCP gene from the E. coli MK01 strain81, which was a kind gift of Sander Tans (Addgene #195090). The genomic deletion was achieved by following the λRed recombination protocol82. The DNA fragment for the recombination was generated by PCR amplification of the pKD13 plasmid82 using primers pr_EB14&15.

The light system encoded on the plasmids pJFR1 and pJFR240 was a kind gift of Christopher Voigt. We modified the blue light system from Fernandez-Rodriguez et al.40 to fit it on a single plasmid (pJP_Azul01). Briefly, we digested pJFR2 with EcoRI-HF and BsaI-HF v2, while yf1-fixJ and t7pol were amplified from pJFR1 (using primers pr_JP49&50 and pr_JP51&52, respectively). After DNA purification, the resulting fragments were assembled together using Gibson assembly and transformed via electroporation into competent E. coli NEB5α.

The hybrid promoter (PT3lacO) was designed by adding two lac binding sites (lacO) immediately downstream of the PT3 promoter sequence and inserted into pJP_Ctrl05. Briefly, we constructed pJP_Ctrl05 by amplifying the backbone and lacI from pLPT107 using the primers pr_JP53&54 (pr_JP54 contains the sequence for PT3lacO) and pr_JP57&58, respectively, and a spacer fragment from one of our plasmids pJ207226 with the primers pr_JP55&56. To avoid any problems related to photo-bleaching with blue light, we changed the fluorescence reporter of the pJP_Ctrl05 from mCerulean to mCherry, generating pJP_Ctrl5.2. To do so, we digested pJP_Ctrl05 with AatII and EcoRI-HF, amplified the mCherry fragment from pCDF-mCherry (from our lab) using primers pr_JP61&62 and assembled the two sequences by Gibson assembly. To more accurately represent the TetR node of the repressilator, the J23100 promoter controlling the lacI transcription was subsequently replaced by the pR promoter. This was done by PCR amplification of pJP_Ctrl5.2 using the primers pr_JP104&105, pr_JP106&107 and pr_JP108&109, followed by Gibson assembly. The final version of this plasmid, which was used for the characterisation of the PT3lacO promoter, is called pJP_Ctrl10.

For the light-inducible repressilator (pJP_Rep00), we started with plasmids pLPT107 and pLPT4124, which were kind gifts from Johan Paulsson (Addgene plasmid #85525 and #85524). To construct pJP_Rep00, we deleted the promoter pLtetO upstream of tetR and replaced it with PT3lacO. To do so, we digested pLPT107 with HpaI and StuI to obtain the backbone and we amplified the remaining fragments from pLPT107 using the primers pr_JP69&70 and pr_JP71&72, and the hybrid promoter (PT3lacO) from pJP_Ctrl05 using primers pr_JP67&68.

Plasmids,and their maps and sequences of pJP_Azul01 (#219670), pJP_Ctrl10 (#219672) and pJP_Rep00 (#219677) are available at Addgene.

Optogenetic experiments

Optogenetic setup

For constant and light pulses conditions, we used a LITOS device 49 for light induction. This device is composed of a LED RGB matrix and a control unit to which we can upload a program to set the stimulation time, wavelength (R = 620–630 nm, G = 520–525 nm, B = 465–470 nm) and intensity and select the positions of the LEDs we want to turn on. In this work, we only used the blue LED, therefore the red and green intensities were set to 0.

To convert the relative light intensities (15%, 20%, 25%, 30%, 35%, 40%, 60%, 80% and 100%) to absolute light values, we measured the light emitted by LITOS in a dark room, using the Skye single channel light sensor device (SKYE instruments LTD). The given unit ( × 10 μmol ⋅ m−2 ⋅ s−1) was then converted to W ⋅ m−2. The graph correlating the light intensities in percentages to absolute values is shown in Supplementary Fig. 2.

Growth of colonies

To test the PT3lacO hybrid promoter, pJP_Ctrl10 and pJP_Azul01 were co-transformed into E. coli MK01 ΔclxCP. A colony was inoculated in a tube containing 3 mL of liquid LB with ampicillin (100 μg/ mL) and spectinomycin (50 μg/ mL). After an overnight incubation at 30 °C, cells were serial diluted 4 × 107 times. 100 μL were homogeneously spread on LB agar plates (15 g/L agar and plates with a diameter of with 90 mm) with ampicillin (100 μg/ mL), spectinomycin (50 μg/ mL) and with or without 1 mM IPTG. The plates were wrapped in aluminum foil and incubated at 30 ∘C for 20 h. Next, the aluminum foil was removed for microscopy imaging to measure the initial size of the colonies. Each plate contained 5 to 10 colonies, 3 (replicates) of them were randomly selected and marked to track initial and final size of respective colonies. Then, the plates were placed upside-down on the LITOS LED matrix with different light conditions (constant light at 15, 20, 25, 30, 35, 40, 60 and 80% of light intensity). The LITOS setup with the plates was placed in a Peltier incubator (IPP 750 Plus, Memmert GmbH). The temperature was set to 21 ∘C and the experiment ran for 96 h. After that, colonies were imaged with a fluorescence microscope to measure fluorescence and the final size of the colonies (see microscopy section for details).

For the ring patterns experiment, we first obtained the optoscillator strain by co-transforming pLPT41, pJP_Rep00 and pJP_Azul01 into E. coli MK01 ΔclxCP. The experimental procedure to obtain the isolated colonies before the light induction was the same as described in the previous paragraph, except that IPTG was not added to the medium and the antibiotics used for inoculation were kanamycin (50 μg/ mL), ampicillin (100 μg/ mL) and spectinomycin (50 μg/ mL). Incubation at 37 °C was avoided as our circuit oscillates even without induction at this temperature, most likely due to increased leakiness of the light-system at higher temperature. For the constant light condition, light intensity was set to 30% until the end of the experiment, and for the light pulses regimes, the intensity of light (I) varied from 0 to 100% in a sinusoidal wave shape (I = I0(1 + sin(2π/Tlight))/2) according to the chosen time period (Tlight). The intensity was set with an eight bit resolution, and we changed the intensity twenty times in the course of one time period. Experiments were performed using at least three biological replicates. All data were reliably replicated in at least one additional experiment.

Microscopy

Pictures were taken with an AxioImager M1 microscope (Zeiss) with an Achromat 2.5X/0.12 Fluar objective and an sCMOS camera (Photometrics, Prime 95B) controlled by the VisiView 4.3.0.4 software (Visitron Systems). DsRed and YFP channels were used to measure the fluorescence of mKate2 (and mCherry) and mVenus, respectively. The exposure time of every channel was set to 100 ms, including the brightfield channel.

Image analysis

Image processing steps to generate quantitative data from the fluorescent ring patterns were carried out in MATLAB (R2023b). We first measured the fluorescence intensity across the radius of the colony (space vs intensity). To determine the oscillator’s time period and to compare its phase to the light pulse period, we transformed the space vs intensity data from our ring pattern experiments to time vs intensity data. Because the bacterial colony does not expand linearly, we first measured a growth curve correlating the radius of the colony and the elapsed time (space vs time). With that, we could transform the space vs intensity plots to time vs intensity graphs. The details of this transformation are described in the SI section 3.

After the transformation, the fluorescence intensity measured across the radius was averaged for each colony, resulting in an oscillation profile shown as a gray line in the figures depicting the quantified measurements of colony intensity. The maxima and minima from each of these oscillation profiles were identified and are represented by filled colored dots in the graphs. To calculate the average oscillation period, T (h), shown in Fig. 4c, we first measured the time intervals between consecutive maxima, and consecutive minima of the oscillation. T (h) was obtained by averaging the combined time intervals from three replicates, for each Tlight condition. The standard error is calculated based on the number of time intervals from three combined replicates. For Figs. 4d and 5b, the amplitude was obtained by subtracting the maximum from the minimum value of fluorescence for each ring. The average amplitude (A) and the standard error for each Tlight condition were obtained by measuring the amplitude of all rings collected from three replicates.

Mathematical model and simulations

The model is described in detail in the supplementary information section 2. Briefly, the deterministic reaction kinetics equations were described with ordinary differential equations (ODEs) and they were solved in a dimensionless form in MATLAB (R2023b) with the SimBiology toolbox, while the stochastic differential equations (SDEs, based on the chemical Langevin equation (CLE)) were solved in C++ with the fully composite Patankar method83 (SI section 2.3.2).

To compare the experimentally observed patterns with the model, we also performed spatial simulations. Details are described in the supplementary information section 2.3. Briefly, simulations are based on the Fisher–KPP (Kolmogorov–Petrovsky–Piskunov)52 equations. These partial differential equations (PDEs) were solved in C++ with the finite difference method, with the forward time–centered space (FTCS) scheme, while the stochastic reaction kinetics equations were solved using the fully composite Patankar method83.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.