Main

Motion of liquid metal in Earth’s core is the source of the geomagnetic field and its time variations, including dramatic polarity reversals wherein the large-scale field switches to point in the opposite direction. The past twenty years have seen considerable advances in our ability to model this process, with the advent of 3D numerical geodynamo models capable of solving the equations of conservation of momentum, magnetic induction and buoyancy transport in a self-consistent manner11,12. Some such models show polarity reversals13,14,15, which proceed by the production and expulsion of inverse magnetic flux by intermittent convective plumes, and subsequent transport by meridional flow6,16. By necessity, such simulations operate in a regime in which viscous effects remain important. However, the values of the two dimensionless parameters that characterize these simulations—the Ekman number Ek = ν/(2Ωd2) and the magnetic Prandtl number Prm = ν/η, where ν is the kinematic viscosity, Ω is the angular rotation rate, d is the thickness of the spherical shell of convecting fluid and η is the magnetic diffusivity—differ greatly from the values estimated for Earth’s core, and so it is possible that other processes operate under such conditions17. Figure 1 summarizes Ek and Prm for a selection of published models that exhibit polarity reversals (see Extended Data Table 1).

Figure 1: Control parameters of a selection of numerical geodynamo models that exhibit polarity reversals.
figure 1

The blue dots are the parameters for published reversing-geodynamo models (see Extended Data Table 1). The red dot shows the parameters for the reversing dynamo S6 discussed here. Ek = ν/(2Ωd2) is the Ekman number and Prm = ν/η is the magnetic Prandtl number, where ν is the kinematic viscosity, Ω is the angular rotation rate, d is the thickness of the spherical shell of convecting fluid and η is the magnetic diffusivity. For case S6, Ek = 1.2 × 10−6 and Prm = 0.05. The Earth lies off to the bottom left in this diagram (as indicated by the arrow), with estimated values of Ek = O(10−15) and Prm = O(10−5).

PowerPoint slide

Full size image

In an effort to push towards the low-viscosity regime, some researchers have experimented with stress-free boundary conditions in geodynamo models, and discovered a wide variety of quadrupolar and hemispheric dynamos, some of which undergo prominent field oscillations, excursions and reversals10,18 via a dynamo-wave mechanism9. Dynamo waves have been extensively studied in both 2D and 3D using prescribed flows2,19,20; they involve cyclic variations in magnetic induction due to the combined action of differentially rotating (shear) flow and helical flow. Up to now, the relevance of such solutions to Earth has been uncertain because they have been found only in kinematic models, or in dynamic models with unusual boundary conditions or forcing modes. Here, we demonstrate that dynamo waves can also produce polarity reversals in a standard geodynamo model set-up, provided that Ek and Prm are sufficiently small and that the rate of convective driving is sufficiently large.

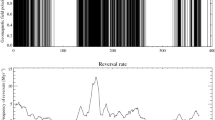
We adopt a numerical approach to solve the equations governing convection-driven magnetohydrodynamics in a rapidly rotating, electrically conducting, spherical shell (see Methods). The calculations reported here were started from an earlier run with parameters and set-up as close as possible to a previously reported dynamo simulation21,22, which uses among the smallest published values for Ek (1.2 × 10−6) and Prm (0.2). In a calculation hereafter referred to as ‘S6’, the convective driving (as measured by the Rayleigh number Ra; see Equation (2) in Methods) was then increased by a factor of 30 and Prm decreased to 0.05, in an effort to break the strong equatorial anti-symmetry of the generated field and to enhance its time variability. Figure 2a shows that, following the change in the control parameters, there is a gradual decrease in the magnitude of the magnetic energy in dynamo S6. Then, after about 1.1 magnetic diffusion times with a steady, dipole-dominated field, nearly periodic reversals of the dipole field set in (Fig. 2b). The period of the reversals is approximately 0.18 magnetic diffusion times and they persist for the 6 magnetic diffusion times that we have been able to calculate so far. We repeated the calculations with increased model resolution, in both angular and radial directions, and continue to find the same reversing behaviour.

Figure 2: Magnetic field time-dependence for dynamo S6.
figure 2

a, Time dependence of the magnetic energy, integrated over the volume of the dynamo region, for dynamo S6. The simulation was started from a previous dipole-dominated run similar to the dynamo of ref. 21, then the Rayleigh number Ra was increased by a factor of 30 and the magnetic Prandtl number Prm decreased by a factor of 4. b, The resultant time dependence of the dipole tilt, determined from the first three Gauss coefficients of the magnetic field at the outer boundary. Polarity reversals set in around 1.1 magnetic diffusion times.

PowerPoint slide

Full size image

Figure 3 presents the detailed structure and time-dependence of the reversing field in dynamo S6. The radial magnetic field Br at the outer boundary of the dynamo is primarily axisymmetric, and consists of bands with alternating polarity that appear at low latitude and subsequently move polewards (Fig. 3b, c and Supplementary Video 1). The northern hemisphere field is stronger and migrates polewards more slowly (see the lines in Fig. 3b, which illustrate that the speed dz/dt, where z = sin(λ) and λ is the latitude, is 50% faster in the southern hemisphere). The reversing field at the outer boundary is linked to deep structures that are evident in meridional sections of the longitudinally averaged azimuthal field (Fig. 3d and Supplementary Videos 2, 3). In the equatorial plane, the sign of alternates, and the field subsequently migrates polewards in each hemisphere, moving parallel to the rotation axis.

Figure 3: Magnetic field polarity reversal process.
figure 3

a, A close up of time dependence of the dipole tilt angle from dynamo S6 (Fig. 2b); orange dots mark the time instances shown in c and d. b, A butterfly plot of the longitudinally averaged radial magnetic field Br at the outer boundary of the dynamo region as a function of z = sin(λ), where λ is the latitude, and time t. c, Sequence showing Br at the outer boundary of the liquid metal region, in a Hammer projection, for the times marked by the orange dots in a. d, Sequence of meridional sections showing the longitudinally averaged azimuthal field within the liquid metal region.

PowerPoint slide

Full size image

In Fig. 4, we examine the underlying flow that generates this distinctive pattern of field reversals. Figure 4a shows the time-averaged kinetic energy spectrum as a function of spherical harmonic degree. The kinetic energy in the reversing regime is much larger than the magnetic energy, and it decays more slowly with spherical harmonic degree. It is nonetheless dominated by degrees below 20, and has a notably large zonal component. Snapshots and animations of the flow (Supplementary Videos 4, 5) reveal columnar flow patterns with strong alignment parallel to the rotation axis, typical of low-Ek rotating convection. The time and longitudinally averaged flow in S6 is presented in Fig. 4b, c, which shows meridional sections of the angular velocity (differential rotation) and radial flow. There is a strong retrograde jet close to the tangent cylinder; this produces substantial shear perpendicular to the rotation axis and is associated with weaker, but persistent, radial flow. There is a surprising difference between the angular velocities in the northern and southern hemispheres: prograde zonal flow at low latitudes in the southern hemisphere is absent in the northern hemisphere. This may be linked to the southern hemisphere being colder at the outer boundary (see Supplementary Video 6). Flow asymmetry between the northern and southern hemispheres, and a substantial quadrupolar component in the generated field, are conditions known to favour reversing behaviour in dynamos23,24. Neither the kinetic energy nor the structure of the flows varies much during the reversals.

Figure 4: Time-averaged flow in dynamo S6.
figure 4

a, Volume-averaged spectra of the kinetic energy (blue) compared to the magnetic energy (red), time-averaged over the reversing interval. b, A meridional section showing the time and longitudinally averaged angular velocity ω, with blues denoting retrograde velocities and reds denoting prograde velocities. c, Similar meridional section for the radial flow (ur, radial velocity); reds show radially outward flow.

PowerPoint slide

Full size image

To further investigate the nature of the reversal process, we carried out a series of additional calculations, in which we varied the control parameters and set-up of the dynamo (see Extended Data Table 2). Upon increasing Ra, which enhances the magnetic Reynolds number Rem and the amplitude of the zonal flow, we continue to find similar reversals, but with shorter periods and increasing time variability (runs S6.04–S6.08). Decreasing Prm much further is difficult without losing the dynamo, but small decreases slightly shorten the reversal period (runs S7.02, S7.03). Replacing the electrically conducting inner core with an insulating inner core makes little difference (the reversal period becomes very slightly shorter; see run S6_InsIC), presumably because the reversals result primarily from processes outside the tangent cylinder. We also carried out one calculation with the Lorentz force switched off (case S6_LorOff). Very similar reversals were then obtained, but with a shorter period of only 0.07 magnetic diffusion times. The helicity of the flow did not change much upon switching off the Lorentz force, but the energy in the zonal part of the toroidal flow increased by a factor of five. A calculation using a revised model ‘S6ε0’, in which the internal heating is set to zero (and all other parameters remain the same as in S6; see Extended Data Table 2), has established that in this case the dynamo continues to reverse in a similar manner, with its period differing by less than 5% from that of S6 (see Methods).

We next consider whether these reversals can be the result of a dynamo-wave process. A first clue is that Parker’s theory2,9 predicts poleward propagation of dynamo waves along cylinders parallel to the rotation axis, in the case that the magnitude of the (westward) angular velocity decreases with distance away from the tangent cylinder and helicity is negative in the northern hemisphere. This is in agreement with our results. In addition, the period of dynamo waves can be estimated by10,18

where TParker is the predicted reversal period, γ is a constant, is the modulus of the volume-integrated kinetic helicity of the non-axisymmetric flow that we evaluate in the northern hemisphere, and is the zonal toroidal flow energy. Both quantities were time-averaged over the reversing interval. Upon comparing the predictions of this theory with the reversal periods found in our numerical calculations (Extended Data Table 2) we find a reasonable agreement (Extended Data Fig. 1), especially regarding the decrease in reversal period as the energy of toroidal zonal flow increases.

Dynamo S6 thus demonstrates that field oscillations and reversals can result from dynamo waves produced by rapidly rotating convection in a spherical shell, even in the presence of no-slip boundary conditions, provided that Ek and Prm are sufficiently small. Dynamo waves are apparently a very robust phenomenon, relevant to dynamos across a range of planetary25,26,27 and astrophysical28 scenarios. A common aspect of such dynamos is that they possess a relatively large toroidal magnetic field, obtained by stretching due to differential rotation. Strong azimuthal fields just outside the tangent cylinder, which are related to an omega effect taking place at this location, are a characteristic feature of the reversing dynamos reported here.

Our more Earth-like parameter regime brings further surprises. The conventional wisdom is that the local Rossby number Rol (see Methods) is important for delineating two regimes of behaviour7: for Rol < 0.1 the dynamos are generally dipolar and of stable polarity, whereas, as the driving is increased and inertial effects play a more important part, the dynamos become multipolar and reversing29. In these previous studies, the dynamos have viscous and Ohmic diffusivities that are broadly similar (Prm = O(1)). S6, with its small Prm and Ek, has Rol = 0.06 (Extended Data Table 2) and so contradicts the accepted regime division by lying in the purportedly stable dipolar regime. Similarly, our dynamo S6 should lie close to the non-reversing regime (Rol < 0.05) according to a study of magnetic reversal frequency scaling8. Conversely, it exhibits a reversal frequency that is predicted to occur only at Rol = 0.4 according to dynamos for which Ek > 3 × 10−4 and 3 ≤ Prm ≤ 20.

The polarity reversals exhibited by S6 are nearly periodic, but if the Rayleigh number is increased, for example, as in S6.07, the time dependence becomes more variable, and Earth-like events such as dipole excursions become possible (Extended Data Fig. 2). Moreover, at a radius corresponding to Earth’s surface, the field in S6 is dipole-dominated between reversals (Supplementary Video 7). Our results therefore indicate that dynamo waves could indeed play a part in long-term geomagnetic variability2,33. Unfortunately, it is currently a huge computational undertaking to produce the long time series needed to fully characterize the statistics of reversals in the low-Ek regime: S6 required 4 × 106 CPU hours (approximately 457 CPU years) to integrate for 6.5 magnetic diffusion times. More complete studies of the dynamics of polarity reversals in dynamos at low viscosity may therefore have to wait for new numerical tools that are capable of more efficiently exploring this challenging regime.

Methods

Governing equations and non-dimensionalization

We adopt the Boussinesq approximation for convection-driven, rotating magnetohydrodynamics, which results in the following non-dimensional equations:

where

The variables u, B and T are the velocity, magnetic field and temperature, respectively. is the modified pressure that contains information about conservative forces. The axis of rotation of the system is z and is a unit vector in that direction. Time is denoted as t. A uniform heat source ε is included. Solenoidal conditions ∇·B = 0 and ∇·u = 0 are integrated into the solution technique through use of a poloidal-toroidal decomposition of the vector field. The non-dimensional parameters are

where Ro is the magnetic Rossby number, Ek is the Ekman number, Ra is the modified Rayleigh number and q is the Roberts number.

The units of length, time, magnetic field and temperature for the non-dimensional governing equations are chosen as

The following symbols denote the parameters of the system: is the rotation rate, μ0 is the permeability of free space, ρ0 is the density, ν, κ and η are the kinematic viscosity, thermal diffusivity and magnetic diffusivity, respectively, α is the thermal expansivity and d is the thickness of the spherical shell of convecting fluid. The unit of temperature ΔT is chosen to be βd/β*, where β and β* = −2(1 − ri/ro) are the dimensional and non-dimensional temperature gradients at the core–mantle boundary (CMB), respectively, and ri,o are the inner and outer radii of the shell, respectively. Gravity is assumed to vary linearly with radius and has value g on the outer boundary. The spherical coordinates are denoted (r, θ, φ).

Boundary conditions and internal heating

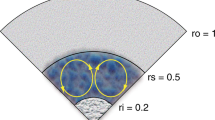
The modelled fluid is enclosed in a rotating spherical shell between radii ri and ro with c = ri/ro = 0.35. Both boundaries are no-slip and impermeable. The outer boundary is electrically insulating, the inner core has the same electrical conductivity as the outer core. In case S6_InsIC the inner core is insulating. The inner-core temperature is kept constant at ; the gradient of the temperature on the outer boundary is β* = −2/(1 − c). A uniform heat source with ε = 3q is adopted throughout the outer core. In run S6ε0, the uniform heat source ε is set to zero.

Diagnostics

The dipole latitude is calculated as where are the first three Gauss coefficients of the magnetic field at the outer boundary. The kinetic and magnetic energies are defined as and , where the volume integral is over the entire outer core. The local Rossby number8 is defined as ; the magnetic Reynolds number Rem is Ud/η; is the mean harmonic degree; is the kinetic energy per harmonic degree l; ; and V is the volume of the spherical shell.

Numerical set-up

We solve the governing equations using a parameterization in spherical harmonics up to degree and order 255 for the angular component and 528 finite-difference points in radius. A second-order predictor–corrector scheme is used for the time integration34. The time-step is adaptive and varies throughout the run. In the case S6, the time-step started from 10−7 magnetic diffusion times at the initial stage of the run with a very turbulent flow, and later increased up to 2.5 × 10−6 magnetic diffusion times during the reversing interval. Parallelization is carried out in radius. In the linear parts of the code, data are split over the spherical harmonics. 528 cores were used simultaneously for one simulation. The bulk of the simulations and visualizations were performed on the supercomputer Piz Daint (Cray XC 30) at the Swiss National Supercomputing Centre. The code was originally developed by Willis35 and then subsequently optimized for the Cray XC 30 and successfully benchmarked against other dynamo codes36.

Importance of the heating mode

We carried out an additional simulation S6ε0 to test how the particular choice of the internal homogeneous heating influences the reversing behaviour. In the two runs S6 and S6ε0, the internal heating ε is set to 3q and 0, respectively. Other parameters are the same. The run S6ε0 was started from S6. As a consequence of changing the heating mode, the temperature drop between the inner core boundary (ICB) and the CMB is modified (see Extended Data Fig. 3). An important transient effect is the secular cooling that can be defined as the decrease in the thermal energy in the shell per unit time: (to evaluate Qsec, the mean radial temperature gradient on the ICB is measured; see Equation (5) and Extended Data Fig. 4). We plot the ratio of the secular cooling to the heat coming from the ICB in the steady (Qsec = 0) state in Extended Data Fig. 5. In the modified run S6ε0, Qsec constitutes less than 5% of the heat flux from the ICB during the final magnetic diffusion time. So, we conclude that the contribution of the secular cooling term to the heat flux equation is small at this stage.

The reversal period in S6ε0 increased by less than 5% in comparison with that in S6 (see dipole latitude time dependencies for both runs in Extended Data Fig. 6). This test suggests that the inclusion or not of the internal heating term is not crucial to the dynamo-wave reversals exhibited by our dynamos. Changes in the internal heating term do nevertheless slightly alter the value of the reversal period obtained.

Volume-integrated terms of the heat equation

The heat flux equation is

In a quasi-stationary state  , if no-slip boundary conditions (uφ = uθ = 0) are applied, then

and the integrated heat flux equation is

This is equivalent to Qi + Qint = Qo, whereby the sum of the heat supplied by internal heating Qint and that from the inner core Qi is equal to the heat leaving through the outer boundary Qo.

The temperature gradient at the CMB was held fixed at with c = ri/ro = 0.35. In S6 the internal heating Qint = 3qV. The heat leaving through the outer boundary . The temperature gradient on the ICB in run S6 is

In the case S6ε0 without internal heating, the temperature gradient at ri is

Without internal heating, in a steady case the heat from the ICB goes through the shell and leaves without losses or gains at the CMB. The power flowing through the CMB and the ICB is equal, although the heat flux is smaller at the CMB because it is inversely proportional to the surface area, yielding the coefficient (ro/ri)2 = 1/c2 in equation (4).

Let us consider the non-steady case:

where is the secular cooling. If the heat flux from the inner core in the steady case is , the . So, the difference between the steady state and the actual value of the heat flux from the inner boundary is the secular cooling. The relative influence of the secular cooling can be calculated as