1 Introduction

In the field of data mining, classification analysis is an essential component. It learns from and trains a training set of labeled samples, builds a model for classification, and finally uses the constructed model to identify class labels of the test set samples. We can use our established model to predict future trends and receive more valuable data. There have been several popular algorithms for classification in the past, such as naive Bayesian algorithms, support vector machines, decision trees, etc. There are a number of factors contributing to the increase in data, which also increases the requirements for classification algorithms. As data processing becomes more complex, classical algorithms are no longer able to cope. The demand for classifiers with improved classification accuracy and lower error rates is pressing. It is among the top ten algorithms in data mining because of its value in pattern classification, and it can also be used in other directions. As an example, in reference [1], a new overlapping community detection algorithm (NOCD) is proposed based on an improved KNN algorithm aimed at detecting overlapping communities in large networks. In addition, in reference [2], the improved KNN algorithm is also applied to discover the DDoS attack. A recent discussion on how to resolve the issue of KNN algorithms not being accurate and effective due to proximity measurement attracted many experts and scholars.

We have developed in [3] an effective method of weighting different nearest neighbor samples, Dudani [3] proposed a classical distance weighted k-nearest neighbor (WKNN) classification algorithm. As a result of this algorithm, the closest neighbor samples are used to weigh the voting process of the algorithm, rather than the k value, eliminating the influence of the k value on algorithm accuracy; Wangmeng Zhou et al. [4] presented a kernel difference weighted k-nearest neighbor classification algorithm, which defines the weighted KNN rule as a constrained optimization problem, and a novel approach is proposed for calculating different nearest neighbor weights; Jianping Gou et al. [5] proposed a KNN classification algorithm based on double-weighted voting rules (Dual Weighted voting for k-nearest Neighbor rule, DWKNN); the algorithm establishes a double-weighted voting function which is used for voting, effectively overcoming the problem of how to select nearest neighbors based on size k, and improves the quality of the classification. Local mean k-nearest neighbor algorithm (LMKNN) algorithm is a classifier proposed by Mitani. Y and Hamamoto. Y [6]. To accomplish this task, it is necessary to find the k-nearest neighbors of the samples to be classified in each training set class, obtain local mean points for each class, and finally determine the class of test samples based on the shortest distance. Three methods of determining k value are discussed in literature [7, 8], and [9] respectively, but the last one is an adaptive selection method for k value. Yong Zeng et al. [10] presented a classification algorithm based on the pseudo-nearest neighbor rule and referred to it as PNN. It is an extension of the LMKNN algorithm, which uses pseudo-nearest neighbor instead of the real nearest neighbor. Althrough the research on a large number of improved algorithms based on KNN, we find that the algorithms in the above documents have improved the first problem of KNN mentioned in this paper, that is, the accuracy and stability of KNN algorithm can be easily measured by different k values.

Another problem is that the KNN algorithm selects the closest neighbor samples based on Euclidean distance measurements, ignores correlations and redundancy, and any errors in the similarity distance measurement would affect the accuracy of classification. Zhibin pan et al. [11] proposed a locally adaptive k-nearest neighbor algorithm based on discriminant class. In a study by Weinberger et al. [12], similarity was measured using Manhattan distance, which makes it so the similarity between classes is large, whereas the dissimilarity between classes is small; Xiao X et al. [13] developed the k-nearest neighbor algorithm using attribute information entropy. It is proposed that the similarity measure is calculated as the average information entropy of sample values of the same attribute. According to average information entropy, a set of k-nearest neighbors similar to the sample to be tested is selected, and finally, the class label of the sample to be tested is calculated according to the reliability. Despite this, when the class reliability of the samples to be tested in each category is very close, it is not possible to achieve the proper classification effect. T. Denoeux [14] proposed a k-nearest neighbor classification rule based on Dempster Shafer. The related algorithms involved in this paragraph have solved the second problem of KNN algorithm proposed in the abstract, which is instructive to the algorithm proposed in this paper.

Inspired by the concept of non-parametric [8, 15,16,17,18,19] and the way of seeking sample center [20,21,22,23,24,25,26,27,28,29,30,31], a non-parametric nearest neighbor classification algorithm based on global variance difference (VKNN) rule is proposed in this paper. As an extension of KNN rule, the purpose of our VKNN is to use global variance differences, thereby solving the problem that KNN nearest neighbors contribute equally and the effectiveness is affected by proximity measurements without affecting the accuracy. When considering the problem, variance has been added in this paper, as opposed to the previous methods. In probability theory and statistics, variance is a measure of the dispersion of random variables. In many practical situations, it is of great importance. As a first step, we calculate the difference of variance before and after adding the sample to be tested in order to obtain an optimal distance metric. After that, we divide the difference by the variance before adding the sample to be tested, and we take the minimum value of the quotient as the objective function, so as to analyze the problem more intuitively and effectively. In experiments using real data, the proposed algorithm effectively resolves the problem that KNN accuracy and effectiveness are somewhat affected by proximity measurement, and improves the accuracy of the classification algorithm significantly.

With its advantages such as simplicity, effectivity, and competitive performance, KNN classification has become the most attractive classification method in countless practical applications. Nevertheless, as described in Section 2.1, it is susceptible to problems such as sensitive selection of nearest neighbor parameters and the simple maximum voting classification decision-making principle, especially in the case of a small sampling size. It has been clearly known that the selection of neighborhood size plays a very important role in KNN algorithm. When k is too small, the near neighborhood may include noise points and outliers, causing overfitting and incorrect classification rules; when k is too large, the nearest neighbor may include more noise points and outliers, resulting in a reduction in classification accuracy.

Furthermore, the proximity measurement method will also affect the performance of the KNN algorithm. In many improved KNN algorithms, the k-nearest neighbor samples of each test sample are usually selected by the dissimilarity measure, and the Euclidean distance measure is commonly used to select the nearest neighbor set. The accuracy and effectiveness of the KNN algorithm are affected by proximity measurement. Sometimes the similarity between test samples and nearest neighbor samples cannot be accurately reflected.

A large number of studies have proposed various methods to solve various problems in KNN algorithm, such as adaptive selection of appropriate k value, changing classification decision rules, etc. As far as we know, the difference of ergodic global variance has not attracted the attention of researchers. Therefore, our proposed algorithm pays attention to this breakthrough. The main reasons why the experimental results of this paper are significantly better than other algorithms are as follows: (1) the parameter k is not used. Because according to the previous experimental analysis, the value of k is too large or too small will affect the experimental results. (2) The sample center is selected as the sample mean, and the global variance difference is traversed. The feasibility of this method has been clearly proved in the previous theoretical proof, which is also one of the important reasons why the experimental results of our algorithm are obviously better than other algorithms.

The main contributions of this paper can be summarized as follows: (1) a new scheme of designing classification rules do not involve k-value and other parameters, the VKNN algorithm avoids the influence of k-value and other parameters on the classification effect. (2) A non-parametric nearest neighbor classification based on global variance difference (VKNN) rule is proposed by introducing a global variance difference in the dissimilarity, rather than using the traditional Euclidean distance formula to select the nearest neighbor set. (3) The effectiveness of VKNN is explored by extensive experiments in terms of the classification error and the good classification of VKNN is credibly demonstrated by non-parametric statical tests.

The remainder of this paper is structured as follows. In Sect. 2, we briefly summarize KNN and the classification algorithms used in the comparative experiment. In Sect. 3, we introduce the objective function of the VKNN algorithm and the feasibility of the algorithm. At the same time, we give the pseudocode of the algorithm. In Sect. 4, we conduct experiments for all the competing methods using accuracy and recall on the real UCI datasets. Finally, the conclusions are mentioned in Sect. 5.

2 Related Algorithm

In machine learning, the k-nearest neighbor (KNN) rule has been used extensively in non-parametric classifiers. A variety of KNN-based approaches has also been developed to address the challenges in KNN-based classification, such as the pseudo-nearest neighbor classification (LMPNN) [32], a globally adaptive k-nearest neighbor classifier based on local mean optimization(LMO-GAKNN) [33] and a new locally adaptive k-nearest neighbor algorithm based on discrimination class (DC-LAKNN) [11]. In this section, we briefly review LMPNN, LMO-GAKNN and DC-LAKNN classifiers that motivate our work.

2.1 The Classical KNN Algorithm

In the field of data mining, the KNN algorithm is a classical classification algorithm. This algorithm is the classification algorithm proposed by Cover et al. [34] in 1967. In addition, it has several advantages: (1) its concept is very simple and easy to implement, (2) there is no need to generate additional data to describe the rules, and there will be noise in the data, (3) in category decision-making, it is only related to a very small number of adjacent samples, which allows for better avoiding the imbalance of sample numbers. Its performance, however, is easily affected by the sensitivity of nearest neighbor parameter selection and the maximization of voting in the classification decision, so its performance needs to be further improved.

In the general classification problem, suppose a training set \(T={\{y_{i}=R^{d}\}_{i = 1}^N}\) with M classes consists of N training samples in a d-dimensional feature space and the class label of one sample \(y_{i}\) is \(c_{n}\), where \(c_{n}=\{\omega _{1},\omega _{2},\ldots ,\omega _{M}\}\). Let \(T(\omega _1)={\{y_{i}^j=R^{d}\}_{i = 1}^N}\) denote a class subset of T from the class \(y_{i}\), with the number of the training samples \(N_{i}\). Given a query point x, the KNN rule is carried out as follows:

Step 1: Calculate the Euclidean distance from the sample x to \(T={\{y_{i}=R^{d}\}_{i = 1}^N}\):

$$\begin{aligned}{} & d(x,y_{i}) =\sqrt{(x-y_{1})^2+(x-y_{2})^2+\cdots +(x-y_{n})^2}\nonumber \\ &\quad = \sqrt{\sum \limits _{k= 1}^n {(x-y_{i})^2}} \end{aligned}$$
(1)

Step 2: Sort all distances in ascending order: \(d(x-y_{1})<d(x-y_{2})<\cdots<d(x-y_{N})\)

Step 3: Take the first k neighbors: \(y_{1},y_{2},\ldots ,y_{k}\)

Step 4: Predict the class label of the sample x that needs to be tested:

$$\begin{aligned} \begin{array}{c} c=argmax_v {\sum \limits _{y_{i},\omega _{i}\epsilon {T}}I(v=\omega _{i})} \end{array} \end{aligned}$$
(2)

Among them, the class label is expressed as v, and the indicator function is expressed as I(\(\cdot\)), as shown in the following formula:

$$\begin{aligned} {I(a,b)} = \left\{ {\begin{array}{*{20}{l}} {1,\,if\, a=b }\\ {0,\mathrm{{otherwise}}} \end{array}} \right. \end{aligned}$$
(3)

2.2 Pseudo-Nearest Neighbor Algorithm was Based on Local Mean (LMPNN)

LMPNN is another successful KNN-based classifier. Motivated by the ideas of the LMKNN [6] and PNN [10] rules, it is a pseudo-nearest neighbor algorithm based on each test sample, which makes extensive use of the local information of the sample and minimizes the impact of outliers on the classification accuracy. The advantage of this algorithm is straightforward, efficient, and easy to execute. It still widely uses in the field of classification algorithms.

Given a query point x and a training set T, the class label of x in the LMPNN rule is determined through the following steps:

Step 1: Calculate the Euclidean distance from the sample x to \({T_{\omega _j}}(j=1,2,\ldots ,L)\):

$$\begin{aligned}{} & {} d(x,y_{i}) =\sqrt{(x-y_{1})^2+(x-y_{2})^2+\cdots +(x-y_{n})^2}\nonumber \\& \quad =\sqrt{\sum \limits _{k= 1}^n {(x-y_{i})^2}} \end{aligned}$$
(4)

Step 2: Arrange the Euclidean distances in the category \(\omega _j\) in ascending order, and take the first k-nearest neighbors: \(y_{1}^j,y_{2}^j,\ldots ,y_{k}^j\)

Step 3: Calculate the local mean vector of the first i nearest neighbors of the sample x in the category \(\omega _j\):

$$\begin{aligned} \begin{array}{c} {{\bar{y}}}_{i}^j =\frac{1}{i} {\sum \limits _{l = 1}^i {y_{l}^j}} \end{array} \end{aligned}$$
(5)

Use \({{\bar{T}}_{\omega _{j}}}={\{{\bar{y}}_{i}^j\epsilon {R^{d}\}_{i = 1}^k}}\) to denote the set of local mean vectors in \(\omega _j\). \(d(x,{\bar{y}}_{i}^j)\) represents the Euclidean distance from the sample x to the local mean in the category \(\omega _j\).

Step 4: Assign different weights to the local mean vector in each category. In the class \(\omega _j\), the weight of the ith local mean vector is

$$\begin{aligned} \begin{array}{c} W_{i} =\frac{1}{i} (i=1,2,\ldots ,k) \end{array} \end{aligned}$$
(6)

Step 5: Calculate the pseudo-nearest neighbors in each category \(\omega _j\):

$$\begin{aligned} \begin{array}{c} d(x,y_{PNN}^j) = W_{1}\times {d(x,{\bar{y}}_{1}^j)}+W_{2}\times {d(x,{\bar{y}}_{2}^j)}+\cdots +W_{k}\times {d(x,{\bar{y}}_{k}^j)} \end{array} \end{aligned}$$
(7)

Step 6: Predict the class label c of the sample x that need to be tested:

$$\begin{aligned} \begin{array}{c} c=argmin_{\omega _{j}} d(x,y_{PNN}^j) \end{array} \end{aligned}$$
(8)

2.3 A Globally Adaptive k-Nearest Neighbor Classifier Based on Local Mean Optimization (LMO-GAKNN)

In the LMKNN classifier, the unreliable nearest neighbor selection rule and the single local average vector strategy have serious defects that have a negative impact on its classification performance. Considering these problems in LMKNN, a globally adaptive k-nearest neighbor classifier based on local mean optimization [33], which has been proposed in 2021, utilizes the globally adaptive nearest neighbor selection strategy and the implementation of local mean optimization to obtain more convincing and reliable local mean vectors.

Given a query point x and a training set T, the class label of x in the LMO-GAKNN rule is determined through the following steps:

Step 1: Calculate the Euclidean distance from the sample x to \(T={\{y_{i}=R^{d}\}_{i = 1}^N}\):

$$\begin{aligned}{} & {} d(x,y_{i}) =\sqrt{(x-y_{1})^2+(x-y_{2})^2+\cdots +(x-y_{n})^2}\nonumber \\&\quad =\sqrt{\sum \limits _{k= 1}^n {(x-y_{i})^2}} \end{aligned}$$
(9)

Step 2: Sort all distances in ascending order: \(d(x-y_{1})<d(x-y_{2})<\cdots<d(x-y_{N})\).

Step 3: Select the first r samples as r nearest neighbors for class \(\omega _j\) based on sorted \(d(x,y_{i})\).

Step 4: Find k-nearest neighbors of x in the ascending order of sorted Euclidean distances to x, where \(k={r}\times {M}\).

Step 5: Select \(r_{j}\) nearest neighbors for class \(\omega _j\) in the initial k-nearest neighbors, where \({0}\leqslant {r_j} \leqslant k\) and \({\sum \nolimits _{j = 1}^M} {r_{j}=k}\).

Step 6: Compute \(MLMV_{j}^{r_{j}}\) for class \(\omega _j\) according to equation as follows:

$$\begin{aligned} \begin{array}{c} {m_{j}^s}=\frac{1}{s}\sum \limits _{i = 1}^s {y_{i}},y_{i}\epsilon {NN_{j}^r} \end{array} \end{aligned}$$
(10)

Step 7: Select optimal local mean vector \(m_{j}^*\) in \(MLMV_{j}^{r_{j}}\) according to the equation as follows:

$$\begin{aligned} \begin{array}{c} {m_{j}^*}=argmin_s d(x,{m_{j}^s}),{m_{j}^s}\epsilon {MLMV_{j}^{r_{j}}} \end{array} \end{aligned}$$
(11)

Step 8: Classify x into the class \(\omega _c\) based on minimum Euclidean distance between x and optimal local mean vectors of all classes according to the equation as follows:

$$\begin{aligned} \begin{array}{c} {\omega _c}=argmin_{\omega _j}d(x,m_{j}^*) \end{array} \end{aligned}$$
(12)

2.4 A New Locally Adaptive k-Nearest Neighbor Algorithm Based on Discrimination Class (DC-LAKNN)

A new locally adaptive k-nearest neighbor algorithm based on discrimination class(DC-LAKNN) [11] has been proposed in 2020. In this method, the role of the second majority class in classification is for the first time considered. Firstly, the discrimination classes at different values of k are selected from the majority class and the second majority class in the k-neighborhood of the query. Then, the adaptive k value and the final classification result are obtained according to the quantity and distribution information on the neighbors in the discrimination classes at each value of k.

Given a query point x and a training set T, the class label of x in the DC-LAKNN rule is determined through the following steps:

Step 1: Select its k-nearest neighbors \(NN_{k}(x)={{({y_{i}^{NN}},{c_{i}^{NN}})}_{i=1}^k}\) in the training set T according to the ascending order of Euclidean distances between x and all training instances.

Step 2: Find the majority classes \({({\omega _{1st,i}^{k}})}_{i=1}^{{num_{1st}}^{k}}\) and second majority classes \({({\omega _{2nd,i}^{k}})}_{i=1}^{{num_{2nd}}^{k}}\) in the k-neighborhood of the query x consisting of \(NN_{k} (x)\), where \(num_{1st}^{k}\) and \(num_{2nd}^{k}\) are the number of the majority classes and second majority classes, respectively. Record the number of the majority class neighbors and the second majority class neighbors \(r_{1st}^{k}\) and \(num_{2nd}^{k}\).

Step 3: Compute the centroids of nearest neighbors in different majority classes and different second majority classes \({({cent_{1st,i}^{k}})}_{i=1}^{{num_{1st}}^{k}}\),\({({cent_{2nd,i}^{k}})}_{i=1}^{{num_{2nd}}^{k}}\).

Step 4: Select discrimination class \(\omega _{disc}^{k}\) from the majority classes \({({\omega _{1st,i}^{k}})}_{i=1}^{{num_{1st}}^{k}}\) and second majority classes \({({\omega _{2nd,i}^{k}})}_{i=1}^{{num_{2nd}}^{k}}\). Specifically, the selection process is divided into the following cases:

Case 1: If \({num_{1st}}^{k}=1\), then compute \(\delta ={r_{1st}^{k}}/{r_{2nd}^{k}}\);

Case 1.1: If \(\delta ={r_{1st}^{k}}/{r_{2nd}^{k}}>{\theta }\), then this sole majority class is selected as the discrimination class, that is,

$$\begin{aligned} \begin{array}{c} \omega _{disc}^{k}=\omega _{1st,1}^{k} \end{array} \end{aligned}$$
(13)

Case 1.2: If \(\delta ={r_{1st}^{k}}/{r_{2nd}^{k}}\leqslant {\theta }\), then the class with the closest centroid to the query x among the sole majority class and the \(num_{2nd}^{k}\) second majority classes is selected as the discrimination class, that is,

$$\begin{aligned} \begin{array}{c} \omega _{disc}^{k}=argmin{(d(x,cent_{1st,1}^{k}),d(x,cent_{2nd,i}^{k}))} \end{array} \end{aligned}$$
(14)

Case 2: If \({num_{1st}}^{k}>1\), then the majority class with the closest centroid to the query x is selected as the discrimination class, that is,

$$\begin{aligned} \begin{array}{c} \omega _{disc}^{k}=argmin{d(x,cent_{1st,i}^{k})} \end{array} \end{aligned}$$
(15)

Step 5: Record the number and centroid of nearest neighbors in the discrimination class, \(r_{disc}^{k}\) and \(cent_{disc}^{k}\), based on the above results.

Step 6: Compute the ratio of the number of nearest neighbors in the discrimination class to the number of all nearest neighbors, \(ratio^{k}={r_{disc}^{k}}/k\), and the distance between the centroid of nearest neighbors in the discrimination class and the query x, \(d^{k}=d(x,cent_{disc}^{k}), k =1, 2,\ldots , kmax\).

Step 7: Generate two rankings \({rank_{ratio}}={({rank_{ratio}^{k}})}_{k=1}^{kmax}\) and \({rank_{d}}={({rank_{d}^{k}})}_{k=1}^{kmax}\) of the discrimination classes corresponding to different values of k according to the descending order of \(ratio^{k}\) and the ascending order of \(d^{k}, k = 1, 2,\ldots , kmax\).

Step 8: Compute the average ranking of the discrimination classes for each value of k:

$$\begin{aligned} \begin{array}{c} {rank_{ave}^{k}=\left( \frac{{rank_{ratio}^{k}}}{max_{k=1,2,\ldots ,kmax}rank_{ratio}^{k}}+\frac{{rank_{d}^{k}}}{max_{k=1,2,\ldots ,kmax}rank_{d}^{k}}\right) }/2 \end{array} \end{aligned}$$
(16)
$$\begin{aligned} \begin{array}{c} k=1,2,\ldots ,kmax \end{array} \end{aligned}$$
(17)

Step 9: Select the discrimination class with the minimum average ranking as the classification result of the query x, and the corresponding value of k is the adaptive k value for x, that is,

$$\begin{aligned} \begin{array}{c} k_{adap}=argmin_{k=2,\ldots ,kmax}(rank_{ave}^{k}) \end{array} \end{aligned}$$
(18)
$$\begin{aligned} \begin{array}{c} \omega _{c}=\omega _{disc}^{k_{adap}} \end{array} \end{aligned}$$
(19)

3 The VKNN Algorithm

As a further improvement to KNN-based classification, we present the non-parametric nearest neighbor classification based on global variance difference (VKNN) in this section. Using the VKNN approach, we further improve KNN-based classification accuracy.

3.1 The VKNN Classification Rule

The VKNN method, as an extension of the KNN rule, is presented in this subsection. The idea of the VKNN algorithm is: first, the training samples are divided into categories, and the mean value of each sample is taken as the sample center; Then, according to the sample center, the variance before and after adding the sample to be tested in each class is calculated respectively, and the obtained variance is processed as the difference, and then the difference is divided by the variance before adding the sample to be tested, and the quotient obtained is used as the objective function; finally, the samples are classified into the class with the smallest objective function.

Take the mean value of \(N_i\) samples in each class as the sample center and record it as M. In the proposed VKNN rule, the class label of a query point x is yielded by the following steps:

Step 1: Suppose a training dataset \(T={\{y_{i}=R^{d}\}_{i = 1}^N}\) is given;

Step 2: Select samples from the training samples, and divide the samples according to classes, and the corresponding classes are marked as set \({T_{\omega _{j}}}={\{y_{i}^j={R^{d}\}_{i = 1}^{N^{j}}}}\);

Step 3: For each class, select the sample center \(x_{ij}\) of \(N_{i}\) a sample and record it as M, then we have

$$\begin{aligned} \begin{array}{c} {M_i} = \frac{{\sum \limits _{j = 1}^{N_i} {{x_{ij}}}}}{N_{i}} \end{array} \end{aligned}$$
(20)

Step 4: According to sample center, calculate the global variance between the sample point to be tested and the sample center of each category, then we have the objective function \(D_{i}(x)\), that is

$$\begin{aligned} \begin{array}{c} {D_i(x)} = \frac{{\sum \limits _{i = 1}^{n+1} {{(x_{i}-M_{i})^2}}}-{\sum \limits _{i = 1}^{n} {{(x_{i}-M_{i})^2}}}}{{\sum \limits _{i = 1}^{n} {{(x_{i}-M_{i})^2}}}} \end{array} \end{aligned}$$
(21)

Step 5: Finally find the minimum value of the objective function, and classify the sample to be tested into the class with the minimum objective function \(D_{i}(x)\):

$$\begin{aligned} \begin{array}{c} c=argmin_{\omega _{i}} D_{i}(x) \end{array} \end{aligned}$$
(22)

3.2 The Pseudo Codes of VKNN

As discussed in this section, the proposed VKNN method is summarized in Algorithm 1 by means of pseudocodes.

figure a

3.3 Theoretical Proofs

The objective function is mainly composed of the variance before and after adding the sample to be tested:

$$\begin{aligned} \begin{array}{c} {var_1} = {\sum \limits _{i = 1}^{n} {{(x_{i}-M_{i})^2}}}={\sum \limits _{i = 1}^{n} {{(x_{i}-{\frac{x_{1}+x_{2}+\cdots +x_{n}}{n}})^2}}}\\ {var_2} = {\sum \limits _{i = 1}^{n+1} {{(x_{i}-M_{i})^2}}}={\sum \limits _{i = 1}^{n+1} {{(x_{i}-{\frac{x_{1}+x_{2}+\cdots +x_{n}+x_{n+1}}{n+1}})^2}}} \end{array} \end{aligned}$$
(23)

If the two are treated as differences, there are

$$\begin{aligned} \begin{array}{c} {var_2-var_1} = {\sum \limits _{i = 1}^{n+1} {{(x_{i}-{\frac{x_{1}+x_{2}+\cdots +x_{n}+x_{n+1}}{n+1}})^2}}}-{\sum \limits _{i = 1}^{n} {{(x_{i}-{\frac{x_{1}+x_{2}+\cdots +x_{n}+x_{n}}{n}})^2}}}\\ =(x_{n+1}-{\frac{x_{1}+x_{2}+\cdots +x_{n}+x_{n+1}}{n+1}})\\ +{\sum \limits _{i = 1}^{n} {{(x_{i}-{\frac{x_{1}+x_{2}+\cdots +x_{n}+x_{n+1}}{n+1}})^2}}}-{\sum \limits _{i = 1}^{n} {{(x_{i}-{\frac{x_{1}+x_{2}+\cdots +x_{n}+x_{n}}{n}})^2}}} \end{array} \end{aligned}$$
(24)

Then, find the partial derivative of \(x_{n+1}\) for the above formula:

$$\begin{aligned} \begin{array}{c} \frac{\partial {D_{i}(x)}}{\partial {x_{n+1}}}={\sum \limits _{i = 1}^{n} {{2(x_{i}-\frac{x_{1}+x_{2}+\cdots +x_{n}+x_{n+1}}{n+1})}}}{(-\frac{1}{n+1})}\\ +{2(x_{n+1}-\frac{x_{1}+x_{2}+\cdots +x_{n}+x_{n+1}}{n+1})}{(1-\frac{1}{n+1})} \end{array} \end{aligned}$$
(25)

After simplification, the following formula can be obtained:

$$\begin{aligned}{} & {} {\sum \limits _{i = 1}^{n+1} \left({{\frac{x_{i}}{n}-\frac{x_{1}+x_{2}+\cdots +x_{n}+x_{n+1}}{n}+\frac{x_{1}+x_{2}+\cdots +x_{n}+x_{n+1}}{n+1}}}\right)}\nonumber \\ & =x_{n+1}-{\frac{x_{1}+x_{2}+\cdots +x_{n}}{n}} \end{aligned}$$
(26)

where

$$\begin{aligned} \begin{array}{c} {\sum \limits _{i = 1}^{n+1} ({{\frac{x_{i}}{n}-\frac{x_{1}+x_{2}+\cdots+x_{n}+x_{n+1}}{n}}})}=-(x_{1}+x_{2}+\cdots+x_{n}+x_{n+1}) \end{array} \end{aligned}$$
(27)

In addition,

$$\begin{aligned} \begin{array}{c} {\sum \limits _{i = 1}^{n+1} {{\frac{x_{1}+x_{2}+\cdots +x_{n+1}}{n+1}}}={(n+1)}{\frac{x_{1}+x_{2}+\cdots +x_{n+1}}{n}}}={x_{1}+x_{2}+\cdots +x_{n+1}} \end{array} \end{aligned}$$
(28)

Therefore, there are

$$\begin{aligned} \begin{array}{c} {\sum \limits _{i = 1}^{n+1} ({{\frac{x_{i}}{n}-\frac{x_{1}+x_{2}+\cdots +x_{n}+x_{n+1}}{n}+\frac{x_{1}+x_{2}+\cdots +x_{n}+x_{n+1}}{n+1}}})}=0 \end{array} \end{aligned}$$
(29)

That is

$$\begin{aligned} \begin{array}{c} {x_{n+1}-\frac{x_{1}+x_{2}+\cdots +x_{n}}{n}}=0 \end{array} \end{aligned}$$
(30)

The final result is

$$\begin{aligned} \begin{array}{c} {x_{n+1}}=\frac{x_{1}+x_{2}+\cdots +x_{n}}{n} \end{array} \end{aligned}$$
(31)

The objective function obtained in this paper is obtained by calculating the difference between the variance of the sample to be tested and the variance of all sample centers. As shown in Formula 14, the difference between the variance of the sample to be tested and the variance of the sample center as a whole is a variable. This section also analyzes theoretically, and gives the variances of the sample to be tested and all sample centers respectively, and makes a difference between them. The final results show that this method is completely feasible in theory. In this way, it is proved theoretically that when the sample center of each sample is the sample mean, the value of the objective function \(D_{i}(x)\) can be the minimum, and it is most appropriate to divide the samples to be tested into the class with the minimum value of the objective function.

4 Experimental

To validate the proposed VKNN on the classification performance, we compare VKNN with competing classifiers: KNN, LMKNN, LMPNN, LMO-GAKNN, DC-LAKNN. During the experiment, real datasets were used to verify the accuracy of this algorithm. Moreover, we use recall to further verify superiority of the proposed method on all real datasets, since non-parametric statistical tests play an important role in comparing the performance of the competing classifiers over multiple datasets so as to demonstrate the effectiveness of a new method in machine learning. The comparison between algorithms shows the performance of each algorithm. In the next section, we will discuss dataset selection, experimental setting, evaluation index selection, and comparison with other classification algorithms. The results and analysis of the experiments will be described in detail.

4.1 Selection of Datasets

In this subsection, we briefly give the information of all the datasets used in our experience. The 12 real datasets are selected from the UCI machine learning repository. For short, among these datasets, the abbreviations of ‘wine’, ‘seeds’, ‘sonar’, ‘wrd’, ‘haber’, ‘glass’, ‘trans', ‘iris’, ’aus’, ‘iono’ ‘ozone’ and ‘segment’. The name and relevant information of the data are shown in Table  1. The main characteristics of these 12 datasets are introduced in detail, including the number of samples, the number of attributes, the number of categories, and the test sets.

Table 1 Detailed information about datasets
Full size table

As shown in Table  1, there are seven two-class classification problems among all the real datasets, while the others are the multi-class classification problems. In these datasets, the largest and lowest numbers of the samples are 2536 and 146, and the largest and lowest numbers of dimensionality are 73 and 3.

4.2 Experimental on Real UCI Datasets

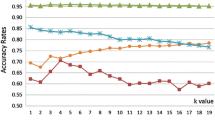
Our algorithm is designed for the problem of KNN nearest neighbors having the same contribution and the effectiveness being affected by proximity measurement. For changing the traditional Euclidean distance formula to select the nearest neighbors, an improved KNN algorithm is proposed. These performances are performed by 10-fold cross validation by means of the classification accuracy and racall. As a comparative experiment, we chose a variety of KNN algorithms, including classical KNN algorithm, LMKNN [6], LMPNN [32], LMO-GAKNN and DC-LAKNN. The four comparison algorithms adopt the method of identifying and verifying the k value one by one, the specific settings are as follows: firstly, the value range of k is 1 \(\sqrt{n}\) (n indicating the number of samples); next, perform the m-fold cross validation five times to obtain the average accuracy for each k value, and select the k value with the highest average accuracy as the optimal k value. For the comparative experiment, we choose the best k value. In Fig. 1, we show the optimal k values for four comparison algorithms for 12 datasets. The best classification of each method with highest accuracy is obtained in the interval of k on each data set.

Fig. 1
figure 1

The best value k of each method on different datasets

Full size image

4.3 Experimental Result

We use two performance indicators to measure the classification ability of different algorithms. One is the accuracy rate (Acc), the other is the recall rate (Recall). The following is a detailed introduction of the two performance indicators:

a. Accuracy (Acc): indicates the percentage of correctly classified samples. The formula is as following:

$$\begin{aligned} \begin{array}{c} Acc=\frac{\sum \nolimits _{i = 1}^{m} {{\delta (r_{i},map(p_{i}))}}}{m} \end{array} \end{aligned}$$
(32)

where m is the total amount of data objects in a given dataset; \(p_{i}\) and \(r_{i}\) labels, respectively, representing the classification of data objects and the real situation; \(\delta (x,y)\)is Dirac function, when \(x=y\), \({\delta (x,y)}=1\), otherwise, \({\delta (x,y)}=0\);\(map(p_{i})\) is a permutation mapping function, which maps the classification division \(p_{i}\) obtained by classification to the equivalent real label. In addition, the value ranges of Acc being [0, 1]. The greater the classification accuracy, the better the classification effect.

b. Recall: refers to the ratio of the number of samples correctly identified as this category to the total number of samples belonging to this category in the original sample set. The specific definition is as following:

$$\begin{aligned} \begin{array}{c} Recall=\frac{n_{k}^{m}}{n_{m}} \end{array} \end{aligned}$$
(33)

where \(n_{k}^{m}\) represents the number of data objects shared by the kth class in the classification result and the mth class in the real classification result, \(n_{m}\) represents the number of data objects in the mth class in the real classification result. The larger the value of the Recall, the better the classification effect.

Tables 2 and 3 show the best accuracy and recall rate of each method respectively, bold values are shows that the classification ability of corresponding classifier performs the best among all comparative classifier. There are also corresponding standard deviations in brackets in the table. Note that in the competitive method, the best value for each dataset is expressed in bold.

Table 2 Accuracy on different datasets
Full size table
Table 3 Recall on different datasets
Full size table

We draw the results of Tables 2 and  3 into the histogram of Figs. 2 and 3, which can more clearly compare the performance of several algorithms.

Fig. 2
figure 2

Average accuracy of different algorithms

Full size image
Fig. 3
figure 3

Average recall of different algorithms

Full size image

5 Discussion

5.1 Analysis of Experimental Results

The experimental results in Tables 2 and 3 clearly illustrate that our proposed VKNN is almost as effective as the other five competitive methods in these real UCI datasets. The average classification accuracy of the VKNN algorithm is higher than that of the other five classification algorithms on the 12 datasets in Table 2. The classification accuracy of this algorithm for sonar dataset is 81.61\(\%\), which is lower than 83.03\(\%\) of DC-LAKNN algorithm, the difference is 1.42, but still better than 80.30\(\%\) of KNN, 81.06\(\%\) of LMKNN and 80.38\(\%\) of LMPNN, and the difference is acceptable. In addition, in the glass dataset, the accuracy of VKNN is lower than that of LMO-GAKNN, but it is significantly higher than that of the other four compared algorithms. However, in terms of classification accuracy, the comparison between competing classifiers is not statistically convincing. Here, we further use recall to compare the performance of classifiers. It can be seen from Table  3 that the recall rate of 10 datasets is significantly better than that of other algorithms. Especially in the sonar dataset, the recall rate of VKNN algorithm is the lowest, which is 86.20\(\%\). The difference between VKNN algorithm and the other four algorithms is 1.18\(\%\), 6.63\(\%\), 1.98\(\%\) and 1.42\(\%\) respectively, and the difference between VKNN algorithm and LMKNN algorithm is the largest. In the wrd dataset, the recall rate of VKNN is 50.11\(\%\), significantly higher than 45.11\(\%\) of KNN, but also lower than 58.01\(\%\) of LMKNN, 53.83\(\%\) of LMPNN, 54.26\(\%\) of LMO-GAKNN and 52.12\(\%\) of DC-LAKNN. In general, the average of the two evaluation indexes of the algorithm in 12 datasets is significantly better than the other three algorithms, indicating that the algorithm improves the classification performance on the whole. This also means that our algorithm can be better applied to data classification (Table 4).

5.2 Algorithm Complexity Analysis

In the process of classifier design, complexity can be used as an index to evaluate the classifier. Suppose the size of the dataset is n, the data dimension is d, the number of nearest neighbors is k, the number of found nearest neighbors is r, the number of categories is c, \(num_{1st}^{k}\) and \(num_{2nd}^{k}\) are the number of the majority classes and second majority classes, respectively. The complexity of several comparison algorithms used in the experiment is as follows:

(1) KNN: In reference [32], we can clearly get that the complexity of KNN and WKNN are \(O(nd+nk+k)\) and \(O(nd+nk+2k)\).

(2) LMKNN: The complexity of LMKNN algorithm comes from four aspects: (a) calculate the distance from the test sample to each class, and the complexity is \(O(n_{1}d+n_{2}d+\cdots +n_{c}d)\); (b)find k-nearest neighbors from each class, the complexity is \(O(n_{1}k+n_{2}k+\cdots +n_{c}k)\); (c) calculate the local average vector of k-nearest neighbors in each class, then the complexity of this step is O(ckd);(d) assign the samples to be classified to the class with the nearest local average vector, and the complexity is \(O(cd+c)\). Therefore, in general, the complexity of LMKNN is \(O(nd+nk+ckd+cd+c)\).

(3) LMPNN: On the basis of LMKNN algorithm, calculate the distance from the test sample to each class, and find k-nearest neighbors from each class, then the complexity is \(O(nd+nk)\). The other three complexities come from the following three aspects: (a) calculate k local average vectors corresponding to k-nearest neighbors, and calculate the distance between the sample to be tested and k local average vectors, the complexity is O(2ckd); (b) the weight is assigned to the local mean vector of each class to find out the pseudo-nearest neighbor of each class, the complexity is O(3ck); (c) determine the type of sample to be tested, with a complexity of O(c). Therefore, in general, the complexity of LMPNN is \(O(nd+nk+2ckd+3ck+c)\).

(4) LMO-GAKNN: In reference [33], we can clearly get that LMO-GAKNN can be summarized into three aspects. Therefore, the time complexity of the algorithm can be summarized as: \(O(nk+2Mr)\).

(5) DC-LAKNN: According to the discussion in reference [11], we can accurately obtain that the complexity of DC-LAKNN can be summarized as: \(O(num_{1st}^{k}+num_{2nd}^{k}+k_{max})\).

(6) VKNN: The steps of VKNN algorithm can be summarized into two aspects: (a) according to sample center, calculate the global variance between the sample point to be tested and the sample center of each category; (b) classify the sample to be tested into the class. Then, the complexity of VKNN is \(O({n^2}+cd)\).

By analyzing the complexity of the above algorithms, it is not difficult to see that the complexity of VKNN algorithm is greater than others. However, considering that the VKNN algorithm avoids the influence of k value, these increased calculations are acceptable.

Table 4 Abbreviations
Full size table

6 Conclusion

In this paper, we propose a non-parametric nearest neighbor classifier to solve the problem that KNN classifier depends on nearest neighbor measurement and is sensitive to k-value selection. Distinct from the aforementioned improved methods, in the existing improved algorithms, the nearest neighbor of each test sample is typically selected by the traditional distance measurement, which will drastically reduce the effect of classification. The improved method of this paper is to introduce variance, divide the difference between the variance before and after additional samples, take the minimum value of the result as the objective function, and determine the rules of the algorithm by optimizing the objective function for classification. It is also demonstrated here that the central sample point of each nearest neighbor class may be replaced by the mean value of all sample points within it. To some extent, the sensitivity of k-value selection and the influence of proximity have been solved. Finally, experimental results on 12 real datasets show that the improved algorithm overcomes the problems of k-value sensitivity and proximity measurement of KNN algorithm to a certain extent.

The advantages of VKNN algorithm is that its classification rules do not involve k-value and other parameters, effectively avoiding the influence of k-value and other parameters on the classification effect. Furthermore, the traditional Euclidean distance formula is not used to select the nearest neighbor set in the dissimilarity measurement of VKNN, but rather a global variance difference is introduced. Thus, it avoids to an extent the impact of k value and the nearest neighbor measurements on the classification performance, compared to other improved classification algorithms based on KNN.

However, as the algorithm complexity analysis in 5.2 shows, the time complexity of VKNN algorithm is relatively complex. In the next step, the proposed algorithm must be applied to complex practical problems. It is necessary to reduce the algorithm complexity without reducing the accuracy of the algorithm on the basis of existing algorithms. In addition, the most important thing of the classifier is to use and practice. How to combine the classifier with the actual situation, and what kind of dataset is applicable to, are also issues we need to consider in the future.