1 Introduction

A permanent magnet synchronous machine (PMSM) has the advantages of a high efficiency and a high power density, which is suitable for many industrial applications [1, 2]. To achieve a reliable startup of a PMSM with the sensorless control method, the main motor parameters should be obtained including the initial rotor position, the d-q axis inductances, and the winding resistances. The initial rotor position is used for field-oriented control. The parameter design of the controller and observer can be realized according to the inductances and resistances. High-frequency (HF) voltage signal injection is the conventional method for estimating the rotor position and d-q axis inductances at standstill, including the HF rotating signal injection method and the HF pulsating signal injection method [3,4,5].

The rotor position can be obtained from measured HF signals utilizing the mechanical or magnetic saturation saliencies. To solve the defects of conventional methods such as complicated signal demodulation and HF noise, many improved methods have been proposed in the past decade. In [6], a discrete Fourier transform is adopted for detecting the rotor sector so the time of initial position estimation is only half of an injection cycle. In [7], a conventional band-pass filter is substituted for an all-pass filter to eliminate the phase lag of the HF signal demodulation process. In [8], a pseudorandom HF square wave voltage was used for suppressing HF noise.

Keeping the rotor stationary is critical for initial rotor position estimation. Thus, the injected HF signal should have a low amplitude to mitigate the additional torque caused by the injected signal. However, inverter nonlinearity, especially dead-time and ZCC effects, can result in additional current harmonics, output voltage vector variations, and distortion of the injected signal [9,10,11]. At low and zero speeds, inverter nonlinearity has a severe influence on parameter estimations [12]. In [13], the inverter nonlinearity effects on HF signal injection were investigated, and voltage error and harmonic current are described. In [14], adaptive linear neurons were adopted for estimating and suppressing current harmonics with inverter nonlinearity. In [15], a vectorial disturbance estimator was proposed to estimate and compensate the voltage vector variation. In [16], voltages in a trapezoidal form were utilized to compensate for inverter nonlinearity.

Although many conventional HF signal injection methods have been used for estimating rotor position and inductances, their analyses of dead-time effect are insufficient, especially the ZCC effect. In the conventional methods, the output voltage variation caused by dead-time is considered to be a constant, which is incorrect under low amplitude HF excitation. In this paper, a method for simultaneously estimating initial rotor position and inductances was proposed based on HF pulsating voltage signal injection using the ZCC effect under the condition of low-amplitude HF excitation and a severe dead-time.

The remainder of this paper is organized as follows. Dead-time and ZCC effects are both analyzed in detail in Sect. 2. A method for initial rotor position and d-q axis inductance estimations is derived in Sect. 3. In Sect. 4, a PMSM driven experimental system is built and tested to verify the proposed method. Although many advanced algorithms have been proposed for parameter estimations or for reducing dead-time effect, the method proposed in this paper can avoid complex signal demodulation and observer design processes. In addition, it can obtain the initial rotor position and inductances easily.

2 Dead-time effect analysis

2.1 Asymmetric currents caused by dead-time

Figure 1 shows a diagram of a three-phase voltage source inverter (VSI) with PMSM. Udc is the DC bus voltage. Sa+, Sa−, Sb+, Sb−, Sc+, and Sc− are the A, B, and C phase upper and lower arm driving signals of the power switches, respectively. The phase current direction shown in Fig. 1 denotes that the current polarity is positive. According to the space vector pulse width modulation (SVPWM), the non-zero basic space voltage vectors and the corresponding switching states (Sa+, Sb+, Sc+) are shown in Fig. 2. The amplitudes of these basic space voltage vectors are the same, 2Udc/3, except for the zero vectors ‘000’ and ‘111’.

Fig. 1
figure 1

Three-phase voltage source inverter

Full size image
Fig. 2
figure 2

Basic voltage vectors based on SVPWM

Full size image

The inverter switching period is recorded as Ts. Meanwhile, the three-phase currents are sampled at the beginning of each switching period. The injected voltage signal is a pulsating square wave signal, where the amplitude and period are set as Uo and 4Ts, respectively. According to the SVPWM, the resultant output voltage vectors consist of U3, U4 and zero vectors when the direction of the HF voltage signal injection is ‘a’, as shown in Fig. 2. Furthermore, the power switches of the B and C phases operate at the same duty ratio. If two-phase power switches operate at the same duty ratio, the same HF voltage signals are injected. Moreover, the resistive voltage drop can be neglected in comparison with the inductive voltage drop under HF signal excitation. Therefore, their currents have the same frequencies and phases and cross the zero level simultaneously in the steady state. For the Y-connected windings of the PMSM, if the two-phase currents are zero, the third phase current is also zero. Therefore, the three-phase currents simultaneously cross the zero level, which is essential for the analysis of the dead-time effect. Figure 3 shows simulations of the reference voltage and the corresponding steady-state three-phase currents (Ts is 0.1 ms). The reference voltage is given in Fig. 3a and it produces symmetric steady-state currents as shown in Fig. 3b without dead-time. In practice, dead-time can distort actual voltage and cause asymmetric steady-state currents, as shown in Fig. 3c.

Fig. 3
figure 3

Reference voltage and corresponding steady-state three-phase currents under a 10 kHz switching frequency: a reference voltage; b three-phase currents without dead-time; c three-phase currents with dead-time

Full size image

2.2 Dead-time effect analysis with different HF voltage amplitudes

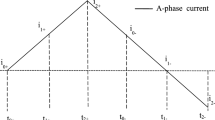
The phase A current is taken as an example to analyze the dead-time effect on an injected signal. Its waveform in an injected signal period is detailed in Fig. 4, where T1-T5 is one injected signal period including four switching periods: T1−T2, T2−T3, T3−T4, and T4−T5. It can be seen that the phase A current crosses the zero level at T1* and T2*. I−, i−, i+, and I+ are the sampling values of the phase A current at T1, T2, T3, and T4, respectively.

Fig. 4
figure 4

Phase A current in an injected signal period

Full size image

During T1-T2 or T2-T3, the reference voltage amplitude is Uo. Ta, Tb, and Tc are the conducting times of the power switches of the A, B, and C phase upper arms, respectively. Ta, and Tb can be expressed according to SVPWM algorithm as:

$$\left\{ \begin{gathered} T_{a} = \frac{1}{2}(1 + \frac{{3U_{o} }}{{2U_{dc} }})T_{s} \hfill \\ T_{b} = T_{c} = \frac{1}{2}(1 - \frac{{3U_{o} }}{{2U_{dc} }})T_{s} \hfill \\ \end{gathered} \right.$$
(1)

According to the different switching states of the inverter, every switching period can be divided into nine intervals noted as tk (k = 1, 2, …, 9), as shown in Fig. 5.

Fig. 5
figure 5

Nine switching states in a switching period

Full size image

The dead-time effect on the reference voltage is mainly related to the three-phase current polarities. Since the power switches of phases B and C operate at the same duty ratio, the three-phase current polarities have three possible states: (a) ia > 0, ib < 0, ic < 0; (b) ia < 0, ib > 0, ic > 0; and (c) ia = ib = ic = 0. Figure 6 shows the phase A current during the dead-time. The lower arm can be considered to turn on when ia > 0, and the upper arm can be considered to turn on when ia < 0. If the phase A current crosses the zero level during the dead time, it clamps to zero and remain at the zero level until the switching states change, which is the ZCC effect. The phase B and C currents are similar to the phase A current. In regard to the different current polarities and switching states, the basic voltage vector corresponding to each interval tk is recorded as uk. Table 1 lists tk and uk, where ‘0’ denotes the zero vector and Td denotes the dead-time. The basic voltage vector is derived from Fig. 5. For example, at t3, Sa+ = 1, Sb+ = 0, and Sc+ = 0. Thus, the voltage vector is U4 (100). In the dead-time, according to Fig. 6, Sa+ = 0(ia > 0 or ia = 0), Sa+ = 1(ia < 0). The phase B and phase C currents are similar to those of phase A.

Fig. 6
figure 6

Phase A current during dead-time

Full size image
Table 1 Output basic voltage vectors in a switching period
Full size table

It can be found from Table 1 that the resultant voltage vector still consists of U4 and zero vectors even though the dead-time has already led to a distortion. It states that the dead-time is unable to change the voltage vector direction in this case. Consequently, U4 can be substituted by its amplitude 2Udc/3 to calculate the resultant voltage vector. During T2-T3, the phase A current polarity is positive. According to Table 1, the resultant voltage amplitude Uavg in a switching period can be expressed as:

$$U_{avg} = \sum\limits_{k = 1}^{9} {\frac{{t_{k} }}{{T_{s} }}} u_{k} = \frac{{T_{a} - T_{b} - 2T_{d} }}{{T_{s} }} \cdot \frac{2}{3}U_{dc}$$
(2)

By submitting (1) into (2), the distorted voltage drop Uerr can be obtained as:

$$U_{err} = U_{o} - U_{avg} = \frac{{T_{d} }}{{T_{s} }} \cdot \frac{4}{3}U_{dc}$$
(3)

This indicates that Uerr is actually independent of Uo. During the time period T1-T2, the polarities of the three-phase currents are changed. From Fig. 4, under the assumption that the variations of inductance and resistance are neglected, I− (ia < 0) and I+ (ia > 0) can be expressed as:

$$\left\{ {\begin{array}{*{20}l} { - L_{a} \frac{{I^{ - } }}{{T_{s} }} = \sum\limits_{k = 1}^{j - 1} {\frac{{t_{k} }}{{T_{s} }}u_{k} + \frac{{t_{j} - t_{x} }}{{T_{s} }}u_{j} } } \hfill \\ {L_{a} \frac{{I^{ + } }}{{T_{s} }} = U_{o} - U_{err} + \sum\limits_{k = j + 1}^{9} {\frac{{t_{k} }}{{T_{s} }}u_{k} + \frac{{t_{x} }}{{T_{s} }}u_{j} } } \hfill \\ {0 < t_{x} < t_{j} } \hfill \\ \end{array} } \right.$$
(4)

where tj (j = 2, 3, 4, 6, 7) is one of nine intervals shown in Fig. 5. During this interval, the phase A current crosses the zero level. In addition, ia < 0 during tj–tx, and ia = 0 or ia > 0 during tx. La is the phase A inductance, which is a constant value at standstill. Since the average value of the HF voltage signal is zero in each injected signal cycle, the relationship between I− and I+ can be described as:

$$I^{ + } + I^{ - } = 0$$
(5)

In addition, i+ in Fig. 4 can be expressed as:

$$L_{a} \frac{{i^{ + } }}{{T_{s} }} = \sum\limits_{k = j + 1}^{9} {\frac{{t_{k} }}{{T_{s} }}u_{k} + \frac{{t_{x} }}{{T_{s} }}u_{j} }$$
(6)

According to (4–6), Uo and i+ can be derived corresponding to different values of j and shown in Table 2.

Table 2 Relationship between Uo and i+
Full size table

where r is defined as Uo/Uerr for the sake of simplicity. Due to symmetry, the analytical methods and results during T3−T5 are similar to those during T1−T3.

In fact, the phase A current shown in Fig. 4 corresponds to r > 2.5. Figure 7 shows the phase A current when 1.25 < r < 1.5. In Fig. 4 and Fig. 7, both of the currents do not clamp to the zero level. Figure 8 shows the phase A current when 1.5 < r < 2.5. It is evident that the phase A current clamps to zero during T1*−T3* and T2*−T4*. This operating state is used for realizing the parameter estimation.

Fig. 7
figure 7

Phase A current when 1.25 < r < 1.5

Full size image
Fig. 8
figure 8

Phase A current when 1.5 < r < 2.5

Full size image

Obviously, dead-time is a main factor that leads to inverter nonlinearity. In addition, the threshold voltages of the active switch, the freewheeling diode, and the turn-on and turn-off time delays of the switch incur signal distortions. The variation of the output voltage amplitude caused by inverter nonlinearity can be measured more accurately through a simple experiment. The inverter generates a constant voltage vector that is equal to the DC voltage, which has the same direction along with U4. This means that the phase A upper arm turns on, and the phase B and phase C lower arms turn on while the inverter outputs non-zero voltage. An equivalent circuit of this simple experiment is shown in Fig. 9. Here, La, Lb, and Lc are the three-phase inductances, Rs is the phase resistance, and iavg is the steady-state average current of phase A.

Fig. 9
figure 9

Equivalent circuit measuring the variation of the output voltage amplitude caused by inverter nonlinearity

Full size image

In the steady-state, the inductive average voltage drop is zero. The relationship between the output voltage Uo and the steady-state phase A average current iavg can be obtained as:

$$U_{o} = 1.5R_{s} i_{avg} + U_{err}$$
(7)

The least-square method can be adopted for fitting different values of Uo and iavg. The slope of the fitting line is 1.5Rs and its intercept is Uerr.

3 Initial rotor position and inductance estimations

As discussed in Sect. 2, the relationship between the HF voltage amplitude and the dead-time effect as well as a sufficient condition for the ZCC effect are presented, based on which a parameter estimation method is used. The voltage equations of a PMSM at a standstill and the HF excitation in the d-q frame can be expressed as:

$$\left\{ \begin{gathered} u_{d} = R_{h} i_{d} + L_{d} \frac{{di_{d} }}{dt} \hfill \\ u_{q} = R_{h} i_{q} + L_{q} \frac{{di_{q} }}{dt} \hfill \\ \end{gathered} \right.$$
(8)

where ud and uq are the d-q axis voltages. id and iq are the d-q axis currents. Ld and Lq are the d-q axis inductances. Rh is the HF resistance. Generally, Ld\(\le\) Lqfor a PMSM.

According to (8), the d-axis voltage equation in the time domain can be obtained as:

$$i_{de} = i_{ds} e^{ - \lambda } + \frac{{u_{d} }}{{R_{h} }}(1 - e^{ - \lambda } )$$
(9)

where ids and ide are the values of the d-axis current at the beginning and end moments of the d-axis voltage pulse, respectively. λ is ThRh/Ld and Th is the duration during which the currents are not zero. Since HF resistance causes current amplitude attenuation, the HF resistance has less influence on the d-axis current with a shorter Th. Δid denotes the variation of the d-axis current and can be calculated as:

$$\Delta i_{d} = i_{de} - i_{ds} = \frac{{u_{d} - R_{h} i_{ds} }}{{R_{h} }}(1 - e^{ - \lambda } )$$
(10)

Similarly, Δiq denotes the variation of the q-axis current and can be calculated as:

$$\Delta i_{q} = \frac{{u_{q} - R_{h} i_{qs} }}{{R_{h} }}(1 - e^{ - \eta } )$$
(11)

where iqs is the value of the q-axis current at the beginning of a voltage pulse and η is ThRh/Lq.

As previously mentioned, the range of r should be set to 1.5–2.5 to utilize the ZCC effect, and the phase A current is shown in Fig. 8. Δia+ denotes the variation of the phase A current during T3*−T2, where Δia+ = i+. From Table 1, the interval corresponding to U4 is t7, and the intervals corresponding to the zero vectors are t8 and t9. Therefore, Th can be expressed as:

$$T_{h} = t_{7} + t_{8} + t_{9} = \frac{1}{2}(T_{s} - T_{b} - T_{d} )$$
(12)

By submitting (1) and (3) into (12), Th can be rewritten as:

$$T_{h} = \left( {\frac{{U_{o} }}{{2U_{{err}} }} - \frac{1}{2}} \right)T_{d} + \frac{1}{4}T_{s} = \frac{{r - 1}}{2}T_{d} + \frac{1}{4}T_{s}$$
(13)

Since the range of r is 1.5–2.5, the maximum value of Th is 0. 75Td + 0.25Ts. Generally, the dead-time Td is very short. Thus, Th is also very short and is about a quarter of a switching period. The average output voltage Uh corresponding to Th can be obtained as:

$$U_{h} = \frac{{t_{7} }}{{T_{h} }} \cdot \frac{2}{3}U_{dc}$$
(14)

Utilizing the Taylor series for linearization, e−λ and e−η can be expressed as:

$$\left\{ \begin{gathered} e^{ - \lambda } = 1 - \lambda + o(\lambda^{2} ) \approx 1 - \lambda \hfill \\ e^{ - \eta } = 1 - \eta + o(\eta^{2} ) \approx 1 - \eta \hfill \\ \end{gathered} \right.$$
(15)

where o(λ2) and o(η2) are the second-order errors with respect to the extremely short Th, which can be neglected. Since the currents clamp to zero during T1*−T3*, ids and iqs are equal to zero.

$$i_{ds} = i_{qs} = 0$$
(16)

Since the direction of the HF voltage signal injection is ‘a’ in the three-phase frame, the equations of the coordinate transformation can be expressed as:

$$\left\{ \begin{gathered} u_{d} = U_{h} \cos \theta_{a} \hfill \\ u_{q} = - U_{h} \sin \theta_{a} \hfill \\ \Delta i_{a}^{ + } = \Delta i_{d} \cos \theta_{a} - \Delta i_{q} \sin \theta_{a} \hfill \\ \end{gathered} \right.$$
(17)

where θa is the electrical angle between the a-axis and the d-axis. According to (10) through (17), Δia+ can be derived as:

$$\frac{{\Delta i_{a}^{ + } }}{{U_{h} T_{h} }} = \frac{{\cos^{2} \theta_{a} }}{{L_{d}^{ + } }} + \frac{{\sin^{2} \theta_{a} }}{{L_{q}^{ + } }}$$
(18)

where Ld+ and Lq+ are the d-q axis inductances during T3*−T2, which are defined as:

$$\left\{ {\begin{array}{*{20}c} {L_{d}^{ + } = \frac{{\Delta \psi_{d} }}{{\Delta i_{d} }}} \\ {L_{q}^{ + } = \frac{{\Delta \psi_{q} }}{{\Delta i_{q} }}} \\ \end{array} } \right.$$
(19)

where Δid and Δiq are variations of the d-q axis currents, while Δψd and Δψq are variations of the d-q axis flux linkages during T3*−T2. It is worth mentioning that Rh is absent from (18), which means that the HF resistance caused by variation of the current is a second-order error and can be neglected. By substituting (1) and (3) into (18), Δia+ can be rewritten as:

$$\frac{{2\Delta i_{a}^{ + } }}{{(U_{o} - U_{err} )T_{s} }} = \frac{{\cos^{2} \theta_{a} }}{{L_{d}^{ + } }} + \frac{{\sin^{2} \theta_{a} }}{{L_{q}^{ + } }}$$
(20)

Similarly, during T4*−T4, Δia− denotes the variation of the phase A current, where Δia− = i−. The average output voltage is − Uh, and Δia− can be derived as:

$$\frac{{2\Delta i_{a}^{ - } }}{{(U_{o} - U_{err} )T_{s} }} = - \frac{{\cos^{2} \theta_{a} }}{{L_{d}^{ - } }} - \frac{{\sin^{2} \theta_{a} }}{{L_{q}^{ - } }}$$
(21)

where Ld− and Lq− are the d-q axis inductances during T4*-T4.

Magnetic saturation results in a slight variation of the inductance under a low-amplitude injected current. Nevertheless, the d-axis inductance gets greater when id < 0, and it gets smaller when id > 0. For simplified analyses, the average value of Ld− and Ld+ can be considered to be almost constant, and the q-axis inductance is analyzed similarly, which can be expressed as:

$$\left\{ \begin{gathered} \frac{2}{{L_{d} }} \approx \frac{1}{{L_{d}^{ + } }} + \frac{1}{{L_{d}^{ - } }} \hfill \\ \frac{2}{{L_{q} }} \approx \frac{1}{{L_{q}^{ + } }} + \frac{1}{{L_{q}^{ - } }} \hfill \\ \end{gathered} \right.$$
(22)

From (18) to (22), in order to reduce the influence of magnetic saturation on the inductances and to eliminate the DC component of the HF current, Ka is defined as:

$$K_{a} = 2\frac{{\Delta i_{a}^{ + } - \Delta i_{a}^{ - } }}{{(U_{o} - U_{err} )T_{s} }} = \frac{{2\cos^{2} \theta_{a} }}{{L_{d} }} + \frac{{2\sin^{2} \theta_{a} }}{{L_{q} }}$$
(23)

Correspondingly, when the directions of the HF voltage signal injection are ‘b’ or ‘c’, as shown in Fig. 2, Kb and Kc are defined as:

$$\left\{ \begin{gathered} K_{b} = 2\frac{{\Delta i_{b}^{ + } - \Delta i_{b}^{ - } }}{{(U_{o} - U_{err} )T_{s} }} = \frac{{2\cos^{2} \theta_{b} }}{{L_{d} }} + \frac{{2\sin^{2} \theta_{b} }}{{L_{q} }} \hfill \\ K_{c} = 2\frac{{\Delta i_{c}^{ + } - \Delta i_{c}^{ - } }}{{(U_{o} - U_{err} )T_{s} }} = \frac{{2\cos^{2} \theta_{c} }}{{L_{d} }} + \frac{{2\sin^{2} \theta_{c} }}{{L_{q} }} \hfill \\ \end{gathered} \right.$$
(24)

where Δib+ and Δib− are variations of the phase B currents corresponding to the average output voltages Uh and − Uh, when the direction of the HF voltage signal injection is ‘b’. In addition, Δic+ and Δic− are variations of the phase C currents corresponding to the average output voltages Uh and − Uh, when the direction of the HF voltage signal injection is ‘c’.

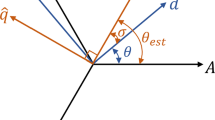
The estimated initial rotor position is defined as θa. From Fig. 2, θb and θc can be expressed as:

$$\left\{ \begin{gathered} \theta_{b} = \theta_{a} - \frac{2}{3}\pi \hfill \\ \theta_{c} = \theta_{a} - \frac{4}{3}\pi \hfill \\ \end{gathered} \right.$$
(25)

According to (23) through (25), the solutions of the equations are:

$$\left\{ {\begin{array}{*{20}l} {M_{1} = \frac{1}{3}(K_{a} + K_{b} + K_{c} ) = \frac{1}{{L_{d} }} + \frac{1}{{L_{q} }}} \hfill \\ {M_{2} = \frac{\sqrt 3 }{3}(K_{c} - K_{b} ) = (\frac{1}{{L_{d} }} - \frac{1}{{L_{q} }})\sin 2\theta_{a} } \hfill \\ {M_{3} = \frac{1}{3}(2K_{a} - K_{b} - K_{c} ) = (\frac{1}{{L_{d} }} - \frac{1}{{L_{q} }})\cos 2\theta_{a} } \hfill \\ \end{array} } \right.$$
(26)

Here, Ld, Lq, and θa can be obtained as:

$$\left\{ \begin{gathered} L_{d} = \frac{2}{{M_{1} + \sqrt {M_{2}^{2} + M_{3}^{2} } }} \hfill \\ L_{q} = \frac{2}{{M_{1} - \sqrt {M_{2}^{2} + M_{3}^{2} } }} \hfill \\ \theta_{a} = \frac{1}{2}\arctan \frac{{M_{2} }}{{M_{3} }} \hfill \\ \end{gathered} \right.$$
(27)

Twice the estimated rotor angle in (26) leads to ambiguity of the magnetic polarity, which means that the position estimation error can be either 0 or π. To clear up this ambiguity, magnetic polarity identification utilizing a short pulse is applied and introduced in Sect. 4.

From (20) and (21), there is a linear relationship between the output voltage amplitude Uo and the current variation Δi. To further reduce the estimation error, the least square method is applied to fitting Uo and Δi. Therefore, Δia+, Δia−, and Ka can be rewritten as:

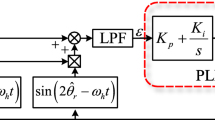
$$\left\{ {\begin{array}{*{20}c} {\Delta i_{a}^{ + } = k_{a}^{ + } U_{o} + b_{a}^{ + } } \\ {\Delta i_{a}^{ - } = k_{a}^{ - } U_{o} + b_{a}^{ - } } \\ {K_{a} = 2\frac{{k_{a}^{ + } - k_{a}^{ - } }}{{T_{s} }}} \\ \end{array} } \right.$$
(28)

where ka+ and ka− are the slopes of the fitting lines, and ba+ and ba− are the intercepts of the fitting lines. Kb and Kc are similar to Ka. It is worth mentioning that Uerr is absent from (28), which means Uerr has no impact on the estimation accuracy when using the least square method. Thus, an accurate value of Uerr is unnecessary. An overall control block diagram of the parameter estimation method is shown in Fig. 10.

Fig. 10
figure 10

Control block diagram of the parameter estimation method

Full size image

4 Experimental results

Figure 11 shows a PMSM driven experimental platform, where the main parameters are shown in Table 3. A PS21865 intelligent power module (IPM) is used for the VSI, and a TMS320F28335 digital signal processor (DSP) is used for the controller.

Fig. 11
figure 11

PMSM driven experimental platform

Full size image
Table 3 PMSM driven experimental system parameters
Full size table

The DC bus voltage Udc, the phase A current ia, and the phase B current ib are sampled at the beginning moment of each switching period. The phase C current ic is equal to –(ia + ib) due to the Y-connected windings of the PMSM. According to (7), Fig. 12 shows the data of Uo and iavg and their fitting line Uo = 0.76Rs + 15. From experimental results, Rs is 0.51 \(\Omega\) and Uerr is 15 V. According to (3), Uerr should be 16.6 V. This error is due to the fact that the other factors that led to inverter nonlinearity are neglected in (3). Nevertheless, the error is not significant which means the dead-time is the main factor causing inverter nonlinearity.

Fig. 12
figure 12

Data of Uo and iavg and their fitting line

Full size image

When the direction of the HF voltage signal injection is ‘a’, Fig. 13 shows the phase A and B steady-state currents under different HF voltages. Figure 13a depicts the currents corresponding to Fig. 4 when r is greater than 2.5 and Uo is set to 50 V. Figure 13b shows the currents corresponding to Fig. 7 when the range of r is 1.25–1.5 and Uo is set to 19 V. Figure 13c shows the currents corresponding to Fig. 8 when the range of r is 1.5–2.5 and Uo is set to 28 V. As can be seen from Fig. 13, there are different phenomena corresponding to the different r ranges when the currents cross the zero level. It is evident that currents clamp to the zero level in Fig. 13c.

Fig. 13
figure 13

Phase A and phase B current waveforms under different HF voltages: a Uo = 50 V; b Uo = 19 V; c Uo = 28 V

Full size image

Figure 14 illustrates the relationship between the HF voltage amplitude Uo and the phase A current i+ in Table 2. There are 14 sampling points in the different r ranges. The corresponding phase B current also is shown in Fig. 14. When Uo is 19–22.5 V (r is 1.25–1.5), the currents are almost constant. When Uo is 22.5–37.5 V (r is 1.5–2.5), the currents increase linearly with Uo. When Uo is greater than 37.5 V (r is greater than 2.5), the currents slowly increase due to the inductance decrease caused by magnetic saturation.

Fig. 14
figure 14

Phase A and phase B current values after the currents cross the zero level

Full size image

From Fig. 14, the range of the HF voltage amplitude should be set to 27–35 V to utilize the ZCC effect and to obtain the linear relationship. Figure 15 illustrates the HF voltage amplitude Uo and the current variations Δi along with their least square method-based fitting lines under different directions of signal injection. The slopes of these fitting lines can be used for parameter estimation to improve accuracy. The duration of the injected HF signal is 50 ms. For the first 20 ms, the steady-state is achieved and then 150 data points of Δi+ and Δi− are sampled for the rest of the time. The values of Δi+ and Δi− in Fig. 15 are the average values of these 150 data points.

Fig. 15
figure 15

Relationship between the HF voltage amplitude Uo and the current variation Δi along with their fitting lines

Full size image

From (27), θa is the estimated rotor position, and the method of magnetic polarity identification is given as follows. When three-phase currents are zero, the inverter outputs a high-amplitude voltage vector in the θa direction in a switching period. At the end of the switching period, the d-axis current is sampled. Similarly, the inverter outputs a voltage vector with the same amplitude in the θa + π direction, and the d-axis current is likewise sampled at the end of the switching period. Figure 16 shows the d-axis currents when the short voltage pulse amplitude is 105 V. For ease of comparison, two periods of generating voltage pulses are overlapped. The d-axis current in the positive d-axis is greater than the other one.

Fig. 16
figure 16

d-axis currents of the magnetic polarity identification

Full size image

The initial rotor position and the d-q axis inductances are estimated using the least square method according to (28). The HF voltage amplitude is the same as the voltage amplitude in Fig. 15. In the conventional method, the output voltage variation caused by the dead-time effect is considered to be constant, and its amplitude is equal to Uerr. According to the analysis in this paper, its amplitude relates to the amplitude of the output voltage. The rotor position estimation error θerr and the estimated d-q axis inductances Ld and Lq are depicted in Fig. 17. There are two experimental results for the conventional methods in Fig. 17. The first is to use the same HF injected signal as the new method, the second is to use a high amplitude HF injected signal. In the experiment with high amplitude HF signal injection, the rotor is fixed to remain stationary. From Fig. 17, under low amplitude HF excitation, the estimation error of the conventional method is greater than the new method since the voltage variation caused by the dead-time effect is incorrect. By increasing the amplitude of the output voltage, the dead-time effect can be mitigated. However, high amplitude current can cause the rotor to rotate. Thus, the rotor has to be fixed. Moreover, high amplitude current can cause serious magnetic saturation. Thus, the estimation values of the inductances are smaller than the actual values.

Fig. 17
figure 17

Estimation results of the conventional method and the proposed method: a rotor position estimation error; b estimation value of the d-axis inductance; c estimation value of the q-axis inductance

Full size image

The experimental results of the new method are shown in detail in Fig. 18. The average error of θerr is 2.0 \(^\circ\). The maximum error of θerr is 5.6 \(^\circ\). The average estimations of Ld and Lq are 1.33mH and 1.68mH, respectively. Their maximum relative errors are 6.1% and 7.9%. In addition, the average values are 1.6% and 2.8%. It can be seen from these experimental results that the proposed method can estimate the rotor position and the d-q axis inductances.

Fig. 18
figure 18

Error of the rotor position estimation and the estimated d-q axis inductances with the least square method

Full size image

5 Conclusion

In this paper, a method for initial rotor position and inductance estimations is proposed for the sensorless control of a PMSM by utilizing the ZCC effect. To simplify the analysis of the dead-time effect, a HF signal must be injected in the three-phase stationary reference frame and its period must be four times the switching period. The amplitude of the HF signal is only 1.5–2.5 times the voltage variation caused by the dead-time effect, which means the dead-time can cause severe distortion of the HF signal. Thus, the conventional method is unable to estimate the initial rotor position and inductances. The voltage variation caused by the dead-time effect is related to the power switches and the DC bus voltage. Generally, the dead-time of the power switches in a definite inverter is constant. Reducing the DC bus voltage means that maximum speed of the PMSM is reduced. However, in order to keep the rotor stationary, the injected HF signal should be a low amplitude and a severe dead-time effect cannot be avoided. The method proposed in this paper can solve this problem easily and without complexity in the signal demodulation process or observer design. It is worth mentioning that an accurate assessment of the voltage variation caused by the dead-time effect is unnecessary in this method. It is only used for determining the range of the HF voltage signal that can cause the ZCC effect. Thus, the proposed method is effective under different dead-time conditions. A longer dead-time means that the parameter estimation data can be sampled in a wider range of HF voltage signals, which is beneficial for improving the estimation accuracy. If the dead-time is short, the conventional method is simple and effective.