1 Introduction

A flywheel is the key inertial actuator for generating high precision control torque to realize the attitude stabilization and adjustment of spacecraft [1,2,3]. When compared with conventional ball bearing flywheels, magnetically suspended flywheels (MSFWs) have aroused widespread concern owing to the remarkable advantages of the no stiction-friction effect, long service life, high control precision, micro vibration, and so on [4, 5]. Depending on the rotor speed, the MSFWs can be divided into the magnetically suspended reaction flywheel [6], the magnetically suspended bias momentum wheel [7] and the magnetically suspended attitude control energy storage flywheel [8]. The angular momentum is changed, and the control torque is obtained for attitude stabilization when the rotor is accelerated or decelerated. However, the torque is too small to achieve the agile maneuvers of spacecraft in orbit. The instantaneous large procession torque of a magnetically suspended gimballing flywheel (MSGFW) is obtained when the rotor angular momentum direction is changed by means of a deflection magnetic bearing (MB) [9]. Thus, the MSGFW is suitable for spacecraft attitude maneuver control.

Two types of MBs, magnetic reluctance MB and Lorentz force-type magnetic bearing (LFMB) [10,11,12,13,14,15], can be used for the deflection control of a MSGFW. Murakami et al. [16] proposed an active–passive MSGFW. The passive MB is used for radial translation suspension, and the three-axis magnetic reluctance MB is adopted for axial translation control and radial deflection. Han et al. [17] presented an active–passive scheme with radial magnetic reluctance MBs for radial translation suspension. Axial translation suspension and radial deflection are realized by the passive MB. Seddon et al. [18] presented another active–passive MSGFW with a pair of radial magnetic reluctance MBs for radial translation and radial deflection control. The suspension precision of the active–passive MSGFW is relatively low due to the passive MB. Coupling between the passive axial suspension and the active deflection is unavoidable. To eliminate the interference torque, Wen et al. [19] introduced a 5 degree of freedoms (DOFs) MSGFW with a pair of radial magnetic reluctance MBs to realize radial deflection. To decrease the axial size of the MSGFW in [19], Tang et al. [20] developed another active MSGFW with a pair of axial magnetic resistance MBs for radial deflection and axial translation controls. Based on the comprehensive sensitivity and cross-factor variance, Jin et al. [21] presented a multi-objective design optimization to simultaneously optimize the radial and axial suspension force. Then, Diao et al. [22] and Sun et al. [23] proposed sequential subspace optimization methods to improve optimization efficiency. However, the deflection torque precision is limited due to magnetic reluctance MBs with nonlinear force. To remedy the limitation of magnetic reluctance MBs, an LFMB with good linearity and no displacement stiffness is adopted for deflection suspension [24]. Gerlach et al. [25] proposed a 5-DOF active scheme that relied on LFMBs. Concerning reference [25], Liu et al. [26] presented a similar 5-DOF active LFMB scheme, and its attitude control and attitude sensitivity were studied in detail.

The bearing capacity of the LFMB scheme for the MSGFW is insufficient during ground experiments. Combining the magnetic reluctance MB with high stiffness and the LFMB with good linearity, Li et al. [10] introduced a 4-DOF hybrid active–passive MSGFW scheme. The magnetic resistance MBs were utilized to realize radial translation and passive axial support, and the LFMB was adopted to achieve high-precision deflection control. To increase the suspension precision, Xiang et al. [11] proposed a 5-DOF active hybrid MSGFW with the conical magnetic resistance MB for 3-DOF translation and the LFMB for 2-DOF deflection. However, interference torque is generated due to the change of the air gap shape in [10, 11] when the rotor is tilted. Ren et al. [12], Liu et al. [13] and Xu et al. [14] presented a hybrid MSGFW with a spherical air gap for eliminating interference torque during rotor deflection.

The LFMB of the hybrid MSGFWs in [10,11,12] is the core component to output gyroscope moments by tilting the rotor at a high rated speed. The magnetic flux density of the conventional LFMBs in [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25] was relatively low due to the single-sided PMs. To increase the magnetic flux density, LFMBs with double-sided PMs were adopted in [11, 12]. Liu et al. [13] proposed a LFMB with double-sided trapezoidal PMs to reduce the magnetic flux leakage at the right-angle area of the rectangular PMs. The above magnetic flux density uniformity was poor due to PM rings with multiple arc PMs. Xu et al. [14] presented the LFMB with magnetic rings to suppress the magnetic flux leakage in the splicing gap. Based on the smoothing function of the magnetic rings for magnetic flux, Zhao et al. [15] proposed a LFMB with conventional double magnetic circuits, which combined the Halbach array PMs main circuit and the auxiliary magnetic circuit. Both the magnetic flux density and its uniformity were improved. However, the magnetomotive force of the Halbach array PMs is not fully utilized due to inconsistency between the magnetization direction and the magnetic vector.

In this paper, a LFMB with improved double magnetic circuits is presented to improve the PMs magnetomotive force efficiency. Inclined magnetization Halbach array PMs and trapezoidal PMs are combined to increase the magnetic flux density. A mathematical model of the magnetic flux density is established. The optimal magnetization angle is obtained, and the related dimension parameters are optimized. An LFMB prototype is developed and experiments on the magnetic flux density are carried out to verify its effectiveness.

2 MSGFW and LFMB

2.1 MSGFW structure and its working principle

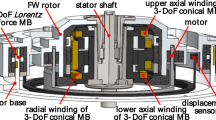
The configuration of a MSGFW is shown in Fig. 1. The MSGFW is mainly composed of a brushless DC motor, a sphere rotor, a pair of axial spherical magnetic resistance MBs, a single radial spherical magnetic resistance MB, the LFMB, eddy current displacement sensors and gyroscope houses. The sphere rotor with a rated speed of 9000 r/min is driven by the brushless DC motor. The radial and axial translations are realized by the radial and axial spherical MBs, respectively. The 2-DOF deflections are controlled by the LFMB. The eddy current displacement sensors are utilized to measure the rotor real-time position and attitude. The gyroscope houses are adopted to provide a vacuum environment.

Fig. 1
figure 1

Configuration of a MSGFW

Full size image

Gyroscope moment is generated when the sphere rotor with a rated speed of ω is tilted by the LFMB. The gyroscope moment M can be expressed as:

$${\varvec{M}} = J_{z} {\varvec{\omega}} \times{\varvec{\varOmega}},$$
(1)

where Jz is the rotary inertial momentum around the Z axis, and Ω is the sphere rotor procession angular velocity. The larger the deflection torque T, the faster the rotor procession, and the larger the gyroscope moment M. When the sphere rotor is tilted around the X axis with a deflection angle of α, the deflection torque Ty can be written as [15]:

$$T_{y} = NRBi\left[ \begin{gathered} 8\left( {1 - 2\sin^{2} \frac{\alpha }{2}} \right)\sin \beta + \frac{16}{3}\sin^{3} \beta \sin^{2} \frac{\alpha }{2} \\ 0 \\ 0 \\ \end{gathered} \right] = \left[ \begin{gathered} K_{i} i \\ 0 \\ 0 \\ \end{gathered} \right],$$
(2)

where N is the number of coil turns, R is the radius of the coils, B is the magnetic flux density, i is the control current in the LFMB coils, β is the half central angle of a single coil, and Ki is the current stiffness of the deflection torque. Similarly, the deflection torque Tx around the Y axis can be obtained. When the dimension parameters of the LFMB are constant, the current stiffness of the deflection torque is in proportion to the magnetic flux density of the LFMB. Therefore, the parameters related to the magnetic flux density are the objects to analyze.

2.2 Comparison between two LFMBs

The two schemes, an LFMB with conventional double magnetic circuits and an LFMB with the improved double magnetic circuits (IDMC), are shown in Fig. 2. The magnetic fluxes of the two schemes are composed of the main magnetic flux generated by Halbach array PMs (defined as Part-A) and the auxiliary magnetic flux produced by auxiliary PMs (defined as Part-B). The main magnetic fluxes plotted in black solid line are, respectively, generated by the conventional and the inclined magnetization Halbach array PMs defined as Part-A(I) and Part-A(II). The auxiliary magnetic fluxes plotted in black dash lines are generated by rectangular and trapezoidal PMs defined as Part-B(I) and Part-B(II), respectively. As shown in Fig. 2, most of the magnetic lines in the blue elliptical region of Part-A(I) are inconsistent with the magnetization direction, which results in low efficiency of the PMs. When compared with the LFMB with the conventional double magnetic circuits, in Part-A, the magnetization directions of the LFMB with the improved double magnetic circuits are consistent with the magnetic lines. Under the same dimensions, the magnetic flux density is improved and the efficiency of the PMs is higher. In Part-B, auxiliary trapezoidal PMs are adopted to replace the auxiliary rectangular PMs to improve the magnetic flux density.

Fig. 2
figure 2

Two LFMB schemes

Full size image

The magnetic flux densities simulated by the finite element method are shown in Fig. 3. In Fig. 3a, the maximum magnetic flux densities generated by Part-A(I) and Part-A(II) are 0.528 T and 0.543 T. When the magnetomotive force strengthens with an increase of the magnetizing length, the magnetic flux density of Part-A(II) with a longer magnetization length is obviously larger than that of Part-A(I). Thus, the magnetomotive force efficiency of Part-A(II) is relatively high since the Halbach array PMs are inclined magnetized. As can be seen in Fig. 2, the magnetization length of the PM of Part-B(II) is longer than that of Part-B(I). Thus, a magnetic flux density with a maximum of 0.0605 T of Part-B(II) is larger than that with a maximum of 0.054 T of Part-B(I), which is shown in Fig. 3b. As shown in Fig. 3c, the total magnetic flux densities of the two LFMB schemes are improved as the superposition of Part-A and Part-B. The maximum magnetic flux density of the LFMB with the improved double magnetic circuits is 0.598 T, which is increased by 4.9% when compared with that of 0.57 T of the LFMB with the conventional double magnetic circuits. The fluctuations of the two LFMBs are approximately equivalent due to the similar dimensions of the auxiliary magnetic rings. Therefore, the LFMB with the improved double magnetic circuits is adopted for deflection control of the MSGFW.

Fig. 3
figure 3

Magnetic flux density of two LFMBs: a part-A; b part-B; c two LFMB schemes

Full size image

3 Theoretical analysis

An LFMB with the improved double magnetic circuits is shown in Fig. 4. The materials of the PMs and the magnetic rings are Sm2Co17 and 1J50, which are the same as those of an LFMB with the conventional double magnetic circuits. Each of the inclined magnetization Halbach array PMs is composed of two inclined magnetization PMs and a radial magnetization PM. The main magnetic flux is generated by two axial magnetization PMs and four sets of inclined magnetization Halbach array PMs. The solid line is the main magnetic flux flowing across the auxiliary magnetic rings, the air gap, the coils and the main magnetic rings. The dashed line denotes the auxiliary magnetic flux passing through the auxiliary magnetic rings, the air gap and the coils. The total magnetic flux in the coil region is obtained by the superposition of the main and auxiliary magnetic fluxes.

Fig. 4
figure 4

LFMB with the improved double magnetic circuits scheme

Full size image

To simplify the calculation of the magnetic flux density generated by the inclined Halbach array PMs, the equivalent surface current method is adopted to obtain the magnetic flux density at an arbitrary point in the coil region. The magnetic flux density of the PM with an arbitrary magnetization direction can be equivalent to that generated by the surface currents I–IV. A model of an arbitrary inclined magnetization PM is shown in Fig. 5, and the center of PM is taken as the coordinate origin.

Fig. 5
figure 5

Equivalent surface current of PMs: a inclined magnetization PM; b axial magnetization PM; c radial magnetization PM

Full size image

As shown in Fig. 5, θ is the magnetization angle, J is the surface current density, Jy, and Jz are the components of J in the Y and Z directions, m and k are the width and height of the arbitrary inclined magnetization PM, r is the vector length from the surface current element to the arbitrary P(y, z), φ is the angle between the vector direction of r and the Y+ direction, and φ1–φ4 are the boundaries of φ. The magnetic flux density at an arbitrary P(y, z) is generated by the inclined magnetization PM in Fig. 5a, which can be equivalent to the superposition of those in Fig. 5b and c. In Fig. 5b, the model is considered as the axial magnetization PM with surface currents I and II. In addition, its surface current density is Jz. The magnetic flux density generated by the arbitrary element of the surface current I is BI, which can be resolved into BIy and BIz in the Y and Z directions. The model in Fig. 5c is the radial magnetization PM with surface currents III and IV. In addition, its surface current density is Jy.

The magnetic flux densities generated by an arbitrary element of the surface currents II–IV are BII, BIII and BIV. Biy and Biz (where i = II, III, IV) are the components in the Y and Z directions. There is no volume magnetizing current due to the uniform magnetization. The surface current density J is equivalent to the magnetization M. The components Jy and Jz can be expressed as:

$$\left\{ \begin{gathered} J_{y} = M\cos \theta \hfill \\ J_{z} = M\sin \theta \hfill \\ \end{gathered} \right..$$

According to the Biot–Savart law, the magnetic flux density BI generated by the surface current I is given by:

$$B_{{\text{I}}} = \frac{{\mu_{0} I}}{2\pi r},$$
(4)

where μ0 is the vacuum permeability, and I is the surface current corresponding to J. The magnetic flux density components BIy and BIz in the Y and Z directions are expressed as:

$$\left\{ \begin{gathered} B_{{{\text{I}}y}} = \int_{{\varphi_{1} }}^{{\varphi_{2} }} {\frac{{\mu_{0} J_{z} }}{2\pi r}\sin \varphi dl} \hfill \\ B_{z} = \int_{{\varphi_{1} }}^{{\varphi_{2} }} {\frac{{\mu_{0} J_{z} }}{2\pi r}\cos \varphi dl} \hfill \\ \end{gathered} \right..$$
(5)

Similarly, the magnetic flux density components BI–BIV in the Y and Z directions at an arbitrary point P(y, z) generated by the four equivalent surface currents can be obtained as:

$$\left[ {\begin{array}{*{20}c} {B_{{{\text{I}}y}} } & {B_{{{\text{III}}y}} } \\ {B_{{{\text{II}}y}} } & {B_{{{\text{IV}}y}} } \\ {B_{{{\text{I}}z}} } & {B_{{{\text{III}}z}} } \\ {B_{{{\text{II}}z}} } & {B_{{{\text{IV}}z}} } \\ \end{array} } \right] = \frac{{\mu_{0} M}}{2\pi }\left[ {\begin{array}{*{20}c} { - \frac{1}{2}\ln \frac{{\cos \varphi_{1} (y,z)}}{{\cos \varphi_{2} (y,z)}}} & {\varphi_{1} (y,z) - \varphi_{3} (y,z)} \\ {\frac{1}{2}\ln \frac{{\cos \varphi_{4} (y,z)}}{{\cos \varphi_{3} (y,z)}}} & {\varphi_{4} (y,z) - \varphi_{2} (y,z)} \\ {\varphi_{2} (y,z) - \varphi_{1} (y,z)} & {\frac{1}{2}\ln \frac{{\cos \varphi_{3} (y,z)}}{{\cos \varphi_{1} (y,z)}}} \\ {\varphi_{4} (y,z) - \varphi_{3} (y,z)} & { - \frac{1}{2}\ln \frac{{\cos \varphi_{4} (y,z)}}{{\cos \varphi_{2} (y,z)}}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\sin \theta } & 0 \\ 0 & {\cos \theta } \\ \end{array} } \right],$$
(6)

where the boundaries φ1–φ4 of φ are given by:

$$\left\{ \begin{gathered} \varphi_{1} (y,z) = \tan^{ - 1} \frac{z - k/2}{{y + m/2}} \hfill \\ \varphi_{2} (y,z) = \tan^{ - 1} \frac{z + k/2}{{y + m/2}} \hfill \\ \varphi_{3} (y,z) = \tan^{ - 1} \frac{z - k/2}{{y - m/2}} \hfill \\ \varphi_{4} (y,z) = \tan^{ - 1} \frac{z + k/2}{{y - m/2}} \hfill \\ \end{gathered} \right..$$
(7)

As shown in Fig. 4, according to the same dimensions and symmetrical location, the PMs are classified into four groups: group1 including PM1, 7, 8, and 14; group2 including PM2, 6, 9, and 13; group3 including PM3, 5, 10, and 12; group4 including PM4 and 11. To simplify the calculation, PM4 and PM15 are combined as an axial magnetization PM. In addition, PM11 and PM16 are dealt with similarly.

O and on are the coordinate origin and the center of PMs, respectively. For a simplified calculation, the operator is used, and it is expressed as:

$$D_{{( - 1)^{p} a,( - 1)^{q} b}}^{m,k} \varphi_{n} (y,z) = \varphi_{n} [y - ( - 1)^{p} a,z - ( - 1)^{q} b]_{m,k} ,$$
(8)

where a and b are the abscissa and ordinate of the vector Oon; φn (i = 1, 2, 3, 4) represent the boundaries; p and q are the constant values; a1 that is equivalent to (− th − ta − 2g − wc)/2 and b1 that is equivalent to (hm − h1)/2 are the abscissa and ordinate of the vector Oo1; th and ta are the Halbach array middle PM thickness and the auxiliary magnetic ring thickness; g and wc are the air gap thickness and the coil width; and hm and h1 are the main magnetic ring height and the PM1 height. It can be seen in Fig. 4 that the height of each PM in group1 is h1, and the corresponding width is the sum of th and ta. The magnetic flux density generated by group1 can be written as:

$$\left\{ \begin{gathered} B_{1y} (y,z) = \frac{{\mu_{0} M}}{2\pi }\sum\limits_{p = 1}^{2} {\sum\limits_{q = 1}^{2} {\left\{ \begin{gathered} \frac{{( - 1)^{p} \sin \theta }}{2}\ln \frac{{\prod\limits_{n = 2,4} {\cos \left[ {D_{{( - 1)^{p} a_{1} ,( - 1)^{q} b_{1} }}^{{t_{h} + t_{a} ,h_{1} }} \varphi_{n} (y,z)} \right]} }}{{\prod\limits_{n = 1,3} {\cos \left[ {D_{{( - 1)^{p} a_{1} ,( - 1)^{q} b_{1} }}^{{t_{h} + t_{a} ,h_{1} }} \varphi_{n} (y,z)} \right]} }} \hfill \\ + ( - 1)^{q} \cos \theta \left[ {\sum\limits_{n = 1,4} {D_{{( - 1)^{p} a_{1} ,( - 1)^{q} b_{1} }}^{{t_{h} + t_{a} ,h_{1} }} \varphi_{n} (y,z)} - \sum\limits_{n = 2,3} {D_{{( - 1)^{p} a_{1} ,( - 1)^{q} b_{1} }}^{{t_{h} + t_{a} ,h_{1} }} \varphi_{n} (y,z)} } \right] \hfill \\ \end{gathered} \right\}} } \hfill \\ B_{1z} (y,z) = \frac{{\mu_{0} M}}{2\pi }\sum\limits_{p = 1}^{2} {\sum\limits_{q = 1}^{2} {\left\{ \begin{gathered} ( - 1)^{p} \sin \theta \left[ {\sum\limits_{n = 2,4} {D_{{( - 1)^{p} a_{1} ,( - 1)^{q} b_{1} }}^{{t_{h} + t_{a} ,h_{1} }} \varphi_{n} (y,z)} - \sum\limits_{n = 1,3} {D_{{( - 1)^{p} a_{1} ,( - 1)^{q} b_{1} }}^{{t_{h} + t_{a} ,h_{1} }} \varphi_{n} (y,z)} } \right] \hfill \\ + \frac{{( - 1)^{q} \cos \theta }}{2}\ln \frac{{\prod\limits_{n = 2,3} {\cos \left[ {D_{{( - 1)^{p} a_{1} ,( - 1)^{q} b_{1} }}^{{t_{h} + t_{a} ,h_{1} }} \varphi_{n} (y,z)} \right]} }}{{\prod\limits_{n = 1,4} {\cos \left[ {D_{{( - 1)^{p} a_{1} ,( - 1)^{q} b_{1} }}^{{t_{h} + t_{a} ,h_{1} }} \varphi_{n} (y,z)} \right]} }} \hfill \\ \end{gathered} \right\}} } \hfill \\ \end{gathered} \right..$$
(9)

It can be seen in Fig. 4 that the coordinates of the vectors Oo2 (a2, b2); Oo3 (a3, b3); and Oo4 (a4, b4) are (− ta − g − (wc + th)/2, hm/2 − h1 − h2/2); (− ta − g − (wc + th)/2, (h4 + h3)/2); and ((− th − ta − 2g − wc)/2, 0), respectively. In addition, h3 and h4 are the heights of PM3 and PM4. Similarly, the magnetic flux densities generated by the PMs of group2–group4 at an arbitrary point P(y, z) can be obtained as follows:

$$\left\{ \begin{gathered} B_{2y} (y,z) = \frac{{\mu_{0} M}}{2\pi }\sum\limits_{p = 1}^{2} {\sum\limits_{q = 1}^{2} {( - 1)^{q} \left[ {\sum\limits_{n = 1,4} {D_{{( - 1)^{p} a_{2} ,( - 1)^{q} b_{2} }}^{{t_{h} ,h_{2} }} \varphi_{n} (y,z)} - \sum\limits_{n = 2,3} {D_{{( - 1)^{p} a_{2} ,( - 1)^{q} b_{2} }}^{{t_{h} ,h_{2} }} \varphi_{n} (y,z)} } \right]} } \hfill \\ B_{2z} (y,z) = \frac{{\mu_{0} M}}{4\pi }\sum\limits_{p = 1}^{2} {\sum\limits_{q = 1}^{2} {( - 1)^{q} \ln \frac{{\prod\limits_{n = 1,4} {\cos \left[ {D_{{( - 1)^{p} a_{2} ,( - 1)^{q} b_{2} }}^{{t_{h} ,h_{2} }} \varphi_{n} (y,z)} \right]} }}{{\prod\limits_{n = 2,3} {\cos \left[ {D_{{( - 1)^{p} a_{2} ,( - 1)^{q} b_{2} }}^{{t_{h} ,h_{2} }} \varphi_{n} (y,z)} \right]} }}} } \hfill \\ B_{3y} (y,z) = \frac{{\mu_{0} M}}{2\pi }\sum\limits_{p = 1}^{2} {\sum\limits_{q = 1}^{2} {\left\{ \begin{gathered} \frac{{( - 1)^{p + q + 1} \sin \theta }}{2}\ln \frac{{\prod\limits_{n = 2,4} {\cos \left[ {D_{{( - 1)^{p} a_{3} ,( - 1)^{q} b_{3} }}^{{t_{h} ,h_{3} }} \varphi_{n} (y,z)} \right]} }}{{\prod\limits_{n = 1,3} {\cos \left[ {D_{{( - 1)^{p} a_{3} ,( - 1)^{q} b_{3} }}^{{t_{h} ,h_{3} }} \varphi_{n} (y,z)} \right]} }} \hfill \\ + ( - 1)^{q} \cos \theta \left[ {\sum\limits_{n = 1,4} {D_{{( - 1)^{p} a_{3} ,( - 1)^{q} b_{3} }}^{{t_{h} ,h_{3} }} \varphi_{n} (y,z)} - \sum\limits_{n = 2,3} {D_{{( - 1)^{p} a_{3} ,( - 1)^{q} b_{3} }}^{{t_{h} ,h_{3} }} \varphi_{n} (y,z)} } \right] \hfill \\ \end{gathered} \right\}} } \hfill \\ B_{3z} (y,z) = \frac{{\mu_{0} M}}{2\pi }\sum\limits_{p = 1}^{2} {\sum\limits_{q = 1}^{2} {\left\{ \begin{gathered} ( - 1)^{p + q + 1} \sin \theta \left[ {\sum\limits_{n = 2,3} {D_{{( - 1)^{p} a_{3} ,( - 1)^{q} b_{3} }}^{{t_{h} ,h_{3} }} \varphi_{n} (y,z)} - \sum\limits_{n = 1,4} {D_{{( - 1)^{p} a_{3} ,( - 1)^{q} b_{3} }}^{{t_{h} ,h_{3} }} \varphi_{n} (y,z)} } \right] \hfill \\ + \frac{{( - 1)^{q} \cos \theta }}{2}\ln \frac{{\prod\limits_{n = 2,3} {\cos \left[ {D_{{( - 1)^{p} a_{3} ,( - 1)^{q} b_{3} }}^{{t_{h} ,h_{3} }} \varphi_{n} (y,z)} \right]} }}{{\prod\limits_{n = 1,4} {\cos \left[ {D_{{( - 1)^{p} a_{3} ,( - 1)^{q} b_{3} }}^{{t_{h} ,h_{3} }} \varphi_{n} (y,z)} \right]} }} \hfill \\ \end{gathered} \right\}} } \hfill \\ B_{4y} (y,z) = \frac{{\mu_{0} M}}{8\pi }\sum\limits_{p = 1}^{2} {\sum\limits_{q = 1}^{2} {( - 1)^{p} \ln \frac{{\prod\limits_{n = 1,4} {\cos \left[ {D_{{( - 1)^{p} a_{4} ,( - 1)^{q} b_{4} }}^{{t_{h} + t_{a} ,h_{4} }} \varphi_{n} (y,z)} \right]} }}{{\prod\limits_{n = 2,3} {\cos \left[ {D_{{( - 1)^{p} a_{4} ,( - 1)^{q} b_{4} }}^{{t_{h} + t_{a} ,h_{4} }} \varphi_{n} (y,z)} \right]} }}} } \hfill \\ B_{4z} (y,z) = \frac{{\mu_{0} M}}{4\pi }\sum\limits_{p = 1}^{2} {\sum\limits_{q = 1}^{2} {( - 1)^{p} \left[ {\sum\limits_{n = 2,4} {D_{{( - 1)^{p} a_{4} ,( - 1)^{q} b_{4} }}^{{t_{h} + t_{a} ,h_{4} }} \varphi_{n} (y,z)} - \sum\limits_{n = 1,3} {D_{{( - 1)^{p} a_{4} ,( - 1)^{q} b_{4} }}^{{t_{h} + t_{a} ,h_{4} }} \varphi_{n} (y,z)} } \right]} } \hfill \\ \end{gathered} \right..$$
(10)

As shown in Fig. 4, all of the PMs are located between the two main magnetic rings. The distance between the two main magnetic rings is dm. Since the magnetomotive force in the interfaces between the four groups of PMs and the main magnetic rings is different from that inside the four groups of PMs, the surface currents in the two interfaces are considered. The main magnetic flux in the two interfaces is obviously changed. According to the images method [28], the surface currents in the two interfaces can be seen as numerous image sources. The total main magnetic flux can be obtained by the superposition of the magnetic fluxes generated by the image sources and four groups of PMs. The magnetic flux densities generated by the image sources of four groups of PMs are similarly calculated as Eqs. (9) and (10), and the results can be defined as B′iy and B′iz (i = 1, 2, 3, 4).

Based on the analysis above, the magnetic flux density components generated by four groups of PMs and their image sources are added together, and the total magnetic flux density components By and Bz at an arbitrary point P(y, z) are given by:

$$\left\{ \begin{gathered} B_{y} (y,z) = \sum\limits_{i = 1}^{4} {(B_{iy} + B^{\prime}_{iy} ) = \frac{{\mu_{0} M}}{2\pi }\left[ {k_{1} (y,z)\sin \theta + k_{2} (y,z)\cos \theta + k_{3} (y,z)} \right]} \hfill \\ B_{z} (y,z) = \sum\limits_{i = 1}^{4} {(B_{iz} + B^{\prime}_{iz} ) = \frac{{\mu_{0} M}}{2\pi }\left[ {k_{4} (y,z)\sin \theta + k_{5} (y,z)\cos \theta + k_{6} (y,z)} \right]} \hfill \\ \end{gathered} \right.,$$
(11)

where ki (y, z) (i = 1, 2, …, 6) are functions related to the position of the arbitrary point P(y, z). In addition, ki can be expressed as:

$$\left\{ \begin{gathered} k_{1} = \frac{1}{2}\sum\limits_{p = 1}^{2} {\sum\limits_{q = 1}^{2} {\sum\limits_{s = 0, \pm 1...}^{\infty } {\left\{ \begin{gathered} ( - 1)^{p} \ln \frac{{\prod\limits_{n = 2,4} {\cos \left[ {D_{{( - 1)^{p} a_{1} - 2sd_{m} ,( - 1)^{q} b_{1} }}^{{t_{h} + t_{a} ,h_{1} }} \varphi_{n} (y,z)} \right]} }}{{\prod\limits_{n = 1,3} {\cos \left[ {D_{{( - 1)^{p} a_{1} - 2sd_{m} ,( - 1)^{q} b_{1} }}^{{t_{h} + t_{a} ,h_{1} }} \varphi_{n} (y,z)} \right]} }} \hfill \\ + ( - 1)^{p + q + 1} \ln \frac{{\prod\limits_{n = 2,4} {\cos \left[ {D_{{( - 1)^{p} a_{1} - 2sd_{m} ,( - 1)^{q} b_{1} }}^{{t_{h} + t_{a} ,h_{1} }} \varphi_{n} (y,z)} \right]} }}{{\prod\limits_{n = 1,3} {\cos \left[ {D_{{( - 1)^{p} a_{1} - 2sd_{m} ,( - 1)^{q} b_{1} }}^{{t_{h} + t_{a} ,h_{1} }} \varphi_{n} (y,z)} \right]} }} \hfill \\ \end{gathered} \right\}} } } \hfill \\ k_{2} = \sum\limits_{p = 1}^{2} {\sum\limits_{q = 1}^{2} {\sum\limits_{s = 0, \pm 1...}^{\infty } {\left\{ \begin{gathered} ( - 1)^{q} \left[ {\sum\limits_{n = 1,4} {D_{{( - 1)^{p} a_{1} - 2sd_{m} ,( - 1)^{q} b_{1} }}^{{t_{h} + t_{a} ,h_{1} }} \varphi_{n} (y,z)} - \sum\limits_{n = 2,3} {D_{{( - 1)^{p} a_{1} - 2sd_{m} ,( - 1)^{q} b_{1} }}^{{t_{h} + t_{a} ,h_{1} }} \varphi_{n} (y,z)} } \right] \hfill \\ + ( - 1)^{q} \left[ {\sum\limits_{n = 1,4} {D_{{( - 1)^{p} a_{3} - 2sd_{m} ,( - 1)^{q} b_{3} }}^{{t_{h} ,h_{3} }} \varphi_{n} (y,z)} - \sum\limits_{n = 2,3} {D_{{( - 1)^{p} a_{3} - 2sd_{m} ,( - 1)^{q} b_{3} }}^{{t_{h} ,h_{3} }} \varphi_{n} (y,z)} } \right] \hfill \\ \end{gathered} \right\}} } } \hfill \\ k_{3} = \sum\limits_{p = 1}^{2} {\sum\limits_{q = 1}^{2} {\sum\limits_{s = 0, \pm 1...}^{\infty } {\left\{ \begin{gathered} ( - 1)^{q} \left[ {\sum\limits_{n = 1,4} {D_{{( - 1)^{p} a_{2} - 2sd_{m} ,( - 1)^{q} b_{2} }}^{{t_{h} ,h_{2} }} \varphi_{n} (y,z)} - \sum\limits_{n = 2,3} {D_{{( - 1)^{p} a_{2} - 2sd_{m} ,( - 1)^{q} b_{2} }}^{{t_{h} ,h_{2} }} \varphi_{n} (y,z)} } \right] \hfill \\ + \frac{1}{4}( - 1)^{p} \ln \frac{{\prod\limits_{n = 1,4} {\cos \left[ {D_{{( - 1)^{p} a_{4} - 2sd_{m} ,( - 1)^{q} b_{4} }}^{{t_{h} + t_{a} ,h_{4} }} \varphi_{n} (y,z)} \right]} }}{{\prod\limits_{n = 2,3} {\cos \left[ {D_{{( - 1)^{p} a_{4} - 2sd_{m} ,( - 1)^{q} b_{4} }}^{{t_{h} + t_{a} ,h_{4} }} \varphi_{n} (y,z)} \right]} }} \hfill \\ \end{gathered} \right\}} } } \hfill \\ k_{4} = \sum\limits_{p = 1}^{2} {\sum\limits_{q = 1}^{2} {\sum\limits_{s = 0, \pm 1...}^{\infty } {\left\{ \begin{gathered} ( - 1)^{p} \left[ {\sum\limits_{n = 2,4} {D_{{( - 1)^{p} a_{1} - 2sd_{m} ,( - 1)^{q} b_{1} }}^{{t_{h} + t_{a} ,h_{1} }} \varphi_{n} (y,z)} - \sum\limits_{n = 1,3} {D_{{( - 1)^{p} a_{1} - 2sd_{m} ,( - 1)^{q} b_{1} }}^{{t_{h} + t_{a} ,h_{1} }} \varphi_{n} (y,z)} } \right] \hfill \\ + ( - 1)^{p + q + 1} \left[ {\sum\limits_{n = 2,4} {D_{{( - 1)^{p} a_{3} - 2sd_{m} ,( - 1)^{q} b_{3} }}^{{t_{h} ,h_{3} }} \varphi_{n} (y,z)} - \sum\limits_{n = 1,3} {D_{{( - 1)^{p} a_{3} - 2sd_{m} ,( - 1)^{q} b_{3} }}^{{t_{h} ,h_{3} }} \varphi_{n} (y,z)} } \right] \hfill \\ \end{gathered} \right\}} } } \hfill \\ k_{5} = \frac{1}{2}\sum\limits_{p = 1}^{2} {\sum\limits_{q = 1}^{2} {\sum\limits_{s = 0, \pm 1...}^{\infty } {\left\{ \begin{gathered} ( - 1)^{q} \ln \frac{{\prod\limits_{n = 2,3} {\cos \left[ {D_{{( - 1)^{p} a_{1} - 2sd_{m} ,( - 1)^{q} b_{1} }}^{{t_{h} + t_{a} ,h_{1} }} \varphi_{n} (y,z)} \right]} }}{{\prod\limits_{n = 1,4} {\cos \left[ {D_{{( - 1)^{p} a_{1} - 2sd_{m} ,( - 1)^{q} b_{1} }}^{{t_{h} + t_{a} ,h_{1} }} \varphi_{n} (y,z)} \right]} }} \hfill \\ + ( - 1)^{q} \ln \frac{{\prod\limits_{n = 2,3} {\cos \left[ {D_{{( - 1)^{p} a_{3} - 2sd_{m} ,( - 1)^{q} b_{3} }}^{{t_{h} ,h_{3} }} \varphi_{n} (y,z)} \right]} }}{{\prod\limits_{n = 1,4} {\cos \left[ {D_{{( - 1)^{p} a_{3} - 2sd_{m} ,( - 1)^{q} b_{3} }}^{{t_{h} ,h_{3} }} \varphi_{n} (y,z)} \right]} }} \hfill \\ \end{gathered} \right\}} } } \hfill \\ k_{6} = \sum\limits_{p = 1}^{2} {\sum\limits_{q = 1}^{2} {\sum\limits_{s = 0, \pm 1...}^{\infty } {\left\{ \begin{gathered} \frac{1}{2}( - 1)^{q} \ln \frac{{\prod\limits_{n = 1,4} {\cos \left[ {D_{{( - 1)^{p} a_{2} - 2sd_{m} ,( - 1)^{q} b_{2} }}^{{t_{h} ,h_{2} }} \varphi_{n} (y,z)} \right]} }}{{\prod\limits_{n = 2,3} {\cos \left[ {D_{{( - 1)^{p} a_{2} - 2sd_{m} ,( - 1)^{q} b_{2} }}^{{t_{h} ,h_{2} }} \varphi_{n} (y,z)} \right]} }} \hfill \\ + \frac{1}{2}( - 1)^{p} \left[ {\sum\limits_{n = 2,4} {D_{{( - 1)^{p} a_{4} - 2sd_{m} ,( - 1)^{q} b_{4} }}^{{t_{h} + t_{a} ,h_{4} }} \varphi_{n} (y,z)} - \sum\limits_{n = 1,3} {D_{{( - 1)^{p} a_{4} - 2sd_{m} ,( - 1)^{q} b_{4} }}^{{t_{h} + t_{a} ,h_{4} }} \varphi_{n} (y,z)} } \right] \hfill \\ \end{gathered} \right\}} } } \hfill \\ \end{gathered} \right..$$
(12)

It can be seen from Eq. (11) that the magnetic flux density depends on the magnetization angle θ. As shown in Eq. (12), the functions ki (i = 1, 2, …, 6) are related to the dimension parameters including g, wc, th, ta, hm, h1, h2, h3, and h4.

4 LFMB design

4.1 Sensitivity analysis

According to Eqs. (11), (12) and the theoretical analysis above, two types of parameters, the magnetization angle θ and the dimension parameters g, wc, th, ta, hm, h1, h2, h3 and h4, are calculated. The main magnetic ring height hm and the radial dimensions g, wc, th, and ta are consistent with the overall dimensions of an LFMB with the conventional double magnetic circuits in [15]. The PM heights in Part-A(II) including PM1 height h1, PM2 height h2, PM3 height h3, and PM4 height h4 are variable dimension parameters. The PM2 height h2 can be calculated by the formula h2 = (hm − h4)/2 − h1 − h3. Therefore, the dimension parameters h1, h3 and h4 together with the magnetization angle θ are adopted as design parameters. To improve the efficiency of the LFMB design, a sensitivity analysis [22, 23] is employed. The sensitivity Si of the magnetic flux density versus the design parameters θ, h1, h3 and h4 are given by:

$$S_{i} = \frac{\partial B}{{\partial x_{i} }}{\kern 1pt} = \frac{\Delta B}{{\Delta x_{i} }} \, (i = 1,2,3,4),$$
(13)

where x1, x2, x3, and x4 denote θ, h1, h3, and h4, respectively. The perturbation ΔB is calculated by the finite element method [27]. The sensitivities Si (i = 1, 2, 3, 4) are 4.2 mT/°, 0.5 mT/mm, 0.4 mT/mm, and 0.1 mT/mm. The sensitivity of the magnetic flux density B to the magnetization angle θ is far greater than the other three sensitivities. The magnetization angle θ can be considered as the critical factor.

4.2 Magnetization angle

The parameters are consistent with those of the LFMB scheme in [15], including the coil width wc of 3.6 mm, the coil height hc of 8 mm, the air gap thickness g of 0.7 mm, the auxiliary magnetic ring thickness ta of 1 mm, the Halbach array mid PM thickness th of 4 mm, the main magnetic ring thickness tm of 4 mm, and the main magnetic ring height hm of 28 mm. As shown in Fig. 2, the heights of the inclined magnetization Halbach array PMs in Part-A(II) are different from those of Part-A(I). In Part-A(II), the PM heights (h1 of 2.5 mm, h2 of 5.2 mm, h3 of 3.9 mm, and h4 of 4.8 mm) are used. A simulation model is established by the finite element method based on the above parameters. The magnetic flux density curves of the theoretical analysis and the simulation are plotted in Fig. 6.

Fig. 6
figure 6

Relationship between magnetic flux density and magnetization angle

Full size image

When the magnetization angle is 20°, the simulation magnetic flux density reaches a maximum of 0.608 T. The optimal magnetization angle of the theoretical analysis is 25°, and its corresponding maximum magnetic flux density is 0.632 T. The deviation between the simulation and theoretical analysis values of the maximum magnetic flux density is about 0.02 T, when ignoring the magnetic flux leakage in the calculation.

4.3 Dimension parameters

Based on the analysis results above, a magnetization angle of 20° is adopted. The dimension parameters h1, h3 and h4 are calculated. The design variable X can be written in vector form as:

$${\varvec{X}} = \left[ {\begin{array}{*{20}c} {h_{1} } & {h_{3} } & {h_{4} } \\ \end{array} } \right].$$
(14)

According to the structure in Fig. 4 and the dimension parameters of the LFMB scheme in [15], the initial bounds of the design variables can be defined as follows:

$$\left\{ \begin{gathered} 2\,{\text{mm}} \le h_{1} \le 4\,{\text{mm}} \hfill \\ 3\,{\text{mm}} \le h_{3} \le 5\,{\text{mm}} \hfill \\ 3.6\,{\text{mm}} \le h_{4} \le 5\,{\text{mm}} \hfill \\ \end{gathered} \right..$$
(15)

The larger the magnetic flux density, the larger the deflection torque of the LFMB, the greater the gyroscope moment of the MSGFW. Thus, the maximum magnetic flux density Bmax is defined as the optimization objective. The optimization objective function with the design variables is expressed as:

$$B_{\max } = \max f(X) = \max f(h_{1} ,h_{3} ,h_{4} ).$$
(16)

The sequential quadratic programming method [29, 30] is utilized to optimize the design variables h1, h3 and h4. The optimization curves are plotted in Fig. 7. As shown in Fig. 7, the curves of the design variables and the objective are convergent after the 50th iteration. The optimal values of the PM1 height h1, the PM3 height h3, and the PM4 height h4 are 3 mm, 3.4 mm, and 4.2 mm, respectively. In addition, its corresponding maximum magnetic flux density is about 0.6153 T.

Fig. 7
figure 7

Optimization curves

Full size image

After optimization of the PMs heights, the magnetic flux densities versus the magnetizations angle are calculated again, and their corresponding curves are shown in Fig. 8. The optimal magnetization angle of the theoretical analysis and simulation are within 22–23° and 20–21°, respectively. These values are nearly equivalent to those before the dimension parameters optimization. In addition, the corresponding optimal magnetic flux densities are 0.6466 T and 0.6153 T. The optimized results show that the optimal magnetization angle is basically invariable before and after the dimension parameters optimization. They also show that the theoretical analysis has a good agreement with the simulation. The design parameters of an LFMB with the improved double magnetic circuits are listed in Table 1.

Fig. 8
figure 8

Magnetic flux density versus magnetization angle

Full size image
Table 1 Design parameters of an LFMB with the improved double magnetic circuits
Full size table

5 Simulation and experiment

5.1 Simulation

The magnetic flux density of an LFMB can be divided into the radial and axial components. The radial component and its fluctuation are related to the stiffness and precision of the deflection control. Interference torque is induced by the axial component. Based on the design parameters in Table 1, the two components in the radial section are simulated by the finite element method, as shown in Fig. 9a and b, respectively. In Fig. 9a, the radial magnetic flux density is relatively low in a position far away from the PMs. That is in accordance with the theoretical analysis in Eqs. (6) and (7), where the radial magnetic flux density Biy increases with a decrease of the abscissa y of the arbitrary P(y, z). Owing to magnetic flux leakage, the radial magnetic flux density decreases gradually along with its position from center to the coil region edge in the axial direction. Therefore, the maximum and minimum radial magnetic flux densities of 0.615 T and 0.58 T are in the axial and radial centers of the coil region edges. Since inclined magnetized PMs are adopted in the LFMB with the improved double magnetic circuits, the maximum and minimum values are increased by 7.9% and 8% when compared with those of 0.57 T and 0.537 T in the LFMB with the conventional double magnetic circuits in [15]. Its corresponding magnetic flux density fluctuation of 0.85% is almost equal to that of 0.75% in [15] due to the auxiliary magnetic rings of Part-B in both schemes. It can be seen in Fig. 9b that the axial component is less than 5% of the radial component. The maximum and minimum axial components in the coil region are 0.03 T and 0.018 T. Both of them are almost the same as those of 0.036 T and 0.024 T in [15].

Fig. 9
figure 9

Magnetic flux density in the radial section: a radial component; b axial component

Full size image

The radial magnetic flux density distributed in the circumferential direction is further analyzed in Fig. 10. As shown in Fig. 10a, the nine circles with axial even distributions in the upper coil region are used. The corresponding nine magnetic flux density curves are plotted in Fig. 10b. The maximum and minimum magnetic flux densities are in the 5th line and the 9th line, respectively. When compared with the scheme in [15], the maximum and minimum magnetic flux densities are increased from 0.564 T and 0.544 T to 0.611 T and 0.585 T. The magnetic flux density is smoothed by the auxiliary magnetic rings in the two LFMBs. For the LFMB with the IDMC, the radial magnetic flux density fluctuation in the circumferential direction is about 0.9% in the coil region, which is about equivalent to that of 0.79% in [15].

Fig. 10
figure 10

Magnetic flux density distributed in the circumferential direction: a sectional view of a nephogram; b magnetic flux density in the middle of upper coil regions

Full size image

For the two LFMB schemes, both the axial magnetic flux density and radial magnetic flux density fluctuations in the circumferential direction are similar. The radial magnetic flux density of the LFMB with the IDMC is larger than that of the LFMB with the conventional double magnetic circuit. Thus, the deflection torque stiffness is improved by the LFMB with the IDMC presented in this paper. The demand of a large deflection torque with high precision for MSGFWs can be fulfilled very well.

5.2 Experiment

A magnetic flux density experimental system of an LFMB is shown in Fig. 11. The PM rings in the LFMB are spliced with 12 arc PM blocks. The LFMB rotor is fixed in the sphere rotor edge groove. The sphere rotor is placed on the rotary table driven by the step motor with 15 s pauses during every 2° interval. The Hall sensor is used to detect the magnetic flux density in the coil region when the step motor is stopped. Radial magnetic flux density experiment results are shown in Fig. 12.

Fig. 11
figure 11

Magnetic flux density experiment system

Full size image
Fig. 12
figure 12

Magnetic flux density experiment results: a radial section; b circumferential direction

Full size image

The radial magnetic flux density in the radial section, measured by the Hall senor, is shown in Fig. 12a. The maximum and minimum radial magnetic flux densities are 0.608 T and 0.575 T. When compared with the simulation values in Fig. 9a, the maximum and minimum values are decreased by 1% and 1.2% due to the demagnetization of the PMs. Curves of the radial magnetic flux density distributed in the circumferential direction are plotted in Fig. 12b. Despite the good smoothing function of the magnetic rings for the magnetic flux, there are still 12 fluctuations induced by the splicing PM rings. The maximum and minimum magnetic flux densities of 0.603 T and 0.576 T are decreased by 1.3% and 1.5% when compared with those of the simulation in Fig. 10a. Both the radial magnetic flux density fluctuations in the radial section and in the circumferential direction are about 1.02%, which are approximately equal to the simulation results. The error between the experiment and the simulation is less than 5%. When compared with the maximum magnetic flux density of 0.6466 T in the analytical results, the error between the experimental and the analytical results is within 6%. Based on the above analysis, the reasonability and feasibility of the LFMB with the improved double magnetic circuits are verified, and the demand for a large deflection torque with a high precision of the MSGFW can be satisfied.

6 Conclusion

In this paper, an LFMB with improved double magnetic circuits applied to a MSGFW is proposed. When compared with a LFMB with the conventional double magnetic circuits, inclined magnetization Halbach array PMs generating the main magnetic flux are adopted to effectively increase the PMs magnetomotive force. In addition, trapezoidal PMs producing auxiliary magnetic flux are utilized to further improve the magnetic flux density. The magnetic flux density is calculated by the equivalent surface current method, which is verified by the finite element method. An optimal magnetization angle of 20° and optimal dimensions are obtained. A magnetic flux density experiment of the LFMB prototype is carried out. Experiment results show that the radial maximum and minimum magnetic flux densities of 0.608 T and 0.585 T are increased by 6.7% and 6.7% when compared with an LFMB with the conventional double magnetic circuits. Both the fluctuation in the radial section and the circumferential direction are about 1.02%, which are approximately equal to those of the LFMB with the conventional double magnetic circuits. This indicates that the demand for high-precision agile maneuvers for the MSGFW can be effectively fulfilled by a LFMB with the improved double magnetic circuits.