Magnetic, electric and magnetocaloric properties of EuFe_0.5Mn_0.5O₃ perovskite: Monte Carlo study and ab-initio calculations

Abstract

Studies on the magnetic and electrical behavior of the perovskite complex EuMn_0.5Fe_0.5O₃, which crystallizes in the orthorhombic structure and belongs to the symmetry group (Pbnm), have been conducted based on this study using numerical techniques More specifically, we investigated the magnetic and electrical properties of the EuMn_0.5Fe_0.5O₃ material using approximations created within the framework of density functional theory, such as a full potential linearized augmented plane wave and the generalized gradient approximation. The magnetization, the transition temperature, as well as the fluctuation of the magnetic entropy, the specific heat, and the variation of the adiabatic temperature and relative cooling power. were analyzed using the Monte Carlo simulations when it was discovered via research that this compound exhibit spin-reorientation phenomena as it behaves like a conducting metal.

1 Introduction

The manganites and ferrites perovskites are rich by magnetic and electrical properties, such as spin flop [1, 2], spin reorientation [3,4,5,6], multiferrocity [7,8,9], giant magnetoresistance [9,10,11], and giant magnetocaloric effect [12, 13]. The double exchange interaction is the main mechanism responsible for the magnetoresistance of manganites [8]. These systems exhibit spin-reorientation transition at the transition temperature. The behavior of perovskite structures is fundamentally governed by the exchange interactions between near neighbors, which lead to an arrangement of magnetic moments parallel to each other. It is noted nevertheless that the various orientations are not equivalent and that it is easier to align the magnetization on certain crystallographic axes called axis of easy magnetization. The rare earths orthoferrites RMO₃ with the ions M³⁺ and R³⁺ are the site of a variety of interactions which exist between these ions and which they are often anisotropic–symmetric, isotropic, and super-exchange interaction type [14]. It, therefore, follows an impact on the physical properties of these perovskites. One of the prominent phenomena, which characterizes these structures, is that of spin-reorientation. RMO₃ is a weak ferromagnetic due to a small canted spin of the antiferromagnetic [15] arrangement of the M³⁺ sub-lattice. The interaction between R and M ions makes the moments belongs the parallel magnetic structure or antiparallel to the moments of M³⁺ ions. The phenomenon of spin reorientation is produced in the system under application of an external magnetic field, which is accompanied by the fact that the symmetry of this magnetic arrangement changes axis of easy magnetization by rotation of the moments [14]. EuFeO₃ is an orthoferrite that crystallizes in the perovskite orthorhombic structure with the Pbmn space group, which is the seat of a distortion of its crystallographic structure [16,17,18]. In this structure, the Eu³⁺ ions are distributed, such that they populate the A and B sites of the dodecahedral and octahedral networks, respectively, this compound is good dielectric material. In this research, the magnetic, electric, and magnetocaloric properties of the EuMn_0.5Fe_0.5O₃ a with Pbmn space group and were examined by using the Ab initio calculations and the Monte Carlo method. The prominent impact of the substitution of Mn³⁺ ions which is a transition metal in the Fe sites of the EuFeO₃ compound, gives rise to the jean teller [19] distortion which causes the microscopic distortion of the oxygen octahedral, thus modifying the anion–cation distances which become long and short, in turn impacting the exchange parameters between Mn^3+͟-Mn³⁺, Mn^3+͟-Fe³⁺ and Fe^3+͟-Fe³⁺. This compound exhibit a spin reorientation [14]. One of the effects that we have studied for this compound is the magnetocaloric effect (EMC) which is a physical property of the magnetic material consisting of warming or cooling of the material around its transition temperature when an external magnetic field is applied. Ab initio (from first principles) DFT calculations using approximations make it possible to study and calculate the behavior of materials based on the theory of quantum mechanics.

The electronic and magnetic properties of a series of perovskites and double perovskites were studied by simulations and experimentally [20,21,22,23].

Using the generalized gradient approximation (GGA) [24], we deduce the electrical and magnetic behavior by calculating the magnetic moments of Mn, Fe, Eu and O in the system. Magnetocaloric effect in perovskite EuFe_0.5Mn_0.5O₃ was studied using the Monte Carlo simulations. We obtain too The Néel temperature T_N of compound EuFe_0.5Mn_0.5O₃. We present the adiabatic temperature variations and relative cooling power (RCP), as well as the dependency of the magnetization on temperature.

Table 1 The values of exchange interactions used in this work are given with Kelvein (K)

Fig. 1

Crystallographic structure of EuFe_0.5Mn_0.5O₃ perovskite

Fig. 2

The total energy vs. volume corresponding to the unit cell of ${\mathrm{EuFe}}_{0.5}{\mathrm{Mn}}_{0.5}{\mathrm{O}}_{3}$ perovskite

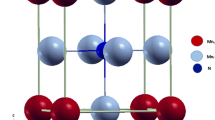
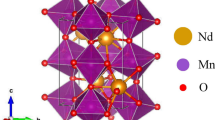
This work intends to study numerically and theoretically, the magnetic, electric properties and the magnetoelectric effect of the EuMn_0.5Fe_0.5O₃ Material (Fig. 1). The approach followed in this paper is as follows: we describe the Ab initio calculations to give the total and partial density of states (DOS) and the band structures of the EuMn_0.5Fe_0.5O₃ perovskite. We have also used the Monte Carlo simulations to give the variations of the magnetization, magnetic entropy changes, relative cooling power, specific heat changes and adiabatic temperature of EuMn_0.5Fe_0.5O₃. Finally, we have finished by conclusion.

Fig. 3

Magnetization a and dM/dT b vs. temperature

Fig. 4

Temperature dependence of the magnetic entropy Changes for different external magnetic fields (a) and (b)

Fig. 5

Variation relative cooling power with several external magnetic field

Fig. 6

Temperature dependence of the adiabatic Temperature

Fig. 7

Dependence temperature of specific heat for several values of external magnetic field

Fig. 8

Hysteresis cycle for several temperatures of EuFe_0.5Mn_0.5O₃

2 Ab initio calculations details

This part of the study is devoted to DFT calculations by the Full Augmented Plane Wave (FLAPW) [25] method and the generalized gradient approximation (GGA). We have solved in a self-consistent way Kohn–Sham equations, the muffin-tin approximation, consists in decoupling the space into two regions, inside the muffin-tin spheres where the local atomic potentials are spherically symmetrical and the outer region (interstitial) where the potential is smooth or varies very slowly which can be considered constant. The spheres do not overlap and the basis function inside each atomic sphere is a linear expansion of the radial solution of a spherical symmetry potential multiplied by spherical harmonics. In the interstitial region, the wave function was considered as an expansion of plane waves. In the nucleus region, core electrons in nuclei move faster and have been described by atomic wave functions solved in the relativistic framework using the current spherical part. The spin-polarized potential and the antiferromagnetic state were taken into consideration. The valence wave functions inside the muffin-tin spheres are expanded in terms of spherical harmonics up to l_max = 10. The energy of separation between the valence and core states is -9.0 Ry. the R_MT taken at 2.5 and 2.5 u for the Mn and Fe atoms, respectively. The k-points used in the calculations were based on 10*10*10 Monkhorst–Pack scheme. The ${R}_{min}^{MT}{k}_{max}$ = 7.0, while the charge density was Fourier expanded G_max = 12. In this work, we are interested in the study of the physical properties of the component with parameters found experimentally by X-ray diffraction method a = 5.347 (Å), b = 5.623 (Å), and c = 7.602 (Å) at 293 K [26]. The component crystallized as an orthorhombic perovskite belonging to the Pbnm space group.

3 Monte Carlo simulations

Along with theory and experiment, Monte Carlo simulation methods are one of the fundamental tenets of scientific investigation. The Monte Carlo simulation approach, which is based on the statistical physics principles, enables one to evaluate the average of physical quantities, such that the link between the Boltzmann factor and the probability of a configuration whose energy is E as: $\mathrm{exp}(\frac{E}{{k}_{B}})$ $=\mathrm{exp}(-\beta E)$ where k_B is the Boltzmann constant, and T is the temperature absolute. The periodic cyclic conditions are imposed in the three dimensions. The Metropolis algorithm [28] will be applied to the Ising model to determine magnetic and magnetocaloric parameters of EuFe_0.5Mn_0.5O₃. This system will be described by the following Hamiltonian:

$$\begin{gathered} H = - J_{FeFe}^1 \sum_{ < i,j > } {S_i S_j } - J_{FeFe}^2 \sum_{ < < i,k > > } {S_i S_k } - J_{MnMn}^1 \sum_{ < l,m > } {\sigma_l \sigma_m } - J_{MnMn}^2 \sum_{ < < l,n > > } {\sigma_l \sigma_n } - J_{EuEu}^1 \sum_{ < p,q > } {q_p q_q } - J_{EuEu}^2 \sum_{ < < p,r > > } {q_p q_r } \hfill \\ - J_{FeMn}^1 \sum_{ < i,l > } {S_i \sigma_l } - J_{FeMn}^2 \sum_{ < < i,m > > } {S_i \sigma_m } - J_{FeEu}^1 \sum_{ < i,n > } {S_i q_n } - J_{FeEu}^2 \sum_{ < < i,p > > } {S_i q_p } - J_{MnEu}^1 \sum_{ < l,p > } {\sigma_l q_p } - J_{MnEu}^2 \sum_{ < < l,q > > } {\sigma_l q_q } - h\left( {\sum_i {S_i } + \sum_k {\sigma_k } + \sum_l {q_l } } \right). \hfill \\ \hfill \\ \end{gathered}$$

The terms in the Hamiltonian S(Fe) = 5/2, σ(Mn) = 2, q(Eu) = 3 are the values of the spin moments of Fe, Mn and Eu, respectively. J_AB is an exchange parameter where A and B represents Fe, Mn and Eu, while the exponents i = 1 and i = 2 in J_ij indicate exchange parameter values between the first and the second neighbors in the environment of each one of Fe, Mn and Eu.

 < , > and <  < , >  > are used to denotes the interactions between first and second neighbors of each spin, respectively; the system is under the action of an external magnetic field h.

The ab initio calculations [25] were used to calculate the exchange parameters with Kevin unity, which take the following values (see Table 1).

The sample contains a spin number for each atom as follows:

Number of S(Fe) in the system is N₁ = 2291, Number of σ(Mn) in the system is N₂ = 2339 and Number of q(Eu) in the system is N₃ = 1300.

The investigations of the magnetic behaviors and magnetocaloric effects of the component can be deduced from the magnetization defined as M = $\frac{1}{\mathrm{N}}$<∑S_i >

 where the internal energy of the system is E = $\frac{1}{\mathrm{N}}$<H > 

The magnetizations by spin of Mn³⁺, Fe³⁺ and Eu³⁺ are

M_Fe³⁺ = $\frac{1}{{N}_{1}}\sum_{i}<{S}_{i}(Fe)>$

M_Mn³⁺ = $\frac{1}{{N}_{2}}\sum_{i}<{\sigma }_{i}(\mathrm{Mn})>$

M_Eu³⁺ = $\frac{1}{{N}_{3}}\sum_{i}<{q}_{i}(Eu)>$where S_i, σ_i and q_i are the magnetic spins of the i^th magnetic ions. In addition, N = N₁ + N₂ + N₃.

The total magnetization is given by

$$M = \frac{{N_1 \times M_{Fe^{3 + } } + N_2 \times M_{Mn^{3 + } } + N_3 \times M_{Eu^{3 + } } }}{N_1 + N_2 + N_3 }.$$

Magnetic specific heat of EuFe_0.5Mn_0.5O₃ is given by

$$C_m = \frac{\beta^2 }{N}\left[ { < {\text{E}}^{2} > - < {\text{E}} >^{2} } \right]{\text{ where }}\beta = \frac{1}{KB}.$$

From the following Maxwell’s thermodynamic equations relations $\left( {\frac{{\partial {\text{Sm}}}}{{\partial {\text{h}}}}} \right)_{\text{T}} = \left( {\frac{{\partial {\text{M}}}}{{\partial {\text{T }}}}} \right)_{\text{h}}$, the entropy variation is associated with the magnetocaloric effect. Considering an isothermal environment, the variation of the corresponding magnetic entropy is given by the following relation:

$$\Delta {\text{S}}_{\text{m}} \left( {{\text{T}},{\text{h}}} \right) \, = {\text{ Sm }}({\text{T}},{\text{ h}} \ne 0) - {\text{ Sm }}\left( {{\text{T }}, \, 0} \right) = \int_0^{h\max } {\left( {\frac{{\partial {\text{M}}}}{{\partial {\text{T }}}}} \right)} h_i {\text{ dh}} \, = \, \sum \limits_i { }(\frac{{\partial {\text{M}}}}{{\partial {\text{T }}}})_{h_i }$$

where h_max is the maximum value of external magnetic field and ${(\frac{\partial \mathrm{M}}{\partial \mathrm{T }})}_{{h}_{i}}$ is the thermal magnetization for a fixed magnetic field hi.

The famous expression of relative cooling power RCP is: ${\text{RCP}}= \int \nolimits_{T_c }^{T_h } {{\Delta }}s(T)dT$, where T_h and T_c are the hot and the cold temperatures, respectively.

4 Results and discussion

Ab initio calculations and Monte Carlo simulations have been used to study the magnetic and electrical properties of EuFe_0.5Mn_0.5O₃ perovskite.

In this work. Murnaghan's equation of state is employed to plot the curve for minimizing total energy in Fig. 2. The model report that the antiferromagnetic magnetic structure is the most stable, such as given in Refs. [27, 28]. The structural parameters a, b and c are obtained and stored in Table. 2.

${\text{E}}_{{\text{Tot}}} = \frac{VB_0 }{{B_0 }}\left( {\frac{1}{1 + B_0 }} \right)\left[ {\frac{V_0 }{V} + B_0 \left( {1 - \frac{V_0 }{{V_0 }}} \right) - 1 } \right] + E_0$ with V₀ is the equilibrium volume, B₀ and B are, respectively, the compressibility modulus and derivative of B₀ is given in Table 2. Then, we have studied by Monte Carlo simulation the variation of the magnetization according to the temperature Fig. 3a which shows that there is a temperature lower than the transition temperature T_N $\approx$ 310 K for which the magnetization becomes zero. This temperature is the compensation temperature which characterizes ferrimagnetic materials. T_comp $\approx$ 270 K. note that the phenomenon of spin reorientation does not appear in this curve. on the other hand, in Fig. 3b which represents how dM/dT varies with temperature, we notice a rise in dM/dT indicating an increase in magnetization which evolves towards a new magnetic order (quasiparamagnetic phase) which is the spin reorientation which produced at temperature T_sr $\approx$ 260 ֩K followed again by a decrease in dM/Dt which will reach its minimum at transition temperature T_N = 310 K. The application of a magnetic field allows to align the magnetic moments thus creating a form of order in the system, the transition from a disordered state to an ordered state is accompanied by a reduction of the entropy. $\Delta$ S in Fig. 4a represents the dependence of magnetic entropy on temperature for several values of the external magnetic field h. we see again and in agreement with the results of Fig. 3a. the spin reorientation which is manifested by the decrease in entropy S from the temperature T 180 K and to reach a minimum value at a temperature of Tsr = 260 K corresponding to a magnetic order then $\Delta S$ begins to increase by increasing the temperature for take the value $\Delta$ S_Max at the transition temperature T_N = 310 K. The same behavior of $\Delta S$ is observed in Fig. 4b. Variation relative cooling power with different several externals is plotted in Fig. 5. After then, changes in magnetic entropy and magnetic specific heat can be used to indirectly determine the adiabatic temperature change ΔT_ad. Figure 6 illustrates the relationship between adiabatic temperature change and temperatures. The ΔT_ad values of the perovskite are under EuMn_0.5 Fe_0.5O₃ action of different values of external magnetic field, and the maximum of ΔT_ad coincides with the transition temperature 310 K. This result confirmed that given in figures before. Moreover, The T_ad curves vary in the same way as the corresponding entropy reaching a maximum in the magnetic transition temperature interval. The maximum of ΔT_ad is situated at the transition temperature point of 310 K. This result is consistent with those found in Fig 4a, b. In the plot of Fig. 7, the magnetic fluctuations are described by the specific heat, a parameter that changes with temperature. It was noted that throughout the period [0.50 K], the specific heat capacity curve does not change and stays at zero. Then, increases to reach a peak and begins to decrease until ΔC_p = 0 at the reorientation temperature T_sr found before. The specific heat continues to decrease until a peak indicating a second-order phase transition arrives. The temperature of the minimum T = 315 K. Coincides with the transition temperature T_N called Néel temperature. The hysteresis cycles plotted in Fig. 8 for different temperature values show a double jump concerning the saturation magnetization, since it jumps discontinuously from one value to another during the symmetrical cycle of magnetization and demagnetization. The more the temperature increases the more the loop of the cycle tightens and disappears near the transition temperature T_N = 315 K. In the perspective of investigating the electronic properties of the compound EuMn_0.5 Fe_0.5O₃, the partial and total densities of the states of this material have been studied using the GGA approximation and the results have been represented in Figs. 9, 10, 11 and 12, where 0 eV is used as the fixed Fermi level. From Figs. 9, 11 and 12, the partial DOS of Mn and Fe atoms were compared, and the results showed that Mn–d and Fe–d atoms have a large contribution in the cases of spin up and spin down, while atoms O and Eu show a weak magnetic contribution in compound EuMn_0.5Fe_0.5O₃. The total, partial and interstitial magnetic moments of each atom in our system were calculated by using GGA (Table 3). Furthermore, it appears that the region of the valence band for the compound is located in the interval [− 7.5; 0] eV is that it is composed essentially by d orbitals of Mn and Fe atoms (see partial DOS of Mn and Fe in Figs. 9, 11, 12 and 13). While the conduction band region for the compound EuMn_0.5Fe_0.5O₃ (Total DOS in Fig. 10) is only created by the s orbital of Eu. As a result of the total and partial DOS results, the contribution of the compound EuMn_0.5Fe_0.5O₃ is mainly due to Fe–d and Mn–d in the valence band regions and due to Eu–s in the conduction band. Moreover, the results showed that the up and down spins of total DOS are symmetric. Thus, proving the ferrimagnetic behavior of the compound. The band structure of the compound shows that there is an overlap between the valence band and the conduction band around the Fermi level and the gap between these two bands is zero. This property is that of a conductive metal.

Fig. 9

Total and partial DOS for both Fe and Mn atoms

Fig. 10

Total DOS of EuFe_0.5Mn_0.5O₃

Fig. 11

Partial and total DOS of oxygen for s and p oribitals

Fig. 12

Partial and total DOS of Europium

Fig. 13

Band structure of EuFe_0.5Mn_0.5O₃ using GGA for both spin up and spin down

Table 2 Lattice parameters${\mathrm{a}}_{0}(\mathrm{A}^\circ )$, ${\mathrm{b}}_{0}(\mathrm{A}^\circ )$,${\mathrm{c}}_{0}(\mathrm{A}^\circ )$, equilibrium volume${\mathrm{V}}_{0}{({\mathrm{A}}^{^\circ })}^{3}$, total energy${\mathrm{E}}_{0 }(\mathrm{Ry})$, bulk modulus ${\mathrm{B}}_{0}(\mathrm{GPa})$ and its pressure derivative ${\mathrm{B}}_{0}^{\mathrm{^{\prime}}}$ for ${\mathrm{EuFe}}_{0.5}{\mathrm{Mn}}_{0.5}{\mathrm{O}}_{3}$ compound

Table 3 Total, partial and interstitial magnetic moments calculated of EuFe_0.5Mn_0.5O₃ using GGA

5 Conclusion

A ferrimagnetic system makes up the perovskite model under study. We looked at the material's magnetic, electrical, and magnetocaloric characteristics using Monte Carlo simulations. Consequently, it is possible to draw the conclusion that the transition from the ferrimagnetic to the paramagnetic phases is of second order. The magnetization vs temperature graph shows the compensating phenomena. While the fluctuation curves of S, dM/dT, and ΔT_ad show the spin reorientation phenomena. In addition, the magnetocaloric effect of EuFe_0.5Mn_0.5O₃ was investigated by using the Monte Carlo simulations. The portion of the investigation based on FLAPW and GGA revealed that Fe–d, Mn–d, and Eu–s in the compound are mostly responsible for the components magnetic. Equally on the electrical side the latter is metallic in character.