Introduction

Alcoholic fermentation is an anaerobic process transforming sugars into ethanol and CO2 alongside energy production. It is catalyzed by enzymes secreted by microorganisms, which produce energy for their physiological activities, growth, and reproduction, producing ethanol as a byproduct (de Almeida Lima 2019).

According to Dias et al. (2015), the fermentation process must be optimized to increase the sugars’ efficiency consumption in this stage. Tesfaw and Assefa (2014) have stated that the temperature, pH, initial sugar concentrations, oxygen concentration, organic acids, and dissolved solids are potential parameters affecting the specific rate of yeast growth and ethanol production.

Simulation software allows users to analyze their design to optimize the process using case studies to evaluate heat integration, different operating conditions and configurations, and raw material compositions. Recently researchers have been devoting efforts to applying simulation tools to simulate the ethanol production from sugarcane bagasse and trash (Carpio and de Souza 2017). There are several studies (da Cunha and Caurin 2017; David et al. 2010; Dhabhai et al. 2013; Esfahanian et al. 2016; Fan et al. 2015; Ahmad 2011; Felix et al., 2014; Gòdia et al. 1988; Liu 2014; Sulieman et al. 2018; Tesfaw and Assefa 2014) that have been addressing the implementation of kinetic models of fermentation processes.

In the last years, single-objective optimization of the fermentation processes has been proposed by some authors, for example, (i) glucose isomerase production (Thi Nguyen and Tran 2018), (ii) ethanol production from sugarcane (Mutran et al. 2020), and (iii) beer production (Rodman and Gerogiorgis 2016). However, in recent years, multi-objective optimization (MOO) has been the focus of research (Yingling et al. 2011; Shadbahr et al. 2018; Andiappan et al. 2015; Wang and Sheu 2000; Garcia and You 2015) since it allows improving the process through different perspectives or objectives. In the work of Shadbahr et al. (2018), a MOO of the simultaneous saccharification and fermentation process for cellulosic ethanol production was conducted to maximize the ethanol yield/cellulose conversion and minimize the enzyme consumption by manipulating the initial sugar concentrations and the cellulose and enzyme loadings. An overall 40% reduction of the enzyme consumption per ethanol produced was attained for the same ethanol yield (32%) as a non-optimized process.Andiappan et al. (2015) proposed the MOO of the synthesis of an integrated biorefinery. They considered different types of biomasses feedstock based on their lignin, cellulose, and hemicellulose compositions. The results permitted analyzing different reaction pathways based on economic, environmental and energy criteria.Garcia and You (2015) developed a comprehensive bioconversion network model for fuel production. They used a multi-objective strategy coupling capital and operating expenditures (CAPEX and OPEX) together with environmental impacts.Ansoni and Seleghim (2016) applied computational fluid dynamics (CFD) to design a continuous flow bioreactor. The MOO was used to search the Pareto frontier characterized by performance parameters such as residence times, shear stress, and geometric parameters. Other relevant works on MOO applied to fermentation processes can be mentioned: Link et al. (2008); Logist et al. (2010); de Medeiros et al. (2019); Rodman et al. (2018) and Xu et al. (2021). Among these works, several advances in the area of multi-objective optimization have been reported, mainly tests and comparison of evolutionary and deterministic algorithms (Link et al. 2008; Rodman et al. 2018), such as NSGA-II algorithm and development of computational packages (Ansoni and Seleghim 2016; Logist et al. 2010).

Different types of biomasses have the potential as raw materials for bioethanol production. Because of their chemical composition, they mostly form three groups: (i) sugar-containing raw materials: sugar beet, sugarcane, molasses, whey and sweet sorghum, (ii) starch-containing feedstocks: grains such as corn, wheat, root crops such as cassava, and (iii) lignocellulosic biomass: straw, agricultural waste, crop and wood residues, barley straw, barley husks, corn stover, sugar cane bagasse, and switchgrass (26).

The Brazilian sugar and ethanol units or industries use sugarcane as their primary raw material. Sugarcane is one of the most planted crops around the world. In Brazil, the sugarcane is the primary feedstock to produce sugar; ethanol is a secondary product. Most of distilleries in Brazil are attached to the sugar factory. Sugarcane has been used as feedstock for ethanol production on a large-scale basis in Brazil for over three decades, where sugarcane plants produce sugar, ethanol and electricity (Dias et al. 2015).

In Brazil, 2 million tons of cashew apples are produced yearly, in which 90–94% of the apples are discarded, as the main industrial product is cashew nuts. In addition, about 10% of cashew apples used for commercial production (e.g., wine and fruit juice) are consumed locally (Deenanath et al. 2013; Luz et al. 2008).

There are other raw materials with great potential, such as the cashew fruit (consisting of a fleshy part and a cashew nut), which currently has a wastage of 90%, as mainly the nuts are sold. Cashew apple juice appears to be a promising alternative raw material to produce ethanol by fermentation. Thus, since the potential of the cashew fruit is not fully exploited, the use of this coproduct to produce ethanol will not only bring economic benefits but also solve issues related to the disposal of the unwanted part of the cashew fruit, adding value to the production chain of cashews.

Some authors (Pereira et al. 2019; Pinheiro et al. 2017) have recently implemented cashew apple juice fermentation simulation, in which some sensitivity analyses were performed. Pinheiro et al. (2017) have simulated the process and applied the response surface methodology (RSM) to study different process configurations. Their results demonstrated that the most important variables for a high volume/low value-added product are product yield per substrate, final titer, and productivity. They also emphasized that the final ethanol percentage per volume of solution (%\({V}_{ethanol}\)/\({V}_{solution}\)) must also be monitored; at least 4% (v/v) is required for efficient distillation. Pinheiro et al. (2020) have proposed a process optimization to maximize the sugar conversion efficiency to ethanol. The model optimization was based on the partial derivative of the efficiency function concerning each decision variable. Response surface graphs were built to illustrate the influence of the evaluated variables on efficiency. Pereira et al. (2021) developed a hybrid neural model obtained by combining mass balance equations with an artificial neural network, predicting reaction-specific rates. They also proposed an optimization based on an objective function of efficiency and productivity by applying the Particle Swarm Optimization (PSO) algorithm.

Table 1 summarizes the main works on the optimization of fermentation processes.

Table 1 Applications of simulation and optimization to fermentation processes
Full size table

As reviewed, there are several applications of MOO to fermentation processes; however, there are still no applications for the problem studied in this manuscript. We believe that the application of MOO can be an extension of the works of Pereira et al. (2019) and Pinheiro et al. (2017). Pereira et al. 2021) aimed to apply MOO for the problem studied in this manuscript, the optimization was simplified by using a geometric mean between the efficiency and productivity in which they turned the MOO into a SOO since it was carried out for one operating point and the Pareto curve could not be obtained.

The main advantages of applying MOO (Pardalos et al. 2017) are :

  1. (i)

    Find optimal solutions to generate a Pareto curve for a problem involving multiple objectives.

  2. (ii)

    Choose the best option from the generated Pareto curve by presenting the solutions to the decision-maker.

  3. (iii)

    Enable the a priori generation of optimal data, avoiding the need to perform new optimization calculations at every objective change.

The present work aims to investigate the optimization of ethanol production from cashew apple juice fermentation in a batch reactor. In the proposed strategy, three goals are simultaneously optimized: (i) the ethanol yield from the cashew juice feed, (ii) the ethanol yield from the cashew juice consumed, and the (iii) volumetric ethanol productivity, optimum temperature, initial concentration of cashew juice, and fermentation time. The WSM (Pardalos et al. 2017) was applied to the MOO with the Nelder–Mead (NM) algorithm.

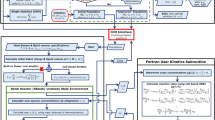
The work is structured as follows: Topic 2 describes the kinetic study, including the mathematical modeling of the process. Topic 3 focuses on the process optimization stage. The results are presented in Topic 4, and Topic 5 concludes with presenting findings and suggestions.

Kinetic study

Mathematical model

The kinetic model was based on the works of Pereira et al. (2019) and Pereira (2016), consisting of a batch bioreactor containing 750 mL of cashew juice. The model used to describe the system is represented by the following Eqs. (1–11):

$$\frac{{dX_{V} }}{{dt}} = \mu \cdot X_{V} - k_{d} \cdot X_{V}$$
(1)
$$\frac{{dX_{d} }}{{dt}} = k_{d} \cdot X_{V}$$
(2)
$$\frac{{dS}}{{dt}} = - \left( {\frac{{\mu _{{mix}} \cdot \mu _{s} }}{{\mu _{{mix}} + \mu _{s} }}} \right) \cdot X_{V}$$
(3)
$$\mu = \mu _{{max}} \cdot \frac{S}{{S + K_{s} + \frac{{S^{2} }}{{K_{i} }}}} \cdot \left( {1 - \frac{P}{{P_{{max}} }}} \right)$$
(4)
$$X_{T} = X_{V} + X_{d}$$
(5)
$$\frac{{dS}}{{dt}} = - \left( {\frac{{\mu _{{mix}} \cdot \mu _{s} }}{{\mu _{{mix}} + \mu _{s} }}} \right) \cdot X_{V}$$
(6)
$$\frac{{dP}}{{dt}} = Y_{{P/X}} \cdot \mu \cdot X_{V}$$
(7)
$$\mu _{{mix}} = \beta _{{mix}} \cdot \left( {S - S^{ * } } \right) \cdot I_{{mix}} ^{n}$$
(8)
$$S^{ * } = \eta \cdot S$$
(9)
$$\eta = {\text{b}} \cdot {\text{e}}^{{{\text{a}} \cdot {\text{X}}_{{\text{V}}} }}$$
(10)
$$\mu _{s} = \left( {\frac{\mu }{{Y_{{X/S}} }} + m_{s} } \right)$$
(11)

in which \({X}_{V}\) denotes the viable cells concentration, \({X}_{d}\) are dead cells concentration, \(S\) is the substrate concentration and \(P\) represents the ethanol concentration in (g/L).

The kinetic equation used to represent the specific cell growth rate (\(\mu\)), indicated in Eq. (3), was proposed by Ghose and Tyagi (1979), which considers inhibition by substrate and product. The parameters \({K}_{s}\) and \({K}_{i}\) correspond to the limiting substrate concentration and the initial substrate concentration at which inhibition starts, respectively, and \({P}_{max}\) corresponds to the maximum ethanol concentration that inhibits microbial growth. \({\mu }_{max}\) is the maximum specific rate of cell growth, \({Y}_{P/X}\) is the cell-to-product conversion, \({Y}_{X/S}\) is the substrate-to-cell conversion, \({\mu }_{s}\) is the specific substrate consumption rate and \({m}_{s}\) is the biomass maintenance coefficient.

The parameter \({\beta }_{mix}\) corresponds to the mass transfer coefficient in the stagnant film. Thus, the cell surface substrate concentration (\({S}^{*}\)) is lower than the free substrate concentration, being an exponential function of the cell concentration inside the reaction (Eqs. 9 and 10). The substrate flow through the boundary layer was defined analogously to Fick’s law, where the boundary layer thickness was given as a function of the stirring velocity (\({I}_{mix}=150 rpm\)) according to a power law.

The temperature effect on the parameters \({\mu }_{max}\), \({Y}_{X/S}\) and \({Y}_{P/X}\) is given by the modified Arrhenius equation (Eq. (12). The values of constants \(A\), \(B\), \(C\) and \(D\) were taken from the reference and are presented in Table 2. It is noteworthy that, as these values were obtained based on experiments performed by Pinheiro et al. (2017), they could only be used in the temperature range, stirring, initial substrate and yeast concentrations of (26–42) °C, (80–800) rpm, (70–170) and (3–10) g/L respectively, which were the ranges used in the experiments.

$${\text{Parameter}} = A \cdot e^{{B/T}} + C \cdot e^{{D/t}}$$
(12)
Table 2 Kinetic coefficients parameters (based on Pinheiro et al. (2017) and Pereira et al. (2019)
Full size table

The other kinetic parameters were considered constant by (Pereira et al. 2019) and their values are given in Table 3.

Table 3 Kinetic parameters (based on Pinheiro et al. 2017,Pereira 2016 and Pereira et al. 2019)
Full size table

The model was implemented into Scilab software (Scilab Enterprises 2012) software (version 6.1). The Adams method (Butcher, 2008) was used to solve the explicit ordinary differential equations system obtained.

Model validation

Pinheiro (2015) conducted a series of experiments that occurred at temperatures of 26, 30, 34, 38 and 42 °C, with initial cell concentrations of 3, 5, 8 and 10 g/L, stirring velocities of 80, 150, 300, 490, 650 and 800 rpm and initial substrate concentrations of 70, 90, 110, 130 and 170 g/L over a period of 12 h.

The residual standard deviation (RSD) (Pinheiro et al. 2017) between the experimental and theoretical data was used to evaluate the kinetic model. The RSD is written according to Eq. (13):·

$$\sum\limits_{{i = 1}}^{n} {\frac{{\left| {y_{i}^{{exp}} - y_{i}^{{th}} } \right|}}{n}}$$
(13)

in which \(y\) are the obtained data, \(\left( \cdot \right)^{{exp}}\) denotes the experimental data and \(\left( \cdot \right)^{{th}}\) are the theoretical data resulting from the simulation and \(\left| \cdot \right|\) is the L2 norm.

Optimization problem

Introduction to optimization problem

Optimization is a mathematical term that refers to the minimization or maximization of one or more functions of interest (objective functions), finding the optimal values of the variables to which these functions are dependent (decision variables) within a set (Nocedal 1999).

A general optimization problem is defined by Eq. 14 a–d:

$${\text{min}}_{x} F\left( x \right)$$
(14a)
$$g_{j} \left( x \right) \le 0; \quad j = 1, \ldots ,m_{i}$$
(14b)
$$h_{i} \left( x \right) = 0; \quad i = 1, \ldots ,m_{e}$$
(14c)
$$x_{{min,k}} \le x_{k} \le x_{{max,k}} ; \quad k = 1, \ldots ,n$$
(14d)

Decision variables are represented by the vector \(\mathbf{x}\), which contains \(n\) elements. \(F\), \(g\) and \(h\) refer to the objective function, inequality constraints and equality constraints, respectively. For a mono-objective problem, function \(F\) is composed of only one objective function, and for a multi-objective problem, \(F\) is composed of a set of objective functions. \({m}_{i}\) corresponds to the total number of inequality constraints, and \({m}_{e}\) represents the total number of equality constraints (Nocedal 1999).

It is possible to transform a constrained optimization problem into an unconstrained problem by using, for example, penalty methods, where \(F\left(\mathbf{x}\right)\) is replaced by a penalty function. An example of a penalty function is the exact penalty function given by Eq. (15), in which \({r}_{1}\) and \({r}_{2}\) are positive weights. The penalty increases for any values of that violate one of the equality or inequality constraints (Biegler 2010).

Penalty methods are generally associated with direct search optimization methods, which do not require derivative information such as Particle Swarm Optimization (PSO) (Marini and Walczak 2015) and Nelder-Mead (NM) (Nelder and Mead 1965).

$${P}_{1}\left(\mathbf{x},{r}_{1},{r}_{2}\right)=F\left(x\right)+\left[\sum _{i=1}^{{m}_{e}}{{r}_{1}}_{i}\left|{h}_{i}\left(\mathbf{x}\right)\right|+\sum _{j=1}^{{m}_{i}}{{r}_{2}}_{j}\text{m}\text{a}\text{x}\left\{0,{g}_{j}\left(\mathbf{x}\right)\right\}\right]$$
(15)

One of the interesting features of multi-objective optimization is that its solution is generally not unique as different tradeoff levels may be desirable (with each tradeoff level yielding a different solution). A set of solutions called Pareto optimal solutions form the complete solution set of the optimization problem.

Weighted sum method (WSM)

In MOO the set of optimal parameters form a Pareto set. Pareto optimal solutions are those for which any improvement in one objective will result in the worsening of at least one other objective. Thus, if a point is Pareto optimal, it can be assured that it is impossible to simultaneously improve all the objectives (Pardalos et al. 2017). The representation of a MOO with two objective functions is sketched in Fig. 1.

Fig. 1
figure 1

Representation of a MOO with two objective functions (minimization): a left, b right

Full size image

Notice in Fig. 1a that a feasible region exists between the two minimum points of objective functions. This region depends on the weights assigned to each function. Figure 1b shows the Pareto front resulting from different assigned weights.

An alternative technique is to reduce the number of objectives by transforming the multi-objective problem into a single-objective problem. This technique takes advantage of effective deterministic single-objective algorithms that handle constraints and converge with high precision in fewer evaluations of the objective functions and constraints (Pardalos et al. 2017).

An important point relates to the normalization of the objective functions, which must be done prior to the aggregation. For the aggregation to be efficient and at the same time to reflect the desired relative influence of each objective, the different objective functions must be normalized using the same normalization formulations as the design variables. The normalization must be done concerning each objective function’s minimum and maximum estimated values.

In this work, the decision variables were final fermentation time (\({t}_{F}\)), initial substrate concentration (\({S}_{o}\)) and temperature (\(T\)), while initial yeast concentration (\({X}_{o}\)) and stirring velocity (\({I}_{mix}\)) were set at 5 g/L and 150 rpm, respectively. The goal was to maximize three functions: (1) the volumetric ethanol productivity (\({Q}_{p}\)), calculated as the ratio between ethanol concentration at the steady state (\({P}_{SS}\)) and the final fermentation time (Eq. 16); (2) the ethanol yield from consumed substrate (\({\text{min}}_{{\,t_{F} ,T,S_{o} }} \left[ {F_{2} } \right]\eta _{{{\text{P}}/\Delta {\text{S}}}}\)) (EYCS), given by Eq. (17); (3) the ethanol yield from the substrate fed to the bioreactor (\(\eta _{{{\text{P}}/S_{o} }} )\) (EYFS) given by Eq. (18).

$$Q_{P} = \frac{{P_{{SS}} }}{{t_{F} }}$$
(16)
$$\eta _{{{\text{P}}/\Delta {\text{S}}}} = \frac{{P_{{SS}} }}{{0.511 \cdot \left( {S_{o} - S} \right)}}$$
(17)
$$\eta _{{{\text{P}}/S_{o} }} = \frac{{P_{{SS}} }}{{0.511 \cdot S_{o} }}$$
(18)

The first step to optimize the system was normalizing the objective functions. As the yields are already normalized, only the productivity had to be normalized, about the maximum productivity value, \({{Q}_{P}}_{max}\) (normalized productivity – NP: \({{{Q}_{P}/Q}_{P}}_{max}\)). In this way, the strategy adopted to find \({{Q}_{P}}_{max}\) was to run a single-objective optimization (SOO) with the objective function defined by Eq. (19):

$$F_{1} \left( {t_{F} ,S_{o} ,T} \right) = - Q_{P} + \wp \cdot \left[ {{\text{max}}\left( {t_{F} - t_{{SS}} ,0} \right) + {\text{ max}}\left( {32 - P,0} \right)} \right]$$
(19)

The objective function used (Eq. 19) is represented by the negative productivity plus the penalty term: \(\wp \cdot \left[ {{\text{max}}\left( {t_{F} - t_{{SS}} ,0} \right) + {\text{ max}}\left( {32.0 - P,0} \right)} \right]\), since it was imposed that the final fermentation time should not exceed the maximum steady state time \(({t}_{SS}=17 \text{h})\) and that the final ethanol concentration should not be lower than 32 g/L. This concentration is equivalent to 4% (v/v), which is the minimum value required to avoid azeotrope formation in the mixture, making the distillation of the fermented mixture difficult.

The function to be minimized is represented by the weighted sum of the negative yields and normalized productivity, according to Eq. (20):

$$F_{2} \left( {t_{F} ,S_{o} ,T} \right) = - w_{1} \cdot \underbrace {{\left( {\frac{{Q_{P} }}{{Q_{{P\max }} }}} \right)}}_{{F_{{2,a}} }} - w_{2} \cdot \underbrace {{\left( {{{\eta _{P} } \mathord{\left/ {\vphantom {{\eta _{P} } {S_{o} }}} \right. \kern-\nulldelimiterspace} {S_{o} }}} \right)}}_{{F_{{2,b}} }} - w_{3} \cdot \underbrace {{\left( {{{\eta _{P} } \mathord{\left/ {\vphantom {{\eta _{P} } {\Delta S}}} \right. \kern-\nulldelimiterspace} {\Delta S}}} \right)}}_{{F_{{2,c}} }} + \cdots \wp \cdot \left[ {\max \left( {t_{F} - t_{{SS}} ,0} \right) + {\text{ }}\max \left( {32 - P,0} \right)} \right]$$
(20)

in which \({w}_{1}\), \({w}_{2}\) and \({w}_{3}\) are the weighting factors, where \({w}_{i}>0, i=1, 2, 3\) and \(\sum _{i=1}^{3}{w}_{i}=1\).

The optimization strategy was divided into two steps:

  1. (i)

    Single-objective optimization with maximization of \({F}_{1}\):

    $${\text{max}}\,_{{t_{F} ,T,S_{o} }} [F_{1} ]$$
    (21)

    subject to:

    Equations. (1–11) [dynamic model]

  2. (ii)

    Multi-objective optimization with minimization of \({F}_{2}\):

    $${\text{min}}_{{\,t_{F} ,T,S_{o} }} \left[ {F_{2} } \right]$$
    (22)

subject to:

Eqs 1–11 [Dynamic model]

The Nelder-Mead (Nelder and Mead 1965) algorithms were used for the MOO coupled to the WSM. The main reasons for using the Nelder-Mead algorithm were: (i) ease of implementation in Scilab software (using the fminsearch function); (ii) Being a direct method (derivative-free), which proved to be robust for solving the problem, with a low computational cost for carrying out the optimization procedure; (iii) The method did not present convergence problems for the analysis of the studied problems, allowing its application together with the weighted-sum strategy. It should be noted that, as this was the first application of the strategy for building the system’s Pareto curve, a performance comparison study of different algorithms was not carried out.

Table 4 lists the parameters of the implemented Nelder-Mead algorithm (Nelder and Mead 1965) (https://github.com/NEOEQ/Fermentation-of-Cashew-Apple-Juice-Process).

Table 4 Nelder Mead’s specifications
Full size table

The following computer configuration was used: Intel(R) Core(TM) i7-8565U CPU @ 1.80 GHz 1.99 GHz, 8.00 GB RAM, and operating system Microsoft® Windows 10.

Simulated results

Comparison with experimental results

The ability of the kinetic model to fit the experimental data was evaluated through graphical analysis and the RSD values. Figure 2 illustrates the dynamic profiles of the biomass, substrate, and ethanol concentrations (in g/L) under different operating conditions: 30 (Fig. 2a and b), 34 (Fig. 2c) and 42 °C (Fig. 2d), at a stirring velocity (\({I}_{mix}\)) of 150 rpm. Notice that the initial concentrations are different for each subplot.

Fig. 2
figure 2

Simulated results: biomass (blue curve), substrate (black curve), ethanol (red curve); experimental results: biomass (circle), substrate (cross), ethanol (square); a, b 30 oC; c 34 oC and d 42 oC

Full size image

As observed in Fig. 2, the model satisfactorily represents the dynamics of the fermentation system studied under different operating conditions. The model reasonably predicts the substrate decrease and the increase of ethanol and biomass concentrations over time.

Table 5 shows that a good adjustment to the experimental data could be obtained for the four evaluated cases, with RSD values below 5%.

Table 5 RSD values
Full size table

Sensitivity analysis

Figure 3 shows the sensitivity analysis of the steady-state values of the substrate, ethanol, and biomass concentrations as a function of temperature for the initial concentrations presented in Fig. 2. Figure 3(a) shows that the final biomass concentration decreases with temperature, indicating that the ethanol production increases, as shown in Fig. 3c. In Fig. 3d, the maximum productivity value is between 6 and 7 \(\text{g}/\text{L}\) in the 34–38 °C temperature range. The maximum ethanol concentration in case (a) reaches approximately 80 g/L. Still, the productivity of case (a) is the lowest of the four cases due to the longer time taken to reach the steady state. This is one reason to consider optimizing the objective function represented by the volumetric ethanol productivity (\({Q}_{p}\)), calculated as the ratio between the ethanol concentration and the final fermentation time: \({Q}_{p}=P/{t}_{f}\). Figure 5 shows the steady-state time, referring to the case study shown in Fig. 4. The steady-state time is between 6 and 8 h for cases (b)–(d). In contrast, case (a) has a steady state time of around 15 h because of its high initial concentration of substrate.

Fig. 3
figure 3

Influence of temperature over biomass, substrate, ethanol concentrations and productivity

Full size image
Fig. 4
figure 4

Influence of temperature over reaction time

Full size image

Optimization results

Single objective optimization for obtaining \({{Q}_{P}}_{max}\)

As explained, a single-objective optimization was performed to calculate the value of \({Q}_{p,max}\). The initial concentrations of \({\text{X}}_{\text{V}0}=5 g/L\) and \({\text{P}}_{0}=0 g/L\) were used. Table 6 summarizes the optimal results and shows that the obtained values of substrate temperature and final time were \({\text{S}}_{0}=112.95 g/L\), \({\text{T = 35}}{\text{.79}}\) °C, and \({t}_{f}=7.63 h\), respectively. The maximum productivity was 7.15 g/L·h. The relative errors of the decision variables to obtain the same objective function value are smaller than 1%. The NM algorithm required a computational time of 5.58 s and 95 iterations. The results presented in Table 6 are close to those observed in Fig. 2.

Table 6 Summary of SOO results with Nelder Mead algorithm
Full size table

Pareto fronts

Figure 5A illustrates the obtained 3D-Pareto front resulting from the MOO procedure. The initial concentrations of \({\text{X}}_{\text{V}0}=5 g/L\) and \({\text{P}}_{0}=0 g/L\) were used. The Pareto graph allows us to analyze the cases where the solutions are non-optimal and optimal dominant. The surface exhibits a collection of possible optimal points, which depends on the weighting values assigned by the decision-maker. The results show that increasing the NP (\({Q}_{P}/{{Q}_{P}}_{max}\)) or EYCS (\(\eta _{{{\text{P}}/\Delta {\text{S}}}}\)) necessarily implies reducing the EYFS (\(\eta _{{{\text{P}}/S_{o} }}\)), and vice versa. This behavior can be better observed in Fig. 5B–D, which show the 2D projections of Fig. 5A. Notice a combination of optimal points depending on the weights assigned to each objective function. The values of the objective functions increase with the values of the weights ( \(\omega \in \left[\text{0,1}\right]\) ), which are chosen by the decision-maker, who must consider the importance of each function.

In Fig. 5B, the relationship between the efficiencies EYFS (\(\eta _{{{\text{P}}/S_{o} }}\)) and EYCS (\(\eta _{{{\text{P}}/\Delta {\text{S}}}}\)) can be examined. The reduction of EYCS favors the increase of EYFS. This behavior can be explained by the effect of \({S}_{o}\) on the ethanol concentration, which is nonlinear, as shown previously in Fig. 3. A considerable increase of \({S}_{o}\), contributes to the rise of ethanol concentration and, consequently, of \(\eta _{{\text{P}}}\). However, in that case, the \({\Delta }\text{S}\) value may be decreased as there may still be an excess of the substrate at the end of the process. Consequently, the denominator of EYCS (\(\eta _{{{\text{P}}/\Delta {\text{S}}}}\)) diminishes, while the denominator of EYFS (\(\eta _{{{\text{P}}/S_{o} }}\)) grows, causing the objectives to have opposite directions. This inverse effect is most noticeable in the right region of Fig. 5B, with a value of \(\text{E}\text{Y}\text{F}\text{S} <0.94\), which is the region of Fig. 5B where \({S}_{o}\) presents higher values.

The relation between the normalized productivity NP (\({Q}_{P}/{{Q}_{P}}_{max}\)) and EYFS (\(\eta _{{{\text{P}}/S_{o} }}\)) is visualized in Fig. 5C in which the interaction between these two functions is also inversely proportional, as in the previous case. In that case, it is more challenging to analyze the individual effects of the decision variables on the objective functions, mainly because \({S}_{o}\) and \({\text{t}}_{F}\) have a nonlinear interaction with productivity, as evidenced in Figs. 2 and 3. In these figures, it can be observed that a high increase in \({S}_{o}\) contributes to the increase of \({\text{t}}_{F}\), causing a decrease or increase in the NP. Temperature, on the other hand, can either decrease or increase the NP and EYFS (because of \({\eta }_{P}\)), as also evidenced in Fig. 3. These factors explain the nonlinear profile of the Pareto curve in this region.

Figure 5D shows that the NP (\({Q}_{P}/{{Q}_{P}}_{max}\)) and EYCS (\(\eta _{{{\text{P}}/\Delta {\text{S}}}}\)) have the same optimization direction, which characterizes the linear relation between these two functions, as corroborated by Fig. 5B and C. This behavior suggests that choosing these two objective functions would be redundant since both functions present the same direction of variation.

Table 7 summarizes the cause-effect matrix based on the relation of decision variables and objective function. Table 8 summarizes the interaction of the objective functions.

Table 7 Decision variables vs. Objective functions
Full size table
Table 8 Interaction of objective functions
Full size table
Fig. 5
figure 5

MOO solution: A 3D Pareto surface; B Pareto front: \(\eta _{{{\text{P}}/S_{o} }}\) × \(\eta _{{{\text{P}}/\Delta {\text{S}}}}\); C Pareto front: \({Q}_{P}/{{Q}_{P}}_{max}\) × \(\eta _{{{\text{P}}/{\text{S}}_{0} }}\); D \({Q}_{P}/{{Q}_{P}}_{max}\) × \(\eta _{{{\text{P}}/\Delta {\text{S}}}}\)  

Full size image

The analysis of Table 8 shows that the NP and EYCS objective functions are not conflicting, suggesting one can be removed from the study. The NP and EYFS functions are conflicting, characterizing a bi-objective problem. This case is represented by Fig. 5C.

Figure 6A–D displays the set of optimal points the decision variables represent. In Fig. 6A, the optimal temperature range is approximately 35.8 to 36.2 °C. The optimal substrate concentration varies from about 70 g/L to 110 g/L, and, according to Fig. 6A–D, the reaction time changed from around 3 to 8 h.

We can notice in Fig. 6 that all optimal solutions of the decision variables present a dispersion, resulting in the 3D surface of Fig. 6A. Tests were not carried out to investigate this behavior, which may occur due to the very characteristic of the optimization problem solution or the optimization methodology using the Nelder Mead algorithm (due to the sensitivity of the solution to the initial estimates, for example).

In Fig. 6B, it is possible to visualize three points: I, II (not optimal), and III (optimal). These three points were simulated from the proposed model to analyze the results. The results are presented in Fig. 7.

Figure 7 illustrates the biomass, substrate, and ethanol concentrations over time, for a temperature of 36 °C and initial substrate concentrations (\({S}_{0}\)) of 70, 100, and 110 g/L, corresponding to points (I), (II), and (III), respectively. The experimental values for the substrate concentration of 108 g/L and temperature of 34 °C were also plotted in all the graphs.

Fig. 6
figure 6

Decision variables: a 3D plot of decision variables; b \({\text{S}}_{0}\) × \(\text{T}\); c \({\text{t}}_{F}\) × \(\text{T}\); d \({\text{t}}_{F}\) × \({\text{S}}_{0}\)

Full size image

Figure 7i shows that point (i) presents a final ethanol concentration value of 32 g/L and a steady state time of 3.8 h. It is possible to observe that the ethanol concentration was significantly lower than the experimental concentration of approximately 50 g/L. Also, the results show that the initial substrate concentration substantially influences the final ethanol concentration, as previously observed in Fig. 2. Figure 7ii shows that the final ethanol concentration was very close to the experimental concentration, 49.2 g/L, and the steady state time (\({t}_{F}\)) of 6 h. Figure 7iii shows that the final ethanol concentration reached 50 g/L with a steady state time (\({t}_{F}\)) of around 7.8 h.

These results indicate that points (i) and (ii), which are outside the optimal curve of points, present ethanol production values (and consequently productivity for constant So) lower than the optimal values (point (iii).

Fig. 7
figure 7

Optimal results: biomass (blue curve), substrate (black curve), ethanol (red curve); experimental results for \({S}_{0}=108 \text{g}/\text{L}\): biomass (circle), substrate (cross), ethanol (square)

Full size image

Conclusions

This work simulated the fermentation process of cashew apple juice in the Scilab software. The results were compared with the literature results in which values lower than 6% of the residual standard deviation (RSD) of substrate, ethanol and biomass concentrations could be reached.

The results highlight four aspects:

  1. I.

    First, it was possible to get the Pareto curve by applying the WSM-NM algorithm, enclosing different optimization scenarios with the three objective functions.

  2. II.

    Among the three objective functions analyzed, we verified that the volumetric ethanol productivity (\({Q}_{P}/{{Q}_{P}}_{max}\)), and the substrate fed to the bioreactor (\(\eta _{{{\text{P}}/{\text{S}}_{0} }}\)) presented conflicting objectives.

  3. III.

    The results showed that temperature and initial substrate concentration greatly influence the reported objective functions.

  4. IV.

    The final batch time is an important optimization parameter, as it is related to productivity and the required initial substrate concentration. Also, time minimization requires higher substrate concentrations.

Additionally, some suggestions for improving the work can be highlighted:

  1. (i)

    The Nelder-Mead is a deterministic algorithm that depends on initial estimates of the decision variables. Therefore, an investigation of the sensitivity of the solution in relation to the initial estimates could help to improve the optimization result.

  2. (ii)

    The WS strategy is often used for multi-objective optimization. However, the true Pareto curve cannot always be obtained, especially for solutions that have non-convex profiles. Therefore, using evolutionary algorithms for multi-objective optimization, such as NSGA-II, could be useful to evaluate the results and compare them with the performance of the Nelder-Mead algorithm.

  3. (iii)

    Other optimization methods could also be tested and compared to the NM method, such as stochastic methods (Particle Swarm Optimization, Nelder Mead, Genetic) or Gradient-based algorithms (BFGS, Sequential Quadratic Programming, Interior Point). The main aspects observed would be computational cost, values of decision variables and objective functions.

From the industrial point of view, this is a valuable computational tool, as the multi-objective optimization strategy allows obtaining the set of optimal solutions necessary for an offline analysis, where the decision maker can choose the values of the decision variables to obtain a specific optimal solution. One of the main advantages of this type of tool is that new solutions (Pareto curves) can be obtained if there is any change in the initial conditions (of biomass or ethanol) or the stirring speed values. Thus, the number of experimental tests can be reduced to obtain optimal solutions.