1 Introduction

Ship weather routing is currently generating a lot of interest with the development of maritime transport. The problem consists in programming the route of a vessel through the ocean to its final destination within a given time window, in order to optimize one or more criteria, taking into account various environmental factors such as the wind, the waves or the currents, which have an impact on the progression of the vessel. The route specifies the trajectory of the vessel on the surface of the ocean and its speed at each point along the trajectory. In general the criteria to be optimized is the cost, correlated to fuel oil consumption, but it can also be necessary to consider other parameters such as time or various aspects concerning the safety or the preservation of the environment [1]. The evaluation of the criteria depends on the weather conditions, which change dynamically with the time (the values of these different factors are given in the form of forecasts covering the region and the period).

A particularity of ship weather routing in comparison to other routing problems such as vehicle routing, is that potentially the route can pass by any point on the surface of the ocean. This continuous aspect makes the problem all the more difficult. Many existing approaches operate on the basis of a discretization of the ocean surface, which takes the form of a grid [2, 3] or a meshing developed from departure and destination points around the orthodromic route [4,5,6], or a graph expanded dynamically applying course changes [7]. The routes are then defined by series of waypoints and by values specifying the speed of the vessel between the waypoints, assuming that between two successive waypoints the vessel sails in straight line, i.e., following the great circle route, and at constant speed. Some approaches are based on isochrones [7, 8], others on Dijkstra (and A*) algorithm [6, 9], on dynamic programming [5, 10, 11], or on evolutionary algorithms. In this last category genetic algorithms are the most common [4, 12,13,14,15,16], but there are also approaches based on ant colony optimization [17] or particle swarm optimization [3]. Optimizing the speed of the vessel while searching for a trajectory is an important point as there is a strong correlation between the two. All recent approaches take this aspect into account. Finally, it is also necessary to give the possibility to penalize or to forbid the navigation in some areas, or in certain weather conditions, or when some constraints are not met. This is useful for example to avoid regions with risks of piracy or unsafe sailing conditions, or to enforce time constraints [12]. A complete survey of weather routing and voyage optimization research in maritime transportation can be found in [18].

We propose a metaheuristic algorithm called WRM. The method solves the weather routing problem in the case time is not a criteria to optimize but a constraint. It searches the least costly routes within a given time window, optimizing the trajectory and the speed of the vessel. The approach proceeds somewhat as a greedy randomized adaptive search procedure (GRASP) [19]), and more particularly to its extension to the domain of continuous global optimization (C-GRASP) [20], where a parameter controls the density of the discretization. An advantage of the approach lies in the facility with which constraints concerning the regions which are traversed or the conditions of navigation that are encountered can be introduced.

The paper is organized as follows: in Sect. 2 we present the metaheuristic algorithm for the ship weather routing problem, in Sect. 3 we describe the experimentations that we have conducted using a basic evaluation of the fuel oil consumption of the vessel and we discuss the advantages of the method compared to other approaches. We conclude in Sect. 4.

2 The Metaheuristic Algorithm WRM

The problem we are interested in, denoted SWRTCP (for Ship Weather Routing with Time Constraint Problem), is to find the less costly routes from a point to another within a given period of time. Thus, time is not a criteria to be optimized but a constraint. In this section we will consider the surface of the ocean as a plane. A point in this plane is identified by its coordinates. The routes are represented by

  • a finite sequence of points \((p_{0},p_{1},\ldots ,p_{k})\),

  • a sequence of values that represent the speed, \((s_{0},\ldots ,s_{k-1})\),

  • a date \(t_{start}\).

Thus, a route is composed of a sequence of legs, each one connecting a pair of consecutive points of the sequence \((p_{0},p_{1},\ldots ,p_{k})\) following the orthodromic route. \(t_{start}\) specifies the departure date and \((s_{0},\ldots ,s_{k-1})\) specifies the speed of the vessel on each leg. This parameter can refer to the speed on the ground of the vessel (SOG), the power level of the engine, the number of revolutions per minute of the engine, or any other value that enables to determine the duration and the cost of the navigation. In the rest of the paper the term speed will be used to refer to this parameter.

We assume the functions cost and duration with parameters (u, v, s, t) are given, that return respectively the cost and the duration for crossing from the point u to the point v at speed s at the date t. The function duration is required to return a strictly positive value, provided that u and v coordinates are finite and v is positive. If this value is \(+\infty\) then it means that at speed s and at date t it is impossible to reach v from u. Finally, we will admit that \(\forall t, t',\ \text {if} \ t<t',\ \text {then}\ t+duration(u,v,s,t) \le t'+duration(u,v,s,t')\), that is, in other words, when crossing from a point u to a point v at a given speed s, it is not possible leaving u later to reach v earlier. The dates \(d_{0},d_{1},\ldots ,d_{k}\) at which the route reaches the points \(p_{0},p_{1},\ldots ,p_{k}\) and the corresponding costs \(c_{0},c_{1},\ldots ,c_{k}\), are calculated as follows: the date \(d_{0}\) is \(t_{start}\), and the date \(d_{i}\) with \(i>0\), is defined recursively:

$$\begin{aligned} d_{i} = d_{i-1} + duration(p_{i-1}, p_{i}, s_{i-1}, d_{i-1}) \end{aligned}$$

assuming that \(duration(p_{i-1}, p_{i}, s_{i-1}, d_{i-1}) \ne \infty\). If this is not the case the route is unfeasible. The cost to reach the first point of the route is \(c_{0}=0\), and the cost to reach the point \(p_{i}\) if the route is feasible, is

$$\begin{aligned} c_{i} = c_{i-1} + cost(p_{i-1}, p_{i}, s_{i-1}, d_{i-1}) \end{aligned}$$

Given two points denoted departure and arrival and a time interval \([{t_{min}}, {t_{max}}]\), the SWRTCP consists in finding the less costly feasible routes from departure to arrival that leave departure after date \({t_{min}}\) and reach arrival not later than \({t_{max}}\). We propose an algorithm called WRM  for this problem. The idea consists in solving successively simplified versions of the problem generated from random graphs. Each time, the results of the previous runs are utilized to refine the search space and limit the possible choices for the current run. This reduction-densification of the search space is achieved by limiting the region of the plane in which the route is searched, and by reducing the ranges for the values of the speed and the passage dates at each waypoint. The algorithm stops after a given number of runs.

2.1 Simplified Versions of the Problem

A simplified version of the problem is defined by:

  • P: a finite set of points defined by their coordinates, containing at least departure and arrival,

  • \(G=(P,A)\): a directed graph whose vertices are the points of P,

  • \(D_{dep}\): a set of dates,

  • I: time intervals associated to the vertices of G,

  • S: finite sets of values of the speed, associated to the arcs of G,

  • cost, duration: the functions introduced in previous section.

A solution of the simplified version of the problem is a feasible route \(((p_{0},p_{1},\ldots ,p_{k}),\) \((s_{1},\ldots ,s_{k}), t_{start})\) such that

  • \(\{p_{0},p_{1},\ldots ,p_{k}\} \subseteq P\), \(p_{0}=departure\) and \(p_{k}=arrival\),

  • \(\{(p_{0},p_{1}),(p_{1},p_{2}),\ldots ,(p_{k-1},p_{k})\}\subseteq A\),

  • \(t_{start} \in D_{dep}\) and \(\forall i\in \{0,1,\ldots ,k\},\ d_{i}\in I_{p_{i}}\),

  • \(\forall i\in \{0,\ldots ,k-1\},\ s_{i}\in S_{(p_{i},p_{i+1})}\),

where \(d_{i}\) is the date at which the point \(p_{i}\) is reached, as defined previously using the function duration. The simplified problem consists of finding the less costly solutions, that is those whose total cost \(c_{k}\) as defined above is minimal. This problem is not very different from the Weight Constrained Shortest Path Problem (WCSPP), if we substitute in G each arc (u, v) with as many arcs as there are values of the speed in \(V_{u,v}\). The WCSPP is NP-hard, even if the graph is acyclic and all weights and costs are positive, but it can be solved in pseudopolynomial time [21]. In our case the graph is dynamic, that is the weights and the resource consumption of the arcs change with the time. From WRM’s perspective it is not necessary to work with exact solutions, since the objective is just to identify the regions in which good quality routes are likely to be found. We have developed a simple and efficient (but not exact) algorithm called searchAGoodRoute, which requires the graph G to be acyclic. In practice this constraint is achieved when generating the graphs in WRM, using the lengths of the direct routes (that is the great circle routes) from departure to the points of P. The arcs which are considered are those whose origin is closer to departure than the destination. In the case of ship weather routing in open sea (that is without obstacles) it is unlikely that better routes can be obtained by going backwards. In fact, to our knowledge, this possibility is not considered in the existing approaches, whether they are based on meshings of the surface of the ocean expanded from departure, or they use genetic algorithms.

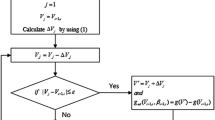
The function searchAGoodRoute is presented in Algorithm 1. It consists of a forward search that propagates dated costs in the graph. A dated cost associated to a vertex u is a pair (t, c) where t is a date and c is a cost. It indicates that the algorithm has discovered a route starting from departure that reaches u at date t for a total cost c. Initially, null dated costs corresponding to the dates of \(D_{dep}\) are created and associated to departure (lines 1-4). Then the vertices are considered one after the other in topological order. For each vertex u, its dated costs are propagated to its neighbors, considering successively the values of the speed available for the corresponding leg (line 5-11). Thus, for each dated cost \((t,c)\in costs(u)\), and for each neighbor v of u, \(|S_{(u,v)}|\) dated costs are generated and possibly added to the costs of v (line 9, function add). It can be useful at this stage to record, for each new dated cost, that it was generated from u with the cost (t, c), in order to be able to reconstruct the route if necessary. If a maximal bound of the total cost is given, it is possible to discard the dated costs that will lead to an excessive total cost, using minimal bounds of the costs to reach arrival. These bounds can be calculated determining the minimal and maximal arrival dates of each vertex (with the function duration), then estimating the minimal cost for each arc over the period (with the function cost) and finally performing a backward exploration of the graph.

The function searchAGoodRoute discovers valid routes joining departure to arrival with a departure date in \(D_{dep}\), that is routes that respect the time windows associated to the vertices and the potential speeds associated to the arcs. If all the dated costs that are generated during the process are saved, their number can grow exponentially with the number of vertices, even if the graph is reduced to a single path. For the method to be feasible in practice, it is necessary to discard some dated costs during the process. The parameter \(\delta\) is used for this purpose: it specifies the minimal time gap that must separate consecutive dated costs of a same vertex. If the addition of a new dated cost does not satisfy this constraint, one or more costs are removed. Note that there is no reason to prefer one to the other. Indeed even Pareto-optimal dated costs are not more likely to lead to best routes than non Pareto-optimal costs, since depending of the cost function it is possible that arriving later with a higher cost on an intermediate vertex results in a less costly route in the end (and since there are no cycles with null costs, which reflects the fact that the vessel is not allowed to stop and wait in the middle of the ocean). The number of costs propagations performed when running searchAGoodRoute is

$$O(|A| \times ns_{max} \times k_{max})$$

where \(ns_{max}=MAX_{(u,v)\in A}|S_{(u,v)}|\) and \(k_{max}=1+MAX_{u\in P}\lfloor I_{u}/\delta \rfloor\), which makes the method suitable if the graph is not too large.

figure a

2.2 The Metaheuristic Algorithm WRM

The procedure searchAGoodRoute can be used directly for SWRTCP. It suffices (1) to generate at random a set of points P containing at least departure and arrival, (2) to generate at random an acyclic graph G whose vertices are the points of P, (3) to select a set S of potential speeds for the vessel, and (4) to call searchAGoodRoute assigning to each vertex of G the time interval \([{t_{min}}, {t_{max}}]\). However, there are many parameters and the search space can be very large if the required level of accuracy is high. Moreover, a large part of the search effort will be spent exploring regions of the search space in which there is no chance to discover good quality routes. The idea behind the metaheuristic algorithm WRM is to use searchAGoodRoute as a tool to discard parts of the search space that are of no interest, and to progressively focus on the most promising regions. The procedure searchAGoodRoute is called many times. Each time a simplified problem is generated at random, based on the best route discovered in previous calls. The convergence is achieved by restricting the region of the ocean where the route is searched, the dates of passage and the speed of the vessel. We used the following parameters:

  • perimeter: the maximal distance from the waypoints to the best route,

  • speed range: the width of the range in which the potential values of the speed are chosen, for each crossing ; the minimal and maximal values are set from the values of the speed in the best route,

  • dates range: the length of the time period during which the vessel can transit, for each waypoint ; the periods are set from the dates of passage of the best route.

The objective is to converge quickly while not taking the risk of excluding regions of the search space that could contain optimal solutions. The following parameters are also useful:

  • number of vertices,

  • number of outgoing arcs for each vertex,

  • maximal (resp. minimal) length of the crossings corresponding to the arcs,

  • maximal number of dated costs for each vertex,

  • speed step (in practice, the speeds are enumerated between the minimal and maximal values associated to the leg, with increment speed step).

These parameters are likely to evolve during the execution of the algorithm to intensify the search. Figure 1 shows two graphs generated by WRM from given routes (in blue) with perimeters of value 400 (on the left) and 100 (on the right). There are 100 vertices in each graph, each vertex with at most 8 outgoing arcs. departure and arrival are respectively at the top right and at the bottom left. Each point is connected to its closest neighbors which are further away from departure.

Fig. 1
figure 1

Graphs generated with values 400 and 100 for the perimeter (chart \(4200\times 1800\))

Full size image

WRM is described in Algorithm 2. For a given number of runs a simplified version of the problem is generated and solved with searchAGoodRoute. The restrictions for the choice of the points, dates and speeds are set up using a marking of the chart (function markChart). The chart is divided into cells, and the marking specifies for each cell if it can contain points, and if so, what are the dates of transit and what is the speed of the vessel in the current best route when it crosses or passes close to this cell. The chart is marked after each call of searchAGoodRoute. For the first run the cells in a wide perimeter around the direct route from departure to arrival are marked, so as not to eliminate potentially promising areas (line 4). The function generateSimplifiedProblem generates a simplified problem, taking into account the marking, the set of parameters \(\mathcal {P}\) and the minimal departure and maximal arrival dates (line 6). It chooses at random the positions of the points, the connections between them, the sets of potential speeds associated to the connections, and the time intervals attached to the points. At this stage it is possible to refine the time intervals, propagating the minimal dates forward and the maximal dates backwards with the minimal and maximal durations of the crossings. Similarly minimal bounds of the costs to reach arrival can be calculated for each point. These bounds can serve to ignore useless dated costs in searchAGoodRoute. The function also returns the set \(D_{dep}\) of potential departure dates, consisting of all dates of the form \({t_{min}}+i\times \delta\) in the interval \([{t_{min}}, {t_{max}}]\). Then searchAGoodRoute is launched on the generated simplified problem. The variable bestRoute represents the best route discovered so far. Each time a better route is discovered, bestRoute is updated (lines 8-11). After each run, the parameters of \(\mathcal {P}\) are reinforced (function intensifyParameters) and the chart is marked again with the current best route (lines 12-13).

figure b

3 Experimentations

We have implemented WRM and we have tested it on the crossing of the North Atlantic Ocean. The computation of the durations and costs of the crossings depends of the speed parameter. This evaluation is difficult since many factors are involved, and the problem is not easily modelled. Recent approaches based on statistical models [22], regression modeling [23] or machine learning and neural networks [24] are predicting ship speed and fuel oil consumption successfully. They are all suitable for WRM. Indeed WRM just needs the duration and the cost of the crossing from one point to another at a given date and time for a given value of the speed parameter. We have developed a rough evaluation to perform the experiments. The speed parameter is the power level of the engine. We have supposed that the consumption grows linearly with the power level. Thus, the cost is the product of the power level of the engine by the duration of the crossing.

The environmental factors which are taken into account are the wind and the waves. Both have an influence on the progression of the vessel, depending on its speed and on its direction. We have considered that the power needed to move the vessel at the speed v given constant weather conditions is defined by

$$\begin{aligned} P = c_{0} + (P_{calm} + P_{wind}) \times C_{waves} \end{aligned}$$

where

$$\begin{aligned} P_{calm} = c_{1}\times v^{2.5} \end{aligned}$$

is the power required in calm water to make the vessel progress at speed v, and

$$\begin{aligned} P_{wind} = c_{2}\times A\times w_{a}^{2}\times \mathrm {cos}\,\theta _{a} \end{aligned}$$

is the power required to compensate for the effect of the wind on the progression, where A is the projected surface area of the emerged part of the vessel, and \(w_{a}\) and \(\theta _{a}\) are the apparent wind speed and the apparent wind to vessel direction (the apparent wind is the wind experienced by an observer on the ship). The coefficient \(C_{waves}\) represents the resistance due to the waves. It depends on the waves length \(\lambda\), the length L of the vessel at waterline, and the angle \(\theta _{w}\) between the waves and the longitudinal axis of the vessel

$$\begin{aligned} C_{waves} = f(\lambda , L, \theta _{w}, v) \end{aligned}$$

We have developed the function f from the results of G. Papageorgiou [25]. The maximum of the added resistance is observed when the angle is between \(130^\circ\) and \(180^\circ\) (\(180^\circ\) corresponds to head waves), depending of the ratio \(\lambda /L\) (the normalized wave length) and of the speed of the vessel. For example if the speed is 12 knots and the ratio \(\lambda /L\) is 1.25, the maximum resistance is reached when the value of \(\theta\) is \(160^\circ\). At 6 knots if the ratio is 0.8, the maximum resistance is reached at \(130^\circ\).

The coefficient \(c_{0}\) corresponds to the fuel oil consumption of the vessel when the engine is not engaged, the coefficient \(c_{1}\) weights the hull resistance, that is the cost of the progression of the vessel in calm weather conditions, and the coefficient \(c_{2}\) weights the effect of the wind on the superstructures of the vessel. We have considered that \(P_{calm}+P_{wind}\) cannot be negative. If this is the case P is set to \(c_{0}\). A table based on these formulas provides the speed on ground of the vessel from the power level of the engine and the weather conditions.

The values of the parameters used in the experiments are listed in Table 1. The very first runs are parameterized differently. Indeed, it is important at the beginning to not restrict the search space, in order to give the algorithm the possibility to discover very diverse routes. Thus, during the first ten runs, called the preliminary phase, the number of waypoints is important and the perimeter is very large. For the remaining runs, the normal phase, the value of some parameters evolve during the search. We have specified for these parameters their values at the first and at the last run. Depending on the values of the coefficients \(c_{0}\), \(c_{1}\) and \(c_{2}\), the wind and waves have more of less influence on the power needed by the vessel to progress. We set their values so that the strengths of the method can be seen clearly. Thus, the effect of the environmental factors is probably overestimated compared to the ships usually encountered today.

Table 1 Values of the parameters used for testing
Full size table

Figure 2 shows the execution of the procedure at different steps: at the end of the preliminary phase (top left drawing), at run 40 (top right drawing), and after the final run (bottom drawings, the left one with only the wind being represented, the right one with only the waves). We got weather data from NOAAFootnote 1 (GFS atmospheric model and GFS waves model, for a period of 16 days starting from January 20, 2022, with 3 hours intervals and a resolution of one degree). The region represented in the figure extends from 0\(^\circ\) N, 77\(^\circ\) W to 70\(^\circ\) N, 2\(^\circ\) E. The problem is to find a route from Cap Lizard (50\(^\circ\) 00’ N, 5\(^\circ\) 20’ W) to New-York (40\(^\circ\) 45’ N, 73\(^\circ\) 50’ W) within the period from January 29, 2022, at 10:00 pm to February 06, 2022, at 10:00 am, that is the duration of the voyage is at most 180 hours. The figure represents the chart, the points, the wind speed and direction, and the current best route (best route legs are represented by straight lines, although for the computations the great circle distance is used). The different colors correspond to different speeds, both for the wind and for the ship on the best route. The wind along the route is the wind at the moment the vessel passes. Similarly, at any position p in the chart, if the orthodromic distance from p to departure is d, the wind reported at p is the wind at the moment at which a vessel following the best route should be at the orthodromic distance d from departure. This explains why the representation of the wind may differ from one run to another. The program is written in Java and runs on a laptop equipped with a 2,5 GHz processor and 8GB of RAM. The orthodromic route from departure to arrival represented with a thin black line in the drawing is 2844.9 NM long. If the ship followed this route at minimal engine power so as to arrive before the deadline the cost should be about 5561352. The program stopped after 77.6 seconds, and returned a route of 55 legs that leaves departure at 10:00 pm on February 29 (which is \({t_{min}}\)) and reaches arrival 180.0 hours later (that is exactly at \({t_{max}}\)). The best route discovered during the preliminary phase (top left image) is 3041 NM long and its cost is 3911224. The final best route is 2981.8 NM long and its total cost is 3613024 (bottom left image). If we look at the graph after the preliminary phase, at run 40 and at the final run, we can see that the algorithm gradually refines the area in which good solutions are likely to be found. Figure 3 shows the power level of the engine and the speed over ground of the vessel along the final route (left drawing). On each leg the value of the speed is the average of the speed along the leg in knots. Note that the power level is continuously adjusted along the route. There is a strong correlation between the speed and the itinerary, which allows the vessel to avoid headwinds and to take advantage of favorable winds.

Fig. 2
figure 2

WRM best route after preliminary phase, at run 40 and at final run

Full size image
Fig. 3
figure 3

Engine power level on the best route returned by WRM, and all the routes discovered by WRM

Full size image

At each run, searchAGoodRoute is launched with the maximal number of dated costs associated to departure, with dates uniformly distributed between \({t_{min}}\) and the deadline for leaving departure. However, the departure and arrival dates of the best route returned by searchAGoodRoute are in most cases very close to \({t_{min}}\) and \({t_{max}}\). Lower speed means lower fuel oil consumption, so, unless the weather conditions are very special or if the navigation in certain conditions is strongly penalized, the more profitable routes will extend over the longest possible period. Nevertheless, during the search the algorithm discovers many routes with various departure and arrival dates. Figure 3 (right drawing) shows the 8465 dated costs corresponding to the valid routes that were generated by WRM over all runs. The solutions that are Pareto-optimal in this set are plotted in dark blue. It is likely that these solutions were generated during the last runs. They can be easily extracted if needed. However, optimizing all these solutions is not the objective of the method.

While WRM is running the positions of the potential waypoints change constantly and the meshing of the space gets more and more dense. This has little effect on the execution time of each run. Indeed, the size of the simplified problem varies relatively little (within the limits of the maximum values given as parameters), and the cost of the execution of searchAGoodRoute increases linearly with the size of the instance. Many approaches represent the potential waypoints as the nodes of a graph, based on a square grid, or on a meshing around the orthodromic route or expanded from the departure node applying predefined course changes. The possible positions of the waypoints are then limited in number and in most cases clearly defined when the search is launched. Thus, the potential crossings from a given waypoint are determined by the neighbors in the mesh or by the course changes to be considered. On the contrary, WRM generates new potential waypoints as it runs. This results in potentially more detailed routes. By adjusting various parameters, such as the number of runs, the number of waypoints or the perimeter, it is possible to increase the level of detail of the generated routes. Furthermore, time is indirectly discretized in WRM, since for each leg only few values are considered for the power level. However, the sets of available values become more and more dense as the algorithm proceeds, and even more if the engine power step is assigned a low value for the last runs. Thus, WRM can deliver solutions with the desired level of precision in a reasonable amount of computation time (the computation time grows linearly with the number of runs, the number of points and the number of values of the power level which are considered).

3.1 Avoiding Bad Weather Conditions

With the growth of sea shipping and the development of larger and larger ships, maintaining safety at sea has become critical. Navigation in severe weather conditions can be dangerous for the ship and its crew, and also for the other ships, for example if containers are lost at sea, and can have dramatic consequences from an ecological point of view. For this reason, navigation in fair conditions must be favored, and it is important to take this issue into consideration in a ship routing system. This kind of constraints can easily be implemented in WRM. If it is required to completely forbid navigation if the conditions are considered dangerous, it suffices to ignore the corresponding dated costs (Algorithm 1, line 9). For our experimentations we chose instead to just penalize the navigation when the conditions are bad by increasing the cost when some parameters, wind speed and direction, and waves height and direction, exceed given thresholds. For example we have supposed that a significant swell coming from the side could be dangerous for the vessel and its load, as well as a strong wind coming from the bow. If this is the case the consumption is multiplied by a factor depending on the amount of exceeding, in terms of speed for the wind or height for the waves. Table 2 lists the conditions in which the navigation is considered as unsafe.

Table 2 Conditions under which navigation is considered unsafe in our experiments
Full size table

A solution discovered by WRM is shown in Fig. 4 (same instance as the one presented before). It takes 88.1 seconds to the algorithm to return this route, the safe route, composed of 53 legs. It is 3117 NM long and its cost is 3861303. The safe route is significantly different from the basic route pictured in Fig. 2. It passes further north around the 50th meridian west, in order to bypass the low-pressure area whose center is at 50\(^\circ\) north and 47\(^\circ\) west and which is moving northeast, and crosses at the north of the island (corresponding to Newfoundland island) to avoid adverse conditions more to the south. On the entire route penalized conditions are never encountered. Compared to the basic route, the safe route is 6.9% more costly, not because the navigation is penalized, but because the route is longer. In contrast, on the basic route the vessel encounters severe weather conditions, in particular winds of more than 25 knots from the front and from the side.

Fig. 4
figure 4

WRM best route when bad weather conditions are penalized

Full size image

3.2 Emissions Control Areas

The protection and preservation of the environment are a major challenge for maritime shipping. Indeed transport by sea contributes significantly to the emission of greenhouse gases and other air pollutants. Emission Control Areas (ECA) have been created, with restrictive rules concerning in particular the quality of the fuel used for the engine. Such requirements can be satisfied by different means, but in most cases it makes navigation more costly in these areas. In WRM this specificity is simply implemented by increasing the cost when the ship is in an ECA. For our experiments we assumed the existence of a large ECA along the east coast of the United States, within which navigation is significantly more costly. Figure 5 shows the result obtained on the crossing Cap Lizard-New York. The ECA is colored in green. Sailing with bad weather conditions is not penalized. The route discovered by WRM is very different from the basic route shown in Fig. 2. It passes far to the south, in order to completely bypass the easternmost part of the ECA. However, to avoid the strong westerly winds between the 45th and 50th meridians west, the route had to stay above the 45th parallel and execute a sharp turn to the south. Then the vessel had to use its maximum power in order to cross the ECA in the final section at very low engine power level. It takes 71.6 seconds to WRM to discover this route which is 3120 NM long and costs 5522676. This cost is high because the route is long, the weather conditions encountered to avoid the eastern part of the ECA are not favorable, and finally the crossing of the western part of the ECA results in a significant additional cost.

Fig. 5
figure 5

Penalization of Emission Control Areas (ECA)

Full size image

4 Conclusion

In this paper we have described a metaheuristic algorithm called WRM for the ship weather routing problem with time constraint. The problem is to find the route of a vessel from one point to another that respects given departure and arrival dates, while minimizing the total cost. This one depends of the power level setting of the engine of the ship, and also of environmental factors such as the wind or the waves. We have implemented the algorithm, and performed experimentations, using a simplified evaluation of the cost. The results are convincing. It is easy to forbid or to penalize the navigation in certain situations, whether it concerns a region, a time period or specific weather conditions. The method discovers optimized routes. Compared to other approaches, WRM is not based on a predefined meshing of the space, nor on the discretization of the time. This particularity ensures a high level of detail to the solutions produced by WRM. Furthermore, the low computation time and the volume of weather data (20Mb in our example) makes the method suitable for use on board a ship as well as by a centralized service which would broadcast the results to the ship.

We plan to develop WRM in two directions. First, by taking into account several optimization criteria. Indeed, more and more, elements related to safety and environmental preservation must be considered, and cannot always be modeled with constraints or penalties. Several existing approaches, based on genetic algorithms, support the multi-criteria aspect [4, 6, 14, 15]. The part that can be a problem with WRM is the marking of the chart, which currently operates on the basis of a unique route, and that should take into account all Pareto-optimal routes discovered so far. Secondly, in the field of transport by sea, the weather routing problem is part of the more general framework of designing complete ship journeys. We believe that WRM can be very useful in this domain as a tool to provide statistical data, taking advantage of the fact that it requires low computational time.