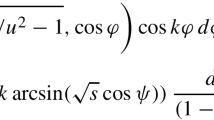Almost everywhere convergence of the Bochner–Riesz means for the Dunkl transforms of weighted $L^{p}$-functions

Abstract

For the Dunkl transforms associated with the weight functions $h_{\kappa }^2(x)=\prod _{j=1}^d |x_j|^{2{\kappa }_j}$, ${\kappa }_1,\ldots , {\kappa }_d\ge 0$ on ${{\mathbb {R}}}^d$, it is proved that if $p\ge 2$ and ${\delta }>{\delta }_{\kappa }(p):=\max \{(2l_{\kappa }+1) |\frac{1}{2}-\frac{1}{p}|-\frac{1}{2},0\}$, the Bochner–Riesz means $B_{R}^{\delta }(h_{\kappa }^2; f)$ converges to f at almost everywhere for all $f\in L^p({{\mathbb {R}}}^d; h_{\kappa }^2dx)$. This extends a well known result of Carbery et al. for the classical Fourier transforms (J Lond Math Soc 38:513–524, 1988).

1 Introduction and main results

In this paper, we consider weight functions

$$\begin{aligned} h^2_{\kappa }(x)=\prod _{j=1}^d |x_j|^{2{\kappa }_j},\quad k=({\kappa }_1,\ldots , {\kappa }_d),\quad k_j\ge 0, \quad j=1,\ldots , d. \end{aligned}$$

(1)

Let ${\sigma }_j$ be the reflection with respect to the coordinate plane $x_{j}=0$ ($j=1,\ldots ,d$). Namely,

$$\begin{aligned} x {\sigma }_j =(x_1, \ldots , x_{j-1}, -x_j, x_{j+1},\ldots , x_d),\quad x\in {{\mathbb {R}}}^d. \end{aligned}$$

Denote by ${{\mathbb {Z}}}_2^d$ the Abelian reflection group generated by ${\sigma }_1,\ldots , {\sigma }_d$. Clearly, $h^2_{\kappa }(x)$ is invariant under ${{\mathbb {Z}}}_2^d$.

For $1\leqslant p\leqslant \infty$, let $L^{p}({\mathbb {R}}^{d}; h_{{\kappa }}^{2})\equiv L^{p}({\mathbb {R}}^{d}; h_{{\kappa }}^{2}dx)$ be the $L^{p}$-space defined with respect to the measure $h_{{\kappa }}^{2}(x)dx$ on ${{\mathbb {R}}}^d$, and $\Vert \cdot \Vert _{{\kappa },p}$ the norm of $L^{p}( {{\mathbb {R}}}^d; h_{\kappa }^2)$. For a set $E\subset {{\mathbb {R}}}^d$, write ${{\,\mathrm{meas}\,}}_{\kappa }(E):=\int _E h_{\kappa }^2(x)\, dx.$ And denote by $\Vert \cdot \Vert$ and ${\langle }\cdot , \cdot {\rangle }$ the Euclidean norm and the Euclidean inner product on ${{\mathbb {R}}}^d$, respectively. Let $B(x,r):=\{ y\in {{\mathbb {R}}}^d:\ \Vert y-x\Vert \le r\}$ be the ball with center $x\in {{\mathbb {R}}}^d$ and radius $r>0$.

The Dunkl transform ${\mathcal {F}}_{\kappa }f$ of $f\in L^{1}({{\mathbb {R}}}^d; h_{\kappa }^2)$ is defined by

$$\begin{aligned} {\mathcal {F}}_{\kappa }f(x)=c_{\kappa } \int _{{\mathbb {R}}^{d}}f(y)E_{\kappa }(-{\mathbf {i}}x,y)h^{2}_{\kappa }(y)dy, \quad x\in {{\mathbb {R}}}^d, \end{aligned}$$

(2)

where $c_{\kappa }^{-1}=\int _{{{\mathbb {R}}}^d}h_{\kappa }^2(y)e^{-\Vert y\Vert ^2/2}\, dy$, $E_{\kappa }(-{\mathbf {i}}x, y)=V_{\kappa }\Bigl [ e^{-{\mathbf {i}}\langle x, \cdot \rangle }\Bigr ](y)$ is the weighted analogue of the character $e^{-{\mathbf {i}}\langle x, y\rangle }$ on ${{\mathbb {R}}}^d$, and $V_{{\kappa }}:\ C({{\mathbb {R}}}^d)\rightarrow C({{\mathbb {R}}}^d)$ denotes the Dunkl intertwining operator. In the case of ${\kappa }=0$ (i.e., the unweighted case), $V_{\kappa }$ is simply the identity operator on $C({{\mathbb {R}}}^d)$, and the Dunkl transform ${\mathcal {F}}_{\kappa }f$ becomes the classical Fourier transform. Furthermore, in the case when $f(\cdot )=f_0(\Vert \cdot \Vert )$ is a radial function, ${\mathcal {F}}_{\kappa }f$ becomes a Hankel transform of $f_0$.

It is clear that $h_{\kappa }$ is invariant under a reflection group. And Dunkl transform is an isometry of $L^2({{\mathbb {R}}}^d; h_{\kappa }^2dx)$, which has applications in physics for the analysis of quantum many body systems of Calogero–Moser–Sutherland type (see, for instance, [15, 16, 10, Section 11.6], [14]). From the mathematical analysis point of view, the importance of the Dunkl transform lies in that it generalizes the classical Fourier transform, and plays the similar role as the Fourier transform in classical Fourier analysis.

Many properties of Dunkl transform are very similar to those of the classical Fourier transform (see [7, 15, 16]). For instance, if the Dunkl transform ${\mathcal {F}}_{\kappa }f$ of $f\in L^1({{\mathbb {R}}}^d; h_{\kappa }^2)$ is also in $L^1({{\mathbb {R}}}^d; h_{\kappa }^2)$, then f can be recovered by ${\mathcal {F}}_{\kappa }f$ via inverse Dunkl transform. However, to check whether ${\mathcal {F}}_{\kappa }f\in L^1({{\mathbb {R}}}^d; h_{\kappa }^2)$ is sometimes difficult. To weaken this condition, a very useful tool is the Bochner–Riesz means of f, which are defined as

$$\begin{aligned} B_R^{\delta }(h_{\kappa }^2; f)(x)= c_{\kappa }\int _{\Vert y\Vert \le R} \left( 1-\frac{\Vert y\Vert ^2}{R^2}\right) ^{\delta }{\mathcal {F}}_{\kappa }f(y)E_{\kappa }({\mathbf {i}}x, y) h_{\kappa }^2 (y) \, dy, \quad x\in {{\mathbb {R}}}^d, \end{aligned}$$

where $R>0$, $f\in L^{1}( {{\mathbb {R}}}^d; h_{\kappa }^2)$, and ${\delta }>-1$ is the order of the Bochner–Riesz means. As in classical Fourier analysis, $B_R^{\delta }(h_{\kappa }^2; f)(x)$ can be expressed as an integral

$$\begin{aligned} B_{R}^{\delta }(h_{\kappa }^2; f)(x)=c_{\kappa }\int _{{\mathbb {R}}^{d}}f(y)K_R^{\delta }(h_{\kappa }^2;x, y) h_{\kappa }^2(y)\, dy,\quad x\in {{\mathbb {R}}}^d, \end{aligned}$$

(3)

which further extends $B_{R}^{\delta }(h_{\kappa }^2; f)$ to a bounded operator on $L^p({{\mathbb {R}}}^d; h_{\kappa }^2)$ for all $1\le p<\infty$ and $R>0$.

Summability of the Bochner–Riesz means $B_R^{\delta }(h_{\kappa }^2; f)$ for the Dunkl transform was studied in the pioneering paper by Thangavelu and Xu [15, Theorem 5.5], where it was proved that¹

$$\begin{aligned} \sup _{R>0} \Vert B_R^{\delta }(h_{\kappa }^2; f)\Vert _{{\kappa }, p} \le c \Vert f\Vert _{{\kappa },p},\quad \forall f\in L^p({{\mathbb {R}}}^d; h_{\kappa }^2) \end{aligned}$$

(4)

for all $1\le p\le \infty$ if and only if ${\delta }>l_{\kappa }: =\frac{d-1}{2}+|{\kappa }|$, where $|{\kappa }|=\sum _{j=1}^d {\kappa }_j$. Moreover, it was proved in [4, Theorem 4.3] that if $1\le p\le \infty$ and $|\frac{1}{p}-\frac{1}{2}|\ge \frac{1}{2l_{\kappa }+2}$, then (4) holds for all $f\in L^p({{\mathbb {R}}}^d; h_{\kappa }^2)$ if and only if

$$\begin{aligned} {\delta }>{\delta }_{\kappa }(p):=\max \Bigl \{(2l_{\kappa }+1)\Bigl |\frac{1}{p}-\frac{1}{2}\Bigr |-\frac{1}{2},0\Bigr \}. \end{aligned}$$

(5)

This last result extends the celebrated Thomas–Stein theorem for the Fourier transforms [17].

Thangavelu and Xu [15] also studied the maximal Bochner–Riesz operators:

$$\begin{aligned} B_{*}^{{\delta }}(h_{{\kappa }}^{2};f)(x):=\sup _{R>0} |B_{R}^{{\delta }}(h_{{\kappa }}^{2};f)(x)|,\quad x\in {{\mathbb {R}}}^d. \end{aligned}$$

They proved that:

$$\begin{aligned} \Vert B_{*}^{{\delta }}(h_{{\kappa }}^{2};f)\Vert _{{\kappa },p}\le C\Vert f\Vert _{{\kappa },p}, \quad \text { for }1<p\leqslant \infty \text { and } \delta >\lambda _{\kappa }. \end{aligned}$$

(6)

Feng Dai and Wenrui Ye gave a stronger result in [6] under the condition $\frac{1}{2}-\frac{1}{p}\ge \frac{1}{2l_{\kappa }+2}$. They proved that (6) holds for all $f\in L^p({{\mathbb {R}}}^d; h_{\kappa }^2)$ if and only if ${\delta }>{\delta }_{\kappa }(p)$. This result is due to Christ [2]. And by a standard density argument, this result directly implies that if $\frac{1}{2}-\frac{1}{p}\ge \frac{1}{2l_{\kappa }+2}$, ${\delta }>{\delta }_{\kappa }(p)$ and $f\in L^p({{\mathbb {R}}}^d; h_{\kappa }^2)$, then

$$\begin{aligned} \lim _{R\rightarrow \infty } B_R^{\delta }(h_{\kappa }^2; f)(x)=f(x) \quad \hbox { a.e.}\ x\in {{\mathbb {R}}}^d. \end{aligned}$$

(7)

In [6], it was also claimed, but not proved, the condition $\frac{1}{2}-\frac{1}{p}\ge \frac{1}{2l_{\kappa }+2}$ for (7) can be dropped. In this paper, we are devoted to give the proof of this fact. Our main result is stated as follows:

Theorem 1.1

If $p\ge 2$and ${\delta }>{\delta }_{\kappa }(p):=\max \{(2l_{\kappa }+1) |\frac{1}{2}-\frac{1}{p}|-\frac{1}{2},0\}$, then for all $f\in L^p({{\mathbb {R}}}^d, h_{\kappa }^2)$,

$$\begin{aligned} \lim _{R\rightarrow \infty } B_R^{\delta }(h_{\kappa }^2; f)(x)=f(x) \quad \hbox { a.e.}\ x\in {{\mathbb {R}}}^d. \end{aligned}$$

(8)

We point out that in the unweighted case of Fourier transform (i.e., the case of ${\kappa }=0$), Theorem 1.1 is well known and is due to Carbery et al. [1]. However, the proof of the weighted case is rather involved and more difficult.

This paper is organized as follows. Section 2 contains some preliminary materials on analysis associated with the Dunkl transform. Then, in Sect. 3, we prove our main result, Theorem 1.1. The proof relies on a technical result Theorem 3.3 which will be proved in Sect. 5. And in Sect. 4, we will prove some lemmas as preparations.

2 Preliminaries

In this section, we shall present some preliminary materials on Dunkl analysis associated with the group ${{\mathbb {Z}}}_2^d$ and the weight $h_{\kappa }^2(x)$ given in (1), most of which can be found in [5, 8,9,10, 14, 15, 16].

2.1 Dunkl intertwining operators

Let $E_j$ be the difference operator given by $E_j f(x):=\frac{f(x) -f(x{\sigma }_j)}{ x_j}$. The Dunkl operators ${{\mathcal {D}}}_{{\kappa },j}$ are defined by

$$\begin{aligned} {{\mathcal {D}}}_{{\kappa },j}:=\frac{\partial }{\partial x_j} +{\kappa }_j E_j,\quad j=1,\ldots , d, \end{aligned}$$

(9)

These operators are mutually commute, and map ${{\mathbb {P}}}_n^d$ to ${{\mathbb {P}}}_{n-1}^d$, where ${{\mathbb {P}}}_n^d$ denotes the space of homogeneous polynomials of degree n in d variables. A fundamental result in the Dunkl theory states that there exists a linear operator $V_{\kappa }$ on the space of all algebraic polynomials on ${{\mathbb {R}}}^d$, called the Dunkl intertwining operator, determined uniquely by the following conditions:

$$\begin{aligned} V_{\kappa }({{\mathbb {P}}}^d_n)\subset {{\mathbb {P}}}^d_n,\ \ V_{\kappa }(1) =1,\ \ \text {and}\ \ {\mathcal {D}}_{{\kappa },i} V_{\kappa }=V_{\kappa }\frac{\partial }{\partial x_i},\ \ 1\le i\le d . \end{aligned}$$

(10)

It was proved by Yuan Xu [18] that

$$\begin{aligned} V_{\kappa }f(x)= \int _{[-1,1]^{d}}f(x_{1}t_{1},\ldots ,x_{d}t_{d}) \prod _{j=1}^{d}d\mu _j(t_j), \end{aligned}$$

(11)

where $d\mu _j(s)=c_{{\kappa }_j} (1+s)(1-s^{2})^{\kappa _{j}-1}ds$ with $c_{{\kappa }_j}:=\frac{ \varGamma ({\kappa }_j+1/2)}{\sqrt{\pi }\varGamma ({\kappa }_j)}$ if ${\kappa }_j>0$, and $d\mu _j$ is the dirac measure supported at $s=1$ if ${\kappa }_j=0$. In particular, the formula (11) extends $V_{\kappa }$ to a positive operator on the space of continuous functions on ${{\mathbb {R}}}^d$.

For the Dunkl intertwining operator associated with a general finite reflection group, we refer to the work of Rösler [12].

2.2 Dunkl transforms

The Dunkl transform ${\mathcal {F}}_{\kappa }f$ of $f\in L^{1}({\mathbb {R}}^{d}; h_{\kappa }^{2})$ is defined by

$$\begin{aligned} {\mathcal {F}}_{\kappa }f(x)=c_{\kappa } \int _{{\mathbb {R}}^{d}}f(y)E_{\kappa }(-{\mathbf {i}}x,y)h^{2}_{\kappa }(y)dy, \quad x\in {{\mathbb {R}}}^d, \end{aligned}$$

(12)

where $c_{\kappa }^{-1}=\int _{{{\mathbb {R}}}^d}h_{\kappa }^2(y)e^{-\Vert y\Vert ^2/2}\, dy$,

$$\begin{aligned} E_{\kappa }(-{\mathbf {i}}x, y)= V_{\kappa }\Bigl [ e^{-{\mathbf {i}}{\langle }x, \cdot {\rangle }}\Bigr ](y) =\prod _{j=1}^d c_{{\kappa }_j}\Bigg [\frac{J_{{\kappa }_{j}-\frac{1}{2}}(x_jy_j)}{(x_jy_j)^{{\kappa }_{j}-\frac{1}{2}}} -{\mathbf {i}}x_jy_j\frac{J_{{\kappa }_{j}+\frac{1}{2}}(x_jy_j)}{(x_jy_j)^{{\kappa }_{j}+\frac{1}{2}}}\Bigg ], \end{aligned}$$

and $J_{\alpha }$ denotes the Bessel function of order ${\alpha }$ of the first kind:

$$\begin{aligned} J_{\alpha }(t)=\Bigl (\frac{t}{2}\Bigr )^{\alpha }\sum _{n=0}^\infty \frac{(-1)^n}{n! \varGamma (n+{\alpha }+1)}\Bigl (\frac{t}{2}\Bigr )^{2n}, \quad t\in {{\mathbb {R}}}. \end{aligned}$$

(13)

If ${\kappa }=0$, then the Dunkl transform coincides with the usual Fourier transform. And in this paper, we also use ${\widehat{f}}$ to denote the Dunkl transform of f.

The Dunkl transform ${\mathcal {F}}_{\kappa }$ restricted on the class ${\mathcal {S}}({{\mathbb {R}}}^d)$ of Schwartz functions on ${{\mathbb {R}}}^d$ satisfies the Plancherel formula $\Vert f\Vert _{{\kappa },2}=\Vert {\mathcal {F}}_{\kappa }f\Vert _{{\kappa },2}$. Thus, it extends to an isometric isomorphism on the space $L^2({{\mathbb {R}}}^d; h_{\kappa }^2)$. As a result, the Dunkl transform can also be defined on the space $L^1+L^2\supset \bigcup _{1\le p\le 2} L^p$.

The Dunkl transforms have properties similar to those of the classical Fourier transform. We collect some of these properties in the following lemma.

Lemma 2.1

[7, 13]

• (i) If $f\in L^1({{\mathbb {R}}}^d; h_{\kappa }^2)$then ${\mathcal {F}}_{\kappa }f\in C({{\mathbb {R}}}^d)$and $\lim _{\Vert \xi \Vert \rightarrow \infty } {\mathcal {F}}_{\kappa }f(\xi ) =0$.

• (ii) The Dunkl transform ${\mathcal {F}}_{\kappa }$is an isomorphism of the Schwartz class ${\mathcal {S}}({{\mathbb {R}}}^d)$onto itself, and ${\mathcal {F}}_{\kappa }^2 f(x) = f (-x)$for $f\in {\mathcal {S}}({{\mathbb {R}}}^d)$.

• (iii) If f and ${\mathcal {F}}_{\kappa }f$are both in $L^1({{\mathbb {R}}}^d; h_{\kappa }^2)$then the following inverse formula holds:

  $$\begin{aligned} f(x)=c_{\kappa }\int _{{{\mathbb {R}}}^d} {\mathcal {F}}_{\kappa }f(y) E_{\kappa }({\mathbf {i}}x, y) h_{\kappa }^2(y)\, dy ,\quad x\in {{\mathbb {R}}}^d. \end{aligned}$$

• (iv) If $f, g\in L^1({{\mathbb {R}}}^d; h_{\kappa }^2)$then

  $$\begin{aligned} \int _{{{\mathbb {R}}}^d} {\mathcal {F}}_{\kappa }f(x) g(x)\, h_{\kappa }^2(x)\, dx =\int _{{{\mathbb {R}}}^d} f(x) {\mathcal {F}}_{\kappa }g(x)\, h_{\kappa }^2(x)\, dx . \end{aligned}$$

  (14)

• (v) If $1\le p\le 2$and $\frac{1}{p}+\frac{1}{p'}=1$, then

  $$\begin{aligned} \Vert {\mathcal {F}}_{\kappa }f\Vert _{{\kappa },p'}\le \Vert f\Vert _{{\kappa },p}. \end{aligned}$$

  (15)

• (vi) Given $\varepsilon >0$, let $f_\varepsilon (x) =\varepsilon ^{-(2l_{\kappa }+1)}f(\varepsilon ^{-1} x)$with $l_{\kappa }:=\frac{d-1}{2} +|{\kappa }|$. Then ${\mathcal {F}}_{\kappa }f_\varepsilon (\xi ) ={\mathcal {F}}_{\kappa }f (\varepsilon \xi )$.

• (vii) If $f(x)=f_0(\Vert x\Vert )$is a radial function in $L^p({{\mathbb {R}}}^d; h_{\kappa }^2)$with $1\le p\le 2$, then ${\mathcal {F}}_{\kappa }f (\xi ) = H_{l_{\kappa }} f_0 (\Vert \xi \Vert )$is again a radial function, where $H_{{\alpha }}$denotes the Hankel transform defined by

  $$\begin{aligned} H_{\alpha }g(s) = \frac{1}{\varGamma ({\alpha }+1)} \int _0^\infty g(r) \frac{J_{\alpha }(rs)}{(rs)^{\alpha }} r^{2{\alpha }+1}\, dr,\ \ {\alpha }>-\frac{1}{2}. \end{aligned}$$

We will also consider the Dunkl transform on the space ${\mathcal {M}}$ of finite Borel measures on ${{\mathbb {R}}}^d$:

$$\begin{aligned} {\mathcal {F}}_{\kappa }(d\mu )(\xi )= c_{\kappa } \int _{{\mathbb {R}}^{d}}E_{\kappa }(-i\xi ,y)h^{2}_{\kappa }(y)d\mu (y),\quad \xi \in {{\mathbb {R}}}^d,\quad \mu \in {\mathcal {M}}. \end{aligned}$$

Many identities in this paper are interpreted in a distributional sense. Denote by ${\mathcal {S}}'({{\mathbb {R}}}^d)$ the space of all tempered distributions on ${{\mathbb {R}}}^d$. We shall identify a function f in $L^p({{\mathbb {R}}}^d; h_{\kappa }^2)$, $1\le p\le \infty$ with a tempered distribution in ${\mathcal {S}}'({{\mathbb {R}}}^d)$ given by

$$\begin{aligned} (f, \varphi ):=\int _{{{\mathbb {R}}}^d} f(x) \varphi (x) h_{\kappa }^2(x)\, dx,\quad \hbox { }\ \forall \varphi \in {\mathcal {S}}({{\mathbb {R}}}^d). \end{aligned}$$

According to (14), we may define the distributional Dunkl transform ${\mathcal {F}}_{\kappa }f$ of $f\in \bigcup _{p>2} L^p({{\mathbb {R}}}^d, h_{\kappa }^2)$ via

$$\begin{aligned} ({\mathcal {F}}_{\kappa }f, \varphi ) :=(f, {\mathcal {F}}_{\kappa }\varphi )\equiv \int _{{{\mathbb {R}}}^d} f(x) {\mathcal {F}}_{\kappa }\varphi (x) h_{\kappa }^2(x)\, dx, \ \ \forall \varphi \in {\mathcal {S}}({{\mathbb {R}}}^d). \end{aligned}$$

2.3 Generalized translations

Definition 2.2

[13, 14, 15] Given $y\in {{\mathbb {R}}}^d$, the generalized translation $T^y f$ of $f\in {\mathcal {S}}({{\mathbb {R}}}^d)$ is defined by

$$\begin{aligned} T^y f(x):=c_{\kappa }\int _{{{\mathbb {R}}}^d} {\mathcal {F}}_{\kappa }{f}(\xi ) E_{\kappa }(-{\mathbf {i}}y, \xi )E_{\kappa }({\mathbf {i}}\xi , x) h_{\kappa }^2(\xi )\, d\xi ,\quad x\in {{\mathbb {R}}}^d.\end{aligned}$$

(16)

It was proved in [6, Proposition 2.5] and [15] that the generalized translations are bounded operators on $L^p({{\mathbb {R}}}^d; h_{\kappa }^2)$ for all $1\le p\le \infty$. Throughout the paper, we will use (16) as the definition of the generalized translation $T^y f$ of $f\in \bigcup _{p\ge 1} L^p({{\mathbb {R}}}^d; h_{\kappa }^2)$.

According to the inverse formula, if $f\in {\mathcal {S}}({{\mathbb {R}}}^d)$ and $x, y\in {{\mathbb {R}}}^d$, then

$$\begin{aligned} {\mathcal {F}}_{\kappa }(T^y f)(x)=E_{\kappa }(-{\mathbf {i}}x, y) {\mathcal {F}}_{\kappa }f(x). \end{aligned}$$

(17)

Moreover, it was shown in [13, Lemma 2.2] that $T^y$ is a linear operator from the space ${\mathcal {S}}({{\mathbb {R}}}^d)$ to itself, and for any $f, g\in {\mathcal {S}}({{\mathbb {R}}}^d)$,

$$\begin{aligned} \int _{{{\mathbb {R}}}^d} T^y f(x) g(x) h_{\kappa }^2(x)\, dx =\int _{{{\mathbb {R}}}^d} f(x) T^{-y} g(x) h_{\kappa }^2(x)\, dx. \end{aligned}$$

(18)

And the property (17) of the generalized translation operators carries over to $L^p$ spaces as well:

Lemma 2.3

([6, Propsition 2.7]) If $y\in {{\mathbb {R}}}^d$and $f\in L^p({{\mathbb {R}}}^d; h_{\kappa }^2)$with $1\le p\le \infty$, then (17) holds almost everywhere (a.e.) on ${{\mathbb {R}}}^d$for $1\le p\le 2$, and holds in a distributional sense for $1\le p\le \infty$:

$$\begin{aligned} \Bigl ( {\mathcal {F}}_{\kappa }(T^y f), \varphi \Bigr ) =\Bigl ({\mathcal {F}}_{\kappa }{f}, E_{\kappa }(-{\mathbf {i}}y,\cdot ) \varphi \Bigr ), \ \forall \varphi \in {\mathcal {S}}({{\mathbb {R}}}^d). \end{aligned}$$

(19)

Moreover, the generalized translation has the following integral representation on the space ${\mathcal {S}}({{\mathbb {R}}}^d)$.

Lemma 2.4

([15, Theorem 7.1]) For $y=(y_1,\ldots , y_d), x=(x_1,\ldots , x_d)\in {{\mathbb {R}}}^d$and $f\in {\mathcal {S}}({{\mathbb {R}}}^d)$,

$$\begin{aligned} T^y f(x)=T_{1, y_1} T_{2, y_2}\cdots T_{d, y_d} f(x). \end{aligned}$$

(20)

Here the operators $T_{j,y_j}$are defined by

$$\begin{aligned} T_{j, y_j} f(x) :=&\int _{-1}^1 \Bigg [f_{j, e} (u_j (x, y, t))+\frac{(x_j-y_j)f_{j,o} (u_j(x,y, t))}{v_j(x_j,y_j,t)}\Bigg ] \, d\mu _j(t), \end{aligned}$$

(21)

where $v_j(x_j, y_j, t):= \sqrt{x_j^2+y_j^2 -2x_jy_j t}$, $u_j(x, y, t): =\Bigl (x_1, \ldots , x_{j-1}, v_j(x_j, y_j, t), x_{j+1}, \ldots x_d\Bigr )$, $f_{j,e} (x): = \frac{1}{2} \Bigl ( f(x) + f(x{\sigma }_j)\Bigr )$, $f_{j,o} (x) = \frac{1}{2} \Bigl ( f(x) - f(x{\sigma }_j)\Bigr ),$ and the measure $d\mu _j$is the same as in (11).

According to (21), we have

$$\begin{aligned} T^y f(x):=\int _{{{\mathbb {R}}}^d} f(z) \, d\mu _{x,y}(z),\quad x,y\in {{\mathbb {R}}}^d, \end{aligned}$$

(22)

where $d\mu _{x,y}$ is a signed Borel measure supported on

$$\begin{aligned} \Bigl \{z=(z_1,\ldots , z_d)\in {{\mathbb {R}}}^d:\ \ \bigl ||x_i|-|y_i|\bigr |\le |z_i|\le |x_i|+|y_i|,\quad i=1,2,\ldots , d\Bigr \}. \end{aligned}$$

2.4 Generalized convolutions

We start with the definition on the space ${\mathcal {S}}({{\mathbb {R}}}^d)$.

Definition 2.5

The generalized convolution of $f, g\in {\mathcal {S}}({{\mathbb {R}}}^d)$ is defined by

$$\begin{aligned} f*_{\kappa }g(x) =\int _{{{\mathbb {R}}}^d} f(y) T^y g (x) h_{\kappa }^2(y)\, dy,\quad x\in {{\mathbb {R}}}^d. \end{aligned}$$

(23)

The generalized convolution has the following basic property: for $f, g\in {\mathcal {S}}({{\mathbb {R}}}^d)$,

$$\begin{aligned} {\mathcal {F}}_{\kappa }( f*_{\kappa }g)(\xi ) ={\mathcal {F}}_{\kappa }f(\xi ) {\mathcal {F}}_{\kappa }g(\xi ),\quad \xi \in {{\mathbb {R}}}^d. \end{aligned}$$

(24)

Since the generalized translation operators are uniformly bounded on $L^p$-spaces with $1\le p\le \infty$, the following Young’s inequality can be established (see [15, Proposition 7.2]):

$$\begin{aligned} \Vert f*_{\kappa }g\Vert _{{\kappa },r}\le \Vert f\Vert _{{\kappa },p}\Vert f\Vert _{{\kappa },q},\ \ \end{aligned}$$

(25)

where $1\le p, q, r\le \infty$ and $1+\frac{1}{r}=\frac{1}{p}+\frac{1}{q}$. This implies that $f*_{\kappa }g$ can be defined for $f\in L^p({{\mathbb {R}}}^d; h_{\kappa }^2)$ and $g\in L^q({{\mathbb {R}}}^d; h_{\kappa }^2)$ with $1\le p, q\le \infty$ and $\frac{1}{p}+\frac{1}{q}\ge 1$. And is has the following property.

Lemma 2.6

([6, Corollary 2.9]) If $f\in L^p({{\mathbb {R}}}^d; h_{\kappa }^2)$, $1\le p\le \infty$and $g\in {\mathcal {S}}({{\mathbb {R}}}^d)$, then

$$\begin{aligned} {\mathcal {F}}_{\kappa }( f*_{\kappa }g)(\xi ) ={\mathcal {F}}_{\kappa }f(\xi ) {\mathcal {F}}_{\kappa }g(\xi ) \end{aligned}$$

(26)

holds in a distributional sense.

2.5 Spaces of homogeneous type

A straightforward calculation shows that

$$\begin{aligned} {{\,\mathrm{meas}\,}}_{\kappa }(B(x,r))\sim r^d \prod _{j=1}^d (|x_j|+r)^{2{\kappa }_j},\quad x\in {{\mathbb {R}}}^d,\quad r>0. \end{aligned}$$

(27)

This, in particular, implies that the measure $d\mu _{\kappa }(x) =h_{\kappa }^2(x)\, dx$ satisfies the doubling condition on the space ${{\mathbb {R}}}^d$, and hence $({{\mathbb {R}}}^d, d\mu _{\kappa })$ is a space of homogeneous type in the sense of Coifman, and Weiss [3]. In this subsection, we will review briefly some basic definitions and facts on homogeneous spaces, most of which can be found in [3, 11].

Definition 2.7

A space of homogeneous type $(X, \rho , \mu )$ is a topological space X endowed with a quasi-metric $\rho$ and a nonnegative Borel measure $\mu$ such that

• (i) $\rho$ is continuous on $X\times X$ and every ball $B_\rho (x,r):=\{y\in X:\ \ \rho (x,y)<r\}$ is open in X;

• (ii) the measure $\mu$ satisfies the doubling condition:

  $$\begin{aligned} \mu (B_{\rho }(x, 2r))\le C \mu (B_{\rho }(x,r)),\ \ \forall x\in X,\ \ \forall r>0; \end{aligned}$$

• (iii) $0<\mu (B_\rho (x,r))<\infty$ for every $x\in X$ and $r>0$.

Definition 2.8

A weight w (any nonnegative measurable function) on a homogeneous space $(X,\rho ,\mu )$ satisfies the $A_p$ condition for $1\le p<\infty$ if

$$\begin{aligned} {[}w]_{A_p}:=\sup _B \Bigl (\frac{1}{\mu (B)}\int _B w\, d\mu \Bigr )\Bigl (\frac{1}{\mu (B)}\int _B w^{-\frac{1}{p-1}}\, d\mu \Bigr )^{p-1}<\infty , \end{aligned}$$

and in the case of $p=1$, we replace $\Bigl (\frac{1}{\mu (B)}\int _B w^{-\frac{1}{p-1}}\, d\mu \Bigr )^{p-1}$ with $\Vert w^{-1}\Vert _\infty$.

The $A_p$ classes are increasing with respect to p; that is, $A_{p_1}\subset A_{p_2}$ for $1\le p_1<p_2$. As a result, we can define $A_\infty$ class by $A_\infty =\bigcup _{p>1} A_p$.

Next, we define a modified Hardy–Littlewood maximal function on the homogeneous space $({{\mathbb {R}}}^d, d\mu _{\kappa })$ by

$$\begin{aligned} M_{\kappa }f(x):=\sup _{B} \frac{1}{\mu _{\kappa }(B)}\int _{\widetilde{B}} |f(y)| d\mu _{\kappa }(y), \end{aligned}$$

where the supremum is taken over all the balls B in ${{\mathbb {R}}}^d$ such that $x\in \widetilde{B}=\{x\sigma :\ \ x\in B,\ \ \sigma \in {{\mathbb {Z}}}_2^d\}$. Since $\mu _{\kappa }$ is a ${{\mathbb {Z}}}_2^d$-invariant doubling measure on ${{\mathbb {R}}}^d$, it follows that

$$\begin{aligned} \mu _{\kappa }\Bigl \{ x\in {{\mathbb {R}}}^d:\ \ M_{\kappa }f(x)>{\alpha }\Bigr \} \le C_{\kappa }\frac{\Vert f\Vert _{{\kappa },1}}{{\alpha }},\quad \forall {\alpha }>0, \end{aligned}$$

(28)

and

$$\begin{aligned} \Vert M_{\kappa }f\Vert _{{\kappa },p}\le C_p\Vert f\Vert _{{\kappa },p},\quad 1<p\le \infty . \end{aligned}$$

(29)

2.6 The Hardy–Littlewood–Sobolev inequality

Recall that ${\mathcal {D}}_{{\kappa },j}$, $1\le j\le d$ denote the Dunkl operators as defined in (9). The Dunkl h-Laplacian $\varDelta _{\kappa }$ is defined by $\varDelta _{{\kappa }}=\sum _{j=1}^d {\mathcal {D}}_{{\kappa }, j}^2,$ and it plays the role similar to that of ordinary Laplacian. It is known that

$$\begin{aligned} \varDelta _{{\kappa }} =\varDelta + 2\sum _{j=1}^d {\kappa }_j \delta _j \end{aligned}$$

(30)

where $\varDelta =\sum _{j=1}^d \partial _j^2$ and

$$\begin{aligned} {\delta }_j :=\frac{{\langle }\nabla f(x), e_j{\rangle }}{x_j}-\frac{f(x)-f(x{\sigma }_j)}{4x_j^2}. \end{aligned}$$

Furthermore, $(-\varDelta _{\kappa }f)^{\wedge }(x)=\Vert x\Vert ^2 \widehat{f}(x)$ for $f\in {\mathcal {S}}({{\mathbb {R}}}^d)$. As a result, we may define fractional power of the h-Laplacian $\varDelta _{\kappa }$ in a distributional sense by ${\mathcal {F}}_{\kappa }(-\varDelta _{\kappa })^\beta f(x)=\Vert x\Vert ^{2\beta } \widehat{f}(x)$ for $\beta \in {{\mathbb {R}}}$.

In the case when $0<\beta <2l_{\kappa }+1$, the fractional h-Laplacian $(-\varDelta _{\kappa })^{\beta /2} f$ becomes the weighted Riesz potential, which we denote by $I_{\kappa }^\beta$. It is known ([16, Section 4]) that for $0<\beta <2l_{\kappa }+1$ and $f\in {\mathcal {S}}({{\mathbb {R}}}^d)$,

$$\begin{aligned} I_{\kappa }^\beta f(x) = c({\kappa },\beta )^{-1} \int _{{{\mathbb {R}}}^d} f(y) T^y K_{\beta }(x) h_{\kappa }^2(y)\, dy, \end{aligned}$$

where $K_\beta (y)=\Vert y\Vert ^{\beta -2l_{\kappa }-1}$ and

$$\begin{aligned} c({\kappa },\beta ):=2^{\beta -l_{\kappa }-\frac{1}{2}} \frac{\varGamma (\beta /2) }{ \varGamma \left( {\lambda }_{\kappa }+\frac{1}{2} -\frac{\beta }{2}\right) }. \end{aligned}$$

Lemma 2.9

[16, Theorem 4.3] Let $1<p< q<\infty$and $0<\beta <2l_{\kappa }+1$be such that $\beta =(2l_{\kappa }+1) (\frac{1}{p}-\frac{1}{q})$. Then

$$\begin{aligned} \Vert I_{\kappa }^\beta f\Vert _{{\kappa },q}\le C \Vert f\Vert _{{\kappa },p},\ \ \forall f\in L^p(h_{\kappa }^2). \end{aligned}$$

In the rest three sections of this paper, we use both $\widehat{f}$ and ${\mathcal {F}}_{\kappa }f$ to denote the Dunkl transforms of f for convenience.

3 Proof of Theorem 1.1

In this section, we will prove Theorem 1.1. Let $\xi$ be a $C^\infty$-function on ${{\mathbb {R}}}$ satisfying that $\xi (x)=1$ for $|x|\le 1$ and $\xi (x)=0$ for $|x|\ge 2$, and set $\theta (x)=\xi ( x)-\xi (2x)$. Clearly, $\text {supp}\, {\theta }\subset \{x:\ \ \frac{1}{2}\le |x|\le 2\}$, and $\sum _{j=0}^\infty {\theta }(2^j x)=\xi (x)=1$ for all $x\in [-1,1]{\setminus }\{0\}$. Thus, we can write, for $\beta >-1/2$,

$$\begin{aligned} (1-\Vert \xi \Vert ^2)_+^\beta =(1-\Vert \xi \Vert ^2)_+^\beta \sum _{j=0}^\infty \theta \Bigl (2^j(1-\Vert \xi \Vert ^2)\Bigr )=\sum _{j=0}^\infty 2^{-j \beta } m_j^\beta (\xi ), \end{aligned}$$

where $m_j^\beta (\xi )=2^{j\beta }\theta \bigl (2^j(1-\Vert \xi \Vert ^2)\bigr ) (1-\Vert \xi \Vert ^2)_+^\beta$. As a result, the operator $B_R^\beta (h_{\kappa }^2; f)$ can be decomposed as

$$\begin{aligned} B_R^\beta (h_{\kappa }^2; f)(x)=\sum _{j=0}^\infty 2^{-j \beta }T_{R, j}^\beta f(x), \end{aligned}$$

(31)

where the operators $T_{R,j}^\beta$ are given by $\widehat{T_{R,j}^\beta f}(\xi )=m_j^\beta (R^{-1}\xi ) \widehat{f}(\xi )$.

Since $m_0^\beta , m_1^\beta , m_2^\beta \in {\mathcal {S}}({{\mathbb {R}}}^d)$, by [6, Lemma 4.6],

$$\begin{aligned} \sup _{R>0}|T_{R, j}^\beta f(x)|\le C M_{\kappa }f(x),\ \ j=0,1,2, \end{aligned}$$

(32)

Definition 3.1

Let $\varPhi$ be a $C^\infty$-function supported on $[-\frac{1}{2}, \frac{1}{2}]$. For a parameter ${\alpha }\in (0,1/2]$, set

$$\begin{aligned} \phi (x):=\varPhi \Bigl ( \frac{1-\Vert x\Vert }{{\alpha }}\Bigr ),\ \ x\in {{\mathbb {R}}}^d, \end{aligned}$$

and let $\psi (x)={\widehat{\phi }}(x)$ for $x\in {\mathbb {R}}^{d}$.

An important tool in the proof of Theorem 1.1 is the maximal operator defined below.

Definition 3.2

For $t>0$, define the operator $S_t^{\alpha }$ by $S_t^{\alpha }f (x) =f*_{\kappa }\widehat{\phi }_{t^{-1}}(x)$, where $\widehat{\phi }_{t^{-1}}(x)=t^{2{\lambda }_{\kappa }+1} \widehat{\phi }(tx)$. The maximal operator $S_*^{\alpha }$ is then defined by $S_*^{\alpha }f(x)=\sup _{t>0}|S_t^{\alpha }f(x)|$.

The proof of Theorem 1.1 can be reduced to the following estimate on the maximal operator $S_*^{\alpha }$.

Theorem 3.3

For $p\ge 2$, ${\delta }>{\delta }_{\kappa }(p):=\max \{(2l_{\kappa }+1) |\frac{1}{2}-\frac{1}{p}|-\frac{1}{2},0\}$and $0\le \beta <2l_{\kappa }+1$,

$$\begin{aligned} \int _{{{\mathbb {R}}}^d} |S_*^{\delta } f(x)|^2 h_{\kappa }^2(x)\frac{dx}{\Vert x\Vert ^\beta }\le C_\beta A_\beta ({\delta })\int _{{{\mathbb {R}}}^d} |f(x)|^2 h_{\kappa }^2(x)\frac{dx}{\Vert x\Vert ^\beta }, \end{aligned}$$

where for $0<t\le 1$,

$$\begin{aligned} A_\beta (t)={\left\{ \begin{array}{ll} 1,&{}\ \ \text {if }0\le \beta<1,\\ |\ln t|,&{}\ \ \text {if }\beta =1,\\ t^{1-\beta },&{}\ \ \text {if }1<\beta <2l_{\kappa }+1.\end{array}\right. } \end{aligned}$$

(33)

The proof of Theorem 3.3 will be given in the next two sections. For the rest of this section, we take this theorem for granted and proceed with the proof of Theorem 1.1.

Proof of Theorem 1.1

Let ${\delta }>{\delta }_{\kappa }(p)$ with $p\ge 2$. Without loss of generality, we may assume that $0<{\delta }\le {\lambda }_{\kappa }$ since otherwise the result follows directly from (6).

We decompose a function $f\in L^p({{\mathbb {R}}}^d; d\mu _{\kappa })$ as $f=f_1+f_2$, where $f_{1}(x)=f(x)\chi _{\Vert x\Vert \leqslant 1}$, $f_{2}(x)=f(x)\chi _{\Vert x\Vert >1}$ and we recall that $d\mu _{\kappa }(x)=h_{\kappa }^2(x)\, dx$. Since $p\ge 2$, it follows by Hölder’s inequality that $\Vert f_{1}\Vert _{L^{2}({\mathbb {R}}^{d}, d\mu _{\kappa })} \leqslant C \Vert f\Vert _{L^{p}({\mathbb {R}}^{d}, d\mu _{\kappa })}<\infty$. Hence, (6) and a standard density argument imply that (8) holds with $f=f_1$.

It remains to show (8) holds with f being replaced by $f_2$. Since $(2\lambda _{{\kappa }}+1)(1-\frac{2}{p})<1+2\delta ,$ we may choose a constant $\beta$ such that $(2\lambda _{{\kappa }}+1)(1-\frac{2}{p})<\beta <1+2\delta$. By Hölder’s inequality, we then have

$$\begin{aligned} \int _{{{\mathbb {R}}}^d}|f_{2}(x)|^{2} \frac{d\mu _{\kappa }(x)}{\Vert x\Vert ^{\beta }}&\leqslant \left( \int _{{\mathbb {R}}^{d}}|f_{2}(x)|^{p} d\mu _{\kappa }(x)\right) ^{\frac{2}{p}} \left( \int _{\Vert x\Vert >1}\Vert x\Vert ^{-\frac{\beta p}{p-2}}d\mu _{\kappa }(x)\right) ^{1-\frac{2}{p}}\\&\leqslant \Vert f_{2}\Vert _{L^{p}({\mathbb {R}}^{d};d\mu _{\kappa })}^{2} \left( \int _{1}^{\infty }r^{2\lambda _{{\kappa }}- \frac{\beta p}{p-2}}\int _{{\mathbb {S}}^{d-1}}h_{{\kappa }}^{2}(x')d \sigma (x')dr\right) ^{1-\frac{2}{p}}\\&\leqslant C\Vert f\Vert _{L^{p}({\mathbb {R}}^{d}; d\mu _{\kappa })}^{2}<\infty , \end{aligned}$$

where the third step uses the fact that $\frac{\beta p}{p-2}-2l_{\kappa }>1$. This means that $f_{2}\in L^{2}({\mathbb {R}}^{d};\Vert x\Vert ^{-\beta }d\mu _{\kappa })$. Thus, we reduce the proof of Theorem 1.1 to the estimate:

$$\begin{aligned} \Vert B_{*}^{\delta }(h_{{\kappa }}^{2};f) \Vert _{L^{2}({\mathbb {R}}^{d};\Vert x \Vert ^{-\beta } d\mu _{\kappa })} \leqslant C\Vert f\Vert _{L^{2} ({\mathbb {R}}^{d};\Vert x\Vert ^{-\beta }d\mu _{\kappa })},\quad \forall f\in L^{2}({\mathbb {R}}^{d};\Vert x\Vert ^{-\beta }d\mu _{\kappa }). \end{aligned}$$

(34)

To show (34), we use the decomposition (31) and the estimate (32) to obtain

$$\begin{aligned} |B_R^{\delta }(h_{\kappa }^2; f)(x)|\le C M_{\kappa }f(x)+\sum _{j=3}^\infty 2^{-j {\delta }}|T_{R, j}^{\delta }f(x)|, \end{aligned}$$

(35)

where $\widehat{T_{R,j}^{\delta }f}(\xi )=m_j^{\delta } (R^{-1}\xi ) \widehat{f}(\xi )$, $m_j^{\delta } (\xi )=\varPhi (2^{j-2}(1- \Vert \xi \Vert ^2))$, $\varPhi$ is a $C^\infty$ function supported in the interval $[-\frac{1}{2}, \frac{1}{2}]$. Thus, with the notations of Definition 3.2, we have

$$\begin{aligned} |B_*^{\delta }(h_{\kappa }^2; f)(x)|\le C M_{\kappa }f(x)+\sum _{j=3}^\infty 2^{-j {\delta }} S_*^{2^{-j+2}} f(x). \end{aligned}$$

(36)

Since $\Vert x\Vert ^{-\beta }$ for $0\le \beta <2{\lambda }_{\kappa }+1$ is an $A_1$-weight on the homogeneous space $({{\mathbb {R}}}^d, d\mu _{\kappa })$, it follows by Theorem 3.3 that

$$\begin{aligned} \Vert B_{*}^{\delta }(h_{{\kappa }}^{2};f) \Vert _{L^{2}({\mathbb {R}}^{d};\Vert x\Vert ^{-\beta }d\mu _{\kappa })}&\leqslant C \Vert f\Vert _{L^{2} ({\mathbb {R}}^{d};\Vert x\Vert ^{-\beta }d\mu _{\kappa })}\\&\quad +C_{\beta }\Bigl [\sum _{j=0}^{\infty } 2^{-j{\delta }} \bigl (2^{j(\beta -1)/2}+1+\sqrt{j}\bigr )\Bigr ]\Vert f\Vert _{L^{2} ({\mathbb {R}}^{d};\Vert x\Vert ^{-\beta }d\mu _{{\kappa }})}\\&\leqslant C\Vert f\Vert _{L^{2}({\mathbb {R}}^{d};\Vert x\Vert ^{-\beta } d\mu _{\kappa })}, \end{aligned}$$

where the last step uses the fact that $\beta <2{\delta }+1$. This shows (34) and hence completes the proof of Theorem 1.1. $\square$

4 Some lemmas

Lemma 4.1

Let $0<\beta <2l_{\kappa }+1$and $0<\varepsilon <100d$. Set $u_\beta (x) =\Vert x\Vert ^{\beta -2l_{\kappa }-1}$and $E=\{ x\in {{\mathbb {R}}}^d:\ \ ||x|-1|\le \varepsilon$. Then for $x, y\in E$,

$$\begin{aligned} h_{\kappa }^2(x)|T^y u_\beta (x)| \le {\left\{ \begin{array}{ll} C \Vert {\bar{x}}-{\bar{y}}\Vert ^{\beta -d}, &{}\ \text {if }0<\beta<d,\\ C \Bigl |\ln \Vert {\bar{x}}-{\bar{y}}\Vert \Bigr |, &{}\ \text {if }\beta =d,\\ C, &{} \ \hbox { if}\ d<\beta <2l_{\kappa }+1, \end{array}\right. } \end{aligned}$$

where ${\bar{x}}=(|x_{1}|,\ldots ,|x_{d}|)$for $x=(x_{1},\ldots ,x_{d})\in {\mathbb {R}}^{d}$.

Proof

Let $\psi \in C_c^\infty ({{\mathbb {R}}}^d)$ be a radial function supported in $[\frac{1}{2}, 4]$ such that $\sum _{k\in {{\mathbb {Z}}}} \psi (2^{k} x)=1, \ \ \forall x\ne 0.$ Then setting $\varphi (x)=\Vert x\Vert ^{\beta -2l_{\kappa }-1} \psi (x)$, we obtain that for $x\ne 0$,

$$\begin{aligned} u_\beta (x)&=\sum _{k\in {{\mathbb {Z}}}} \Vert x\Vert ^{\beta -2l_{\kappa }-1} \psi (2^{k}x)=\sum _{k\in {{\mathbb {Z}}}} 2^{k(2l_{\kappa }+1-\beta )} \varphi (2^{k} x)=\sum _{k\in {{\mathbb {Z}}}} 2^{-k\beta } \varphi _{2^{-k}}(x), \end{aligned}$$

where $\varphi _t(x)=t^{-2l_{\kappa }-1} \varphi (x/t)$. It follows by [6, Lemma 4.6] that for $\ell >2l_{\kappa }+3$,

$$\begin{aligned} |T^y u_\beta (x)|&=|\sum _{k\in {{\mathbb {Z}}}} 2^{-k\beta } T^y \varphi _{2^{-k}}(x)| \le C \sum _{k\in {{\mathbb {Z}}}} \frac{2^{-k\beta } }{\bigl ( 1+2^{k}\bigl \Vert {\bar{x}}-{\bar{y}}\bigr \Vert \bigr )^{\ell }\int _{B(x,2^{-k})} h_{\kappa }^2(z)\, dz}\\&\le C\sum _{k\in {{\mathbb {Z}}}} 2^{k(d-\beta )} \bigl ( 1+2^k\bigl \Vert {\bar{x}}-{\bar{y}}\bigr \Vert \bigr )^{-\ell }\prod _{j=1}^d (|x_j|+2^{-k})^{-2{\kappa }_j}. \end{aligned}$$

For simplicity, we set $\rho =\Vert {\bar{x}}-{\bar{y}}\Vert$. If $0<\beta <d$, then

$$\begin{aligned} h_{\kappa }^2(x) |T^y u_\beta (x)|&\le C \sum _{2^k \rho \le 1} 2^{k(d-\beta )} +C\sum _{2^k \rho >1} 2^{k(d-\beta )} (2^k \rho )^{-\ell } \le C \rho ^{\beta -d}. \end{aligned}$$

If $\beta =d$, then

$$\begin{aligned} h_{\kappa }^2(x) |T^y u_\beta (x)|&\le C \sum _{2^k \rho \le 1} 1 +C\sum _{2^k \rho >1} (2^k \rho )^{-\ell } \le C |\ln \rho |. \end{aligned}$$

Finally, if $d<\beta <2l_{\kappa }+1$, then

$$\begin{aligned} h_{\kappa }^2(x) |T^y u_\beta (x)| \le&C h_{\kappa }^2(x)\sum _{k\le 0} 2^{k(2l_{\kappa }+1-\beta )} +C \sum _{\begin{array}{c} 2^k \rho \le 1\\ k\ge 0 \end{array}} 2^{k(d-\beta )} + C \sum _{2^k \rho \ge 1}2^{k(d-\beta )} (2^k\rho )^{-\ell }\\ \le&C h_{\kappa }^2(x) +C+C \rho ^{\beta -d}\le C. \end{aligned}$$

$\square$

Lemma 4.2

For $0<\varepsilon <100d$and $0\le \beta <2l_{\kappa }+1$, we have

$$\begin{aligned} \int _{\bigl |1-\Vert \xi \Vert \bigr |\le \varepsilon } |\widehat{f}(\xi )|^2h_{\kappa }^2(\xi )\, d\xi \le C_\beta A_\beta (\varepsilon ) \varepsilon ^\beta \int _{{{\mathbb {R}}}^d} |f(x)|^2 \Vert x\Vert ^\beta h_{\kappa }^2(x)dx, \end{aligned}$$

(37)

where

$$\begin{aligned} A_\beta (t)={\left\{ \begin{array}{ll} 1,&{}\ \ \text {if }0\le \beta<1,\\ |\ln t|,&{}\ \ \text {if }\beta =1,\\ t^{1-\beta },&{}\ \ \text {if} 1<\beta <2l_{\kappa }+1.\end{array}\right. } \end{aligned}$$

Furthermore, for any $M>2l_{\kappa }+1$and $\beta > 0$,

$$\begin{aligned} \int _{{{\mathbb {R}}}^d} |\widehat{f}(\xi ) |^2 (1+\Vert \xi \Vert )^{-M} h_{\kappa }^2(\xi )\, d\xi \le C_{M,d,\beta } \int _{{{\mathbb {R}}}^d} |f(x)|^2 \Vert x\Vert ^\beta h_{\kappa }^2(x)\, dx. \end{aligned}$$

(38)

Proof

We start with the proof of (37). Without loss of generality, we may assume $\beta >0$. Set $E:=\{ x\in {{\mathbb {R}}}^d:\ \ \bigl |1-\Vert x\Vert \bigr |\le \varepsilon \}$, and denote by $L^2(E; h_{\kappa }^2)$ the subspace of $L^2(h_{\kappa }^2)$ consisting of all functions supported in the set E. We first claim that (37), is a consequence of the following estimate: for any function $g\in L^2(E; h_{\kappa }^2)$,

$$\begin{aligned} \int _{{{\mathbb {R}}}^d}|\widehat{g}(x)|^2 \Vert x\Vert ^{-\beta } h_{\kappa }^2(x)\, dx \le C_\beta A_\beta (\varepsilon ) \varepsilon ^\beta \int _E |g(x)|^2 h_{\kappa }^2(x) \, dx. \end{aligned}$$

(39)

To see this, consider the operator $T: L^2(\Vert x\Vert ^{\beta }h_{\kappa }^2(x))\rightarrow L^2(E; h_{\kappa }^2)$ given by $Tf =\widehat{f}\Bigl |_{E}$, and note that for any $g\in L^2(E; h_{\kappa }^2)$,

$$\begin{aligned} {\langle }Tf, {\bar{g}}{\rangle }_{L^2(E; h_{\kappa }^2)}&= \int _E \widehat{f}(\xi ) g(\xi ) h_{\kappa }^2(\xi )\, d\xi =\int _{{{\mathbb {R}}}^d} f(x) \Bigl (\Vert x\Vert ^{-\beta }\widehat{g}(x)\Bigr ) \Vert x\Vert ^\beta h_{\kappa }^2(x) dx. \end{aligned}$$

This means that $T^*{\bar{g}} (x)=\Vert x\Vert ^{-\beta }\overline{\widehat{g}(x)}$ where $T^*: L^2(E; h_{\kappa }^2)\rightarrow L^2(\Vert x\Vert ^\beta h_{\kappa }^2(x))$ denotes the dual operator of T. The claim then follows.

By the standard density argument, it suffices to show (39) for $g\in L^2(E;h_{\kappa }^2)\cap C_c^\infty ({{\mathbb {R}}}^d)$. Indeed, invoking [16, Lemma 4.1], we obtain that for $g\in L^2(E;h_{\kappa }^2)\cap C_c^\infty ({{\mathbb {R}}}^d)$,

$$\begin{aligned} \int _{{{\mathbb {R}}}^d}|\widehat{g}(x)|^2 \Vert x\Vert ^{-\beta } h_{\kappa }^2(x)\, dx&=\int _{{{\mathbb {R}}}^d} ( g *_{\kappa }\overline{\widetilde{g}})^{\wedge }(\xi )\Vert \xi \Vert ^{-\beta } h_{\kappa }^2(\xi )\, d\xi \\&=\int _{{{\mathbb {R}}}^d} ( g *_{\kappa }\overline{\widetilde{g}})(\xi ){\mathcal {F}}_{\kappa }(\Vert \cdot \Vert ^{-\beta })(\xi ) h_{\kappa }^2(\xi )\, d\xi \\&=c({\kappa },\beta )\int _{{{\mathbb {R}}}^d} g *_{\kappa }\overline{\widetilde{g}}(x)\Vert x\Vert ^{\beta -2l_{\kappa }-1} h_{\kappa }^2(x)\, dx \\&=c({\kappa },\beta ) \int _{E}g(y)\overline{g*_{\kappa }u_{\beta }(y)} \, h_{\kappa }^2(y) dy\\&=c({\kappa },\beta ) {\langle }g, Lg{\rangle }_{L^2(E; h_{\kappa }^2)}\le C \Vert Lg\Vert _{L^2(E; h_{\kappa }^2)}\Vert g\Vert _{L^2(E; h_{\kappa }^2)}, \end{aligned}$$

where

$$\begin{aligned} Lg (x):=\int _{E} g(y) T^y u_{\beta }(x)\, dy,\ \ x\in E. \end{aligned}$$

Clearly,

$$\begin{aligned} \Vert Lg\Vert _{L^2(E; h_{\kappa }^2)} \le B_\beta \Vert g\Vert _{L^2(E; h_{\kappa }^2)}, \end{aligned}$$

where $B_\beta$ is the Lebesgue constant of the operator L; that is,

$$\begin{aligned} B_\beta =\sup _{x\in E}\int _E T^y u_{\beta }(x) h_{\kappa }^2(y)\, dy. \end{aligned}$$

According to Lemma 4.2, if $0<\beta <d$, then

$$\begin{aligned} B_\beta&\le C\sup _{x\in E}\int _E \Vert {\bar{x}}-{\bar{y}}\Vert ^{\beta -d}\, dy \le C \sum _{{\sigma }\in {{\mathbb {Z}}}_2^d} \sup _{x\in E}\int _E \Vert \sigma x-y\Vert ^{\beta -d}\, dy\le C \sup _{x\in E}\int _E \Vert x-y\Vert ^{\beta -d}\, dy\\&\le C_\beta \varepsilon ^\beta A_\beta (\varepsilon ); \end{aligned}$$

if $\beta =d$, then

$$\begin{aligned} B_\beta&\le C \sup _{x\in E}\int _E \Bigl |\ln \Vert {\bar{x}}-{\bar{y}}\Vert \Bigr |\, dy \le C \sup _{x\in E}\int _E \Bigl |\ln \Vert x-y\Vert \Bigr |\, dy \\&\le C \sup _{x\in E}\int _{\{y\in E:\ \Vert y-x\Vert \le 4\varepsilon \}} \Bigl |\ln \Vert x-y\Vert \Bigr |\, dy+ C \sup _{x\in E}\int _{\{y\in E:\ \Vert y-x\Vert > 4\varepsilon \}} \Bigl |\ln \Vert x-y\Vert \Bigr |\, dy\\&\le C \int _0^{4\varepsilon } r^{d-1} \ln r\, dr + C \int _{1-\varepsilon }^{1+\varepsilon } r^{d-1} dr \max _{x'\in {\mathbb {S}}^{d-1}} \int _{\{ y'\in {\mathbb {S}}^{d-1}:\ \Vert x'-y'\Vert \ge 2{\delta }\}} \Bigl |\ln \Vert x'-y'\Vert \Bigr |\\&\le C \varepsilon \int _{2\varepsilon }^\pi |\ln {\theta }| \sin ^{d-2}{\theta }\, d{\theta }\le C \varepsilon ; \end{aligned}$$

and finally, if $d<\beta <2l_{\kappa }+1$, then $B_\beta \le C \sup _{x\in E}\int _E \, dy\le C \varepsilon .$

Now we turn to the proof of (38). Note that

$$\begin{aligned} \int _{{{\mathbb {R}}}^d} |f(x)|^2 \Vert x\Vert ^\beta h_{\kappa }^2(x)\, dx =C \int _{{{\mathbb {R}}}^d} \bigl |(-\varDelta _{{\kappa },0})^{\beta /2} \widehat{f}(\xi )\bigr |^2 h_{\kappa }^2(\xi )\, d\xi =\Bigl \Vert (-\varDelta _{{\kappa },0})^{\beta /2} \widehat{f}\Bigl \Vert _{{\kappa },2}^2. \end{aligned}$$

Thus, it suffices to show that

$$\begin{aligned} \int _{{{\mathbb {R}}}^d} |f(x)|^2 (1+\Vert x\Vert )^{-M}h_{\kappa }^2(x)\, dx \le C \Vert (-\varDelta _{{\kappa }})^{\beta /2}f\Vert _{{\kappa },2}^2. \end{aligned}$$

(40)

(40) is an easy consequence of Lemma 2.9. Indeed, let $q\ge 2$ be such that $(2l_{\kappa }+1) (\frac{1}{2}-\frac{1}{q})=\frac{\beta }{2}$. Then using Hölder’s inequality and Lemma 2.9, we obtain

$$\begin{aligned} \int _{{{\mathbb {R}}}^d} |f(x)|^2 (1+\Vert x\Vert )^{-M}h_{\kappa }^2(x)\, dx \le C \Vert f\Vert _{{\kappa },q}^2&=C \Bigl \Vert I_{\kappa }^{\beta }(-\varDelta _{{\kappa }})^{\beta /2}f\Bigr \Vert _{{\kappa },q}^2 \le C \Bigl \Vert (-\varDelta _{{\kappa }})^{\beta /2}f\Bigr \Vert _{{\kappa },2}^2. \end{aligned}$$

$\square$

5 Proof of Theorem 3.3

Definition 5.1

Let $\ell \in {{\mathbb {N}}}$ and $0<\beta <\ell$. Define

$$\begin{aligned} D^\beta f(x):=\Bigg ( \int _{{{\mathbb {R}}}^d} \frac{|\triangle _y^\ell f(x)|^2}{\Vert y\Vert ^{2l_{\kappa }+1+2\beta }}h_{\kappa }^2(y)\, dy\Bigg )^{\frac{1}{2}}, \end{aligned}$$

where

$$\begin{aligned} \triangle _y^\ell f(x) =\sum _{j=0}^\ell \left( {\begin{array}{c}\ell \\ j\end{array}}\right) (-1)^j T^{jy} f(x). \end{aligned}$$

By (22),

$$\begin{aligned} \triangle _y^\ell f(x)=\int _{{{\mathbb {R}}}^d} f(z)d\mu _{ x, y,\ell }(z), \end{aligned}$$

(41)

where $d\mu _{x,y,\ell }$ is a signed Borel measure supported in $\{z\in {{\mathbb {R}}}^d:\ \ \Vert {\bar{z}}-{\bar{x}}\Vert \le \ell |y|\}.$

Lemma 5.2

For $\ell \in {{\mathbb {N}}}$and $0<\beta <\ell$,

$$\begin{aligned} \Vert (-\varDelta _{{\kappa }})^{\beta /2} f\Vert _{{\kappa },2}\sim \Vert D^\beta f\Vert _{{\kappa },2}. \end{aligned}$$

Proof

By definition, we have

$$\begin{aligned} (\triangle _y^\ell f)^{\wedge } (x) =A_\ell (x,y) \widehat{f}(x), \end{aligned}$$

where

$$\begin{aligned} A_\ell (x,y)&=\sum _{j=0}^\ell \left( {\begin{array}{c}\ell \\ j\end{array}}\right) (-1)^j V_{\kappa }\Bigl [ e^{-i j {\langle }y, \cdot {\rangle }}\Bigr ](x)\\&=V_{\kappa }\Bigl [\sum _{j=0}^\ell \left( {\begin{array}{c}\ell \\ j\end{array}}\right) (-1)^j (e^{-i{\langle }y,\cdot {\rangle }})^j \Bigr ](x)=V_{\kappa }\Bigl [ (1-e^{-i{\langle }y, \cdot {\rangle }})^\ell \Bigr ](x)\\&=c_{\kappa }\int _{[-1,1]^d} \Bigl ( 1-\exp \Bigl ( -i \sum _{j=1}^d t_j x_jy_j\Bigr )\Bigr )^\ell \prod _{j=1}^d (1-t_j^2)^{{\kappa }_j-1}(1+t_j)\, dt_j. \end{aligned}$$

It is easily seen that the function $A_\ell (x,y)$ has the following properties:

• (i) For $x, y\in {{\mathbb {R}}}^d$, $|A_\ell (x,y)|\le 2^\ell .$

• (ii) As $\Vert y\Vert \rightarrow 0$,

  $$\begin{aligned} A_\ell (x,y)= q_\ell (x,y)+O(\Vert y\Vert ^{\ell +1})\end{aligned}$$

  (42)

  holds uniformly in $x\in {\mathbb {S}}^{d-1}$, where

  $$\begin{aligned} q_\ell (x,y)&= i^\ell V_{\kappa }\Bigl [ ({\langle }y, \cdot {\rangle })^\ell \Bigr ](x)= c_{\kappa }i^{\ell } \int _{[-1,1]^d} \Bigl ( \sum _{j=1}^d t_j x_jy_j\Bigr )^\ell \prod _{j=1}^d (1-t_j^2)^{{\kappa }_j-1}(1+t_j)\, dt_j.\end{aligned}$$

• (iii) For any $r>0$ and any $x, y\in {{\mathbb {R}}}^d$, $A_\ell (rx, y)=A_\ell (x, ry)$.

On the other hand, using Plancherel’s formula, we obtain

$$\begin{aligned} \Vert D^\beta f\Vert _{{\kappa },2}^2&=\int _{{{\mathbb {R}}}^d}\frac{h_{\kappa }^2(y)}{\Vert y\Vert ^{2l_{\kappa }+1+2\beta }}\int _{{{\mathbb {R}}}^d} \Bigl |A_\ell \Bigl (\frac{\xi }{\Vert \xi \Vert },\Vert \xi \Vert y\Bigr )\Bigr |^2 |\widehat{f}(\xi )|^2 h_{\kappa }^2(\xi )\, d\xi \, dy\\&=\int _{{{\mathbb {R}}}^d} |\widehat{f}(\xi )|^2 \Vert \xi \Vert ^{2\beta } h_{\kappa }^2(\xi ) B(\xi /\Vert \xi \Vert )\, d\xi , \end{aligned}$$

where

$$\begin{aligned} B(x)&=\int _{{{\mathbb {R}}}^d} \frac{|A_\ell (x,y)|^2 }{\Vert y\Vert ^{2l_{\kappa }+1+2\beta }}h_{\kappa }^2(y)\, dy. \end{aligned}$$

Thus, it suffices to show that

$$\begin{aligned} B(x)\sim _{{\kappa },d} 1,\quad \forall x\in {\mathbb {S}}^{d-1}. \end{aligned}$$

(43)

To this end, let $\varepsilon =\varepsilon _{d,{\kappa }}\in (0,1)$ be a small constant depending only on d and ${\kappa }$, and set

$$\begin{aligned} B(x, \varepsilon ):=\int _{\Vert y\Vert \le \varepsilon } \frac{|A_\ell (x,y)|^2 }{\Vert y\Vert ^{2l_{\kappa }+1+2\beta }}h_{\kappa }^2(y)\, dy. \end{aligned}$$

Clearly,

$$\begin{aligned} B(x,\varepsilon ) \le B(x)\le B(x, \varepsilon )+ O_{\varepsilon ,\ell } (1).\quad \forall x\in {\mathbb {S}}^{d-1}. \end{aligned}$$

Thus, for the proof of (43), it is sufficient to show that

$$\begin{aligned} B(x, \varepsilon )\sim _\varepsilon 1,\ \ \forall x\in {\mathbb {S}}^{d-1}. \end{aligned}$$

(44)

Indeed, using (42), we obtain that for $x\in {\mathbb {S}}^{d-1}$,

$$\begin{aligned} B(x,\varepsilon )&=\int _{\Vert y\Vert \le \varepsilon } \frac{|q_\ell (x,y)|^2 }{\Vert y\Vert ^{2l_{\kappa }+1+2\beta }}h_{\kappa }^2(y)\, dy +O(1) \int _{\Vert y\Vert \le \varepsilon } \frac{\Vert y\Vert ^{2\ell +1}}{\Vert y\Vert ^{2l_{\kappa }+1+2\beta }} h_{\kappa }^2(y)\, dy \\&=\int _0^{\varepsilon } r^{2\ell -2\beta } \int _{{\mathbb {S}}^{d-1}} |q_\ell (x, y')|^2h_{\kappa }^2 (y')\, d{\sigma }(y') dr +O(1) \varepsilon ^{2\ell +2-2\beta }\\&=\frac{ M_\ell (x)}{2\ell -2\beta +1} \varepsilon ^{2\ell -2\beta +1} +O(1) \varepsilon ^{2\ell +2-2\beta }, \end{aligned}$$

where

$$\begin{aligned} M_\ell (x):=\int _{{\mathbb {S}}^{d-1}} |q_\ell (x, y)|^2h_{\kappa }^2 (y)\, d{\sigma }(y). \end{aligned}$$

Thus, (44) is a consequence of the following estimate:

$$\begin{aligned} M_\ell (x)\sim _\ell 1,\quad \forall x\in {\mathbb {S}}^{d-1}. \end{aligned}$$

Since $M_\ell$ is a homogeneous polynomial of degree $2\ell$ on ${\mathbb {S}}^{d-1}$ and ${\mathbb {S}}^{d-1}$ is compact, it is enough to show that

$$\begin{aligned} M_\ell (x):=\int _{{\mathbb {S}}^{d-1}} |q_\ell (x, y)|^2h_{\kappa }^2 (y)\, d{\sigma }(y) >0,\quad \forall x\in {\mathbb {S}}^{d-1}. \end{aligned}$$

(45)

Assume (45) were not true, that is, there exists $x=(x_1,\ldots , x_d)\in {\mathbb {S}}^{d-1}$ such that $M_\ell (x)=0$. This would imply that $q_\ell (x, y)=0$ for all $y\in {\mathbb {S}}^{d-1}$. However, this is impossible because for $y=e_{j_0}$ with $j_0\in \{1,\ldots , d\}$ satisfying $|x_{j_0}|=\max _{1\le j\le d}|x_j|$, we have

$$\begin{aligned} |q_\ell (x, y)|&=c_{{\kappa }_{j_0}} \Bigl |\int _{-1}^1 (tx_{j_0})^\ell (1-t^2)^{{\kappa }_{j_0}-1}(1+t)\, dt\Bigr |\\&\ge c_{{\kappa }_{j_0}} d^{\ell /2}\int _{-1}^1 t^\ell (1-t^2)^{{\kappa }_{j_0}-1}(1+t)\, dt>0. \end{aligned}$$

$\square$

Recall that $\phi _t(x)=\phi (x/t)$ for $t>0$, and

$$\begin{aligned} \phi (\xi )=\varPhi \Bigl ( \frac{1-\Vert \xi \Vert }{{\delta }}\Bigr ),\ \ \xi \in {{\mathbb {R}}}^d,\ \ {\delta }\in \left( 0,\frac{1}{4}\right) , \end{aligned}$$

where $\varPhi \in C_c^\infty ({{\mathbb {R}}})$ be such that $\text {supp}\ \varPhi \subset [-\frac{1}{2}, \frac{1}{2}]$.

By Definition 3.2,

$$\begin{aligned} \widehat{S_t^{\delta }f}(\xi )=\phi (\Vert \xi \Vert /t) \widehat{f}(\xi ). \end{aligned}$$

Lemma 5.3

For $f\in L^2(\Vert x\Vert ^{-\beta }h_{\kappa }^2(x))$and $0<\beta <d$,

$$\begin{aligned} \int _{{{\mathbb {R}}}^d} |S_1^{\delta }f(x)|^2 \frac{h_{\kappa }^2(x) dx}{\Vert x\Vert ^\beta }\le C_\beta A_\beta ({\delta })\int _{{{\mathbb {R}}}^d} |f(x)|^2 \frac{h_{\kappa }^2(x) dx}{\Vert x\Vert ^\beta }. \end{aligned}$$

Proof

It is easy to see

$$\begin{aligned} S_1^{\delta }f(x):=\sum _{j=i}^\infty f*_{\kappa }(\widehat{\phi }\eta _j)(x)=\sum _{j=i}^\infty f*_{\kappa }K_j(x), \end{aligned}$$

(46)

where $K_j(x)=\widehat{\phi }(x)\eta _j(x)$ and $2^{-i}\sim {\delta }$. By [6, Lemma 6.4], for any $N\ge 1$,

$$\begin{aligned} |\widehat{K_j}(x)|&=|\phi *\widehat{\eta _j}(x)|\le {\left\{ \begin{array}{ll} C 2^{-(j-i)N} \bigl (1+{\delta }^{-1}\bigl |1-\Vert x\Vert \bigr |\bigr )^{-N},\ \ &{} { \frac{1}{4}\le \Vert x\Vert \le 8,}\\ C 2^{-(j-i)N} {\delta }^N (1+\Vert x\Vert )^{-N},\ \ &{}\text {otherwise.}\end{array}\right. } \end{aligned}$$

In particular, this implies that

$$\begin{aligned} |\widehat{K_j}(x)|\le {\left\{ \begin{array}{ll} C 2^{-(j-i)N},\ \ &{}\text { for all }x\in {{\mathbb {R}}}^d,\\ C 2^{-(j-i)N} 2^{-kN},\ \ &{}\text {if }\bigl |1-\Vert x\Vert \bigr |\ge 2^k {\delta }\hbox { and } k\ge 4,\\ C 2^{-(j-i)N} {\delta }^N (1+\Vert x\Vert )^{-N},\ \ &{} \hbox { if}\ \Vert x\Vert \le \frac{1}{4} \hbox { or } \Vert x\Vert \ge 8. \end{array}\right. } \end{aligned}$$

(47)

For $j\ge i$, we set $T_j f=f*_{\kappa }K_j$, and claim that

$$\begin{aligned} \int _{{{\mathbb {R}}}^d}|T_j f(x)|^2 h_{\kappa }^2(x)\, dx \le C 2^{-N(j-i)} {\delta }^\beta A_\beta ({\delta }) \int _{{{\mathbb {R}}}^d} |f(x)|^2 \Vert x\Vert ^\beta h_{\kappa }^2(x)\, dx. \end{aligned}$$

(48)

Here and throughout the proof, N is a large positive integer whose exact value is not important. Indeed,

$$\begin{aligned} \int _{{{\mathbb {R}}}^d} |T_j f(x)|^2h_{\kappa }^2(x) \, dx&=\int _{{{\mathbb {R}}}^d}|\widehat{f}(x)|^2 |\widehat{K_j}(x)|^2 h_{\kappa }^2(x)\, dx \\&=\int _{\bigl |1-\Vert x\Vert \bigr |\le 16 {\delta }}\cdots +\int _{16{\delta }<\bigl |1-\Vert x\Vert \bigr |\le 9}\cdots +\int _{\bigl |1-\Vert x\Vert \bigr |>9}\cdots =: I_1+I_2+I_3. \end{aligned}$$

For the first integral $I_1$, using (47) and Lemma 4.2, we have

$$\begin{aligned} I_1&\le C 2^{-N(j-i)} \int _{\bigl |1-\Vert x\Vert \bigr |\le 16 {\delta }} |\widehat{f}(x)|^2 h_{\kappa }^2(x)\, dx\le C {\delta }^\beta A_\beta ({\delta }) 2^{-N(j-i)}\int _{{{\mathbb {R}}}^d} |f(x)|^2 \Vert x\Vert ^\beta h_{\kappa }^2(x)\, dx. \end{aligned}$$

For $I_2$, using (47) and Lemma 4.2 again, we obtain

$$\begin{aligned} I_2&=\sum _{ 16 {\delta }\le 2^k{\delta }\le 9} \int _{2^k{\delta }\le \bigl |1-\Vert x\Vert \bigr |\le 2^{k+1}{\delta }} |\widehat{f}(x)|^2 |\widehat{K_j}(x)|^2 h_{\kappa }^2(x)\, dx \\&\le C 2^{-N(j-i)} \sum _{ 16\le 2^k \le 9/{\delta }} 2^{-kN}\int _{\bigl |1-\Vert x\Vert \bigr |\le 2^{k+1}{\delta }} |\widehat{f}(x)|^2h_{\kappa }^2(x) \, dx \\&\le C 2^{-N(j-i)} \sum _{ 16\le 2^k \le 9/{\delta }} 2^{-kN} A_\beta (2^{k+1}{\delta }) (2^{k+1}{\delta })^\beta \int _{{{\mathbb {R}}}^d}|f(x)|^2 \Vert x\Vert ^\beta h_{\kappa }^2(x)\, dx\\&\le C 2^{-N(j-i)} {\delta }^\beta A_\beta ({\delta })\int _{{{\mathbb {R}}}^d}|f(x)|^2 \Vert x\Vert ^\beta h_{\kappa }^2(x)\, dx \sum _{k=1}^\infty 2^{-kN} 2^{k(\beta +1)}\\&\le C 2^{-N(j-i)} {\delta }^\beta A_\beta ({\delta })\int _{{{\mathbb {R}}}^d}|f(x)|^2 h_{\kappa }^2(x) \Vert x\Vert ^\beta \, dx. \end{aligned}$$

For $I_3$, we have

$$\begin{aligned} I_3&\le C {\delta }^N 2^{-(j-i)N} \int _{\bigl |1-\Vert x\Vert \bigr |\ge 9} |\widehat{f}(x)|^2 (1+\Vert x\Vert )^{-N} h_{\kappa }^2(x)\, dx\\&\le C {\delta }^N 2^{-(j-i)N}\int _{{{\mathbb {R}}}^d} |f(x)|^2 \Vert x\Vert ^\beta h_{\kappa }^2(x)\, dx\\&\le C 2^{-(j-i)N} {\delta }^\beta A_\beta ({\delta }) \int _{{{\mathbb {R}}}^d} |f(x)|^2 \Vert x\Vert ^\beta h_{\kappa }^2(x)\, dx. \end{aligned}$$

Now combining the above estimates of $I_1,I_2, I_3$, we deduce the estimate (48).

Second, we show that (48) implies that for $j\ge i$,

$$\begin{aligned} \int _{{{\mathbb {R}}}^d}|T_j f(x)|^2 h_{\kappa }^2(x)\frac{dx}{\Vert x\Vert ^\beta }\le C 2^{-N(j-i) } {\delta }^\beta A_\beta ({\delta }) \int _{{{\mathbb {R}}}^d} |f(x)|^2 h_{\kappa }^2(x)\, dx. \end{aligned}$$

(49)

Indeed, the dual operator $T_j^*: L^2(h_{\kappa }^2)\rightarrow L^2(\Vert x\Vert ^{\beta }h_{\kappa }^2(x))$ of the operator $T_j: L^2(\Vert x\Vert ^\beta h_{\kappa }^2(x)) \rightarrow L^2(h_{\kappa }^2)$ can be obtained as follows:

$$\begin{aligned} {\langle }T_j f, g{\rangle }_{L^2(h_{\kappa }^2)}&={\langle }f, T_j g{\rangle }_{L^2(h_{\kappa }^2)}={\langle }f, T_j^*g{\rangle }_{L^2(\Vert x\Vert ^\beta h_{\kappa }^2(x))}, \end{aligned}$$

where $T_j^*g(x)=\Vert x\Vert ^{-\beta } T_j g(x)$. The asserted estimate (49) then follows by (48) and duality.

Third, we show that for $j\ge i$,

$$\begin{aligned} \int _{{{\mathbb {R}}}^d} |T_j f(x)|^2 h_{\kappa }^2(x) \frac{dx}{\Vert x\Vert ^\beta }\le C 2^{-N(j-i)} A_\beta ({\delta })\int _{{{\mathbb {R}}}^d} |f(x)|^2 h_{\kappa }^2(x) \frac{dx}{\Vert x\Vert ^\beta }. \end{aligned}$$

(50)

To this end, we recall the following local property of the operator $T_j$: If f is supported in a cube Q of side length $c 2^{j}$, then $T_j f$ is supported in the set

$$\begin{aligned} Q^*=\bigcup _{{\sigma }\in {{\mathbb {Z}}}_2^d} {\sigma }\bigl (c_d Q\bigl ). \end{aligned}$$

We decompose ${{\mathbb {R}}}^d$ as an almost pairwise disjoint union of cubes $Q_k$, $k\in {{\mathbb {Z}}}$, where $Q_0$ is a cube centered at the origin of side length $2^{\ell }2^j$, and the $Q_k$, $k\ne 0$ are cubes of side length $2^j$. We choose $\ell \in {{\mathbb {N}}}$ large enough so that $Q^*_k\cap \frac{1}{2} Q_0=\emptyset$ for all $k\ne 0$. With this decomposition, we have

$$\begin{aligned} \Vert x\Vert&\le C 2^j,\ \ \hbox { for all }\ x\in Q_0^*,\\ \Vert x\Vert&\sim \Vert x'\Vert \ \ \hbox { for all }\ x, x'\in Q^*_k \hbox { and } k\ne 0. \end{aligned}$$

Set $f_k=f\chi _{Q_k}$ for $k\in {{\mathbb {Z}}}$. Then $f =\sum _{k\in {{\mathbb {Z}}}} f_k$. For $k=0$, we use (49) to obtain

$$\begin{aligned} \int _{{{\mathbb {R}}}^d} |T_j f_0(x)|^2 \Vert x\Vert ^{-\beta } h_{\kappa }^2(x)\, dx&\le C 2^{-N(j-i)} {\delta }^\beta A_\beta ({\delta }) \int _{Q_0}|f(x)|^2 h_{\kappa }^2(x)\, dx \\&\le C 2^{-N(j-i)} {\delta }^\beta A_\beta ({\delta }) 2^{j\beta } \int _{Q_0}|f(x)|^2 h_{\kappa }^2(x) \, \frac{dx}{\Vert x\Vert ^\beta }\\&\le C 2^{-(j-i)(N-\beta )} A_\beta ({\delta }) \int _{Q_0}|f(x)|^2 h_{\kappa }^2(x) \frac{dx}{\Vert x\Vert ^\beta }. \end{aligned}$$

For $k\ne 0$, we use Plancerel’s theorem to obtain

$$\begin{aligned} \int _{Q_k^*} |T_j f_k(x)|^2 h_{\kappa }^2(x)\, dx&=\int _{{{\mathbb {R}}}^d}|\widehat{f_k}(x)|^2 |\widehat{K_j}(x)|^2 h_{\kappa }^2(x)\, dx \le C 2^{-(j-i)N} \int _{Q_k}|f(x)|^2 h_{\kappa }^2(x)\, dx. \end{aligned}$$

Since $\Vert x\Vert \sim \Vert x'\Vert$ for all $x, x'\in Q^*_k$, it follows that for $k\ne 0$,

$$\begin{aligned} \int _{Q_k^*} |T_j f_k(x)|^2 h_{\kappa }^2(x) \, \frac{dx}{\Vert x\Vert ^\beta }&\le C 2^{-(j-i)N} \int _{Q_k}|f(x)|^2 h_{\kappa }^2(x)\, \frac{dx}{\Vert x\Vert ^\beta }\\&\le C 2^{-(j-i)N} A_\beta ({\delta })\int _{Q_k}|f(x)|^2 h_{\kappa }^2(x)\frac{dx}{\Vert x\Vert ^\beta }. \end{aligned}$$

On the other hand, since $\text {supp}\ T_j f_k \subset Q_k^*$ for all $k\in {{\mathbb {Z}}}$ and $\sum _{k\in {{\mathbb {Z}}}} \chi _{Q_k^*}(x)\le C_d$, we have

$$\begin{aligned} |T_j f(x)|^2&\le \Bigl (\sum _{k\in {{\mathbb {Z}}}} |T_j f_k(x)|\chi _{Q_k^*}(x)\Bigr )^2\le C_d^2 \sum _{k\in {{\mathbb {Z}}}} |T_j f_k(x)|^2 \chi _{Q_k^*}(x). \end{aligned}$$

It follows that

$$\begin{aligned} \int _{{{\mathbb {R}}}^d} |T_j f(x)|^2 h_{\kappa }^2(x) \frac{dx}{\Vert x\Vert ^\beta }&\le C \sum _{k\in {{\mathbb {Z}}}} \int _{Q_k^*} |T_j f_k(x)|^2 h_{\kappa }^2(x) \frac{dx}{\Vert x\Vert ^\beta }\\&\le C A_\beta ({\delta })2^{-(j-i)N} \sum _{k\in {{\mathbb {Z}}}} \int _{Q_k} |f_k(x)|^2 h_{\kappa }^2(x) \frac{dx}{\Vert x\Vert ^\beta }\\&=C A_\beta ({\delta })2^{-(j-i)N} \int _{{{\mathbb {R}}}^d} |f(x)|^2 h_{\kappa }^2(x) \frac{dx}{\Vert x\Vert ^\beta }. \end{aligned}$$

This proves (50).

Finally, using (46) and Minkowskii’s inequality, we obtain

$$\begin{aligned} \Vert S_1^{\delta }f\Vert _{L^2(\Vert x\Vert ^{-\beta }h_{\kappa }^2(x))}&\le \sum _{j=i}^\infty \Vert T_j f\Vert _{L^2(\Vert x\Vert ^{-\beta }h_{\kappa }^2(x))}\le C \sqrt{A_{\beta }({\delta })}\sum _{j=i}^\infty 2^{-(j-i)} \Vert f\Vert _{L^2(\Vert x\Vert ^{-\beta }h_{\kappa }^2(x))}\\&\le C \sqrt{A_{\beta }({\delta })}\Vert f\Vert _{L^2(\Vert x\Vert ^{-\beta }h_{\kappa }^2(x))}. \end{aligned}$$

$\square$

Remark 5.1

Lemma 5.3 and a duality argument imply that for $0\le \beta <2l_{\kappa }+1$ and $t>0$,

$$\begin{aligned} \int _{{{\mathbb {R}}}^d} |S_t^{\delta }f(x)|^2 \Vert x\Vert ^\beta h_{\kappa }^2(x)\, dx\le C_\beta A_\beta ({\delta })\int _{{{\mathbb {R}}}^d} |f(x)|^2 \Vert x\Vert ^\beta h_{\kappa }^2(x)\ dx. \end{aligned}$$

(51)

Note that by Lemma 5.2,

$$\begin{aligned} \int _{{{\mathbb {R}}}^d} |f(x)|^{2}\Vert x\Vert ^{\beta }h_{{\kappa }}^{2}(x)\, dx \sim \Vert D^{\beta /2} \widehat{f}\Vert _{{\kappa },2}^2 =\int _{{{\mathbb {R}}}^d}\int _{{{\mathbb {R}}}^d} \frac{|\triangle _y^r f(x)|^2}{\Vert y\Vert ^{2l_{\kappa }+1+\beta }}h_{\kappa }^2(y)\, dy h_{\kappa }^2(x)\, dx, \end{aligned}$$

(52)

where

$$\begin{aligned} \triangle _y^r f(x) =\sum _{j=0}^r \left( {\begin{array}{c}r\\ j\end{array}}\right) (-1)^j T^{jy} f(x) \end{aligned}$$

and r is the smallest integer bigger than $\beta /2$. Note that if f is supported in a set $\widetilde{B}(x_0, t)=\bigcup _{{\sigma }\in {{\mathbb {Z}}}_2^d} B(\sigma x_0, t)$, then $\triangle ^r_y f(x)$ is supported in the domain $\widetilde{B}(x_0, t+r\Vert y\Vert )$.

Lemma 5.4

For $0\le \beta <2l_{\kappa }+1$and $k\in {{\mathbb {Z}}}$,

$$\begin{aligned} \int _{2^k}^{2^{k+1}} \int _{{{\mathbb {R}}}^d} |S_t^{\delta }f(x)|^2 h_{\kappa }^2(x)\frac{dxdt}{t\Vert x\Vert ^\beta }\le C_\beta {\delta }A_\beta ({\delta })\int _{{{\mathbb {R}}}^d} |f(x)|^2 h_{\kappa }^2(x)\frac{dx}{\Vert x\Vert ^\beta }. \end{aligned}$$

(53)

Proof

It suffices to prove the asserted conclusion for $k=0$. For simplicity, we denote by $L^2_{x,t}$ the Hilbert $L^2$-space defined with respect to the measure $t^{-1}\Vert x\Vert ^{-\beta }h_{\kappa }^2(x) dtdx$ on ${{\mathbb {R}}}^d\times [1,2]$. Consider the operator $T: L^2(\Vert x\Vert ^{-\beta }h_{\kappa }^2(x))\rightarrow L_{x,t}^2$ given by $f\mapsto S_t^{\delta }f(x)$. Its dual $T^*: L_{x,t}^2\rightarrow L^2(\Vert x\Vert ^{-\beta }h_{\kappa }^2(x))$ can be obtained as follows: for $\{g_t\}_{1\le t\le 2}\in L_{x,t}^2$,

$$\begin{aligned} {\langle }S_t^{\delta }f, g_t{\rangle }_{L^2_{x,t}}&=\int _{{{\mathbb {R}}}^d} \int _1^2 S_t^{\delta }f(x) g_t(x)h_{\kappa }^2(x) \frac{dtdx}{t\Vert x\Vert ^\beta }\\&=\int _1^2 \int _{{{\mathbb {R}}}^d} f(x) \Bigl [ \Vert x\Vert ^\beta S_t^{\delta }\Bigl (\Vert \cdot \Vert ^{-\beta } g_t(\cdot )\Bigr )(x)\Bigr ]h_{\kappa }^2(x)\frac{ dx dt}{t\Vert x\Vert ^\beta }\\&=\left\langle f(x), \int _1^2 \Bigl [ \Vert x\Vert ^\beta S_t^{\delta }\Bigl (\Vert \cdot \Vert ^{-\beta } g_t(\cdot )\Bigr )(x)\Bigr ]\, \frac{dt}{t}\right\rangle _{L^2(\Vert x\Vert ^{-\beta }h_{\kappa }^2(x))}. \end{aligned}$$

Thus,

$$\begin{aligned} T^*(g_t)(x)=\int _1^2 \Bigl [ \Vert x\Vert ^\beta S_t^{\delta }\Bigl (\Vert \cdot \Vert ^{-\beta } g_t(\cdot )\Bigr )(x)\Bigr ]\, \frac{dt}{t}, \end{aligned}$$

and it is sufficient to show that

$$\begin{aligned} \Bigl ( \int _{{{\mathbb {R}}}^d} \Bigl | \int _1^2 S_t^{\delta }\bigl (\Vert \cdot \Vert ^{-\beta } g_t(\cdot )\bigr )(x)dt\Bigr |^2 \Vert x\Vert ^\beta h_{\kappa }^2(x) dx\Bigr )^{\frac{1}{2}}\le&C {\delta }^{\frac{1}{2}} A_\beta ({\delta })^{\frac{1}{2}}\Bigl (\int _1^2 \int _{{{\mathbb {R}}}^d}|g_t(x)|^2 h_{\kappa }^2(x)\frac{dxdt}{\Vert x\Vert ^\beta }\Bigr )^{\frac{1}{2}} . \end{aligned}$$

Setting $f_t(x)=\Vert x\Vert ^{-\beta }g_t(x)$, we then conclude that (53) is a consequence of the following estimate:

$$\begin{aligned} \int _{{{\mathbb {R}}}^d} \Bigl |\int _1^2 S_t^{\delta }f_t(x)dt\Bigr |^2 \Vert x\Vert ^\beta h_{\kappa }^2(x)\, dx \le C {\delta }A_\beta ({\delta })\int _1^2 \int _{{{\mathbb {R}}}^d}|f_t(x)|^2\Vert x\Vert ^\beta h_{\kappa }^2(x)\, dxdt . \end{aligned}$$

(54)

Note that by (52),

$$\begin{aligned} \int _{{{\mathbb {R}}}^d} \Bigl |\int _1^2 S_t^{\delta }f_t(x)dt\Bigr |^2 \Vert x\Vert ^\beta h_{\kappa }^2(x)\, dx&=C \int _{{{\mathbb {R}}}^d}\Bigl |D^{\beta /2} \int _1^2 \phi _t(x) \widehat{f_t} (x)dt\Bigr |^2 h_{\kappa }^2(x)dx\\&=C \int _{{{\mathbb {R}}}^d}\int _{{{\mathbb {R}}}^d} \Vert y\Vert ^{-2l_{\kappa }-1-\beta } \Bigl |\int _1^2 \triangle _y^r (\phi _t \widehat{f})(x)\, dt \Bigr |^2 h_{\kappa }^2(y)h_{\kappa }^2(x) \, dy dx \end{aligned}$$

Since for $t\in [1,2]$, $\phi _t$ is supported in $\{z\in {{\mathbb {R}}}^d:\ \ (1-\frac{{\delta }}{2}) t\le \Vert z\Vert \le (1+\frac{{\delta }}{2})t\}$, $\triangle _y^r ( \phi _t \widehat{f_t})(x)= 0$ unless

$$\begin{aligned} \{z\in {{\mathbb {R}}}^d:\ \ \Vert x\Vert -r\Vert y\Vert \le \Vert z\Vert \le \Vert x\Vert +r\Vert y\Vert \}\cap \Bigg \{z:\ \ \Bigg (1-\frac{{\delta }}{2}\Bigg ) t\le \Vert z\Vert \le \Bigg (1+\frac{{\delta }}{2}\Bigg )t\Bigg \}\ne \emptyset , \end{aligned}$$

which holds either

$$\begin{aligned} \Bigg (1-\frac{{\delta }}{2}\Bigg ) t\le \Vert x\Vert -r\Vert y\Vert \le \Bigg (1+\frac{{\delta }}{2}\Bigg )t\quad \text{ or } \quad \Bigg (1-\frac{{\delta }}{2}\Bigg ) t\le \bigl |\Vert x\Vert +r\Vert y\Vert \bigr |\le \Bigg (1+\frac{{\delta }}{2}\Bigg )t \end{aligned}$$

In the first case, setting $a_{x,y}=\frac{\Vert x\Vert -r\Vert y\Vert }{1+\frac{{\delta }}{2}}$, we have that

$$\begin{aligned} 0\le t-a_{x,y}&\le \bigl |\Vert x\Vert -r\Vert y\Vert \bigr |\Bigg (\frac{1}{1-\frac{{\delta }}{2}}-\frac{1}{1+\frac{{\delta }}{2}}\Bigg )\\&\le \Bigg (1+\frac{{\delta }}{2}\Bigg )t {\delta }\Bigg (1-\frac{1}{4} {\delta }^2\Bigg )^{-1}\le 2\Bigg (1+\frac{{\delta }}{2}\Bigg ) {\delta }\Bigg (1-\frac{1}{4} {\delta }^2\Bigg )^{-1}\le c{\delta }. \end{aligned}$$

Similarly, in the second case, $0\le t-a'_{x,y}\le c{\delta }$, where $a'_{x,y}=\frac{\Vert x\Vert +r\Vert y\Vert }{1+\frac{{\delta }}{2}}$. Thus, for fixed $x, y\in {{\mathbb {R}}}^d$, the function $A_{x,y}(t):=\triangle _y^r ( \phi _t \widehat{f_t})(x)$ is supported in the set

$$\begin{aligned} I_{x,y}=\Bigl ([a_{x,y}, a_{x,y}+c{\delta }]\bigcup [a_{x,y}', a'_{x,y}+c{\delta }]\Bigr )\bigcap [1,2]. \end{aligned}$$

Using Hölder’s inequality, we then deduce that

$$\begin{aligned} \Bigl |\int _1^2 \triangle _y^r (\phi _t \widehat{f_t})(x)\, dt \Bigr |^2&\le C {\delta }\int _1^2 |\triangle _y^r (\phi _t \widehat{f_t})(x)|^2\, dt. \end{aligned}$$

This implies that

$$\begin{aligned}&\int _{{{\mathbb {R}}}^d} \Bigl |\int _1^2 S_t^{\delta }f_t(x)dt\Bigr |^2 \Vert x\Vert ^\beta h_{\kappa }^2(x)\, dx\\&\quad \le C {\delta }\int _{{{\mathbb {R}}}^d}\int _{{{\mathbb {R}}}^d} \Vert y\Vert ^{-2l_{\kappa }-1-\beta } \int _1^2 \bigl |\triangle _y^r (\phi _t \widehat{f_t})(x)\bigr |^2\, dt h_{\kappa }^2(x)h_{\kappa }^2(y) \, dy dx\\&\quad =C{\delta }\int _1^2 \int _{{{\mathbb {R}}}^d} |D^{\beta /2} (\phi _t \widehat{f_t})(x)|^2\, h_{\kappa }^2(x) dx dt\\&\quad =C{\delta }\int _1^2 \int _{{{\mathbb {R}}}^d}|S_t ^{\delta }f_t(x)|^2 \Vert x\Vert ^\beta h_{\kappa }^2(x) dx dt, \end{aligned}$$

which, by (51), is estimated above by

$$\begin{aligned} C {\delta }A_\beta ({\delta }) \int _1^2 \int _{{{\mathbb {R}}}^d}| f_t(x)|^2 \Vert x\Vert ^\beta h_{\kappa }^2(x)dx dt. \end{aligned}$$

This shows the asserted estimate (54). $\square$

Lemma 5.5

For $0\le \beta <2l_{\kappa }+1$,

$$\begin{aligned} \int _{0}^{\infty } \int _{{{\mathbb {R}}}^d} |S_t^{\delta }f(x)|^2 h_{\kappa }^2(x)\frac{dx}{\Vert x\Vert ^\beta }\frac{dt}{t}\le C_\beta {\delta }A_\beta ({\delta })\int _{{{\mathbb {R}}}^d} |f(x)|^2 h_{\kappa }^2(x)\frac{dx}{\Vert x\Vert ^\beta }. \end{aligned}$$

Proof

Recall that $(L_j f)^{\wedge } (\xi )=\widehat{f}(\xi ) \varphi (2^j\xi )$, where $\varphi \in C_c^\infty ({{\mathbb {R}}}^d)$ is supported in [1, 3] and satisfies that $\sum _{j\in {{\mathbb {Z}}}} \varphi (2^j\xi )=1$ for all $\xi \in {{\mathbb {R}}}^d{\setminus }\{0\}$. Thus,

$$\begin{aligned} S_t^{\delta }f(x)=f*_{\kappa }\widehat{\phi _t}(x) =\sum _{j\in {{\mathbb {Z}}}} (L_j f)*_{\kappa }\widehat{\phi _t}(x), \end{aligned}$$

where $((L_j f)*_{\kappa }\widehat{\phi _t})^{\wedge } (\xi ) =\varphi (2^j\xi ) \widehat{f}(\xi ) \phi (t^{-1}\xi ).$ Note that $\varphi (2^j\xi ) \phi (t^{-1}\xi )$ is identically zero unless

$$\begin{aligned} 2^{-j}\le \Vert \xi \Vert \le 3\cdot 2^{-j}\quad \text{ and } \quad \frac{3}{4} \Vert \xi \Vert ^{-1} \le t\le \frac{5}{4} \Vert \xi \Vert ^{-1}, \end{aligned}$$

which also implies that

$$\begin{aligned} 2^{j-2}\le \frac{3}{4} ( 3\cdot 2^{-j})^{-1}\le t \le \frac{5}{4} (2^{-j})^{-1}\le 2^{j+1}. \end{aligned}$$

This means that

$$\begin{aligned} S_t^{\delta }f(x)= f*_{\kappa }\widehat{\phi _t}(x) =\sum _{j\in {{\mathbb {Z}}}:\ \ 2^{j-2}\le t\le 2^{j+1}} (L_j f)*_{\kappa }\widehat{\phi _t}(x), \end{aligned}$$

and hence

$$\begin{aligned} |S_t^{\delta }f(x)|^2 \le C \sum _{j\in {{\mathbb {Z}}}:\ \ 2^{j-2}\le t\le 2^{j+1}} |(L_j f)*_{\kappa }\widehat{\phi _t}(x)|^2. \end{aligned}$$

It follows by Lemma 5.4 that

$$\begin{aligned} \int _{{{\mathbb {R}}}^d}\Bigg (\int _0^\infty |S_t^{\delta }f(x)|^2\frac{dt}{t}\Bigg ) h_{\kappa }^2(x)\frac{dx}{\Vert x\Vert ^\beta }&\le C \sum _{j\in {{\mathbb {Z}}}} \int _{{{\mathbb {R}}}^d}\int _{2^{j-2}}^{2^{j+1}} |S_t^{\delta }L_jf (x)|^2 \frac{dt}{t} h_{\kappa }^2(x) \frac{dx}{\Vert x\Vert ^\beta } \\&\le C A_\beta ({\delta }) \sum _{j\in {{\mathbb {Z}}}} \int _{{{\mathbb {R}}}^d}|L_j f|^2 h_{\kappa }^2(x)\frac{dx}{\Vert x\Vert ^\beta } \\&= C A_\beta ({\delta }) \Bigl \Vert \bigl (\sum _{j\in {{\mathbb {Z}}}}|L_j f|^2\bigr )^{1/2}\Bigr \Vert _{L^2(\Vert x\Vert ^{-\beta } h_{\kappa }^2(x))}^2. \end{aligned}$$

Since for $0\le \beta <2l_{\kappa }+1$, $w(x)=\Vert x\Vert ^{-\beta }\in A_1$, it follows by the weighted Paley-Littlewood inequality (see [6, Theorem 5.2]) that

$$\begin{aligned} \Bigl \Vert \bigg (\sum _{j\in {{\mathbb {Z}}}}|L_j f|^2\bigg )^{1/2}\Bigr \Vert _{L^2(\Vert x\Vert ^{-\beta }h_{\kappa }^2(x))}^2\le C \Vert f\Vert _{L^2(\Vert x\Vert ^{-\beta })}^2=C \int _{{{\mathbb {R}}}^d} |f(x)|^2 h_{\kappa }^2(x) \frac{ dx}{\Vert x\Vert ^\beta }. \end{aligned}$$

This completes the proof. $\square$

Let $\widehat{\phi }(u)={\delta }\phi '(u) u$ for $u\ge 0$. Define $\widetilde{S_t^{\delta }} f(x)$ by

$$\begin{aligned} \Bigl (\widetilde{S_t^{\delta }} f\Bigr )^{\wedge }(\xi ) =\widetilde{\phi }_t (\Vert \xi \Vert ) \widehat{f}(\xi ),\quad t>0, \end{aligned}$$

where $\widetilde{\phi }_t (\Vert \xi \Vert )=\widetilde{\phi }(t^{-1}\Vert \xi \Vert )$. It is easily seen that

$$\begin{aligned} \frac{d}{dt} S_t^{\delta }f(x) =-\frac{1}{t{\delta }}\widetilde{S_t^{\delta }} f(x). \end{aligned}$$

(55)

By Lemma 5.5 and (55), we can easily get the following lemma.

Lemma 5.6

For $0\le \beta <2l_{\kappa }+1$,

$$\begin{aligned} \int _{0}^{\infty } \int _{{{\mathbb {R}}}^d} |\widetilde{S_t^{\delta }} f(x)|^2 h_{\kappa }^2(x)\frac{dx}{\Vert x\Vert ^\beta }\frac{dt}{t}\le C_\beta {\delta }A_\beta ({\delta })\int _{{{\mathbb {R}}}^d} |f(x)|^2 h_{\kappa }^2(x)\frac{dx}{\Vert x\Vert ^\beta }. \end{aligned}$$

We are now in a position to prove Theorem 3.3.

Proof of Theorem 3.3

For $t>0$,

$$\begin{aligned} \Bigl ||S_t^{\delta }f(x)|^2-|S_1^{\delta }f(x)|^2\Bigr |&=2\Bigl |\int _1^t (S_u^{\delta }f(x))\bigg (\frac{d}{du} S_u^{\delta }f(x)\bigg )\, dx \Bigr |=\frac{2}{{\delta }}\Bigl |\int _1^t (S_u^{\delta }f(x))(\widetilde{S_u^{\delta }}f(x))\frac{du}{u}\Bigr |\\&\le \frac{2}{{\delta }}\int _0^\infty |S_u^{\delta }f(x)||\widetilde{S_u^{\delta }}f(x)|\frac{du}{u} \\&\le \frac{2}{{\delta }}\Bigg ( \int _0^\infty |S_u^{\delta }f(x)|^2\frac{du}{u}\Bigg )^{\frac{1}{2}}\Bigg ( \int _0^\infty |\widetilde{S_u^{\delta }} f(x)|^2\frac{du}{u}\Bigg )^{\frac{1}{2}}\\&=: \frac{2}{{\delta }}G^{\delta }f(x) \widetilde{G^{\delta }} f(x), \end{aligned}$$

where

$$\begin{aligned} G^{\delta }f(x)= \Bigg (\int _0^\infty |S_t^{\delta }f(x)|^2\frac{dt}{t}\Bigg )^{\frac{1}{2}}\quad \text{ and } \quad \widetilde{G^{\delta }} f(x)= \Bigg ( \int _0^\infty |\widetilde{S_t^{\delta }} f(x)|^2\frac{dt}{t}\Bigg )^{\frac{1}{2}}. \end{aligned}$$

It follows that

$$\begin{aligned} \int _{{{\mathbb {R}}}^d} |S_*^{\delta }f(x)|^2 h_{\kappa }^2(x)\frac{dx}{\Vert x\Vert ^\beta }&\le C \int _{{{\mathbb {R}}}^d} |S_1^{\delta }f(x)|^2 h_{\kappa }^2(x)\frac{dx}{\Vert x\Vert ^\beta }\\&\quad +C {\delta }^{-1} \int _{{{\mathbb {R}}}^d} G^{\delta }f(x) \widetilde{G^{\delta }} f(x) h_{\kappa }^2(x) \frac{dx}{\Vert x\Vert ^\beta }\\&\le C A_\beta ({\delta })\int _{{{\mathbb {R}}}^d} | f(x)|^2 h_{\kappa }^2(x)\frac{dx}{\Vert x\Vert ^\beta }\\&\quad + C{\delta }^{-1} \Bigg (\int _{{{\mathbb {R}}}^d}| G^{\delta }f(x)|^2 h_{\kappa }^2(x) \frac{dx}{\Vert x\Vert ^\beta }\Bigg )^{\frac{1}{2}}\Bigg (\int _{{{\mathbb {R}}}^d}|\widetilde{ G^{\delta }} f(x)|^2 h_{\kappa }^2(x) \frac{dx}{\Vert x\Vert ^\beta }\Bigg )^{\frac{1}{2}}\\&\le C A_\beta ({\delta })\int _{{{\mathbb {R}}}^d} | f(x)|^2 h_{\kappa }^2(x)\frac{dx}{\Vert x\Vert ^\beta }. \end{aligned}$$

$\square$

The last inequality follows from Lemmas 5.3 and 5.4.