Finite element approximation of invariant manifolds by the parameterization method

Abstract

We combine the parameterization method for invariant manifolds with the finite element method for elliptic PDEs, to obtain a new computational framework for high order approximation of invariant manifolds attached to unstable equilibrium solutions of nonlinear parabolic PDEs. The parameterization method provides an infinitesimal invariance equation for the invariant manifold, which we solve via a power series ansatz. A power matching argument leads to a recursive systems of linear elliptic PDEs—the so called homological equations—whose solutions are the power series coefficients of the parameterization. The homological equations are solved recursively to any desired order N using finite element approximation. The end result is an N-th order polynomial approximation of a chart map of the manifold, with coefficients in an appropriate finite element space. We implement the method for a variety of example problems having both polynomial and non-polynomial nonlinearities, on non-convex two dimensional polygonal domains (not necessary simply connected), for equilibrium solutions with Morse indices one and two. We implement a-posteriori error indicators which provide numerical evidence in support of the claim that the manifolds are computed accurately.

1 Introduction

The present work concerns nonlinear stability analysis for parabolic partial differential equations (PDEs). In particular, we develop high order numerical methods for approximating local unstable manifolds attached to equilibrium solutions of finite Morse index (finite number of unstable eigenvalues counted with multiplicity) for parabolic PDEs formulated on spatial domains with non-trivial geometry. We show that the Taylor coefficients of an appropriate parameterization of the local unstable manifold solve a homological equation which is strongly related to the eigenvalue problem/resolvent of the linearization at equilibrium. Our main goal is to leverage this result in the development of efficient numerical algorithms. We stress that, since we compute the Taylor coefficients order by order by directly solving the homological equations, our method does not require numerical integration of the parabolic PDE.

Recall that the equilibrium solutions of a parabolic PDE are found by solving the steady state equation, and that this equation usually reduces to an elliptic BVP. Likewise, the eigenvalue problems which determine the linear stability of an equilibrium solution are linear elliptic BVPs of the same kind. Because of this, there are dramatic differences between parabolic problems in the case of one spatial variable and in the case of two or more. For problems with one spatial variable, equilibrium and eigenvalue problems lead to two point BVPs for ordinary differential equations (ODEs). Such problems are generally amenable to spectral methods (Fourier series) which diagonalize both differential operators and multiplication (in Fourier and function space respectively) and which typically have excellent convergence properties. Parabolic PDEs in two or more spatial variables posed on domains with non-trivial geometry require fundamentally different theoretical and numerical tools. Finite element analysis is invaluable in this context, and—since finite element methods typically employ lower regularity approximation schemes—it is often necessary to study a weak formulation of the BVP.

Our approach is rooted in the tradition of the qualitative theory of dynamical systems, and exploits the parameterization method of Cabré, Fontich, and de la Llave [10,11,12]. The idea of the parameterization method is to study an auxiliary functional equation, whose solutions correspond to chart maps of the invariant object. The method is used widely in the field of computational dynamics. The basic mathematical setup and some additional references are discussed in Sect. 2.1. We extend the parameterization method to parabolic PDEs on non-trivial domains, and illustrate it’s utility by implementing numerical computations for a number of example systems.

• The Fisher Equation: scalar reaction/diffusion equation with logistic nonlinearity. This pedagogical example illustrates the main steps of our procedure in the easiest possible setting.

• The Ricker Equation: a modification of the Fisher equation with a more realistic exponential nonlinearity. We show how non-polynomial problems are treated using ideas from automatic differentiation for formal power series.

• A modified Kuramoto-Shivisinsky Equation: a scalar parabolic PDEs with the bi-harmonic Laplacian as the leading term and lower order derivatives in the nonlinearities. The system is a toy model of fluid dynamics.

For each example we derive the homological equations, and implement numerical procedures for solving them. In the case of a non-polynomial nonlinearity, the necessary formal series manipulations are simplified by coupling the given PDEs to auxiliary equations describing the transcendental nonlinear terms. We provide examples of this procedure, and develop power series expansions for unstable manifolds attached to equilibria with Morse indices 1 and 2. This provides examples of computations for one and two dimensional unstable manifolds. The Fisher and Ricker Equations are nonlinear heat equations, and we use piecewise linear finite elements to approximate the coefficients of the parameterization. Kuramoto-Shivisinsky is a bi-harmonic Laplacian equation, so that higher order elements are appropriate. Here we utilize the Argyris element. We implement a-posteriori error indicators for each of the examples, giving evidence that the manifolds have been computed correctly.

Remark 1.1

(Invariant manifolds for 1D domains) We remark that Fourier-Taylor methods for computing invariant manifolds for parabolic problems in one spatial dimension are treated in a number of places, for example in [2, 38, 54], and higher dimensional problems with periodic boundary conditions (including Dirchlet/Neumann boundary conditions on rectangles/boxes) can also be studied using multivariate Fourier series. We refer to the works of [7, 8, 14, 23, 35] for more discussion of invariant manifolds in this context.

The remainder of the paper is organized as follows. In Sect. 2 we review the finite element method for elliptic PDEs, and the parameterization method for invariant manifolds on Hilbert spaces. We also provide an elementary example of the formal series analysis for the unstable manifold in a simple finite dimensional example. In Sect. 3 we extend the parameterization method to a class of parabolic problems. Section 4 contains the main calculations of the paper, as we derive the homological equations for the main examples. We also implement the recursive solution of the homological equations for the main examples and report on some numerical results. Some conclusions and reflections are found in Sect. 5.

2 Background

While the material in this section is standard in some circles, the methods of the present work combine tools from different fields and it is worth reviewing some basic ideas. Our hope is that some brief review will help to make the paper more self contained. The reader familiar with these ideas may want to skip ahead to Sect. 3, and refer back to these sections only as needed.

2.1 The parameterization method

The parameterization method is a general functional analytic framework for studying invariant manifolds, originally developed for fixed points for maps on Banach spaces [10,11,12], and for whiskered tori of quasi-periodic maps [25,26,27]. Since then it has been extended to a number of settings for both discrete and continuous dynamical systems, in both finite and infinite dimensions. A complete overview of the literature is beyond the scope of the present brief introduction, and the interested reader will find a much more complete overview—including a wealth of references to the literature—in the recent book on the topic [24]. Several papers more closely related to the present work include works of [22, 28, 29] on delay differential equations, KAM for PDEs [17], and unstable manifolds for PDEs defined on compact intervals [38], and on the whole line [2]. More recently the parameterization method has been used to develop a mathematically rigorous approach to optimal mode selection in nonlinear model reduction by projecting onto spectral submanifolds [6, 9, 33]. This research direction has been further developed and combined with large finite element systems demonstrating its potential for industrial applications [48, 56].

2.1.1 Parameterization method for vector fields on Hilbert spaces

We give a brief review the parameterization method, in the context of evolution problems on Hilbert spaces. The main application we have in mind is the dynamics of a semi-flow generated by parabolic PDE. In particular, we discuss the invariance equation for the local unstable manifold attached to an equilibrium solution.

Let ${\mathcal {H}}$ be an $L^2$ Hilbert space ($H^k$ or $H_0^k$ for some k) and $F :{\mathcal {H}} \rightarrow L^2$ be a Frechet differentiable mapping. We adopt also the standard requirement that DF(x), when viewed as an operator on $L^2$, is densely defined and sectorial. Consider the evolution equation

$$\begin{aligned} \frac{\partial }{\partial t} u(t) = F(u(t)), \quad \quad \quad \text {with } u(0) \in {\mathcal {H}} \text { given}. \end{aligned}$$

(2.1)

An orbit segment (or solution curve) for Eq. (2.1) is a smooth curve $\gamma :(a, b) \rightarrow {\mathcal {H}}$ having

$$\begin{aligned} \frac{d}{dt} \gamma (t) = F(\gamma (t)), \end{aligned}$$

for each $t \in (a, b)$. If $b = \infty$ then $\gamma$ is a said to be a full forward orbit. Since F dose not depend on time, we can always choose $a = 0$.

The simplest type of orbits are equilibria, that is, solutions which do not change in time. For $u_0 \in {\mathcal {H}}$, the curve $\gamma (t) = u_0$ is a constant solution of Eq. (2.1) if and only if

$$\begin{aligned} F(u_0) = 0. \end{aligned}$$

For a given equilibrium solution $u_0$, we would like to understand first it’s linear stability, and then it’s nonlinear stability. That is, we would like to understand how orbits in a neighborhood of $u_0$ escape from that neighborhood.

Let $A = DF(u_0)$, and define the Morse index of $u_0$ to be the number of unstable eigenvalues of A, counted with multiplicity. We assume that Eq. (2.1) is parabolic, so that A generates a compact semi-group $e^{At}$. This insures that the Morse index of A is finite. Let $\lambda _1, \ldots , \lambda _M$ denote the unstable eigenvalues ordered so that

$$\begin{aligned} 0 < \text {real}\left( \lambda _1\right) \le \cdots \le \text {real}\left( \lambda _M\right) . \end{aligned}$$

Suppose for the sake of simplicity that each unstable eigenvalue has multiplicity one, and that they are all real (though both assumptions can be removed—see [10, 55]), and let $\xi _1, \ldots , \xi _M \in {\mathcal {H}}$ denote associated eigenfunctions, so that

$$\begin{aligned} A \xi _j = \lambda _j \xi _j, \quad \quad \quad 1 \le j \le M. \end{aligned}$$

Suppose that $\gamma :(-\infty , 0] \rightarrow {\mathcal {H}}$ is a solution curve for Eq. (2.1) and that $u \in {\mathcal {H}}$. We say that $\gamma$ is an infinite pre-history for u, accumulating in backward time to the equilibrium $u_0$, if

$$\begin{aligned} \gamma (0) = u, \quad \quad \quad \text {and} \quad \quad \quad \lim _{t \rightarrow -\infty } \gamma (t) = u_0. \end{aligned}$$

The unstable manifold attached to $u_0$, denoted $W^u(u_0)$, is the set of all $u \in {\mathcal {H}}$ which have an infinite pre-history, accumulating at $u_0$. The intersection of $W^u(u_0)$ with a neighborhood U of $u_0$ is called a local unstable manifold for $u_0$, and is denoted by

$$\begin{aligned} W^u(u_0) \cap U = W_{\text {loc}}^u(u_0, U). \end{aligned}$$

By the unstable manifold theorem, there exists a neighborhood U of $u_0$ so that $W_{\hbox {loc}}^u(u_0, U)$ is a smooth manifold, diffeomorphic to an M-disk, and tangent to the unstable eigenspace of A at $u_0$. Moreover, if A is hyperbolic (that is, if A has no eigenvalues on the imaginary axis), then $W_{\text {loc}}^u(u_0, U)$ is the set of all $u \in U$ which have well-defined backwards history remaining in a neighborhood of $u_0$ for all time $t \le 0$.

Fig. 1

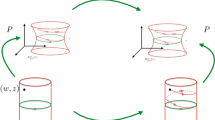
Schematic representation of the invariance equation given in Eq. (2.5). The idea is the DP pushes forward the vector field $\Lambda$ modeling the dynamics on the unstable manifold. This push forward should be equal, on the image of P, to the vector field F generating the full dynamics

We are now ready to introduce the parameterization method. Let ${\mathbb {B}} = [-1, 1]^M$ denote the M-dimensional unit hypercube. We seek a

$P :{\mathbb {B}} \rightarrow {\mathcal {H}}$ having that

$$\begin{aligned} P(0)= & {} u_0, \end{aligned}$$

(2.2)

$$\begin{aligned} \partial _j P(0)= & {} \xi _j, \quad \quad \quad \quad 1 \le j \le M, \end{aligned}$$

(2.3)

and that

$$\begin{aligned} P\left( [-1,1]^M\right) \subset W_{\hbox {loc}}^u(u_0, U), \end{aligned}$$

for some open set U containing $u_0$. Any such P is a local unstable manifold attached to $u_0$. Since any reparameterization of P is again a parameterization of a local unstable manifold, the problem has infinitely many freedoms and we need to impose an additional (infinite dimensional) constraint to isolate a single parameterization.

Write

$$\begin{aligned} \Lambda = \left( \begin{array}{ccc} \lambda _1 &{} \ldots &{} 0 \\ \vdots &{} \ddots &{} \vdots \\ 0 &{} \ldots &{} \lambda _{M} \end{array}\right) . \end{aligned}$$

(2.4)

The main idea of the parameterization method is to look for P which, in addition to satisfying the constraint Eqs. (2.2) and (2.3), is a solution of the invariance equation

$$\begin{aligned} F(P(\theta ))=DP(\theta )\Lambda \theta , \quad \quad \quad \text {for all } \theta \in {\mathbb {B}} = [-1,1]^M. \end{aligned}$$

(2.5)

We remark that the choice of “unit” domain is a normalization which will become more clear as we proceed.

Figure 1 illustrates the geometric meaning of Eq. (2.5). The equation requires that the push forward of the linear vector field $\Lambda$ by DP equals the vector field F restricted to the image of P. Loosely speaking, since the two vector fields match on the image of P they must generate the same dynamics—with the dynamics generated by $\Lambda$ well understood. We then expect that P maps orbits of $\Lambda$ in ${\mathbb {B}}$ to orbits of F on the image of P. Since P maps orbits to orbits, Eq. (2.5) is called an infinitesimal conjugacy equation. The geometric meaning of Eq. (2.5) is illustrated in Fig. 2, and is made precise by the following lemma, whose proof appears in Appendix C

Lemma 2.1

(Orbit correspondence) Assume that the unstable eigenvalues $\lambda _1, \ldots , \lambda _M$ are real and distinct. Suppose that $P :[-1,1]^M \rightarrow {\mathcal {H}}$ satisfies the first order constraints of Eqs. (2.2) and (2.3), and that P is a smooth solution of Eq. (2.5) on ${\mathbb {B}} = (-1,1)^M$. Then P parameterizes a local unstable manifold for $u_0$.

We remark that if F generates a semi-flow $\Phi$ near $u_0$, then Lemma 2.1 says that P satisfies the flow conjugacy

$$\begin{aligned} P(e^{\Lambda t} \theta ) = \Phi (P(\theta ), t), \end{aligned}$$

(2.6)

for all t such that $e^{\Lambda t} \theta \in (-1,1)^M$. That is, P conjugates the flow generated by $\Lambda$ to the flow generated by F.

An example illustrating the formal series solution of Eq. 2.5 for a simple ODE is given in Appendix A, with some numerical calculations given in Appendix B. These appendices are included for the reader who would like to see how the method works in the simplest possible setting before moving on to the more sophisticated applications to PDEs considered in the next section, in hopes of making the present work self contained. Other similar worked examples are found in the literature, and we refer the interested reader to [4, 13, 21, 53] for more details.

Fig. 2

The orbit correspondence induced by the invariance Equation. The orbits generated by the vector field $\Lambda$ accumulate in backwards time to the origin in ${\mathbb {B}}$. Then P lifts these orbits to orbits in ${\mathcal {H}}$ which accumulate at the equilibrium $u_0$. From this it follows that image of P is a local unstable manifold. or (2.5)

Remark 2.2

(Complex conjugate unstable eigenvalues) Complex conjugate eigenvalues are easily incorporated into this set-up by choosing associated complex conjugate eigenfunctions and proceeding as above. This results in complex conjugate coefficients for the parameterization P. The use of complex conjugate variables (in the appropriate components of $\theta$) results in P having real image, i.e. recovers the parameterization of the real manifold. The only difference is that one has to adjust the domain of the parameterization in the variables corresponding to the complex conjugate eigenvalues, choosing unit disks instead of unit intervals. In this sense the PDE case is no different from the ODE case described in detail in [36], where the interested reader can find more a complete discussion.

2.2 Finite element methods for elliptic linear elliptic PDE

In this section we briefly review some basic finite element analysis for elliptic BVPs needed for our numerical implementations. Excellent reference for this now classic material include [16, 19]. Let $\Omega \subset {\mathbb {R}}^d$ denote an open set and let ${\mathcal {H}}$ be an $L^2$ Sobolev space on $\Omega$ (and hence a Hilbert space). Let ${\mathcal {H}}^{\vee }$ denote the dual space consisting of all bounded linear functionals on ${\mathcal {H}}$.

Consider for example a uniformly elliptic linear PDE of the form

$$\begin{aligned} {\mathcal {L}}u= f, \end{aligned}$$

with Dirichlet boundary conditions $u |_{\partial \Omega } = 0$. We ask that ${\mathcal {L}}$ is densely defined on ${\mathcal {H}} \subset L^2$, and that $f \in L^2$.

A weak formulation of the problem is obtained after multiplying by a test-function $v\in {\mathcal {H}}$, applying Green’s formula (integration by parts), and imposing the boundary conditions. This results in the variational problem

$$\begin{aligned} \text {Find} u\in {\mathcal {H}} \text {such that} \forall v \in {\mathcal {H}}, \langle u,v \rangle _{{\mathcal {L}}}=\langle f, v \rangle , \end{aligned}$$

(2.7)

where

$$\begin{aligned} \langle f, v \rangle = \int _\Omega f v, \end{aligned}$$

and $\langle u,v \rangle _{{\mathcal {L}}}$ is a bilinear form. More generally, one can ask that ${\mathcal {L}} :{\mathcal {H}} \rightarrow {\mathcal {H}}^{\vee }$ and that $f \in {\mathcal {H}}^{\vee }$, where ${\vee }$ denotes the dual space.

The classical Lax-Milgram lemma insures that the problem has a unique solution u, assuming that $\langle \cdot ,\cdot \rangle _{{\mathcal {L}}} :{\mathcal {H}} \times {\mathcal {H}} \rightarrow {\mathbb {R}}$ is a continuous ${\mathcal {H}}$-elliptic bilinear form and $\langle f,\cdot \rangle :{\mathcal {H}} \rightarrow {\mathbb {R}}$ is a bounded linear functional (i.e, $\langle f,\cdot \rangle \in {\mathcal {H}}^{\vee }$). Neumann boundary conditions are handled using the same technology, after restricting to a space ${\mathcal {H}}$ of test functions which vanish on $\partial \Omega$. The treatment of more general boundary conditions using penalty methods, Lagrange multipliers, or projection methods is also classical. We refer to [1, 3, 15, 20, 52] for more general discussion of boundary conditions.

The finite element method (FEM) is a Galerkin projection approach to numerically solving Eq. (2.7), and consists of three main steps:

• 1. Triangulate $\Omega \subset {\mathbb {R}}^d$: obtain (often polygonal) mesh which discretizes the problem domain.

• 2. Choose interpolants for ${\mathcal {H}}$ on the mesh: construct a basis for the interpolant space where the basis functions have nearly disjoint support over mesh elements. This is the finite element basis and its span is a finite element space.

• 3. Solve the sparse linear system obtained by projecting the the weak formulation of the PDE (Eq. (2.7)) onto the finite element basis. This reduces the problem to numerical linear algebra.

In the present work we focus on $\Omega \subset {\mathbb {R}}^2$ a polygonal domain. However, we do not require $\Omega$ to be convex or even simply connected, and use the domains illustrated in Fig. 3. The next three subsections discuss the three steps listed above in more detail.

Fig. 3

Three example domains used in this paper. Note that they are non-convex, and non-simply connected. Left: the $\textit{L}$ domain: it has a reemergent corner. Center: the Door domain: not simply connected. Right: the Polygon with holes domain: toy model of a “natural” domain like a lake with islands

2.2.1 Triangulation of $\Omega \subset {\mathbb {R}}^2$

Let $\{T_i\}_{i = 1}^{{ne}}$ denote the elements of the triangulation so that

$$\begin{aligned} \Omega =\bigcup \limits _{i=1}^{{ne}} T_i. \end{aligned}$$

Here $T_i$ is the $i^{th}$ triangle, and ne is the number of triangles. We require that if the boundary of two triangles meet, then their intersection must be at a common edge. We remark that other discretizations can be considered, for example as in the Bogner-Fox-Schmit elements [16] (quadrilaterals), or even a combination of rectangles and triangles. Also, the discretization does not need to be uniform but can be adapted to the model and domain, leading to more efficient approximations.

2.2.2 Constructing the basis elements

The basis elements, which are required to have “small” compact support in ${\mathcal {H}}$, are typically chosen to be piecewise polynomial. In this paper we use linear polynomials for second order problems (Laplacian operator), and fifth degree polynomials for some fourth order examples (Bi-harmonic Laplacian). These Argyris elements are discussed in more detail in Sect. 4.4. More general basis elements can be considered such as special rational functions (for example Zienkiewicz triangles [16]).

A finite element is denoted by $E=[z_1, \ldots ,z_{{nn}}] \subset T$, where T is an arbitrary triangle and the $z_i$ are control points or nodes. $S_i:=\{L_{ij}: 1\le j \le s_i\}$ denotes a corresponding sets of control operators evaluated at $z_i$ (nn is the number of nodes in T and $s_i$ denotes the total number of operators assigned to the node $z_i$). Typically, the nodes consist of the vertices along with a few other carefully chosen points. In general, they are not required to be uniformly distributed in T.

Denote by ${lnb}:=\sum \limits _{k=1}^{{nn}} s_k$ and define

$$\begin{aligned} S=\bigcup \limits _{i=1}^{{nn}} S_i = \{L_i : 1\le i \le {lnb}\}. \end{aligned}$$

the set of operators associated with the finite element E. The letters lnb appropriately stand for “local number of basis” since the operators are used to determine the basis elements associated with T. That is, for each k, the system $L(\phi ):= (L_1(\phi ), \cdots , L_{{lnb}}(\phi ))= e_k$ is required to have a unique solution $\phi ^E_k$ in some vector space ${\mathcal {B}} \subset {\mathcal {H}}$. Here $e_k$ is the $k^{th}$ elementary basis vector in ${\mathbb {R}}^{{lnb}}$.

It follows that if we would like to work with

$$\begin{aligned} {\mathcal {B}}={\mathbb {P}}_k:=\{p: p \text {is a polynomial of degree at most} k \}, \end{aligned}$$

then we must have ${lnb}=\frac{(k+1)(k+2)}{2}$. Imposing regularity conditions (for example continunity) on the solution u imposes further restrictions on the finite elements. For ${\mathcal {B}}={\mathbb {P}}_1$ the elements are of the form $E=[n_1, n_2, n_3]$ where the $n_i$’s are the vertices of the triangles, and $S_i=\{{id}\}$ for all i’s, with ${id}(\phi )(n_i)=\phi (n_i)$.

Finally, let $V_h:=\text {span}\{\phi _i\}_{i=1}^{{nb}}\subset {\mathcal {H}}$ denote an interpolation space for ${\mathcal {H}}$, where nb is the total number of basis elements. Constructing this space involves collecting and indexing all the local basis functions.

2.2.3 Computing the projection

Let $u \in {\mathcal {H}}$ denote the solution of Eq. (2.7). The projection of u into $V_h$ is found by solving a weak formulation of Eq. (2.7) on $V_h$. More precisely, write $u_h=\sum \limits _{i=1}^{{nb}} c_i \phi _i$ and solve the linear system

$$\begin{aligned} \sum _{j=1}^{{nb}}c_j \langle \phi _j, \phi _i \rangle _{{\mathcal {L}}} = \langle f, \phi _i \rangle . \end{aligned}$$

(2.8)

It follows that the matrix $\Big ( \langle \phi _j, \phi _i \rangle _{{\mathcal {L}}} \Big )$ is invertible under the assumption that $\langle .,. \rangle _{{\mathcal {L}}}$ is ${\mathcal {H}}$-elliptic and the $\phi _i$ are linearly independent.

In general, a Lagrange type interpolation of a function f over T with control set $\{S_i\}$ is given by

$$\begin{aligned} \Pi _T(f)(x,y)=\sum _{i=1}^{{lnb}}L_i (f)(z_{n(i)}) \frac{det(A_i(x,y))}{det(A)} \end{aligned}$$

where $L_i\in S=\bigcup \limits _{i=1}^{{nn}} S_i$, and the index $n(i)=k$ for i such that $s_0+\cdots s_{k-1} + 1 \le i \le s_0+\cdots s_{k}$. Here we define $A_{ij}=\Big ( L_i(x^m y^n)(z_{n(i)})\Big )$, and ${(A_k(x,y))}_{ij}= (1-\delta _{ki})A_{ij} + \delta _{ki} x^my^n$, where $j=\frac{(m+n)(m+n+1)}{2} + (n+1)$. The operators $L_i$ are acting on the monomials $x^my^n$ where m, n range from 0 to the order of the polynomial interpolation, and the the coordinate j depends on m, n as described above. Notice that the only term that survives the evaluation of $L_i(\Pi _T(f))$ at a node gives the prescribed value. We let $S_0:=\emptyset$ for convenience of expressing n(i).

For low order polynomial bases the integrals appearing in (2.8) can be evaluated exactly. For higher order bases it is often more practical to use quadrature rules of sufficiently high degree to approximate the integrals. Such rules have the form

$$\begin{aligned} \int _{\Omega } f=\sum _{i=1}^{{ne}}\int _{T_i} f \approx \sum _{i=1}^{{{ne}}} \sum _{j=1}^{{nq}} w_{j}^{T_i} f(q_{j}^{T_i}), \end{aligned}$$

where nq is the degree of the quadrature rule, $q_j^{T_i}$ are the quadratures points, and $w_j^{T_i}$ are some appropriately chosen weights. Then

$$\begin{aligned} \Big ( \langle \phi _j,\phi _i \rangle _{{\mathcal {L}}}^{q} \Big ) c^q=\Big ( \langle f, \phi _i \rangle ^{q} \Big ), \end{aligned}$$

where $\langle \cdot ,\cdot \rangle _{{\mathcal {L}}}^{q}$ and $\langle f,\cdot \rangle ^{q}$ denote the quadrature approximation of the bilinear form and linear functional respectively. The solution to this approximated problem is denoted by $c^q$.

Suppose that the quadrature formula converges to the exact integral as $nq \rightarrow \infty$. If $\langle \cdot ,\cdot \rangle _{{\mathcal {L}}}$ is ${\mathcal {H}}$-elliptic, it follows that $\langle \cdot ,\cdot \rangle _{{\mathcal {L}}}^{q}$ is $V_h$-elliptic ($V_h \subset {\mathcal {H}}$) for nq large enough, which implies that $\Big ( \langle \phi _j,\phi _i \rangle _{{\mathcal {L}}}^{q} \Big )$ is invertible. In general, the ${\mathcal {H}}$-elliptic property of $\langle \cdot ,\cdot \rangle _{{\mathcal {L}}}$ is established using the Sobolev embedding theorems/Poincaré inequalities.

For any polynomial basis and Gaussian quadratures there is nq large enough so that $\langle \phi _j,\phi _i \rangle _{{\mathcal {L}}}^{q}=\langle \phi _j,\phi _i \rangle _{{\mathcal {L}}}$, in which case

$$\begin{aligned} \Vert c^q - c\Vert \le \left\| \Big (\langle f, \phi _i \rangle ^{q} - \langle f, \phi _i \rangle \Big )\right\| \left\| \Big ( \langle \phi _j,\phi _i \rangle _{{\mathcal {L}}}^{q} \Big )^{-1} \right\| , \end{aligned}$$

and approximating $f=p+\epsilon$, with p polynomial, we have

$$\begin{aligned} \left\| \Big ( \langle f, \phi _i \rangle ^{q} - \langle f, \phi _i \rangle \Big ) \right\| \le 2 \sup (|\epsilon |) \left\| \Big (\langle 1, |\phi _i| \rangle \Big ) \right\| . \end{aligned}$$

Bounding the projection error for a polynomial basis of order k requires assumptions about the domain $\Omega$. It follows, for example, by the the Bramble-Hilbert lemma that $\Vert u-u_h\Vert _{1,\Omega } = O(h^k)$, where $u_h$ denotes the projection of the solution u to the finite dimensional vector space $V_h$. Of course, more sophisticated and practical ways of estimating these errors can be found in the literature.

3 Formal power series and the homological equations for parabolic PDEs

We now turn to the main problem of this paper, which is to extend the kinds of calculations illustrated in Section A to the “vector fields” on Sobolev spaces generated by parabolic PDEs. To this end we introduce a fairly simple class of nonlinear heat equations which we find sufficient to highlight the main issues. Nevertheless, the discussion in this section generalizes to parabolic equations involving more general elliptic operators, to problems formulated on spatial domains of three or more dimensions with more general boundary conditions, and even to systems of PDEs. Indeed, our goal in this section is not to describe the most general possible setting but rather to illustrate the application parameterization method, and especially the solution of Eq. (2.5), for an interesting class of PDEs. Some extensions are given in Sect. 4.

Let $\Omega \subset {\mathbb {R}}^2$ denote bounded, planar, polygonal domain and $f :{\mathbb {R}} \times \Omega \rightarrow {\mathbb {R}}$ be a smooth function, satisfying mild growth conditions at infinity. Consider the class of scalar parabolic PDEs given by

$$\begin{aligned} \frac{\partial }{\partial t} u(t, x,y) = \Delta u(t, x, y) + f(u(t, x, y), x, y), \end{aligned}$$

(3.1)

with the Neumann boundary conditions

$$\begin{aligned} \frac{\partial }{\partial \textbf{n}} u(t, x, y) = 0 \quad \text {for } (x, y ) \in \partial \Omega . \end{aligned}$$

Fix ${\mathcal {H}} = H^1$. We are interested in the dynamics of the semi-flow generated by the vector field $F :{\mathcal {H}} \rightarrow {\mathcal {H}}^{\vee }$ given by

$$\begin{aligned} F(u) = \Delta u + f(u, x,y). \end{aligned}$$

These spaces are appropriate for defining a weak version of F(u).

We now consider an equilibrium solution. That is, suppose that $u_0 :\Omega \rightarrow {\mathbb {R}}$ is in ${\mathcal {H}}$ and is a solution of the weak form of the elliptic nonlinear boundary value problem

$$\begin{aligned} \Delta u(x, y) + f(u(x, y), x, y) = 0, \end{aligned}$$

subject to the Neumann boundary conditions. More precisely, this means that $u_0$ satisfies

$$\begin{aligned} -\int _{\Omega } \nabla u(x,y) \cdot \nabla \phi (x,y) + \int _{\Omega } f(u, x, y) \phi (x,y) = 0, \end{aligned}$$

for all $\phi \in {\mathcal {H}}$.

Suppose also that $u_0$ has Morse index M. That is, we assume that $\lambda _1, \ldots , \lambda _M\in (0, \infty )$ are the unstable eigenvalues, each with multiplicity one. Let $\xi _1, \ldots , \xi _M :\Omega \rightarrow {\mathbb {R}}$ denote associated unstable eigenfunctions, i.e. solutions in ${\mathcal {H}}$ of the weak form of the eigenvalue problem

$$\begin{aligned} \Delta \xi (x,y) + \partial _1 f(u_0,x,y) \xi = \lambda \xi (x,y), \end{aligned}$$

again subject to the boundary conditions.

We look for $P :[-1, 1]^M \rightarrow {\mathcal {H}}$ solving Eq. (2.5), with P given by the formal power series

$$\begin{aligned} P(\theta _1, \ldots , \theta _M, x,y) = \sum _{n_1 = 0}^\infty \ldots \sum _{n_M = 0}^\infty p_{n_1, \ldots , n_M}(x,y) \theta _1^{n_1} \ldots \theta _M^{n_M}. \end{aligned}$$

Here each coefficient $p_{n_1, \ldots , n_M} \in {\mathcal {H}}$ is required to satisfy the boundary conditions. Moreover, imposing the constraints of Eqs. (2.2) and (2.3) gives that the first order coefficients of P are

$$\begin{aligned} p_{0, \ldots , 0}(x,y) = u_0(x,y), \end{aligned}$$

and

$$\begin{aligned} p_{1, \ldots , 0}(x,y) = \xi _1(x,y), \quad \quad \quad \ldots \quad \quad \quad p_{0, \ldots , 1}(x,y) = \xi _M(x,y). \end{aligned}$$

To work out the higher order coefficients we follow the blueprint of Section A. Begin by letting $\Lambda$ denote the diagonal matrix of unstable eigenvalues as in Eq. (2.4). Calculating the push forward of $\Lambda$ by DP on the level of power series gives

$$\begin{aligned} DP(\theta , x,y) \Lambda \theta= & {} \left[ \partial _1 P(\theta , x,y), \ldots , \partial _M P(\theta , x,y) \right] \left( \begin{array}{c} \lambda _1 \theta _1 \\ \vdots \\ \lambda _M \theta _M \end{array} \right) \\{} & {} =\lambda _1 \theta _1 \frac{\partial }{\partial \theta _1} P(\theta , x,y) + \ldots + \lambda _M \theta _M \frac{\partial }{\partial \theta _M} P(\theta , x,y) \\{} & {} =\sum _{n_1 = 0}^\infty \ldots \sum _{n_M = 0}^\infty (n_1 \lambda _1 + \ldots + n_M \lambda _M) p_{n_1, \ldots , n_M}(x,y) \theta _1^{n_1} \ldots \theta _M^{n_M}. \end{aligned}$$

Observe that the value of this series at $\theta = 0$ is zero.

Next consider

$$\begin{aligned} F(P(\theta , x,y))&= \Delta P(\theta , x, y) + f(P(\theta , x,y), x, y). \end{aligned}$$

Proceeding formally, we commute the Laplacian with the infinite sum, and have that

$$\begin{aligned} \Delta P(\theta , x, y) = \sum _{n_1 = 0}^\infty \ldots \sum _{n_M = 0}^\infty \Delta p_{n_1, \ldots , n_M}(x,y) \theta _1^{n_1} \ldots \theta _M^{n_M}. \end{aligned}$$

If f is analytic then $f(P(\theta , x,y), x,y)$ admits a power series representation. (For f only $C^k$ regularity the argument below is modified accordingly). Let us write

$$\begin{aligned} f(P(\theta , x,y), x,y) = \sum _{n_1 = 0}^\infty \ldots \sum _{n_M = 0}^\infty q_{n_1, \ldots , n_M}(x,y) \theta _1^{n_1} \ldots \theta _M^{n_M}, \end{aligned}$$

where the $q_{n_1, \ldots , n_M}$ are the formal Taylor coefficients of the composition, and each depends on the coefficients of P. Efficient computation of the $q_{n_1, \ldots , n_M}$ best illustrated through examples in the next section and for the moment we remark that, for any given multi-index $(n_1, \ldots , n_M) \in {\mathbb {N}}^M$, the dependence of $q_{n_1, \ldots , n_M}$ on $p_{n_1, \ldots , n_M}$ has

$$\begin{aligned} q_{n_1, \ldots , n_M} = D_1 f (u_0, x,y) p_{n_1, \ldots , n_M} + S_{n_1, \ldots , n_M}, \end{aligned}$$

where $S_{n_1, \ldots , n_M}$ depends only on coefficients of P of lower order. This follows from the Faá di Bruno formula.

Matching like powers in Eq. (2.5) leads to

$$\begin{aligned}&(n_1 \lambda _1 + \ldots + n_M \lambda _M) p_{n_1, \ldots , n_M}\\&\quad = \Delta p_{n_1, \ldots , n_M} + q_{n_1, \ldots , n_M}\\&\quad = \Delta p_{n_1, \ldots , n_M} + D_1 f (u_0, x,y) p_{n_1, \ldots , n_M} + S_{n_1, \ldots , n_M}, \end{aligned}$$

so that

$$\begin{aligned}{} & {} \Delta p_{n_1, \ldots , n_M} + D_1 f (u_0, x,y) p_{n_1, \ldots , n_M} - (n_1 \lambda _1 + \ldots + n_M \lambda _M) p_{n_1, \ldots , n_M}\\{} & {} \quad = - S_{n_1, \ldots , n_M}. \end{aligned}$$

That is, $p_{n_1, \ldots , n_M}$ solves the linear equation

$$\begin{aligned} \left( DF(u_0) - (n_1 \lambda _1 + \ldots + n_M \lambda _M) \text {Id}_{{\mathcal {H}}} \right) p_{n_1, \ldots , n_M} = - S_{n_1, \ldots , n_M}, \end{aligned}$$

(3.2)

where the right hand side depends only on lower order terms.

Equation (3.2) is the homological equation for the unstable manifold for F at $u_0$. Observe that Eq. (3.2) is a linear elliptic PDE with the same boundary conditions as the original reaction/diffusion Eq. (3.1). Indeed, the linear operator on the left hand side is the resolvent of $DF(u_0)$, evaluated at the complex numbers $n_1 \lambda _1 + \ldots + n_M \lambda _M$. Then each Taylor coefficient of P is the solution of a linear problem no more complicated than the linearized equation at $u_0$, so that these equations are themselves amiable to finite element analysis under mild assumptions on the domain $\Omega$.

This is a general fact which makes the parameterization method so useful. The homological equations determining the jets of the invariant manifold parameterization are linear equations, as complicated as the linearized problems at the steady state itself. For example when considering a finite dimensional problem in Section  A, the steady state equations were systems of n nonlinear algebraic equations in n unknowns, and in this case the homological equations turned out to be systems of n linear equations in n unknowns. Moreover, the homological equations involved the characteristic matrix for the derivative of the vector field at the equilibrium.

In the calculations just discussed, the steady state equation is a nonlinear elliptic BVPs, and the homological equations turn out the be linear elliptic BVPs on the same domain with the same boundary conditions. In fact the linear operator is just the resolvent of the differential, in direct analogy with the finite dimensional case. In the remarks below, we expand on several similarities between the results just derived and the simple example calculation considered in Section A.

Remark 3.1

(Non-resonance conditions and existence of a formal solution) Observe that Eq. (3.2) has a unique solution if and only if the non-resonance condition

$$\begin{aligned} n_1 \lambda _1 + \ldots + n_M \lambda _M \notin \text {spec}(DF(u_0)), \end{aligned}$$

(3.3)

is satisfied whenever $n _1 + \ldots + n_M \ge 2$. Since $\lambda _1, \ldots , \lambda _M$ are the only unstable eigenvalues of $DF(u_0)$, and since $DF(u_0)$ generates a compact semi-group, we have that the countably many remaining eigenvalues are stable. (In practice we check that the remaining eigenvalues of the numerically computed derivative have negative real part).

Since the $n_1, \ldots , n_M$ are all positive, there are only finitely many opportunities for $n_1 \lambda _1 + \ldots + n_M \lambda _M$ to be an eigenvalue. If Eq. (3.3) is satisfied for all multi-indices $(n_1, \ldots , n_M) \in {\mathbb {N}}^M$ with $n_1 + \ldots + n_M \ge 2$ then we say that the unstable eigenvalues are non-resonant, and in this case we have that the parameterization P is formally well defined to all orders. That is, Eq. (2.5) has a well defined formal series solution satisfying the first order constraints of Eqs. (2.2) and (2.3).

Remark 3.2

(Uniqueness up to rescaling of the first order data) The unique solvability of the homological equations, assuming non-resonance of the unstable eigenvalues, gives that the solution P at $u_0$ is unique up to the choice of the scalings of the eigenfunctions. The choice of the scaling of the eigenfunctions directly effects the decay of the coefficients $p_{n_1, \ldots , n_M}$ as discussed in [4, 38]. For this reason we always fix the domain of the parameterization to be ${\mathbb {B}} = [-1,1]^M$, and choose the scaling of the eigenvectors so that the coefficients decay rapidly. Of course while choosing smaller scalings for the eigenvectors provides faster coefficient decay, it also means that the image of ${\mathbb {B}}$ is smaller in ${\mathcal {H}}$. That is, smaller scalings stabilize the numerics but reveal a smaller portion of the local unstable manifold. In practice we must strike a balance between the polynomial order of the calculation (at what order do we truncate the formal series?) the scaling of the eigenvectors and the size of the local unstable manifold we compute.

3.1 Automatic differentiation of power series

This section deals with the problem of working out the power series coefficients of nonlinear functions of known power series. Classic references for this material (which focus on the one variable case) are [31, 32]. The discussion will focus on the multivariable case.

A critical step in any explicit example application of the parameterization method is to work out the dependence of the coefficients $q_{n_1, \ldots , n_M}$ of the nonlinear composition on the unknown coefficients $p_{n_1, \ldots , n_M}$. This is essential for defining the right hand side $S_{n_1, \ldots , n_M}$ of the Homological equation (3.2). This challenge reduces to repeated application of the Cauchy product formula whenever $f(\cdot , x,y)$ has polynomial nonlinearity.

For example consider the case where f is a quadratic function of the form

$$\begin{aligned} f(u, x,y) = a(x,y) u^2. \end{aligned}$$

Then, the standard Cauchy product formula for two power series gives that

$$\begin{aligned}&f(P(\theta , x,y), x,y)\\&\quad = a(x,y) \left( \sum _{n_1 = 0}^\infty \ldots \sum _{n_M = 0}^\infty p_{n_1, \ldots , n_M}(x,y) \theta _1^{n_1} \ldots \theta _M^{n_M} \right) \\&\qquad \times \left( \sum _{n_1 = 0}^\infty \ldots \sum _{n_M = 0}^\infty p_{n_1, \ldots , n_M}(x,y) \theta _1^{n_1} \ldots \theta _M^{n_M} \right) \\&\quad = \sum _{k_1 = 0}^{n_1} \ldots \sum _{k_M = 0}^{n_M} q_{n_1, \ldots , n_M}(x,y) \theta _1^{n_1} \ldots \theta _M^{n_M}, \end{aligned}$$

where

$$\begin{aligned} q_{n_1, \ldots , n_M}(x,y)&= \sum _{k_1 = 0}^{n_1} \ldots \sum _{k_M = 0}^{n_M} a(x,y) p_{n_1 - k_1, \ldots , n_M - k_M}(x,y) p_{k_1, \ldots , k_M}(x,y) \\&= 2 a(x,y) p_{0, \ldots , 0}(x,y) p_{n_1, \ldots , n_M}(x,y) + \text {``lower order terms''} \\&= 2 \frac{\partial }{\partial u} f(u_0, x,y) p_{n_1, \ldots , n_M}(x,y) + \text {``lower order terms''}, \end{aligned}$$

as promised in the previous section. We see that the “lower order terms” have the explicit form

$$\begin{aligned} S_{n_1, \ldots , n_M} = \sum _{k_1 = 0}^{n_1} \ldots \sum _{k_M = 0}^{n_M} \hat{\delta }_{n_1, \ldots , n_M}^{k_1, \ldots , k_M} a(x,y) p_{n_1 - k_1, \ldots , n_M - k_M}(x,y) p_{k_1, \ldots , k_M}(x,y) \end{aligned}$$

where the coefficient

$$\begin{aligned} \hat{\delta }_{n_1, \ldots , n_M}^{k_1, \ldots , k_M} = {\left\{ \begin{array}{ll} 0 &{} \text {if } k_1 = \ldots = k_M = 0 \\ 0 &{} \text {if } k_1 = n_1, \ldots , k_M = n_M \\ 1 &{} \text {otherwise} \end{array}\right. }, \end{aligned}$$

appears in the sum to indicate that both of the terms with $p_{n_1, \ldots , n_M}(x,y)$ have been removed.

When f contains non-polynomial terms, calculating the $q_{n_1, \ldots , n_M}$ is more delicate. We employ a semi-numerical technique based on the idea that many typical nonlinearities appearing in applications are themselves solutions of polynomial differential equations. This is exploited in fast recursion schemes.

Consider for example the case of

$$\begin{aligned} f(u, x,y) = a(x,y) e^{-u}. \end{aligned}$$

Let

$$\begin{aligned} P(\theta , x, y) = \sum _{n_1 = 0}^\infty \ldots \sum _{n_M = 0}^\infty p_{n_1, \ldots , n_M}(x,y) \theta _1^{n_1} \ldots \theta _M^{n_M}, \end{aligned}$$

and write

$$\begin{aligned} Q(\theta , x,y) =\sum _{n_1 = 0}^\infty \ldots \sum _{n_M = 0}^\infty q_{n_1, \ldots , n_M}(x,y) \theta _1^{n_1} \ldots \theta _M^{n_M} = f(P(\theta , x, y)). \end{aligned}$$

(3.4)

The following idea is described in detail in Chapter 2 of [24]. We apply the radial gradient—the first order partial differential operator given by

$$\begin{aligned} \nabla _{\theta } = \theta _1 \frac{\partial }{\partial \theta _1} + \ldots + \theta _M \frac{\partial }{\partial \theta _M}, \end{aligned}$$

to both sides of Eq. (3.4) and obtain

$$\begin{aligned} \nabla _\theta f(P(\theta , x,y), x,y) = \nabla _\theta Q(\theta , x,y). \end{aligned}$$

That is

$$\begin{aligned}&\nabla _\theta f(P(\theta , x,y), x,y)\\&\quad = \theta _1\frac{\partial }{\partial u} f(u,x,y)\left| _{u = P(\theta , x,y)} \right. \frac{\partial }{\partial \theta _1} P(\theta ,x,y) + \ldots \\&\qquad + \theta _M\frac{\partial }{\partial u} f(u,x,y)\left| _{u = P(\theta , x,y)} \right. \frac{\partial }{\partial \theta _M} P(\theta , x,y) \\&\quad = -a(x,y) e^{- P(\theta , x,y)} \left( \theta _1 \frac{\partial }{\partial \theta _1} P(\theta , x,y) + \ldots + \theta _M \frac{\partial }{\partial \theta _M} P(\theta , x,y) \right) \\&\quad = - Q(\theta , x,y) \nabla _\theta P(\theta , x,y)\\&\quad = - \left( \sum _{n_1 = 0}^\infty \ldots \sum _{n_M = 0}^\infty q_{n_1, \ldots , n_M}(x,y) \theta _1^{n_1} \ldots \theta _M^{n_M} \right) \\&\quad \left( \sum _{n_1 = 0}^\infty \ldots \sum _{n_M = 0}^\infty (n_1 + \ldots + n_M) p_{n_1, \ldots , n_M}(x,y) \theta _1^{n_1} \ldots \theta _M^{n_M} \right) \\&\quad \qquad = - \! \sum _{n_1 = 0}^\infty \ldots \sum _{n_M = 0}^\infty \left( \sum _{k_1 =0}^{n_1} \ldots \sum _{k_M =0}^{n_M} (k_1 + \ldots + k_M)q_{n_1 - k_1, \ldots , n_M - k_M} p_{k_1, \ldots , k_M} \right) \theta _1^{n_1} \ldots \theta _M^{n_M}, \end{aligned}$$

on the left, and

$$\begin{aligned} \nabla _\theta Q(\theta , x,y) = \sum _{n_1 = 0}^\infty \ldots \sum _{n_M = 0}^\infty (n_1 + \ldots + n_M) q_{n_1, \ldots , n_M}(x,y) \theta _1^{n_1} \ldots \theta _M^{n_M} \end{aligned}$$

on the right. Matching like powers and isolating $q_{n_1, \ldots , n_M}$ leads to

$$\begin{aligned} q_{n_1, \ldots , n_M} = \frac{-1}{n_1 + \ldots + n_M} \sum _{k_1 =0}^{n_1} \ldots \sum _{k_M =0}^{n_M} (k_1 + \ldots + k_M)q_{n_1 - k_1, \ldots , n_M - k_M} p_{k_1, \ldots , k_M}. \end{aligned}$$

Then the complexity of computing the power series coefficients of $a(x,y) e^{-P(\theta , x,y)}$ is the complexity of a single Cauchy product. The additional cost is that the coefficients of Q have to be stored in addition to those of P.

Such methods for formal series manipulations are referred to by many authors as automatic differentiation for power series, and they facilitate rapid computation of the formal series coefficients of compositions with all the elementary functions. A classic reference, which includes an in depth historical discussion, is found in Chapter 4, Section 6 of [32]. See also the discussion of software implementations found in [31].

4 Applications

4.1 A first worked example: Fisher’s Equation

Consider the parabolic PDE

$$\begin{aligned} \frac{\partial }{\partial t}u=\Delta u +\alpha u (1-u), \end{aligned}$$

on the ${\mathbb {L}}$ domain $\Omega$ illustrated in the left-most frame of Fig. 3, subject to the Neumann boundary conditions

$$\begin{aligned} \nabla u \cdot {\textbf {n}}|_{\partial \Omega }=0. \end{aligned}$$

Here n is a unit vector normal to $\partial \Omega$. This reaction-diffusion equation was introduced by Ronald Fisher in the context of population dynamics, as a toy model for the propagation of advantageous genes. It is essentially a nonlinear heat equation with logistic nonlinearity. Letting

$$\begin{aligned} F(u) = \Delta u +\alpha u (1-u), \end{aligned}$$

we see that the problem describes an evolution equation as in Eq. (2.1). For this example we let ${\mathcal {H}} = H^1(\Omega )$.

The example provides an interesting first study both because it has the simplest possible nonlinearity, and also because the well understood bifurcation structure of the problem gives us easy access to non-trivial equilibrium solutions with any desired Morse index as we now discuss.

Recall that an equilibrium solution has $F(u) = 0$, so that the constant function 0 is always an equilibrium solution of Fisher’s Equation. This is referred to as the homogeneous background solution. Note that when $\alpha = 0$, the homogeneous background solution is stable, as the problem reduces to the heat equation. For $\alpha \ne 0$ the problem has two constant equilibrium solutions, $u \equiv 0$ and $u \equiv 1$.

Increasing $\alpha$ causes an eigenvalue to crosses the imaginary axis (in fact it pass through zero as all eigenvalues are real) so that the homogeneous background solution looses stability. This is a symmetry breaking, or pitch-fork bifurcation and it gives rise to a pair of non-constant equilibrium solutions. The new branches of equilibrium solutions carry the pre-bifurcation Morse index of background state, so that after the first bifurcation they are stable. The eigenvalue-eigenvector problem is specified below.

As $\alpha$ increases more and more eigenvalues pass through zero, increasing the morse index of the homogeneous solution. Each of these bifurcations gives rise to a new branch of equilibrium solutions, and we can follow any of these branches using numerical continuation methods. The first pair of non-trivial equilibria to appear are initially stable, however they also undergo symmetry breaking bifurcations of their own, and loose stability as $\alpha$ is increased further. For example, at $\alpha =2.7$ the first non-trivial branch of equilibrium solutions have Morse index 1, and Morse index 2 when $\alpha = 9$. These equilibrium solutions then have one and two dimensional attached unstable manifolds respectively. In the remainder of this section we discuss in detail the parameterization of the two dimensional unstable manifold for this otherwise simple example.

To find equilibria, we study the nonlinear elliptic BVP

$$\begin{aligned} F(u) = \Delta u + \alpha u (1-u) = 0, \end{aligned}$$

subject to the same natural boundary conditions on $\Omega$. The weak formulation is

$$\begin{aligned} {\mathcal {F}}(u)\phi =-\int _{\Omega } \nabla u \cdot \nabla \phi +\int _{\Omega } \alpha u(1-u)\phi =0, \end{aligned}$$

and, using the notation of Sect. 2.2, triangulate $\Omega$ and solve for the coefficients of the finite element representation $u_h=\sum _{j=1}^{{nb}} c_j \phi _j$ of u. In order to construct this projection, define the linear basis functions $\phi _j$ as

$$\begin{aligned} \phi _j(n_i)= {\left\{ \begin{array}{ll} 1 &{} j = i \\ 0 &{} j \ne i \end{array}\right. }, \end{aligned}$$

where $n_i$ denotes the $i-th$ vertex in the triangulation. Note that in this case, ${nb}={nn}$. Letting $\phi =\phi _i$ for $1\le i\le {nb}$ leads to the nonlinear system of nb equations in nb unknowns, given by

$$\begin{aligned} {\mathcal {F}}^{h}_i(c)=-\int _{\Omega } \left( \sum _{j=1}^{{nb}} c_j \nabla \phi _j \right) \cdot \nabla \phi _i + \int _{\Omega } \alpha \left( \sum _{j=1}^{{nb}} c_j \phi _j \right) \left( 1-\sum _{j=1}^{{nb}} c_j \phi _j \right) \phi _i =0, \end{aligned}$$

which we solve using the Newton’s Method (for $c=(c_1,c_2,...,c_{nb})$). More precisely, let ${\mathcal {F}}^{h}(c)=({\mathcal {F}}^{h}_1(c),...,{\mathcal {F}}^{h}_{{nn}}(c))=({\mathcal {F}}(u_h)\phi _1,...,{\mathcal {F}}(u_h)\phi _{nn})$. The k’th Newton’s step is given by

$$\begin{aligned} c^{(k)}= c^{(k-1)} -{D{\mathcal {F}}^{h}\left( c^{(k-1)}\right) }^{-1}{\mathcal {F}}^{h}\left( c^{(k-1)}\right) , \end{aligned}$$

where $u_h^{(k)}= \sum _{j=1}^{{nb}} c^{(k)}_j \phi _j$ and $D{\mathcal {F}}^{h}(c)= -\left( \int _{\Omega } \nabla \phi _j \cdot \nabla \phi _i\right) + \left( \int _{\Omega } \frac{ \partial N(c)}{ \partial c_j} \phi _i\right)$.

Fig. 4

Fisher’s equation with $\alpha =9$, $ne=515$. Left: Equilibrium solution, with Morse index 2. Center: Eigenfunction for $\lambda _1=9.04$. Right: Eigenfunction for $\lambda _2=7.16$

Once the approximate solution $u_0$ is computed we proceed to solve the eigenvalue-eigenvector problem

$$\begin{aligned} \Delta \xi + \alpha (1-2 u_0) \xi -\lambda \xi =0, \quad \quad \nabla \xi \cdot {\textbf {n}}|_{\partial \Omega }=0. \end{aligned}$$

That is, we compute the projection $\xi _h=\sum \limits _{j=1}^{{nb}} c_j \phi _j$ in the weak formulation, which leads to

$$\begin{aligned} -\int _{\Omega } \left( \sum _{j=1}^{{nb}} c_j \nabla \phi _j \right) \cdot \nabla \phi _i + \int _{\Omega } \alpha (1-2u_0) \left( \sum _{j=1}^{{nb}} c_j \phi _j \right) \phi _i =\int _{\Omega } \lambda \left( \sum _{j=1}^{{nb}} c_j \phi _j \right) \phi _i \end{aligned}$$

or

$$\begin{aligned} \Big (- \int _{\Omega } \nabla \phi _j \cdot \nabla \phi _i + \alpha (1-2u_0)\phi _j \phi _i\Big )c = \lambda \Big (\int _{\Omega }\phi _j \phi _i\Big )c. \end{aligned}$$

After computing the unstable eigenvalues $\lambda _1$ and $\lambda _2$ and the associated eigenfunctions $\xi _1$ and $\xi _2$, we proceed to solve the invariance Eq. (2.5) specialized to the present situation. That is, we consider the weak form of the equation

$$\begin{aligned} F(P(\theta ))=\lambda _1 \theta _1 \frac{\partial }{\partial \theta _1} P(\theta ) +\lambda _2 \theta _2 \frac{\partial }{\partial \theta _2} P(\theta ), \end{aligned}$$

where

$$\begin{aligned} P(\theta )=\sum \limits _{m=0}^{\infty }\sum \limits _{n=0}^{\infty }p_{m,n}(x,y)\theta _1^m \theta _2^n, \end{aligned}$$

with $p_{0,0}=u_0$, $p_{1,0}=\xi _1$ and $p_{0,1}=\xi _2$. Taking the projection $p_{m,n}=\sum \limits _{j=1}^{{nb}}c_j^{(m,n)} \phi _j$, leads to

$$\begin{aligned} \Big (- \int _{\Omega } \nabla \phi _j \cdot \nabla \phi _i + \alpha ( 1-2u_0- m\lambda _1 -n\lambda _2 ) \phi _j \phi _i\Big ) \Big ( c_i^{(m,n)}\Big ) = \Big (\int _{\Omega } s_{(m,n)} \phi _i \Big ), \end{aligned}$$

for $m +n\ge 2$, which is

$$\begin{aligned} \Big (D{\mathcal {F}}^{h}(c^{(0)})-(\lambda _1 m + \lambda _2 n) \int _{\Omega } \phi _j \phi _i \Big ) c^{(m,n)}=\Big ( \int _{\Omega } s_{(m,n)} \phi _i \Big ), \end{aligned}$$

with

$$\begin{aligned} s_{(m,n)}=\alpha \sum \limits _{i=0}^{m} \sum \limits _{j=0}^{n} \delta (i,j) p_{i,j}p_{m-i,n-j}, \end{aligned}$$

and

$$\begin{aligned} \delta (i,j)= {\left\{ \begin{array}{ll} 0 &{} (i,j)=(0,0) \text {or} (i,j)=(m,n) \\ 1 &{} \text {otherwise} \end{array}\right. }. \end{aligned}$$

As anticipated in Sect. 3.1, the homological equations are linear elliptic PDEs, and we solve them recursively to any desired order using the Finite Element Method. Figure 6 shows a few functions in the fast manifold (1d manifold associated to the largest positive eigenvalue) and slow manifold (1d manifold associated to the smallest positive eigenfunction) approximated up to order $N=30$.

The effect of the scaling of the eigenvectors on the decay of the coefficients is illustrated in Fig. 5 .

Fig. 5

Coefficient growth: three plots of the magnitude of the parameterization coefficients as a function of the order of the coefficients. (Horizontal axis is the order of the coefficient and vertical axis is the base ten logarithm $L^2$ norm of the coefficient function). Left: The scaling of the eigenvector is too small, and the coefficients decay too fast. Coefficients after order then are below machine precision in $L^2$ norm (smaller than $10^{-16}$) and hence do not contribute significantly to the accuracy of the polynomial approximation. Center: The eigenvector scaling is choosen too large, and now the $p_{m,n}$’s grow exponentially fast. This introduces numerical instabilities into the approximation. Right: The scaling is chosen just right: they decay exponentially fast at a rate chosen so that the N-th order coefficients reach machine precision

Fig. 6

Left: 10 functions on the fast manifold approximated to order $N=30$ with Invariance equation error of 1.34e−8 with respect to the $L^2$ norm, and 5.98*e−8 with respect to the $H^1$ norm. Right: 10 functions on the slow manifold approximated to order $N=30$ with Invariance equation error of 4.56e−07 with respect to the $L^2$ norm, and 2.19e−06 with respect to the $H^1$ norm

4.2 A reaction diffusion equation with non-polynomial nonlinearity: one unstable eigenvalues

In this section we derive the homological equations for a non-polynomial problem. We consider the reaction diffusion equation with Ricker type exponential nonlinearity given by

$$\begin{aligned} u_t=\Delta u + \alpha u \left( 0.5-e^{-u} \right) , \end{aligned}$$

(4.1)

over the ${\mathbb {L}}$ domain with Neumann boundary conditions and ${\mathcal {H}} = H^1(\Omega )$.

We refer to this problem as the Fisher-Ricker (FR) equation, and take parameter $\alpha = -4.7$. Letting

$$\begin{aligned} F(u) = \Delta u + \alpha u \left( 0.5-e^{-u} \right) , \end{aligned}$$

we obtain an evolution equation of the kind given in Eq. (2.1).

To find the equilibrium solution consider the weak form of the equation $F(u) = 0$, project into a finite element space of piecewise linear functions, and solve

$$\begin{aligned} {\mathcal {F}}^{h}_i(c)= -\int _{\Omega } \left( \sum _{j=1}^{{nb}} c_j \nabla \phi _j \right) \cdot \nabla \phi _i + \int _{\Omega } \alpha \left( \sum _{j=1}^{{nb}} \phi _j\right) \left( 0.5- \exp \{-\sum _{j=1}^{{nb}} c_j \phi _j\}\right) \phi _i =0. \end{aligned}$$

The corresponding eigenvalue-eigenfunction problem is

$$\begin{aligned} D{\mathcal {F}}^{h}(c^{(0)})c = \lambda \Big ( \int _{\Omega } \phi _j \phi _i \Big )c. \end{aligned}$$

Suppose now that $u_0$ is an equilibrium solution with Morse index 1, let $\lambda$ denote the unstable eigenvalue, and $\xi$ be a corresponding eigenfunction. We seek a parameterization of the form $P(\theta )=\sum \limits _{n=0}^{\infty }p_n \theta ^n$ solving the 1D Invariance Equation

$$\begin{aligned} F(P(\theta )) = \theta \lambda \frac{d}{d \theta } P(\theta ), \end{aligned}$$

which, after expanding $P(\theta )$ as a power series becomes

$$\begin{aligned} \sum \limits _{n=0}^{\infty }\Delta p_n \theta ^n +\alpha \left( \sum \limits _{n=0}^{\infty }p_n \theta ^n\right) \left( 0.5- \exp \left( -\sum \limits _{n=0}^{\infty }p_n \theta ^n \right) \right) =\lambda \sum \limits _{n=0}^{\infty } n p_n \theta ^n. \end{aligned}$$

Here, the $p_n = p_n(x,y)$ are functions defined on $\Omega$ satisfying the boundary conditions.

We compute the power series coefficients of the exponential nonlinearity as in Sect. 3.1. That is, we introduce the new variable

$$\begin{aligned} Q(\theta ):= e^{-P(\theta )}=\sum \limits _{n=0}^{\infty } q_n \theta ^n, \end{aligned}$$

and note that $Q'=-QP'$. Then

$$\begin{aligned} q_n=-p_n q_0 - \frac{1}{n} \sum \limits _{j=0}^{n-2}(j+1)p_{j+1}q_{n-1-j}. \end{aligned}$$

(4.2)

Note that Eq. (4.2) involves only sums and products of the functions $p_i(x,y), q_j(x,y)$, for $0 \le i,j \le n$, and that these operations are well defined for $p_n, q_n$ in any finite element space. Equation (4.2) then allows us to compute $q_n$ to any desired order, assuming that $p_n, \ldots , p_0$, and $q_{n-1}, \ldots , q_0$ are known.

Returning to the Invariance Equation and using the recursive formula for $q_n$ we obtain that for $n \ge 2$, the $p_n$ solve

$$\begin{aligned} \Delta p_n +\alpha ( 0.5-q_0-\lambda n )p_n -\alpha p_0 q_n = \alpha \sum \limits _{j=1}^{n-1} p_j q_{n-j}, \end{aligned}$$

or

$$\begin{aligned} \Delta p_n +\alpha (0.5-q_0+p_0q_0- \lambda n)p_n= s_n, \end{aligned}$$

where

$$\begin{aligned} s_n=\alpha \sum \limits _{j=1}^{n-1} p_j q_{n-j} - \frac{\alpha p_0}{n} \sum \limits _{j=0}^{n-2} (j+1) p_{j+1}q_{n-1-j}. \end{aligned}$$

Passing to the weak form, we find that the coefficients $p_{n}=\sum \limits _{j=1}^{{nb}}c_j^{(n)} \phi _j$ solve the homological equations

$$\begin{aligned} \Big (D{\mathcal {F}}^{{h}}(c^{(0)})-\lambda n \int _{\Omega } \phi _j \phi _i \Big ) c^{(n)} =\Big ( \int _{\Omega } s_n \phi _i \Big ), \end{aligned}$$

(4.3)

for $n \ge 2$. Notice that $s_n$ only depends on $p_k$’s and $q_k$’s with $0< k<n$. Then if $p_0, \ldots , p_{n-1}$ and $q_0, \ldots , q_{n-1}$ are known, $p_n$ is computed by solving Eq. (4.3). Once $p_n$ is known, we update Eq. (4.2) to obtain $q_n$.

4.3 A reaction diffusion equation with non-polynomial nonlinearity:two unstable eigenvalues

A modification of the method just discussed allows us to compute higher dimensional manifolds in problems with non-polynomial nonlinearities. Consider again Eq. (4.1),

this time with $\alpha =-4.41$. At this parameter value there is a non-trivial equilibrium $u_0$ with Morse index 2. Let $\lambda _1$ and $\lambda _2$ denote the unstable eigenvalues and $\xi _1$, $\xi _2$ denote an associated pair of unstable eigenfunctions.

Fig. 7

Fisher-Ricker equation with $\alpha =-4.7$, $ne=515$. Left: Equilibrium solution. Center: Eigenfunction $\xi _1$ with $\lambda _1=2.41$. Right: Eigenfunction $\xi _2$ with $\lambda _2=0.05$

Recall that for an equilibrium with Morse index 2, the invariance equation becomes

$$\begin{aligned} F(P(\theta ))=\lambda _1 \theta _1 \frac{\partial }{\partial \theta _1} P(\theta ) +\lambda _2 \theta _2 \frac{\partial }{\partial \theta _2} P(\theta ), \end{aligned}$$

and we seek a power series solution of the form

$$\begin{aligned} P(\theta )=\sum \limits _{m=0}^{\infty }\sum \limits _{n=0}^{\infty }p_{m,n}(x,y)\theta _1^m \theta _2^n, \end{aligned}$$

with

$$\begin{aligned} p_{00} = u_0, \quad \quad \quad p_{10} = \xi _1, \quad \text {and} \quad p_{01} = \xi _2, \end{aligned}$$

and where $p_{m,n}$ for $m+n \ge 2$ are to be determined.

Once again, we exploit the technique developed in Sect. 3.1 to work out the exponential nonlinearity, and define the auxiliary equation

$$\begin{aligned} Q:=\exp \left( -P(\theta )\right) =\sum \limits _{m=0}^{\infty }\sum \limits _{n=0}^{\infty }q_{m,n}(x,y)\theta _1^m \theta _2^n, \end{aligned}$$

and take the radial gradient to obtain that

$$\begin{aligned} q_{m,n}=-\frac{1}{(m+n)} \sum \limits _{i=1}^{m}\sum \limits _{j=1}^{n}(i+j)p_{i,j}q_{m-i,n-j}. \end{aligned}$$

Note that this requires only additions and multiplications, all well defined operations for finite element basis functions.

Returning to the Invariance Equation and using the recursive formula for $q_{m,n}$ we have

$$\begin{aligned} \Delta p_{m,n} +\alpha ( 0.5-q_{0,0}-\lambda _1 m -\lambda _2 n )p_{m,n} -\alpha p_{0,0} q_{m,n}= \alpha \sum \limits _{i=0}^{m}\sum \limits _{j=0}^{n}q_{i,j}p_{m-i,n-j} \delta (i,j), \end{aligned}$$

so that the strong form of the homological equation is

$$\begin{aligned} \Delta p_{m,n} +\alpha (0.5-q_{0,0} + p_{0,0}q_{0,0} - \lambda _1 m - \lambda _2 n)p_{m,n}= s_{m,n}, \end{aligned}$$

with

$$\begin{aligned} s_{m,n}=\alpha \sum \limits _{i=0}^{m}\sum \limits _{j=0}^{n}q_{i,j}p_{m-i,n-j} \delta (i,j) - \frac{\alpha p_{0,0}}{(m+n)}\sum \limits _{i=1}^{m-1}\sum \limits _{j=1}^{n-1} (i+j) p_{i,j}q_{m-i,n-j}, \end{aligned}$$

a linear, elliptic BVP for each $m + n \ge 2$ as desired. Passing to the weak form leads to

$$\begin{aligned} \Big (D{\mathcal {F}}^{h}(c^{(0)})-(\lambda _1 m +\lambda _2 n) \int _{\Omega } \phi _j \phi _i \Big ) c^{(m,n)} =\Big ( \int _{\Omega } s_n \phi _i \Big ), \end{aligned}$$

which we solve recursively via the finite element method, obtaining the parameterization coefficients to any desired order (updating the equation for $q_{mn}$ as we go). Results are illustrated in Fig. 8.

Fig. 8

Left: 10 functions on the fast manifold approximated to order $N=30$ with Invariance equation error of 9.21e−8 with respect to the $L^2$ norm, 3.69e−07 with respect to the $H^1$ norm. Right: 10 functions on the slow manifold approximated to order $N=30$ with Invariance equation error of 6.12e−06 with respect to the $L^2$ norm, 2.50e−05 with respect to the $H^1$ norm

4.4 Higher order PDEs: a Kuramoto-Sivashinsky small term

We now consider a higher order problem, with leading diffusion term given by the biharmonic Laplacian. The biharmonic operator often appears in models of thin structures that react elastically to external forces. The Kuramoto-Sivashinsky equation (or KS equation) is given by

$$\begin{aligned}{} & {} F(u)=-\Delta ^2 u - \Delta u -0.5|\nabla u|^2,\\{} & {} u|_{\partial \Omega }=0 \quad \quad \quad \nabla u \cdot {\textbf {n}}|_{\partial \Omega }=0. \end{aligned}$$

for $u \in H_0^2(\Omega )$. It models flame front propogation, and is known to exhibit chaotic dynamics. We refer to [30, 34, 35, 47, 60] for more complete discussion of the physics and dynamics of the KS equation.

Since the differential operator is fourth order, higher regularity Finite Elements are required. The purpose of this section is to illustrate the use of the parameterization method in a higher order problem. To simplify the discussion, we start with a known solution of Fisher, and introduce the biharmonic term and nonlinearity as a perturbation with Neumann boundary conditions.

Specifically, we consider $u \in H^2(\Omega )$ and take

$$\begin{aligned} F_0(u)= \Delta u + \alpha u(1-u) \quad \quad \quad \nabla u \cdot {\textbf {n}}|_{\partial \Omega }=0, \end{aligned}$$

with weak formulation

$$\begin{aligned} {\mathcal {F}}_{0}(u) \phi = -\int _{\Omega } \nabla u \cdot \nabla \phi +\int _{\Omega } \alpha u(1-u)\phi =0, \end{aligned}$$

and let ${\mathcal {F}}_{\epsilon }(u) \in {H^2(\Omega )}^{\vee }$ for the perturbation problem given by

$$\begin{aligned} {\mathcal {F}}_{\epsilon }(u)\phi = {\mathcal {F}}_0(u)\phi + \int _{\Omega } \epsilon _1 \Delta u \Delta \phi + \int _{\Omega } \epsilon _2 N(u)\phi =0. \end{aligned}$$

Notice that regular enough solutions of the weak equation above correspond to strong solutions (with $\beta =1$) of the problem

$$\begin{aligned} F_{\epsilon }(u)= \epsilon _1 \Delta ^2 u + \beta \Delta u + \alpha u(1-u) + \epsilon _2 N(u)=0, \end{aligned}$$

with Neumann boundary conditions.

Indeed, starting with

$$\begin{aligned} \int _{\Omega } \epsilon _1 \left( \Delta ^2 u \right) \phi + \int _{\Omega } \beta (\Delta u)\phi + \int _{\Omega } (\alpha u(1-u) + \epsilon _2 N(u))\phi =0, \end{aligned}$$

and applying Green’s formula we have:

$$\begin{aligned}{} & {} \int _{\Omega } -\epsilon _1 \nabla (\Delta u) \cdot \nabla \phi + \oint _{\partial \Omega } \epsilon _1 (\nabla (\Delta u) \cdot n)\phi \\{} & {} \quad - \int _{\Omega } \beta \nabla u \cdot \nabla \phi + \oint _{\partial \Omega } \beta (\nabla u \cdot n) \phi + \int _{\Omega } ( \alpha u(1-u) + \epsilon _2 N(u) )\phi =0. \end{aligned}$$

Assuming that the boundary integrals vanish, we apply Green’s formula once more and now have:

$$\begin{aligned} \int _{\Omega } \epsilon _1 \Delta u \Delta \phi - \oint _{\partial \Omega } \epsilon _1 (\nabla \phi \cdot n) \Delta u - \int _{\Omega } \beta \nabla u \cdot \nabla \phi + \int _{\Omega } (\alpha u (1-u) + \epsilon _2 N(u))\phi =0. \end{aligned}$$

Noting that the boundary integral vanish , we obtain the weak equations

$$\begin{aligned} \int _{\Omega } \epsilon _1 \Delta u \Delta \phi - \int _{\Omega } \beta \nabla u \cdot \nabla \phi + \int _{\Omega } (\alpha u(1-u) + \epsilon _2 N(u))\phi =0, \end{aligned}$$

i.e

$$\begin{aligned} \int _{\Omega } \epsilon _1 \Delta u \Delta \phi - \int _{\Omega } \beta \nabla u \cdot \nabla \phi + \int _{\Omega } \alpha u \phi = \int _{\Omega } (\alpha u^2 - \epsilon _2 N(u))\phi . \end{aligned}$$

In this last form, one easily identify the perturbation problem from Fisher’s equation, $u_t = F_{\epsilon }(u)$, where

$$\begin{aligned} F_{\epsilon }(u)=\epsilon _1 \Delta ^2 u + \beta \Delta u + \alpha u(1-u) + \epsilon _2 N(u) = F_0(u) + \epsilon _1 \Delta ^2 u + \epsilon _2 N(u). \end{aligned}$$

We will choose $N(u)=-0.5|\nabla u|^2$ for our computations (and $\beta =1$), and $\epsilon _1$ will be a small negative parameter. In this way, for $\beta =0$ and $\alpha =0$ (and with Dirichlet boundary conditions instead) we recover the Kuramoto-Sivashinsky model. On the other hand, with $\epsilon _1=0$ and $\epsilon _2=0$ we obtain again Fisher’s equation.

Remark 4.1

The computations in the Matlab scripts are formulated as $u_t= -\alpha \Delta ^2 u -\beta \Delta u + \mu u(1-u) -\delta 0.5|\nabla u|^2,$ with $\alpha$ small and positive, $\beta$ negative of absolute value close to 1, $\mu$ close to the parameters used for Fisher’s equation, and $\delta$ small and positive.

Because the weak form of the equation contains the Laplacian (instead of just the gradient) we use $C^1$ Argyris elements which offer high convergence rate. We refer to [16] for the mathematical theory of the Argyris elements and to [18] for a useful discussion of numerical the implementation.

We recall that the Argyris elements are fifth order polynomials in two space variable constructed as follows. Define the operators $L_1 = {id}$, $L_2 = \partial _{10}$, $L_3 = \partial _{01}$, $L_4 = \partial _{20}$, $L_5 = \partial _{11}$ and $L_6 = \partial _{02}$. For an element $[n_1, n_2, n_3, m_1, m_2, m_3]$ with nodes $n_1$, $n_2$ and $n_3$ and midpoints of the edges $m_1$, $m_2$ and $m_3$, the nodal basis $\phi _k^{n_i}$ are defined by

$$\begin{aligned}{} & {} L_{\ell } (\phi _k^{n_i}(n_j)) = \delta _{ij} \delta _{\ell k},\\{} & {} \frac{\partial }{\partial n} \phi _k^{n_i}(m_j) = 0, \end{aligned}$$

and the basis associated to the edge midpoints by

$$\begin{aligned}{} & {} \frac{\partial }{\partial n} \phi ^{m_i}(m_j) = \delta _{ij},\\{} & {} L_\ell \phi ^{m_i}(n_j) = 0, \end{aligned}$$

where $1 \le i, j \le 3$ and $1 \le k, \ell \le 6$.

These are 21 constraints for each $\phi$ which uniquely defines a fifth order polynomials of the form

$$\begin{aligned} \phi (x,y) = \sum _{0 \le i + j \le 5} c_{ij} x^i y^j. \end{aligned}$$

We solve a $21 \times 21$ linear system $Ac=b$ for the coefficients $c_{ij}$ for each of the 21 basis associated with an element. In practice, we only do this for a reference triangle and transfer these basis to an arbitrary element using the method of Dominguez and Sayas [18].

In the notation presented earlier, $S_i=\{L_k: 1\le k \le 6\}$ for $i=1,2,3$ and $S_i=\{\frac{\partial }{\partial n}\}$ for $i=4,5,6$. After some indexing and renaming we let $S= \bigcup \limits _i S_i = \{L_k\}$ and

$$\begin{aligned} \phi _i=\frac{det(A_i)}{det(A)} \end{aligned}$$

for $1\le i\le 21$. Recall that the coordinates of A, $A_{ij}=\Big ( L_i(x^m y^n)(z_{n(i)})\Big )$, and the coordinates of $A_k$, ${(A_k(x,y))}_{ij}= (1-\delta _{ki})A_{ij} + \delta _{ki} x^my^n$, where $j=\frac{(m+n)(m+n+1)}{2} + (n+1)$.

The global representation of u becomes:

$$\begin{aligned} u = \sum _{k = 1}^6 \sum _{\hbox {all } n_i} c_k^{n_i} \phi _k^{n_i} + \sum _{\hbox {all } m_i} c^{m_i} \phi ^{m_i}. \end{aligned}$$

This interpolation is indexed in some convenient way: $u=\sum _{j=1}^{{nb}}c_j\phi _j$ with ${nb}=6{nv}+{ned}$ where nv is the number of vertices and ned is the number of edges in the triangulation.

After computing an equilibrium solution and eigendata $\lambda$ and $\xi$ as in the previous examples, we proceed to solve Eq. (2.5) in the case of Morse index one, interpreted in ${H^2(\Omega )}^{\vee }$ as

$$\begin{aligned} F(P(\theta ))=\lambda \theta \frac{\partial P}{\partial \theta }. \end{aligned}$$

Fig. 9

FKS equation with $\epsilon _1=-10^{-2}$, $\beta =1$, $\alpha =2.61$, and $\epsilon _2=10^{-3}$ Left: Equilibrium solution, ne=705. Right: Eigenfunction $\xi$ with $\lambda =3.48$

First comparing powers and then solving for

$$\begin{aligned} p_n=\sum \limits _{j=1}^{{nb}}c_j^{(n)}\phi _j, \end{aligned}$$

leads to

$$\begin{aligned} \langle \epsilon _1 \Delta ^2 p_n +\beta \Delta p_n +\alpha (1-2p_0)p_n - \epsilon _2 \left( \frac{\partial p_0}{\partial x}\frac{\partial p_n}{\partial x} + \frac{\partial p_0}{\partial y}\frac{\partial p_n}{\partial y} \right) -\lambda p_n, \phi \rangle = \langle s_n, \phi \rangle \end{aligned}$$

where

$$\begin{aligned} s_n=\frac{\epsilon _2}{2} \left( \sum _{k=1}^{n-1}\frac{\partial p_k}{\partial x}\frac{\partial p_{n-k}}{\partial x} + \frac{\partial p_k}{\partial y}\frac{\partial p_{n-k}}{\partial y} \right) -\alpha \sum _{k=1}^{n-1} p_k p_{n-k}, \end{aligned}$$

and so the projected weak formulation of the homological equation is of the form

$$\begin{aligned} \left( D {\mathcal {F}}^{h}(c^{(0)})-\lambda n \int _{\Omega } \phi _j \phi _i \right) c^{(n)} = \left( \int _{\Omega } s_n \phi _i \right) . \end{aligned}$$

In the Fig. 10, we show the manifolds computed over two additional irregular domains. In Fig. 11 the manifold is approximated to order 10 and 120, using the same scaling of the eigenvector. The error improves significantly by increasing the order of the approximation. Equivalently, if we set a tolerance level for the error in our computations, the local manifold obtained for order 10 is significantly smaller.

Fig. 10

Unstable manifolds for the FKS equation posed on non-convex domains with holes. Left: $ne=522$, $\epsilon _1=-10^{-3}$, $\beta =1$, $\alpha =3$, and $\epsilon _2=10^{-4}$, 10 points on the 1d manifold, $N=30$. $L^2$ error on the invariance equation 1.48e−07, $H^1$ error on the invariance equation 1.17e−06. Right: $ne=391$, $\epsilon _1=-10^{-2}$, $\beta =1$, $\alpha =3$, and $\epsilon _2=10^{-3}$, 10 points on the 1d manifold, $N=30$. $L^2$ error on the invariance equation 1.13e−06, $H^1$ error on the invariance equation 1.57e−05

Fig. 11

Unstable manifold for the FKS equation on the ${\mathbb {L}}$ domain with eigenvector scaled by 0.8 and parameters $\epsilon _1=-10^{-2}$, $\beta =1$, $\alpha =2.61$, and $\epsilon _2=10^{-3}$ Left: 10 points on the 1d manifold, $N=10$, Invariance equation error $L^2$ norm 0.012, $H^1$ norm 0.075. Right: 10 points on the 1d manifold, $N=120$, Invariance equation error $L^2$ norm 1.55e−05, $H^1$ norm 1.49e−04

4.5 A-posteriori error estimation

In this section we define a-posteriori error indicators for the parameterization method and illustrate their use in the examples from above. For the first indicator, consider the $L^2$ norm of the defect associated with the invariance equation. That is, for the N-th order parameterization

$$\begin{aligned} P^N(\theta , x,y) = \sum _{n = 0}^N p_n(x,y) \theta ^n, \end{aligned}$$

of a 1D unstable manifold, define the defect function

$$\begin{aligned} E_{1, N}(\theta , x, y):= F(P_N(\theta ,x,y))- \lambda \theta \frac{\partial }{\partial \theta } P_N(\theta ,x,y), \end{aligned}$$

for $\theta \in (-1,1)$ and $(x,y) \in \Omega$, and the $L^2$ indicator

$$\begin{aligned} \epsilon _{N,1} = \int _{|\theta | \le 1}\left\| E_{1, N}(\theta ) \right\| _{L^2(\Omega )}. \end{aligned}$$

Note that $\epsilon _{N,1} = 0$ for an exact solution.

Similarly we define, for the parameterization

$$\begin{aligned} P^N(\theta _1, \theta _2, x,y) = \sum _{m + n = 0}^N p_{mn}(x,y) \theta _1^m \theta _2^n, \end{aligned}$$

of a two dimensional unstable manifold, the defect function

$$\begin{aligned} E_{N,2}(\theta _1, \theta _2, x, y)= & {} F(P_N(\theta _1, \theta _2,x,y)) - \lambda _1 \theta _1 \frac{\partial }{\partial \theta _1} P_N(\theta _1, \theta _2,x,y) \\ {}{} & {} - \lambda _2 \theta _2 \frac{\partial }{\partial \theta _2} P_N(\theta _1, \theta _2,x,y), \end{aligned}$$

and the indicator

$$\begin{aligned} \epsilon _{N,2} =\int _{|\theta _1|, |\theta _2| \le 1}\left\| E_{2, N}(\theta _1, \theta _2) \right\| _{{\mathcal {H}}}. \end{aligned}$$

In practice these indicators are approximated by computing the $L^2(\Omega )$ norms and average for a finite number of parameter points.

Table 1 $L^2$, $H^1$ norms of the error in the Invariance Equation for 1d and 2d unstable manifolds in the Fisher model over the ${\mathbb {L}}$ domain: $\alpha =2.7$, $\alpha =9$ respectively

Table 2 $L^2$, $H^1$ norms of the error in the Invariance Equation for 1d and 2d manifolds in the Fisher model with exponential nonlinearity over the ${\mathbb {L}}$ domain: $\alpha =-4.7$, $\alpha =-4.41$ respectively

Another class of indicators is obtained by considering the dynamical conjugacy error discussed in Equation (2.6). That is, with fixed $T > 0$ define the dynamical defect

$$\begin{aligned} \text {conjError}(T)_{N,1}(\theta , x,y) = P^N(e^{\lambda T} \theta , x,y) - \Phi (P^N(\theta , x,y), T), \end{aligned}$$

$\theta \in (-1,1)$ and $(x,y) \in \Omega$, for the 1D manifold and

$$\begin{aligned} \text {conjError}(T)_{N,2}(\theta _1, \theta _2, x,y) = P^N(e^{\lambda _1 T} \theta _1, e^{\lambda _2 T} \theta _2, x,y) - \Phi (P^N(\theta _1,\theta _2, x,y), T), \end{aligned}$$

$\theta _1, \theta _2 \in [-1,1]\times [-1,1]$ and $(x,y) \in \Omega$ for the 2D manifold. Then we have the indicators

$$\begin{aligned} \varepsilon _{N,1} = \sup _{|\theta | \in [-1,1]} \left\| \text {conjError}(T)_{N,1}(\theta ) \right\| _{{\mathcal {H}}}, \end{aligned}$$

and

$$\begin{aligned} \varepsilon _{N,2} = \sup _{|\theta _1|, |\theta _2| \le 1} \left\| \text {conjError}(T)_{N,2}(\theta _1, \theta _2) \right\| _{{\mathcal {H}}} \end{aligned}$$

Note that the calculation of these indicators depends on the (fairly arbitrary) choice of T, and more over requires numerical approximation of the flow map $\Phi (P(\theta ,x,y),t)$, which in turn requires implementation of a numerical integration scheme for the parabolic PDE. Then the computation of the $\epsilon$-indicators is in general much simpler than the $\varepsilon$-indicators. For this reason, we much prefer the former in the present work. Nevertheless, the latter can be very valuable for debugging purposes, and we always check the conjugacy errors before claiming with confidence that we have working codes.

Tables 1 - 6 below report the results of a number of defect calculations for the manifold computations of the previous section. We observe that in general the defect decreases as the number of elements increases (and hence the mesh size decreases) and tends to improve as the order N of the approximation increases. It should also be stressed that using finite elements of higher order in a given problem seems to have a dramatic effect on the error. This is illustrated in Table 6, which compares the defect for the 1D manifold in the Fisher equation using piecewise linear versus Argyris elements. While the piecewise linear elements proved approximately 6 figures of accuracy on the L-shaped domain, using the higher order elements we obtain defects on the order of machine precision. The later are considerably more difficult to implement, but offers significant advantages, and are especially encouraging for potential future applications in computer assisted proofs.

Table 3 $L^2$, $H^1$ norms of the error in the Invariance Equation for the 1d unstable manifold over the ${\mathbb {L}}$ domain: $\epsilon _1=-10^{-2}$, $\beta =1$, $\alpha =2.61$, and $\epsilon _2=10^{-3}$

Table 4 $L^2$, $H^1$ norms of the error in the Invariance Equation for the 1d unstable manifold over the door domain: $\epsilon _1=-10^{-3}$, $\beta =1$, $\alpha =3$, and $\epsilon _2=10^{-4}$

Table 5 $L^2$, $H^1$ norms of the error in the Invariance Equation for the 1d unstable manifold over the polygon with holes: $\epsilon _1=-10^{-2}$, $\beta =1$, $\alpha =3$, and $\epsilon _2=10^{-3}$

Table 6 $L^2$ norms of the error in the Invariance Equation for 1 dimensional manifolds in the Fisher model over the ${\mathbb {L}}$ domain with piecewise linear and Argyris basis: $\alpha =2.7$

5 Conclusions

We have combined the parameterization method with finite element analysis to obtain a new approximation method for unstable manifolds of equilibrium solutions for parabolic PDEs. The method is applied to several PDEs defined on planar polygonal domains and is implemented for number of example problems with both polynomial and non-polynomial nonlinearities, for unstable manifolds of dimension one and two, for a number of non-convex and non-simply connected domains, and for problems involving both Laplacian and bi-harmonic Laplacian diffusion operators. The method is easy to implement for computing the approximation to arbitrary order: the same code that computes the second order approximation will compute the approximation to order 50—this is just a matter of changing a loop variable. The method is amenable to a-posteriori analysis of errors and we employ these indicators to show that our calculations are accurate far from the equilibrium solution.

Interesting future projects would be to apply the method to problems with other boundary conditions such as Dirichlet or Robin, to apply it to problems formulated on spatial domains of dimension 3 or more, to extend the method for the computation of unstable manifolds attached to periodic solutions of parabolic PDEs, or to extend the method to study invariant manifolds attached to equilibrium or periodic solutions of systems of parabolic PDEs.

Finally we mention that there is a thriving literature on mathematically rigorous computer assisted proof for elliptic PDEs based on finite element analysis. See for example the works of [5, 37, 39,40,41,42,43,44,45,46, 49,50,51, 57,58,59] for validated numerical methods for solving nonlinear elliptic PDE (equilibrium solutions of parabolic PDEs) and their associated eigenvalue/eigenfunction problems. We refer also the references just cited for more complete review of this literature. From the point of view of the present discussion the important point is this: that the present work reduces the problem of computing jets of unstable manifolds to the problem of solving elliptic boundary value problems—and moreover that a number of authors have developed powerful methods of computer assisted proof for solving such problems. A very interesting line of future research would be to combine the results of the present work validated numerical methods for elliptic BVPs.

Appendices

Appendix A: Formal solution of Eq. (2.5): an ODE example

In this section we illustrate the use of the parameterization method as a computational tool for a simple example. The idea is to develop a formal series solution of Eq. (2.5). Such formal calculations play a critical role in the remainder of the present work, and are much more involved for PDEs than for ODEs. To separate those complications which are inherent to the method from those which are due to PDEs, we explain the procedure for the planar vector field $F :{\mathbb {R}}^2 \rightarrow {\mathbb {R}}^2$ (Hilbert space is the plane) given by

$$\begin{aligned} F(x,y) = \left( \begin{array}{c} x + y \\ 1 - x^2 \end{array} \right) . \end{aligned}$$

(A.1)

We are interested in the orbit structure of ${\mathbb {R}}^2$ generated by the ODE

$$\begin{aligned} \frac{d \gamma }{dt} = F(\gamma ), \end{aligned}$$

where

$$\begin{aligned} \gamma (t) = \left( \begin{array}{c} x(t) \\ y(t) \end{array} \right) . \end{aligned}$$

Note for future use that

$$\begin{aligned} DF(x,y) = \left( \begin{array}{cc} 1 &{} 1 \\ -2x &{} 0 \end{array} \right) . \end{aligned}$$

(A.2)

Suppose that $p_0 \in {\mathbb {R}}^2$ has $F(p_0) = 0$, so that $p_0$ is an equilibrium solution of the ODE. Suppose further that $DF(p_0)$ has one unstable eigenvalue $\lambda > 0$ and that the remaining eigenvalue is stable. Let $\xi \in {\mathbb {R}}^2$ denote an eigenvector associated with $\lambda$.

We look for a function $P :[-1, 1] \rightarrow {\mathbb {R}}^2$ with

$$\begin{aligned} P(0) = p_0 \quad \quad \text {and} \quad \quad P'(0) = \xi , \end{aligned}$$

parameterizing the one dimensional unstable manifold attached to $p_0$. In the one dimensional case the invariance equation of Equation (2.5) reduces to

$$\begin{aligned} \lambda \theta \frac{d}{d \theta } P(\theta ) = F(P(\theta )), \end{aligned}$$

(A.3)

for $\theta \in (-1, 1)$. We look for a formal power series solution of Equation (A.3) of the form

$$\begin{aligned} P(\theta ) = \left( \begin{array}{c} P_1(\theta ) \\ P_2(\theta ) \end{array}\right) = \sum _{n = 0}^\infty \left( \begin{array}{c} a_n \\ b_n \end{array} \right) \theta ^n, \end{aligned}$$

and impose first order constraints

$$\begin{aligned} \left( \begin{array}{c} a_0 \\ b_0 \end{array} \right) = p_0, \quad \quad \text {and} \quad \quad \left( \begin{array}{c} a_1 \\ b_1 \end{array} \right) = \xi . \end{aligned}$$

To work out the higher order coefficients we note that, on the level of formal power series, the left hand side of Eq. (A.3) is

$$\begin{aligned} \lambda \theta \frac{d}{d\theta } P(\theta ) = \sum _{n = 0}^\infty \lambda n \left( \begin{array}{c} a_n \\ b_n \end{array} \right) \theta ^n, \end{aligned}$$

(A.4)

and that the right hand side of Eq. (A.3) is

$$\begin{aligned} F(P(\theta ))= & {} \left( \begin{array}{c} P_1(\theta ) + P_2(\theta ) \\ 1 - P_1(\theta )^2 \end{array} \right) \nonumber \\{} & {} = \sum _{n = 0}^\infty \left( \begin{array}{c} a_n + b_n \\ \delta _n - \sum _{k=0}^n a_{n-k} a_k \end{array} \right) \theta ^n. \end{aligned}$$

(A.5)

Here we have used the Cauchy product formula for the coefficients of $P_1(\theta )^2$, and defined

$$\begin{aligned} \delta _n = {\left\{ \begin{array}{ll} 1 &{} n = 0 \\ 0 &{} n \ge 1 \end{array}\right. }. \end{aligned}$$

Returning to the invariance Eq. (A.3), we set the right hand side of Eq. (A.4) equal to Eq. (A.5), match like powers of $\theta$, and recall the definition of $\delta _n$ to obtain

$$\begin{aligned} \lambda n \left( \begin{array}{c} a_n \\ b_n \end{array} \right) = \left( \begin{array}{c} a_n + b_n \\ - \sum _{k=0}^n a_{n-k} a_k \end{array} \right) , \end{aligned}$$

(A.6)

for $n \ge 1$. We seek to isolate terms of order n, and derive a equation for $p_n$ in terms of lower order coefficients. Since there are still some terms order n locked in the sum, we note that for $n \ge 2$

$$\begin{aligned} \sum _{k = 0}^n a_{n-k} a_k =2 a_0 a_n + \sum _{k = 1}^{n-1} a_{n-k} a_k, \end{aligned}$$

where the new sum on the right contains no terms of order n. Exploiting this identity, Eq. (A.6) becomes

$$\begin{aligned} n \lambda \left( \begin{array}{c} a_n \\ b_n \end{array} \right) = \left( \begin{array}{c} a_n + b_n \\ -2 a_0 a_n - \sum _{k = 1}^{n-1} a_{n-k} a_k \end{array} \right) , \end{aligned}$$

or

$$\begin{aligned} \left( \begin{array}{c} a_n + b_n - n\lambda a_n \\ -2 a_0 a_n - n \lambda b_n \end{array} \right) = \left( \begin{array}{c} 0 \\ \sum _{k = 1}^{n-1} a_{n-k} a_k \end{array} \right) . \end{aligned}$$

This is

$$\begin{aligned} \left[ \begin{array}{cc} 1 - n\lambda &{} 1 \\ -2 a_0 &{} - n \lambda \end{array} \right] \left( \begin{array}{c} a_n \\ b_n \end{array} \right) = \left( \begin{array}{c} 0\\ \sum _{k = 1}^{n-1} a_{n-k} a_k \end{array} \right) , \end{aligned}$$

which, after referring back to Eq. (A.2), we rewrite as

$$\begin{aligned} \left( DF(a_0, b_0) - n\lambda \text {Id} \right) p_n = s_n, \quad \quad \quad n \ge 2, \end{aligned}$$

(A.7)

where

$$\begin{aligned} p_n = \left( \begin{array}{c} a_n \\ b_n \end{array} \right) , \quad \quad \text {and} \quad \quad s_n = \left( \begin{array}{c} 0 \\ \sum _{k = 1}^{n-1} a_{n-k} a_k \end{array} \right) . \end{aligned}$$

Again, note that $s_n$ depends only on terms of order less than n.

We refer to Eq. (A.7) as the homological equations for P, and note that they are linear algebraic equations for the power series coefficients of the parameterization. We now ask, are the homological equations solvable? To answer this we note that since $P(0) = p_0 = (a_0, b_0)$ is an equilibrium solution, the left hand side of Eq. (A.7) is the characteristic matrix for the derivative $DF(p_0)$. The characteristic matrix is invertible if and only if $n \lambda$ is not an eigenvalue of $DF(p_0)$. Since $\lambda > 0$, and since the remaining eigenvalue of $DF(p_0)$ is negative, we see that for $n \ge 2$, $n \lambda$ is never an eigenvalue. Then the homological equations are uniquely solvable to all orders, and the power series solution of Eq. (A.3), when F is given by Eq. (A.1), is well defined. Convergence of this series is another issue, not treated here.

Nevertheless, we see that the coefficients of P are uniquely determined by the first order data (equilibrium and eigenvector). Then the only freedom in determining the solution is the choice of the scaling of the eigenvector $\xi$. This non-uniqness is used to control the growth rate of the coefficients of P, providing numerical stability.

Remark A.1

(Non-resonance and the parameterization method) The condition

$$\begin{aligned} n \lambda \notin \text {spec} DF (p_0) \quad \quad \quad n \ge 2, \end{aligned}$$

(A.8)

is called a non-resonance condition. In fact it is an inner non-resonance condition as we are computing the unstable manifold, and Eq. (A.8) involves linear combinations of the (in this case unique) unstable eigenvalues. We will see in Sect. 3 that the non-resonance conditions are similar, but somewhat more subtle for higher dimensional unstable manifolds.

Remark A.2

(Stable manifolds for ODEs) Note that replacing $\lambda$ with a stable eigenvalue in the above discussion changes nothing. This reflects the general fact that in finite dimensions, the parameterization method applies equally well to both stable and unstable manifolds. However, an equilibrium solution of a parabolic PDE typically has infinitely many stable eigenvalues which make it impossible to overcome the non-resonance conditions. This is why the present work focuses on unstable manifolds for parabolic PDEs.

Appendix B: A numerical example

The vector field of Eq. (A.1) has equilibrium solutions $f(x_{1,2}, y_{1,2}) = (0,0)$ at

$$\begin{aligned} \left( \begin{array}{c} x_1 \\ y_1 \end{array} \right) = \left( \begin{array}{c} -1 \\ 1 \end{array} \right) , \quad \quad \text {and} \quad \quad \left( \begin{array}{c} x_2 \\ y_2 \end{array} \right) = \left( \begin{array}{c} 1 \\ -1 \end{array} \right) , \end{aligned}$$

and one can check that

$$\begin{aligned} DF(-1, 1) = \left( \begin{array}{cc} 1 &{} 1 \\ 2 &{} 0 \end{array} \right) , \end{aligned}$$

(B.1)

has eigenvalues $2, -1$. Hence the equilibrium $(-1, 1)$ is a hyperbolic saddle. Let $\lambda = 2$ denote the unstable eigenvalue. One can check that

$$\begin{aligned} \xi = \left( \begin{array}{c} 1 \\ 1 \end{array} \right) , \end{aligned}$$

is an associated unstable eigenvector.

The zero-th and first order terms of the parameterization are

$$\begin{aligned} \left( \begin{array}{c} a_0 \\ b_0 \end{array} \right) = \left( \begin{array}{c} -1 \\ 1 \end{array} \right) \quad \quad \text {and} \quad \quad \left( \begin{array}{c} a_1 \\ b_1 \end{array} \right) = \left( \begin{array}{c} 1 \\ 1 \end{array} \right) , \end{aligned}$$

and the second order term is determined by solving the homological equation of Eq. (A.7) with $n = 2$ as follows. Recalling the definition of $s_n$, and noting that $a_1 = 1$, when $n = 2$ we have that

$$\begin{aligned} \left. \sum _{k = 1}^{n-1} a_{n-k} a_k \right| _{n = 2} = a_1^2 = 1, \end{aligned}$$

and that

$$\begin{aligned} s_2 = \left( \begin{array}{c} 0 \\ 1 \end{array} \right) . \end{aligned}$$

Moreover, since $\lambda = 2$ and $a_0 = -1$ we recall Eq. (B.1), and have that

$$\begin{aligned} DF(-1,1) - 2 \lambda \text {Id} = \left[ \begin{array}{cc} 1 - 2 \lambda &{} 1 \\ 2 &{} - 2 \lambda \end{array} \right] = \left[ \begin{array}{cc} -3 &{} 1 \\ 2 &{} - 4 \end{array} \right] . \end{aligned}$$

Solving

$$\begin{aligned} \left[ DF(-1,1) - 2 \lambda \text {Id} \right] p_2 = s_2, \end{aligned}$$

gives

$$\begin{aligned} p_2 = \left( \begin{array}{c} -0.1 \\ -0.3 \end{array} \right) . \end{aligned}$$

From this we conclude that the second order local unstable manifold approximation is

$$\begin{aligned} P^N(\theta ) = \left( \begin{array}{c} -1 \\ 1 \end{array} \right) + \left( \begin{array}{c} 1 \\ 1 \end{array} \right) \theta + \left( \begin{array}{c} -0.1 \\ - 0.3 \end{array} \right) \theta ^2, \end{aligned}$$

(B.2)

for $N = 2$. Third and higher order terms are computed recursively following the same recipe.

Roughly speaking, how accurate is the approximation above? Since the remainder term in the approximation given by $P^2$ in Eq. (B.2) is cubic in $\theta$, we expect that the size of the truncation error has

$$\begin{aligned} E_2(\theta ) = \Vert P(\theta ) - P^2(\theta ) \Vert \le C |\theta |^3, \end{aligned}$$

for some constant C. Suppose that we restrict the domain of our parameterization to

$$\begin{aligned} \theta \in [-10^{-5}, 10^{-5}]. \end{aligned}$$

Then $E_2$ is of order $(10^{-5})^3 = 10^{-15}$, so that the size of the truncation error is roughly 5 multiples machine precision. In practice, we prefer to rescale the length of the eigenvector, and take the domain of $P^N$ normalized to a unit cube. See the following remark.

Remark B.1

(Rescaling the eigenvector to optimizing the coefficient decay) Suppose now that we compute the coefficients of $P^N$ to order $N = 20$, using the same eigenvector $\xi = [1,1]$. Rather than listing the resulting coefficients order by order, we remark that the coefficients decay like

$$\begin{aligned} \Vert p_n\Vert \approx 65 \times 10^{-1.18 n}, \end{aligned}$$

(found by taking an exponential best fit algorithm) and that

$$\begin{aligned} \Vert p_{20}\Vert \approx 1.56 \times 10^{-22}, \end{aligned}$$

a quantity far smaller than machine precision. Note that coefficients below machine precision do not contribute (numerically) to the approximation, and this is wasted effort.

Fig. 12

Stable/unstable manifold visualization: dynamics generated by the vector field given in Eq. (A.1). Several reference orbits are illustrated by black curves. These are obtained by numerical integration of several arbitrarily chosen initial conditions. The main features of the phase space are the saddle equilibrium at $(-1,1)$ and the repelling equilibrium at $(1,-1)$. We compute the local unstable and local stable manifold parameterizations $P^N$ and $Q^N$ for the saddle stable equilibrium $(-1,1)$ to order $N = 100$. The unstable and stable eigenvectors to lengths of 13 and 10.5 respectively, The images $P^N([-1,1])$ and $Q^N([-1,1])$ are plotted as blue (unstable) and red (stable) curves. In both cases the plots of the manifolds are generated only by plotting the approximating polynomials: the manifolds are not extended using numerical integration. This illustrates that it is often possible to approximate a substantial portion of the unstable manifold using the parameterization method. (Of course numerical integration could be used to extend the manifolds even further). We observe that the unstable manifold parameterization (blue curve) follows a “fold”, that is, the curve is not the graph over the unstable eigenspace of any function. The stable manifold on the other hand seems have been approximated up to very near it’s maximal radius of convergence, as computing additional terms has very little effect on the picture, and we are not able to reach a fold

To obtain a more significant result, we increase the scaling of the unstable eigenvector, taking $P'(0) = s \xi$ with some $s > 1$. For example, rescaling the eigenvector by $s = 2.5$ and recomputing the coefficients leads to a 20-th order polynomial whose final coefficient vector has magnitude $1.4 \times 10^{-14}$. Since the final coefficient is close to, but still above machine precision—and hence numerically significant—this choice of scaling is nearly optimal for the order $N=20$ calculation.

Experimenting a little more in this way, we find that taking $s = 13$, and computing the parameterization to order $N = 100$, gives coefficients which decay exponentially fast and in such at way that the last coefficient had magnitude roughly machine epsilon. A plot illustrating the results of the order $N = 100$ calculation is given in Fig. 12. Note that the unstable manifold, which is shown as the blue curve, is not the graph of a function over the tangent space (span of the eigenvector). This illustrates the well known fact that the parameterization method can “follow folds” in the manifold. The reader interested in more refined approaches to choosing the computational parameters in the parameterization method might consult [4], where methods for optimizing the calculations under certain constraints are discussed in detail.

Remark B.2

(Visualization in a Function space) The parameterization method is extremely valuable for visualizing invariant manifolds when the dimension of the phase space is low. However the remainder of the paper concerns infinite dimensional problems, and visualization is much more problematic. For the parabolic PDEs studied below, the phase space is a Sobolev space, and each point on the manifold is actually a function represented as a linear combination of finite elements. In this setting it is more natural to plot the points on the manifolds as functions over the given domain. That is, we visualize the manifold as a curve or surface of functions. Nevertheless, it is valuable to keep in mind the picture in Fig. 12 when trying to interpret the results.

Appendix C: Proof of Lemma 2.1

Observe that the constraint given in Eq. (2.3) implies that P is tangent to the unstable eigenspace of $DF(u_0)$ at $u_0$. Since the eigenvalues are real and distinct, the eigenvectors are linearly independent, and P maps a small enough neighborhood of the origin diffeomorphically into ${\mathcal {H}}$.

Fix $\theta \in (-1, 1)^M$, and define the curve $\gamma _{\theta } :(-\infty , 0] \rightarrow {\mathcal {H}}$ by

$$\begin{aligned} \gamma _{\theta }(t) = P\left( e^{\Lambda t} \theta \right) . \end{aligned}$$

We observe that $\gamma _{\theta }$ is a solution curve for F. To see this, we first note that $\gamma _\theta$ is well defined for all backward time, as for all $t \in (-\infty , 0]$ we have that

$$\begin{aligned} {\hat{\theta }} := e^{\Lambda t} \theta \in {\mathbb {B}}. \end{aligned}$$

This is because the entries of $\Lambda$ are unstable, real, and distinct. To see that $\gamma _\theta (t)$ solves the differential equation, note that

$$\begin{aligned} \frac{d}{dt} \gamma _{\theta }(t)&= \frac{d}{dt} P\left( e^{\Lambda t} \theta \right) \\&= D P\left( e^{\Lambda t} \theta \right) \Lambda e^{\Lambda t}\theta \\&= D P ({\hat{\theta }}) \Lambda {\hat{\theta }} \\&= F(P({\hat{\theta }})) \\&= F(P (e^{\Lambda t} \theta )) \\&= F(\gamma _{\theta }(t)), \end{aligned}$$

as desired.

In addition to being a solution curve, we have that $\gamma _{\theta }$ accumulates at $u_0$ in backward time. To see this, we simply compute the limit

$$\begin{aligned} \lim _{t \rightarrow - \infty } \gamma _{\theta }(t)&= \lim _{t \rightarrow - \infty } P\left( e^{\Lambda t} \theta \right) \\&= P\left( \lim _{t \rightarrow - \infty } e^{\Lambda t} \theta \right) \\&=P\left( 0 \right) \\&= u_0, \end{aligned}$$

where we have used the assumption that P is smooth, and hence continuous on $[-1,1]^M$. Since $\theta$ was arbitrary, we see that every point $P(\theta )$ on the image of P has a backward orbit which accumulates at $u_0$. That is

$$\begin{aligned} \text {image}(P) \subset W^u(u_0). \end{aligned}$$

Since $\text {image}(P)$ is locally an M-dimensional disk containing $u_0$ and contained in the unstable manifold, we have that $\text {image}(P)$ is a local unstable manifold as desired.