1 Introduction

Time series dynamics often change due to external events or internal systematic fluctuations. One common structural change is the mean shift, and changepoint analyses allow the researcher to identify whether and when abrupt changes in the mean of the series take place. Evolving from the original treatise for a single location parameter shift in Page (1954), the majority (but not all) of changepoint analyses check for shifts in the mean of the series. Since Page (1954), considerable changepoint work has been conducted, including recursive segmentation algorithms such as binary segmentation and wild binary segmentation Fryzlewicz (2014), dynamic programming based approaches such as Jackson et al. (2005) and Killick et al. (2012), moving sum (MOSUM) procedures (Eichinger and Kirch 2018; Chen et al. 2021), and simultaneous multi-scale changepoint estimators (SMUCE) Frick et al. (2014). Additional changepoint work includes applications in climatatology (Hewaarachchi et al. 2017), economics (Norwood and Killick 2018), and disease modelling (Hall et al. 2000).

Many changepoint techniques assume independent and identically distributed (IID) model errors; however, time series data are typically correlated (e.g., daily temperatures, stock prices, and DNA sequences Chakravarthy et al. (2004)). Changepoint techniques tend to overestimate the number of changepoints should positive autocorrelation be ignored (Shi et al. 2022). In addition, some multiple changepoint models for time series allow all model parameters, including those governing the correlation structure of the series, to change at each changepoint time. These scenarios are easier to handle computationally as dynamic programming techniques can quickly optimize penalized likelihood objective functions; see Killick et al. (2012) and Maidstone et al. (2017). In these cases, the objective function optimized is additive in its segments (regimes). A more parsimonious model allows series means to shift with each changepoint time, but keeps error autocovariances constant across all regimes. These models do not lead to objective function additivity and fast dynamic programming techniques cannot be directly applied (See Shi et al. 2022).

Remedies typically seek to incorporate the autocorrelation structure in the changepoint analysis or to pre-whiten the series prior to any changepoint analysis. In either case, one needs to quantify the autocovariance structure and/or long-run variance of the series. With a good estimate of the series’ autocovariance structure, one-step-ahead prediction residuals can be computed—and these residuals are always uncorrelated (independent up to estimation error for Gaussian series). Indeed, a principle of (Shi et al. 2022; Robbins et al. 2011) is that good multiple changepoint detection routines can be devised by applying IID methods to the series’ one-step-ahead prediction residuals (also called pre-whitening). Perhaps owing to this, considerable recent research has sought to find changepoints in dependent time series. Among these, Dette et al. (2020) estimate the long-run variance of the error process via a difference-type variance estimator calculated from local means from different blocks; this estimate is then used to modify SMUCE for dependent data. The authors Chen et al. (2021) propose a robust covariance estimation procedure from \(M-\)estimation to modify a moving sum procedure. Other proposed long-run variance (or time-average variance) estimators for mean shift problems based on robust methods include (Chan 2022; Romano et al. 2021; Chakar et al. 2017).

This paper studies autocovariance and long-run variance estimation in the presence of mean shifts in more detail. We devise a method based on first order differencing that outperforms robust and rolling window methods. The scenario is asymptotically quantified when the model errors obey a causal autoregressive (AR) process.

The rest of this paper proceeds as follows. The next section narrates our setup and discusses approaches to the problem. Section 3 then develops an estimation technique based on lag one differences of the series. Section 4 proves consistency and asymptotic normality of these estimators and Sect. 5 assesses their performance in simulations. Section 6 applies the results to an annual precipitation series and Sect. 7 concludes with brief comments.

2 Model and estimation approaches

Suppose that \(\{ X_t \}_{t=1}^N\) is a time series having an unknown number of mean shift changepoints, denoted by m, occurring at the unknown ordered times \(1< \tau _1< \tau _2< \cdots < \tau _m \le N\). These m changepoints partition the series into \(m+1\) distinct segments, each segment having its own mean. The model is written as

$$\begin{aligned} X_t= \kappa _{s(t)} + \epsilon _t. \end{aligned}$$
(1)

Here, s(t) denotes the series’ regime number at time t, which takes values in \(\{0, 1, \ldots , m \}\). Then \(\kappa _{s(t)} = \mu _i\) is constant for all times in the \(i\mathrm{th}\) regime:

$$\begin{aligned} \kappa _{s(t)}= {\left\{ \begin{array}{ll} \; \mu _0, \quad &{}1 \le t \le \tau _1,\\ \; \mu _1, \quad &{}\tau _1+1 \le t \le \tau _2,\\ \; \; \qquad \vdots \\ \; \mu _m, \quad &{}\tau _{m}+1 \le t \le N \end{array}\right. }. \end{aligned}$$

We assume that \(\{ \epsilon _t \}\) is a stationary causal AR(p) time series that applies to all regimes. The AR order p is assumed known for the moment; BIC penalties will be examined later to select the order of the autoregression should it be unknown. While more general ARMA(p, q) \(\{ \epsilon _t \}\) could be considered, we work with AR(p) errors because this model class is dense in all stationary short-memory series (Brockwell and Davis 1991), and estimation, prediction, and forecasting are easily conducted. Adding a moving-average component \(q \ge 1\) induces considerably more work and is less commonly found in changepoint applications. The AR(p) \(\{ \epsilon _t \}\) obeys

$$\begin{aligned} \epsilon _t=\phi _1 \epsilon _{t-1}+\cdots +\phi _{p}\epsilon _{t-p}+Z_t, \quad t \in \mathbb {Z}, \end{aligned}$$
(2)

where \(\{ Z_t \}\) is IID white noise with a zero mean, variance \(\sigma ^2\), and a finite fourth moment (this enables consistent estimation of the autoregressive parameters \(\phi _1, \ldots , \phi _p\)).

The next section develops a difference based moment estimation procedure for the mean shift setting. Under this scenario, first-order differences of the series will have a non-zero mean only at the changepoint times. At this point, it might seem prudent to apply ARMA estimation methods that are robust to outliers to the differenced series. Indeed, many previous authors have considered outlier-robust estimators for ARMA models. For examples, the M-estimators of Muler et al. (2009) are shown to be consistent and tractable and the bounded influence propagation (BIP) \(\tau\)-estimators in Muma and Zoubir (2017) merit mention. However, these estimators require the ARMA series to be causal and invertible. In our application, the differenced series has a unit root in its MA component and is hence not invertible. Perhaps worse, future simulations demonstrate that BIP \(\tau\)-estimators do not perform well in our setting.

3 Moment estimates based on differencing

This section derives a system of linear equations that relate the autocorrelations of the differenced series to the AR(p) coefficients. First-order differencing a series eliminates any piecewise constant mean except at times where shifts occur. Authors have previously used differencing to estimate global parameters in the changepoint literature. For example, Tecuapetla-Gómez and Munk (2017) discuss a class of difference– based estimators for autocovariances in nonparametric changepoint segment regression when the errors are from a stationary m- dependent process. The paper Fryzlewicz (2014) uses differencing to get an estimate of \(\text {Var}(X_t)\), although IID errors are assumed in this work. The estimator in (16) below comes from Chakar et al. (2017) and is also based on differencing. This said, there seems to be no previous literature using differencing to estimate AR(p) parameters in a setting corrupted by mean shifts. As an aside, differencing also detrends a time series; the estimators below perform well if a time series has both changepoints and a linear trend.

Let \(\{ X_t \}\) be a stationary series satisfying the causal AR(p) difference equation

$$\begin{aligned} X_t = \mu + \sum _{j=1}^p \phi _j (X_{t-j}-\mu ) + Z_t, \end{aligned}$$
(3)

with \(\{ Z_t \}\) a zero mean IID sequence with a finite fourth moment. Since \(X_t\) may be causally expressed in terms of \(Z_t, Z_{t-1}, \ldots\), the autoregressive coefficients are uniquely determined by the pth order recursion

$$\begin{aligned} \gamma _X(h) = \phi _1\gamma _X(h-1) + \cdots + \phi _p\gamma _X(h-p), \quad h = 1,2,\ldots \end{aligned}$$
(4)

and its boundary conditions Brockwell and Davis (1991). Here, \(\gamma _X(h)=\text {Cov}(X_t,X_{t-h})\) and we use the analogous notation \(\rho _X(h)=\text {Corr}(X_t, X_{t-h})\). Consider the sequence of first differences defined by \(d_t=X_t-X_{t-1}\). Then \(\{ d_t \}\) is stationary with

$$\begin{aligned} \gamma _d(h):=\text {Cov}(d_t, d_{t+h})= 2\gamma _X(h) -\gamma _X(h-1)-\gamma _X(h+1), \end{aligned}$$
(5)

and

$$\begin{aligned} \rho _d(h):=\text {Corr}(d_t, d_{t+h})= \frac{2\rho _X(h) -\rho _X(h-1)-\rho _X(h+1)}{2[1-\rho _X(1)]}. \end{aligned}$$
(6)

One can also show that \(\{ d_t \}\) satisfies an ARMA(p, 1) difference equation with a first-order moving average parameter of \(-1\). We now show that \(\phi _1, \ldots , \phi _p\) can be recovered from the autocorrelation function of the differences.

Let \(P(A\Vert B)\) denote the best linear predictor (BLP) of a random variable A from linear combinations of elements in the set B. We assume that B includes a constant term to allow for cases with a nonzero mean. It is well known that for a stationary causal ARMA process, the linear representation of the best linear prediction of future series values from past series values is unique Brockwell and Davis (1991). Equations determining the autoregressive coefficients can be derived by equating two different expressions for the BLP.

Executing on the above, (3) gives

$$\begin{aligned} P(d_{p+1}\Vert 1; X_j, 1 \le j \le p)= & {} P(X_{p+1}\Vert 1; X_j, 1 \le j \le p)-X_p \\= & {} \kappa \mu + (\phi _1-1)X_p+\sum _{j=2}^p \phi _j X_{p+1-j}, \end{aligned}$$

where \(\kappa =1-\sum _{j=1}^p\phi _j\) (\(\kappa \ne 0\) by causality). Substituting \(X_{p-j}=X_p-\sum _{j=0}^{p-2}d_{p-j}\) for \(j=1, \ldots , p-1\) into the last line above yields

$$\begin{aligned} P(d_{p+1}\Vert 1; X_j, 1 \le j \le p) = \kappa (\mu - X_p) -\sum _{j=0}^{p-2} d_{p-j}\sum _{i=2+j}^p \phi _i. \end{aligned}$$

To express the BLP in terms of \(\mathbf {d}=(d_p, \ldots , d_1)^T\) only, use the prediction equations to obtain

$$\begin{aligned} P(X_p\Vert 1; \mathbf {d})=\mu +\text {Cov}(X_p,\mathbf {d}) \varvec{\Gamma }_d^{-1}\mathbf {d}, \end{aligned}$$

where \(\varvec{\Gamma }_d\) is the \(p \times p\) covariance matrix of \(\mathbf {d}\), which is known to be invertible for a causal stationary ARMA \(\{ d_t \}\) (see Proposition 5.1 in Brockwell and Davis (1991)). Combining the above gives

$$\begin{aligned} P(d_{p+1}\Vert 1; \mathbf {d})= - \kappa v_p d_1 + \sum _{j=1}^{p-1} \left( d_{p+1-j} - \kappa v_j -\sum _{i=j+1}^p\phi _i \right) , \end{aligned}$$
(7)

with \((v_1,v_2,\ldots ,v_p)=\text {Cov}(X_p,\mathbf {d})\varvec{\Gamma }_d^{-1}\).

The coefficients \(\mathbf {v}^T=(v_1,\ldots , v_p)\) can be written in terms of the correlation function of the differences in (6):

$$\begin{aligned} \mathbf {v}^T= & {} \gamma _d(0)^{-1}\text {Cov}(X_p,\mathbf {d}) (\varvec{\Gamma }_d/\gamma _d(0))^{-1}\\= & {} \varvec{c}{} \mathbf{R}_d^{-1}, \end{aligned}$$

where \(\mathbf{R}_d\) is the \(p \times p\) autocorrelation matrix of \(\mathbf{d}\) and

$$\begin{aligned} \mathbf{c}^T= \gamma _d(0)^{-1} \text {Cov}(X_p, \mathbf{d})= \left( 1/2, 1/2 + \rho _d(1), \ldots , 1/2 + \sum _{k=1}^{p-1} \rho _d(k) \right) \end{aligned}$$
(8)

can be extracted from (5) and the relation

$$\begin{aligned} \gamma _X(h)-\gamma _X(h+1)= \frac{\gamma _d(0)}{2}+\sum _{k=1}^{h-1}\gamma _d(k). \end{aligned}$$

A second representation of the BLP is given by the prediction equations:

$$\begin{aligned} P(d_{p+1}\Vert 1; \mathbf {d})= \sum _{j=1}^p u_jd_{p+1-j}, \end{aligned}$$
(9)

where the predicting coefficients are \((u_1, u_2, \ldots , u_p) = \text {Corr}(d_{p+1}, \mathbf {d})\mathbf{R}_d^{-1}\). Here, \(u_p\) is the lag p partial autocorrelation of \(\{ d_t \}\). Equating the coefficient of \(d_1\) in (7) and (9) yields \(- \kappa v_p= u_p\). If \(v_p \ne 0\), which we tacitly assume to avoid trifling work, we can set \(\kappa =-u_p/v_p\). Equating the coefficients on the right hand sides of (7) and (9), and solving for \(\varvec{\phi }\) produces an expression of the autoregressive coefficients in terms of the autocorrelations of \(\{ d_t \}\):

$$\begin{aligned} \phi _k = (u_{k}-u_{k-1})-\frac{u_p}{v_p}(v_{k}-v_{k-1}), \quad k=1,\ldots , p, \end{aligned}$$
(10)

where \(v_0=1\) and \(u_0=-1\). If \(\{ X_t \}\) satisfies (3), then \(\phi _1, \ldots , \phi _p\) satisfy (10). Now let \(\{ d_t \}\) be a stationary sequence with \(v_p \ne 0\) and suppose that \(\varvec{\phi }^T=(\phi _1,\ldots , \phi _p)\) satisfies (10):

$$\begin{aligned} \varvec{\phi } = \varvec{A}\mathbf {R}_d^{-1} \left( \text {Corr}(d_{p+1},\mathbf {d})- \frac{u_p}{v_p}\varvec{c}\right) + \left( 1 + \frac{u_p}{v_p}, 0, \ldots , 0 \right) ^T, \end{aligned}$$

with

$$\begin{aligned} \mathbf {A}= \left[ \begin{array}{rrrrrr} 1&{}0&{}0&{}\cdots &{}0 &{}0\\ -1&{}1&{}0&{}\cdots &{}0&{}0\\ \vdots &{}\vdots &{}\vdots &{}\ddots &{}\vdots &{}\vdots \\ 0&{}0&{}0&{}\cdots &{}1 &{}0\\ 0&{}0&{}0&{}\cdots &{}-1 &{}1 \\ \end{array} \right] . \end{aligned}$$

Since \(u_p\) is the partial correlation of \(\{ d_t \}\) at lag p,

$$\begin{aligned} u_p=(0,0,\ldots ,1)\mathbf {R}_d^{-1} \varvec{\rho }_d, \end{aligned}$$

with \(\varvec{\rho }_d^T=\left( \rho _d(1), \ldots , \rho _d(h) \right)\). Substituting this into the above linear equation for \(\varvec{\phi }\) and simplifying gives

$$\begin{aligned} \varvec{\phi } = \varvec{M} \varvec{\rho }_d + (1,0,\ldots ,0)^T, \end{aligned}$$
(11)

where

$$\begin{aligned} \mathbf{M} =\mathbf {A}\mathbf {R}_d^{-1}\left( \mathbf {I}-\mathbf {c}^*(0,0,\ldots ,1)\mathbf {R}_d^{-1}\right) , \end{aligned}$$

with \(\mathbf {c}^*=\left( -1/2, 1/2 + \rho _d(1), \ldots , 1/2 + \sum _{k=1}^{p-1} \rho _d(k) \right) ^T\). Note that each element in \(\varvec{M}\) is a function of \(\rho _d(1), \ldots , \rho _d(p)\).

The \(p=1\) case will shed light on the above calculations. Here, (10) and (6) give

$$\begin{aligned} \phi _1 = 1 + 2\rho _d(1)=\frac{\rho _X(1)-\rho _X(2)}{1-\rho _X(1)}, \end{aligned}$$

which exceeds unity whenever \(\rho _X(2) < 2\rho _X(1)-1\), which can happen for some AR(p) models. However, if \(\{ X_t \}\) follows

$$\begin{aligned} X_t=\phi X_{t-1}+Z_t, \quad t=0,\pm 1, \pm 2, \ldots , \end{aligned}$$

and \(|\phi |< 1\),

$$\begin{aligned} \frac{\rho _X(1)-\rho _X(2)}{1-\rho _X(1)}=\frac{\phi -\phi ^2}{1-\phi }=\phi . \end{aligned}$$

In general, if \(\varvec{\phi }\) is from a causal AR(p) model satisfying (4), then (11) provides a one-to-one transformation between \(\rho _{d}(1), \ldots , \rho _d(p)\) and \(\varvec{\phi }\). However, if \(\{X_t\}\) does not follow a causal AR(p) recursion, there is no guarantee that \(\varvec{\phi }\) satisfying (10) corresponds to a causal AR(p) model. In practice, this presents no issue since it is easy to check to see if a fitted AR(p) model is causal. If our fitted model is not causal, this is an indication that \(\{X_t\}\) is inadequately described by an AR(p) series. In this case, we simply change p and refit until causality is achieved.

Given observations \(X_1, \ldots , X_N\), we estimate the lag h sample autocorrelation of the differences from

$$\begin{aligned} \hat{\rho }_d(h) = \frac{\hat{\gamma }_d(h)}{\hat{\gamma }_d(0)}= \frac{\sum _{t=1}^{N-h} (d_t-\bar{d})(d_{t+h}-\bar{d})}{\sum _{t=1}^N (d_t-\bar{d})^2}, \quad h \ge 0. \end{aligned}$$

Here, \(\bar{d}= (N-1)^{-1}\sum _{t=1}^{N-1} d_t\) is the sample mean. The AR(p) model will be fit using (10) with \(\gamma _d(h)\) replaced by the sample version \(\hat{\gamma }_d(h)\):

$$\begin{aligned} {\hat{\mathbf{{u}}}}={\hat{\mathbf{{R}}}}_d^{-1} {\hat{\varvec{\rho }}}_d \quad \text {and} \quad {\hat{\mathbf{{v}}}}={\hat{\mathbf{{R}}}}_d^{-1}{\hat{\mathbf{{c}}}}, \end{aligned}$$
(12)

where \({\hat{\mathbf{{c}}}}\) is obtained from (8) by replacing all elements with their estimates.

To ensure that the estimated \(v_p\) is not zero, one simply checks this in practice. It is also recommended to check to see if the fitted AR(p) model is causal.

Summarizing, our proposed algorithm for fitting an AR(p) model using differences is

  1. 1.

    Compute \({\hat{\mathbf{{u}}}}\) and \({\hat{\mathbf{{v}}}}\). If \(\hat{v}_p=0\), reduce the AR order to \(p-1\) and refit.

  2. 2.

    Use (10) with \(\mathbf {u}={\hat{\mathbf{{u}}}}\) and \(\mathbf {v}={\hat{\mathbf{{v}}}}\) to find \(\hat{\varvec{\phi }}\), and check to see that the estimates correspond to a causal model. If the solution is non-causal, change p and refit.

The above algorithm produces a \(\hat{\varvec{\phi }}\) for a causal AR(p) process satisfying (11):

$$\begin{aligned} \hat{\varvec{\phi }}= \hat{\mathbf {M}} {\hat{\varvec{\rho }}}_d+ (1,0,\ldots ,0)^T, \end{aligned}$$
(13)

where each element in \(\hat{\mathbf{M}}\) corresponds to an element of \(\mathbf{M}\) with \(\rho _d(h)\) replaced by \(\hat{\rho }_d(h)\) for each h. For any stationary sequence of first differences \(\{ d_t \}\), each element of \(\hat{\mathbf{M}}\) converges almost surely to its theoretical value. In particular, as \(N \rightarrow \infty\), \(\hat{\mathbf{M}} \rightarrow \mathbf{M}\) in the almost sure sense.

We end this section by estimating \(\sigma ^2\). There are several moment equations that can be used to estimate \(\sigma ^2\). For example, multiplying both sides of the ARMA(p, 1) difference equation,

$$\begin{aligned} d_t=\phi _1 d_{t-1}+\cdots +\phi _p d_{t-p}+z_t-z_{t-1}, \end{aligned}$$

by \(d_t\), taking expectations, and solving for \(\sigma ^2\) yields,

$$\begin{aligned} \sigma ^2=\gamma _d(0)\left( \frac{1-\sum _{k=1}^p \phi _k \rho _d(k)}{2-\phi _1}\right) . \end{aligned}$$

A moment based estimator of the variance is hence

$$\begin{aligned} \hat{\sigma }^2=\hat{\gamma }_d(0)\left( \frac{1-\sum _{k=1}^p \hat{\phi }_k \hat{\rho }_d(k)}{2-\hat{\phi }_1}\right) . \end{aligned}$$
(14)

In the next section, we show that \(\hat{\sigma }^2\) is a \(\sqrt{N}\)-consistent estimator of \(\sigma ^2\).

4 Asymptotic normality

This section shows that if \(m=m(N)\) grows slowly enough in N, the estimators in the last section will be consistent and asymptotically normal. If the number of changepoints m is small relative to N, then the mean shifts should have a negligible impact on the estimated autocovariance of the differences, since \(X_t-X_{t-1} = d_t-d_{t-1}\) except at the changepoint times \(\tau _1, \ldots , \tau _m\). In particular, to obtain asymptotic normality, we assume that as \(N \rightarrow \infty\), for some finite B,

  1. A.1

    \(\max _{0 \le k\le m(N)} \mid \mu _{k+1}-\mu _k \mid \le B\).

  2. A.2

    \(m(N)=o(\sqrt{N})\).

Condition A.1 imposes existence of some bound on the mean shift sizes and Condition A.2 regulates the number of changepoints that can occur.

We begin with asymptotic normality of the autocorrelations for first-order differences in the general ARMA(p, q) case, which may be of distinct interest. The asymptotic normality of the AR(p) estimators is a corollary to Theorem 1.

Theorem 1

If \(\{ X_t \}_{t=1}^N\) obeys (1) with \(\{\epsilon _t \}\) satisfying (2) where \(\{ Z_t \}\) is IID white noise having a finite fourth moment, then for each fixed positive integer k, as \(N \rightarrow \infty\),

$$\begin{aligned} \sqrt{N} \left( \begin{array}{c} \hat{\rho }_d(1) - \rho _d(1) \\ \vdots \\ \hat{\rho }_d(k) - {\rho }_d(k) \\ \end{array} \right) \xrightarrow {\mathbf {D}} \mathbf {N}_k{(\mathbf {0}}, { \mathbf {BWB}^T}). \end{aligned}$$

Here, the elements in the \((k+1) \times (k+1)\) dimensional \(\mathbf {W}\) are from Bartlett’s formula for the asymptotic covariance matrix of \((\hat{\rho }_\epsilon (1), \ldots , \hat{\rho }_\epsilon (k+1))^T\), (see Chapter 8 of Brockwell and Davis 1991) and \(\mathbf {B}\) is \(k \times (k+1)\) dimensional with form

$$\begin{aligned} \mathbf {B}= \frac{1}{2(1-\rho _X(1))} \begin{bmatrix} 2 &{} -1 &{} 0 &{} 0 &{}\cdots &{} 0 &{}0 &{}0 \\ -1 &{} 2 &{}-1 &{} 0 &{}\cdots &{} 0 &{}0 &{}0 \\ 0 &{} -1 &{} 2 &{}-1 &{}\cdots &{} 0 &{}0 &{}0 \\ \vdots &{}\vdots &{}\vdots &{} \vdots &{}\ddots &{} \vdots &{} \vdots &{} \vdots \\ 0 &{}0 &{}0 &{}0 &{}\cdots &{}-1 &{}2 &{}-1 \\ \end{bmatrix} . \end{aligned}$$

Proof

We first show that the changepoints have negligible impact on estimated autocorrelations in the limit. To do this, write \(d_t=X_t-X_{t-1}= (\epsilon _t - \epsilon _{t-1}) +\delta _t\), with \(\delta _t=(\mu _k-\mu _{k-1}) I_{[t=\tau _{k+1}]}\), and \(I_A\) the indicator of the set A. Letting

$$\begin{aligned} \tilde{\gamma }_d(h)= \frac{\sum _{t=2}^{N-h} (\epsilon _t-\epsilon _{t-1}) (\epsilon _{t+h}-\epsilon _{t+h-1})}{N}, \end{aligned}$$

then

$$\begin{aligned} \sqrt{N} \mid \hat{\gamma }_d(h)-\tilde{\gamma }_d(h) \mid\le & {} \frac{m}{\sqrt{N}} \left[ m^{-1} \sum _{t \in \mathcal{T}} \delta _t(\epsilon _{t+h}-\epsilon _{t+h-1} +\epsilon _{t-h}-\epsilon _{t-h-1}+\delta _t)\right] , \end{aligned}$$

where \(\mathcal{T} = \{ \tau _1, \ldots , \tau _m \}\) denote all changepoint times. The term on the right hand side converges to zero if \(N^{-1/2}m \rightarrow 0\) as \(N \rightarrow \infty\) (this is Condition A.2) and the sum is bounded in probability (this is guaranteed by Conditions A.1, A.2, and the properties of \(\{ \epsilon _t \}\)). We see that the asymptotic distribution of \(\hat{\gamma }_d(h)\) is the same as that of \(\tilde{\gamma }_d(h)\).

It is easy to see that

$$\begin{aligned} \sqrt{N}\left[ \tilde{\gamma }_d(h)-(2\hat{\gamma }_\epsilon (h)- \hat{\gamma }_\epsilon (h-1)-\hat{\gamma }_\epsilon (h+1))\right] =o_P(1), \end{aligned}$$
(15)

where \(o_P(1)\) denotes a term that converges to zero in probability as \(N \rightarrow \infty\). Using the above and \(\hat{\gamma }_d(0)/\gamma _\epsilon (0) \rightarrow 2(1-\rho _\epsilon (1))\) in the almost sure sense, we have

$$\begin{aligned} \sqrt{N}\left( \hat{\rho }_d(h)-\rho _d(h)\right) = \frac{\sqrt{N}}{2(1-\rho _\epsilon (1))}\left( -1,2,-1\right) ^T \begin{bmatrix} \hat{\gamma }_\epsilon (h-1)-{\gamma }_\epsilon (h-1)\\ \hat{\gamma }_\epsilon (h)-{\gamma }_\epsilon (h) \\ \hat{\gamma }_\epsilon (h+1)-{\gamma }_\epsilon (h+1) \end{bmatrix}+o_p(1) \end{aligned}$$

for each \(h = 1, \ldots , k\). Hence,

$$\begin{aligned} \sqrt{N}({\hat{\varvec{\rho }}}_d-{\varvec{\rho }}_d)=\mathbf {B}\sqrt{N}({\hat{\varvec{\rho }}}_\epsilon -{\varvec{\rho }}_\epsilon ) +o_p(1). \end{aligned}$$

\(\square\)

Theorem 1 now follows from classic results for asymptotic normality for sample autocorrelations of ARMA processes (see Chapter 8 of Brockwell and Davis 1991).

Corollary 2

Suppose that \(\{ X_t \}\) follows (1) with \(\{ \epsilon _t \}\) satisfying (2) with \(\{ Z_t \}\) IID white noise having a finite fourth moment. For the estimator in (11), as \(N \rightarrow \infty\),

$$\begin{aligned} \sqrt{N} \left( \begin{array}{c} \hat{\phi }_1 - \phi _1 \\ \vdots \\ \hat{\phi }_p - \phi _p \\ \end{array} \right) \xrightarrow {\mathbf {D}} \mathbf {N}_p(\mathbf{0}, \varvec{\Sigma }), \end{aligned}$$

Here, \(\varvec{\Sigma }=\mathbf {M} \mathbf {B W} (\mathbf {M} \mathbf {B})^T\).

Proof of Corollary 2

Since \(\{ d_t \}\) is stationary and ergodic, the elements of \(\hat{\varvec{M}}\) converge to those in \(\varvec{M}\) in the almost sure sense; specifically, (15) gives

$$\begin{aligned} \sqrt{N}\left( \hat{\varvec{\phi }}-\varvec{\phi }\right) = \mathbf {M}\sqrt{N}\left( {\hat{\varvec{\rho }}}_d-\varvec{\rho }_d \right) +o_P(1). \end{aligned}$$

The conclusion of Corollary 2 now follows. \(\square\)

Theorem 1 and Corollary 2 imply that \({\hat{\varvec{\rho }}}_d\) and \(\hat{\varvec{\phi }}\) are both consistent estimators, so that \(\hat{\sigma }^2\) given by (14) is a consistent estimator of the white noise variance.

5 A simulation study

A simulation study with AR(p) errors is now conducted. Our Yule-Walker moment estimator based on first-order differencing is now compared to several estimators, including the robust AR(1) estimator of Chakar et al. (2017), the BIP \(\tau\)-estimators of Muma and Zoubir (2017), and the rolling window methods employed in Beaulieu and Killick (2018).

The paper Chakar et al. (2017) studies the AR(1) case and proposes an estimator that is robust to mean shifts:

$$\begin{aligned} \hat{\phi } := \frac{\displaystyle \displaystyle \left( {\mathrm{median}}_{1 \le t \le N-2} \mid X_{t+2} -X_t\mid \right) ^2}{\displaystyle \displaystyle \left( {\mathrm{median}}_{1 \le t \le N-1} \mid X_{t+1} -X_t \mid \right) ^2} - 1. \end{aligned}$$
(16)

It is not clear how to extend this work to cases where \(p > 1\).

The rolling window methods of Beaulieu and Killick (2018) estimate autocorrelations via window-based methods as follows. For a window length w, with \(w \le N\), a moving window scheme generates \(N-w+1\) subsegments, the \(i\mathrm{th}\) subsegment containing the data at times \(i, \ldots , i+w-1\). Each subsegment is treated as a stationary series (even though some may contain mean shifts and are thus truly nonstationary) and the time series parameters are estimated in subsegment i from the data in this subsegment only. The final estimates are taken as medians of the estimates over all subsegments. The hope is that most windows will be “changepoint free”, and medians over all subsegments will not be heavily influenced by the few windows containing changepoints. Of course, such a scheme may not use all data efficiently in estimation. Moreover, Beaulieu and Killick (2018) demonstrates that the success of this procedure depends heavily on the choice of w. As we show below, these robust autocovariance estimation methods do not perform particularly well for this problem.

In each simulation, the series length is \(N=1,000\) and m is randomly generated from the discrete uniform distribution \(\text {Uniform} \{ 0, 1, \ldots , 10 \}\), which roughly corresponds to the changepoint frequency in our data example in the next section. All changepoint times are generated randomly within \(\{ 2, 3, \ldots , N \}\) with equal probability — we do not impose any minimal spacing between successive changepoint times. The segment means \(\mu _i\) are randomly generated from a \(\text {Uniform}(-1.5,1.5)\) distribution. Ten thousand independent runs are conducted for all cases.

We first consider AR(1) errors, simulating \(\phi\) randomly from the \(\text {Uniform}(-0.95, 0.95)\) distribution and \(\{ Z_t \}\) as Gaussian white noise with a unit variance. Our Yule-Walker difference estimator in (12) is denoted by Diff in future figures. This estimator will be compared to a variety of alternative approaches. The robust AR(1) estimator in (16) is denoted by AR1seg. Averaged rolling window estimators, using different window lengths, are denoted by their lengths: N, N/2, N/5, N/10, N/20, and N/50. We also compare to the general ARMA robust estimator of Muma and Zoubir (2017) applied to the differenced data, which is denoted by BIP. Here, we fit a general ARMA(1,1) model for the errors, which does not take into account that the MA(1) parameter should be -1. This extra flexibility should make the BIP method appear better than it truly is. Finally, we include an estimator based on our approach but with the outlying observations in \(\{ d_t \}\) first removed, which we denote by Outlier. Since our method is “corrupted" by non-zero means at the changepoint times, removing outliers (which are likely to occur at the changepoint observations) should improve our approach. For outlier detection, we use a simple nonparametric Tukey fence and acknowledge that other detection schemes could be used.

Our simulation results are summarized in Fig. 1. The obvious winner is the Yule-Walker estimator based on first-order differencing. Indeed, this estimator is unbiased and has the smallest variance. The AR1seg estimator is unbiased; however, it has a larger variability than the Yule-Walker difference estimators. The performance of the rolling window estimators depends on the choice of the window length, but appears to be inferior to the difference based estimator, even with the optimal window size selected (which is likely somewhere between N/20 and N/50 in this simulation). It is hard to decide the optimal window length in practice and smaller window lengths considerably increase computation time. While the general BIP robust estimator appears unbiased, it has a much larger variance than all other estimators. Indeed, this estimator seems to be the worst of all. Our outlier removal approach has a slightly positive bias and slightly larger variance, likely induced by the tendency to remove true observations as outliers.

Fig. 1
figure 1

Box plots of estimates of the AR(1) parameter \(\phi\). Our differenced based method appears to be unbiased and has the smallest variability; the BIP robust method has the largest variability of all methods

Full size image

We now move to AR(2) errors. In each AR(2) simulation, the AR coefficients were uniformly generated from the triangular region guaranteeing model causality: \(\phi _1 + \phi _2 < 1\), \(\phi _2 - \phi _1 < 1\), and \(|\phi _2 |< 1\). In these simulations, the changepoint total is fixed at \(m=9\) and all segments have equal lengths. All mean shifts alternate in sign with an absolute magnitude of 2.0, the first shift moving the series upwards. The series length varies with \(N \in \{ 1000, 2000, 5000, 10000, 20000 \}\). Since \(p > 1\), the AR1seg estimator is not applicable. The rolling-window estimator and general BIP robust estimator were dropped from consideration due to their poor AR(1) performance and computational time requirements. The simulation results show that estimator bias and variance decreases as the length of the series increases, reinforcing the consistency results in the last section Fig. 2.

Fig. 2
figure 2

Box plots of AR(2) coefficient estimates. Variability and bias decrease as the series length increases

Full size image

Moving to AR(4) simulations, to meet model causality requirements, the AR(4) characteristic polynomial is factored into its four roots, denoted by \(1/r_1, 1/r_2, 1/r_3\), and \(1/r_4\). That is,

$$\begin{aligned} \phi (z)=(1-r_1z)(1-r_2z)(1-r_3z)(1-r_4z). \end{aligned}$$

Causality implies that all \(r_i\) should lie inside the complex unit circle. To meet this, \(r_1\) and \(r_2\) will be randomly generated from the Uniform\((-0.9, 0.9)\) distribution, and \(r_3\) is a randomly generated complex number with modulus \(\vert r_3 \vert <0.9\). The root \(r_4\) is taken as the complex conjugate of \(r_3\). This mixes real and complex roots in the AR(4) characteristic polynomial. All other simulation settings are identical to those in the AR(2) case. Figure 3 shows our results, which exhibit the same pattern as the AR(2) case, with decreasing bias and variance as N increases.

Fig. 3
figure 3

Box plots of AR(4) coefficient estimates. Again, estimator variabilities and biases decrease with increasing sample size

Full size image

Our next simulation returns to the AR(1) setting and conducts a sensitivity analysis to mean shift sizes. Here, estimator accuracy is more greatly influenced by the magnitude of the mean shifts than changepoint locations. We take all mean shifts to have the same size \(\Delta\) and introduce the signal-to-noise ratio (SNR), defined as the absolute mean shift magnitude over the marginal series standard deviation of \(X_t\):

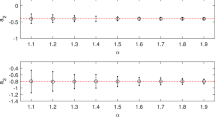
$$\begin{aligned} \text {SNR} = \frac{\mid \Delta \mid }{\sqrt{\frac{\sigma ^2}{1-\phi ^2}}}. \end{aligned}$$
(17)

For simplicity, \(\sigma ^2\) is set to unity. The number of changepoints is fixed at \(m=9\) and their locations are randomly generated over \(\{ 2, \ldots , N \}\) with \(N=1,000\). In each run, the true \(\phi\) is simulated from the \(\text {Uniform}(-0.95, 0.95)\) distribution. The nine mean shifts alternate signs, with \(|\Delta |\) varied in [0,5]. Boxplots of the difference between the estimated \(\hat{\phi }\) and the true \(\phi\) are presented in Fig. 4.

Fig. 4
figure 4

An AR(1) mean shift size sensitivity plot. The larger the mean shifts are, the more the estimates of \(\phi\) degrade

Full size image

The horizontal line in Fig. 4 marks zero bias in \(\hat{\phi }\); the solid curve depicts the average differences between \(\hat{\phi }\) and \(\phi\). Obviously, the larger the mean shift magnitude, the more our estimator degrades. This said, in practice, larger mean shift sizes can usually be identified as outliers in the differenced series (Chen and Liu 1993; McQuarrie and Tsai 2003) or can easily be identified in the original series, despite the AR contamination. As such, the essential challenge lies with estimating the AR(p) parameters in the presence of smaller mean shifts.

Two more simulations are included. Our first simulation shows how AR(p) processes can approximate MA(q) errors in changepoint problems. The specifications of the series and changepoints are the same as the first AR(1) case of this section, but the model errors obey the MA(1) model

$$\begin{aligned} \epsilon _t = Z_t + \theta Z_{t-1}, \end{aligned}$$

with \(\theta = 0.5\). The plot in Fig. 5 shows the autocorrelation function of our fitted AR(10) process from one simulation run only. Notice that the fitted AR(10) autocovariance is essentially zero at most lags that exceed unity, indicating the overall quality of the AR(10) approximation (an MA(1) model is characterized by an autocovariance that is non-zero only at lag 1).

Fig. 5
figure 5

Autocorrelations of the AR(10) process used to approximate our MA(1) errors. The dashed lines demarcate 95% pointwise confidence thresholds for white noise

Full size image

Our final simulation considers order selection of p for AR errors by adding the Bayesian Information Criterion (BIC) penalty \((p+1)\ln (N)\) to minus two times the log likelihood of the model. The mean shifts in \(\{ X_t \}\) “contaminate” the likelihood for \(\{ X_t \}\) away from a likelihood for an AR series with a fixed (constant) mean. Our remedy here is to demean \(\{ X_t \}\) before estimating p. While other methods of order estimation are possible, this procedure worked the best amongst several that were experimented with. More specifically, the AR(p) coefficients are first estimated via \(\{ d_t \}\) for each candidate AR order \(p \in \{ 1, 2, \ldots , p_\mathrm{{max}} \}\), where \(p_\mathrm{{max}}\) is some preset maximum AR order to consider. Then, one-step-ahead prediction residuals were computed and the changepoint configuration was estimated by some changepoint technique. The pruned exact liner time (PELT) algorithm of Killick et al. (2012) was used here. The estimated changepoint configuration is then used to demean \(\{ X_t \}\). The likelihood and BIC scores are then calculated from the demeaned series for each order p and the order with the smallest penalized likelihood BIC score is selected.

$$\begin{aligned} \text {BIC}(p) = -2 \log (\hat{\sigma }^2) + (p+1)\log (N) \end{aligned}$$
(18)

In our simulation, \(N=1,000\), nine equally-spaced mean shifts of size 2.5 corrupt the series, and the errors are generated from a causal AR(4) process with coefficients \(\varvec{\phi }=(0.3, -0.3, -0.2, -0.1)\). The estimated AR order for 1, 000 simulations is plotted in the Fig. 6 histogram. While BIC selects \(p=4\) the majority of the time, it is also prone to overestimation, selecting the order 5 in more than 20% of the runs. AR order overestimation by BIC is classically appreciated in even changepoint-free settings (Brockwell and Davis 1991).

Fig. 6
figure 6

Estimated AR orders via a Bayesian information criterion penalty. The mode of the histogram is correct at four, but some overestimation of p is also present

Full size image

6 Applications

6.1 Changepoints in AR(p) Series

As previously discussed, most changepoint techniques mistakenly flag changepoints when underlying positive dependence is ignored. For example, (Lund and Shi 2020) argues that shifts identified in the London house price series of Fryzlewicz (2020) may be more attributable to the positive correlations in the series than to actual mean shifts. CUSUM based techniques are known to degrade with positive correlation (Shi et al. 2022). To remedy this, authors recommend detecting changepoints from estimated versions of the one-step-ahead prediction residuals of the series (Bai 1993; Robbins et al. 2011). This requires estimation of the autocovariance structure of the series in the presence of the unknown changepoints. As such, a major application of our methods serves to decorrelate (pre-whiten) series without any prior knowledge of the changepoint configuration of the series. IID-based changepoint techniques, applied to the estimated one-step-ahead prediction residuals, can then be used to estimate any mean shifts in the series. The Yule–Walker difference estimator proposed here is extensively used in Shi et al. (2022) to do just this. In addition, our difference estimator supplies a long-run variance estimate needed in the changepoint methods in Eichinger and Kirch (2018), Romano et al. (2021), and Dette et al. (2020).

Table 1 demonstrates the improved performance of two popular multiple changepoint methods, wild binary segmentation (WBS) Fryzlewicz (2014) and PELT Killick et al. (2012). In each run, an AR(1) series of length \(N=500\) is simulated with \(\phi\) fixed within \(\{ 0.25, 0.50, 0.75 \}\), and \(\sigma ^2=1\). The series has either no changepoints or three equally spaced changepoints; all mean shift sizes are the same, are denoted by \(\Delta\), and are chosen to induce the constant signal-to-noise requirement of \(\text {SNR}=2\) in (17). All simulations are aggregated from 1, 000 independent runs. In Table 1, \(\overline{\hat{m}}\) and \(SE_{\hat{m}}\) denote the average and standard error of the estimated number of changepoints when WBS and PELT are directly applied to the series. The quantities \(\overline{\hat{m}^d}\) and \(SE_{\hat{m}^d}\) denote the average and standard error of the estimated number of changepoints from the one-step-ahead prediction residuals after fitting an AR(1) series to the differences by our methods.

Table 1 Results for AR(1) series with three and no changepoints
Full size table

It is apparent that IID based WBS and PELT methods overestimate the number of changepoints in a dependent series when positive correlation is ignored; PELT appears to be more resistant to dependence issues than WBS. In contrast, with the help of the proposed Yule-Walker difference estimator and decorrelation techniques, both WBS and PELT become much more accurate.

6.2 New Bedford precipitation

Annual precipitations from New Bedford and Boston, Massachusetts are studies in Li and Lund (2012). The data are available from https://w2.weather.gov/climate/xmacis.php?wfo=box. The ratio of these series (New Bedford to Boston) is displayed in Figure 7, along with a fitted mean of a model that allows for both multiple changepoints and AR errors. Three documented changepoints, occurring at the years 1886, 1917, and 1967 are indicated. After adjusting for four regime means, Fig. 8 shows the sample ACF plot of the precipitation ratio series, suggesting that the series is correlated. The Bayesian Information Criterion estimates \(p=1\) as the AR order. Although this order does not seem to adequately describe all non-zero autocorrelations, we use it anyway to illustrate our points.

Fig. 7
figure 7

New Bedford to Boston annual precipitation ratios with three identified changepoints

Full size image
Fig. 8
figure 8

Sample autocorrelations of the demeaned precipitation ratio series with 95% pointwise confidence bands for zero correlation

Full size image

The AR(1) parameter estimates fluctuate wildly over distinct methods. Specifically, our difference Yule-Walker estimator and BIP \(\tau\)-estimators produce antipodal estimates as can be seen in Table 2. Our estimate agrees closely with an estimate computed by assuming the three changepoint times are known, but the level of autocorrelation is significantly less than that estimated in a Yule–Walker scheme that ignores all three changepoint times. The results show that one needs to be careful in changepoint problems with correlated data—mean shifts and correlation can inject similar features into time series.

Table 2 AR(1) \(\phi\) estimates for the precipitation ratio series. The individual estimates highly depend on the method
Full size table

7 Conclusions

Differencing methods can effectively be used to estimate the autocovariance structure of an AR(p) series corrupted by mean shift changepoints. Our Yule–Walker estimator for autoregressive models is easy to implement, computationally fast, consistent, and asymptotically normal. While the proposed estimator is adversely impacted by large mean shifts, large shifts appear as large outliers in the differenced series and can be removed. When changepoints are present, the difference methods developed here significantly improve changepoint techniques developed for IID errors. The techniques are also applicable if the series has a linear trend (constant across all regimes) with intercept shifts.