Node line semimetal states in tungsten-based materials

Abstract

Node line semimetals (NLSMs) were characterized by one-dimensional band crossings in their bulk electronic structures. The nontrivial band topology of NLSM gives rise to "drumhead" surface electronic excitations that exhibits exotic physical properties. The symmetries of crystalline provide the needed protection of node line from being gapped out by the perturbations that preserve the symmetry. The progress of NLSM in tungsten-based materials is reviewed with an emphasis on their symmetry-based protection, characteristic electronic band structures and their response to the spin–orbit coupling (SOC) and breaking of time-reversal symmetry. The potential exploration directions of tungsten-based NLSM in the future are also discussed.

1 Introduction

Generally, the crystalline materials are classified into metals and insulators based on their conductivity. The explanation of the conductivity of electrons in a crystalline material was built on the progress of solid-state physics in which symmetry plays a key role. Recently, the topology of wavefunction has emerged as another powerful tool to classify matters, by which the insulators and metals are found to host more exotic phases beyond the traditional symmetry paradigm. The search for new phases of topologically nontrivial insulators and metals quickly becomes one of the most exciting frontiers of condensed matter physics and materials science [1,2,3,4,5]. After a complete classification of gapped system given by Ryu et al. [6], much more attention has been drawn to the topological semimetal (TSM) since the successful design [3] and experimental observations of the Weyl semimetal (WSM) state in transition-metal monophosphides, a family of tungsten-related materials [4, 5]. WSM is a topological electronic state whose valence and conduction bands touch at discrete node points in the Brillouin zone (BZ) shown in Fig. 1a. These touching points, also named as Weyl points, are doubly degenerated, and topologically robust against weak disorder under the protection of their nontrivial band topology.

Fig. 1

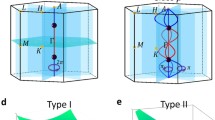
Node point and NL in materials. a Node (Weyl) point in a band crossing system without other symmetry except the translation one; b NL band crossing protected by $S$ symmetry; c NL band crossing protected by mirror symmetry and confined to the mirror plane ${k}_{z}=0$; d NL band crossing protected by nonsymmorphic screw-axis symmetry and confined to the BZ boundary

Heikkilä et al. [7, 8] extended the idea of fermionic node points to node-line semimetals (NLSMs) that host one-dimensional (1D) crossing points of conduction and valence bands. One of the significant properties of NLSMs is that they support "drumhead" like flat surface band [9, 10] which may potentially support high transition temperature superconductivity due to their high density of states [11]. The node-line fermions have been proposed in realistic materials such as Graphene-network [10], Cu₃N [12], Cu₃PdN [13] and Ca₃P₂ [14]. Recently, there rises a new trend in investigating NLSMs with multiple node line (NL) loops [15,16,17,18,19,20,21]. In those NLSMs, NL loops may intersect with each other and entangle into a variety of structures, such as node-net [21], node-chain [15] and Hopf-link [17,18,19,20, 22, 23], etc. Three types of NLs have been discovered based on their protecting mechanism [24]. The first type of NLs is protected by the combination of time-reversal symmetry ${\it T}$ and inversion symmetry ${\it P}$, i.e., $S=PT$. This type of NLs can present in any region of the BZ as shown in Fig. 1b, since $S$ is restored at every point of BZ. The second type of NLs are those protected by mirror symmetries. This type of NLs is always pinned to the high-symmetry planes of the mirror symmetries as shown in Fig. 1c. The last type of NLs is protected by nonsymmorphic symmetries and usually appears at the boundary of BZ, shown in Fig. 1d [25, 26].

In this mini review, we introduce progress of the materials realization of NLSM in the tungsten-related materials. The remaining part of this paper is organized as follows. In Sect. 2 the theory foundation of NLSM is briefly discussed. In Sect. 3 we introduce some materials families which show NLs in their bulk band structure. Discussions and outlook are presented in Sect. 4. As the present mini review only focuses on the tungsten-based NLSMs, for those who are interested in the general theory and material realization of NLSM beyond this type of materials are suggested to read some excellent reviews [27, 28].

2 Theory of node line semimetals

In this section, we first discuss the basic theoretical mechanism of the NLSMs in their electronic structures. To describe the node structure, we adopted an effective 2 $\times$ 2 Hamiltonian near the Fermi level, which is generally expressed in the form,

$$H\left({\varvec{k}}\right)={a}_{0}\left({\varvec{k}}\right){\hat{{\varvec{\sigma}}}}_{0}+{b}_{x}\left({\varvec{k}}\right){\hat{{\varvec{\sigma}}}}_{{\varvec{x}}}+{b}_{y}\left({\varvec{k}}\right){\hat{{\varvec{\sigma}}}}_{{\varvec{y}}}+{b}_{z}\left({\varvec{k}}\right){\hat{{\varvec{\sigma}}}}_{{\varvec{z}}},$$

(1)

where ${\hat{{\varvec{\sigma}}}}_{0}$ denotes the unit matrix and ${\hat{{\varvec{\sigma}}}}_{{\varvec{i}}} (i=x, y, z)$ the isospin operators of the crossing bands. Here we omit the spin degree of freedom for simplicity and leave the discussion of the spin effect to the end of this section. The two eigenvalues of this effective model are easily computed as ${E}_{\pm }({\varvec{k}})={a}_{0}^{2}({\varvec{k}})\pm \sqrt{{b}_{x}^{2}({\varvec{k}})+{b}_{y}^{2}({\varvec{k}})+{b}_{z}^{2}({\varvec{k}})}$. The existence of crossing points of bands then poses the constraints for Hamiltonia Eq. (1),

$${b}_{x}({\varvec{k}})={b}_{y}({\varvec{k}})={b}_{z}({\varvec{k}})=0.$$

(2)

The solution of each equality ${b}_{i}({\varvec{k}})=0$ is represented by a surface in the 3D Brillouin zone and the intersection of them should generally be discrete points, which are also named as Weyl points. The existence of the Weyl point in a two-band system thus only needs the translation invariant of the materials and is satisfied obviously in a crystalline. Some tungsten-related materials were discovered as the first material representations of Weyl node matter, such as TaAs [3,4,5].

Besides the translation symmetry, there exist other symmetries which enforce Eq. (2) to hold. With the help of these symmetries, the Weyl node point can even be promoted to higher dimensions. One of the most discussed symmetry is the compound symmetry $S$ that combines the space inversion ${\it P}$ and time-reversal symmetry ${\it T}$, i.e., $S={P}{T}$. Its component symmetry ${\it P}$ and ${\it T}$ impose below constraints to the Hamiltonian Eq. (1),

$$\begin{array}{l} {P}H({\varvec{k}}){P}^{-1}=H(-{\varvec{k}})\\ {T}H({\varvec{k}}){T}^{-1}={H}^{*}(-{\varvec{k}}).\end{array}$$

(3)

One immediately finds that the above equalities lead to the real condition of Hamiltonian for a $S$-invariant system,

$$H\left({\varvec{k}}\right)={H}^{*}\left({\varvec{k}}\right).$$

(4)

It is worthy to note an important fact of $S$ that its induced reality condition Eq. (4), or equally ${b}_{y}({\varvec{k}})=0$, holds in the entire BZ, rather than some discrete points in the case of a ${\it P}$- or ${\it T}$-invariant system. One quickly concludes that for a crossed two-band system with $S$ symmetry, the intersection of conduction and valence bands is prompted to a one-dimensional line of the BZ, i.e., a node line, because in this case the three parameters of BZ $\left({k}_{x},{k}_{y},{k}_{z}\right)$ are only imposed with two constraints ${b}_{x}({\varvec{k}})=0$ and ${b}_{z}({\varvec{k}})=0$.

Other symmetries supporting node structure in bulk band structure are the mirror symmetries. For example, if a system has a mirror symmetry ${M}_{z}$ and the two orbitals in Hamiltonian Eq. (1) have opposite sign after the mirror operation, one then easily finds,

$${M}_{z}{H}_{12}\left({k}_{x},{k}_{y},{k}_{z}\right){M}_{z}^{-1}=-{H}_{12}\left({k}_{x},{k}_{y},-{k}_{z}\right),$$

(5)

which further ensures that on ${k}_{z}=0$ or ${k}_{z}=\uppi$ plane,

$$\begin{array}{c}{d}_{x}\left({k}_{x},{k}_{y},0\right)={d}_{x}\left({k}_{x},{k}_{y},\uppi \right)=0\\ {d}_{y}\left({k}_{x},{k}_{y},0\right)={d}_{y}\left({k}_{x},{k}_{y},\uppi \right)=0.\end{array}$$

(6)

If there are band crossings on the ${k}_{z}=0$ or ${k}_{z}=\uppi$ plane, the geometry of band crossing is solely determined by the equation ${d}_{z}\left({k}_{x},{k}_{y},{k}_{z}=0\,\mathrm{ or \,\pi }\right)=0$ and generally forms a one-dimensional NL rather than some Weyl points. The above two types of NLs are robust under the protection of the associated symmetries. Any external perturbations that preserve these symmetries only shift or distort but not eliminate the NLs. Since the symmetry $S$ holds in the entire BZ, the NL protected by $S$ can therefore present at any part of the BZ, while the NL protected by mirror symmetry is readily pinned to the high symmetry plane of the mirror symmetries.

An important type of symmetry supporting the existence of NL is off-center nonsymmorphic symmetry. The nonsymmorphic symmetry $\tilde{g}=\left\{g|{\varvec{t}}\right\}$ where $g$ is the normal point-group operation and the ${\varvec{t}}$ is a translation with the translate distant being the fraction of the primary vectors. Typical nonsymmorphic symmetries are glide mirrors and screw rotations. Take screw rotation ${G}_{z}=\left\{{C}_{2z}|{\varvec{c}}/2\right\}$ as an example. Since the fractional translation ${\varvec{t}}$ is ${\varvec{c}}/2$, we have ${G}_{z}^{2}={\mathrm{e}}^{-i2{\varvec{k}}\cdot {\varvec{t}}}$ and the eigenvalues of the screw axis are $\pm {\mathrm{e}}^{-i{\varvec{k}}\cdot {\varvec{t}}}$. If the valence band and conduction band have distinct eigenvalues of ${G}_{z}$, they may cross at the boundary of BZ from being gapped out.

The above discussion has omitted the effect of spin–orbit coupling (SOC). When one introduces the SOC, the two-band system in Eq. (1) will be enlarged to a four-band one. It is easy to find that for a $S$-invariant system, any band should be doubly degenerated. In the case that one has ${S}^{2}=-1$, which ensures that any eigenstate of the system $|\varPsi ({\varvec{k}})\rangle$ must be degenerated with the partner $S|\varPsi ({\varvec{k}})\rangle$ due to the Kramers degeneracy [29].

In the case of SOC, the enlarge four-band Hamiltonian is now expanded by fifteen Dirac matrices and thus in the momentum space, the three parameters $\left({k}_{x},{k}_{y},{k}_{z}\right)$ are not enough to fulfill the conditions of reducing all fifteen coefficients of Dirac matrices to zero simultaneously, which generally lifts the node degeneracy of no SOC. Nevertheless, the existence of Node degeneracy with SOC is allowed by additional crystalline symmetries. Consider a system poses the two-fold screw rotation ${S}_{z}$ as well as ${\it P}$ and ${\it T}$ symmetries. The combination of ${G}_{z}$ and ${P}$,${M}={G}_{z}P$ will act as,

$${M}:(x,y,z)\to (x,y,c/2-z)$$

(7)

It is also easy to verify the following commutation relation between ${P}$ and ${M}$ ,

$${M}{P}={T}_{001}{\rm P}{\rm M}$$

(8)

where the unit translation ${T}_{001}$ along ${\varvec{c}}$ direction is induced by the partial translation of ${ G}_{z}$. The is a compound symmetry that resembles a mirror plane but off-centered away from the inversion center. One of the high-symmetry plane ${k}_{z}=\uppi$, ${T}_{001}$ leads to an additional phase ${\mathrm{e}}^{i{k}_{z}c}=-1$, which makes ${\rm P}$ (also $S={P}{T}$) anti-commute with $M$,

$$\{S/{P},M\}=0.$$

(9)

In the spinful case, one has ${M}^{2}=-1$ because the reflection also acts on the spin degrees of freedom. Therefore, each eigenstate on the high-symmetry plane ${k}_{z}=0$ is also associated with an $M$-eigenvalue of $\pm i$. An interesting fact is that acting $M$ on $\left|{\varPsi }_{+}({\varvec{k}})\right.\rangle$ will not change the eigenvalue of $S$, namely,

$$\begin{array}{l} M\left(PT\left|{\varPsi }_{+}({\varvec{k}})\right.\rangle \right)=-PTM\left|{\varPsi }_{+}({\varvec{k}})\right.\rangle \\ =-PT\left(+i\left|{\varPsi }_{+}({\varvec{k}})\right.\rangle \right)=+i\left(PT\left|{\varPsi }_{+}({\varvec{k}})\right.\rangle \right).\end{array}$$

(10)

When the conduction band and valence band have opposite $M$-eigenvalue on the ${k}_{z}=\uppi$ plane, there is no hybridization between them and a one-dimensional node structure, i.e., a NL, is produced. And because $PT$ will not change the $M$-eigenvalue of the crossed states, the partner pair also will not repel to each other.

3 Node line semi-metal in quasi-one-dimensional materials BaMX₃

The = BaMX₃ (M $=$ V, Nb or Ta; X $=$ S or Se) is a group of quasi-one-dimensional crystals adopting hexagonal structure with the No.194 space group, P6₃/mmc [30, 31]. The P6₃/mmc space group is associated with the point group of ${D}_{6h}={D}_{6}\otimes \{i\mid 0\}$, which contains a six-fold rotation along $z$-axis, a two-fold screw rotation along the axis $a-b$ and its two replicas construct by the $\left\{{C}_{3z}\mid {\varvec{c}}/2\right\}$, a horizonal mirror plane ${\sigma }_{h}$, a vertical mirror $\left\{{\sigma }_{d}^{A}\mid 0\right\}$ crossing and ${\varvec{c}}$ and its two replicas made by $\left\{{C}_{3z}\mid {\varvec{c}}/4\right\}$, a vertical slide mirror $\left\{{\sigma }_{v}^{A}\mid {\varvec{c}}/2\right\}$ and its two replicas, a inversion center. The combinations of other symmetries and inversion center also make the symmetries of the system. The nonsymmorphic symmetries, the screw rotations and slide mirrors provide the possibility of nontrivial NLSM in the materials [32].

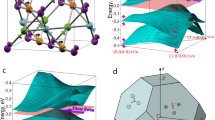
The crystal structure of BaMX₃ is shown in Fig. 2a. These materials are considered as quasi-one-dimensional crystals in which MX₆ octahedrons sharing common surfaces form linear chains lining up along the $z$-axis and arranged into a trigonal lattice in the $x-y$ plane with Ba atoms filling the space between the chains. In Fig. 2b, we also show the evolution of $\mathrm{d}$-orbitals character of M under the crystal fields. The $\mathrm{d}$-orbitals of M are split into a two-fold ${\mathrm{e}}_{\mathrm{g}}$ and a three-fold ${\mathrm{t}}_{2\mathrm{g}}$ manifolds under the crystal field of MX₆ octahedra. The ${C}_{3z}$ symmetry of the system further splits the three-fold ${\mathrm{t}}_{2\mathrm{g}}$ orbitals into a two-fold ${\mathrm{e}}_{\mathrm{g}}^{\mathrm{^{\prime}}}$ orbitals and a single ${\mathrm{a}}_{\mathrm{g}}$ orbital. The Brillouin Zone of BaMX₃ is also plotted in Fig. 2c where the high-symmetry paths of the system are highlighted.

The first-principles calculations of BaMX₃'s band structure without the inclusion of SOC in Fig. 3a verifies that the electronic states near the fermi level attributes to the ${\mathrm{d}}_{z}$-orbitals of M. An interesting fact in this band structure is that on the high-symmetry path $A-L-H$ the energy band is two-fold degenerate. This degeneracy actually extends to the entire high-symmetry plane ${k}_{z}=\uppi$ as one sees the 2D band structure on the ${k}_{z}=\uppi$ plane in Fig. 3b. Away from the ${k}_{z}=\uppi$ plane, for saying on the ${k}_{z}=0.9\uppi$ plane, the degenerated bands start to split. This two-fold degeneracy on the entire high symmetry plane at the BZ boundary is, therefore, named as a node-surface as in Ref. [32].

Fig. 2

a Unit cell of Hexagonal BaMX₃. Large (green), mediate (yellow) and small (brown) spheres denote the Ba, M and X atoms; b Splitting of $\mathrm{d}$-orbitals under the crystal fields. The crystal field of MX₃-octahedron splits the five-fold d orbitals into two-fold ${\mathrm{e}}_{\mathrm{g}}$ and three-fold ${\mathrm{t}}_{2\mathrm{g}}$ orbitals. The crystal field of the hexagonal lattice further splits the three-folded ${\mathrm{t}}_{2\mathrm{g}}$ orbitals into two-fold ${\mathrm{e}}_{\mathrm{g}}^{\mathrm{^{\prime}}}$ and ${\mathrm{a}}_{\mathrm{g}}$ orbitals. ${\mathrm{a}}_{\mathrm{g}}$ has the character of ${\mathrm{d}}_{{3z}^{3}-{r}^{2}}$ orbital shown in the inset; c Brillouin zone of MX₃. Shadowed planes are the projected 2D Brillouin zone to different crystal facets. Reproduced with permission from Ref. [32]. Copyright 2016, APS

The symmetry argument of this two-fold degeneracy in the spinless case on the ${k}_{z}=\uppi$ plane for BaMX₃, is given as follows. The time-reversal symmetry ${T}$, inversion symmetry ${P}$ and nonsymmorphic screw rotation ${G}_{z}=\left\{{C}_{2z}\mid {\varvec{c}}/2\right\}$ together give BaMX₃ two compound symmetries, $S=PT$ and $C=P{G}_{z}$.$S$ is preserved at any ${\varvec{k}}$-point of BZ, while $S$ is respected at the ${k}_{z}=0$ and ${k}_{z}=\uppi /c$ planes. Applying $C$ twice on the lattice can bring the system back to its starting point, one has ${C}^{2}=1$ and the corresponding eigenvalues of $S$ are $\pm 1$, which can be used to label the eigenstates of the Hamiltonian. Due to the anti-commutation of $C$ and $S$ of Eq. (9) on ${k}_{z}=\uppi$ plane, the action of $C$ switches each eigen-state to its degenerate partner of opposite $S$-label, ensuring the two-fold degeneracy of energy bands on the entire ${k}_{z}=\uppi /c$ plane as found in Fig. 3b.

When we consider the spin degree of freedom the two-dimensional Hilbert space of the two-band model will be enlarged into a four-dimensional one. The degeneracy of the node-surface on the ${k}_{z}=\uppi$ plane is then lifted by introducing the SOC. Because the SOC of BaVS₃ is minor and the node-surface can still possibly be observed. In BaTaX₃, However, the strong SOC of Ta atom cannot be ignored and the node-surface is not a good approximation anymore to describe the electronic structure around the fermi level for BaTaX₃. Nevertheless, we still find a 1D NL four-fold degeneracy on the three high-symmetry paths $L-A$. In Fig. 4a, we plot the band structure of BaTaS₃ with SOC. One can see the band degeneracy along the high symmetry path $L-H-A$ is lifted while on the path $L-A$ it is maintained. For a more clear demonstration of the band degeneracy on $L-A$ one can inspect this point by comparing the two-dimensional band structure on the ${k}_{z}=\uppi$ plane in Fig. 4b with the one in Fig. 3b.

Fig. 3

Node-surface in BaVS₃ under room-temperature paramagnetic phase with negligible spin–orbit coupling. a Band dispersion of BaVS₃. The orbital nature is represented by circle (red), square (green) and triangle (blue) symbols for the ${\mathrm{d}}_{{3z}^{3}-{r}^{2}}$,${\mathrm{d}}_{{x}^{3}-{y}^{2}}$ and ${\mathrm{d}}_{xy}$ orbitals; b 3D plot of the bands in ${k}_{z}=\uppi /c$ (left) and ${k}_{z}=0.9\uppi /c$ (right) plane; c Fermi-surface of BaVS₃. Dashed lines highlight the contact boundary between two partitions of the Fermi surface around ${ k}_{z}=\uppi /c$. Reproduce with permission from Ref. [32]. Copyright 2016, APS

Fig. 4

Node-lines in BaTaS₃ with strong spin–orbit coupling. a Band structure of BaTaS₃. The orbital characteristic of ag band is highlighted by circle (red) symbols; b 2D plot of the bands in ${k}_{z}=\uppi /c$ plane. The gradually varied colors indicate the splitting of the bands. The darkest lines along $A-L$ paths are node-lines denoted in the bottom contour plot by dashed lines; c Full view of Fermi surface of BaTaS₃. The contact points between the two partitions of the fermi surface around ${k}_{z}=\uppi /c$ are highlighted by solid circles (white). Reproduce with permission from Ref. [32]. Copyright 2016, APS

Fig. 5

a Hexagonal lattice of PbTaSe₂; b BZ of PbTaSe₂; c Bulk band structure of PbTaSe₂; d, e Zoom-in band structure around $H$ without/with the inclusion of SOC; f, g Same as (d, e) but for band structure around $K$; The bands in e, g correspond to those in the red rectangular boxes in (c); Mirror eigenvalues of bands around fermi level are labeled in (e, g). Reproduced with permission from Ref. [33]. Copyright 2016, Nature

Fig. 6

a The NL band structure of TlTaSe₂ with various SOC; b The energy difference between the two bands b₂ and b₃ as a function of SOC, showing the changing of the number of NLs at varying SOC; c The spin polarization ofsurface bands of Tl-terminated surface. Reproduced with permission from Ref. [34]. Copyright 2016, APS

Fig. 7

a The crystal structure of centrosymmetric PbTaS₂ with SOC; b Calculated band structure of PbTaS₂ without SOC; c Zoom-in band structures around $K$ without/with SOC. The colour code shows the orbital components; d Three-dimensional band structure on ${k}_{x}-{k}_{y}$ plane of ${k}_{z}=0$. The NL2 is highlighted by the light blue; e Surface band structure of PbTaS₂ along $M-K-\varGamma$. The surface states are pointed by white arrows; f The isoenergic contour shows the NL and SS states, which can be seen clearly in g. Reproduce with permission from Ref. [35]. Copyright 2020, ACS

Fig. 8

a Rock-salt crystal structure of ZrCo₂Sn with Fm $\overline{3 }$ m space group; b Brillouin zone (BZ) of the rock-salt structure; c The NL in the x–y plane has a large dispersion; d Three NLs in three planes in three-dimensional k-space; e Dispersion of NL in the ${k}_{x}-{k}_{y}$ plane; f Intersecting of three NLs around $\varGamma$. Reproduced with permission from Ref. [36]. Copyright 2016, APS

Fig. 9

a Conventional and b primitive unit cell of crystal structure for LiV₂O₄; c Corresponding Brillouin zone with the considered high-symmetry paths. d The electronic band structures and projected density of states (PDOS) of LiV₂O₄ compound in the absence of SOC. The upper half is for the spin-up ones, which is metallic showing crossed bands around Fermi level and red downner half is for the spin-down channel, which has a large insulating band gap of 3.27 eV; e and f are schematic illustrations of the NL1 and NL2 in the Brillouin zone, respectively. g The schematic illustrations of the nodal chain in LiV₂O₄;. The green and blue lines in e and f denote NL1 and NL2, respectively. Reproduced with permission from Ref. [37]. Copyright 2020, APS

The symmetry protection of the four-fold degenerate node-lines in presence of SOC is given as follows. In the spinful case, time-reversal operator is expressed as $T=i{s}_{y}K$ and thus ${T}^{2}=-1$. One then finds that the square of $M=P{G}_{z}$ becomes ${M}^{2}=-1$ at its invariant plane ${k}_{z}=\uppi /c$. Thus the eigenstates of Bloch Hamiltonian are labeled by the eigenvalues $\pm i$ of $M$,$M\left|{\phi }^{\pm }({\varvec{k}})\right.\rangle =\pm i\left|{\phi }^{\pm }({\varvec{k}})\right.\rangle$. Unlike in the spinless case, in the spinful case applying $S=PT$ on $\left|{\phi }^{\pm }({\varvec{k}})\right.\rangle$ translates it to a partner state of the same $M$-eigenvalue, and extra symmetry is needed to provide the protection of NLs. In BaMX₃, the mirror plane ${M}_{x}$ which takes an anti-commutation relation with $M$ on the intersection line of its invariant plane ${k}_{x}=0$ and the invariant plane of $M$,${k}_{z}=\uppi /c$ plays this role of protection. Because of $\left\{{M}_{x},M\right\}=0$, applying ${M}_{x}$ on $\left|{\phi }^{\pm }({\varvec{k}})\right.\rangle$ translates it to a partner state with an opposite $M$-eigenvalue, which enforces the existence of a four-fold degenerate NLs.

4 Spinful node line semi-metal in Pb(Tl)TaX₂

PbTaSe₂ is a layered, non-centrosymmetric compound in space group P $\overline{6 }$ m2 (No.187), lacking an inversion symmetry. The crystal of PbTaSe₂ consists of one hexagonal Pb atom layer, one Ta atom layer and Two Se atom layers stacking along the z-direction alternatively, as shown in Fig. 5a. The Ta and Se layers are more tightly packed and can be considered a primary layer. The cutting plane where the Ta atom layer sits is a mirror plane of the system that reflects ${k}_{z}$ to −${k}_{z}$, providing the essential need for protecting the NLs.

Bian et al. [33] report, based on a systematic theoretical study and a detailed experimental characterization, the existence of topological NL states in PbTaSe₂ with strong SOC [33]. Figure 5c shows the bulk band structures of PbTaSe₂ with the inclusion of SOC. Crossings and anti-crossings of bulk bands around $K$ and $H$ are highlighted by dashed boxes. The zoom-in band structures around $K$ and $H$ are also shown in Fig. 5e, g, respectively. By comparing the band structure with SOC with the one without SOC (see in Fig. 5d, f), we find SOC lifts the two-fold degeneracy of the band structure. For the states on the ${k}_{z}=0$ and ${k}_{z}=\uppi$, each band is labeled by a mirror eigenvalue, which is either “$+$” or “$-$”. Two bands with opposite eigenvalues will cross each other, while they anti-cross when they have the same eigenvalues. From Fig. 5e and g we can easily find there are two NLs around $H$ and one NL around $K$. These NLs are robust even under the strong strength of SOC of Ta atoms. The Angle-Resolved Photoemisson Specroscopy (APRES) spectrum reproduced the first-principles band structure very well. Even topological surface states connecting the NLs have also been detected in the APRES measurement, supporting the nontrivial NLSM state of PbTaSe₂.

Since PbTaSe₂ are non-centrosymmetric, there is no Kramers-degeneracy in their bands structure. Bian et al. [34] theoretically proposed the existence of topological spinful NL fermions in TlTaSe₂, an isostructural material of PbTaSe₂, given by the strong spin–orbit coupling and protected by the mirror reflection symmetry. Detailed DFT calculation with a fine tuning of the SOC strength even reveals an electronic transition from a two NLSM state to a single NLSM state in this compound, shown in Fig. 6a, b. An even more interesting property of TlTaSe₂ is found for their topological surface state on the Tl-terminated surface that these surface bands are spin polarized, resembling the spin-momentum locked surface states on a topological insulator surface, shown in Fig. 6c.

It is found recently that quite different from noncentrosymmetric PbTaSe₂, PbTaS₂ is a centrosymmetric crystal with space group P6₃/mmc [35]. The unit cell PbTaS₂ consists of alternatively stacked TaS₂ and Pb atom layers. Two TaS₂ transfer inversely with respect to a Pb atom in between them, shown in Fig. 7a. Figure 7b presents the band structure of PbTaS₂ without SOC, showing several bands crossing the Fermi level. The zoom-in figure of the band crossing around $K$ without SOC shown in Fig. 7c also indicates there exist six band crossing points along $M-K$ and $K-\varGamma$ directions. These NLs are protected by compound symmetry $S=PT$ of the system. When SOC is turned on, the bands split into two branches with opposite spin orientations and the NLs are gapped out, as indicated by the zoom-in figure of band structure around $K$ with SOC. The NLs and band inversion also result in the characteristic “drumhead-like” surface state, which have been shown in Fig. 7e–g.

5 Node line half metal in pipeline MM’O₄

Recent progress of NLSM is that such concept of node line permissions has been extended to half-metallic state in which the spin degree of freedom is completely quenched [36,37,38,39,40,41,42,43]. Wang et al. [36] predict a new family of Weyl semimetals in the Co-based Heusler materials XCo₂Z (X $=$ IVB or VB; Z $=$ IVA or IIIA). The authors focus on the representative compound ZrCo₂Sn and calculate the spinful band structures and density of states (see in Fig. 8c, d), which suggests that this material is in a half-metallic state. Such half-metallic signature has also been experimentally verified in another partner compound TiCo₂Sn [44]. From the spin-polarized band structure in Fig. 8c, one observes that two-band crossing occurs along $\varGamma -X$, $\varGamma -W$, and $\varGamma -K$ in the majority spin. The crossing bands are further found to belong to different mirror eigenvalues with respect to the mirror symmetry ${M}_{z}$, giving rise to an NL in the ${k}_{x}-{k}_{y}$ plane. Due to the cubic symmetry of the material, two NLs on the ${k}_{x}-{k}_{z}$ and ${k}_{y}-{k}_{z}$ plane are also found in addition to the NL in the ${k}_{x}-{k}_{y}$ plane. The three NLs intersect at six points on the three-axis of the k-space and form a cage-like structure centering at the $\varGamma$. When the SOC is turned on, the spin degree of freedom will couple with the orbital degree of freedom. When the spins are aligned to [100] direction, the coupling of spin and orbital degree of freedom will break the mirror symmetries ${M}_{x},{M}_{y}$ and ${M}_{z}$ simultaneously, which lifts the degeneracy of the NLs and gives rise to a number of pairs of Weyl point located around the coordinate axis of the momentum space.

Using first-principles calculations and symmetry analysis, Zhang et al. [37] predicted the realization of a fully spin-polarized NL state in another tungsten-related material family called spinel half metals, including LiV₂O₄, VMg₂O₄, FeAl₂O₄, and NiAl₂O₄. Taking LiV₂O₄ (see in Fig. 9a) as an example, the authors show that one spin channel is fully gapped and only the band structures from the other spin channel are present near the Fermi level for the ferromagnetic state. The bands near the Fermi level cross and form two types of NLs, which are protected by the glide mirror symmetries. Remarkably, it is found that the NL join with each other and form a chainlike nodal structure, shown in Fig. 9e–g. The fully spin-polarized bulk NLSM is stable under the variation of electron correlation and lattice strains. The effect of SOC, however, is more complex. When the spin is pointing to the [001] direction, most of the glide mirrors are broken except the one ${G}_{z}=\left\{{m}_{z}|{\varvec{c}}/2\right\}$. As a result, only the NL in the high symmetry plane ${k}_{z}=0$ of ${G}_{z}$ remains and all other NLs are gapped out by the SOC. Therefore, the spinel half metals provide an excellent platform through which to investigate fully spin-polarized nodal chain fermions in realistic materials.

6 Outlook

We have reviewed the research of NLSM in tungsten-related materials, however, many interesting progresses have not been included in this mini review. For example, ZrSiS(Se) is considered as an ideal NLSM whose fermi level is mainly consisted of crossing valence and conduction bands without any other trivial band. The research of ZrSiS and its intrinsic NLSM properties is still ongoing and some reviews have already published on this material [45, 46]. It is also of great interest to explore the interplay between the nontrivial topology of NLSM and other effects, including e–e interactions, superconductivity, magnetism, etc. NLSMs Tl(MoS)₆ [47] and TaPbSe₂ [33] have been found to be superconductors at low temperature. Fundamentally fascinating time-reversal-invariant topological superconducting ground state is proposed in these materials. The signature of topological superconductivity such as Majorana fermions is yet to be detected to verify the nontrivial topology of the superconducting ground state. In addition, at the beginning of the exploration of NLSM, topological surface state, i.e., the “drumhead” state, is expected to work as a platform of high transition temperature superconductivity when strong electron correlation is introduced. However, no such signature has been detected yet. With the continuous efforts of theoretical and experimental research, more and more breakthroughs are expected in these research directions.