1 Introduction

Compared with ordinary generators, switched reluctance generators (SRG) have the advantages of simple structure, low cost, high power density and strong working ability. In addition, the double stator motor has high precision, fast response and large acceleration. Under the condition of limited space, the volume and weight of the mechanical system can be greatly reduced. When used as a generator, the two stators can simultaneously output induced voltage, which has a wide application prospects [1,2,3]. Combined with the existing deflectable multi-degree-of-freedom motor, this paper proposes a new deflection double stator switched reluctance generator (DDS-SRG). The unique structural design and flexibility enhance the reliability, fault tolerance and application field. Because of the periodic variation and the serious local saturation of the magnetic circuit in SRG, the non-sinusoidal flux density in the core and nonlinear space vector make magnetic density analysis and iron loss calculation more complicated. Iron loss is one of the important factors affecting the efficiency of generators, so the calculation of core magnetic density and loss of generators is of great significance [4,5,6,7].

In this paper, the magnetic flux analysis method is used to analyze the magnetic flux in the core. In the transient state, the output current, load current and the magnetic density of the stator and rotor are calculated by electromagnetic analysis software. On the basis of this, the ellipse method is used to calculate the core loss of the generator. Finally, the iron loss data is indirectly measured by the experimental platform to verify the accuracy of the calculation scheme.

2 Structure and Control Method of DDS-SRG

2.1 Introduction of Generator Structure

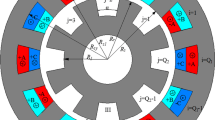
The overall structural model of DDS-SRG is shown in Fig. 1.

Fig. 1
figure 1

Overall structure of DDS-SRG

Full size image

The outer stator of the generator is directly connected to the outer housing, and the inner stator is fixed to the base by the inner stator bracket. A joint bearing is connected between the shaft and the inner stator bracket, so that the rotor can be deflected within a certain range.

In Fig. 2a, b show the stator structure and the rotor structure of DDS-SRG, respectively. From the Fig. 2, the stator structure consists of two parts: the inner stator and the outer stator. The outer teeth of the inner stator and the outside rotor are convex spherical, and the inner teeth of the outer stator and the inside rotor are concave spherical. The teeth of stator and rotor have 12 and 8, respectively, and the rotor teeth staggered. The diaphragm is located between the inside and outside of the rotor, which separates the inner and outer magnetic circuits of the rotor and does not interfere with each other. Therefore, the whole generator can be regarded as an outer rotor generator (inner generator) consisting of inner stator and inner rotor, and an inner rotor generator (outer generator) comprising of outer stator and outer rotor. The main structural parameters of the generator are shown in Table 1.

Fig. 2
figure 2

Internal structure of the generator

Full size image
Table 1 Structural parameters of generator
Full size table

2.2 Winding Connection Mode of Generator

The winding connection mode of the generator is shown in Fig. 3. The outer and inner stators are each divided into three phases, respectively, namely A B C and D E F. In the Fig. 3, the blue arrow indicates the current direction inside the winding. It can be seen that the current between the adjacent two-phase windings is opposite in direction and different in polarity. The winding connection of the inner stator and the outer stator is NSNS…NSNS distribution.

Fig. 3
figure 3

The winding connection mode of the generator

Full size image

3 Flux Waveform of DDS-SRG

3.1 Basic Frequency of Magnetic Flux Density of Generator Core

According to the structural characteristics of the generator, the switching frequency of the inner stator winding and the outer stator winding are the same, so the basic frequency of the flux density of the two cores is the same. When the outer stator windings A, B and C (or inner stator windings D, E and F) complete a switching period at one time, the rotor rotates a pole distance, so the flux frequency of the outer stator (inner stator) pole is [8, 9]:

$$f_{s} = \frac{1}{{T_{s} }} = \frac{{nZ_{r} }}{60} = \frac{{\omega Z_{r} }}{2\pi }$$
(1)

where, fs represents the fundamental frequency of flux density of the outer stator (inner stator), Ts is a switching period of the electrified winding, Zr is the number of teeth poles on the outside or inside of the rotor, n is the rotational speed of the rotor driven by the prime mover, and ω is the angular speed of the rotor. The expression of the basic frequency of the flux density of the rotor core is:

$$f_{r} = \frac{Kn}{60} = \frac{K\omega }{2\pi }$$
(2)

where, K represents the number of cycles of the magnetic field polarity distribution of the outer stator (inner stator) (1 ≤ K ≤ Zs/2). Since the outer stator and the inner stator windings are connected by NSNS…NSNS, the value of K is 6 [10,11,12]. Zs is the teeth number of the outer stator or the inner stator. The stator magnetic flux frequency is related to the rotor speed and the number of rotor teeth. In the core of the rotor, the basic frequency of magnetic density is related not only to the speed, but also to the connection mode of the windings.

3.2 Analytical Calculation of Generator Flux

Because the internal electromagnetic relationship and operation characteristics of the generator are complex and changeable, the linearization of its mathematical model can facilitate the analysis and calculation of various physical variables. The relationship between phase winding flux ψ and rotor position angle θ in the linear model of generator is shown in Fig. 4. The rotor speed is 300 r/min. In the internal generator, the turn-on angle and turn-off angle of the switch are 17.5° and 32.5°, respectively. In the external generator, the switching-on angle is 8° and the switching-off angle is 23°, so that DDS-SRG operates in a low-speed power generation state.

Fig. 4
figure 4

Diagram of phase winding flux linkage of generator

Full size image

Within an inductance period, the expression of winding flux linkage is:

$$\psi_{\text{z}} = \left\{ {\begin{array}{*{20}l} {\frac{{U_{\text{s}} }}{{\omega_{\text{r}} }}(\theta - \theta_{\text{on}} ),} \hfill &\quad {(\theta_{\text{on}} \le \theta \le \theta_{\text{off}} )} \hfill \\ {\frac{{U_{\text{s}} }}{{\omega_{\text{r}} }}( 2\theta_{\text{off}} - \theta_{\text{on}} - \theta ),} \hfill &\quad {(\theta_{\text{off}} \le \theta <le 2\theta_{\text{off}} - \theta_{\text{on}} )} \hfill \\ {0,} \hfill &\quad {({\text{Other}}{\mkern 1mu} {\text{location}})} \hfill \\ \end{array} } \right.$$
(3)

where, ψz represents the phase winding flux linkage of the generator, and z represents the A to F six phases. Us is the excitation voltage of the outer stator winding (inner stator winding) of the generator, ωr is the angular velocity of the rotor, and θ represents the rotor position angle. θon and θoff are the position angles of the rotor corresponding to the moment when the power supply of the stator winding is turned on and is turned off, respectively [13].

As shown in Fig. 5, 1, 2, 3, 1′, 2′, and 3′ represent the yoke between the two teeth of the outer stator. 4, 5, 4′, and 5′ is the teeth on the outer side of the rotor. 6, 7, 6′, and 7′ represent the yoke between the two teeth on the outside of the rotor. 8, 9, 8′, and 9′ represent the yoke between the two teeth on the inside of the rotor. 10, 11, 10′ and 11′ represent the teeth on the inside of the rotor. 13, 14, 15, 13′, 14′ and 15′ represent the yoke between the two teeth of the inner stator.

Fig. 5
figure 5

Part flux structure diagram of generator

Full size image

Since the working principle of the internal generator and the external generator is the same, only the conduction time of the internal generator is 7.5° behind the external generator, and the excitation voltage is small, so the generator composed of the outer stator and the outer side of the rotor is the main analysis object. The variation law of the three-phase magnetic flux of A, B and C is analyzed under the ideal linear model. ψA, ψB and ψC are the flux linkages of the each phase windings, ФspA, ФspB and ФspC are the magnetic fluxes of the each phase windings, and Nph is the number of windings for each phase. It is prescribed that the generator rotor rotates counterclockwise to the positive direction, and the direction from the inner diameter to the outer diameter is the positive direction of the magnetic flux in the stator and the rotor teeth. The counterclockwise direction is the positive direction of the magnetic flux in the stator and the rotor yoke. Excitation in the order of A–B–C–A, the magnetic flux expression of the teeth of the outer stator can be obtained as [14,15,16]:

$$\left[ {\begin{array}{*{20}c} {\varPhi_{{\text{spA}}} } \\ {\varPhi_{{\text{spB}}} } \\ {\varPhi_{{\text{spC}}} } \\ \end{array} } \right] = - \left[ {\begin{array}{*{20}c} {\varPhi_{{\text{spA'}}} } \\ {\varPhi_{{\text{spB'}}} } \\ {\varPhi_{{\text{spC'}}} } \\ \end{array} } \right] = \frac{1}{{N_{{\text{ph}}} }}\left[ {\begin{array}{*{20}c} 1 &\quad 0 &\quad 0 \\ 0 &\quad { - 1} &\quad 0 \\ 0 &\quad 0 &\quad 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\varPsi_{\text{A}} } \\ {\varPsi_{\text{B}} } \\ {\varPsi_{\text{C}} } \\ \end{array} } \right]$$
(4)

The expression of the flux at the yoke of the outer stator is:

$$\left[ {\begin{array}{*{20}c} {\varPhi_{{\text{sc1}}} } \\ {\varPhi_{{\text{sc} 2}} } \\ {\varPhi_{{\text{sc} 3}} } \\ \end{array} } \right] = - \left[ {\begin{array}{*{20}c} {\varPhi_{{\text{sc1'}}} } \\ {\varPhi_{{\text{sc} 2 '}} } \\ {\varPhi_{{\text{sc} 3 '}} } \\ \end{array} } \right] = \frac{1}{2}\left[ {\begin{array}{*{20}c} 1 &\quad { - 1} &\quad 1 \\ 1 &\quad { - 1} &\quad { - 1} \\ 1 &\quad 1 &\quad { - 1} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\varPhi_{{\text{spA}}} } \\ {\varPhi_{{\text{spB}}} } \\ {\varPhi_{{\text{spC}}} } \\ \end{array} } \right]$$
(5)

The magnetic flux expression of the outer tooth of the rotor is:

$$\varPhi_{{\text{rp1}}} = - \varPhi_{{\text{rp1'}}} = \left[ {\begin{array}{*{20}c} 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} 1 &\quad 0 &\quad { - 1} \\ 0 &\quad 1 &\quad 0 \\ { - 1} &\quad 0 &\quad 1 \\ 0 &\quad { - 1} &\quad 0 \\ 1 &\quad 0 &\quad { - 1} \\ 0 &\quad 1 &\quad 0 \\ { - 1} &\quad 0 &\quad 1 \\ 0 &\quad { - 1} &\quad 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\varPhi_{{\text{spA}}} } \\ {\varPhi_{{\text{spB}}} } \\ {\varPhi_{{\text{spC}}} } \\ \end{array} } \right]$$
(6)
$$\varPhi_{{\text{rp} 2}} = - \varPhi_{{\text{rp} 2\text{'}}} = \left[ {\begin{array}{*{20}c} 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} 0 &\quad 1 &\quad 0\\ { - 1} &\quad 0 &\quad 1\\ 0 &\quad { - 1} &\quad 0\\ 1 &\quad 0 &\quad { - 1} \\ 0 &\quad 1 &\quad 0 \\ { - 1} &\quad 0 &\quad 1 \\ 0 &\quad { - 1} \quad 0 \\ 1 &\quad 0 &\quad { - 1} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\varPhi_{{\text{spA}}} } \\ {\varPhi_{{\text{spB}}} } \\ {\varPhi_{{\text{spC}}} } \\ \end{array} } \right]$$
(7)

The magnetic flux expression of the outer yoke of the rotor is:

$$\varPhi_{{\text{cr1}}} = - \varPhi_{{\text{cr1'}}} = \left[ {\begin{array}{*{20}c} 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} { - 1} &\quad 1 &\quad 1 \\ { - 1} &\quad { - 1} &\quad 1 \\ 1 &\quad { - 1} &\quad { - 1} \\ 1 &\quad 1 &\quad { - 1} \\ { - 1} &\quad 1 &\quad 1 \\ { - 1} &\quad { - 1} &\quad 1 \\ 1 &\quad { - 1} &\quad { - 1} \\ 1 &\quad 1 &\quad { - 1} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\varPhi_{{\text{spA}}} } \\ {\varPhi_{{\text{spB}}} } \\ {\varPhi_{{\text{spC}}} } \\ \end{array} } \right]$$
(8)
$$\varPhi_{{\text{cr2}}} = - \varPhi_{{\text{cr2'}}} = \left[ {\begin{array}{*{20}c} 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} { - 1} &\quad { - 1} &\quad 1 \\ 1 &\quad { - 1} &\quad { - 1} \\ 1 &\quad 1 &\quad { - 1} \\ { - 1} &\quad 1 &\quad 1 \\ { - 1} &\quad { - 1} &\quad 1 \\ 1 &\quad { - 1} &\quad { - 1} \\ 1 &\quad 1 &\quad { - 1} \\ { - 1} &\quad 1 &\quad 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\varPhi_{{\text{spA}}} } \\ {\varPhi_{{\text{spB}}} } \\ {\varPhi_{{\text{spC}}} } \\ \end{array} } \right]$$
(9)

The Фsc1, Фsc2, Фsc3, Фsc1′, Фsc2′, Фsc3′ in (5)–(9) represent the magnetic fluxes at the outer stator yokes 1, 2, 3, 1′, 2′, 3′, respectively in Fig. 5. Фrp1, Фrp1′, Фrp2, Фrp2′ represent the magnetic fluxes at the outer tooth pole 4, 4′, 5, 5′ of the rotor, respectively and Фcr1, Фcr1′, Фcr2, Фcr2′ correspond to the magnetic flux of the outer yoke of the rotor, respectively. Each row in the flux matrix corresponds to the external stator three-phase winding wheel circulating once, that is, one switching cycle. Each column corresponds to the magnetic flux pulse of the tooth or yoke when the phase winding is energized. Therefore, the phase difference between the lines and the columns is one switching period, and one power supply period, respectively.

According to (4)–(9), the magnetic flux waveforms of the generator stator and the rotor tooth portion and the yoke portion are obtained, as shown in Fig. 6. Since the structure of the generator is completely symmetrical, the rotor rotating one full cycle is two complete cycles, so the magnetic flux waveform of 0°–180° is selected for analysis. Figure 6a, b are the magnetic flux waveforms of the yoke portion of the stator tooth portion. It is apparent that there are four complete small periods in the range of 0°–180°, each of which is 45°. The magnetic flux waveform of the rotor tooth portion and the yoke portion is shown in Fig. 6c, d, which are divided into three small periods with 60°. The magnetic flux waveforms on the inner stator and the inside of the rotor are substantially identical to that on the outer stator and the outside of the rotor. The internal motor has a flux amplitude of 0.025 Wb and the external motor has a flux amplitude of 0.2 Wb. This corresponds to the excitation voltage of the inner motor being 1/8 of the external motor excitation voltage. The conduction time of the driving circuit connected to the inner stator winding sequentially lags the outer stator winding by 7.5°, which is consistent with the angle of the internal and external motor magnetic flux waveforms in Fig. 6.

Fig. 6
figure 6

Flux waveform of generator stator and rotor

Full size image

4 Analysis of Finite Element Simulation Results

The core loss of DDS-SRG is closely related to the internal magnetic field of the motor. The magnitude and frequency of the core magnetic density have a decisive influence on the iron loss. In order to make a better comparison between the finite element method and the analytical method, the electromagnetic simulation software is used for the overall modeling analysis of DDS-SRG itself and the power circuit.

4.1 Macroscopic Magnetic Field Analysis

According to the structural characteristics of the generator, the connection modes of the inner stator winding and the outer stator winding are all reverse parallel, and the magnetic pole distribution mode is a symmetrical magnetic field of NSNS…NSNS (N pole and S pole alternate connection). In the case of rated load, the aligned, intermediate and misaligned position of the rotor are analyzed. The alignment position indicates the timing at which the rotor tooth center line is aligned with the stator tooth center line, the middle position indicates the moment when the rotor tooth pole partially overlaps the stator tooth pole, and the misalignment position indicates the rotor tooth center line coincides with the stator slot center line [17]. Since the inner stator and the outer stator are the same, only the outer stator is analyzed. Figure 7 shows the distribution of the magnetic lines of the rotor at different positions.

Fig. 7
figure 7

Magnetic field line diagram of generator at different positions

Full size image

According to the distribution of the magnetic field lines of the generator in Fig. 7, it generates a corresponding current to form a magnetic field when a phase winding is turned on. In the aligned position, almost most of the magnetic lines of force reach the outer teeth of the rotor from the outer stator teeth and pass through the air gap. Since the magnetic resistance between the magnetic poles is small relative to the air gap, the main magnetic flux is the largest. The intermediate position shown in Fig. 7b indicates the distribution of magnetic lines of force when the rotor reaches the misaligned position from the aligned position. Only a small part of the magnetic lines pass through the air gap and reaches the yoke of the outer rotor directly from the tooth pole. In the unaligned position, the magnetic lines of force pass through the two poles very rarely, indicating that the air gap reluctance is relatively small at this position.

4.2 Microscopic Magnetic Density Analysis

The DDS-SRG model is used for the instantaneous simulation of the circuit-magnetic field coupling, and the waveforms of the magnetic flux density of the stator and rotor core with time are obtained. The working principle of SRG determines that the magnetic density of different parts of the core changing with the rotor position. That is, the magnetic density of each unit is a space vector whose magnitude and direction change with time (rotor position). Expression is:

$$\vec{B}_{\text{t}} = B_{{r{\text{t}}}} \vec{e}_{\text{r}} + B_{{\theta {\text{t}}}} \vec{e}_{\theta }$$
(10)

where \(\vec{B}_{t}\) represents the composite vector of the magnetic density of each unit. Brt represents the magnitude of the radial component of the magnetic density, and Bθt represents the magnitude of the tangential component of the magnetic density. \({\vec{\text{e}}}_{\text{r}}\) represents a radial unit vector, and \({\vec{\text{e}}}\)θ represents a tangential unit vector. In order to study the specific situation of the magnetic field changes in the core, some representative points in the core were selected as the key analysis objects. Figure 8 shows the distribution of the points in the outer stator core and the outside core of the rotor. The three points a, b and c in Fig. 8, respectively represent the tip of the tooth, the middle of the tooth and the root of the tooth in the outside stator core. The three points d, e, and f represent the yoke between the AB phases, the yoke between the BC phases and the yoke between the CA phases of the outer stator. In the outer core of the rotor, the four points a′, b′, c′ and d′, respectively represent the tip of the tooth, the middle of the tooth, the root of the tooth and the yoke.

Fig. 8
figure 8

Unit node distribution diagram of generator core

Full size image

In the transient state, the synthetic magnetic density and magnetic density components of each unit node in Fig. 8 are simulated. The rotor position angle is used instead of time as the abscissa, and the amplitude of the magnetic density component is the ordinate. The direction of each physical quantity is consistent with the magnetic circuit analysis method. When the rotor is rotated by 180°, the waveform of magnetic flux density varying with the position of the rotor at each point is obtained.

The simulation waveform of magnetic flux density at each point of the outer stator tooth pole of the generator is shown in Fig. 9. The simulation results show that the radial component Br of magnetic flux density is much larger than the tangential component Bθ. In the radial magnetic density component of the tooth pole, the maximum amplitude of the point at the middle of the tooth can reach 2.1 T, while the point at the tip and root of the tooth is relatively small about 1.5 T. Figure 9d shows the synthetic magnetic density in the teeth of the three phases A, B, and C. The amplitudes are basically the same about 1.3 T, the frequency of change is the same, and the difference is only 15° in phase.

Fig. 9
figure 9

Magnetic density waveform of generator’s outer stator teeth

Full size image

The yoke magnetic density waveform of the generator outer stator is shown in Fig. 10. From Fig. 10a, there is almost no radial component Br in the yoke magnetic density between AB phases of the outer stator. The tangential component Bθ of the magnetic density is near 1.3 T, and the rotor angle corresponding to a period is 45°, in which the positive direction is 2/3 of the magnetic density period and the negative direction is 1/3. The waveforms of the tangential components of the magnetic density of the outer stator yoke BC and the yoke CA are shown in Fig. 10b. Combining with Fig. 10a, it is found that the waveform shape and amplitude of the magnetic oscillating component at the three element nodes are basically the same, which is consistent with the tooth pole part, except that the phase difference is 15° in turn, and the direction of the yoke BC is opposite to that of the yoke AB and CA, due to the connection of the outer stator using NSNS…NSNS.

Fig. 10
figure 10

Magnetic density waveform of generator’s outer stator yoke

Full size image

It can be seen from Fig. 11 that the radial magnetic density component Br is larger in the tooth pole outside the rotor, while the tangential magnetic density component Bθ is larger in the yoke. According to Fig. 11a–c, it can be concluded that the period of each element node in the tooth pole is 60°, the change frequency is the same, and the magnetic density is in positive and negative staggered distribution, which is also determined by the NSNS…NSNS of the outer stator windings. When the rotor rotates at 60°, the magnetic polarity of the stator winding corresponding to the outer tooth pole of the rotor is the same, but the direction changes.

Fig. 11
figure 11

Magnetic density waveform of the outer tooth pole and yoke of the rotor

Full size image

The results of magnetic density analysis by finite element method are shown in Figs. 9, 10 and 11. Compared with the flux waveform Fig. 6 analyzed by the previous analytical method, it can be found that the amplitudes of the two methods are different, which is determined by the number of turns of each phase winding and the unit magnetic flux area. However, the waveform change trend is basically the same, and the same as the period, which verifies the availability of the analytical method.

4.3 Air Gap Magnetic Density Analysis

Since the generator is a double stator structure, there is an air gap inside and outside the rotor. Taking the inner air gap of the rotor as an example, the analysis is performed under the condition of the generator rotating. Considering the special structure of the generator and the distribution of the air gap magnetic field, the air gap magnetic field model is established by the spherical coordinate system shown in Fig. 12, and the P point is any point in the magnetic field outside the rotor air gap. Figure 13 is a 3D distribution diagram of the outer air gap magnetic field magnetic density of the generator in the spherical coordinate system. Figure 13a is the distribution of the magnetic flux density B of the external air gap magnetic field along the spatial angle φ, θ. In the spherical coordinate system, the r, φ, and θ of external air gap magnetic field magnetic density are, respectively shown in the parts (b), (c) and (d) of Fig. 13.

Fig. 12
figure 12

Angle definition diagram

Full size image
Fig. 13
figure 13

Three-dimensional distribution of inner air gap magnetic field magnetic vector of generator rotation

Full size image

As shown in Fig. 13a, the φ ranges from 0° to 360°, corresponding to one revolution of the generator. Under the influence of the φ, the changing period of B is 180°, and the maximum value appears near φ = 40° and φ = 220°. It corresponds to the position where the generator rotor tooth is aligned with the inner stator tooth pole in one cycle. At this time, the magnetic resistance is the smallest and the magnetic density is the largest with the maximum value 0.7 T. Under the influence of the θ, the changing period of the air gap magnetic density B is 60°. During a change period, the curve of B is rectangular, corresponding to the magnetic field lines emanating from the N pole and flowing to the S poles on the adjacent sides of the same phase. As shown in Fig. 13b, the change in the radial magnetic density Br in the θ direction has the same distribution tendency as the magnetic density B, but the amplitude is slightly smaller, which is 0.5 T. The changing period of the radial magnetic density Br is 180° under the influence of φ, and two peaks appear in one period, which are around 30° and 120°. Figure 13c shows that the amplitude of the air gap magnetic density component Bφ is small overall, which is 0.1 T, and the distribution trend is not obvious. Figure 13d shows that the change in the air gap magnetic density component Bθ in the φ direction is the same as Br. It has a rectangular wave in the range of 0°–60° in the θ direction, and the amplitude is 0.35 T. The amplitude of Bθ in the range of 0°–60° is gradually reduced from 0.15 to 0 T. It can be seen that the air gap magnetic field of the rotor inside is mainly composed of the radial component Br and the θ direction of component Bθ when the generator is in the rotation state.

5 Iron Loss Calculation of The Generator

5.1 Non-sinusoidal Magnetic Field Core Loss Calculation

The non-sinusoidal and non-linear core flux density of SRG makes the calculation of core loss more complicated [18,19,20,21]. At present, the theory of iron core loss separation proposed by Bertotti et al. is commonly used in engineering. That is, the iron loss mainly has three parts: eddy current loss Pe, hysteresis loss Ph and residual loss Pc. In the region of low frequency medium magnetic field and strong magnetic field, iron loss is mainly expressed as Pe and Ph. The specific expressions are as follows:

$$P_{{\text{Fe}}} = P_{\text{e}} + P_{\text{h}} + P_{\text{c}}$$
(11)

where, PFe represents iron loss per unit volume, Pe and Ph are eddy current loss and hysteresis loss per unit volume, respectively, and Pc is residual loss per unit volume. When calculating the iron loss, the residual loss Pc is generally ignored. If the core is in a sinusoidal magnetic field, the formula for calculating iron loss is as follows:

$$P_{{F{\text{e}}}} = P_{\text{e}} + P_{\text{h}} = C_{\text{e}} f^{2} B_{\text{m}} + C_{\text{h}} fB_{\text{m}}^{\text{n}}$$
(12)

where, Ce and Ch are eddy current loss coefficients and hysteresis loss coefficients, which are related to the properties of core materials. f is the sine flux frequency, and Bm is the average flux density. When Bm < 1, n takes 1.6, and when Bm > 1, n takes 2.

However, the magnetic field in most electromagnetic devices is not sinusoidal. In this case, the influence of harmonics on the core loss should be considered. Due to the nonlinearity of the ferromagnetic material, the calculation of the core loss does not satisfy the superposition principle, and that is, the core loss generated by the total magnetic density is not equal to the sum of the fundamental wave generated by the magnetic dense Fourier decomposition and the core loss generated by a series of harmonics. Therefore, the calculation of the core loss of a non-sinusoidal magnetic field is very difficult. Lavers et al. proposed in 1976 to consider the eddy current loss correction coefficient Ke and the hysteresis loss correction coefficient Kh of the laminated core in consideration of harmonics to correct the iron loss calculation formula (12), which can analyze the eddy current loss of non-sinusoidal flux. The specific expressions of Ke and Kh are as shown in Eqs. (13) and (14), respectively:

$$K_{e} = \left( {\frac{{B_{1} }}{{B_{p} }}} \right)^{2} \sum\limits_{i = 1}^{n} {\left( {\frac{{iB_{i} }}{{B_{p} }}} \right)^{2} }$$
(13)
$$K_{h} = 1 + \frac{k}{{B_{p} }}\sum\limits_{i = 1}^{N} {\nabla B_{\text{i}} }$$
(14)

where, Bp is the peak of magnetic density, B1 is the amplitude of the fundamental magnetic density, i is the harmonic order, n is the highest harmonic order counted, k is a constant (between 0.6 and 0.7), and N is magnetic density. The number of pulsations of the waveform in one cycle, ∆Bi is the pulsating peak-to-peak value of the ith harmonic magnetic-density waveform.

When calculating the core loss of a non-sinusoidal magnetic field, the Fourier decomposition of the magnetically dense waveform is first performed, and the iron loss value generated by each harmonic is calculated by the fundamental wave and each harmonic according to the formula (12). The correction yields an estimate of the core loss under a non-sinusoidal magnetic field, as shown in Eq. (15):

$$P_{Fe} = K_{e} C_{e} f^{2} \sum\limits_{k = 1}^{n} {k^{2} B_{m}^{2} + } K_{h} C_{h} f\sum\limits_{k = 1}^{n} {kB_{m}^{a} }$$
(15)

5.2 Ellipse Method

According to the previous analysis, the magnetic density waveforms of each unit in the generator core are obtained. In this paper, the ellipse method is selected to calculate the core loss of the generator, which is solved by the orthogonal equivalent theory of core loss and the core loss separation theory. The orthogonal equivalent theory of core loss refers to the fact that the magnetic field of any unit in the stator and rotor core of a generator can be decomposed into two orthogonal alternating magnetic fields, and the hysteresis loss and eddy current loss can be calculated, respectively. The magnetic field in the core of a rotating motor can be divided into alternating and rotating magnetic field, where the magnetic density amplitude changes and the direction remains unchanged is alternating magnetic field. The magnetic density amplitude is constant, and the direction changes is a rotating magnetic field.

The elliptical magnetic field at point A of the tooth tip of the external stator is shown in Fig. 14a. The radial magnetic density component Br of the point is in the longitudinal coordinate, the tangential magnetic density component Bθ is in the abscissal coordinate, and the vector from the coordinate origin to a point in Fig. 14a is the composite magnetic density vector. It can be seen that the direction and amplitude of the composite magnetic density of the outer stator tip have changed, so there are alternating magnetic field and rotating magnetic field in the core magnetic field at the same time. Figure 14b is an elliptical magnetic field formed by the 1, 2, 3, and 4th harmonic magnetic components of the point after the magnetic dense Fourier decomposition, in which the long and short axis magnetic density is, respectively Bkmax and Bkmin.

Fig. 14
figure 14

Elliptical magnetic field diagram

Full size image

5.3 Core Loss Analysis Results

Figure 15 is the amplitude of each harmonic of the radial magnetic density component Br and the tangential magnetic density component Bθ of point A.

Fig. 15
figure 15

Magnetic-density harmonic diagram of outer stator tip unit

Full size image

From the above analysis, hysteresis loss and eddy current loss of each element of core can be obtained. According to (11), the expression of calculating iron loss by ellipse method can be obtained as follows:

$$\left\{ {\begin{array}{*{20}c} {P_{{\text{e}}}^{\prime } = C_{{\text{e}}} f^{2} \sum\limits_{{k = 1}}^{m} {k^{2} \left( {B_{{k_{{{\text{max}}}} }}^{2} + B_{{k_{{{\text{min}}}} }}^{2} } \right)} } \\ {P_{{\text{h}}}^{\prime } = C_{{\text{h}}} f\sum\limits_{{k = 1}}^{m} {k\left( {B_{{k_{{{\text{max}}}} }}^{n} + B_{{k_{{{\text{min}}}} }}^{n} } \right)} } \\ \end{array} } \right.$$
(16)

where, Pe′ and Ph′ are, respectively the eddy current loss and hysteresis loss of each unit, f is the flux frequency of stator or rotor, k is the number of harmonics, and m is the highest harmonic number. Bkmax and Bkmin represent the maximum and minimum amplitudes of kth harmonics, respectively. Therefore, the total core loss of the generator is shown in the following formula:

$$P_{{F{\text{e}}}} = \sum\limits_{j = 1}^{N} {(P_{\text{ej}} + P{}_{\text{hj}})} V_{j}$$
(17)

where, N is the total number of generator stator and rotor units, Pej and Phj are the eddy current loss and hysteresis loss of the jth unit, respectively, and Vj represents the volume of the jth unit. The type of silicon steel sheet used in the stator and rotor cores of the generator is DW465-50. The eddy current loss coefficient Ce is 0.0001494 and the hysteresis loss coefficient Ch is 0.0319. The eddy current loss and hysteresis loss of each part of the generator are calculated as shown in Table 2.

Table 2 Core loss under rotation
Full size table

From the Table 2, it can be seen that the different parts of the generator core produce different loss values. Obviously, the iron loss of the outer stator and the outside of the rotor is much greater than that of the inner stator and the inner rotor. Among them, the proportion of stator iron loss relative to the whole core is 53.27%, the iron loss value of teeth is slightly larger than that of yoke, the proportion of rotor is 46.73%, and the iron loss value of teeth is slightly smaller than that of yoke, contrary to that of stator. In addition, in the type of iron loss, the proportion of eddy current loss of stator core is about 80% and that of rotor core is about 60%. Both of them are larger than the value of hysteresis loss, which is mainly affected by the flux frequency of stator and rotor.

6 Experimental Verification of Generator Core Loss

When DDS-SRG is in steady-state operation, the internal loss of the core cannot be directly measured. It is necessary to obtain the results indirectly by means of the copper loss, mechanical loss and stray loss of the generator. The expressions for calculating core loss are as follows:

$$P_{Fe} = P_{1} - P_{2} - P_{Cu} - P_{fw} - P_{s}$$
(18)

where, P1 represents input power, P2 represents output power, PCu represents copper loss, Pfw represents mechanical loss, Ps represents stray loss.

The winding wire gauge is 1 − Φ0.95, ignoring the skin effect of the winding surface, and the copper loss of the winding can be calculated as shown in (19):

$$P_{{C{\text{u}}}} = qI_{rms}^{2} R_{p}$$
(19)

where, q represents the number of phases, Irms represents the effective value of the phase winding current, Rp represents the resistance, and the effective value of the phase current can be obtained by (20):

$$I_{rms} = \sqrt {\frac{{N_{r} }}{2\pi }\int_{{\theta_{\text{on}} }}^{{\theta_{p} }} {i^{2} \left( \theta \right)d\theta } }$$
(20)

where, θon is the opening angle of the switching tube, and θp represents the rotor angle corresponding to the freewheeling of the phase winding. Mechanical losses mainly include friction loss and ventilation loss of bearings, which are generally estimated according to (21) and (22):

$$P_{f} = 0.15\frac{F}{d}v \times 10^{ - 5}$$
(21)
$$P_{v} = K_{v} \left( {\frac{v}{10}} \right)^{2} Q$$
(22)

where, Pf is the bearing friction loss, Pv is the ventilation loss, F is the bearing load, d is the diameter of the ball, v is the circumferential speed of the rotor, and Kv is the coefficient related to the structure and temperature of the generator, which is 0.18. The stray loss is estimated as 6% of the total loss:

$$P_{s} = (P_{1} - P_{2} ) \times 6\%$$
(23)

As shown in Fig. 16, the experimental platform is composed of generator, power supply, driver and oscilloscope.

Fig. 16
figure 16

Experimental device

Full size image

Experimental test results and simulation calculation data are shown in Table 3. The test results of the prototype show that the calculation error of the core loss is within the allowable range, which verifies the accuracy of the core loss calculation scheme.

Table 3 Comparison of measured and calculated values of generator iron loss
Full size table

7 Conclusion

The DDS-SRG has special applicable value because of its high efficiency and flexibility. In this paper, the basic structure and control principle of the generator are introduced. The core magnetic density and core loss of the generator under the condition of rotation are mainly studied. The magnetic flux waveforms of dual-stators and rotor cores are analyzed by magnetic circuit analysis method, and the overall qualitative analysis and calculation of magnetic flux components are carried out by FEM. Fourier transform is made according to the results of magnetic density calculation, and the harmonics are analyzed. The ellipse method is selected to calculate the iron loss of the generator, and the accuracy of the calculation scheme is verified by the indirect measured experimental data, which has a certain reference value for the follow-up study of the generator.

Because of the particularity of the generator’s structure, its design and performance analysis are quite different from those of ordinary SRG. Therefore, the magnetic flux density analysis in deflection state is the next key research object.