1 Introduction

Electrical conductivity is one of the main properties of polymer nanocomposites, which is necessary for practical applications in electronics, sensors and electrical industries [1,2,3,4,5,6,7,8,9,10,11,12]. The combination of polymer matrix and conductive nanofillers such as carbon nanotubes (CNTs) can present high conductivity in addition to good mechanical properties, which are desirable for different applications [13,14,15,16,17,18]. The conductivity of nanocomposites needs to conductive networks in polymer matrix which form at a critical concentration as percolation threshold [19, 20]. The percolation threshold in polymer nanocomposites is correlated with several factors such as aspect ratio, orientation, dispersion, distribution, surface energy and agglomeration of fillers, mixing method and phase structure [21, 22]. The percolation threshold can be experimentally determined by the measurement of electrical conductivity at different filler concentrations.

There are many parameters, which control the electrical conductivity of polymer nanocomposites. The content, conductivity, size, orientation, waviness and wettability of nanoparticles were reported to be effective in nanocomposite conductivity [23,24,25]. The effective parameters are not independent, and it is difficult to separate the effect of each parameter on the percolation threshold and conductivity. The effects of these parameters can be studied by modeling process, which is a low-cost and effective methodology to study on general properties of nanocomposites.

Many methods were used for modeling of electrical conductivity in polymer composites such as numerical simulation, image processing, analytical and micromechanical modeling [26, 27]. However, some models include some complex parameters such as orientation angle which are not easily manageable [28]. Most available models are appropriate for microparticles and cannot consider the poor filler concentration for percolation threshold of nanocomposites [29]. The widely used model for conductivity of polymer nanocomposites is a power-law equation based on conventional percolation theory [30,31,32]. This model well agrees to the measurements of electrical conductivity of polymer nanocomposites. Similarly, some micromechanics models were developed accounting the tunneling effect, agglomeration and waviness of CNT [28, 33], but their complex and indistinct equations are not useful in practice. Accordingly, there is not a simple model, which can show the conductivity of polymer nanocomposites by the properties of conductive nanoparticles and networks.

The main drawback of available models for conductivity of polymer nanocomposites is ignoring the interphase regions around nanoparticles in nanocomposites. The interphase between polymer matrix and nanoparticles commonly forms in polymer nanocomposites, due to the extraordinary interfacial area and interactions between polymer matrix and filler [34,35,36,37,38]. The roles of interphase properties in the mechanical properties of polymer nanocomposites were well discussed [39, 40]. Also, simple micromechanics models were developed which can predict the interphase properties by the experimental results of tensile test [41, 42]. Moreover, some researchers have reported that the interphase regions can form continuous networks that cause faster percolation and bigger networks in nanocomposites which effectively improve the mechanical properties [43, 44]. However, the role of interphase areas in the electrical conductivity of nanocomposites has not been reported, well.

In this paper, an analytical model proposed by Taherian [29] is developed to describe the effects of aspect ratio, concentration, waviness, conduction and percolation threshold of nanoparticles, interphase thickness, wettability between polymer and filler, tunneling distance between nanotubes and network fraction on the electrical conductivity of polymer/CNT nanocomposites. This development is performed based on the available models and some equations, which highlight the roles of interphase and waviness in the network properties. The developed model explicitly suggests the influences of some parameters such as aspect ratio, effective concentration, conduction and percolation threshold of nanoparticles as well as tunneling distance, wettability and network fraction on the electrical conductivity of polymer nanocomposites. Moreover, the developed model implicitly expresses the roles of interphase thickness and waviness on the conductivity. The developed model is examined by the experimental results from the literature and parametric studies. The author hopes that the developed model can replace the conventional and improper models for electrical conductivity of polymer nanocomposites.

2 Theoretical analysis

Taherian [29] developed an analytical equation to predict the electrical conductivity of composites containing conductive fillers in which three effective parameters including filler conduction, filler aspect ratio and wettability between polymer and nanoparticles were considered as:

$$\sigma = \sigma_{0} + \frac{{A\alpha \sigma_{N} }}{{1 + B\exp \left( { - \,\frac{\text{roundness}}{\cos \theta }} \right)}}$$
(1)

where “σ0” and “σN” are conductions of polymer and nanoparticles, “α” is filler aspect ratio, cos (θ) shows the wettability between components and roundness is a function of “α.” “A” and “B” are also adjustable parameters. Obviously, the negligible level of “σ0” can be disregarded from this model. In this study, this model is developed for conductivity of polymer/CNT nanocomposites by different effective parameters. We try to express the adjustable parameters by sensible properties of nanocomposite components.

Deng and Zheng [45] suggested a model for electrical conductivity of polymer/CNT nanocomposites containing random distribution of CNT above percolation threshold as:

$$\sigma = \sigma_{0} + \frac{{f\phi_{f} \sigma_{N} }}{3}$$
(2)

where “\(\phi_{f}\)” is volume fraction of nanofiller and “f” is the fraction of nanoparticles which belong to network phase after percolation. This model was successfully applied to predict the electrical conductivity of polymer/CNT nanocomposites. We can conclude that the conductivity of polymer nanocomposites directly depends on “\(\phi_{f}\)” and “f” parameters. So, “A” parameter in Eq. 1 can be a function of “\(\phi_{f}\)” and “f” parameters.

Ryvkina et al. [46] also assumed that the main mechanism for electrical conductivity of polymer/CNT nanocomposites includes the electron tunneling, where electrons are transferred by tunneling effect, even though the nanotubes are not connected. The tunneling effect among the electron conduction mechanisms considers the direct contact conductance between nanofillers in close proximity. According to Landauer–Buttiker formula [47, 48], the nanoscale CNT–CNT contact resistance assumes both tunneling and direct contact resistances in nanocomposites. The Landauer formula defines a ballistic or quasi-ballistic conduction among a two-terminal configuration. Nevertheless, a full plan including transmission rates in the matrix form is essential for random geometry with many terminals. Buttiker [49] developed this generalization to describe edge transport in the quantum Hall influence, which is identified as Landauer–Buttiker formula.

Maiti et al. [50] also suggested an equation for conductivity based on tunneling distance as:

$$\sigma = D\exp ( - \,Ed)$$
(3)

where “d” is tunneling distance between nanotubes and “D” and “E” are constant parameters. According to this equation, the conductivity of CNT nanocomposites inversely relates to the tunneling distance. As a result, “B” parameter in Eq. 1 may be a factor, which shows the tunneling distance between adjacent nanotubes in nanocomposites.

Taherian [29] also suggested the “roundness” factor as inverse aspect ratio of filler. It means that by decreasing the filler aspect ratio, the roundness grows. The roundness was defined in the range of 0–1. The aspect ratio of 1000 results in the roundness of 0, while the aspect ratio of 1 expresses the roundness of 1. Therefore, we develop an equation for roundness as:

$${\text{roundness}} = \frac{1000 - \alpha }{1000}$$
(4)

Also, the surface energies of polymer and nanoparticles control the wettability of fillers by polymer chains which can affect the filler distribution and agglomeration [51]. So, the wettability can change the conductivity of nanocomposites. Taherian [29] proposed the role of wettability in conductivity by cos (θ) as:

$$\cos \theta = \frac{{\gamma_{\text{f}} - \gamma_{\text{fp}} }}{{\gamma_{\text{p}} }}$$
(5)

where “γp,” “γf” and “γfp” are the surface energies of polymer, filler and filler/polymer interface and “θ” is wetting angle. Also, “γfp” can be defined based on the surface energies of polymer and filler as:

$$\gamma_{\text{fp}} = \gamma_{\text{f}} + \gamma_{\text{p}} - 2(\gamma_{\text{f}} \gamma_{\text{p}} )^{1/2}$$
(6)

According to above explanations, the conductivity of nanocomposites correlates with CNT size, CNT concentration, network fraction (f), interphase thickness and tunneling distance. When the roles of these factors in the conductivity are properly considered, the developed model is obtained as:

$$\sigma = \frac{{10^{ - 5} f\phi_{f} \alpha \sigma_{N} }}{{1 + \frac{d}{z}\exp \left[ { - \,\frac{{\frac{1000 - \alpha }{1000}}}{{\frac{{\gamma_{\text{f}} - \gamma_{\text{fp}} }}{{\gamma_{\text{p}} }}}}} \right]}}$$
(7)

where “z” is tunneling parameter as 1 nm. When the ranges of all parameters are considered in Eq. 7, the calculations of conductivity are much higher than the experimental data. Therefore, a factor “10−5” was added to the equation to obtain the reasonable results. Also, the conductivity inversely correlates with “B” parameter (Eq. 1). So, “B” correlates with the tunneling distance, because a large tunneling distance decreases the conductivity. However, “d” has nm unit, while “B” is a dimensionless parameter. Accordingly, “B” was considered as d/z and the tunneling parameter was considered.

This equation assumes the roles of the concentration, network fraction, aspect ratio and conduction of filler as well as the tunneling distance and wettability in the conductivity of polymer nanocomposites.

Percolation threshold for random distribution of CNT in nanocomposite was suggested based on the volume and excluded volume of nanoparticles [52] as:

$$\phi_{p} = \frac{V}{{V_{\text{ex}} }}$$
(8)

where “V” and “Vex” parameters show the volume and excluded volume of particles, respectively. The excluded volume includes the volume about an object, which does not permit the center of a similar object to enter.

“V” and “Vex” parameters in polymer/CNT nanocomposites containing dispersed CNT are given [52] as:

$$V = \pi R^{2} l + (4 /3)\pi R^{3}$$
(9)
$$V_{\text{ex}} = \frac{32}{3}\pi R^{3} \left[ {1 + \frac{3}{4}\left( {\frac{l}{R}} \right) + \frac{3}{32}\left( {\frac{l}{R}} \right)^{2} } \right]$$
(10)

where “R” and “l” denote the radius and length of CNT, respectively. By substituting the latter equations into Eq. 8, “\(\phi_{p}\)” is expressed as:

$$\phi_{p} = \frac{{\pi R^{2} l + (4 /3)\pi R^{3} }}{{\frac{32}{3}\pi R^{3} \left[ {1 + \frac{3}{4}\left( {\frac{l}{R}} \right) + \frac{3}{32}\left( {\frac{l}{R}} \right)^{2} } \right]}}$$
(11)

On the other hand, the authors in previous articles have related the “\(\phi_{p}\)” in nanocomposites to the aspect ratio of filler [53, 54]. The aspect ratio of nanoparticles is defined as:

$$\alpha = \frac{l}{2R}$$
(12)

where “2R” is the diameter of nanotubes. The researchers have presented different inverse relations between “\(\phi_{p}\)” and “α.” However, the best relation, which agrees with the levels of “\(\phi_{p}\)” derived from Eq. 11, is suggested as:

$$\phi_{p} = \frac{0.5}{\alpha } = \frac{R}{l}$$
(13)

Figure 1 shows the effects of “R” and “l” parameters on the levels of “\(\phi_{p}\)” expressed by Eqs. 11 and 13 by contour plots. It is shown that the different ranges of “R” and “l” parameters show similar results for percolation threshold using Eqs. 11 and 13. A small “\(\phi_{p}\)” is obtained by thin and long nanotubes, while the worst level of “\(\phi_{p}\)” is shown by the thickest and the shortest nanotubes. Accordingly, thin and long nanotubes create desirable percolation level and “\(\phi_{p}\)” can be correlated with “α” by Eq. 13.

Fig. 1
figure 1

Contour plots to show the roles of “R” and “l” parameters in “\(\phi_{p}\)” according to a Eq. 11 and b Eq. 13

Full size image

As stated, the interphase layer surrounding CNT can speed up the formation of conductive networks in nanocomposites. The interphase regions do not affect the main volume of nanoparticles, but they increase the excluded volume [44] as:

$$V_{\text{ex}} = \frac{32}{3}\pi (R + t)^{3} \left[ {1 + \frac{3}{4}\left( {\frac{l}{R + t}} \right) + \frac{3}{32}\left( {\frac{l}{R + t}} \right)^{2} } \right]$$
(14)

where “t” is interphase thickness.

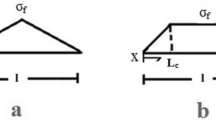
In addition, CNTs are commonly curved in nanocomposites, due to the large aspect ratio, which affects their specifications. An equivalent length as “leq” can be considered for curved nanotubes (Fig. 2). Also, the relation between the length of straight and curved CNT can be considered by a waviness parameter as:

$$u = \frac{l}{{l_{\text{eq}} }}$$
(15)

where u = 1 demonstrates the straight CNT (no waviness), but a higher level of “u” shows more waviness which decreases the effective length.

Fig. 2
figure 2

Schematic illustrations of straight and curved CNT in polymer nanocomposites

Full size image

The influence of curved nanotubes on the excluded volume beside interphase thickness can be taken into account as:

$$V_{\text{ex}} = \frac{32}{3}\pi (R + t)^{3} \left[ {1 + \frac{3}{4}\left( {\frac{l /u}{R + t}} \right) + \frac{3}{32}\left( {\frac{l /u}{R + t}} \right)^{2} } \right]$$
(16)

which results in an equation for percolation threshold by the roles of interphase and waviness as:

$$\phi_{p} = \frac{{\pi R^{2} l + (4 /3)\pi R^{3} }}{{\frac{32}{3}\pi (R + t)^{3} \left[ {1 + \frac{3}{4}\left( {\frac{l /u}{R + t}} \right) + \frac{3}{32}\left( {\frac{l /u}{R + t}} \right)^{2} } \right]}}$$
(17)

This equation was examined by the experimental results of percolation threshold in polymer/CNT nanocomposites. The predictions of percolation threshold show good agreement with the experimental data in several samples such as ultra-high-molecular-weight polyethylene/MWCNT [55], epoxy/MWCNT [56], polycarbonate/acrylonitrile butadiene styrene/MWCNT [53] and epoxy/MWCNT [31]. As a result, Eq. 17 is valuable to analyze the percolation threshold in nanocomposites supposing the interphase and waviness.

The interphase regions also increase the effectiveness of nanoparticles in the general performances of nanocomposites. The effective volume fraction of nanoparticles [28] can be defined based on interphase and waviness by:

$$\phi_{\text{eff}} = \frac{{(R + t)^{2} (l /u + 2t)}}{{R^{2} l /u}}\phi_{f}$$
(18)

Also, only a number of nanotubes participate in the conductive networks after percolation threshold and others are evenly dispersed in nanocomposite.

The fraction of networked CNT can be given by effective filler concentration and percolation threshold [28] as:

$$f = \frac{{\phi_{\text{eff}}^{1/3} - \phi_{p}^{1/3} }}{{1 - \phi_{p}^{1/3} }}$$
(19)

Furthermore, the conduction of transversely isotropic CNT changes by the waviness. Many papers indicated that the waviness weakens the conduction of CNT and suggested an inverse relation between “σN” and “u” [23, 24, 57] as:

$$\sigma_{Nw} = \frac{{\sigma_{N} }}{u}$$
(20)

Assuming the above parameters, the developed model based on Taherian equation can be presented for conductivity of polymer/CNT nanocomposites as:

$$\sigma = \frac{{10^{ - 5} f\phi_{\text{eff}} \alpha \sigma_{Nw} }}{{1 + \frac{d}{z}\exp \left[ { - \,\frac{{\frac{1000 - \alpha }{1000}}}{{\frac{{\gamma_{\text{f}} - \gamma_{\text{p}} }}{{\gamma_{\text{fp}} }}}}} \right]}}$$
(21)

When the aspect ratio of filler is related to percolation threshold by Eq. 13, the developed model is expressed by the effect of percolation threshold as:

$$\sigma = \frac{{10^{ - 5} f\phi_{\text{eff}} \sigma_{Nw} }}{{2\phi_{p} + 2\phi_{p} \frac{d}{z}\exp \left( { - \,\frac{{\frac{{1000 - \frac{0.5}{{\phi_{p} }}}}{1000}}}{{\frac{{\gamma_{\text{f}} - \gamma_{\text{p}} }}{{\gamma_{\text{fp}} }}}}} \right)}}$$
(22)

which generally suggests the impacts of nanoparticles dimensions and waviness, network fraction, interphase thickness, CNT conduction, percolation threshold, tunneling distance and wettability between polymer and nanoparticles on the conductivity of polymer nanocomposites.

3 Results and discussion

The developed model can be evaluated by its predictions for electrical conductivity of polymer nanocomposites. Also, the roles of effective parameters in the conductivity of nanocomposites can be analyzed to confirm the predictability of the developed model.

3.1 Comparison between experimental and theoretical conductivities

Figure 3 exhibits the experimental data and calculations of the developed model for ultra-high-molecular-weight polyethylene/multi-walled CNT (MWCNT) (R = 8 nm, l = 8 μm, u ≈ 1.2) [55] and epoxy/MWCNT (R = 8 nm, l = 30 μm, u ≈ 1.2) [56]. CNT size for these samples was obtained from Refs. [55, 56]. Also, “u” values were approximated based on the morphological images illustrated for the samples. A good agreement between the experimental conductivity and the calculations is observed in all samples, which approves the predictability of the developed model. As a result, the developed model can approximate the electrical conductivity of polymer nanocomposites by the influences of effective parameters.

Fig. 3
figure 3

Experimental and theoretical conductivities based on the developed model for a ultra-high-molecular-weight polyethylene/MWCNT [55] and b epoxy/MWCNT [56] samples at different filler concentrations

Full size image

The values of “t” and “d” parameters can be also obtained by the comparison of experimental data and the predictions of the developed model. When the experimental levels of percolation threshold are applied to Eq. 11, the values of “t” can be calculated. “\(\phi_{p}\)” was reported as 0.0007 and 0.0002 for ultra-high-molecular-weight polyethylene/MWCNT [55] and epoxy/MWCNT [56] samples, respectively, by the experimental results of conductivity. When Eq. 11 is considered, the best values of “t” are estimated as 7 nm for these samples. Moreover, the “d” levels of 3 and 7 nm are obtained by the comparison between experimental conductivity of ultra-high-molecular-weight polyethylene/MWCNT [55] and epoxy/MWCNT [56] samples and the calculations of the developed model. Accordingly, the developed model can estimate the levels of interphase and tunneling distance in the nanocomposites.

3.2 Parametric studies

The effects of different parameters on the conductivity of nanocomposites are assessed based on the developed model. By this evaluation, the predictability of the developed model as well as the efficiencies of parameters in conductivity is determined.

Figure 4 demonstrates the roles of “\(\phi_{f}\)” and “α” factors in the conductivity of nanocomposites at average levels of R = 10 nm, l = 15 μm, u = 1.3, t = 10 nm, d = 3 nm, σN = 105 S/m, γp = 40 mN/m and γf = 45 mN/m by three-dimensional (3D) and contour plots. The maximum levels of “\(\phi_{f}\)” and “α” parameters result in the highest conductivity. As observed, σ = 5.5 S/m is obtained at \(\phi_{f}\) = 0.02 and α = 1000. However, the least conductivity is observed at the poorest levels of “\(\phi_{f}\)” and “α” parameters, where \(\phi_{f}\) = 0.005 and α = 200 calculate σ = 0.3 S/m. Therefore, “\(\phi_{f}\)” and “α” directly control the conductivity of nanocomposites which means that a high conductivity is achieved by great concentration of CNT with large aspect ratio.

Fig. 4
figure 4

The conductivity of polymer nanocomposites at different levels of “\(\phi_{f}\)” and “α” parameters and average R = 10 nm, l = 15 μm, u = 1.3, t = 10 nm, d = 3 nm, σN = 105 S/m, γp = 40 mN/m and γf = 45 mN/m: a 3D and b contour plots

Full size image

As mentioned, CNTs form conductive networks in nanocomposites after percolation threshold. So, the volume fraction of nanoparticles below percolation cannot form the networks which result in the poor conductivity. When the filler concentration reaches percolation level, the networks of CNT produce a large level of electron current which is a sign of conductivity. Moreover, the higher levels of “\(\phi_{f}\)” above percolation threshold help the development of dimensions and density of network. Therefore, the conductivity shows a direct relation with nanofiller volume fraction, due to the better conductivity and networkability of CNT in nanocomposites. Additionally, reducing the particle size and increasing the filler aspect ratio make it easier to form conductive networks which reduce at percolation threshold. The effect of aspect ratio is more obvious at low filler concentrations. A high aspect ratio by long and thin nanotubes increases the ratio of surface to volume which promotes the inter-particle contacts and leads to more probability of networking. In other words, a high aspect ratio develops the properties of conductive networks which positively affect the conductivity of nanocomposites. Many reports on polymer nanocomposites have also indicated the positive influence of aspect ratio on the conductivity [58]. As a result, it is meaningful to correlate the electrical conductivity of nanocomposites with aspect ratio of filler.

Figure 5 also shows the effects of “f” and “d” parameters as the fraction of networked filler and tunneling distance on the conductivity of nanocomposites at \(\phi_{f}\) = 0.01, R = 10 nm, l = 15 μm, u = 1.3, t = 10 nm, σN = 105 S/m, γp = 40 mN/m and γf = 45 mN/m. The highest conductivity as σ = 7 S/m is observed at f = 0.5 and d = 1 nm, while the slightest conductivity as 0.37 S/m is reported at f < 0.2 and d > 5 nm. Accordingly, the conductivity is differently correlated with the fraction of percolated CNT and tunneling distance between nanotubes. A better conductivity is obtained by a higher level of percolated nanoparticles and a smaller distance between nanoparticles. On the other hand, a poor conductivity is shown when more nanoparticles cannot be involved in the networks and a far distance existed between nanotubes.

Fig. 5
figure 5

a 3D and b contour plots to show the dependences of conductivity on “f” and “d” parameters at average \(\phi_{f}\) = 0.01, R = 10 nm, l = 15 μm, u = 1.3, t = 10 nm, σN = 105 S/m, γp = 40 mN/m and γf = 45 mN/m

Full size image

The role of “f” parameter in the conductivity of nanocomposites is reasonable, because it fixes the dimensions of conductive networks. A high level of “f” clearly displays the large number of nanotubes in the conductive networks which gives a high level of charge transportation. However, a small number of nanotubes in the networks decrease their dimensions resulting in a deprived conductivity. The direct role of network properties in the conductivity of nanocomposites was also reported in the literature [24, 57, 59], which confirms the development of this model for conductivity of polymer nanocomposites.

The conductivity of nanocomposites based on the electron tunneling mainly depends on the separation distance between CNT [46, 60]. When the separation distance of CNT is larger than a determinate range, the nanocomposite is insulated or very poor conductivity is observed, due to the absence of electron transferring. However, when CNT volume fraction increases, the conductive networks begin to form and the separate distance between CNT decreases which permits the nanotubes for electron tunneling. As a result, the distance between nanotubes is much important which controls the networking of nanoparticles and conductivity of nanocomposites. Feng and Jiang [28] indicated that the critical separation distance to form conductive networks with electrical contacts rather than physical contacts is 1.8 nm. They also indicated that the nanotubes keep this distance even after percolation threshold, due to the van der Waals attractions. Conclusively, the developed model logically predicts the effect of tunneling distance on the conductivity of nanocomposites.

The conductivity as a function of “t” and “σN” parameters is also plotted in Fig. 6 at average levels of other factors. A direct correlation is observed between the conductivity of nanocomposites and these parameters. As shown, t = 20 nm and σN = 105 S/m produce the conductivity of 18 S/m, while a poor conductivity of 0.38 S/m is reported at an average t < 8 nm and σN < 1.25 × 105 S/m. So, a thick interphase and a high conduction of CNT produce an extraordinary conductivity in nanocomposites. On the other hand, a low conductivity in nanocomposites is calculated in the case of thin interphase and poor-conductive CNT.

Fig. 6
figure 6

The effects of “t” and “σN” parameters on the conductivity of nanocomposites at \(\phi_{f}\) = 0.01, R = 10 nm, l = 15 μm, u = 1.3, d = 3 nm, γp = 40 mN/m and γf = 45 mN/m: a 3D and b contour plots

Full size image

A thick interphase around nanoparticles accelerates the formation of conductive networks in the nanocomposites, because it extends the dimensions of CNT. Moreover, a thicker interphase participates more nanotubes in the networks which expands their size and density. Additionally, the interphase areas increase the effective volume fraction of nanoparticles in nanocomposites, due to their contributions in the general behavior of nanocomposites. Accordingly, a thicker interphase causes more positive impacts on the conductivity of nanocomposites, as suggested by the expressed equations. The positive role of interphase regions in the percolation threshold was indicated by previous researchers [43, 61], but its effects on the network properties and nanocomposite conductivity were not well studied.

Since the polymer matrices are approximately insulated, the CNT conduction mainly controls the conductivity of polymer nanocomposites. By increasing in the CNT conduction, the conductivity of nanocomposites linearly improves and a better maximum conductivity is obtained by more conductive CNT [29]. The main reason for this occurrence can be expressed by the large difference between the conductions of polymers and CNT which highlights the role of CNT conduction in the conductivity of whole nanocomposite. In view of that, the developed model correctly suggests that the CNT conduction linearly affects the conductivity of produced nanocomposites.

The roles of surface energies of polymer and filler on the conductivity of nanocomposites are depicted in Fig. 7 at average levels of other parameters. The best conductivity is observed at the highest and the least surface energies of polymer and nanoparticles, respectively, while the conductivity decreases by poor “γp” and maximum “γf.” However, it is found that these parameters cannot significantly change the conductivity of nanocomposites. As observed, σ = 2.25 S/m is obtained at γp = 50 mN/m and γf = 30 mN/m, but low conductivity of about 2 S/m is exhibited at γp = 20 mN/m and γf = 60 mN/m. As a result, polymers with high surface energy and low surface energy nanofillers produce the nanocomposites with high conductivity.

Fig. 7
figure 7

a 3D and b contour plots for the variations of conductivity at different surface energies of polymer and filler and average \(\phi_{f}\) = 0.01, R = 10 nm, l = 15 μm, u = 1.3, d = 3 nm, t = 10 nm and σN = 105 S/m

Full size image

The surface tensions of polymer matrix and nanoparticles regulate the wettability of filler by polymer which affects the filler distribution and agglomeration. A high wettability facilitates the surrounding of filler by polymer chains which inhibits the direct contacts between nanoparticles and weakens the conductivity of nanocomposite [29]. In addition, a lower wettability leads to more agglomeration of nanoparticles in the matrix which is appropriate for electrical conductivity, because the conductive networks are formed by weak distribution of nanoparticles [29]. So, a low wettability is suitable for the formation of filler networks and improvement of electrical conductivity of nanocomposites. The wettability between polymer and nanofiller is shown by cos (θ) parameter in Eq. 5. Since higher differences between the surface energies of polymer and nanoparticles as well as the great surface energy of polymer and poor surface energy of filler produce worse wetting of filler by polymer matrix, the developed model correctly exhibits the correlations between the conductivity of nanocomposites and the surfaces energies of polymer and filler.

Figure 8 also demonstrates the conductivity of nanocomposites as a function of “\(\phi_{p}\)”and “\(\phi_{\text{eff}}\)” parameters at average values of other variables. A desirable conductivity of 3.5 S/m is estimated at \(\phi_{p}\) = 0.001 and \(\phi_{\text{eff}}\) = 0.08, whereas σ = 0.1 S/m is calculated at \(\phi_{p}\) = 0.005 and \(\phi_{\text{eff}}\) = 0.02. Therefore, the smallest and the highest levels of “\(\phi_{p}\)” and “\(\phi_{\text{eff}}\)” parameters result in the best conductivity representing that low percolation threshold and numerous effective nanoparticles can considerably grow the conductivity of nanocomposites.

Fig. 8
figure 8

The dependences of conductivity of nanocomposite on “\(\phi_{p}\)”and “\(\phi_{\text{eff}}\)” parameters based on Eq. 22 at average values of u = 1.3, d = 3 nm, σN = 105 S/m, γp = 40 mN/m and γf = 45 mN/m via a 3D and b contour plots

Full size image

The percolation threshold shows the least volume fraction of nanoparticles which can form the conductive networks. Beside this, the percolation threshold controls the fraction of nanotubes which creates the networks based on Eq. 19. As a result, the roles of “\(\phi_{p}\)” in the networks formation and their properties are not deniable which affect the conductivity of nanocomposites. All experimental and modeling studies have indicated that a lower percolation threshold is more desirable for conductivity of nanocomposites [28, 58]. Therefore, it is proper to express an inverse relation between the conductivity of nanocomposites and percolation threshold, as suggested by the developed model.

On the other hand, a more level of “\(\phi_{\text{eff}}\)” parameter shows the further efficiencies of nanoparticles and interphase in the conductivity of nanocomposites. According to Eq. 20, a high “\(\phi_{\text{eff}}\)” is obtained by thin and long nanotubes, thick interphase and less waviness. All these ranges are required to produce effective conductive networks capable to significantly improve the conductivity of nanocomposites. Therefore, the role of “\(\phi_{\text{eff}}\)” parameter as a function of filler and interphase specifications in the conductivity of nanocomposites is well given by the developed model.

4 Conclusions

An analytical model was developed for electrical conductivity of polymer nanocomposites based on Taherian approach considering the main effects of aspect ratio, concentration, waviness, conduction and percolation threshold of nanoparticles, interphase thickness, wettability, tunneling distance and network fraction. The developed model was examined by experimental results and parametric analysis. Good agreement between the experimental data and the calculations is observed which validates the predictability of the developed model. Moreover, the developed model can approximate the interphase thickness and tunneling distance by experimental results. The concentration and aspect ratio of nanoparticles directly change the conductivity of nanocomposites, because they affect the nanotubes contacts and network probability. Additionally, a better conductivity is obtained by a higher level of percolated nanoparticles, which produces a larger network. Also, a smaller distance between nanoparticles causes more desirable conductivity, due to the tunneling effect. A thick interphase yields an extraordinary conductivity in nanocomposites, because it well contributes to the effective filler fraction and network level. The high conduction of CNT also manages the conductivity of polymer nanocomposites, because polymers are commonly insulated. Moreover, a high conductivity is observed at great and low surface energies of polymer and nanoparticles, respectively, because they suggest a low wettability between polymer and filler. However, it is shown that these parameters cannot significantly control the conductivity of nanocomposites. The smallest and the highest levels of “\(\phi_{p}\)” and “\(\phi_{\text{eff}}\)” parameters also result in the finest conductivity, because “\(\phi_{p}\)” affects the fraction of networked filler and “\(\phi_{\text{eff}}\)” shows the efficiencies of nanoparticles and interphase in the conductivity.