Regression Modelling on Reliability Variation of a Parallel Series System of (m, n_i) Order with Addition and Removal of Parallel Paths

Abstract

A regression model is fitted on variation of reliability of parallel series system of (m, n_i) order (called initial system) by adding (or removing) the arbitrary number of parallel paths. The initial system is transformed by adding (or removing) the ‘p’ (or ‘k’) parallel paths. A reliability variation method is devised to obtain directly the reliability of the transformed system in terms of reliability of the initial system and reliability of the added (or removed) system. The variation in reliability is evaluated in both cases to see the effect of parallel paths on initial system reliability. Also, the variation in reliability of a particular parallel series system of order (4, 1) is obtained by assuming constant failure rate of the components. The effect of parallel paths and failure rate of the components on variation of reliability of the system is examined by fitting the linear regression model. The values of R² and adjusted R² are calculated to see the best fit of the model in order reduce the computing efforts to obtain the reliability of the transformed system. The results are shown numerically and graphically. The application of the study is discussed with justification.

1 Introduction

It is universally known that change is the law of nature and it applies to all the systems. This is also true that every system either needs to be upgraded or it deteriorates with time. In view of these facts, several systems have been created knowingly or unknowingly by human beings for the development of their civilization. Now, we are in position to enjoy man made or natural systems with least possible snags may because of advancement in technology. But, the failure of systems cannot be ignored completely and in that situation the purpose is to develop the systems with a considerable lifetime. The system designers and researchers have jointly made efforts in this direction and they have succeeded somehow to provide faultless systems to the users. Also, the manufacturers are now prioritizing on the production of flawless commodities and dispensing incessant services to the customers at least for a given time period in terms of warranty or guarantee. The reliability improvement methods including better structural design of the components and provision of redundancy have been suggested by the researchers working in the field of reliability engineering.

The series, parallel, series–parallel and parallel-series structures are the most frequently used system configurations in mechanical, electrical and communication systems. The parallel structure of the components has been considered as the best one over the series structure so far as reliability is concerned [1]. The reliability of any system increases with an increase in number of parallel paths while it decreases with an increase in number of components in series [1]. Sharma et al. [9] analysed Bayesian reliability of a parallel system using time truncated failure and prior information about the failure of system components.By adopting a beta-binomial model for components reliabilities, Benkamara et al. [3] proposed a risk-averse solution to the problem of estimating the reliability of a parallel-series system. They also studied a hybrid two-stage design which can be useful to estimate the reliability of a parallel–series and/or by duality a series–parallel system [2]. On the other hand, to improve reliability or by the demand of the configuration, we came across systems which are neither simple series nor parallel. The reliability of a non-series parallel system in fuzzy and possibility context is discussed by Sharma [10]. Recently, Nitika et al. [8] have studied about the reliability evaluation of non-series parallel systems of five components. The logic diagram technique has been used to deal with such complex systems. Some others methods available for reliability improvement are reduction and duplication. Ezzati et al. [6] revealed that cold duplication method improves system reliability much better than the warm duplication method. However, reduction and duplication methods have no such comparative statement. The block diagram of any complex system can be converted into a logic diagram by identifying all the possible simple parallel paths between IN and OUT terminals.

Thus, the main objective of the system designers and reliability engineers is to examine the change in reliability of the systems affected by several factors including failure rate of the components, number of components/parallel paths added (or removed). For analysing, multi-factor data regression analysis is one of the most widely used techniques. Its broad appeal and usefulness result from the conceptually logical process of using an equation to express the relationship between a variable of interest (the response) and a set of related predictor variables [4]. It is a statistical technique for investigating and modelling the relationship between variables [4].

Life time distributions are mainly used to study failure rate of the components in the field of reliability theory. Exponential distribution is the most preferred distribution as it assumes constant failure rate of the components. Epstein et al. [5] obtained some important results on life testing using exponential distribution. Gupta et al. [7] studied exponential distribution, its properties and models, and illustrated its applications.

Here, a regression model is fitted on variation of reliability of parallel series system of (m, n_i) order (called initial system) by adding (or removing) the arbitrary number of parallel paths. The initial system is transformed by adding (or removing) the ‘p’ (or ‘k’) parallel paths. A reliability variation method is devised to obtain directly the reliability of the transformed system in terms of reliability of the initial system and reliability of the added (or removed) system. The variation in reliability is evaluated in both cases to see the effect of parallel paths on initial system reliability. Also, the variation in reliability of a particular parallel series system of order (4, 1) is obtained by assuming constant failure rate of the components. The effect of parallel paths and failure rate of the components on variation of reliability of the system is examined by fitting the linear regression model. The values of R² and adjusted R² are calculated to see the best fit of the model in order reduce the computing efforts to obtain the reliability of the transformed system. The results are shown numerically and graphically. The application of the study is discussed with justification.

2 Notations

Let’s define the following notations to represent different functions:

$R_{{s_{i} }} \left( t \right)$	Reliability of the initial system	$R_{{s_{f} }} \left( t \right)$	Reliability of the final system
$p_{i} \left( t \right)$	Reliability of the ith component	$C_{{\left( {i,j} \right)}}$	jth component in ith subsystem
$R_{i} \left( t \right)$	Reliability of ith path	$p\left( t \right)$	Reliability for identical component,
t	Operating Time of the Components	T	Life time of the system
$\Delta_{i}$R(t)	Variation in reliability due to addition of parallel paths	$\Delta_{d}$R(t)	Variation in reliability due to removal of parallel paths
$R_{a} \left( t \right)$	Reliability of the added system	$R_{r} \left( t \right)$	Reliability of the removed system
m	Number of parallel paths in initial system	$n_{i}$	Number of components in series in ith subsystem
p	Number of added parallel paths	k	Number of removed parallel paths
df	Degree of freedom	NA	Not applicable
SS	Sum of squares	MS	Mean sum of squares
ANOVA	Analysis of variance	F	F statistic

3 System Description

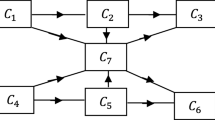
Here, we consider initially parallel series system having ‘m’ parallel paths where each path consists of $\left\{ {n_{i} ,i = 1,2, \ldots ,m} \right\}$ components in series as shown in Fig. 1:

Fig. 1

Block diagram of initial parallel-series system

The reliability of this system is given by

$$\begin{aligned} R_{{s_{i} }} \left( t \right) = {\text{Reliability of the initial system}} = \left\{ {1 - \mathop \prod \nolimits_{i = 1}^{m} \left( {1 - R_{i} \left( t \right)} \right)} \right\} \\ = \left\{ {1 - \mathop \prod \nolimits_{i = 1}^{m} \left( {1 - \mathop \prod \nolimits_{j = 1}^{{n_{i} }} p_{{\left( {i,j} \right)}} } \right)} \right\},\quad {\text{where }}R_{i} \left( t \right) = \mathop \prod \nolimits_{j = 1}^{{n_{i} }} p_{{\left( {i,j} \right)}} \\ \end{aligned}$$

4 To Determine Variation in Reliability

Here we shall consider the following two cases:

Case 1::

Suppose ‘p’ Parallel Paths are Added to the Initial System

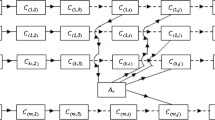
If we add ‘p’ parallel paths to the initial system, where each additional path consists of $\left\{ {n_{i} ,i = m + 1,m + 2, \ldots ,m + p} \right\}$ components in series. The block diagram of the added system is shown in Fig. 2 as:

Fig. 2

Block diagram of added system

The reliability of this added system is given by

$$\begin{aligned} R_{a} \left( t \right) & = {\text{Reliability of the added system}} \\ & = \left\{ {1 - \mathop \prod \nolimits_{i = m + 1}^{m + p} \left( {1 - R_{i} \left( t \right)} \right)} \right\} \\ & = \left\{ {1 - \mathop \prod \nolimits_{i = m + 1}^{m + p} \left( {1 - \mathop \prod \nolimits_{j = 1}^{{n_{i} }} p_{{\left( {i,j} \right)}} } \right)} \right\} \\ \end{aligned}$$

Now, the upgraded final system has ‘m + p’ parallel paths where each path consists of $\left\{ {n_{i} ,i = 1,2, \ldots ,m + p} \right\}$ components in series. The block diagram of the transformed final system is shown in Fig. 3 as:

Fig. 3

Block diagram of the transformed final system

The reliability of the upgraded final system is given by

$$\begin{aligned} R_{{s_{f} }} \left( t \right) & = {\text{Reliability of the upgraded final system}} = { }\left\{ {1 - \mathop \prod \nolimits_{i = 1}^{m + p} \left( {1 - R_{i} \left( t \right)} \right)} \right\} \\ & = \left\{ {1 - \mathop \prod \nolimits_{i = 1}^{m + p} \left( {1 - \mathop \prod \nolimits_{j = 1}^{{n_{i} }} p_{{\left( {i,j} \right)}} } \right)} \right\} \\ \end{aligned}$$

Now, we shall determine variation in reliability due to the addition of parallel paths to the initial system. Let’s define

$$\begin{aligned} \Delta_{i} R\left( t \right) & = {\text{Variation in reliability}} \\ & = {\text{ Reliability of the upgraded final system}} - {\text{ Reliability of the initial system}} \\ & = R_{{s_{f} }} \left( t \right) - R_{{s_{i} }} \left( t \right) \\ & = R_{a} \left( t \right)\left\{ {1 - R_{{s_{i} }} \left( t \right)} \right\} \\ & = {\text{ Reliability of added system}}\left\{ {1 - {\text{Reliability of initial system}}} \right\} \\ & = {\text{ Reliability of added system}}\left\{ {\text{Unreliability of initial system}} \right\}. \\ \end{aligned}$$

To check:

Here, $R_{{s_{f} }} \left( t \right) = {\text{Reliability of the upgraded final system}} = \left\{ {1 - \mathop \prod \nolimits_{i = 1}^{m + p} \left( {1 - R_{i} \left( t \right)} \right)} \right\},$

and

$$R_{{s_{i} }} \left( t \right) = {\text{Reliability of the initial system}} = \left\{ {1 - \mathop \prod \nolimits_{i = 1}^{m} \left( {1 - R_{i} \left( t \right)} \right)} \right\}.$$

$$\begin{aligned} {\text{Therefore, }}\Delta_{i} R\left( t \right) & = R_{{s_{f} }} \left( t \right) - R_{{s_{i} }} \left( t \right) \\ & = \left\{ {1 - \mathop \prod \nolimits_{i = 1}^{m + p} \left( {1 - R_{i} \left( t \right)} \right)} \right\} - \left\{ {1 - \mathop \prod \nolimits_{i = 1}^{m} \left( {1 - R_{i} \left( t \right)} \right)} \right\} \\ & = - \left\{ {\mathop \prod \nolimits_{i = 1}^{m} \left( {1 - R_{i} \left( t \right)} \right)\mathop \prod \nolimits_{i = m + 1}^{m + p} \left( {1 - R_{i} \left( t \right)} \right)} \right\} + \mathop \prod \nolimits_{i = 1}^{m} \left( {1 - R_{i} \left( t \right)} \right) \\ & = \mathop \prod \nolimits_{i = 1}^{m} \left( {1 - R_{i} \left( t \right)} \right)\left\{ {1 - \mathop \prod \nolimits_{i = m + 1}^{m + p} \left( {1 - R_{i} \left( t \right)} \right)} \right\} \\ & = \left[ {1 - \left\{ {1 - \mathop \prod \nolimits_{i = 1}^{m} \left( {1 - R_{i} \left( t \right)} \right)} \right\}} \right]\left\{ {1 - \mathop \prod \nolimits_{i = m + 1}^{m + p} \left( {1 - R_{i} \left( t \right)} \right)} \right\} \\ & = \left[ {1 - R_{{s_{i} }} \left( t \right)} \right]\left\{ {R_{a} \left( t \right)} \right\} \\ & = {\text{Reliability of added system}}\left\{ {1 - {\text{Reliability of initial system}}} \right\} \\ & = {\text{ Reliability of added system}}\left\{ {\text{Unreliability of initial system}} \right\} \\ \end{aligned}$$

where $R_{a} \left( t \right)$ = $\left\{ {1 - \mathop \prod \nolimits_{i = m + 1}^{m + p} \left( {1 - R_{i} \left( t \right)} \right)} \right\}$.

$$\begin{aligned} {\text{Now, }}R_{{s_{f} }} \left( t \right) & = R_{{s_{i} }} \left( t \right) + \Delta_{i} {\text{R}}\left( {\text{t}} \right) \\ & = R_{{s_{i} }} \left( t \right) + {\text{Reliability of added system}}\left\{ {\text{Unreliability of initial system}} \right\} \\ \end{aligned}$$

Case 2::

Suppose ‘k’ Parallel Paths are Removed from the initial system

If we remove ‘k’ parallel paths from the initial system, where each removed path consists of $\left\{ {n_{i} ,i = m - k + 1,m - k + 2, \ldots ,m} \right\}$ components in series. The block diagram of the removed system is shown in Fig. 4. as:

Fig. 4

Block diagram of the removed system

The reliability of the removed system is given by

$$\begin{aligned} R_{r} \left( t \right) & = {\text{Reliability of the removed system}} \\ & = \left\{ {1 - \mathop \prod \nolimits_{i = m - k + 1}^{m} \left( {1 - R_{i} \left( t \right)} \right)} \right\} = \left\{ {1 - \mathop \prod \nolimits_{i = m - k + 1}^{m} \left( {1 - \mathop \prod \nolimits_{j = 1}^{{n_{i} }} p_{{\left( {i,j} \right)}} } \right)} \right\} \\ \end{aligned}$$

Now, the reduced final system has ‘m − k’ parallel paths where each path consists of $\left\{ {n_{i} ,i = 1,2, \ldots ,m - k} \right\}$ components in series. The block diagram of the reduced final system is shown in Fig. 5 as:

Fig. 5

Block diagram of the reduced final system

The reliability of the reduced final system is given by

$$\begin{aligned} R_{{s_{f} }} \left( t \right) & = {\text{Reliability of the reduced final system}} = \left\{ {1 - \mathop \prod \nolimits_{i = 1}^{m - k} \left( {1 - R_{i} \left( t \right)} \right)} \right\} \\ & = \left\{ {1 - \mathop \prod \nolimits_{i = 1}^{m - k} \left( {1 - \mathop \prod \nolimits_{j = 1}^{{n_{i} }} p_{{\left( {i,j} \right)}} } \right)} \right\}. \\ \end{aligned}$$

Therefore,

$$\begin{aligned} \Delta_{d} {\text{R}}\left( {\text{t}} \right) & = {\text{Variation in reliability}} = R_{{s_{i} }} \left( t \right) - R_{{s_{f} }} \left( t \right) \\ & \quad \quad \quad \quad = \left\{ {1 - R_{{s_{i} }} \left( t \right)} \right\}\left[ {\frac{{R_{r} \left( t \right)}}{{1 - R_{r} \left( t \right)}}} \right] \\ & = \left\{ {1 - {\text{Reliability of initial system}}} \right\}\left[ {\frac{{\text{Reliability of removed system}}}{{1 - {\text{Reliability of removed system}}}}} \right] \\ & = \left\{ {\text{Unreliability of initial system}} \right\}\left[ {\frac{{\text{Reliability of removed system}}}{{\text{Unreliability of removed system}}}} \right]. \\ \end{aligned}$$

To check:

Here, $R_{{s_{f} }} \left( t \right) = {\text{Reliability of the reduced final system}} = \left\{ {1 - \mathop \prod \nolimits_{i = 1}^{m - k} \left( {1 - R_{i} \left( t \right)} \right)} \right\},$

and

$$\begin{aligned} R_{r} \left( t \right) & = {\text{Reliability of the removed system}} \\ & { = }\left\{ {1 - \mathop \prod \nolimits_{i = m - k + 1}^{m} \left( {1 - R_{i} \left( t \right)} \right)} \right\} = \left\{ {1 - \mathop \prod \nolimits_{i = m - k + 1}^{m} \left( {1 - \mathop \prod \nolimits_{j = 1}^{{n_{i} }} p_{{\left( {i,j} \right)}} } \right)} \right\} \\ R_{{s_{i} }} \left( t \right) & = {\text{Reliability of the initial system}} = \left\{ {1 - \mathop \prod \nolimits_{i = 1}^{m} \left( {1 - R_{i} \left( t \right)} \right)} \right\} \\ \Delta_{d} {\text{R}}\left( {\text{t}} \right) & = R_{{s_{i} }} \left( t \right) - R_{{s_{f} }} \left( t \right) \\ & = \left\{ {1 - \mathop \prod \nolimits_{i = 1}^{m} \left( {1 - R_{i} \left( t \right)} \right)} \right\} - \left\{ {1 - \mathop \prod \nolimits_{i = 1}^{m - k} \left( {1 - R_{i} \left( t \right)} \right)} \right\} \\ & = \left\{ {1 - \mathop \prod \nolimits_{i = 1}^{m} \left( {1 - R_{i} \left( t \right)} \right)} \right\} - \left[ {1 - \frac{{\mathop \prod \nolimits_{i = 1}^{m - k} \left( {1 - R_{i} \left( t \right)} \right)\mathop \prod \nolimits_{i = m - k + 1}^{m} \left( {1 - R_{i} \left( t \right)} \right)}}{{\mathop \prod \nolimits_{i = m - k + 1}^{m} \left( {1 - R_{i} \left( t \right)} \right)}}} \right] \\ & = \left\{ {1 - \mathop \prod \nolimits_{i = 1}^{m} \left( {1 - R_{i} \left( t \right)} \right)} \right\} - \left[ {1 - \frac{{\mathop \prod \nolimits_{i = 1}^{m} \left( {1 - R_{i} \left( t \right)} \right)}}{{\mathop \prod \nolimits_{i = m - k + 1}^{m} \left( {1 - R_{i} \left( t \right)} \right)}}} \right] \\ & = - \mathop \prod \nolimits_{i = 1}^{m} \left( {1 - R_{i} \left( t \right)} \right) + \frac{{\mathop \prod \nolimits_{i = 1}^{m} \left( {1 - R_{i} \left( t \right)} \right)}}{{\mathop \prod \nolimits_{i = m - k + 1}^{m} \left( {1 - R_{i} \left( t \right)} \right)}} \\ & = \mathop \prod \nolimits_{i = 1}^{m} \left( {1 - R_{i} \left( t \right)} \right)\left\{ {\frac{1}{{\mathop \prod \nolimits_{i = m - k + 1}^{m} \left( {1 - R_{i} \left( t \right)} \right)}} - 1} \right\} \\ & = \mathop \prod \nolimits_{i = 1}^{m} \left( {1 - R_{i} \left( t \right)} \right)\left\{ {\frac{{1 - \mathop \prod \nolimits_{i = m - k + 1}^{m} \left( {1 - R_{i} \left( t \right)} \right)}}{{\mathop \prod \nolimits_{i = m - k + 1}^{m} \left( {1 - R_{i} \left( t \right)} \right)}}} \right\} \\ & = 1 - 1 + \mathop \prod \nolimits_{i = 1}^{m} \left( {1 - R_{i} \left( t \right)} \right)\left\{ {\frac{{1 - \mathop \prod \nolimits_{i = m - k + 1}^{m} \left( {1 - R_{i} \left( t \right)} \right)}}{{1 - 1 + \mathop \prod \nolimits_{i = m - k + 1}^{m} \left( {1 - R_{i} \left( t \right)} \right)}}} \right\} \\ & = \left[ {1 - \left\{ {1 - \mathop \prod \nolimits_{i = 1}^{m} \left( {1 - R_{i} \left( t \right)} \right)} \right\}} \right]\left\{ {\frac{{1 - \mathop \prod \nolimits_{i = m - k + 1}^{m} \left( {1 - R_{i} \left( t \right)} \right)}}{{1 - \left( {1 - \mathop \prod \nolimits_{i = m - k + 1}^{m} \left( {1 - R_{i} \left( t \right)} \right)} \right)}}} \right\} \\ & = \left[ {1 - {\text{Reliability of initial system}}} \right]\left[ {\frac{{\text{Reliability of removed system}}}{{1 - {\text{Reliability of removed system}}}}} \right] \\ & = \left[ {\text{Unreliability of initial system}} \right]\left[ {\frac{{\text{Reliability of removed system}}}{{\text{Uneliability of removed system}}}} \right]. \\ \end{aligned}$$

$$\begin{aligned} {\text{Now}},R_{{s_{f} }} \left( t \right) & = R_{{s_{i} }} \left( t \right) - \Delta_{i} {\text{R}}\left( {\text{t}} \right) \\ & = R_{{s_{i} }} \left( t \right) - \left[ {\text{Unreliability of initial system}} \right]\left[ {\frac{{\text{Reliability of removed system}}}{{\text{Uneliability of removed system}}}} \right]. \\ \end{aligned}$$

5 Application

The application of the present work can be visualised in call centres, customer care centre or feedback centres. These types of service centres are mainly used in telecom and communication sectors. Now a days, many manufacturing firms also use customer care centres to solve the queries of their customers and get feedback about their products which in turn help them to in improving the product quality. Call centres mainly use vocal communication. The call centre executives form a parallel structure i.e. when one calls a service centre any of the available executive can respond to the request or complaint reported by the customer. Let’s consider a case where there are four customer care executives available in the initial system as shown below in Fig. 6

Fig. 6

Initial system of four executives working in parallel

If we are interested in increasing the reliability of the above system by employing more people, then we need to increase the number of parallel paths. Suppose, three more people are employed, the final system can be represented by the following Fig. 7

Fig. 7

Transformed final system after adding more people

Here, we have taken initial system of four employees and final system contains seven employees for illustration purpose only. In real-life a call centre may have hundreds or thousands of employees which is quite a big system and calculating reliability of such systems is complex and difficult. If some more people are hired and this will involve more computation to obtain reliability of the final system. Reliability variation comes to aid in such situations and helps in obtaining reliability of the final system with less computation and save our time.

Sometimes, one of the customer care executives is already busy or absent from the initial system, then this reduces the number of parallel paths of the system as shown in Fig. 8

Fig. 8

Reduced final system after removing some people

We can use reliability variation here to find reliability of the final system and this avoids lengthy and complex calculation.

6 Illustration

Let’s consider an initial system of four identical components connected in parallel and following exponential failure laws as shown below in Fig. 9:

Fig. 9

Parallel system of four components

If all the components in initial system are identical and follow Exponential Failure Laws with failure rate λ, then

$$\begin{aligned} R_{{s_{i} }} \left( t \right) & = {\text{Reliability of the initial system}} = 1 - \mathop \prod \nolimits_{j = 1}^{4} \left( {1 - e^{ - \lambda t} } \right) \\ & = 4e^{ - \lambda t} - 6e^{ - 2\lambda t} + 4e^{ - 3\lambda t} - e^{ - 4\lambda t} . \\ \end{aligned}$$

Case 1: Suppose ‘p’ parallel paths are added to initial system given in Fig. 8, if added system components also follow exponential failure laws with failure rate λ′ and at t = 5, then reliability variation is obtained for the arbitrary values of the initial system components failure rate (λ), added system components failure rate (λ′) and number of added parallel paths (p). The results are shown numerically and graphically as:

Regression analysis:

ANOVA
	df	SS	MS	F	Significance F
Regression	3	2.61515	0.871717	267.3847	1.14E−34
Residual	61	0.19887	0.00326
Total	64	2.81402

	Coefficients	Standard error	t stat	P-value	Lower 95%	Upper 95%
Intercept	0	NA	NA	NA	NA	NA
λ	0.930418	0.052931	17.57792	1.47E−25	0.824576	1.036261
λ′	−0.58183	0.052931	−10.9923	4.22E−16	−0.68768	−0.47599
p	0.028157	0.005293	5.31949	1.57E−06	0.017572	0.038741

Regression statistics
Multiple R	0.964017
R 2	0.929329
Adjusted R2	0.910618
Standard error	0.057098
Observations	64

The linear regression model for reliability variation due to added parallel paths is given by.

$\Delta R = \left( {0.930418} \right)\lambda - \left( {0.58183} \right)\lambda^{^{\prime}} + \left( {0.028157} \right)p$.

From regression statistics, we have.

$R^{2} = 0.929329, \;{\text{adjusted }}R^{2} = 0.910618$ which show that the fitted regression model is a good fit.

Case 2: Suppose ‘k’ parallel paths are removed from initial system given in Fig. 8, then reliability variation is obtained for the arbitrary values of the initial system components failure rate (λ) and number of removed parallel paths (k). The results are shown numerically and graphically as:

Regression analysis:

ANOVA
	df	SS	MS	F	Significance F
Regression	2	0.839056	0.419528	91.76626	3.86E−09
Residual	16	0.073147	0.004572
Total	18	0.912204

	Coefficients	Standard error	t stat	P-value	Lower 95%	Upper 95%
Intercept	0	NA	NA	NA	NA	NA
λ	−0.22694	0.073773	−3.07621	0.007231	−0.38334	−0.07055
k	0.131375	0.0133	9.878023	3.26E-08	0.10318	0.159569

Regression statistics
Multiple R	0.959069
R 2	0.919813
Adjusted R2	0.852301
Standard error	0.067614
Observations	18

The linear regression model for reliability variation due to removed parallel paths is.

$\Delta R = \left( { - 0.22694} \right)\lambda + \left( {0.131375} \right)k$.

From regression statistics, we have.

$R^{2} = 0.919813, \;{\text{adjusted }}R^{2} = 0.852301$ which show that the fitted regression model is a good fit.

7 Discussion

An attempt has been made to determine the variation in reliability of a parallel series system of (m, n_i) order due to adding (or removing) arbitrary number of parallel paths. The study will serve the purpose to obtain the reliability of the transformed system with the help of reliability of the initial system and reliability of the added (or removed) system. The method devised in the manuscript will be applicable to other systems like series, parallel, series parallel and non-series parallel. This would help in determining directly the reliability of complex systems by avoiding the cumbersome computations.

8 Conclusion

The reliability variation has been obtained for a parallel series system of (m, n_i) order. The linear regression model is fitted to the reliability variation by taking a particular case of (4, 1) order system for both the cases (addition or removal of parallel paths). The values of R² and adjusted R² are calculated to check the best fit of the regression model to the data. It is observed that variation in reliability (increment/decrement) keeps on increasing with the addition/removal of parallel paths. Further, the variation in reliability (increment) becomes more with increase in failure rate of the components in the initial system, while it declines when failure rate of components on added system is increased. The reliability variation (decrement) decreases with the increase in failure rate of components of initial system. As, the values of R² and adjusted R² are very high, so we conclude that variation in reliability can be best predicted the linear regression model. The results are shown numerically and graphically, respectively, by Tables 1, 2 and Figs. 10, 11.

Table 1 Reliability versus failure rate of the components in initial system (λ), failure rate of the components in added system (λ′) and number of added parallel paths (p)

Table 2 Reliability versus failure rate of the components in initial system (λ) and Number Of Removed Parallel Paths (k)

Fig.10

Reliability versus failure rate of the components in initial system (λ), failure rate of the components in added system (λ′) and number of added parallel paths (p)

Fig.11

Reliability vs failure rate of the components in initial system (λ) and number of removed parallel paths (k)