1 Introduction

Composite materials are widely used in industry due to their excellent mechanical properties. High strength, stiffness, and lightness are some of the advantages for which composites are preferred over traditional materials [1]. The autoclave process [2] is vastly used to manufacture composites. The composite part is placed on the tool and subjected to a controlled high-pressure and high-temperature cycle. During this process, the resin polymerizes, i.e., a 3D network of bonds is created at the microscopic level, increasing the stiffness of the matrix. This increases the performance of the final part, reduces voids, and generates residual stresses and deformations induced by the curing process [3].

Many factors influence the stresses and deformations of the part, which may be intrinsic to the material—geometry, material properties—or extrinsic-tool/part interaction, curing cycle [4, 5]. During the process, the composite volume varies due to the different thermal expansion coefficients of the matrix and fiber. The non-homogeneous thermal expansion in different directions leads to stresses in the matrix along the fiber direction. On the other hand, chemical reactions due to resin polymerization that occur during the process cause volumetric contraction, i.e., chemical shrinkage. Residual stresses are also formed in this case. The geometric shape can also affect the formation of defects in the part after the curing cycle. U or L sections are more susceptible to deformation after demolding due to curved parts [6, 7]. Another factor affecting final performances is the difference between the thermal expansion coefficients of the tool and the part [8, 9]. As the tool heats up, it expands, causing high tensile stresses in the part. These stresses are most significant at the contact surface and decrease along the thickness of the composite, creating a stress gradient.

Part of the stress generated during the process is released, and induced deformations occur when the composite part is demoulded. The resulting deformations are warpages for flat parts and spring-in angles for curved parts. These deformations are strongly influenced by the change in mechanical properties of the matrix during the polymerization process. The mechanical properties of the composite are highly dependent on the degree of cure of the part. For this reason, numerous models have been proposed to describe the curing process. Loos and Springer [10] proposed a one-dimensional thermochemical model to predict temperature, degree of cure, viscosity, void size, and residual stress in a flat plate. Bogetti and Gillespie [11] performed a one-dimensional simulation analysis of the curing process to predict the stresses and strains induced by the process. They used a micromechanical model based on the law of mixtures to determine the composite’s mechanical properties, shrinkage, and thermal expansion coefficients. To determine the mechanical behavior of the resin, Johnston [12] proposed the cure hardening instantaneous linear elastic (CHILE) constitutive model. According to this approach, the material properties are calculated as the sum of the average values at each time step during the process. Takagaki [13, 14] used the CHILE model to solve C-shape and L-shape geometries. The CHILE model is not time-dependent. Viscoelastic or thermo-viscoelastic [15, 16] models were used to include time dependence.

Composite structures for aerospace applications usually have very stringent geometric tolerance requirements. Therefore, process-induced deformations are undesirable and lead to assembly difficulties, reduced fatigue life, and reliability problems [17, 18]. One way to evaluate the influence of different parameters on the final performance is to perform experimental tests [19,20,21]. However, this approach results in high costs, material waste, and long lead times. In addition, trial and error combined with experience does not always lead to the best configuration. Another approach is to use analytical solutions [21, 22], which often require simplifying assumptions. For this reason, utilizing numerical simulations proves highly beneficial in obtaining more accurate solutions and optimizing and improving composites’ performance. The Finite-Element Method (FEM) [23] is the most widely used approach to analyze even complex structures [24]. There are many applications where this method is used, such as in nonlinear analysis [25] and micromechanics [26]. Parambil et al. [27] used a computational FE model to evaluate residual thermal stresses at the microscale for a carbon fiber-reinforced composite. Qiao et al. [28] used a FE model to determine the deformations, considering the tool-part interaction. Kim et al. [29] evaluated the effects of material parameters on induced deformations using FE analysis.

The complexity of three-dimensional problems often results in high computational costs for the analysis. The present work adopts a different approach in which 1D models are used to lower the computational overhead. The 1D model is based on the Carrera Unified Formulation (CUF) [30] and was first used to analyze 2D plate and shell structures [31] and later extended to beams [32]. The significant advantage of CUF is its ability to provide accurate results comparable to 3D/FE models while limiting the computational cost. Over the years, CUF has been used in a wide range of problems, such as micromechanical analysis [33, 34], progressive damage assessment [35, 36], and analysis to evaluate process-induced deformations and stresses in composites [37, 38].

This work extends previous CUF models using a one-dimensional thermochemical model to predict the evolution of the degree of cure, temperature, and mechanical properties during the curing process of an epoxy resin and carbon fiber composite [11]. The process analysis is carried out using the CHILE method. Unlike conventional approaches reliant on commercial software like RAVEN [37], the new methodology of this work integrates inputs from the thermochemical model directly into the numerical simulation using CUF to assess final performances.

The paper is structured as follows: Sect. 2 describes the thermochemical and structural models, Sect. 3 presents numerical results, and Sect. 4 draws the conclusions.

2 Thermochemical and Structural Models

This section first describes the thermochemical model used to assess the degree of cure and the temperature of the composite part during the curing cycle. Then, the evaluation of the part’s mechanical properties over time and the refined one-dimensional (1D) structural model.

2.1 Thermochemical Model

In the thermochemical model considered, the one-dimensional heat transfer governing equation through thickness is coupled with the curing kinetics of the composite and the coupled system of equations is solved through an iterative procedure [11]. Temperature and degree of cure remain uncoupled at the time steps of the curing process, during which the two variables are considered constant. This can be assumed to be valid if the time steps are sufficiently small. The 1D Fourier equation for the heat transfer through thickness is

$$\begin{aligned} \dot{Q}+k\frac{\partial ^2T}{\partial z^2}=\rho C_p \frac{\partial T}{\partial t} \quad \textrm{for} \; T(z,t) \; \textrm{in} \; (0<z<l) \end{aligned}$$
(1)

where k is the thermal conductivity, \(\rho\) is the density of the material, and \(C_p\) is the specific heat. The thickness of the laminate is l. The temperature T varies along the direction z normal to the median plane and in time t. The internally generated heat per unit volume \(\dot{Q}\) results from the exothermic chemical reaction of the resin and is equal to

$$\begin{aligned} \dot{Q}=\rho H_{{\textrm{r}}}\frac{{\textrm{d}} \alpha }{{\textrm{d}} t} \end{aligned}$$
(2)

where \(H_{{\textrm{r}}}\) is the total heat released by the resin reaction, \(\alpha\) is the degree of cure and \({\textrm{d}} \alpha /{\textrm{d}} t\) is the cure rate. The degree of cure is expressed as a function of the instantaneous cure rate through the following expression:

$$\begin{aligned} \alpha (t)=\int _{0}^{t}\frac{{\textrm{d}} \alpha }{{\textrm{d}}t}{\textrm{d}}t \end{aligned}$$
(3)

Concerning the reaction kinetics model of the resin, several models are available. In this paper, the cure rate relationship is a function of temperature and degree of cure according to semi-empirical relationships, which differ depending on the type of resin chosen. The model used by Bogetti and Gillespie [11] for graphite/epoxy composites made from 3501-6 epoxy with AS4 carbon fibers is adopted:

$$\begin{aligned} \begin{aligned}&\frac{{\textrm{d}} \alpha }{{\textrm{d}} t}=(k_1+k_2 \alpha )(1-\alpha )(0.47-\alpha )&\quad \textrm{for} \; (\alpha \le 0.3) \\&\frac{{\textrm{d}} \alpha }{{\textrm{d}} t}=k_3(1-\alpha )&\quad \textrm{for}\; (\alpha > 0.3) \end{aligned} \end{aligned}$$
(4)

\(k_1\), \(k_2\) and \(k_3\) are the parameters defined by the following Arrhenius equation:

$$\begin{aligned} k_i=A_i {\textrm{e}}^{\frac{-\Delta E_i}{RT}}\quad \textrm{for} \; i=1, 2, 3 \end{aligned}$$
(5)

where \(A_1\), \(A_2\) and \(A_3\) are the pre-exponential coefficients while \(\Delta E_1\), \(\Delta E_2\) and \(\Delta E_3\) are the activation energies. The parameter R is the universal gas constant. The kinematic model proposed by Hubert and Johnston [39, 40] for a carbon fiber-reinforced Hexcel 8552 resin is described by a single modified autocatalytic equation:

$$\begin{aligned} \begin{aligned}&\frac{{\textrm{d}} \alpha }{{\textrm{d}} t}=\frac{K \alpha ^m (1-\alpha ^n)}{1+\textrm{e}^{C[\alpha -(\alpha _{C0}+\alpha _{CT}T)]}} \\&K=A \textrm{e}^{-\frac{\Delta E}{RT}} \end{aligned} \end{aligned}$$
(6)

where m, n, C, A, \(\alpha _{C0}\) and \(\alpha _{CT}\) are experimentally obtained parameters, while \(\Delta E\) is the activation energy. The values of the cure kinetic parameters for the two models are given in Table 1.

Table 1 Cure kinetic parameters for AS4/3501-6 and AS4/8552 materials
Full size table

In the thermochemical model, generalized boundary conditions can be expressed through the following relation: [40]:

$$\begin{aligned} a\frac{\partial T_{{\textrm{s}}}}{\partial z}+bT_{{\textrm{s}}}+cT(t)=0 \quad \textrm{for}\,\, z=0 \quad \textrm{and} \,\,z=l \end{aligned}$$
(7)

where \(T_{{\textrm{s}}}\) is the temperature on the surface and T is the temperature of the autoclave. The direction z is along the thickness. The values of the constants a, b, and c, given in Table 2, depend on the type of boundary condition that is applied.

Table 2 Generalized boundary condition coefficients
Full size table

Dirichlet boundary conditions impose a surface temperature on a part equal to the ambient temperature. Instead, the Neumann condition sets the temperature derivative at the boundary. The convection conditions are defined by Robin. The parameter \((h/k)_{{\textrm{eff}}}\) represents the ratio of the actual heat transfer coefficient to the actual thermal conductivity. In this work, convection is applied to the top surface, while at the bottom end, the temperature is assumed to be equal to that of the autoclave, assuming that the tool has a high thermal conduction.

2.2 Finite Elements for the Thermochemical Model

The finite-element method (FEM) is used to solve the system of equations of the thermochemical model. The composite part is modeled using a 1D model and discretized in the z direction of thickness in a number of finite elements.

The heat transfer equation is transformed into the weak form using the Galerkin method of weighted residuals. The terms of the equation are multiplied by the Galerkin weight function v(x) and integrated into the single element domain \([z_i \;z_j]\):

$$\begin{aligned} \int _{z_i}^{z_j} v(z)\frac{\partial T}{\partial t}{\textrm{d}}z=\frac{k}{\rho C_p}\int _{z_i}^{z_j} v(z) \frac{\partial ^2 T}{\partial z^2}{\textrm{d}}z+\frac{1}{\rho C_p}\int _{z_i}^{z_j} v(z) \dot{Q} {\textrm{d}}z \end{aligned}$$
(8)

Using integration by parts, the following relationship is obtained:

$$\begin{aligned}{} & {} \int _{z_i}^{z_j} v(z)\frac{\partial T}{\partial t}{\textrm{d}}z+\frac{k}{\rho C_p}\int _{z_i}^{z_j}\frac{\partial v(z)}{\partial z} \frac{\partial T}{\partial z}{\textrm{d}}z\nonumber \\{} & {} \quad =\frac{k}{\rho C_p} \bigg [v(z)\frac{\partial T}{\partial z}\bigg ]_{z_i}^{z_j}+\frac{1}{\rho C_p}\int _{z_i}^{z_j} v(z) \dot{Q} {\textrm{d}}z \end{aligned}$$
(9)

The temperature \(T^e(z,t)\) at each point along the thickness of the element is modeled through the shape functions \(\textbf{N}\):

$$\begin{aligned} T^e(z,t)=\textbf{N}(z) \textbf{T}^{e}(t) \end{aligned}$$
(10)

with

$$\begin{aligned} \textbf{N}&=\big [N_1(z), N_2(z),\ldots , N_m(z)\big ] \end{aligned}$$
(11)
$$\begin{aligned} \textbf{T}^{e^T}&=\big [T^e_1(t), T^e_2(t),\ldots , T^e_m(t)\big ] \end{aligned}$$
(12)

where \(\textbf{T}^e\) is the vector of nodal temperatures and m is the number of nodes in the element. Since \(\textbf{N}\) depends only on z and \(\textbf{T}\) depends only on t, the derivatives are defined as

$$\begin{aligned} \frac{\partial T^e}{\partial z}&=\frac{\partial }{\partial z} (\textbf{N} \textbf{T}^e)= \frac{\partial \textbf{N}}{\partial z} \textbf{T}^e= \textbf{B}(z) \textbf{T}^{e}(t) \end{aligned}$$
(13)
$$\begin{aligned} \frac{\partial T^e}{\partial t}&=\frac{\partial }{\partial t} (\textbf{N} \textbf{T}^e)= \textbf{N}\frac{\partial \textbf{T}^e}{\partial t} = \textbf{N}(z) \dot{\textbf{T}}^{e}(t) \end{aligned}$$
(14)

where \(\textbf{B}\) contains derivatives of the shape functions. The internally generated heat \(\dot{Q}\) can also be expressed by applying the finite-element approximation:

$$\begin{aligned} \dot{Q}(z,t)=\textbf{N}(z)\textbf{b} \end{aligned}$$
(15)

with:

$$\begin{aligned} \textbf{b}^T=[\dot{Q}_1(t), \dot{Q}_2(t),\ldots ,\dot{Q}_m(t)] \end{aligned}$$
(16)

By substituting Eqs. 13, 14 and 15 into Eq. 9 and imposing the weight function v(x) equal to the shape function \(\textbf{N}^T\), the following compact form is obtained:

$$\begin{aligned} \textbf{C}^e \dot{\textbf{T}}^e+\textbf{K}^e \textbf{T}^e=\textbf{q}^e+\textbf{M}^e \textbf{b} \end{aligned}$$
(17)

where

$$\begin{aligned} \begin{aligned} \textbf{C}^e&=\int _{z_i}^{z_j}\textbf{N}^T \textbf{N} {\textrm{d}}z\\ \textbf{K}^e&=\frac{k_c}{\rho C_p}\int _{z_i}^{z_j}\textbf{B}^T \textbf{B}{\textrm{d}}z\\ \textbf{q}^e&=\frac{k}{\rho C_p} \bigg [\textbf{N}^T \textbf{B} \textbf{T}^{e} \bigg ]_{z_i}^{z_j}\\ \textbf{M}^e&=\frac{1}{\rho C_p}\int _{z_i}^{z_j} \textbf{N}^T \textbf{N}{\textrm{d}}z \end{aligned} \end{aligned}$$
(18)

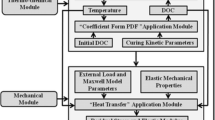
An approximate solution of the Eq. 17 to find temperature and degree of cure is possible by considering the two variables uncoupled in the individual time steps \(\Delta t\) [41]. The accuracy of the solution is higher if the steps are sufficiently small. In this work, this approach is sufficient to obtain accurate results with low computational times, given the model’s simplicity. More efficient methods, such as an Euler forward scheme, may also be used and considered in future works. The flowchart in Fig. 1 shows the iterative procedure. It is assumed that \(\mathbf {T_n}\) is the temperature at time instant \(t_n\), while \(\mathbf {T_{n+1}}\) is the temperature at the next time instant \(t_{n+1}\).

2.3 Material Properties

The Young’s modulus of the resin can be expressed as a function of the degree of cure through the following relationship [11]:

$$\begin{aligned} E_m=(1-\alpha _{{\textrm{mod}}})E_m^0+\alpha _{{\textrm{mod}}}E_m^{\infty } \end{aligned}$$
(19)

with

$$\begin{aligned} \alpha _{{\textrm{mod}}}=\frac{\alpha -\alpha _{{\textrm{gel}}}^{{\textrm{mod}}}}{\alpha _{{\textrm{diff}}}^{{\textrm{mod}}}-\alpha _{{\textrm{gel}}}^{{\textrm{mod}}}} \end{aligned}$$
(20)

where the parameters \(E_m^0\) and \(E_m^{\infty }\) are the fully uncured and fully cured modules, respectively. \(\alpha _{{\textrm{gel}}}^{{\textrm{mod}}}\) is the gelation point, and \(\alpha _{{\textrm{diff}}}^{{\textrm{mod}}}\) is the degree of cure value that the resin reaches at the end of the process. The instantaneous shear modulus is obtained from the isotropic relationship of the material:

$$\begin{aligned} G=\frac{E_m}{2(1+\nu _m)} \end{aligned}$$
(21)

where \(\nu _m\) is the Poisson’s coefficient, it is assumed constant. The mechanical properties of the fibers, on the other hand, do not vary during the process. During the curing cycle, in addition to the change in the elastic properties of the composite, there is a volume change caused by the heat flow to which the part is subjected in the autoclave and by the exothermic chemical polymerization reactions that occur during the process. The change in volume makes an essential contribution to the generation of internal stresses, which consequently cause macroscopic deformations in the part. The increase in the chemical shrinkage \(\Delta V_m\) is directly proportional to the rise in the degree of cure \(\Delta \alpha\) through the following relationship [11]:

$$\begin{aligned} \Delta V_m=\frac{\Delta \alpha }{\alpha _{{\textrm{diff}}}^{sh}}V_{\textrm{sh}} \end{aligned}$$
(22)

where \(V_{\textrm{sh}}\) is the total shrinkage volume when the resin is fully cured and \(\alpha _{{\textrm{diff}}}^{sh}=1\). The isotropic shrinkage strain \(\Delta \epsilon _m\) is calculated as

$$\begin{aligned} \Delta \epsilon _m=\root 3 \of {1+\Delta V_m}-1 \end{aligned}$$
(23)

To find the homogeneous elastic properties of the composite, the chemical shrinkage strains, and the thermal expansion coefficients along the thickness, a micromechanical model based on the law of mixtures presented exhaustively by Bogetti et al. [11] is adopted.

Fig. 1
figure 1

Flowchart of the curing process simulation

Full size image

2.4 Carrera Unified Formulation

The material properties obtained from the thermochemical model are used to derive the deformations and stresses induced by the curing process. A refined one-dimensional model based on the Carrera unified formulation (CUF) is used for this purpose. More details on CUF can be found in the book by Carrera et al. [30]. The reference system of the 1D model consists of the y axis aligned with the beam axis, while the x and z axes are relative to the beam cross-section, as shown in Fig. 2. The vector of displacements is defined as

$$\begin{aligned} \textbf{u}^T=\{u_x,\; u_y, \;u_z\} \end{aligned}$$
(24)

where \(u_x\), \(u_y\) and \(u_z\) are the displacement components in the three directions.

Fig. 2
figure 2

Reference coordinate system of the beam

Full size image

Strains can be calculated from displacements using the geometric relation:

$$\begin{aligned} \varvec{\epsilon }=\textbf{D}\textbf{u} \end{aligned}$$
(25)

where \(\textbf{D}\) is the matrix of linear differential operators. The constitutive equation is

$$\begin{aligned} \varvec{\sigma }=\textbf{C}\varvec{\epsilon } \end{aligned}$$
(26)

where \(\textbf{C}\) is the matrix of material stiffness coefficients. The strain and stress vectors consist of the following components:

$$\begin{aligned} \varvec{\epsilon }^T&=\{\epsilon _{xx},\; \epsilon _{yy},\; \epsilon _{zz},\; \epsilon _{xz},\; \epsilon _{yz},\; \epsilon _{xy}\}\end{aligned}$$
(27)
$$\begin{aligned} \varvec{\sigma }^T&=\{\sigma _{xx},\; \sigma _{yy},\; \sigma _{zz},\; \sigma _{xz},\; \sigma _{yz},\; \sigma _{xy}\} \end{aligned}$$
(28)

According to the CUF-based 1D kinematic model, the cross-section displacement field can be written as an expansion of Lagrange functions:

$$\begin{aligned} \textbf{u}=\textbf{u}_{\tau }(y)F_{\tau }(x,z), \quad \tau =1,\ldots ,M \end{aligned}$$
(29)

where \(F_{\tau }(x,z)\) is the expansion function on the cross-section, M is the number of terms of the expansion function, and \(\textbf{u}_{\tau }(y)\) is the vector containing the unknown displacements along the axis of the beam. If a 9-node Lagrange element (L9) is used for the cross-section, the displacement field is written as

$$\begin{aligned} \textbf{u}=\sum _{\tau =1}^{9} \textbf{u}_\tau F_\tau \end{aligned}$$
(30)

The unknowns \(\textbf{u}_{\tau }(y)\) can be approximated using FEM, Eq. 29 becomes

$$\begin{aligned} \textbf{u}=\textbf{u}_{i\tau }N_i(y)F_{\tau }(x,\;z), \quad \tau =1,\ldots ,M; \quad i=1,\ldots ,N_n \end{aligned}$$
(31)

where \(N_i(y)\) are the shape functions of the FE model, \(\textbf{u}_{i\tau }\) are the nodal unknowns and \(N_n\) are the number of element nodes.

The CHILE [12] approach is used to simulate the curing process. The process is discretized into a number of steps in which the material properties are considered constant and equal to the average value in that step. The final solution is the sum of all solutions in each step. In the i-th step, a static linear problem can be solved as follows [37]:

$$\begin{aligned} \textbf{K}^i \Delta \textbf{u}^i=\Delta \textbf{F}^i \end{aligned}$$
(32)

where \(\textbf{K}^i\) is the stiffness matrix of the model evaluated in the i-th step, \(\textbf{F}^i\) is the load vector in the i-th step and \(\Delta \textbf{u}^i\) are the unknown displacement increments. The model consists of the part, the tool and the interface shear layer. The shrinkage increments and thermal strains, \(\Delta \varvec{\epsilon }_{{\textrm{s}}}^i\) and \(\Delta \varvec{\epsilon }_t^i\), represent the external loads at the i-th step. Once the linear system of a given step has been solved, the strain and stress increments can be found through the geometrical and constitutive laws, respectively. The matrix \(\textbf{K}^i\) and the force vector \(\textbf{F}^i\) contain the stiffness and force contributions of the part, the tool and the interface. The forces acting on the part are due to shrinkage and thermal loads but also to interface forces. It is possible to calculate the magnitude of the interface forces \(\textbf{F}_{tr}\) and, consequently, the displacements caused by tool removal can be calculated by solving the following linear system:

$$\begin{aligned} \textbf{K}_p \Delta \textbf{u}_{tr}=\textbf{F}_{tr} \end{aligned}$$
(33)

where \(\textbf{K}_p\) is the stiffness matrix of the composite part. Residual displacements, strains and stresses can be calculated as the sum of the contributions due to the of curing cycle and those due to the removal of the tool:

$$\begin{aligned} \textbf{u}^f&=\sum _{i_1}^{N} \Delta \textbf{u}_p^i+\textbf{u}_{tr} \end{aligned}$$
(34)
$$\begin{aligned} \varvec{\epsilon }^f&=\sum _{i_1}^{N} \Delta \varvec{\epsilon }_p^i+\varvec{\epsilon }_{tr} \end{aligned}$$
(35)
$$\begin{aligned} \varvec{\sigma }^f&=\sum _{i_1}^{N} \Delta \varvec{\sigma }_p^i+\varvec{\sigma }_{tr} \end{aligned}$$
(36)

Figure 1 shows the flowchart of the iterative procedure.

3 Numerical Results

In this section, the numerical approach introduced in the previous chapter is used to evaluate a composite plate’s deformation and stress field induced by the curing process. The thermochemical model is initially verified using the solution proposed in Ref. [11]. Then, the model is used to evaluate the change in mechanical properties during the process and the impact of process parameters on the temperature and degree of cure of a flat plate. Furthermore, process-induced stresses along the thickness are evaluated using the refined one-dimensional kinematic model, and the influence of process parameters is investigated.

3.1 Thermochemical Model Verification

The laminate is made of 3501-6 epoxy resin and unidirectional AS4 graphite fibers. The thickness of the composite is \(2.54 \;\textrm{cm}\), and the fiber volume fraction is 67%. The cure kinetic parameters are shown in Table 1, while the density \(\rho =1.52 \times 10^3\; \frac{{\textrm{kg}}}{{\textrm{m}}^3}\), the specific heat \(c_p=942\; \frac{{\textrm{J}}}{{\textrm{W}}^{\circ }{\textrm{C}}}\) and the thermal conductivity \(k=4.457 \times 10^{-1}\; \frac{{\textrm{W}}}{{\textrm{m}}^{\circ }{\textrm{C}}}\). The curing process for this material involves two holding temperatures at \(161 ^{\circ }{\textrm{C}}\) and \(177 ^{\circ }{\textrm{C}}\) for 70 min and 127 min, respectively, and a heating rate of \(2.24 \; \frac{{\textrm{K}}}{{\textrm{min}}}\), as shown in Fig. 3.

The thermochemical 1D FE model that discretizes the structure consists of ten elements along the thickness. Convection boundary conditions are applied to both the top and bottom faces. Figure 3 compares the degree of cure and temperature during the cure cycle with the reference results of Bogetti et al. [11]. As expected, the exothermic nature of the polymerization reaction results in a peak when the autoclave temperature is kept constant. The good match between the results demonstrates the accuracy of the thermochemical model used in this work. The slight differences in the cure degree results may be due to a different choice of initial cure degree, as this was not specified in the reference.

Fig. 3
figure 3

Comparison of temperature and degree of cure prediction for a given curing cycle with Bogetti’s reference results [11]

Full size image

3.2 Effect of Process Parameters

The composite material adopted for the following results consists of an 8552 matrix reinforced with AS4 carbon fibers. The part is a plate 2.54 cm thick and consists of eight layers of equal thickness. The fiber volume fraction is 57.3%, whereas the density \(\rho =1.58 \times 10^3\; \frac{{\textrm{kg}}}{{\textrm{m}}^3}\), the specific heat \(c_p=870\; \frac{{\textrm{J}}}{{\textrm{W}} ^{\circ } {\textrm{C}}}\) and the thermal conductivity \(k=0.69\; \frac{{\textrm{W}}}{{\textrm{m}} ^{\circ } {\textrm{C}}}\). The stacking sequence is \((90/0/90/0)_{{\textrm{s}}}\). The lamination angle is zero when the fibers are aligned with respect to the x axis of the part. The composite component is placed on an Invar tool of thickness 0.01 m, Young’s modulus of \(150 \; \textrm{GPa}\), Poisson ratio of 0.28 and density of \(8140 \; \frac{{\textrm{kg}}}{{\textrm{m}}^3}\). The thermal expansion coefficient is \(1.56 \times 10^{-6} \; /^{\circ }\textrm{C}\). Friction between the tool and the part is not considered. A convection boundary condition is applied at the top of the structure. A Dirichlet boundary condition is applied at the bottom to simulate the presence of the tool. The cure cycle consists of a heating rate of \(1.8 \; ^{\circ }{\mathrm {C/min}}\) and a holding temperature of \(177 \; ^{\circ }{\textrm{C}}\) for \(200 \; \textrm{min}\) as shown in Fig. 4. The degree of cure and temperature are obtained using a 1D thermochemical model, whose cure kinetic parameters are shown in Table 1. In Fig. 4, the two process variables are evaluated in the center of the structure thickness.

Fig. 4
figure 4

Curing cycle adopted

Full size image

During the cure cycle, the temperature and degree of cure do not remain homogeneous along the thickness. Figure 5 shows the temperature and degree of cure distributions along the thickness after the gelation point. The heat from the autoclave heats the surfaces first, making them warmer than the center of the part. As the chemical reactions progress, the temperature profile changes, and the intermediate layers become warmer as the exothermic reaction heat is generated. After the autoclave temperature is maintained, the temperature in the layers becomes homogenous. Finally, the surface temperature decreases earlier during the cooling phase until the entire part reaches room temperature. The degree of cure profiles also varies depending on the time step considered (Fig. 5b). As the process goes on, the degree of cure increases and becomes uniform throughout the part.

Fig. 5
figure 5

Distributions of temperature and degree of cure along the thickness at various stages of the curing cycle

Full size image

The mechanical properties were obtained from the law of mixtures and vary during the curing process, depending on the degree of cure of the part. Young’s moduli, shear moduli, and Poisson’s ratios are shown in Fig. 6 starting from the gelation point, which is 0.469 and evaluated at the middle layer.

Fig. 6
figure 6

Material properties evolution during the curing process

Full size image

The effect of varying process parameters on temperature and degree of cure is evaluated by considering variations of individual parameters and starting from the reference cycle considered in Fig. 2; all other parameters are fixed. The temperature of the autoclave is indicated by \(T_a\), while the temperature and degree of cure of the part are T and \(\alpha\), respectively.

Figure 7a shows the effect of the fiber volume fraction on the temperature and degree of cure. The effect of the maximum temperature holding time, heating, and cooling rate are shown in Fig. 7b, and 8a, b, respectively. Figure 9 shows the effect of the holding temperature; first, consider different temperature values, then consider a decreasing value. The results show that

  • Variations in fiber volume fraction, holding time, heating, and cooling rate do not lead to significant variations in the curing of the part.

  • Varying the holding temperature significantly impacts the cycle. Considering lower temperatures than the reference cycle leads to slower curing and a lower degree of cure.

  • The last case considered, with a decreasing holding temperature, shows no significant variations in the final curing values. Such a result could help decrease the energy required for the curing process.

Fig. 7
figure 7

Comparison of temperature and degree of cure considering three different fiber volume fractions and three holding times

Full size image
Fig. 8
figure 8

Comparison of temperature and degree of cure considering three different heating rates and three cooling rates

Full size image
Fig. 9
figure 9

Comparison of temperature and degree of cure considering three different holding temperatures and with a modified holding phase

Full size image
Table 3 Final degree of cure and \(\sigma _{xx}\) at the mid-plane of the part thickness for various process parameters
Full size table

3.3 Process-Induced Stress Evaluation

The FE model of the part consists of two cubic beam elements, as shown in Fig. 10. Only one-quarter of the structure is considered due to the double symmetry of the structure. An additional symmetry plane is used at the bottom of the tool to prevent displacement in the z direction. The tool/part interface is modeled to simulate the absence of friction with a very low shear stiffness of the shear layer. One nine-node Lagrange element (L9) is used for the tool, one for the shear layer, and one for each part layer (Fig. 10). Overall, the FE model has 1323 degrees of freedom. The part’s material properties are considered constant in thickness and equal to the values found at the structure’s mid-plane.

Fig. 10
figure 10

Structural model

Full size image

The influence of the variation of the process parameters on the residual stresses of the part is evaluated. In Figs. 11, 12 and 13, the in-plane and transverse shear stress distributions after tool removal are compared by varying the fiber volume fraction, the temperature holding, and the curing cycle, respectively. Table 3 reports the final degree of cure and the \(\sigma _{xx}\) residual stress of the mid-plane of the thickness for various values of the volume fraction (\(V_{{\textrm{f}}}\)), holding time (HT), heating and cooling rate (HR and CR), holding temperature (\(T_{{\textrm{max}}}\)). The results show that

  • The use of layer-wise structural models has led to the continuity at the layer interfaces of \(\sigma _{xz}\) and null shear stress at the free surfaces.

  • The variation of the fiber volume fraction does not result in a significant variation in residual stresses after removing the tool. In contrast, variation in the maximum holding temperature of the curing cycle greatly impacts the final stress state of the part, as shown in Fig. 12. The higher the temperature, the higher are the in-plane and transverse stresses.

  • The modified cycle brings no significant differences in the residual stresses.

Fig. 11
figure 11

Comparison of stress distributions through the thickness with varying fiber volume fractions

Full size image
Fig. 12
figure 12

Comparison of stress distributions through the thickness with varying holding temperatures

Full size image
Fig. 13
figure 13

Comparison of stress distributions in the modified and reference cycles

Full size image

4 Conclusion

This paper has presented numerical results concerning the residual stresses induced by the curing process of a composite part. The influence of various process parameters on the stress state at the end of curing was investigated. A 1D thermochemical model was used to assess the temperature evolution and degree of cure during the process. A composite plate was considered. The mechanical properties were evaluated as a function of the degree of cure. The cure hardening instantaneously linear elastic (CHILE) approach was used to simulate the curing process. The evolution of the mechanical properties during the process is used by a refined 1D model based on the Carrera unified formulation (CUF) to accurately determine the residual stresses from the process in the thickness. The structural model is layer-wise, i.e., each layer retains the thermochemical and mechanical properties as the curing process proceeds. The following conclusions may be drawn:

  • The holding temperature greatly impacts the final degree of cure. On the other hand, varying the holding time, cooling rate, and heating rate do not significantly affect the final degree of cure.

  • The variation of the holding temperature leads to significant changes in the in-plane and transverse stresses. The higher the maximum temperature reached during the cure cycle, the higher the process-induced stresses once the part has been removed from the tool.

  • A modified cure cycle was proposed, involving a gradual decrease in the holding temperature. This modification was aimed at reducing the energy consumption of the process. The results indicated that this modified cycle had no significant impact on the final cure degree and induced stress of the cured part.

Future work should involve the experimental validation and the optimization of the curing process on more complex configurations, e.g., curved parts and spars.