1 Introduction

Supersonic ejectors are well accepted in many fields of application. They are simple mechanical devices, with ease of manufacturing, no moving parts, and can be powered by low-grade or waste heat [1]. It utilizes the venturi effect to convert enthalpy of motive primary fluid into kinetic energy to pump [2], compress, mix, and/or recompression of two streams by momentum and energy transfer. The high-pressure motive fluid is accelerated to a supersonic fluid through the converging–diverging nozzle. The pressure at the nozzle exit is below that of the secondary (entrained) flow at the inlet, which results in the secondary fluid being induced into the suction chamber. Both primary and secondary streams enter the mixing section, where complex interactions take place between the primary supersonic flow and subsonic secondary flow. During the intense interaction of primary and secondary streams and exchange of their momentum, kinetic and internal energies into the mixing section generate alternate oblique shocks and expansion waves. The mixed stream enters to diffuser section to convert its kinetic energy into enthalpy and hence rise in static pressure.

The global performance parameter of the ejector is often measured by the entrainment ratio (ω), which is a ratio of secondary to primary mass flow rate. The previous efforts on ejector performance improvement were focused on design approaches [3,4,5] and optimization of geometrical parameters [6,7,8,9] and operating parameters [10, 11].

To reduce the optimization cost, the ejector geometry needs to be calculated based on the variation of the flow energy along with the system for the given operating conditions [8]. The first isentropic/adiabatic CRMC one-dimensional gas dynamic model for the design of the diffuser section was proposed by Eames [3]. This approach was based on the assumption that the rate of momentum change shall be constant along with the diffuser. The later study [12] modified the CRMC approach considering the frictional effect in the model to design the complete ejector system. A similar method, i.e., Constant Rate Kinetic Energy change, is proposed by Kumar et al. [13].

Design improvement and optimization of geometrical parameters of the ejector system and its performance have been a challenge for researchers in recent years. The mixing section of a supersonic ejector geometry is critical among the other sub-sections (nozzle, suction, and diffuser), generating the highest entropy during mixing. Due to this, geometry computation of the mixing section is noted as the most crucial step toward physics-based ejector design. In the literature, the researchers considered for the mixing part a straight cylindrical (constant area design) [4] duct and determined its length using experimental and numerical trials. Later studies considered the mixing section to a converging cone (constant-pressure mixing approach) [5] and variable area over a selected length [14].

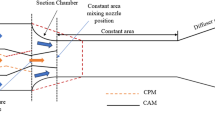
The shape of the mixing section and nozzle exit position (NXP) are important geometrical parameters of the ejector system. The nozzle exits position (NXP) of an ejector system not only controls the jet expansion angles, but also controls the converging space for secondary flow to be entrained in the mixing/entrainment region. The literature states that moving the NXP away or into the mixing chamber affects the performance of the system [15,16,17]. It has also been found that NXP is one of the most influential geometrical parameters after the geometry of the mixing section, among others, which affect the overall system performance.

So the present study is divided into two parts: The first part describes the CRMC theory with frictional effect for the computation of high-performance variable area mixing section profile and the second part on effect of NXP on the ejector performance. It is expected that CRMC-based variable area mixing geometry will help in minimize mixing losses, optimization of nozzle exit position, and selection of high-performance ejector system.

2 One-dimensional theory for mixing section design

The ejector performance is directly affected by the irreversibility associated due to the intense mixing and shock generation in the mixing region. So, a clear understanding of mixing effect, compression of streams, occurrence of alternate oblique and/or expansion waves, and the role of the geometrical profile of the mixing section is essential to compute high-performance ejector. For this, an axis-symmetric ejector is considered in the present work. In this section, the one-dimensional compressible flow theory has been used to determine the mixing section geometrical profile and flow parameters. The methodology of internal profile computation of the CRMC mixing section is based on adiabatic SSSF equations of mass, momentum, and energy [8].

The baseline equation for CRMC mixing region is enunciated as follows:

$$\frac{{{\text{d}}\dot{M}}}{{{\text{d}}x}} = \dot{m}_{p} \left( {1 + \omega } \right)\frac{{{\text{d}}V}}{{{\text{d}}x}} = \lambda$$
(1)

where λ (kg/s2) is the rate of momentum change constant. The CRMC constant is varied to get a variety of mixing section profiles for given design conditions. The value of λ is + ve while moving toward section 1-1’ from section 2-2’ (refer Fig. 1). The velocity gradient is computed for selected CRMC constant (λ) using the following equation, deduced from Eq. (1).

Fig. 1
figure 1

CRMC mixing section [13]

Full size image
$$\frac{{{\text{d}}V}}{{V_{i,x} }} = \frac{{\lambda {\text{d}}x}}{{\dot{m}_{p} \left( {1 + \omega } \right)V_{i,x} }}$$
(2)

The deduced set of relations for change in the area of the mixing section and corresponding change in flow parameters of interest at any ith location along flow direction (x) are enumerated as follows.

Change in the local cross-sectional area \(\left( {{\text{d}}A} \right)\):

$$\frac{{{\text{d}}A}}{{A_{i,x} }} = \frac{\gamma }{2}M_{i,x}^{2} \frac{{4f_{i,x} {\text{d}}x}}{{D_{i,x} }} + \left( {M_{i,x}^{2} - 1} \right)\frac{{\lambda {\text{d}}x}}{{\dot{m}_{p} \left( {1 + \omega } \right)V_{i,x} }}$$
(3)

where local Fanning friction factor f is defined as:

$$f = \frac{0.0625}{{\mathop {\left[ {\mathop {\log }\nolimits_{10} \left( {\frac{K}{3.7D} + \frac{5.74}{{\mathop {\text{Re} }\nolimits^{0.9} }}} \right)} \right]}\nolimits^{2} }}$$
(3a)

The local Fanning friction factor (f) was derived by using the Darcy friction factor and Swami Jan equation [13].

Change in local static pressure \(\left( {dP} \right){:}\)

$$\frac{{{\text{d}}P}}{{P_{i,x} }} = - \left[ {1 + \left( {\gamma - 1} \right)M_{i,x}^{2} } \right]\frac{\lambda dx}{{\dot{m}_{p} \left( {1 + \omega } \right)V_{i,x} }} - \frac{{{\text{d}}A}}{{A_{i,x} }}$$
(4)

Change in local static temperature \(\left( {{\text{d}}T} \right){:}\)

$$\frac{{{\text{d}}T}}{{T_{i,x} }} = \left[ {\left( {1 - \gamma } \right)M_{i,x}^{2} } \right]\frac{{\lambda {\text{d}}x}}{{\dot{m}_{p} \left( {1 + \omega } \right)V_{i,x} }}$$
(5)

Change in local Mach number \(\left( {{\text{d}}M} \right){:}\)

$$\frac{{{\text{d}}M}}{{M_{i,x} }} = \left[ {1 + \frac{\gamma - 1}{2}M_{i,x}^{2} } \right]\frac{{\lambda {\text{d}}x}}{{\dot{m}_{p} \left( {1 + \omega } \right)V_{i,x} }}$$
(6)

The flow properties at the next location (i + 1) at a distance of dx from the ith location are calculated by adding the values calculated at an ith location in the change in the local area, pressure, temperature, and Mach number.

The total pressure and temperature in the mixing region at the i + 1th location is calculated using Eqs. (7) and (8).

$$P_{0,i + 1, x} = P_{i + 1, x} \left[ {1 + \frac{\gamma - 1}{2}M_{i + 1,x}^{2} } \right]^{\gamma /\gamma - 1}$$
(7)
$$T_{0,i + 1, x} = T_{i + 1, x} \left[ {1 + \frac{\gamma - 1}{2}M_{i + 1,x}^{2} } \right]^{{}}.$$
(8)

3 Method of solution and computation of geometrical profile

For the mixing region of the ejector, a separate program was developed based on the CRMC theory discussed in Sect. 2. The internal profile of the mixing section is computed using a separate MATLAB program by employing Euler’s method. The changes in the radius of the profile and corresponding flow parameters were computed at each small step (say dx = 0.5 mm) locally. To reduce computational time and manufacturing cost, the results were rounded off to three significant decimal places. The design parameters listed in Table 1 are used to compute the geometrical profile, numerical, and experimental study.

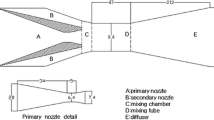
Table 1 List of parameters for computation of CRMC mixing section and ejector profile
Full size table

The mixing section geometry computation starts with the calculation of the static pressure at virtual section A-A’ and thermodynamic properties at the exit of the mixing section 2-2’. Thermodynamic properties at the exit of the mixing section (2-2’) and section A-A’ were computed based on constant pressure mixing theory presented by Kumar et al. [13]. The flow area and corresponding flow parameters of the mixing section were calculated at any ith location by moving toward section (1-1’) from section (2-2’). The flowchart for the overall computation for CRMC mixing section profile and flow parameters is shown in Fig. 2. The selected value of CRMC constant (λ) was 58.5 kg/s2 for CFD and experimental validation as it generates a mixing section with \(L_{\text{m}} /D_{\text{m}}^{*} \approx 7\), as recommended by ESDU [18], where \(D_{\text{m}}^{*}\) is the diffuser throat, while in the present case it is equal to the mixing section exit diameter \(\left( {D_{\text{m, e}} } \right).\) The nozzle and diffuser profiles of the ejector system were computed based on the theory presented by Kumar et al. [12]. The geometrical specification of computed ejector geometry at selected locations is given in Table 2.

Fig. 2
figure 2

Execution flowchart for the mixing section computation

Full size image
Table 2 Geometrical specification of ejector at specific locations
Full size table

3.1 Computational fluid dynamic (CFD) study

The actual flow through the ejector system considered in this study is an axisymmetric, steady, turbulent, and compressible flow. All the flow variables are expected to vary along with axial and radial directions. One-dimensional gas dynamics theory can be considered equivalent to area-averaged axisymmetric flow. Due to this simplification, an ejector geometry, which is based on one-dimensional theory, cannot be directly manufactured for experimental study. An intermediate verification step, namely the gas dynamic computational study of the geometry, is essential. So, a detailed CFD study for the ejector geometry was performed using ANSYS-Fluent 14.0.

3.2 Mesh generation

The geometry of ejector and mesh generation was performed using GAMBIT software. The structured quadrilateral mesh was used in axisymmetric 2D computational domain. This type of mesh has better control of alignment with surface profile and cell aspect ratio. The adaptive grid technique was employed in the region of higher gradients of velocity. Near the wall, higher velocity gradients and in mixing region dense mesh used to capture boundary layer and mixing phenomenon. The ejector performance parameter, the entrainment ratio (ω) was considered to study grid dependency by increasing meshes from the coarse level to a fine level. The performance parameter was not found to change significantly with an increase in cells beyond a mesh no. 38858. Increasing the number of cells beyond 38858 was seen to be unnecessary as the variation was found to be less than 2%.

3.3 Governing equations and turbulence model

The steady-state, axis-symmetric, compressible flow equations in conservation form deal the fluid flow in a supersonic ejector system. The Favre averaged Navier–Stokes equation was used for variable-density flow. The viscous dissipation and total energy equations are coupled with the ideal gas law. The compact Cartesian form of governing equations can be written as [13]:

Continuity equation:

$$\frac{\partial }{{\mathop {\partial x}\nolimits_{i} }}(\mathop {\rho u}\nolimits_{i} ) = 0$$
(9)

Momentum equation:

$$\frac{\partial }{{\mathop {\partial x}\nolimits_{j} }}\left[ {\mathop {\rho u}\nolimits_{i} \mathop u\nolimits_{j} } \right] = - \frac{\partial P}{{\mathop {\partial x}\nolimits_{i} }} + \frac{{\mathop {\partial \tau }\nolimits_{ij} }}{{\mathop {\partial x}\nolimits_{j} }}$$
(10)
$$where\;\;\mathop \tau \nolimits_{ij} = \mathop \mu \nolimits_{eff} \left( {\frac{{\mathop {\partial u}\nolimits_{i} }}{{\mathop {\partial x}\nolimits_{j} }} + \frac{{\mathop {\partial u}\nolimits_{j} }}{{\mathop {\partial x}\nolimits_{i} }}} \right) - \frac{2}{3}\mathop \mu \nolimits_{eff} \frac{{\mathop {\partial u}\nolimits_{k} }}{{\mathop {\partial x}\nolimits_{k} }}\mathop \delta \nolimits_{ij}$$
(10a)

Here \(\mathop \delta \nolimits_{ij}\) is Kronecker delta, and is ‘1’ for \(i = j\) and is ‘0’ for \(i \ne j\) energy equation:

$$\frac{\partial }{{\mathop {\partial x}\nolimits_{i} }}\left[ {\mathop u\nolimits_{i} \left( {\rho E + P} \right)} \right] = \overrightarrow {\nabla } \cdot \left( {\alpha_{\text{eff}} \frac{\partial T}{{\mathop {\partial x}\nolimits_{i} }} + \mathop u\nolimits_{j} \left( {\mathop \tau \nolimits_{ij} } \right)} \right)$$
(11)

The equation of state:

$$\rho = \frac{P}{RT}$$
(12)

The semi-empirical standard \(k - \varepsilon\) transport model for turbulence kinetic energy (k) and its dissipation rate (ε) is used in this study, which relies on the Boussinesq hypothesis. It makes the Reynolds stress tensor from averaging to be proportional to the mean deformation rate tensor. The major advantage of this hypothesis is the relatively low computational cost. But the drawback is the isotropic turbulence assumption

$$\rho \overline{{\mathop u\nolimits_{i}^{'} \mathop u\nolimits_{i}^{'} }} = \mathop u\nolimits_{t} \left( {\frac{{\partial \mathop u\nolimits_{i} }}{{\partial \mathop x\nolimits_{i} }}} \right) - \frac{2}{3}\left( {\rho k + \frac{{\delta \mathop u\nolimits_{i} }}{{\delta \mathop x\nolimits_{i} }}} \right)\mathop \delta \nolimits_{ij}$$
(13)

The \(k - \varepsilon\) turbulence model reduces computational cost with no loss in accuracy compared to another two-equation turbulence model. The dissipation rate (ε) and turbulence kinetic energy \(\left( k \right)\) can be computed using the following transport equations:

$$\frac{\partial }{{\mathop {\partial x}\nolimits_{i} }}\left( {\mathop {\rho ku}\nolimits_{i} } \right) = \frac{\partial }{{\mathop {\partial x}\nolimits_{j} }}\left[ {\left( {\mu + \frac{{\mathop \mu \nolimits_{\text{t}} }}{{\mathop \sigma \nolimits_{\text{k}} }}} \right)\frac{\partial k}{{\mathop {\partial x}\nolimits_{j} }}} \right] + \mathop G\nolimits_{\text{k}} + \mathop G\nolimits_{\text{b}} - \rho \varepsilon - \mathop Y\nolimits_{\text{M}}$$
(14)
$$\frac{\partial }{{\mathop {\partial x}\nolimits_{i} }}\left( {\mathop {\rho \varepsilon u}\nolimits_{i} } \right) = \frac{\partial }{{\mathop {\partial x}\nolimits_{j} }}\left[ {\left( {\mu + \frac{{\mathop \mu \nolimits_{t} }}{{\mathop \sigma \nolimits_{\varepsilon } }}} \right)\frac{\partial \varepsilon }{{\mathop {\partial x}\nolimits_{j} }}} \right] + \mathop C\nolimits_{1\varepsilon } \frac{\varepsilon }{k}\left( {\mathop {\mathop {\mathop G\nolimits_{k} + G}\nolimits_{3\varepsilon } G}\nolimits_{b} } \right) - \mathop C\nolimits_{2\varepsilon } \rho \frac{{\mathop \varepsilon \nolimits^{2} }}{k}$$
(15)

\(G_{\text{k}} , G_{\text{b}} {\text{and}} Y_{\text{M}}\) are turbulence kinetic energy generation due to mean velocity gradients, buoyancy, and fluctuating dilation in compressible turbulence, respectively. \(C_{1\varepsilon } , C_{2\varepsilon } {\text{and}} C_{3\varepsilon }\) are constants. \(\delta_{\text{k}}\) and \(\delta_{\varepsilon }\) are the turbulent Prandtl number for \(k\) and \(\varepsilon\), respectively.

$$\mathop G\nolimits_{\text{k}} = - \rho \overline{{\mathop u\nolimits_{i}^{'} \mathop u\nolimits_{j}^{'} }} \,\frac{{\partial \mathop u\nolimits_{j} }}{{\partial \mathop x\nolimits_{i} }}$$
(15a)
$$\mathop Y\nolimits_{\text{M}} = 2\rho \varepsilon \mathop N\nolimits_{t}^{2}$$
(15b)
$$\mathop N\nolimits_{t}^{2} = \sqrt {\frac{k}{{\mathop a\nolimits^{2} }}}$$
(15c)
$$\mathop \mu \nolimits_{\text{t}} = \rho \mathop C\nolimits_{\mu } \frac{{\mathop k\nolimits^{2} }}{\varepsilon }$$
(15d)
$$\mathop C\nolimits_{1\varepsilon } = 1.44,\,\mathop C\nolimits_{2\varepsilon } = 1.92,\,\mathop C\nolimits_{\mu } = 0.09,\,\mathop \sigma \nolimits_{k} = 1.0,\,\,\mathop \sigma \nolimits_{\delta } = 1.3$$

The ANSYS-Fluent 14.0 was utilized to discretize and solve the governing equations based on the control volume technique. All the convective terms of equations are discretized using a second-order upwind scheme. Coupled solver with the implicit scheme is used to obtain a relation for compressible flow, and pressure is linked to density. It is found that the implicit approach is more stable, accurate, and less expensive as compared to the explicit approach to capture shock waves.

3.4 Boundary conditions and convergence criterion

The pressure-based boundary condition is employed at the inlet and exit of the ejector with standard, no-slip, and adiabatic wall conditions. A suitable under-relaxation factor is applied to achieve convergence for momentum and turbulence. Based on root mean square density, the convergence criterion for residual was set as \(1 \times 10^{ - 9}\) and \(1 \times 10^{ - 5}\) for continuity and other parameters, respectively.

3.5 Experimental test rig

The test rig was developed based on computed geometry, followed by numerical validation. The internal profile of each section of the ejector components was generated using electro discharge machining (EDM) in aluminum rods of the required sizes. To generate the profile, the copper alloy profiled cutting tools were employed, which is harder than the aluminum rods being manufactured. The complete experimental test rig (refer Fig. 3) was designed in such a way to be simple to operate and control. The test rig was commissioned after ensuring the adequate safety and proper sealing of air ingress.

Fig. 3
figure 3

Variable area mixing ejector test rig

Full size image

4 Results and discussion

4.1 Validation of mixing section

The purpose of validation is to verify 1D gas dynamic theory (refer Sect. 2) of variable area mixing ejector before to proceed for the manufacturing of the test rig for experimentation. All the parameters which were calculated using 1D gas dynamic theory were used to validate. For this purpose, all the parameters were fixed at the on-design condition, as mentioned in Table 1.

The numerically computed centerline Mach number and pressure are used to validate with corresponding values predicted by 1D gas dynamic CRMC theory. The intense mixing of both primary and secondary streams can be seen in the CFD results in the mixing region of Figs. 4 and 5. The Mach number and static pressure show the presence of expansion and alternate oblique shock waves. The result shows the Mach number largely remains supersonic with significant pressure pulsations in the mixing region followed by shockfree diffusion (refer Fig. 4). The average value of static pressure is nearly 70 kPa passing through the center of the pulsations (refer Fig. 5). However, the local average Mach number predicted by the 1D model is less than the centerline Mach number predicted by CFD.

Fig. 4
figure 4

Variation of Mach number along with the mixing and diffuser section

Full size image
Fig. 5
figure 5

Variation of static pressure along with the mixing and diffuser section

Full size image

4.2 Effect of nozzle exit position (NXP) on ejector performance

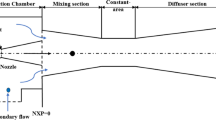
The NXP off-design studies were carried out based on the ejector assembly constraints. The nozzle exit positions were varied in the steps of 1 cm both in upstream (0 to − 3 cm) and downstream (0–3 cm) directions. All other operating parameters were kept constant during the test. The experimentally measured and CFD-predicted entrainment ratio is shown in Fig. 6 with various NXPs.

Fig. 6
figure 6

Effect of NXP on entrainment ratio (ω)

Full size image

From the experimental result, it is noticed that the NXP 1 cm has generated marginally higher entrainment ratio as compared to NXP = 0. The performance of the ejector with negative values of NXPs is lower than that of the design values. However, both experimental and computational results ensure that the decrease in entrainment ratio is reasonable up to NXP = − 1. All these results provide the ruggedness of the NXPs. A small change in NXP from on-design (NXP = 0) is not significantly deterring the performance. Any small error in positioning other than on-design of the nozzle in the variable area mixing ejector system is permissible. It is also observed that the entrainment ratio is higher in the range of NXP values 0–1 cm. Overall, it is seen that moving the nozzle more than 1 cm, away or into the mixing section from zero position, leads to a significant drop in the value of entrainment ratio.

The variation in entrainment with NXP can be explained with the help of the expansion of the jet in the entrainment region. The entrainment region is a self-generated region between nozzle exit and entrance to the mixing zone. This region is not explicitly designed in a 1D gas dynamic analysis. The jet expansion can be seen from the computationally predicted Mach number contours shown in Fig. 7. The NXP of the ejector system controls the jet expansion angles and converging space for secondary flow to be entrained in the entrainment region. When the nozzle starts moving inside the mixing section (+ve NXP) from NXP = 0, the jet expansion angle decreases, and the converging space for secondary flow to be entrain decreases. The smaller jet expansion angle inside the mixing increases the compression effect, which tends to more amount of secondary flow to be entrained. But at the same time, the primary jet is responsible for inducing secondary flow into the suction chamber through suction port moving away from it. Due to the increasing distance from the suction port to the exit of the nozzle, the inducing phenomenon in the entrainment region decreases, resulting in a decrease in entrainment ratio with an increase in the NXPs beyond NXP = 1 cm. Thus, it is found that initially entrainment ratio marginally increases with +ve NXP, and after that it decreases.

Fig. 7
figure 7

CFD predictions of Mach number contours at various NXPs

Full size image

The jet expansion angle increases, and the compression effects decrease as the nozzle starts moving away from the inlet of the mixing section (−ve NXP). Due to the increase in expansion wave angles and the decrease in compression effect away from the mixing section (suction chamber), the entrainment ratio decreases.

The wall static pressure variation with various NXPs is shown in Fig. 8. For the +ve NXPs, the secondary stream starts to interact inside the mixing section little later with the primary flow as compared to −ve NXPs inside the suction chamber. The +ve NXPs also increase the distance between the nozzle exit position inside the mixing section and the suction port of the secondary flow. Due to an increase in the length, the combined momentum of the flow decreases. Due to the interaction of primary and secondary flows away from the inlet section of the mixing, the start of pressure pulsations can be seen away from the inlet and travel even beyond the mixing section also (refer Fig. 8). It is also observed that at NXP = 0, the average static pressure oscillations are less as compared to other NXPs and provide enough momentum to induce secondary flow.

Fig. 8
figure 8

Variation of centerline static pressure along the suction–mixing section

Full size image

For −ve NXPs, the secondary stream starts interacting with the primary stream before it reaches the mixing section. So, the pressure oscillation starts from the suction chamber, and thus the mixed flow loses its momentum and secondary flow dragging phenomenon inside the mixing section, since this pressure pulsation inside the mixing decreases with −ve NXPs.

5 Conclusions

The effect of nozzle exit positions (NXPs) has been studied for variable area mixing ejector. The 1D gas dynamic CRMC theory for variable area mixing section ejector design is utilized for the study of the effect of NXPs. The flow properties computed based on the theory and simulation along the variable area mixing ejector are validated. One of the critical geometrical parameters NXP has been extensively studied. The significant outcome of variation of NXPs has been explained. The results are also used to analyze the system performance and to predict flow physics inside variable area mixing ejector system. It is observed that the entrainment ratio (ω) is very sensitive to the geometrical parameter ‘NXP.’ The experimentally calculated and numerically predicted maximum entrainment ratios corresponding to the on-design condition are 0.512 and 0.591, respectively. The overall best performance is achieved at the on-design operating condition. Hence, the variable area mixing ejector reduces the optimization cost of NXPs. The CFD results help us to visualize the mixing phenomenon inside the mixing section.