Functional magnetoelectric composites with magnetostrictive microwires

Abstract

This paper discusses the electric polarization properties of ferromagnetic microwires at microwave frequencies. At the vicinity of the antenna resonance, a strong magnetic control of the wire polarization is possible owing to the magnetoimpedance (MI) effect. In order to realize efficient tunable properties, magnetic microwires of Co-rich compositions in amorphous state are considered. The absence of the crystalline structure is an important condition to establish well-defined magnetic anisotropies of small magnitudes, which results in the magnetization processes sensitive to the external parameters such as a magnetic field and a mechanical stress. Tunable soft magnetic properties of amorphous microwires are responsible for the MI effect, which can be observed at high frequencies (1–10 GHz). Here we demonstrate that the electric polarization of a microwire depends on its impedance and, hence, can be modulated changing the wire magnetization state in response to the application of a magnetic field and a mechanical stress. The polarization problem is treated theoretically by solving the scattering problem from a cylindrical ferromagnetic wire with the impedance boundary conditions. The modelling results agree well with the available experimental data.

1 Introduction

Competitive technological developments require functional materials that combine several properties which may be tuned by external stimuli. Considering materials with magnetic and (or) electric orders, it is natural to control the magnetization $\varvec{M}$ and permeability $\mu$ with a magnetic field $\varvec{H}$, and the electric polarization $\varvec{P}$ and permittivity $\varepsilon$ with an electric field $\varvec{E}$. The realization of cross-dependences $\varvec{P}\left( \varvec{H} \right)$ and $\varvec{M}\left( \varvec{E} \right)$ is of considerable practical interest which requires strong magnetoelectric coupling. Thus, in magnetically induced ferroelectrics $\varvec{P}$ sensitively changes with $\varvec{H}$ since the origin of electric polarization is ascribed to a complex magnetic order due to the inverse Dzyaloshinskii–Moriya mechanism [1, 2]. A large change in magnetization caused by an electric field was recently observed in hexaferrites with a conical spin structure [3, 4] and also in M-type hexaferrites with a co-linear magnetic structure [5, 6]. In the latter case the mechanism of spontaneous electric polarization can be still related to the magnetic order due to symmetrical exchange striction stimulating the crystal distortions.

The magnetoelectric effects are also realized in composites that combine coupled electric and magnetic dipoles [7]. The coupling mechanism typically involves piezoelectric and magnetostrictive interactions. In the present work we are dealing with the electrical dipoles induced in ferromagnetic wires by a high-frequency electric current generated by the electromagnetic field.

The use of metal inclusions to engineer electric dipoles allows achieving large polarizability in comparison with dielectrics. The inclusion shape significantly determines the polarization properties. A wide variety of polarization effects have been observed in conducting wires with different spatial configurations such as a simple needle or more complex spiral shapes [8, 9]. The dielectric properties of composites with conducting elongated inclusions are formed by the dipole response of the inclusions, which may have a resonance-type frequency dispersion [10,11,12,13]. Similar to the Lorentz oscillator, the electric polarization of a wire inclusion in the vicinity of resonance has the form:

$$P = \mathop \sum \limits_{n} \frac{{A_{n} }}{{\omega_{r,n}^{2} - \omega^{2} - j\omega_{{{\text{rel}},n}} \omega }}$$

(1)

where the summation is carried out over the resonance modes with frequencies $\omega_{r,n}$ which mainly depend on the inclusion shape and $\omega$ is the excitation frequency. The parameter $A_{n}$ represents the resonance mode strength, and $\omega_{{{\text{rel}},n}}$ are the relaxation frequencies. In the case of ferromagnetic wires, each $\omega_{{{\text{rel}},n}}$ includes the internal losses of resistive and magnetic origin; therefore, $P$ may depend on the inclusion magnetization: $\varvec{P}\left( \varvec{M} \right)$. In the present paper we discuss a large change in the electric polarization of ferromagnetic amorphous wires at microwave frequencies in response to a magnetic field $H_{\text{ex}}$ and a mechanical stress $\sigma_{\text{ex}}$.

The underlying mechanism of magnetic control of $\varvec{P}$ is the high-frequency magnetoimpedance (MI) effect which is observed in amorphous microwires of Co-based compositions [14,15,16]. Theoretically, this is explained by solving the scattering problem at a finite length ferromagnetic wire with the impedance boundary conditions imposed at the wire surface [8, 17]. It is demonstrated that the relaxation frequencies $\omega_{{{\text{rel}},n}}$ depend on the wire surface impedance $\varsigma$ and in the vicinity of resonance the wire polarization also strongly depends on $\varsigma$. At certain conditions the variations in the wire magnetic structure caused by the external stimuli $H_{\text{ex}}$ and $\sigma_{\text{ex}}$ lead to large high-frequency impedance changes. This requires a well-defined magnetic anisotropy of a small magnitude which can be established by various annealing treatments [18]. In the case of amorphous alloys with a near-zero magnetostriction the induced anisotropy can be tuned through the magnetoelastic interactions [19,20,21,22] to achieve large stress-MI.

Since the wire polarization depends on a magnetic field the scattering of electromagnetic waves by such wires can be modulated with a low-frequency magnetic field. Then, the scattered signal from a single microwire may be easily detected with lock-in techniques. This was proposed for embedded wireless sensing applications [9, 23, 24]. At certain conditions the amplitude of the modulated signal sensitively depends on the measured parameters such as an applied magnetic field and a mechanical stress.

The other range of applications is related to composite materials containing MI-wires. The effective permittivity of composites also depends on the wire magnetic configuration. Such composites are of interest as tunable electromagnetic materials [25, 26].

2 Electric polarization of a ferromagnetic wire

We consider the polarization properties of a ferromagnetic wire interrogated by a microwave field. The wire of a finite length $l$ is placed in the dielectric medium with the permittivity $\varepsilon_{d}$. The electric field $\varvec{e}_{0}$ along the wire (z-axis) induces the current $\varvec{i}$ which must be zero at the wire ends:

$$i\left( { \pm \,l/2} \right) = 0$$

(2)

This condition implies that there exists some distribution of the current along the wire and the electric charges concentrate at the wire ends generating a dipole moment ${\mathcal{P}}$, which is determined using the continuity equation: $\partial i\left( z \right)/\partial z = j\omega \rho \left( z \right)$ ($\rho$ is charge density per unit length, $i\left( z \right)$ is the linear current density, $j^{2} = - 1$). The value of ${\mathcal{P}}$ is found by integrating the current along the wire

$${\mathcal{P}} = \frac{j}{\omega }\int_{{ - l/2}}^{{l/2}} {i\left( z \right){\text{d}}z}$$

(3)

In order to find the current distribution, we need to solve the scattering problem which is simplified for a thin wire ($l \gg a$, $a$ is the wire radius) with the use of the antenna approximation. Typically, this problem is considered with the zero-impedance boundary conditions. However, this approach ignores completely the effect of internal losses. There are a number of approximations developed to include the resistive losses considering the wire impedance, which results in integro-differential equations for the current distribution [27, 28]. A similar approach was used for a ferromagnetic wire characterized by a scalar permeability independent of frequency [19]. It is not clear if the proposed numerical method could be extended to a general case. We summarize here the approach developed in [8, 17] which is based on finding the scattered electromagnetic field from a cylindrical wire with the use of the impedance boundary conditions imposed at the wire surface:

$$\bar{\varvec{e}}_{t} = \hat{\varsigma }\left( {\bar{\varvec{h}}_{t} \times \varvec{n}_{\varvec{r}} } \right)$$

Here $\hat{\varsigma }$ is the surface impedance tensor which relates the tangential components of electric $\bar{\varvec{e}}_{t}$ and magnetic $\bar{\varvec{h}}_{t}$ fields at the wire surface, and $\varvec{n}_{\varvec{r}}$ is the unit radial vector directed inside the wire. The electric field $\varvec{e}$ is composed of the incident wave field $\varvec{e}_{0}$ and scattered field $\varvec{e}_{s}$. The magnetic field $\varvec{h}$ is induced by the current $\varvec{i}$. In general, the surface impedance $\hat{\varsigma }$ is of a tensor form which may result in some other interesting magnetoelectric properties, for example, inducing the electric polarization by a magnetic field $\varvec{h}_{0}$ of the electromagnetic field. In the case of a diagonal tensor $\hat{\varsigma }$ the boundary condition simplifies:

$$\bar{e}_{z} = \varsigma_{zz} \bar{h}_{\varphi }$$

(4)

The diagonal component $\varsigma_{zz}$ relates the longitudinal electric field $\bar{e}_{z}$ and circular magnetic field $\bar{h}_{\varphi }$.

The fields $\varvec{e}$ and $\varvec{h}$ are expressed in terms of the scalar $\varphi$ and vector $\varvec{A}$ potentials:

$$\varvec{e} = - \nabla \varphi - \frac{4\pi }{{c^{2} }}\frac{{\partial \varvec{A}}}{\partial t}, \quad \varvec{h} = \frac{4\pi }{c}\left( {\nabla \times \varvec{A}} \right)$$

(5)

where $c$ is the velocity of light. Using the Lorentz calibration, the Helmholtz equation can be obtained for $\varvec{A}$:

$$\Delta \varvec{A} + k^{2} \varvec{A} = \varvec{i },\varvec{ }\quad k = \left( {\omega /c} \right)\sqrt {\varepsilon_{d} }$$

(6)

The Green function approach is used for solving Eq. (6) which involves convolutions:

$$\varvec{A}\left( \varvec{r} \right) = \left( {G*\varvec{i}} \right) = \mathop \int \limits_{V}^{{}} \varvec{i}\left( \varvec{z} \right)G\left( {r^{\prime } } \right){\text{d}}V_{z}$$

(7)

$$G\left( r \right) = \exp \left( {jkr} \right)/4\pi r$$

In (7) the integration is done over the wire volume and $r^{\prime } = |\varvec{r} - \varvec{z}|$ is the distance between the point $\varvec{r}$ and the integration point $\varvec{z}$. The circular magnetic field induced by current is found with the help of Eqs. (5) and (7):

$$\varvec{h}\left( \varvec{r} \right) = \frac{2}{{{\text{ca}}^{2} }}\mathop \int \limits_{V}^{{}} \left( {\varvec{i}\left( \varvec{z} \right) \times \varvec{r}^{\prime } } \right)G_{\varphi } \left( r \right){\text{d}}V_{z}$$

(8)

$$G_{\varphi } \left( r \right) = \frac{{a^{2} \left( {1 - jkr^{\prime } } \right)\exp \left( {jkr^{\prime } } \right)}}{{2\left( {r^{\prime } } \right)^{3} }}$$

Using the cylindrical geometry, the surface value of the circular magnetic field is expressed as

$$\bar{h}_{\varphi } \left( z \right) = \frac{2}{\text{ca}}\mathop \int \limits_{ - l/2}^{l/2} G_{\varphi } \left( r \right)i\left( s \right){\text{d}}s, \quad r = \sqrt {\left( {z - s} \right)^{2} + a^{2} }$$

(9)

This can be compared with the static case when $\bar{h}_{\varphi } = 2 I/{\text{ca}}$ where $I$ is the total current. The difference is due to the retarding effects.

The z-component of $\varvec{A}$ describes the scattered electric field from a straight wire and is found from Eqs. (5) and (7). With the use of boundary condition (4) the generalized antenna equation is obtained for the current density in the ferromagnetic wire which has a form of an integro-differential equation:

$$\frac{{\partial^{2} \left( {G*i} \right)}}{{\partial z^{2} }} + k^{2} \left( {G*i} \right) + \frac{{j\omega \varepsilon_{d} \varsigma_{zz} }}{2\pi ac}\left( {G_{\varphi } *i} \right) = \frac{{j\omega \varepsilon_{d} }}{4\pi }e_{0}$$

(10)

Equation (10) involving the second derivatives with respect to $z$ is completed with boundary condition (2) which requires zero current at the ends. The wire surface impedance $\varsigma_{zz}$ and the real part of convolution $\left( {G_{\varphi } *i} \right)$ determine the internal losses. The radiation losses are described by the imaginary parts of $\left( {G*i} \right)$ and $\left( {G_{\varphi } *i} \right)$. In the case of a moderate skin effect, the radiation losses are small. Then, the solution of Eq. (10) is represented as a series over a small parameter involving the imaginary parts of $G$ and $G_{\varphi }$. The zero approximation corresponds to neglecting the radiation losses (putting the imaginary parts to zero). In this case, a simplified analytical solution can be obtained which gives a reasonable approximation if the skin effect is not very strong. Moreover, a moderate skin effect ($a\sim\delta_{m}$, $\delta_{m}$ is the magnetic skin depth) is needed for the manipulation of electric polarization by changing the wire magnetization.

The calculation of the surface impedance tensor $\hat{\varsigma }$ in a ferromagnetic wire with a helical anisotropy and arbitrary frequencies is rather complicated and involves asymptotic expansions of the Maxwell equations [30, 31]. It was demonstrated that the approximation of a strong skin effect gives reasonable results even for $a\sim\delta_{m}$ and is used here. For a uniform magnetization $\varvec{M}_{0}$ directed at a constant angle $\theta$ with respect to the wire axis the component $\varsigma_{zz}$ is defined as:

$$\varsigma_{zz} = \frac{{c\left( {1 - j} \right)}}{4\pi \sigma \delta }\left( {\sqrt {\tilde{\mu }} \cos^{2} \theta + \sin^{2} \theta } \right), \quad \delta = \frac{c}{{\sqrt {2\pi \sigma \omega } }}$$

(11)

Equation (11) contains the permeability parameter $\tilde{\mu }$ which is expressed via the diagonal and off-diagonal components of the internal permeability tensor. It has a meaning of a circular permeability in the cylindrical coordinate system with the dc magnetization $\varvec{M}_{0}$ directed along the $z^{\prime }$ axis; $\sigma$ is the wire electric conductivity.

3 Tunable magnetic configuration in an amorphous wire

As it follows from Eqs. (3), (10) and (11), the current distribution and polarization depend on the surface impedance $\varsigma_{zz}$ and, hence, depend on both the dc magnetization angle $\theta$ and dynamic permeability $\tilde{\mu }$. Then, the magnetic control of ${\mathcal{P}}$ with the help of an external magnetic field $H_{\text{ex}}$ and/or a stress $\sigma_{\text{ex}}$ is mediated by the corresponding dependences of $\theta (H_{\text{ex}} , \sigma_{\text{ex}} )$ and $\tilde{\mu }(H_{ex} , \sigma_{ex} )$ (see Fig. 1). However, at microwave frequencies and moderate values of $H_{\text{ex}}$ the frequency dispersion of permeability $\tilde{\mu }$ is described by the tail of the ferromagnetic resonance where $\tilde{\mu }$ weakly depends on the dc quantities [32]. Therefore, large variations in ${\mathcal{P}}$ require a tunable magnetic configuration in combination with relatively large magnitudes of $\left| {\tilde{\mu }} \right| > 1$.

Fig. 1

Magnetic structure and tuning parameters for amorphous wires with a helical anisotropy

The equilibrium position of $\varvec{M}_{0}$ is decided by minimization of the magnetostatic energy $U_{m}$:

$$U_{m} = - K\frac{{\left( {\varvec{n}_{\varvec{k}} \cdot \varvec{M}_{0} } \right)^{2} }}{{M_{0}^{2} }} - \frac{3}{2}\lambda_{s} \left( {\hat{\sigma }\varvec{M}_{0} } \right) \cdot \frac{{\varvec{M}_{0} }}{{M_{0}^{2} }} - \varvec{M}_{0} \varvec{H}_{\text{ex}}$$

(12)

Here $\varvec{n}_{\varvec{k}}$ and $K$ are the direction and strength of the averaged short-range anisotropy, $\hat{\sigma }$ is the total stress tensor including the internal macroscopic stresses $\hat{\sigma }_{in}$ and external tensile stress $\sigma_{ex}$, and $\lambda_{s}$ is the linear saturation magnetostriction which is uniform in the amorphous state. Typically, the main contribution to the magnetic anisotropy comes from the magnetoelastic interactions. The short-range anisotropy may be enhanced or modified by annealing in the presence of a magnetic field or stress [21, 22].

A near-circumferential anisotropy is required to change sensitively the magnetization direction with the field $H_{\text{ex}}$ applied along the wire. Such anisotropy naturally exists in wires having a negative magnetostriction coupled with a tensile internal stress. Amorphous alloys of Co-rich compositions with small addition of Fe or Mn possess a small negative magnetostriction of the order of $- 10^{ - 7}$. The wires of such compositions produced by Taylor–Ulitovsky technique in glass-coat [33] have a relatively large internal tensile stress, hence a near-circumferential anisotropy. Typical magnetic hysteresis curves for the case of near-circumferential anisotropy in the presence of $\sigma_{\text{ex}}$ are shown in Fig. 2a. The field $H_{\text{ex}}$ rotates the magnetization towards the wire axis causing fast increase in $\cos \theta$. The application of $\sigma_{\text{ex}}$ strengthens the circumferential anisotropy for $\lambda_{s} < 0$, and therefore, its impact on the magnetization direction is seen only in the presence of $H_{\text{ex}}$. The bias-field effect on the stress dependence of the magnetization angle could be of high practical importance. On the other hand, the use of a dc bias field may not be desirable and a “reversed anisotropy” should be established: circumferential for positive magnetostriction and axial for negative magnetostriction. Various annealing treatments are used to modify magnetic anisotropy in amorphous alloys. For example, current annealing induces a circumferential anisotropy in wires with a positive magnetostriction. The corresponding hysteresis loops are shown in Fig. 2b: the application of $\sigma_{\text{ex}}$ increases the remanence magnetization $(\cos \theta$ increases for $H_{\text{ex}} = 0$).

Fig. 2

Influence of the external tensile stress on hysteresis loops of amorphous glass-coated microwires. a: Wires of the composition Co_68.5Mn_6.5Si₁₀B₁₅ having the total diameter of 14.5 μm, the metallic core diameter of 10.2 μm and $\lambda_{s} = - 2 \cdot 10^{ - 7}$. The external stress contributes towards the circular anisotropy. b: Wires of the composition Co₇₁Fe₅B₁₁Si₁₀Cr₃ annealed at 50 mA for 60 min, having the total diameter of 29.5 μm, the metallic core diameter of 23.9 μm and $\lambda_{s} = \left( {3 - 5} \right) \cdot 10^{ - 7}$. The external stress contributes towards the axial anisotropy

4 Tuning the dynamics characteristics: impedance, current distribution and polarization

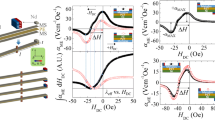
The change in the static magnetic configuration is reflected in the impedance versus magnetic field or impedance versus external stress behaviours, as shown in Fig. 3, where the experimental plots of $Z = \left( {2l/ac} \right)\varsigma_{zz}$ are given. A complex-valued impedance $Z$ is found by measuring $S_{12}$ parameter (forward transmission coefficient) by means of a vector network analyser technique with a specially designed microstrip cell allowing the application of external load at the centre of the wire sample. In the case of a circumferential anisotropy the impedance shows strong variations in the range of magnetic fields $H_{\text{ex}}$ applied along the wire when the static magnetization changes its direction from circumferential to axial (the magnetization angle $\theta$ changes between 0 and $\pi /2$). It is also seen that the impedance sensitively changes with application of the stress and most of the change occurs when a moderate magnetic field is also present. Therefore, in the case of a circumferential anisotropy, the bias magnetic field is favourable to enhance the stress sensitivity. This tendency becomes more pronounced with increasing frequency, as seen in Fig. 3b where the impedance plots versus tensile stress are given for a frequency of 500 MHz. If no field is applied, the impedance does not change in response to $\sigma_{\text{ex}}$ since there is no change in the magnetization direction. However, the impedance sensitivity with respect to $\sigma_{\text{ex}}$ increases greatly in the presence of a $H_{\text{ex}}$ of the order of the anisotropy field $H_{k}$ (a characteristic field required to saturate the wire along the axis).

Fig. 3

Impedance characteristics of Co_68.5Mn_6.5Si₁₀B₁₅ wires with a near-circumferential anisotropy and effect of the tensile stress. a: Impedance versus $H_{\text{ex}}$ for different $\sigma_{\text{ex}}$, frequency is 60 MHz; b: normalized impedance $\left| {Z/Z\left( {H_{\text{ex}} = 0,\sigma_{\text{ex}} = 0} \right) } \right|$ versus $\sigma_{\text{ex}}$ for different $H_{\text{ex}}$, frequency is 500 MHz. The measurement was done with the help of Hewlett-Packard 8753E vector network analyser

The dependence of the impedance on the magnetic field and tensile stress makes it possible to tune the scattering from a single ferromagnetic wire as follows from Eq. (10). Neglecting the radiation losses in (10), the equation for the current distribution is reduced to the ordinary differential equation which is easily solved. Figure 4 demonstrates the effect of tensile stress on the current distribution near the resonance frequency. The bias magnetic field $H_{\text{ex}}$ of about the anisotropy field $H_{K}$ is needed to realize this stress effect (compare with Fig. 3). A very large difference in the current distribution is caused by the application of $\sigma_{\text{ex}} = 650 MPa$, which for the parameters used is sufficient to overcome the effect of $H_{\text{ex}}$ and rotate the magnetization back to the circumferential direction. It should be noted that the antenna resonance frequency defined by the half-wavelength condition is chosen such that the skin effect is not very strong ($a/\delta_{m} \sim a\sqrt {\tilde{\mu }} /\delta \sim1)$ and the permeability parameter $\tilde{\mu }$ substantially differs from unity. (For the parameters used the real part of $\tilde{\mu }$ equals − 4 at a frequency of 2 GHz [32].) For a wire with a diameter of 10–20 micron the frequency range is within few GHz. The antenna resonance frequency $f_{\text{res}} = c/2l\sqrt {\varepsilon_{d} }$ can be adjusted by varying the wire length $l$ and the permittivity of the surrounding medium $\varepsilon_{d}$. If the proper conditions are realized, the induced electric polarization of a ferromagnetic wire shows large variations in response to the applied field and stress. Figure 5 demonstrates the frequency dispersion of the polarizability parameter

Fig. 4

Current distribution along the wire for a frequency $f = 1.9$ GHz (near the resonance) calculated from the zero approximation of Eq. (10) with the use of Wolfram Mathematica. Imaginary part is shown. The effect of external field and tensile stress is demonstrated ($H_{\text{ex}} = 0.8H_{k} , \sigma_{\text{ex}} = 0, 650 {\text{MPa}}$) for a circumferential magnetic anisotropy. Parameters for calculation: $l = 4 {\text{cm}}$, $2a = 10$ μm, $\varepsilon_{d} = 4$, $\sigma = 7.6 \cdot 10^{15} s^{ - 1}$, anisotropy field $H_{K}$ = 5 Oe (the field required to saturate the wire along the axis when $\sigma_{\text{ex}} = 0$), saturation magnetization $M_{0}$ = 500 G, gyromagnetic constant $\gamma = 2 \cdot 10^{7}$ (rad/s)/Oe, spin relaxation parameter is 0.2, internal tensile stress $\sigma_{\text{in}} = 200 {\text{MPa}}$, and internal torsion stress $\sigma_{t} = 40 {\text{MPa}}$. The parameters are chosen such that there is consistency with the hysteresis loops and impedance experimental results shown in Figs. 2a and 3

Fig. 5

Frequency spectra of the real and imaginary parts of the induced polarizability $\alpha = {\mathcal{P}}/Ve_{0}$. Parameters for calculation are the same as for Fig. 4

$$\alpha = \frac{{\mathcal{P}}}{{Ve_{0} }}$$

(13)

in the presence of the external field ($H_{\text{ex}} = H_{K} )$ and for different values of $\sigma_{\text{ex}}$. In (13), $V$ is the wire volume. For $\sigma_{\text{ex}} = 0$, the resonance peaks in the real part of $\alpha$ are suppressed and the peak in the imaginary part is very wide, which corresponds to a relaxation-type frequency dispersion. When a tensile stress is applied together with $H_{\text{ex}}$, the resonance behaviour of the polarizability is well pronounced. Therefore, using a magnetic field and a tensile stress it is possible to control the resonance scattering from a ferromagnetic wire, which is of interest for applications in tunable materials and sensing.

5 Application to tunable dielectrics and wireless sensors

The electric polarizability $\alpha$ of a single wire near the resonance is very strong, so the composites with low concentration of magnetic wires will demonstrate the effective permittivity $\varepsilon_{ef}$ which depends on the wire magnetic properties. For low wire concentrations $p \ll p_{c}$ ($p_{c}$ is the concentration of the percolation threshold) it is considered that the local electric field equals the external field $e_{0}$ and the mutual interactions between the wires can be neglected. Then, the effective permittivity is defined by the summation of the local polarizations:

$$\varepsilon_{\text{ef}} = \varepsilon_{d} + 4\pi p\left\langle \alpha \right\rangle$$

(14)

Here $\left\langle \alpha \right\rangle$ is the averaged polarizability of the magnetic wires. (The averaging could involve different spatial orientations of the wires.) Therefore, the effective permittivity will have a similar to $\alpha$ frequency dispersion (see Fig. 5) and will show strong changes in the presence of external field $H_{\text{ex}}$ and/or stress $\sigma_{\text{ex}}$. The experimental results on scattering spectra (reflection and transmission) of composites with Co₆₈Fe₄Cr₃B₁₄Si₁₁ microwires with induced helical anisotropy confirm this conclusion [12]. Near the dipole resonance, the transmission minimum deepens (from − 12 to − 17 dB at 2 GHz) under the application of $\sigma_{\text{ex}}$ which strengthens the circumferential anisotropy decreasing the impedance and magnetic losses. On the contrary, the application of $H_{\text{ex}}$ rotates the magnetization towards the axis, the impedance increases, and the dipole losses also increase. Therefore, composites with ferromagnetic wires exhibit tunable microwave spectra.

The other range of applications includes wireless sensors for measuring remotely the local stresses inside materials, which is based on the dipole scattering from a ferromagnetic wire. The microwave scattering defined by S-parameters from a single microwire is small in comparison with the incident wave. A special experimental procedure is needed to detect the scattered signal and its dependence on the environment stress. The method is based on the magnetic field dependence of the wire polarization [13, 15]. The wire is subjected to a microwave field and a low-frequency magnetic field $H_{b}$ that modulates the amplitude of the scattered signal. The modulated signal of doubled frequency can be sensitively detected with lock-in techniques. This doubled-frequency signal reflects a symmetric shape of the magnetic hysteresis and impedance versus field plots. The magnitude of these modulations will depend on the external dc stimuli: magnetic field $H_{\text{ex}}$ and stress $\sigma_{\text{ex}}$ that can be originated by strains inside a material.

The scattered signal is proportional to the magnitude of the polarization ${\mathcal{P}}$. Computing ${\mathcal{P}}$ as a function of varying $H_{b}$ at fixed values of $H_{\text{ex}}$, $\sigma_{\text{ex}}$ and frequency (near the resonance) we can deduce the amplitude of the modulations. Figure 6 shows the modulation amplitude as a function of $H_{\text{ex}}$ for various stresses for the case of a wire with a circumferential anisotropy. It is seen that the external stress strongly suppresses the low-frequency modulations since the circumferential anisotropy increases and the impedance becomes insensitive to moderate magnetic fields as follows from Fig. 3. This result is consistent with the experimental investigations of [9, 29].

Fig. 6

Modulation of the dipole moment with ac bias field $H_{b}$ as a function of the dc field $H_{\text{ex}}$ for different external tensile stresses. The parameters are the same as for Fig. 4. The frequency is near the resonance (1.9 GHz). The modulation parameter is defined as $\Delta {\mathcal{P}}/{\mathcal{P}} = {\text{Max}}\left| {\frac{{\left( {{\mathcal{P}}\left( {H_{\text{ex}} + H_{b} } \right) - {\mathcal{P}}\left( {H_{\text{ex}} } \right)} \right)}}{{{\mathcal{P}}\left( 0 \right)}}} \right|$. The amplitude of $H_{b}$ equals $H_{k} /2$

6 Conclusion

We demonstrated that magnetostrictive microwires behave as magnetically tunable electrical dipoles, which is based on microwave magnetoimpedance and resonance scattering. This dynamic magnetoelectric effect can be used for developing tunable microwave materials and wireless stress sensors with remote operation. For practical applications, it is useful to apply a low-frequency magnetic modulation that produces a signal of doubled frequency, the amplitude of which strongly depends on the external stimuli, such as a dc magnetic field or mechanical stress. The signal of a specific low frequency can be sensitively detected.