Numerical Investigation on A Bistable Vibro-Impact Dielectric Elastomer Generator Under Low-Frequency Excitations

Abstract

Purpose

In order to harvest low wide bandwidth frequency vibration energy and enhance the performance of existing energy harvesters using dielectric elastomers (DEs), this paper investigates a bistable vibro-impact dielectric elastomer generator (BVI DEG), which mainly consists of a vibro-impact (VI) DEG, two identical pre-compressed springs, and a base.

Methods

First, the physical model of the BVI DEG is introduced, and its dynamical and electrical analysis models are developed. On this basis, the dynamical behaviors of the BVI DEG under a harmonic excitation are numerically investigated by bifurcation diagrams, phase trajectories and displacement time responses. Rich dynamical behaviors (such as interwell, chaotic and intrawell oscillations) of the system are revealed. Then, the energy harvesting (EH) performance under the harmonic excitation is studied for diverse parameters, including the excitation amplitude and frequency, the initial conditions of the system, the mass of the capsule, the distance between the two membranes, and the different bistable potential wells. Finally, a comparative study is conducted to demonstrate the superiority of the BVI DEG.

Results and conclusion

The system EH performance can be improved by appropriately setting various parameters, including the excitation amplitude and frequency, the initial conditions of the system, the mass of the capsule, the distance between the two membranes, and the different bistable potential wells. However, adjusting the potential barrier and the stable equilibrium position of the bistable potential well is a better way to enhance the EH performance. Moreover, the comparative study demonstrates the superiority of the BVI DEG to harvest ultra-low wide bandwidth frequency vibration energy. This work can help guide the design and optimization of the BVI DEG in the low frequency vibration environment.

Introduction

With the rapid development of microelectronic technology, powering microelectronic devices (e.g., wireless sensors, transmitters, and controllers) with traditional chemical batteries has recently met with the potential challenges. These traditional batteries require regular charging and replacement and have a limited lifetime. To solve this issue, one possible solution is to power these electronic devices via ambient energy harvesting (EH) techniques (e.g., wind, solar and thermal) [1]. Mechanical vibration is another viable source of energy because it is ubiquitous. Most accessible vibrational sources in the ambient environment are commonly in the low frequency range of 0–15 Hz [2,3,4,5,6,7,8,9]. In recent years, dielectric elastomer generators (DEGs) with various models have been developed to convert such vibration energy into electricity [10, 11]. Dielectric elastomer (DE) materials, as smart materials, have attracted many researchers due to its advantages of low cost, large deformation, fast response, high energy density and high energy conversion efficiency [12,13,14]. These advantages can achieve the conversion of vibration energy into electrical energy and improve the EH performance. For example, by designing a novel EH circuit, it was proved from experiments that the DEG can produce an energy density of 780 J/kg, much higher than the energy densities of the piezoelectric (PE), electrostatic (ES) and electromagnetic (EM) energy harvesters [15, 16]. Furthermore, by stacking up DE membranes, the DEG can reach 3.8 μW/mm³ power density, significantly higher than the highest power densities of the EM (2.21 μW/mm³), ES (2.16 μW/mm³) and PE (0.375 μW/mm³) energy harvesters [17, 18].

Currently, in order to fully utilize the advantages of DE materials themselves, DEG models with various structures have been designed for harvesting low-frequency vibration energy. For instance, Fan et al. proposed a DE-based soft pendulum [10] to harvest mechanical vibration energy. The conversion of vibration energy to the electricity is realized due to the stretching and recovery of the membrane when the energy harvester swings under an ultra-low frequency (< 10 Hz) horizontal excitation. However, the proposed device only presents an excellent EH performance in ultra-low frequency narrowband. To harvest vibration energy, a novel vibro-impact (VI) DEG, which has a simpler structure than those of the impact-based EM and PE energy harvesters [19,20,21,22] and the DE-based soft pendulum [10], was designed by Yurchenko’s group [23,24,25]. The VI DEG shows a good EH performance under large-amplitude vibration excitations. However, when the energy harvester is excited by low-amplitude, ultra-low frequency excitations its effective operating frequency range can be narrowed or it may not function properly (because at least it must be ensured that impacts between the ball and the membrane occur under an external excitation). Pan et al. [11] developed an electromechanical coupling model to deeply investigate the dynamics and EH performance of the VI DEG. However, the research findings still show that a good EH performance can be achieved by the VI DEG under high-energy level excitations (i.e., large amplitudes). Moreover, Yurchenko’s group further proposed a VI DEG embedded in a bluff body [26, 27] to harvest wind-induced mechanical vibrations. However, the device can effectively operate within an extremely narrow range of low wind speeds due to the lock-in of the resonant frequency of the beam. Taken together, these studies, on one hand, demonstrate the wide range of potential applications of the VI DEG; On the other hand, the energy harvester has potential shortcomings, especially when working in a low-amplitude, ultra-low frequency (< 10 Hz) vibration environment, the system EH performance can be compromised. However, few studies have investigated in this regard. Thus, it is necessary to further search for more suitable solutions to improve the performance of the existing DEGs in the low frequency vibration environment with a wide operating bandwidth.

Inspired by bistable energy harvesters [28, 29], which possess a broader operational bandwidth than linear ones [30,31,32] and can yield large-amplitude oscillations under low amplitude excitations, one potential solution is to combine DEGs with the bistable property. Currently, studies related to such energy harvesters are very few. One model is a bistable cone DEG, which was proposed by Moretti et al. [33], to harvest ultra-low/low frequency vibration energy. This model, which consists of a dual cone DEG (CDEG) and a negative-rate biasing spring (NBS), exhibits a better EH performance than the DEG without bistability under the ultra-low/low frequency vibration [33]. The authors proposed an arc-cylinder type dielectric elastomer oscillator (ADEO) to harvest vibration energy [34]. When the tilt angle of the ADEO is 90°, the system forms a DE-based bistable energy harvester. The high output power can be produced in the ultra-low frequency range of 5–10 Hz. Another model is a bistable vibro-impact dielectric elastomer generator (BVI DEG) and was applied in the main structure with ultra-low natural frequencies [35]. The research results showed that the proposed device has a better EH performance than the VI DEG and the linear VI DEG (LVI DEG) [35]. However, the proposed BVI DEG system can be also directly subjected to low frequency excitations and exhibit different dynamical behaviors. This is because the BVI DEG installed on the main structure depends on the vibration energy level of the main structure because of the coupling between them, and exhibits an excellent EH performance when the main structure resonates at its natural frequency [35]. Obviously, the BVI DEG directly applied to external excitations does not have this dynamical characteristic, and therefore the design method of the BVI DEG will also be different. At present, the authors also proposed an asymmetric BVI DEG (ABVI DEG) directly applied to ultra-low frequency excitations [36]. The purpose of this work was to provide a possible solution to improve the EH performance of DE-based bistable energy harvesters in the ultra-low frequency vibration environment. Actually, asymmetric bistability are more sensitive to external input energy than symmetric bistability, that is, the ABVI DEG may be applicable to low-energy input excitation but not to high-energy input excitation, and vice versa [36]. Symmetric bistability [36] may not have this defect. Furthermore, from a structural perspective, the AVI DEG requires more springs compared to the BVI DEG. For such a small energy harvester, the design of such springs is relatively difficult, and the increase in the number of springs with different stiffnesses further increases the design difficulty. Note that, the research on the BVI DEG in ref. [36] is also insufficient (i.e., the effects of bistable potential wells on the BVI DEG were only discussed), as it mainly focuses on the ABVI DEG. Thus, the dynamical behavior of the BVI DEG, which decides its EH performance, is unclear for other parameters (such as the mass of the capsule, the system initial conditions, the distance between the two membranes, etc.), and thereby its application in ultra-low/low frequency excitations can be limited.

Therefore, this paper further investigates the dynamical behavior and EH performance of the BVI DEG under low-frequency vibrations, aiming to enhance its performance in the low-frequency vibration environment and provide an insight into the system dynamics. The rest of this paper is organized as follows. Sect. "Theoretical analysis" introduces the structure and operation mechanism of the BVI DEG. In Sect. "System dynamical behavior", the dynamical behaviors of the proposed BVI DEG system under the harmonic excitation are comprehensively studied through numerical simulations. In Sect. "System energy harvesting performance", the EH performance of the BVI DEG under the harmonic excitation is studied for various key parameters. A further comparative study is presented in Sect. "Discussion: comparative study". Key conclusions are drawn in Sect. "Conclusions".

Theoretical Analysis

Physical Model

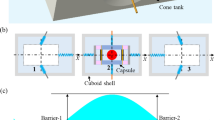
Figure 1a shows a bistable vibro-impact dielectric elastomer generator (BVI DEG), which mainly consists of a vibro-impact (VI) DEG, two identical pre-compressed springs and a base. Each pre-compressed spring is squeezed between the VI DEG and the base and interconnects them. The VI DEG [11, 23] is composed of a cylindrical capsule, an inner free moving ball and two identical pre-stretched circular dielectric elastomer membranes (DEMs) at both ends of the cylindrical capsule. The capsule of the VI DEG is suffered from a bistable elastic potential field due to the combined effects of the springs, as shown in Fig. 1b. The capsule of the VI DEG has three equilibrium positions with balanced external forces: two stable equilibrium positions (position 1 and 3) and one middle unstable equilibrium position (position 2). When the capsule is at position 2, a slight disturbance will make the capsule move leftward or rightward until the horizontal components of the pushing force of the pre-compressed springs are equal to zero, i.e., the capsule is at position 1 or 3. The elastic potential field acting on the capsule is shown in Fig. 1c, which involves two potential wells ($X_{c1}$ and $X_{c3}$, indicating the stable equilibrium positions 1 and 3, respectively) with an identical depth. The potential barrier between each stable equilibrium position (1 or 3) and the unstable equilibrium position (2, which is represented by $X_{c2}$ in the potential field) is denoted as Barrier-1 and Barrier-2, respectively. Hence, a BVI DEG system is formed.

Fig. 1.

a The physical model of the BVI DEG b the schematic diagram of the proposed BVI DEG, the capsule of which has three equilibrium positions c the bistable potential well, which has two potential barriers: barrier-1, barrier-2.

The system parameters of the BVI DEG are presented in Fig. 1a. The masses of the capsule with inner diameter $d_{0}$ and the inner ball with radius $r_{b}$ are $m_{c}$ and $m_{b}$, respectively. $d$ is the distance between the two membranes. The total stiffness of the two pre-compressed springs is $k$. $L$ is the length of the pre-compressed spring with its original length $x_{0}$. In this paper, x-axis is defined as the global coordinate system parallel to the horizontal direction. The absolute coordinates along x-axis of the capsule and the inner ball are $x_{c}$ and $x_{b}$. The static equilibrium position of the capsule (with zero potential energy position) is defined as its coordinate origin. The coordinate origin of the inner ball locates at the center point of the capsule. Here, it should be pointed out that the fixed rods are used to ensure that the capsule can only move along x-axis. The designed cone tank with a hole allows for the translation and rotation of the lightweight connecting rod, thus allowing the capsule to move freely as well. Moreover, the friction between the capsule and the inner ball is quite small and can be ignored, and that between the capsule and the fixed rods is significantly reduced using Teflon lubricant and can also be ignored.

The working principle of the BVI DEG system in EH is as follows: when a continuous external excitation $x_{b0} (t)$ along the x-axis acts on the base, the capsule freely moves under the bistable potential field. The inner ball, meanwhile, moves inside the capsule and impacts both membranes intermittently and regularly, thus generating electricity through the electromechanical conversion mechanism of the DE material. Thus, the vibration energy can be harvested from the BVI DEG system.

Dynamics Modeling

The dynamics model of the proposed system under an external excitation is studied in this subsection. In this paper, the external excitation applied on the base is assumed as a harmonic acceleration one $a_{b0} (t) = A\cos (2\pi f_{0} t)$, where $A$ and $f_{0}$ denote its amplitude and frequency, respectively. Thus, the base’s displacement and velocity can be written as:

$$ \left\{ {\begin{array}{*{20}c} {x_{b0} = - A/(2\pi f_{0} )^{2} \cos (2\pi f_{0} t)} \\ {v_{b0} = \dot{x}_{b0} = A/(2\pi f_{0} )\sin (2\pi f_{0} t)} \\ \end{array} } \right. $$

(1)

According to Fig. 1(a), when the inner ball moves between two membranes, motion equations of the system can be written as [37, 38]:

$$ \left\{ {\begin{array}{*{20}c} {m_{c} \ddot{x}_{c} + k(x_{c} - x_{b0} ) - \frac{{kx_{0} (x_{c} - x_{b0} )}}{{\sqrt {L^{2} + (x_{c} - x_{b0} )^{2} } }} = 0} \\ {m_{b} \ddot{x}_{b} = 0} \\ \end{array} } \right. $$

(2)

where sign $(^{ \bullet } )$ denotes the first derivative with respect to time, and thus $\ddot{x}_{c}$ and $\ddot{x}_{b}$ are absolute accelerations along the x-axis of the capsule and the ball, respectively.

By defining $X_{c} = x_{c} - x_{b0}$ and $X_{b} = x_{b} - x_{b0}$ as the relative displacements of the capsule and the ball with respect to the base, Eq. (2) can be further expressed as:

$$ \left\{ {\begin{array}{*{20}c} {m_{c} \ddot{X}_{c} + kX_{c} \left( {1 - \frac{{x_{0} }}{{\sqrt {L^{2} + X_{c}^{2} } }}} \right) = - m_{c} a_{b0} } \\ {m_{b} (\ddot{X}_{b} + a_{b0} ) = 0} \\ \end{array} } \right. $$

(3)

where $\ddot{X}_{c} = \ddot{x}_{c} - a_{b0}$ and $\ddot{X}_{b} = \ddot{x}_{b} - a_{b0}$ denote the relative accelerations of the capsule and the ball with respect to the base. The second term on the left-hand side of the first equation of Eq. (3) is the restoring force of the capsule and denoted as $F_{s}$. Then, the following equation can be written as:

$$ F_{s} = kX_{c} \left( {1 - \frac{{x_{0} }}{{\sqrt {L^{2} + X_{c}^{2} } }}} \right) $$

(4)

Thus, the potential energy $U(X_{c} )$ of the capsule can be calculated as:

$$ U(X_{c} ) = \frac{1}{2}kX_{c}^{2} - kx_{0} \sqrt {X_{c}^{2} + L^{2} } + kx_{0} L $$

(5)

It can be seen from Eq. (4) that the potential function of the capsule with respect to $X_{c}$ show a bistable pattern with two stable equilibrium positions, whose values and relevant potential energies are:

$$ \left\{ {\begin{array}{*{20}l} {X_{c1,3} = \pm x_{0} \sqrt {1 - \beta^{2} } } \hfill \\ {U(X_{c1,3} ) = - \frac{1}{2}kx_{0}^{2} (1 - \beta )^{2} } \hfill \\ \end{array} } \right. $$

(6)

where $\beta = L/x_{0}$ denotes a proportionality factor.

The governing equations of the system when the ball moves between membranes have been derived. However, it should be noted that the system’s motion conditions will change when the ball impacts the membranes. In this work, $X_{DEG} = x_{b} - x_{c}$ and $V_{DEG} = \dot{x}_{b} - \dot{x}_{c}$ are defined as the relative displacement and relative velocity of the ball with respect to the capsule. Hence, impacts between the ball and the membranes are under the following conditions:

$$ \left\{ {\begin{array}{*{20}l} {X_{DEG} = - (d - 2r_{b} )/2, \, V_{DEG} < 0,{\text{ when the ball imapcts the left membrane}}} \hfill \\ {X_{DEG} = (d - 2r_{b} )/2, \, V_{DEG} > 0,{\text{ when the ball impacts the right membrane}}} \hfill \\ \end{array} } \right. $$

(7)

As the impact time between the ball and the membrane is extremely short, an instantaneous impact model with computational efficiency and accuracy [34] is used to analyze the motions of the capsule and the ball after each impact. The instantaneous impact model was obtained though single-sided impact (SSI) experiments [34, 39] and then further verified by electrical experiments and compared with an elastic impact model [34]. For the instantaneous impact model, a restitution coefficient $r$ between the ball and the membranes can be written as:

$$ r = \frac{{\dot{x}_{c + } - \dot{x}_{b + } }}{{\dot{x}_{b - } - \dot{x}_{c - } }} $$

(8)

where $\dot{x}_{c - }$ and $\dot{x}_{c + }$ denote the velocities of the capsule just before and after each impact; $\dot{x}_{b - }$ and $\dot{x}_{b + }$ denote the velocities of the ball just before and after each impact. The value of $r$, which is related to the impact velocity, was obtained by SSI experiments and is presented in Appendix A.

The momentum conservation equation at each impact can be written as:

$$ m_{c} \dot{x}_{c - } + m_{b} \dot{x}_{b - } = m_{c} \dot{x}_{c + } + m_{b} \dot{x}_{b + } $$

(9)

Thus, $\dot{x}_{c + }$ and $\dot{x}_{b + }$ can be obtained by solving Eqs. (8) and (9):

$$ \left\{ {\begin{array}{*{20}c} {\dot{x}_{c + } = \frac{{(m_{c} - m_{b} r)\dot{x}_{c - } + m_{b} (1 + r)\dot{x}_{b - } }}{{m_{c} + m_{b} }}} \\ {\dot{x}_{b + } = \frac{{m_{c} (1 + r)\dot{x}_{c - } + (m_{b} - m_{c} r)\dot{x}_{b - } }}{{m_{c} + m_{b} }}} \\ \end{array} } \right. $$

(10)

Consequently, the dynamical behavior of the system, including the capsule and the ball, can be obtained through solving Eqs. (3) and (10).

Electrical Modeling

According to the electromechanical conversion mechanism of DE materials, electrical energy can be gained at each impact between the ball and the membranes. Hence, based on the previously obtained dynamics model of the system, the electrical response of the BVI DEG can be further analyzed when the base is subjected to an external excitation.

When the pre-stretched membranes with the pre-stretched ratio $\lambda_{pre}$ are not impacted by the ball, it has an initial surface area of $A_{0} = \pi (d_{0} /2)^{2}$ and an initial thickness of $h_{0}$. While at each impact, the membrane is deformed with an increasing area and a decreasing thickness. The largest surface area $A_{1}$ and the smallest thickness $h_{1}$ achieve when the membrane reaches its largest deformation, which can be calculated as [23]:

$$ A_{1} = 2\pi r_{b}^{2} (1 - \cos \beta_{0} ) + \frac{{\pi R_{0}^{2} - \pi (r_{b} \sin \beta_{0} )^{2} }}{{\cos \beta_{0} }} $$

(11)

$$ h_{1} = \frac{Vol}{{A_{1} }} = \frac{{\pi R_{0}^{2} h_{0} }}{{A_{1} }} $$

(12)

where $Vol = A_{0} h_{0}$ denotes the volume of the membrane, which is a constant due to the incompressibility of the DE materials; the value of $\beta_{0}$ can be obtained from:

$$ \cos \beta_{0} = \frac{{ - 2r_{b} (\delta_{\max } - r_{b} ) + 2R_{0} \sqrt {R_{0}^{2} + \delta_{\max }^{2} - 2\delta_{\max } r_{b} } }}{{2\left[ {R_{0}^{2} + \left( {\delta_{\max } - r_{b} } \right)^{2} } \right]}} $$

(13)

where $\delta_{\max }$ denotes the largest central deflection of the membrane at each impact, which is achieved when the membrane reaches its largest deformation. The value of $\delta_{\max }$, which is related to the impact velocity, can be calculated quantitatively. Their relationship can be obtained through SSI experiments of the ball and the membrane [34, 39], and is presented in Appendix A.

Thus, the minimum and maximal capacitances of the pre-stretched membranes at each impact can be calculated as:

$$ C_{\min } = \frac{{\varepsilon_{0} \varepsilon A_{0} }}{{h_{0} }} = \frac{{\varepsilon_{0} \varepsilon Vol}}{{h_{0}^{2} }} $$

(14)

$$ C_{\max } = \frac{{\varepsilon_{0} \varepsilon A_{1} }}{{h_{1} }} = \frac{{\varepsilon_{0} \varepsilon Vol}}{{h_{1}^{2} }} $$

(15)

where $\varepsilon_{0} = 8.854 \times 10^{ - 12}$ F/m denotes the vacuum permittivity, and $\varepsilon$ is the relative permittivity of the DE materials.

In this paper, the EH circuit with triangular scheme, which was proposed by Shian [40], is adopted due to its high performance, as shown in Fig. 2. The details of the EH circuit with triangular scheme was described in detail in [34, 40]. By harnessing the EH circuit, a higher output voltage $\phi_{out}$ (compared to the input voltage $\phi_{in}$) at each impact can be achieved:

$$ \phi_{out} = \frac{{C_{\max } + C_{T} }}{{C_{\min } + C_{T} }}\phi_{in} $$

(16)

Fig. 2

The EH circuit for DEMs

where $C_{T}$ is the capacitance of the transfer capacitor of the EH circuit. It was reported that most electrical energy can be harvested when $C_{T} = 1.2C_{\min }$ [34, 40].

Thus, the electrical energy gain at each impact is:

$$ W = \frac{1}{2}\phi_{in} \phi_{out} (C_{\max } - C_{\min } ) = \frac{1}{2}\phi_{in}^{2} C_{\min } \left( {\frac{{C_{\max } + C_{T} }}{{C_{\min } + C_{T} }}} \right)\left( {\frac{{C_{\max } }}{{C_{\min } }} - 1} \right) $$

(17)

When the base is subjected to an external excitation, the ball will impact the membranes regularly and electrical energy gain can be obtained intermittently at each impact. Hence, the BVI DEG system operates at a steady-state vibration condition, i.e., impacts occur regularly during a long time, the total energy $W_{total}$ generated from the proposed BVI DEG and the generated output power $P_{sys}$, which can be utilized to evaluate the EH performance of the proposed BVI DEG, can be calculated as:

$$ W_{total} = \sum\limits_{i = 1}^{{N_{T} }} {W_{i} } $$

(18)

$$ P_{sys} = \frac{{W_{total} }}{{t_{2} - t_{1} }} $$

(19)

where $N_{T}$ is the total number of impacts during the given time interval; $W_{i}$ is the energy gain at the $i^{th}$ impact; $t_{1}$ and $t_{2}$ represent the start time and the end time of the time interval for the steady-state vibration of the proposed BVI DEG, respectively.

System Dynamical Behavior

Based on previous theoretical analyses, the proposed BVI DEG system presents a strong nonlinearity. Hence, the fourth-order Runge–Kutta algorithm is adopted in this work to solve the system’s governing equations and reveal its performance. The system dynamical behaviors under an external excitation, which decided the system EH performance, are first studied in this section.

In the numerical simulations, the values of the used parameters are summarized in Table 1 unless otherwise stated. The initial conditions of the system (including the capsule and the inner ball) are set as $x_{c} (0) = 0$, $x_{b} (0) = 0$, $\dot{x}_{c} (0) = 0$ and $\dot{x}_{b} (0) = 0$ in simulations.

Table 1 The values of the parameters used in simulations

First, we preliminarily investigate the effect of a harmonic excitation on the dynamical behaviors of the BVI DEG system (which involves the capsule and the inner ball) using bifurcation diagrams, as shown in Fig. 3. In Fig. 3, $A =$ 0.1g, 0.2g, 0.4g, 0.6g m/s².

Fig. 3

Bifurcation diagrams of the relative displacement $X_{c}$ of the capsule with respect to the base with the excitation frequency $f_{0}$ as a control parameter under a $A = 0.1{\text{g}}$ m/s² b $A = 0.2{\text{g}}$ m/s² c $A = 0.4{\text{g}}$ m/s² d $A = 0.6{\text{g}}$ m/s²; Bifurcation diagrams of the relative displacement $X_{b}$ of the ball with respect to the base and the impact velocity $V_{DEG - }$ of the ball with the excitation frequency $f_{0}$ as a control parameter under e $A = 0.1{\text{g}}$ m/s² f $A = 0.2{\text{g}}$ m/s² g $A = 0.4{\text{g}}$ m/s² h $A = 0.6{\text{g}}$ m/s² (the red and blue points indicate that the impacts occurs at the left and the right membranes, respectively) (color figure online)

Figure 3a–d shows the bifurcation diagrams of $X_{c}$ (the relative displacement of the capsule with respect to the base) with the excitation frequency $f_{0}$ as a control parameter within 140 ~ 200 s (indicating a system’s stable vibration condition). It can be seen from Fig. 3a that when the excitation amplitude $A$ is 0.1g m/s², the capsule experiences single periodic, multiple periodic and chaotic motions as the excitation frequency $f_{0}$ varies. As the excitation amplitude $A$ is increased to 0.2g m/s² (See Fig. 3b), the chaotic motion of the capsule, which can transverse a potential well or double potential wells, is activated under $5.15 \le f_{0} \le 5.25$ Hz. At the remaining excitation frequencies, the pattern of Fig. 3b is similar to that of Fig. 3a, indicating their similar dynamical responses. When the excitation amplitude continues to be increased to 0.4g m/s² (See Fig. 3c), the excitation frequency range of such chaotic motion is expanded and is in the range of 5–5.9 Hz. As the excitation amplitude is further increased to 0.6g m/s² (See Fig. 3d), the capsule will experience the large-scale motion.

The dynamical behavior of the ball is investigated by employing two kinds of bifurcation diagrams. The graphs of Fig. 3e–l show the bifurcation diagrams of $X_{b}$ (the relative displacement of the ball with respect to the base) with the excitation frequency $f_{0}$ as a control parameter to better observe the ball’s motion states. As can be seen, under the same excitation amplitude, the dynamical behaviors of the capsule and the ball are very similar due to their similar bifurcation diagrams. The graphs of Fig. 3e–h II show the bifurcation diagrams of $V_{DEG - }$ (the impact velocity of the ball) with the excitation frequency $f_{0}$ as a control parameter to better observe the ball’s impact states. When the capsule is the single periodic motion (not the large-scale motion), the ball yields a stable 1/1/1 motion (the first ‘1’: single-period motion with respect to the capsule; the second ‘1’: one collision on the left membrane; the third ‘1’: one collision on the right membrane), which means each membrane is impacted once in a response cycle of the ball. When the capsule undergoes the large-scale motion, the ball experiences the multiple periodic motion and multiple collisions. However, when the capsule is the chaotic motion, the ball’s motion is also chaotic and its impact state is disordered. Moreover, it can be further observed from Fig. 3e-II that when the excitation frequency is high, the ball cannot collide with each membrane largely because the impact conditions are not satisfied.

Then, to further investigate the detailed dynamical behaviors of the BVI DEG system under excitation, the dynamical responses of the system are presented in Figs. 5, 6. Here, we noticed that with the increase of the excitation amplitude, the dynamical behaviors of the system are more diverse and more complex, and especially in the low excitation frequency range, new motion states will occur as excitation amplitude increases. At the remaining excitation frequencies, the dynamical behaviors of the system are similar to those under the last excitation amplitude condition. Therefore, in Figs. 5, 6, $A = 0.6{\text{g}}$ m/s². Several representative cases labelled in Fig. 4 are selected, and their corresponding excitation frequencies are 5, 5.3, 6.1, 7.1, 7.6, 8.2, 10.6, 11.5, 12.3 and 14 Hz, respectively.

Fig. 4

The enlarged drawing of Fig. 3d: bifurcation diagrams of the relative displacement $X_{c}$ of the capsule with respect to the base with the excitation frequency $f_{0}$ as a control parameter under $A = 0.6{\text{g}}$ m/s²

Figure 5a shows the phase trajectories of the relative velocity $V_{c}$ ($V_{c} = \dot{x}_{c} - v_{b0}$) and the relative displacement $X_{c}$ of the capsule with respect to the base. It is found that the chaotic motion occurs in cases III and VIII–X, the single-period motion in cases I, II, IV and V, the double-period motion in case VII, the triple-period motion in case VI. Moreover, the capsule experiences the large-scale motion mentioned before, which is the interwell oscillation (See Fig. 5a-I II). The capsule yields intrawell oscillations in cases IV–X. Figure 5b plots the phase trajectories of the relative velocity $V_{b}$ ($V_{b} = \dot{x}_{b} - v_{b0}$) and the relative displacement $X_{b}$ of the ball with respect to the base. As can be seen, the ball experiences the single-period motion in cases IV and V, the double-period motion in case VII, the triple-period motion in case VI, the multiple periodic motion in cases I and II, and the chaotic motion in cases III and VIII–X. Consistent with Fig. 5a, the ball yields interwell oscillations in cases I and II and intrawell oscillations in cases IV–X. Under impacts between the capsule and the ball, the dynamical behaviors of the capsule and the ball are almost the same. The phase trajectories of the relative velocity $V_{DEG}$ and the relative displacement $X_{DEG}$ of the ball with respect to the capsule are presented in Fig. 5c, which clearly exhibits the motion states (with respect to the capsule) and impact states of the ball. It can be seen that the ball experiences the multiple periodic motion and multiple collisions in cases I and II. Chaos and disordered impact states occur in cases III and VIII-X. The ball maintains the stable 1/1/1 motion in cases IV and V, the stable 2/1/2 motion in case VII and the stable 3/2/2 motion in case VI.

Fig. 5

Under $A = 0.6{\text{g}}$ m/s² and different values of $f_{0}$ ($f_{0} =$ 5, 5.3, 6.1, 7.1, 7.6, 8.2, 10.6, 11.5, 12.3, 14 Hz for I-X, respectively), phase trajectories of a the relative velocity $V_{c}$ and the relative displacement $X_{c}$ of the capsule with respect to the base (the red points correspond to Poincaré points), of b the relative velocity $V_{b}$ and the relative displacement $X_{b}$ of the ball with respect to the base (the black points correspond to Poincaré points) and of c the relative velocity $V_{DEG}$ and the relative displacement $X_{DEG}$ of the ball with respect to the capsule (the green points correspond to Poincaré points) (color figure online)

Figure 6 shows the curves of $X_{c}$ and $X_{b}$ against time and the curves of $X_{DEG}$ against time, respectively. Time responses of the system’s displacements are presented here to better understand how the capsule interacts with the ball. It can be seen from Fig. 6a that the fundamental (1:1) resonances mainly govern the dynamical behavior of the system in cases I–VII, whereas the resonances between the capsule and the ball are lost in cases VIII–X. In Fig. 6b, the time response curves of $X_{DEG}$ can clearly show the motion states of the ball (with respect to the capsule) and impact states. As can be seen, the responses of the ball in cases I, II and IV-VII are periodic motions. Chaos occurs in cases III and VIII–X. These results can also be observed from relative phase trajectories of the ball with respect to the capsule shown in Fig. 5c. Moreover, the time response curves of $X_{DEG}$ in cases I and II like a narrow rectangular wave, indicating that the ball periodically collides violently with each membrane. And after a violent collision, it was followed by multiple decaying collisions. The curves in Fig. 6b-IV and V like a triangle wave, inferring that collisions are not as severe compared to cases I and II. As to cases IV and V, there no exists decaying collision. The curves in Fig. 6b-VI and VII exhibit that the ball periodically impacts the membrane. The impact states in cases III and VIII–X are disordered due to system’s chaotic motions.

Fig. 6

Under $A = 0.6{\text{g}}$ m/s² and different values of $f_{0}$ ($f_{0} =$ 5, 5.3, 6.1, 7.1, 7.6, 8.2, 10.6, 11.5, 12.3, 14 Hz for I-X, respectively), time responses of a the relative displacements $X_{c}$ and $X_{b}$ of the capsule and ball with respect to the base and of b the relative displacement $X_{DEG}$ with respect to the capsule (the red dashed lines indicate the ball impacts the bilateral membranes) (color figure online)

By the above analysis, when the excitation amplitude and frequency are different, the system exhibits diverse motion states, such as intrawell and intrawell oscillations and chaotic motions, and complicated impact states. The dynamical behaviors of the system are comprehensively investigated under the excitation in this section. Bases on the above analysis, the system EH performance will be investigated in the next section.

System Energy Harvesting Performance

In this section, the influences of some key parameters on the EH performance of the BVI DEG are studied. Firstly, according to Eq. (3), the excitation parameters ($A$ and $f_{0}$) and system parameters ($m_{c}$, $k$, $x_{0}$ and $L$) can apparently affect dynamical responses of the BVI DEG. Note that $k$, $x_{0}$ and $L$($L$ is replaced by a proportionality factor $\beta$) can vary the bistable potential function (See Eq. (5)). Therefore, the effect of these three parameters on the system EH performance is regarded as that of the bistable potential well on the system EH performance. Secondly, the initial conditions of the system (including the capsule and the ball) can affect the dynamical responses of the system as well. Thirdly, the impact between the ball and the capsule can influence their dynamical and electrical responses. According to Eqs. (7–10), parameters $d$, $m_{c}$, $m_{b}$ and $r$ influence the interaction between the capsule and the ball. Since the parameter $r$ has been first identified by our previous experiments with given $m_{b}$, $r_{b}$, $\lambda_{pre}$, $h_{0}$ and $\phi_{in}$, $r$ is not considered any more in this study. Therefore, the influences of the parameters $A$, $f_{0}$, $m_{c}$ and $d$, initial conditions of the system, and different bistable potential wells on the EH performance of the BVI DEG are fully investigated in this section.

Influences of the Excitation Parameters

In this subsection, the influences of the excitation parameters ($A$ and $f_{0}$) on the EH performance of the BVI DEG are investigated, as shown in Figs. 7, 8. Figure 7 shows $P_{sys} - f_{0}$ curves under different excitation amplitudes. First, it can be noticed that the green solid curve and the brown dashed one almost coincide, indicating that the system can start to harvest energy quickly after a quite short transient state.

Fig. 7

The output power $P_{sys}$ of the BVI DEG against the excitation frequency $f_{0}$ under $A =$ 0.1g, 0.2g, 0.3g, 0.4g, 0.5g, 0.6g m/s². The dashed curve represents the global output power against time over 0– 200 s and the solid curves represent the steady output power against time over 140–200 s

Fig. 8

The output power $P_{sys}$ of the BVI DEG under different sets of $A$ and $f_{0}$

Then, one can see that as the excitation amplitude increases the system EH performance can be enhanced. One can further see that in the excitation frequency range of 5–5.2 Hz, the system output power under $A = 0.5{\text{g}}$ m/s² is significantly higher than that under $A =$ 0.1 g, 0.2 g, 0.3 g, 0.4 g m/s². As $A$ is further increased to 0.6 g m/s², the excitation frequency range of the high output power is broadened and is 5–5.4 Hz. However, when $A = 0.5{\text{g}}$ m/s² and $A = 0.6{\text{g}}$ m/s², the output power plummets at $f_{0} = 5.2$ Hz and $f_{0} = 5.4$ Hz, respectively. The phenomenon can be explained as follows. Taking $A = 0.6{\text{g}}$ m/s² as an example, in the excitation frequency range of 5–5.4 Hz, the high-energy interwell oscillations of the system are excited (See Fig. 6a-I II), and at the same time, the ball collides violently with each membrane, followed by multiple decaying collisions (See Fig. 6b-I II). After $f_{0} = 5.4$ Hz, the system shifts from the interwell oscillation to the chaotic motion (See Fig. 6a-III), while the ball’s impact state is changed to be disordered (See Fig. 6b-III). Thus, the output power drops significantly at $f_{0} = 5.4$ Hz.

As the excitation frequency is further increased from 5.4 Hz, the output power keeps falling slowly under $A =$ 0.1 g, 0.2 g, 0.3 g, 0.4 g m/s², whereas under $A =$ 0.5 g, 0.6 g m/s² the output power is steady first and then decreases slowly. The reason can be explained by Figs. 3a–d and 6. It can be seen from Figs. 3d and 6 that the system experiences the chaotic motion and the intrawell oscillation as excitation frequency increases from 5.4 to 15 Hz. Moreover, the 1:1 resonance mainly governs the dynamical behavior of the system as the excitation frequency increases from 5.4 to 7.7 Hz, whereas there is no resonance between the capsule and the ball in the excitation frequency range of 7.7–15 Hz, except for a few excitation frequencies, at which the system is periodic motions. Thus, the output power keeps steady first and then decreases. For $A =$ 0.1 g, 0.2 g, 0.3 g, 0.4 g m/s² (See Fig. 3a–c), the system shifts from the periodic motion to the chaotic motion, although the system experiences intrawell oscillations. When the system is the chaotic motion in this case, the resonance between the capsule and the ball is lost, resulting in a drop in the output power.

Moreover, we are also concerned with the excitation conditions under which the system can generate the high output power, that is, high-energy interwell motions can be activated. The parameter values corresponding to the sudden increase of the output power are defined as the critical values. To better search for the critical values and observe the combined effect of the excitation amplitude and frequency, the output power under different values of $A$ and $f_{0}$ are presented in Fig. 8. As can be seen, there is a clear boundary between the multi-color area (the high output power area) and the blue area, and the values of excitation parameters ($A$ and $f_{0}$) corresponding to each point on the boundary are the critical values to be sought. Further, it should be noted that the white area, which indicates that the output power is less than 0.0001 mW or that there is no collision between the ball and capsule, tends to appear at high excitation frequencies and generally decreases as the excitation amplitude increases. Regardless, broadband vibration energy harvesting (i.e., the excitation frequency range of the generated output power is very wide) can be achieved at ultra-low/low frequencies with the proposed BVI DEG.

The Influences of the Initial Conditions of the System

In this subsection, the influences of the initial conditions of the system (including the capsule and the ball) on the EH performance of the BVI DEG are investigated, as shown in Fig. 9, where $A = 0.6{\text{g}}$ m/s².

Fig. 9

Under $A = 0.6{\text{g}}$ m/s², the output power $P_{sys}$ of the BVI DEG against the excitation frequency $f_{0}$ for 100 random initial conditions for a $- 0.01 \le x_{c} (0) \le 0.01$ m and $- 1 \le \dot{x}_{c} (0) \le 1$ m/s; and for b $- 0.01 \le x_{b} (0) \le 0.01$ m and $- 1 \le \dot{x}_{b} (0) \le 1$ m/s

It can be seen that the system output power can be increased by properly setting the initial conditions of the system (the increased output power can be compared with the green curve in Fig. 7). Moreover, under different initial conditions, the relationship between the output power and the excitation frequency is not necessarily one-to-one, indicating that there are multiple solutions in the BVI DEG system. To better observe the solution of the system, phase trajectories and basins of attraction are presented in Fig. 10, where $A = 0.6{\text{g}}$ m/s² is kept constant. In this analysis, Figs. 9 and 10 will be combined to discuss the solution of the system.

Fig. 10

Phase trajectories of the relative velocity $V_{c}$ and the relative displacement $X_{c}$ of the capsule with respect to the base for 100 random initial conditions for $- 0.01 \le x_{c} (0) \le 0.01$ m and $- 1 \le \dot{x}_{c} (0) \le 1$ m/s under $A = 0.6{\text{g}}$ m/s² and different values of the excitation frequency $f_{0}$ ($f_{0} =$ 5, 5.35, 5.55, 7.5, 12.5 Hz for a–e, respectively); phase trajectories of the relative velocity $V_{c}$ and the relative displacement $X_{c}$ of the capsule with respect to the base for 100 random initial conditions for $- 0.01 \le x_{b} (0) \le 0.01$ m and $- 1 \le \dot{x}_{b} (0) \le 1$ m/s under $A = 0.6{\text{g}}$ m/s² and different values of the excitation frequency $f_{0}$ ($f_{0} =$ 5, 5.35, 7.5, 10, 12.5 Hz for g–k, respectively); basins of attraction under f $A = 0.6{\text{g}}$ m/s² and $f_{0} = 12.5$ Hz; and under (l) $A = 0.6{\text{g}}$ m/s² and $f_{0} = 10$ Hz. The green color indicates the intrawell motion area of the capsule for the left potential well, the red color indicates the intrawell motion area of the capsule for the right potential well and the blue color indicates the interwell motion area of the capsule for the double potential well

Figure 10a–e shows phase trajectories of the relative velocity $V_{c}$ and the relative displacement $X_{c}$ of the capsule with respect to the base for 100 random initial conditions for $- 0.01 \le x_{c} (0) \le 0.01$ m and $- 1 \le \dot{x}_{c} (0) \le 1$ m/s under different selected representative excitation frequencies labelled in Fig. 9a.

When $f_{0} = 5$ Hz (See Fig. 10a), the capsule is the interwell periodic motion, indicating that the system has only one periodic solution. Combined with Fig. 9a, it can be inferred that in the excitation frequency range of 5–5.3 Hz, the system has only one solution.

When $f_{0} = 5.35$ Hz (See Fig. 10b), the capsule can experience the interwell periodic motion and two types of chaotic motion (one marked with multiple colors and the other with gray), so there are one periodic solution and multiple chaotic solutions in the system. Thus, the system can yield multiple output powers at this excitation frequency.

When $f_{0} = 5.55$ Hz (See Fig. 10c), the capsule can experience the interwell periodic oscillation and chaotic motions, so the system output power has a jump. In the excitation frequency range of 5.35–5.55 Hz, the system has one periodic solution and multiple chaotic solutions. After $f_{0} = 5.55$ Hz, the periodic solution of the system vanishes.

When $f_{0} = 7.5$ Hz (See Fig. 10d), the capsule experiences intrawell periodic motions, so the system has two periodic solutions in the excitation frequency range of 6.65–7.75 Hz. After $f_{0} = 7.75$ Hz, chaotic solutions will appear again. In the excitation frequency range of 8–8.25 Hz, only periodic solutions occur in the system.

When $f_{0} = 12.5$ Hz (See Fig. 10e), the capsule can experience the interwell periodic motion and intrawell chaotic motions, indicating that the system has one periodic solution and multiple chaotic solutions. This results in a jump of the output power. In the excitation frequency range of 9.5–13.6 Hz, the sudden increase in the output power can be attributed to interwell oscillations yielded by the capsule.

Among the graphs in Fig. 10a–e shows that the capsule can experience the interwell oscillation for the double potential well and intrawell oscillations for the right and left potential well. Thus, under the excitation conditions in Fig. 10e, the basin of attraction is presented in Fig. 10f. As can be seen, the total area of green and red colors (intrawell oscillations) is much larger than that of the blue color (interwell oscillations).

Figure 10g–k shows phase trajectories of the relative velocity $V_{c}$ and the relative displacement $X_{c}$ of the capsule with respect to the base for 100 random initial conditions for $- 0.01 \le x_{b} (0) \le 0.01$ m and $- 1 \le \dot{x}_{b} (0) \le 1$ m/s under different representative excitation frequencies labelled in Fig. 9b.

When $f_{0} = 5$ Hz, Fig. 10g shows the same pattern as Fig. 10a. Combining with Fig. 9b, it is inferred that the system has only one periodic solution in the excitation frequency range of 5–5.3 Hz. Figure 10h shows the capsule under $f_{0} = 5.35$ Hz can experience interwell periodic motions and two types of chaotic motion, which means the system has multiple periodic solutions and chaotic solutions. After $f_{0} = 5.35$ Hz, the periodic solutions of the system are lost. When $f_{0} = 7.5$ Hz, Fig. 10i exhibits that the capsule experiences intrawell periodic motions, which is the same as Fig. 10d. Thus, the system has two periodic solutions in the excitation frequency range of 6.65 ~ 7.7 Hz. After $f_{0} = 7.7$ Hz, chaotic solutions will appear again. When $f_{0} = 10$ Hz (See Fig. 10j), the capsule can experience interwell and intrawell chaotic motions, indicating that the system has multiple chaotic solutions. In the excitation frequency range of 9.55–11.25 Hz, the sudden increase in the output power can be ascribed to interwell oscillations of the capsule. When $f_{0} = 12.5$ Hz (See Fig. 10k), the capsule experiences intrawell chaotic motions, so the system has chaotic solutions in the excitation frequency range of 11.3–15 Hz.

Similar to Fig. 10f, the basin of attraction under the excitation conditions in Fig. 10j are presented in Fig. 10l. As can be seen, the area of the red color (intrawell oscillations of the right potential well) is largest. The total area of green and red colors (intrawell oscillations) is much larger than that of the blue color (interwell oscillations).

The Influence of the Mass of the Capsule

The mass $m_{c}$ of the capsule can be adjusted by changing the material density or the thickness of the capsule, and consequently, it is a variable parameter to improve the EH performance of the BVI DEG. By setting $A =$ 0.1g, 0.2g, 0.3g, 0.4g, 0.5g, 0.6g m/s², the output power of the BVI DEG under various sets of $m_{c}$ and $f_{0}$ is presented in Fig. 11.

Fig. 11

The output power $P_{sys}$ of the BVI DEG under different sets of $m_{c}$ and $f_{0}$ when a $A = 0.1{\text{g}}$ m/s² b $A = 0.2{\text{g}}$ m/s² c $A = 0.3{\text{g}}$ m/s² (d) $A = 0.4{\text{g}}$ m/s² e $A = 0.5{\text{g}}$ m/s² f $A = 0.6{\text{g}}$ m/s²

As can be seen, the graphs of Fig. 11 can be divided into two categories according to their pattens. The one category is Fig. 11a–c, where $A =$ 0.1g, 0.2g, 0.3g m/s²; the other one Fig. 11d–f, where $A =$ 0.4g, 0.5g, 0.6g m/s². By comparison, the high output power (See multi-color areas in Fig. 11d–f is produced under $A =$ 0.4g, 0.5g, 0.6g m/s², and $m_{c}$ exerts a complex effect on these multi-color areas. According to the previous analysis, the high output power of the system means that the system yields high-energy interwell oscillations. To demonstrate it, the phase trajectories of the relative velocity $V_{c}$ and the relative displacement $X_{c}$ of the capsule with respect to the base in different representative cases are presented in Fig. 12. The values of $m_{c}$ and $f_{0}$ in each case are selected from one point on the multi-color area of each graph in Fig. 11. As can be seen from Fig. 12, the system experiences intrawell oscillations under $A =$ 0.1g, 0.2g, 0.3g m/s², but interwell oscillations under $A =$ 0.4g, 0.5g, 0.6g m/s².

Fig. 12

Phase trajectories of the relative velocity $V_{c}$ and the relative displacement $X_{c}$ of the capsule with respect to the base in case I: $A = 0.1{\text{g}}$ m/s², $f_{0} = 5.8$ Hz and $m_{c} = 45$ g, case II: $A = 0.2{\text{g}}$ m/s², $f_{0} = 7$ Hz and $m_{c} = 30$ g, case III: $A = 0.3{\text{g}}$ m/s², $f_{0} = 7$ Hz and $m_{c} = 30$ g, case IV: $A = 0.4{\text{g}}$ m/s², $f_{0} = 5$ Hz and $m_{c} = 45$ g, case V: $A = 0.5{\text{g}}$ m/s², $f_{0} = 5.2$ Hz and $m_{c} = 45$ g and case VI: $A = 0.6{\text{g}}$ m/s², $f_{0} = 5$ Hz and $m_{c} = 60$ g

To better observe the effect of $m_{c}$ on the system output power, by setting $f_{0} = 5$ Hz, $P_{sys} - A$ curves under various sets of $m_{c}$ are presented in Fig. 13. As can be seen, there exists a clear boundary between the multi-color area (similar to a triangle) and the blue area. In the multi-color area, as the excitation amplitude increases, the adjustable range of $m_{c}$ become wider; as $m_{c}$ increases, the output power increases as well, although the excitation amplitude range is narrowed. More importantly, the leftmost edge of the boundary is extended to an excitation amplitude of about 0.4g m/s², smaller than that in Fig. 8 under $f_{0} = 5$ Hz, indicating that the system can generate the high output power at a lower amplitude. Hence, by the above analysis, $m_{c}$ is an available adjusting parameter to enhance EH performance of the BVI DEG.

Fig. 13

The output power $P_{sys}$ of the BVI DEG under different sets of $m_{c}$ and $A$ when $f_{0} = 5$ Hz

The Influence of the Distance Between the Two Membranes

The distance $d$ between the two membranes can be adjusted by changing the length of the capsule, and consequently, it is also a variable parameter to enhance the EH performance of the BVI DEG. Similar to Sect. "The influence of the mass of the capsule", the EH performance of the BVI DEG affected by $d$ is studied in this subsection. Figure 14 shows the output power under different sets of $d$ and $f_{0}$; Fig. 15 the output power under different sets of $d$ and $A$. In Fig. 14, $A =$ 0.1g, 0.2g, 0.3g, 0.4g, 0.5g, 0.6g m/s²; in Fig. 15, $f_{0} = 5$ Hz.

Fig. 14

The output power $P_{sys}$ of the BVI DEG under different sets of $d$ and $f_{0}$ when a $A = 0.1{\text{g}}$ m/s² b $A = 0.2{\text{g}}$ m/s² c $A = 0.3{\text{g}}$ m/s² d $A = 0.4{\text{g}}$ m/s² e $A = 0.5{\text{g}}$ m/s² f $A = 0.6{\text{g}}$ m/s²

Fig. 15

The output power $P_{sys}$ of the BVI DEG under different sets of $d$ and $A$ when $f_{0} = 5$ Hz

One can see from Fig. 14 that as $d$ increases from 15 to 70 mm, the system can work normally with given excitation conditions, except for a few excitation frequencies. As $d$ further increases from 70 mm, the system is almost unable to work under most excitation frequencies. One can further see that the graphs in Fig. 14 can also be divided into two categories. By comparison, the high output power of the system is produced under $A =$ 0.4g, 0.5g, 0.6g m/s², and is affected by $d$. It can be seen from Fig. 15 that in the multi-color area, as $d$ increases from 15 to 105 mm the excitation amplitude range of the output power is first narrowed and then widened; and the output power in the multi-color area slightly decreases first and then significantly increases. Moreover, an excitation amplitude of the leftmost edge of the boundary is further reduced to around 0.38g m/s², smaller than that in Fig. 13. Hence, $d$ is another available adjusting parameter to enhance the system EH performance of the BVI DEG.

The Influences of Bistable Potential Wells

In this subsection, the influences of the different bistable potential wells on the system EH performance are investigated. It can be learnt from Eq. (5) that adjusting each of the four parameters forms different symmetric bistable potential functions and can also simultaneously vary their stable equilibrium positions and potential barriers. Thus, we need to adjust stable equilibrium positions and potential barriers separately through appropriately setting parameters $k$, $x_{0}$ and $\beta$, and analyze their influences on the EH performance of the BVI DEG accordingly.

According to Eq. (6), the stable equilibrium position and the potential barrier can be adjusted by only changing values of $k$ and $x_{0}$ with given parameters $\beta$ (the value of $\beta$ is given in Table 1). The influences of $k$ and $x_{0}$ on the bistable potential well are presented in Fig. 16. Figure 16a shows that by only adjusting $k$, the stable equilibrium positions remain constant but the potential barriers are varied. One can further see that with the increase of $k$ the potential barriers also increase. Figure 16b shows that by keeping $kx_{0}^{2}$ constant, adjusting $k$ and $x_{0}$ simultaneously enable the potential barriers to remain constant but make the stable equilibrium positions changed. The value of $kx_{0}^{2}$ is calculated as $4 \times 10^{ - 2}$ ${\varvec{N}} \cdot {\varvec{m}}$ with given $k$ and $x_{0}$ in Table 1 and remain unchanged for the convenience of the analysis. It can be noticed from Fig. 16b that by increasing $x_{0}$ ($k$ naturally decreases as $x_{0}$ increases), the stable equilibrium positions deviate from the origin ($X_{c} = 0$).

Fig. 16

Potential energy function: a under different $k$; b under different $x_{0}$ and $kx_{0}^{2} = 4 \times 10^{ - 2}$ ${\varvec{N}} \cdot {\varvec{m}}$

Then, the influences of the potential barrier and the stable equilibrium position on the EH performance of the BVI DEG are fully investigated, as shown in Figs. 17, 18, 19, 20. In Figs. 17 and 19, $A =$ 0.1g, 0.2g, 0.3g, 0.4g, 0.5g, 0.6g m/s²; in Figs. 18 and 20, $f_{0} = 5$ Hz. Figures 17 and 18 are presented to better reveal the effect of the potential barrier on the system EH performance. As can be seen, the effect law of the potential barrier is completely opposite to that of $m_{c}$ (See Figs. 11 and 13), which indicates that the optimization method of the potential barrier is the opposite of that of $m_{c}$. Moreover, the leftmost edge of the boundary is pushed to an excitation amplitude of about 0.35g m/s², which is smaller than those shown in Figs. 13 and 15.

Fig. 17

The output power $P_{sys}$ of the BVI DEG under different sets of $k$ and $f_{0}$ when a $A = 0.1{\text{g}}$ m/s² b $A = 0.2{\text{g}}$ m/s² c $A = 0.3{\text{g}}$ m/s² d $A = 0.4{\text{g}}$ m/s² e $A = 0.5{\text{g}}$ m/s² f $A = 0.6{\text{g}}$ m/s²

Fig. 18

The output power $P_{sys}$ of the BVI DEG under different sets of $k$ and $A$ when $f_{0} = 5$ Hz

Fig. 19

The output power $P_{sys}$ of the BVI DEG under different sets of $x_{0}$ and $f_{0}$ when a $A = 0.1g$ m/s² b $A = 0.2{\text{g}}$ m/s² c $A = 0.3{\text{g}}$ m/s² d $A = 0.4{\text{g}}$ m/s² e $A = 0.5{\text{g}}$ m/s² f $A = 0.6{\text{g}}$ m/s²

Fig. 20

The output power $P_{sys}$ of the BVI DEG under different sets of $x_{0}$ and $A$ when $f_{0} = 5$ Hz

Figures 19 and 20 are presented to reveal the effect of the stable equilibrium position on the system EH performance. As can be seen, the effect law of the stable equilibrium position is similar to that of $m_{c}$, indicating that both have the same optimization scheme to improve the system EH performance. The leftmost edge of the boundary in Fig. 20 is pushed to an excitation amplitude of about 0.3g m/s², which is noticeably smaller than that shown in Fig. 13. Through above analysis, tuning the potential barrier and the stable equilibrium position can be a better way to improve the EH performance of the BVI DEG.

Discussion: Comparative Study

The EH performance under diverse key parameters is fully investigated in Sect. "System energy harvesting performance". To better demonstrate the superiority of the proposed BVI DEG operating in a wide excitation frequency range under a low excitation amplitude, the proposed BVI DEG system is compared with the VI DEG in this section. For the VI DEG, the external excitation acts directly on the capsule. Moreover, in order to ensure that the membrane can be impacted by the ball (that is, the impact conditions can be satisfied), $d$ is set to be small (e.g., $d = 15$ mm). Then, for a fair comparison between the two EH systems, the parameters in Table 1 continue to be used, and the output power under different values of $A$ and $f_{0}$ are plotted in Fig. 21. As can be seen, with given excitation amplitude, the excitation frequency range of the output power of the BVI DEG is much wider than that of the VI DEG. Moreover, the highest output power produced by the BVI DEG is over 3.5 mW, which is more than 15 times that of the VI DEG.

Fig. 21

The output power $P_{sys}$ of a the BVI DEG and b the VI DEG under different sets of $A$ and $f_{0}$ when $d = 15$ mm. Zero initial conditions are chosen

To further verify broadband effectiveness of the proposed BVI DEG system, a cosine acceleration excitation with a broad frequency band is applied to the BVI DEG and the VI DEG. Figure 22 shows the curves of the frequency spectrum of the excitation with different values of the amplitude $A$ ($A =$ 0.1g, 0.2g, 0.3g, 0.4g, 0.5g, 0.6g m/s²). In this case, the frequency of excitation is varied between 5 and 15 Hz at an increment of 0.1 Hz per second. Then, the output powers of the two energy harvesters under the broadband frequency excitation with different amplitudes are presented in Fig. 23 to investigate the effect of such excitation on the system EH performance. As can be seen from Fig. 23a, b, when $A = 0.6{\text{g}}$ m/s², both energy harvesters can produce a maximum output power. The maximum output power of the BVI DEG is achieved up to 6.98 mW at 6 Hz, and the maximum output power of the VI DEG is 0.3667 mW at 15 Hz. To better compare the EH performance of the two energy harvesters at ultra-low frequencies (5–10 Hz), the enlarged drawing of Fig. 23a, b during 5 Hz and 10 Hz are plotted in Fig. 23c, d. As can be seen, the proposed BVI DEG can harvest a broadband vibration energy and exhibits a better EH performance than the VI DEG in 5–10 Hz. By comparison, the superiority of the proposed BVI DEG system has been demonstrated.

Fig. 22

Curves of frequency spectrum of the variable frequency cosine excitation for $A =$ 0.1g, 0.2g, 0.3g, 0.4g, 0.5g 0.6g m/s²

Fig. 23

When $d = 15$ mm, the output power $P_{sys}$ of a the BVI DEG and b the VI DEG against excitation frequency $f$ under different values of the excitation amplitude $A$; the enlarged drawing of Fig. 23a, b during 5 Hz and 10 Hz are plotted in c and d, respectively. The color data maximum of c is set to be the same as that of d for better comparison between the BVI DEG and the VI DEG. Zero initial conditions are chosen

Conclusions

This paper numerically investigated the dynamical behavior and EH performance of the BVI DEG under low-frequency vibrations. Based on the results of the numerical simulations it can be stated as follows.

1. The proposed BVI DEG exhibits rich dynamical behaviors. The capsule can experience interwell, chaotic and intrawell motions with respect to the base, and the ball exhibits dynamic characteristics similar to that of the capsule. When the capsule undergoes intrawell chaotic motions, resonance between the capsule and the ball disappears; in other cases, the 1:1 resonance is dominant in the system.

2. In terms of the EH performance of the BVI DEG, as the excitation amplitude increases from 0.1 to 0.6 g, the system output power is increased since the system can shift from low-energy intrawell oscillations to high-energy interwell oscillations.

3. The system output power can be further increased by adjusting other key parameters. Adjusting the initial conditions of the system can increase the output power, but it is difficult to achieve this. By adjusting the mass of the capsule, the distance between the two membranes, and the bistable potential well, the proposed BVI DEG can generate the high output power at low excitation amplitudes. However, the generated high output power at a lower excitation amplitude can be further achieved by appropriately setting the bistable potential well, making it a better method to improve the EH performance.

4. By comparing the VI DEG and the proposed BVI DEG, the proposed one has the obvious advantage of operating in a wider excitation frequency under harmonic and variable-frequency excitations.

In conclusion, the research results can help better understand the dynamical behaviors of the proposed BVI DEG and can provide guidelines for the design and optimization of the BVI DEG in the low frequency vibration environment. In future work, investigations on dynamical behaviors and the EH performance of the BVI DEG system will be also presented using experiments and analytical approaches.

Appendix A

The functions of the restitution coefficient $r$ and the largest central deflection of the membrane $\delta_{\max }$ against the impact velocity $V_{DEG - }$ were [34, 39], respectively:

$$ r = 0.5989e^{{ - 1.31\left| {V_{DEG - } } \right|}} + 0.2241 $$

(20)

$$ \delta_{\max } = - 0.006903e^{{ - 0.3498\left| {V_{DEG - } } \right|}} + 0.00832 $$

(21)

where $V_{DEG - } = \dot{x}_{b - } - \dot{x}_{c - }$ denotes the relative velocity between the ball and the membrane (i.e., the velocity of the capsule) before each impact.

In Eq. (20), having known the impact velocity $V_{DEG - }$, the restitution coefficient $r$ can be calculated. Therefore, the dynamical response of the BVI DEG after each impact can be obtained accurately. $\delta_{\max }$, which decides $C_{\max }$ of the DEMs at their largest deformation during impacts, and further determines the output voltage $\phi_{out}$, can be calculated using Eq. (21). Therefore, the output voltage $\phi_{out}$ of the proposed BVI DEG at each impact is decided by $V_{DEG - }$ with the given parameters.