Introduction

Background

As an essential type of transportation, high-speed trains (HSTs) have developed rapidly in recent years. The axle box bearings, which connect the wheelset and the bogie, play an important role for stable and safety operation of HSTs. Fatigue damage of the bearing components happens as the train working under heavy load for enough long time. Researches on the dynamic characteristics of axle box bearings with defects provide a theoretical basis for fault diagnosis, which is of great significance to the safe operation of HSTs.

Literature Survey

A lot of modeling methods for faulty bearings, such as vibration monitoring models, quasi-static models, lumped-parameter models, finite element models and complete dynamic models, have been developed.

For the vibration monitoring model, the defects of the bearing are typically modeled as a pulse sequence. A rolling bearing model under constant radial load was established by McFadden and Smith, and the single and multi-point defects on the inner raceway were described as impulse functions [18, 19]. Multi-event excitation force model was presented by Khanam et al. to analyze the vibration responses of bearings with inner raceway defect [11]. The forcing function was expressed as a function of speed, load, defect edge, and size of defect. The frequency at the component of the spectrum in the response of a bearing with a defect can be correctly predicted by the vibration monitoring model, but the cause of vibration at a bearing defect cannot be clearly revealed by the model.

A quasi-static model of rolling bearings considering the centrifugal force and gyroscopic moment of rolling elements was proposed by Jones, which can determine the elastic compliance of the bearing system under different loads [10]. Bai and Xu studied the nonlinear stability and dynamic characteristics of a rotor-bearing system rotating at high speed by a five-degree-of-freedom dynamic model of ball bearing considering internal clearance and waviness [1]. In addition, some novel methods for bearing stiffness calculation were proposed [4, 6]. The fatigue life of bearings can be estimated more accurately by the quasi-static model. However, due to the assumption of “raceway control”, the model cannot deal with the problems related to lubricant and relative slippage, and most of the research on bearings with defect focused on manufacturing errors.

To make up for the deficiency of quasi-static model, dynamic models were proposed, and the lumped-parameter model was considered first. The varying compliance vibrations of a two-degree-of-freedom bearing model under radial load were investigated by Sunnersjӧ, and the rolling element was modeled as a nonlinear spring according to Hertz theory [25]. Based on the above model, Rafsanjani et al. analyzed the dynamic behaviors of the rolling bearing system with defective component [22]. Dynamic characteristics of rotor-rolling bearing model considering the base excitation and damping rings were investigated by Zhu et al. [35]. Dai et al. considered additional displacement would be caused by a localized defect on the inner raceway, through which the authors studied its effects on the gear-shaft-bearing coupling system [3]. A force model for the inter-shaft bearing containing nonlinear and local defects was addressed by Gao et al., and the nonlinear dynamic characteristics of a dual-rotor system were conducted [5]. Cage collisions, roller skidding and deflection cannot be described in lumped-parameter models because of the simplification of rollers.

Finite element (FE) models are often used to describe complex dynamics of rolling element bearings. Kiral and Karagülle proposed the dynamic loading model of rolling element bearing structure with defects, and the vibration response of the structure was analyzed by FE method [12]. Based on FE method, the uncertainties about the stability threshold of rotating systems supported by cylindrical journal bearings under the influence of bearing clearance and oil temperature were studied by Visnadi and de Castro [27]. A complete dynamic nonlinear FE model of a rolling element bearing with an outer raceway defect was presented by Singh et al., in which the bearing assembly was modeled as a flexible body [23, 24]. The model was addressed numerically by explicit dynamic finite element software package LS-DYNA. However, the detailed interaction between roller and raceway cannot be surveyed by FE model.

To give a more realistic description of the dynamic behavior of bearings, Gupta solved the vibration response of cylindrical roller bearings using classical differential equations of motion [7, 8]. In the proposed model, the interactions between rollers and raceways, rollers and cage were analyzed in detail, and the effect of lubricant was taken into consideration. Wang et al. proposed a cylindrical roller bearing model with centrifugal forces, gravity forces and slipping of the rollers considered, and the dynamic responses of bearing were surveyed with different types and sizes of defects [28]. Dynamic models of rolling ball bearing and cylindrical roller bearing with localized surface defects were developed by Niu et al., considering the finite size of the rolling element, the effect of the cage, changes of contact force directions, and the additional clearance due to material absence [20, 21]. Based on these models, the vibration responses of the defective bearings can be calculated accurately. A cylindrical roller bearing model containing gyroscopic moment, centrifugal force and lubrication traction/slip between roller/raceway, roller/cage, cage/raceway was addressed by Cao et al., and the vibration responses of bearing with single defect, multi-defects and compound faults were investigated [2].

According to the literature, it can be found that the track irregularity is usually considered in the vehicle-track coupled model, in which the bearings were greatly simplified. A three-dimensional vehicle-track coupled dynamics model considering traction drive system and axle box bearing was proposed by Wang et al., in which the effects of unsteady wind load and random track irregularities on dynamic behavior of bearings were investigated [30, 31]. Vehicle-track coupled dynamics models considering the errors were established [14, 26]. Lu et al. conducted a novel bearing-vehicle coupled model to survey the influence of different types of bearing defects on the vibration responses of bearing [15].

Formulation of the Problem of Interest

Prominent achievements have been made in vibration characteristics of defective rolling bearings, but there are still some limitations: (1) When the axle box bearing is modeled as a complete dynamic model, the coupling effect between the bearing and the track is ignored in most literatures. In addition, the modeling of the bearing in the vehicle-track coupled model has been simplified a lot. (2) The vibration mechanism of dynamic model of rolling bearing with rolling element defect is seldom investigated. (3) The motion of outer raceway is rarely considered in the previous bearing dynamics models.

Scope and Contribution of this Study

In this paper, a dynamic model of cylindrical roller bearing coupled with local defects and wheel-rail excitation is proposed based on Gupta’s model. Note that the axle box bearing is modeled as a complete dynamic model and the coupling effect with the track is considered. Time-varying deflection excitation is applied when modeling local defects on the outer raceway, inner raceway and roller. The motion of the outer raceway is taken into account. In addition, gravity of car body, lubrication traction and Hertzian contact force between raceway and roller are included. Furthermore, numerical analyses are carried out in time and frequency domains respectively, and the obtained conclusions provide theoretical support for fault diagnosis of axle box bearings.

Dynamic Model

Model Description

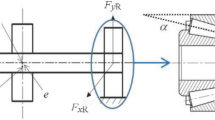
As shown in Fig. 1, the axle box bearing serves as the main body and half of the wheelset is included in the proposed model. The external excitations of the axle box bearing include the gravity of the car body and the wheel-rail contact force. Assuming that the inner raceway of the bearing and the wheelset are one unit, so are the outer raceway and the housing.

Fig. 1
figure 1

A dynamic model of axle box bearing system

Full size image

In consideration of the complexity of the actual axle box bearing, the following assumptions are employed,

  1. 1.

    The axle box bearing is modeled as a cylindrical roller bearing. Compared to the double-row tapered roller bearing with a small contact angle and only radial loads in HST, difference on the contact deformations between rollers and raceways is slight [16].

  2. 2.

    Interactions between cage and other bearing components are ignored.

  3. 3.

    The skewing or tilting of rollers and raceways is not considered in the model.

  4. 4.

    The outer and inner raceways are fixed rigidly to the housing and the shaft, respectively.

  5. 5.

    The lubrication condition of the bearing is assumed to be dry contact, which is close to the operation under elastohydrodynamics lubrication.

  6. 6.

    The contact stiffness does not change at the defect.

The bearing model in the YZ plane is shown in Fig. 2. Axle box bearing is modeled as a cylindrical roller bearing model with 17 rollers. Suppose that the motion of outer raceway can be translated along the Y and Z directions in the outer raceway-fixed coordinate frame, and the motion of inner raceway can be translated along the Y and Z directions and rotated around the X axis in the inner raceway-fixed coordinate frame, respectively. The rollers can be rotated around the X axis and translated radially in the inertial coordinate frame, as well as rotated around the X axis in the roller-fixed coordinate frame.

Fig. 2
figure 2

Bearing model in the YOZ plane

Full size image

Interaction of Roller and Raceway

The interaction between outer raceway and roller is similar to that between the inner raceway and roller, so we discuss only the latter in this part. The relationships between the coordinate frames are shown in Fig. 3. Based on the inertial frame OXYZ, the inner race-fixed coordinate frame OrXrYrZr, the roller-fixed coordinate frame ObXbYbZb, the inner race-fixed azimuth frame OraXraYraZra and the roller azimuthal frame OaXaYaZa are respectively established. The contact frame OcXcYcZc is also introduced to model the contact force between rollers and raceway. The transformation matrix between the coordinate frames is determined by the Cardan angle.

Fig. 3
figure 3

Relationships between coordinate frames

Full size image

The interaction between each slice and the raceway can be calculated as

$$\delta { = } \pm \left( {r_{pr3}^{ra} - r_{r} } \right),$$
(1)

where \(r_{pr3}^{ra}\) is the third element of the vector from the inner race center to the contact point P in the frame OraXraYraZra. rr is the radius of the raceway, and the sign is positive for the outer raceway.

Then, Hertzian contact force can be expressed as [7]

$$Q_{c} = \left\{ \begin{gathered} K_{c} \delta^{10/9} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \delta > 0 \hfill \\ 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \delta \le 0{\kern 1pt} {\kern 1pt} \hfill \\ \end{gathered} \right.,$$
(2)

where Kc is the contact stiffness.

The sliding velocity vector of the raceway relative to the roller at point P in the contact frame is

$$v_{rb}^{c} = v_{r}^{c} - v_{b}^{c} ,$$
(3)

where \(v_{r}^{c}\) and \(v_{b}^{c}\) are the velocity vectors of raceway and roller at point P, respectively.

After the relative sliding velocity is obtained, the contact force vector and the traction force vector can be expressed, respectively, as

$$F_{c}^{c} = \left[ {0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - Q_{c} + c_{rr} v_{rb3}^{c} } \right]^{T} ,$$
(4)
$$F_{t}^{c} = \left[ {0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} sign\left( {v_{rb2}^{c} } \right)\left| {k_{br} } \right|\left| { - Q_{c} + c_{rr} v_{rb3}^{c} } \right|{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0} \right]^{T} ,$$
(5)

where \(v_{rb2}^{c}\) and \(v_{rb3}^{c}\) are the second and third elements of the relative sliding velocity respectively, crr is the damping coefficient and kbr is the traction coefficient, which can be determined based on the following traction model [7]

$$k_{br} = ( - 0.04 + 0.05\left| {v_{rb2}^{c} } \right|)e^{{ - 0.86\left| {v_{rb2}^{c} } \right|}} + 0.04.$$
(6)

Then the forces and moments can be confirmed.

The force vector acting on the roller in the roller azimuthal frame can be written as

$$F_{b}^{a} = \sum\limits_{k = 1}^{n} {T_{ia} T_{ir}^{ - 1} T_{rra}^{ - 1} T_{rac}^{ - 1} \left( {F_{c}^{c} + F_{t}^{c} } \right)} ,$$
(7)

where Tia and Tir are the transformation matrixs from the frame OXYZ to OaXaYaZa and the frame OXYZ to OrXrYrZr, respectively. Trra and Trac are the transformation matrix from the frame OrXrYrZr to OraXraYraZra and the frame OraXraYraZra to OcXcYcZc.

The force vector acting on the raceway in the frame OXYZ is

$$F_{r}^{i} = \sum\limits_{k = 1}^{n} {T_{ir}^{ - 1} T_{rra}^{ - 1} T_{rac}^{ - 1} \left( { - F_{c}^{c} - F_{t}^{c} } \right)} .$$
(8)

The moment vectors acting on the roller and the raceway in the body-fixed frames can be described respectively, as

$$M_{b}^{b} = \sum\limits_{k = 1}^{n} {r_{kc}^{b} \times \left( {T_{ib} T_{ir}^{ - 1} T_{rra}^{ - 1} T_{rac}^{ - 1} \left( {F_{c}^{c} + F_{t}^{c} } \right)} \right)} ,$$
(9)
$$M_{r}^{r} = \sum\limits_{k = 1}^{n} {T_{ir} \left( {r_{rc}^{i} \times \left( {T_{ir}^{ - 1} T_{rra}^{ - 1} T_{rac}^{ - 1} \left( { - F_{c}^{c} - F_{t}^{c} } \right)} \right)} \right)} ,$$
(10)

where rkc is the vector from the inner race center to the center of the kth slice, rrc is the vector of the contact center relative to the raceway center, Tib is the transformation matrix from the frame OXYZ to ObXbYbZb.

Wheel-Rail Force

According to the nonlinear Hertzian elastic contact theory, the vertical force between wheel and rail can be determined as [34]

$$P\left( t \right) = \left[ {\frac{1}{G}\delta Z\left( t \right)} \right]^{3/2} ,$$
(11)

where G is the wheel-rail contact constant (m/N2/3).

Assuming that the rail is always in stationary. The elastic compression deformation between wheel and rail can be expressed as

$$\delta Z\left( t \right){ = }GP_{0}^{2/3} + TI\left( t \right) - z_{r} ,$$
(12)

where P0 is the static wheel load, TI(t) the track irregularity, and zr the displacement of the wheelset in Z direction. Therefore, the wheel-rail force can be written as

$$P\left( t \right) = \left\{ \begin{gathered} \left[ {P_{0}^{2/3} + \frac{1}{G}\left( {TI\left( t \right) - z_{r} } \right)} \right]^{3/2} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \delta Z\left( t \right) > 0 \hfill \\ 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \delta Z\left( t \right) \le 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \hfill \\ \end{gathered} \right..$$
(13)

Modeling of Localized Surface Defect

Defects on Outer and Inner Raceway [28]

In Fig. 4(a), the path of roller as it passes through a defect on the inner raceway can be seen, which is similar to the outer raceway. Assume that H is less than the depth of the defect.

Fig. 4
figure 4

Contact detail with defect in a inner raceway and b roller

Full size image

The elastic deformation within the defective area can be expressed as

$$\delta { = }\left\{ \begin{gathered} \delta { - }\delta_{d} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0 \le \phi_{fr} \le \phi_{d} \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \delta {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{other}} \hfill \\ \end{gathered} \right.,$$
(14)

where the defect deflection excitation is

$$\delta_{d} { = }\left\{ \begin{gathered} H\sin \left( {\frac{\pi }{{\phi_{d} }}\phi_{fr} } \right){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0 \le \phi_{fr} \le \phi_{d} \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{other}} \hfill \\ \end{gathered} \right..$$
(15)

The maximal additional deflection is

$$H = r_{b} - \sqrt {r_{b}^{2} - \left( {W_{d} /2} \right)^{2} } .$$
(16)

The angle of the defect zone can be described by

$$\phi_{d} { = }\left\{ \begin{gathered} W_{d} /r_{o} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{for}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{outer}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{race}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \hfill \\ W_{d} /r_{i} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{for}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{inner}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{race}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \hfill \\ \end{gathered} \right.{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} .$$
(17)

The angle of the roller relative to the initial angular position of the defect in the race-fixed coordinate frame is

$$\phi_{fr} { = }\left\{ \begin{gathered} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \bmod \left( {\theta_{j} ,2\pi } \right){\kern 1pt} - \phi_{0} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{for}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{outer}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{race}} \hfill \\ \bmod \left( {\theta_{j} ,2\pi } \right){\kern 1pt} - \bmod \left( {\omega_{i} t + \phi_{0} ,2\pi } \right){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{for}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{inner}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{race}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \hfill \\ \end{gathered} \right.,$$
(18)

where \(\phi_{0}\) is the initial angular position of the defect zone, rb the radius of the roller, ri and ro the radius of the inner raceway and the outer raceway respectively, Wd the defect width, and ωi is the rotation speed of the inner raceway.

Defect on Roller [33]

The interaction between the defective roller and the inner raceway is shown in Fig. 4(b), and the outer raceway is similar. Assuming that the underside of the roller defect is not touched.

The elastic deformation within the defective area can be expressed as

$$\delta { = }\left\{ \begin{gathered} \delta { - }\delta_{d} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0 \le \phi_{fb} \le \phi_{d} \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \delta {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{other}} \hfill \\ \end{gathered} \right.,$$
(19)

where the defect deflection excitation is

$$\delta_{d} { = }\left\{ \begin{gathered} H\sin \left( {\frac{\pi }{{\phi_{d} }}\phi_{fb} } \right){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0 \le \phi_{fb} \le \phi_{d} \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{other}} \hfill \\ \end{gathered} \right..$$
(20)

The maximal additional deflection as the roller contacts the outer and the inner raceways can be written as

$$H = H_{ro} - H_{o} = \left[ {r_{b} - \sqrt {r_{b}^{2} - \left( {W_{d} /2} \right)^{2} } } \right] - \left[ {r_{o} - \sqrt {r_{o}^{2} - \left( {W_{d} /2} \right)^{2} } } \right],$$
(21)

and

$$H = H_{ri} + H_{i} = \left[ {r_{b} - \sqrt {r_{b}^{2} - \left( {W_{d} /2} \right)^{2} } } \right] + \left[ {r_{i} - \sqrt {r_{i}^{2} - \left( {W_{d} /2} \right)^{2} } } \right],$$
(22)

respectively. The angle of the defect zone can be described as

$$\phi_{d} { = }W_{d} /r_{b} ,$$
(23)

When the initial angular position of the defect zone \(\phi_{0}\) is 0, the angle of the X-axis relative to the initial angular position of the defect zone in the roller-fixed coordinate frame is

$$\phi_{fb} { = }\left\{ \begin{gathered} \bmod \left( {\left| {\eta_{j} } \right|,2\pi } \right){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{for}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{outer}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{race}} \hfill \\ \bmod \left( {\left| {\eta_{j} { + }\pi } \right|,2\pi } \right){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{for}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{inner}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{race}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \hfill \\ \end{gathered} \right.,$$
(24)

where rb is the radius of the roller, ro and ri the radius of the outer raceway and the inner raceway respectively, Wd the defect width, and ηj is the rotation angle.

Simulation of Track Irregularity

German high-speed low disturbance spectrum is used for simulation, which is as [34]

$$S_{v} \left( \Omega \right) = \frac{{A_{v} \Omega_{c}^{2} }}{{\left( {\Omega^{2} + \Omega_{r}^{2} } \right)\left( {\Omega^{2} + \Omega_{c}^{2} } \right)}},$$
(25)

where \(\Omega_{c}\) = 0.8246 rad/m and \(\Omega_{r}\) = 0.0206 rad/m are the cutoff frequencies, \(A_{v}\) = \({4}{\text{.032}} \times 10^{ - 7}\) rad·m the roughness function, and \(\Omega \,{ = }\,2\pi f/V\), the spatial frequency, in which f is the time frequency and V is the train speed.

To facilitate calculation, a method should be adopted to convert the power spectral density function into time-domain signal [34]. The implementation steps are as follows.

  1. 1.

    First, the power spectral density function of track irregularity is transformed into a bilateral spectrum.

  2. 2.

    Then, the spectral moduli of the time-domain sequence are calculated.

  3. 3.

    Assume the spectral phase is random and create a complex sequence by symmetry condition.

  4. 4.

    Finally, the inverse Fourier transform of the obtained complex sequence is used to simulate the disturbance function in time domain.

Equations of Motion of the Bearing System

The equations of translational motion of the outer raceway in the inertial frame are written as

$$\left\{ \begin{gathered} m_{o} \ddot{y}_{o} + k_{o} y_{o} { + }c_{0} \dot{y}_{o} = \sum\limits_{n = 1}^{{N_{b} }} {F_{ob2}^{n} } \hfill \\ m_{o} \ddot{z}_{o} + k_{o} z_{o} { + }c_{0} \dot{z}_{o} = \sum\limits_{n = 1}^{{N_{b} }} {F_{ob3}^{n} - m_{o} g - W} \hfill \\ \end{gathered} \right.,$$
(26)

where mo is the mass of the housing and the outer raceway, ko the stiffness coefficient, co the damping coefficient, \(F_{ob}^{n}\) the force vector of the roller n acting on the outer raceway, and W the weight of the car body acting on the housing. \(\ddot{y}_{o}\), \(\dot{y}_{o}\) and \(y_{o}\) are, respectively, the acceleration, velocity and displacement of the outer raceway in y direction, and \(\ddot{z}_{o}\), \(\dot{z}_{o}\) and \(z_{o}\) are that in z direction.

The equations of translational motion of the inner raceway in the inertial frame are described as

$$\left\{ \begin{gathered} m_{r} \ddot{y}_{r} = \sum\limits_{n = 1}^{{N_{b} }} {F_{rb2}^{n} } \hfill \\ m_{r} \ddot{z}_{r} = \sum\limits_{n = 1}^{{N_{b} }} {F_{rb3}^{n} - m_{r} g + P\left( t \right)} \hfill \\ \end{gathered} \right.,$$
(27)

where mr is the mass of half shaft and the inner raceway, \(F_{rb}^{n}\) the force vector of the roller n acting on the inner raceway, P(t) the wheel-rail force acting on the wheelset, \(\ddot{y}_{r}\) and \(\ddot{z}_{r}\) are the accelerations in y and z directions of the inner raceway respectively.

The motion equations of the roller in the inertial cylindrical frame are expressed as

$$\left\{ \begin{gathered} m_{b} \ddot{r}_{j} - m_{b} r_{j} \dot{\theta }_{j}^{2} = F_{b3}^{a} - m_{b} g\sin \theta_{j} \hfill \\ m_{b} r_{j} \ddot{\theta }_{j} + 2m_{b} \dot{r}_{j} \dot{\theta }_{j} - = - F_{b2}^{a} - m_{b} g\cos \theta_{j} \hfill \\ \end{gathered} \right.,$$
(28)

where mb is the mass of the roller, \(\ddot{r}_{j}\) the radial translational acceleration of the roller j, \(\ddot{\theta }_{j}\) the orbital acceleration of the roller j.

Assuming that the inner raceway and the roller rotate only around their own X-axis in the fixed frame, the rotational equation of motion is

$$I_{x} \dot{\omega }_{x} - \left( {I_{y} - I_{z} } \right)\omega_{y} \omega_{z} = M_{x} ,$$
(29)

where Ix, Iy and Iz are the moment of inertia around X, Y and Z axes, respectively, and ωx, ωy and ωz are the angular velocities. Mx is the moment around its X-axis, and shown as \(M_{r}^{r}\) and \(M_{b}^{b}\) for the inner raceway and the roller, respectively.

Results and Discussions

The flow of numerical simulation is demonstrated in Fig. 5. To obtain the vibration responses of the bearing components, the fourth-order Runge–Kutta method with fixed time step (\(1 \times 10^{{{ - }6}}\) s) is adopted to numerically solve Eqs. (26)–(29). The shaft speed is set to 1590 rpm. The main parameters of axle box bearing are shown in Table 1. The radial clearance is set to 0 for the sake of calculation.

Fig. 5
figure 5

Flow chart of numerical simulation

Full size image
Table 1 Parameters of the bearing system
Full size table

Simulation Results of Track Irregularity

As shown in Fig. 6(a), the amplitude of time series of track irregularity ranges from − 0.007 to 0.007 m, which is consistent with Ref. [34]. In Fig. 6(b), the main frequency components associated with track irregularity are 0.35763 Hz, 0.95367 Hz, 2.86102 Hz, 1.90735 Hz and 5.72205 Hz.

Fig. 6
figure 6

Simulation results of track irregularity in a time domain and b frequency domain

Full size image

Vibration Responses of Bearing Under Different Conditions

In actual structure of axle box, the bearing outer raceway is installed to stationary parts, which makes it more achievable to measure its acceleration, so this signal is chosen for analysis in following sections. The dynamic responses of the axle box bearing which considers track irregularity and local defects are analyzed and compared with the responses of the bearing without track irregularity.

Case Without Defect and Track Irregularity

The vibration responses in the case without fault and track irregularity are shown in Fig. 7. The periodicity can be clearly identified in Fig. 7(a). It can be seen that the time interval between adjacent circles is 0.087 s in Fig. 7(b), which is consistent with the time of one revolution of the roller.

Fig. 7
figure 7

Vibration responses in the case without fault and track irregularity. a Acceleration of outer raceway, b enlarge view of (a), c acceleration envelope spectrum of outer raceway

Full size image

As plotted in Fig. 7(c), there are four main frequency bands in the spectrum. The frequency composition in the first frequency band is clear, major peak frequencies in the spectra include 2fc, 4fc, fvc-3fc, fvc-2fc, 2fvc, 3fvc and 9fvc + fc. For the other three frequency bands, the frequency component distributions are more complex. In the frequency range 4 to 7 kHz, the main peaks are 26fvc + 5fc and 33fvc-2fc. From 10 to 13 kHz, they are 55fvc + 5fc, 57fvc + 5fc, 63fvc + 3fc and 64fvc + 3fc, and from 15 to 18 kHz, they are 80fvc + 5fc, 87fvc + 4fc and 88fvc + 4fc, respectively. One finds that the frequency components are mainly related to fvc and fc.

Case with Only Track Irregularity

The vibration responses in this case are shown in Fig. 8. There is no significant periodicity in Fig. 8(a), while the time interval between the two peaks is about 4.786 ms in Fig. 8(b), which is roughly equal to 1/18fc.

Fig. 8
figure 8

Vibration responses in the case with only track irregularity. a Acceleration of outer raceway, b enlarge view of (a), c acceleration envelope spectrum of outer raceway

Full size image

Two main frequency bands are found in Fig. 8(c). In the first frequency band, the main peaks are 0.9537 Hz, which is the frequency associated with track irregularity, 18fc and 37fc. In the second frequency band, they are 111fc, 129fc, 147fc and 165fc. One finds that, except the frequency associated with the track irregularity, all the other frequency components are harmonic terms close to the product of roller number and rotation frequency of cage.

Case with Only Outer Raceway Defect

In this case, the obvious periodicity can be observed in Fig. 9(a). The time interval between adjacent cycles is about 5.15 ms in Fig. 9(b), which is basically equal to 1/fo.

Fig. 9
figure 9

Vibration responses in the case with only outer raceway defect. a Acceleration of outer raceway, b enlarge view of (a), c acceleration envelope spectrum of outer raceway

Full size image

Two regions with distinct frequency components can be found in Fig. 9(c). In the low-frequency region, the main peaks are 2fc, fo, fo-fc, fo + fc, 2fo-2fc and 2fo + fc. The frequency component distributions are more complex in the high-frequency region, and the main peaks are 67fo-4fc, 69fo-6fc and 72fo-7fc. One finds that the main frequency components are related to fo and fc.

Case with Outer Raceway Defect and Track Irregularity

As shown in Fig. 10(a), there is no obvious periodicity in this case. Whereas the time interval associated with 2.861 Hz, which is the frequency associated with track irregularity, can be found, which is about 0.349 s. In addition, it can be seen that the time interval between adjacent peaks is about 5.082 ms in Fig. 10(b), which is consistent with 1/fo.

Fig. 10
figure 10

Vibration responses in the case with outer raceway defect and track irregularity. a Acceleration of outer raceway, b enlarge view of (a), c acceleration envelope spectrum of outer raceway

Full size image

As plotted in Fig. 10(c), besides the most prominent frequency peak 2.861 Hz, there exist components fo-12fc, fo-9fc, fo-6fc, fo-3fc, fo-fc, fo, fo + 7fc, 2fo-fc and 2fo in the range 50 to 500 Hz, which are related to fo and fc.

Case with Only Inner Raceway Defect

In this case, the obvious periodicity can be observed in Fig. 11(a). It can be found that the time interval between adjacent cycles in Fig. 11(b) is about 0.037 s, matching with fω, and the time interval between two peaks in the same cycle is about 3.742 ms, which is roughly equal to 1/fi.

Fig. 11
figure 11

Vibration responses in the case with only inner raceway defect. a Acceleration of outer raceway, b enlarge view of (a), c acceleration envelope spectrum of outer raceway

Full size image

In Fig. 11(c), the main peaks are fω, 2fω, 3fω, fi, fi + fc, fi + fc-3fω, fi + fc-2fω and fi + fc-fω. One finds that the main frequency components are related to fi, fω and fc.

Case with Inner Raceway Defect and Track Irregularity

As shown in Fig. 12(a), there is no significant periodicity in this case. Similar to the case with outer raceway defect and track irregularity, one also finds a time interval, approximately 0.374 s, associated with 2.861 Hz. It can be observed that the time interval between adjacent cycles in Fig. 12(b) is about 0.038 s, consistent with fω, and the time interval between the two peaks in the same cycle is about 3.964 ms, very close to 1/fi.

Fig. 12
figure 12

Vibration responses in the case with inner raceway defect and track irregularity. a Acceleration of outer raceway, b enlarge view of (a), c acceleration envelope spectrum of outer raceway

Full size image

In Fig. 12(c), the main peaks are fω, 2fω, 5fω, fi and fi + fω. One finds that the amplitude of the frequency related to the track irregularity is larger, and the other major frequency components are related to fi and fω.

Case with Only Roller Defect

In this case, significant periodicity can be found in Fig. 13(a). It can be observed that the time interval between adjacent cycles in Fig. 13(b) is about 0.084 s, which is basically the same time as the roller revolution. The time interval between two adjacent peaks in the same period is about 0.0105 s, which is the time interval between the roller defect and the raceway contact.

Fig. 13
figure 13

Vibration responses in the case with only roller defect. a Acceleration of outer raceway, b enlarge view of (a), c acceleration envelope spectrum of outer raceway

Full size image

In Fig. 13(c), the main peaks are 2fc, 4fc, 2fr-2fc, 2fr, 2fr + 2fc, 3fr and 4fr. One finds that the main frequency components are related to fc and fr.

Case with Roller Defect and Track Irregularity

Similar to the case with only roller defect, the periodicity can be clearly identified in Fig. 14(a). As plotted in Fig. 14(b), the time interval between adjacent cycles is about 0.085 s, and the time interval between two adjacent peaks in the same period is about 0.0105 s.

Fig. 14
figure 14

Vibration responses in the case with roller defect and track irregularity. a Acceleration of outer raceway, b enlarge view of a, c acceleration envelope spectrum of outer raceway

Full size image

In Fig. 14(c), the main peaks are 2fc, fr, 2fr-2fc, 2fr, 2fr + 2fc, 3fr and 4fr. One finds that the main frequency components are related to fc and fr.

Effect of Vehicle Speed on the RMS Value of Acceleration

Figure 15 presents the influence of speed on the root mean square (RMS) value of the outer raceway acceleration under different conditions. As the speed increases, the RMS value of acceleration of the fault-free bearing varies steadily, while the RMS values of the fault bearings increase. In the cases with track irregularities, the RMS values of accelerations of fault-free bearing, bearing with outer raceway defect and bearing with inner raceway defect increase significantly compared with that without considering track irregularity, while the RMS value of acceleration of bearing with roller defect do not change significantly. In the cases of considering the track irregularity, the RMS value of acceleration of the bearing system with outer raceway defect is greater than that of inner raceway, while the inner raceway is greater than that of roller, which indicates that the coupling effect decreases in turn.

Fig. 15
figure 15

The effect of vehicle speed on the RMS values of outer raceway accelerations of a bearing without defect, b bearing with outer raceway defect, c bearing with inner raceway defect, d bearing with roller defect

Full size image

Discussions

In summary, the main frequency peaks are linear combinations of the characteristic frequencies of the bearing with different faults, as shown in the third column of Table 2. When considering the track irregularities, except for the roller defect case, the periodicity is not significant in the whole acceleration time-histories, but it does appear for a short time. The time intervals in the cases with defects can correspond to the frequencies associated with track irregularity and the characteristic frequencies in the spectra. Furthermore, track irregularity makes the frequency components with higher amplitude closer to the low-frequency region. In short, the influence of track irregularity on bearing response is greater under outer raceway and inner raceway defects, but less under roller defect.

Table 2 Main frequency characteristics of different cases
Full size table

The rigid model is used in this paper, so there are deviations between the values of structural damping of the shaft and oil film damping of the bearing and the actual values, resulting in the calculated amplitude of axle box acceleration is different from the experimental and simulation results in the literature [15, 29]. Whereas the frequency-related phenomenon is roughly the same. In addition, the simulated values of characteristic frequencies are in good agreement with the theoretical values, as shown in Table 3, which can also verify the correctness of the model.

Table 3 The values of the characteristic frequencies
Full size table

In the cases with track irregularities, when the outer raceway is defective, the intense wheel-rail excitation escalates the vibration of the roller in the fault zone, which leads to the increase of the contact stiffness between the roller and the outer raceway. In addition, the outer raceway is directly excited by the defect, so the RMS value is quite large. For the case where the inner raceway is defective, the vibration is weakened when transmitted from the inner raceway to the roller and finally to the outer raceway, so the RMS value is relatively small. When the roller is defective, there is only one roller with defect, and the coupling effect with the track irregularity is small. As can be seen from Fig. 15(a), wheel-rail excitation has little influence on the rollers without defects, so the RMS value is the smallest. The simulation results are consistent with those obtained in Ref. [13], which verifies the correctness of the model.

Conclusions

Based on Gupta’s model, a dynamic model of axle box bearing considering localized surface defects and track irregularities is proposed and numerically simulated, so that it can represent the dynamic behaviors of axle box bearing and provide theoretical basis for fault diagnosis of bearing. The acceleration time-histories and spectra of the outer raceway in Z direction are analyzed in detail. Influence of speed on RMS values of vibration signals under different conditions is also discussed. Conclusions are summarized in the following.

In the cases with track irregularities, the greater influence of track irregularity can be observed from the responses of the bearing system with outer raceway defect or inner raceway defect, and frequency components related to track irregularity can be found in both the acceleration time-histories and spectra. In addition, it can be found that the track irregularity causes the main frequency in the frequency domain to be closer to the low-frequency region. However, no obvious effect of track irregularity is found in the response of bearing system with roller defect. It can be seen that the coupling effects between track irregularity and outer raceway defect and inner raceway defect are great, but the coupling effect between track irregularity and roller defect is not obvious.

Track irregularity can aggravate the vibration of bearing, but it has little effect on bearing with roller defect. As the speed increases, the RMS values of accelerations of the bearing with defects show an increasing trend, while the bearing without defect is relatively stable. In the cases of considering the track irregularity, the RMS value of acceleration of the bearing system with outer raceway defect is greater than that of inner raceway, while the inner raceway is greater than that of roller, which indicates that the coupling effect decreases in turn.

With the rapid development of artificial intelligence, the data-driven methods have been extensively applied in fault diagnosis and prognosis, which offer a promising tool for the industrial maintenance problems [17, 32]. Further investigation using deep machine learning techniques will be carried out for monitoring the health states of axle box bearings.