Current Vibration Suppression of Magnetic Bearing Systems Based on Phase Shift Generalized Integrator

Abstract

Purpose

Active Magnetic Bearing (AMB) levitates the rotor with controllable magnetic force, which has been widely applied in high-speed rotating machine. For rotating machine applied AMB, there is vibration in currents in the coils of AMB. Vibration caused by centrifugal force in rotating machine results in noise, collision and other shortcomings. Suppressing vibration in current is an important and meaningful topic.

Methods

In this study, a current vibration suppressing strategy based on phase shift generalized integrator (PSGI) in AMB system is proposed. PSGI is applied to filter out synchronous component in displacement signal of rotor, and therefore vibration in current can be reduced. Firstly, current fluctuation caused by centrifugal force is analyzed. Later, stability of AMB system applied with PSGI is analyzed based on root locus. Principle of selecting phase shift is proposed based on calculating departure angle at the poles in imaginary axis of system. Lastly, simulations and experiments are carried out to demonstrate effectiveness of the proposed vibration suppressing strategy.

Results and conclusion

The results of simulations and experiments show that, the proposed method based on PSGI can suppress the current vibration by over 90%. Compared with traditional method, the proposed method can stabilize the system when rotating frequency is low. In addition, the proposed method is with simpler structure and less calculation, the cost of time for calculation can be reduce by about 66%. This study expands rotating speed range for vibration suppressing and it improves efficiency of algorithm by simpler structure.

Introduction

Active magnetic bearing (AMB) is a novel type of bearing which supports rotor by controllable magnetic force. Levitation of rotor by magnetic force avoids friction, collision and lubricating etc. Because of advantages above, AMB has been applied in high-speed motor, centrifugal compressor, and flywheel suspension etc. AMB detects state information and provides adjustable magnetic force, hence these advantages contribute to design and application of smart rotating machine in the future.

In rotating machines, vibration is a common problem. Main source of vibration is centrifugal force. Unbalance of rotor mass will cause centrifugal force in rotation, whose frequency equals to rotating frequency. Zhang [1] et al. analyzed dynamic performance of AMB system considering centrifugal force and Alford force. In rotational machine applied AMB, vibration mainly performs off-center displacement and electrical current. As a result, there are mainly two types of vibration suppressing method, unbalance compensation, and auto balancing. Unbalance compensation focus on eliminating vibration in displacement and auto balancing focus on eliminating vibration of current. Current vibration may cause saturation of amplifier whereas current vibration will also cause vibration of supporting component, resulting meaningful current suppressed vibration.

This paper proposes a vibration suppressing strategy to reduce current vibration, such as this method belongs to an auto balancing. Basic idea of auto balancing is to filter out synchronous component in displacement signal, so the controller and amplifier will not respond to the synchronous signal. As a result, current fluctuation will be reduced. The frequency of current vibration is varying with rotating speed, so the resonant frequency of notch filter should be adaptive. Adaptive notch filter is the core of vibration suppressing method. Herzog [2] et al. proposed a generalized notch filter (GNF), and applied it to vibration suppressing in AMB system. Liu [3] et al. combined GNF with sliding-mode observer to realize auto balance in AMB system. Zheng [4] et al. proposed a vibration suppressing strategy based on GNF connected in parallel mode. Cui [5] et al. applied GNFs for parallel different resonant frequencies to reduce harmonic vibration in current. Besides GNF, coordinate transformation is usually applied to make up notch filter. Zheng [6] et al. proposed an auto balancing method based on coordinate transformation. Peng [7] et al. proposed force vibration suppression for AMB system based on synchronous rotating frame transformation. Chamroon [8] et al. have proposed a vibration control strategy to prevent nonlinearly coupled rotor–stator whirl response. Kuseyri [9] have proposed adaptive linear parametrically varying (LPV) controllers to suppress vibration in AMB system.

Generalized notch filter applied in AMB requires trigonometric calculation in real time, hence, structure of notch filter is complex. Then, the main disadvantage of GNF is that it cannot stabilize the system when the rotating frequency is relatively low. To overcome these two main shortcomings, this paper applied GI and PSGI to vibration suppressing in AMB. Generalized integrator (GI) performs well in constructing filters and has been applied in power grid control. Yuan [10] et al. applied generalized integrators for active power filters. Allmeling [11] et al. have applied GI to fast harmonics compensation in active filters. Guo [12] et al. have combined GI with extended observer and applied it to suppress sinusoidal disturbance.

The GNF method can be applied to rotational harmonics filtering and can be applied in AMB centrifugal disturbance rejection. However, the major challenge is the computation resource for the method that performs multi trigonometric calculations in the micro-controller. Micro-controller for AMB needs to take responsibilities for multi-axis levitation, which requires more saving of computation resource than power grid harmonics filtering. With GI method, there is a possibility to do the filtering with less computation resources. However, similar to the GNF, and GI method is the instability occurrence for rotation low frequencies.

To simplify the structure of vibration suppressing strategy, this paper proposes a novel current vibration suppressing method of AMB system based on phase shift generalized integrator (PSGI). The structure of proposed vibration suppressing strategy is simpler and with less calculation than notch filter applied commonly in AMB system, and can make the system stable for low frequency. This paper is organized as: In part “Vibration Suppression Strategy”, model of AMB system is established based on transfer functions of each segments. Expression of current fluctuation in theory was calculated. Vibration suppressing strategies based on GI and PSGI are proposed. Next, in part “Analysis of GI and PSGI Applied in AMB”, stability analysis and parameters selecting based on root locus are introduced. In part “Simulation Results”, simulations are carried out to verify effectiveness of proposed strategy. Experiment results carried on a test rig are presented in part “Experimental Results”. Finally, conclusions are summarized in part “Conclusions”.

Vibration Suppression Strategy

In this section, model of AMB system is established and current vibration caused by unbalance effect is analyzed. The main idea of suppressing current fluctuation will be introduced.

Model of AMB System and Current Vibration Analysis

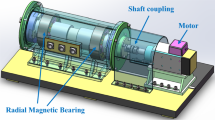
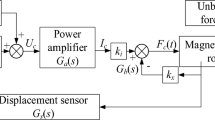
AMB system is composed of sensors, amplifiers, controller, and actuators etc. A radial AMB is shown in Fig. 1. Two displacement sensors are installed on two orthogonal degrees of freedom (DOF). The magnetic force is generated by actuators, and currents in actuators are produced by amplifiers. Controller is the core segment of AMB system. Performance of rotor mainly depends on algorithm of controller. Magnetic force is nonlinear, as a result, AMB system is a typical nonlinear system. The magnetic force can be linearized through controller design. Proportional–integral–differential (PID) controller has been widely used in AMB system. Involving disturbance, the AMB control system applied PID in one DOF is expressed in Fig. 2.

Fig. 1

Structure of radial AMB

Fig. 2

Structure of control system of AMB

The magnetic force can be linearized as a linear model with double-stiffness. When magnetic force operates on the rotor with mass m, the dynamic equation of rotor can be expressed as:

$$k_{i} i + k_{x} x = m\ddot{x},$$

(1)

where k_i is force-current stiffness and k_x is force–displacement stiffness, and they are determined by structure parameters of actuators in AMB [13]. According to the dynamic equation, the transfer function of AMB can be expressed as

$$G\left( s \right) = \frac{X\left( s \right)}{{I\left( s \right)}} = \frac{{k_{i} }}{{ms^{2} - k_{x} }}.$$

(2)

In simulations and experiments presented in this paper, the amplifier is composed of IGBTs and PI current controllers. The amplifier can be expressed as a low-pass segment. The transfer function of the amplifier is

$$G_{{1}} \left( s \right) = \frac{{\omega_{c} }}{{s + \omega_{c} }}.$$

(3)

Transfer function of PID controller should be

$$C\left( s \right) = k_{P} + \frac{{k_{I} }}{s} + k_{D} s.$$

(4)

The sensor is pre-assumed to be a linear segment with gain amplitude k_h. The control system expressed by transfer functions is shown in Fig. 3.

Fig. 3

Structure of control system

The amplifier is regarded as a linear segment temporarily to simplify its expression. The transfer function from centrifugal force to current is

$$\frac{i\left( s \right)}{{F\left( s \right)}} = - \frac{1}{{k_{i} }}\frac{{k_{h} G\left( s \right)C\left( s \right)}}{{1 + k_{h} G\left( s \right)C\left( s \right)}}.$$

(5)

Expanding this transfer function and submitting s = jω, the gain and phase shifting can be expressed as

$$\frac{{i\left( {j\omega } \right)}}{{F\left( {j\omega } \right)}} = \frac{{k_{h} \left( { - jk_{P} \omega + k_{D} \omega^{2} - k_{I} } \right)}}{{j\left( {k_{P} k_{h} k_{i} - k_{x} - m\omega^{2} } \right)\omega^{2} + k_{I} k_{h} k_{i} - k_{D} k_{h} k_{i} \omega^{2} }},$$

(6)

$$\left| {\frac{{i\left( {j\omega } \right)}}{{F\left( {j\omega } \right)}}} \right| = k_{h} \sqrt {\frac{{\left( {k_{D} \omega^{2} - k_{I} } \right)^{2} + k_{P}^{2} \omega^{2} }}{{\left( {k_{P} k_{h} k_{i} - k_{x} - m\omega^{2} } \right)^{2} \omega^{4} + \left( {k_{I} k_{h} k_{i} - k_{D} k_{h} k_{i} \omega^{2} } \right)^{2} }}} ,$$

(7)

$$\angle \frac{{i\left( {j\omega } \right)}}{{F\left( {j\omega } \right)}} = \pi + \tan^{ - 1} \left( {\frac{{k_{P} \omega }}{{ - k_{D} \omega^{2} + k_{I} }}} \right) - \tan^{ - 1} \left( {\frac{{\left( {k_{P} k_{h} k_{i} - k_{x} - m\omega^{2} } \right)\omega^{2} }}{{k_{I} k_{h} k_{i} - k_{D} k_{h} k_{i} \omega^{2} }}} \right).$$

(8)

If the rotor is rotating at a constant speed, the expression of centrifugal force is F(t) = emω²cos(ωt + θ₀). Where e is the eccentricity, ω is the rotating angular speed, and θ₀ is the initial phase of the unbalance mass. Hence, the amplitude of synchronous fluctuation in control current will be

$$\begin{gathered} I_{A} = em\omega^{2} \left| {\frac{{i\left( {j\omega } \right)}}{{F\left( {j\omega } \right)}}} \right|, \hfill \\ = em\omega^{2} k_{h} \sqrt {\frac{{\left( {k_{D} \omega^{2} - k_{I} } \right)^{2} + k_{P}^{2} \omega^{2} }}{{\left( {k_{P} k_{h} k_{i} - k_{x} - m\omega^{2} } \right)^{2} \omega^{4} + \left( {k_{I} k_{h} k_{i} - k_{D} k_{h} k_{i} \omega^{2} } \right)^{2} }}.} \hfill \\ \end{gathered}$$

(9)

From (9), it is clear that with the centrifugal force of emω², AMB control current I_A will have obvious disturbance, with the calculated amplitude in (9). If current fluctuation is too large, there will be saturation in amplifier, which causes control system become unstable. Current fluctuation also causes vibration in motor. Suppressing current vibration contributes to stabilize the system.

Vibration Suppression Strategy for AMB System

The current fluctuation is mainly caused by synchronous component in displacement. A common method is adding a notch filter to filter out synchronous component in displacement signal. Obviously, the resonant frequency of notch filter is supposed to track the rotating frequency, or adaptive. The common strategy to suppress current fluctuation based on generalized notch filter (GNF) is shown in Fig. 4.

Fig. 4

Structure of current fluctuation suppressing with GNF

The core segment of GNF is N(s), which is shown in Fig. 5. It requires three integrators and two times of trigonometric calculations. The aim of GNF is obtaining component with frequency Ω. When Ω is set as rotating angular speed, the synchronous component can be filtered out. However, the complex structure of GNF causes mass of calculation. Then, when the rotating frequency is low, the system cannot be stable.

Fig. 5

Structure of N(s)

To achieve the goal that filtering out synchronous component in displacement signal, considering a generalized integration (GI) segment as

$$N_{0} \left( s \right) = \frac{s}{{s^{2} + \Omega^{2} }}.$$

(10)

The generalized integrator has infinite gain when s = jΩ. When N₀(s) is added a gain ε and applied as feedback, the transfer function is

$$N_{1} \left( s \right) = \frac{1}{{1 + \varepsilon N_{0} \left( s \right)}} = \frac{{s^{2} + \Omega^{2} }}{{s^{2} + \varepsilon s + \Omega^{2} }}.$$

(11)

The bode diagram of N₁(s) with Ω = 400π rad/s is shown in 0 (Fig. 6). It presents a notch-filter feature at s = jΩ.

Fig. 6

Bode diagram of closed-loop GI

To realize a generalized integrator, transforming its transfer function as

$$N_{0} \left( s \right) = \frac{{{1 \mathord{\left/ {\vphantom {1 s}} \right. \kern-\nulldelimiterspace} s}}}{{1 + \frac{1}{s}\frac{{\Omega^{2} }}{s}}}.$$

(12)

It can be realized by forward gain as an integrator and feedback gain as Ω² multiplied with an integrator. As a result, N₀(s) can be realized as Fig. 7.

Fig. 7

Realization of N0(s)

However, in a wide range of rotating speed of AMB system, the phase shift is important to stabilize the system. To adding a phase shift segment, the expression of generalized integrator can be changed as

$$N_{2} \left( s \right) = \frac{s\cos \varphi + \Omega \sin \varphi }{{s^{2} + \Omega^{2} }}.$$

(13)

When phase shift generalized integration (PSGI) is applied to vibration suppression, the transfer function of closed-loop PSGI is

$$N_{{3}} \left( s \right) = \frac{1}{{1 + \varepsilon N_{2} \left( s \right)}} = \frac{{s^{2} + \Omega^{2} }}{{s^{2} + \varepsilon s\cos \varphi + \varepsilon \Omega \sin \varphi + \Omega^{2} }}.$$

(14)

The bode diagram of closed-loop PSGI when Ω = 400π rad/s, φ = π/4 is shown in Fig. 8. It also presents notch-filter feature at s = jΩ, comparing with notch filter composed of GI in Fig. 6, notch filter composed of PSGI has an adjustable phase lead generated by φ at its resonant frequency. The effect of φ will be discussed in next section.

Fig. 8

Bode diagram of closed-loop PSGI

To realize a generalized integrator with phase shift, transforming transfer function of N₂(s) as

$$N_{2} \left( s \right) = \left( {\cos \varphi + \frac{\Omega \sin \varphi }{s}} \right)\frac{{{1 \mathord{\left/ {\vphantom {1 s}} \right. \kern-\nulldelimiterspace} s}}}{{1 + \frac{1}{s}\frac{{\Omega^{2} }}{s}}}.$$

(15)

The phase shift segment can be realized as a proportional–integral (PI) segment, whose realization is shown in Fig. 9. The parameters can be designed as k_IN = Ωsinφ and k_PN = cosφ. Comparing with GNF, PSGI has less calculation, because PSGI does not have to calculate trigonometric in real time. Although there is trigonometric calculation in PI segment, it can be pre-calculated instead of calculating in real time. To apply PSGI to suppress vibration in current, replace N(s) by N₂(s) in Fig. 4 can achieve the goal. The control system applied PSGI is shown in Fig. 10.

Fig. 9

Realization of PSGI

Fig. 10

Control system applied PSGI

Analysis of GI and PSGI Applied in AMB

In this section, AMB control system applied GI and PSGI will be analyzed. Sinusoidal response of GI is calculated. Rotating speed range of AMB system applied GI was analyzed by root locus. Principle of selecting parameter φ was analyzed by calculating departure angle at the pole in imaginary axis of system (Fig. 11).

Fig. 11

Root locus with parameter Ω²

Analysis of AMB System Applied GI

When GI is applied to compose a notch filter, the transfer function of notch filter is N₁(s), the transfer function ratio D_is to N_out is

$$\frac{{N_{{{\text{out}}}} \left( s \right)}}{{{\text{Dis}}\left( s \right)}} = \frac{\varepsilon s}{{s^{2} + \varepsilon s + \Omega^{2} }}.$$

(16)

When Dis is a sinusoidal signal with angular frequency Ω, the N_out is supposed to track Dis to do achieve filtering. It is assumed that Dis(t) = Asin(Ωt), whose Laplace transform expression is

$$L\left( {Dis\left( t \right)} \right) = A\frac{\Omega }{{s^{2} + \Omega^{2} }}.$$

(17)

The response of N_out in time domain is

$$\begin{gathered} N_{{{\text{out}}}} \left( t \right) = L^{ - 1} \left( {L\left( {Dis\left( t \right)} \right)\frac{{N_{{{\text{out}}}} \left( s \right)}}{Dis\left( s \right)}} \right), \hfill \\ = A\sin \left( {\Omega t} \right) - A\frac{{\sinh \left( {\frac{t}{2}\sqrt {\varepsilon^{2} - 4\Omega^{2} } } \right)}}{{\sqrt {\left( {{\raise0.7ex\hbox{$\varepsilon $} \!\mathord{\left/ {\vphantom {\varepsilon {2\Omega }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${2\Omega }$}}} \right)^{2} - 1} }}e^{{ - {\raise0.7ex\hbox{${\varepsilon t}$} \!\mathord{\left/ {\vphantom {{\varepsilon t} 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} , \hfill \\ \end{gathered}$$

(18)

where sinh(x) = (e^x + e^−x)/2. If ε < 2Ω, the expression of response is

$$N_{out} \left( t \right) = A\sin \left( {\Omega t} \right) - A\frac{{\sin \left( {\frac{t}{2}\sqrt {4\Omega^{2} - \varepsilon^{2} } } \right)}}{{\sqrt {1 - \left( {{\raise0.7ex\hbox{$\varepsilon $} \!\mathord{\left/ {\vphantom {\varepsilon {2\Omega }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${2\Omega }$}}} \right)^{2} } }}e^{{ - {\raise0.7ex\hbox{${\varepsilon t}$} \!\mathord{\left/ {\vphantom {{\varepsilon t} 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}} .$$

(19)

The second term of N_out(t) is transient process. Generally, ε is set to be much smaller than 2Ω. As a result, settling time is mainly depend on e^−εt/2, if the error band is set as 2%, the settling time is about 8/ε. If the settling time is designed as 0.4 s, ε should be set as 20. When GI is applied to vibration suppression, the characteristic equation of the control system is

$$\frac{{k_{P} s + k_{I} + k_{D} s^{2} }}{s}\frac{{k_{i} }}{{ms^{2} - k_{x} }}\frac{{\omega_{c} }}{{s + \omega_{c} }}\frac{1}{{1 + \varepsilon \frac{s}{{s^{2} + \Omega^{2} }}}}k_{h} = - 1.$$

(20)

To analyze stability in various speed, root locus about parameter Ω² can be obtained by transforming the characteristic equation as

$$\frac{{\Omega^{2} }}{{\varepsilon \frac{s}{{\frac{{k_{P} s + k_{I} + k_{D} s^{2} }}{s}\frac{{\omega_{c} }}{{s + \omega_{c} }}\frac{{k_{i} }}{{ms^{2} - k_{x} }}k_{h} { + }1}}{ + }s^{2} }} = - 1.$$

(21)

Setting the parameter Ω ² from 0 to + ∞, root locus can be drawn in 0. According to the root locus, when Ω/2π > 72 Hz, the root locus locates at the left of virtual axis, so the system is stable. It means that GI can suppress current vibration when rotating speed is larger than 72 Hz. The system cannot be stable when rotating frequency is lower than 72 Hz, because the root locus locates at right of virtual axis. The parameters for calculation are shown in Table 2 in “Experimental Results”.

Analysis of AMB System Applied PSGI

When PSGI is applied in vibration suppressing, the characteristic equation of whole system is

$$\frac{{k_{P} s + k_{I} + k_{D} s^{2} }}{s}\frac{{k_{i} }}{{ms^{2} - k_{x} }}\frac{{\omega_{c} }}{{s + \omega_{c} }}\frac{1}{{1 + \varepsilon \frac{s\cos \varphi + \Omega \sin \varphi }{{s^{2} + \Omega^{2} }}}}k_{h} = - 1.$$

(22)

To draw root locus, separating ε to transform the characteristic equation as a standard form

$$\varepsilon \frac{s\cos \varphi + \Omega \sin \varphi }{{\left( {s^{2} + \Omega^{2} } \right)\left( {\frac{{k_{P} s + k_{I} + k_{D} s^{2} }}{s}\frac{{\omega_{c} }}{{s + \omega_{c} }}\frac{{k_{i} }}{{ms^{2} - k_{x} }}k_{h} + 1} \right)}} = - 1.$$

(23)

When φ equals to zero, the characteristic equation can also express GI.

$$\varepsilon \frac{s}{{\left( {s^{2} + \Omega^{2} } \right)\left( {\frac{{k_{P} s + k_{I} + k_{D} s^{2} }}{s}\frac{{\omega_{c} }}{{s + \omega_{c} }}\frac{{k_{i} }}{{ms^{2} - k_{x} }}k_{h} + 1} \right)}} = - 1.$$

(24)

According to principle of root locus [14], the root locus begins at poles of open-loop transfer function. In characteristic equations of vibration suppressing control system applied GI and PSGI, there is a pair of poles at imaginary axis s =  ± jΩ. The departure angle at the pole s =  ± jΩ can express stability of the system. Calculating departure angle at the pole s = jΩ of PSGI as

$$\theta = - \varphi - \arg \left( {k_{h} C\left( {j\Omega } \right)G_{1} \left( {j\Omega } \right)G\left( {j\Omega } \right) + 1} \right) + \pi .$$

(25)

Calculating departure angle at the pole s = jΩ of GI, or setting φ = 0, the departure angle is

$$\theta = - \arg \left( {k_{h} C\left( {j\Omega } \right)G_{1} \left( {j\Omega } \right)G\left( {j\Omega } \right) + 1} \right) + \pi .$$

(26)

To make the system stable, the departure angle is supposed to satisfy π/2 < θ < 3π/2, which is prerequisite condition of stable, and this principle can be shown as Fig. 12.

Fig. 12

Prerequisite condition of stable

According to results of departure angle, PSGI can provide φ to improve stability of system. Adequate φ can be chosen to satisfy π/2 < θ < 3π/2 in various speed (Fig. 13). To select φ, defining a function as

$$H\left( s \right) = k_{h} C\left( s \right)G_{1} \left( s \right)G\left( s \right) + 1.$$

(27)

Fig. 13

Phase-frequency response of H(s)

Phase–frequency response of H(s) is shown in 0.

To make the system stable, the parameter φ can be selected as Table 1.

Table 1 Magnitude of φ in various rotating frequency

However, π/2 < θ < 3π/2 is prerequisite condition instead of sufficient prerequisite condition of stable. To verify stability of the system, drawing root locus about Ω as Fig. 14. By sweeping the rotational frequency Ω from zero to above 120 Hz, and applying the value of φ in Table 1, the root of Eq. (23) is displaced in Fig. 14. The root locus is distributed in the left half plane, which indicates parameter φ selected in various rotating frequency can increase the stability of the system. This result shows that with proper parameters, PSGI can obtain better stability in low speed range than GI, whose root appeared in left half plane.

Fig. 14

Root locus about parameter Ω of PSGI

Simulation Results

To verify the proposed vibration suppressing method, simulation model is established based on transfer functions and dynamic equations in Matlab/Simulink. Parameters for simulations are shown in Table 2.

Table 2 Parameters of simulation

Vibration Suppressing by GI

The rotating frequency is set as 140 Hz, the control current is shown in Fig. 15. At 0.5 s, the GI is applied to suppress current fluctuation. After transition process, current fluctuation is reduced to a tiny level.

Fig. 15

Control current with and without GI when Ω/2π = 140 Hz

Vibration Suppressing by PSGI

After applying proposed strategy, the PSGI is supposed to reduce the current fluctuation to suppress the vibration. The rotating speed is set to be: 45 Hz, 60 Hz and 100 Hz, respectively. The current value results are presented in Fig. 16. When rotating frequency is smaller than 72 Hz, the GI is unable to stabilize the system, however, after applying PSGI, vibration in current reduces. In steady state, there is little fluctuation by influence of PSGI. When rotating frequency equals to 100 Hz, applying PSGI can make the current convergence more quickly than applying GI. If rotating speed is in low level, PSGI can also stabilize the system and reduce current fluctuation, which shows effectiveness of proposed strategy in various rotating speed.

Fig. 16

Control current with proposed suppressing strategy

Experimental Results

Experiments are carried out on an AMB test rig to verify the effectiveness of proposed strategy. Two AMBs are arranged in radial shape configuration. The air gap of touch down bearing is ± 250 μm and air gap of radial magnetic bearing is ± 500 μm. A high-speed motor is applied to drive the shaft. The structure of test rig is shown in Fig. 17. Other parameters that are shown in Table 2, are equivalent to the simulation parameters.

Fig. 17

Structure of magnetic bearing test rig

The control board and amplifier are shown in Fig. 18. The amplifier is composed of IGBT circuit, and more details are introduced in the paper [15]. The switching frequency is 20 kHz. The bias current in the coil is 5A.

Fig. 18

Physical figure of amplifier and control board

Vibration Suppressing by GI

In each degree of freedom (DOF), GI is applied to suppress the vibration in the current. Parameters were the same in each DOF. In low speed (< 72 Hz) range, GI will not be able to make system stable, which is also verified by experiment. The experimental results of current vibration for GI are shown for the case of relatively high speed (130 Hz). The AC component of current in coil is shown in Fig. 19. The rotating speed is set as 130 Hz. After applying GI, the current fluctuation reduces effectively.

Fig. 19

Control current with and without GI

The spectrums of control current are shown in Fig. 20. The amplitude of current fluctuation is about 0.55A, after applying GI, the amplitude was reducing to 0.056A. Vibration in control current was reduced by about 90%. Because of noise, the amplitudes of other components have a little difference in Fig. 20a and b.

Fig. 20

Spectrums of control current

Vibration Suppressing by PSGI

Results of vibration suppressing with PSGI are shown in 0. The magnitude of phase shift fits with values in Table 1. PSGI is applied in all four DOFs of the rotor. The rotating frequency was set as 30 Hz, 60 Hz, 100 Hz. In experiments, if rotating frequency equals to 30 Hz or 60 Hz, applying GI or GNF caused the system instability. The current vibration was reduced in various rotating speed in accordance with PSGI, which demonstrates effectiveness of proposed vibration suppressing strategy (Fig. 21).

Fig. 21

Control current with and without PSGI

Implementing fast Fourier transformation (FFT) analysis, the amplitude of synchronous vibration in control current was obtained and presented in Table 3. The synchronous vibration in control current is suppressed in various rotating frequency by proposed vibration suppressing method applied PSGI. Because of harmonic component, there is residual current fluctuation in control current. Recording the time span of one cycle of vibration suppressing algorithm in digital signal process (DSP), whose basic frequency is 200 MHz. The proposed vibration suppressing method costs 197 clock cycles and traditional method costs 589 clock cycles. As a result, the proposed vibration strategy can reduce time of calculation by about 66%.

Table 3 Magnitude of synchronous current fluctuation

Conclusions

Rotational machinery applied AMB with is with the challenge of vibration caused by centrifugal force with synchronous speed. This paper proposed a current vibration suppressing strategy based on PSGI. Comparing with traditional GNF for vibration suppressing, the proposed vibration suppressing strategy does not have to calculate trigonometric in real time and it has a simple structure. As a result, the proposed strategy has less calculation. A PI segment equivalent to phase shift is applied to stabilize the system in various speed range, which avoids the unstable for applying GNF. Phase shift is selected by root locus to make sure stability of the system. Results of simulations and experiments show that the proposed method can suppress vibration in current effectively, which contributes to anti-saturation of amplifiers and improve stability of the system. Recently, varieties of vibration suppressing methods are proposed based on GNF [4, 16], however, GNF is more complex than PSGI. If PSGI is applied in these methods, the complexity will also be reduced.