Study on the Dynamic Characteristics of a Rotor Bearing System with Damping Rings Subjected to Base Vibration

Abstract

Purpose

In this paper, the influence of base excitation on the rotor-rolling bearings’ supports with rubber damping rings coupling dynamics model was studied.

Methods

Using the finite-element theory associated with the lumped mass method, the governing differential equations of the coupling system were established. In this model, the rotor was discretized using Timoshenko beam elements, while the supports and ball bearing outer races were modelled as lumped parameter models.

Results

The dynamic model was verified by varying compliance (VC) vibration impact analysis, the influence of the rubber damping ring, and the rotor unbalanced response. On this basis, the effect of the dynamic characteristics of the rotor coupling system subjected to base vibration was analysed.

Conclusion

The base excitation frequency near the natural frequency of the rotor not only exerts an effect on the rotor vibration in the direction of excitation but also the rotor oscillation in the other directions. The amplitude of the axial trajectory is influenced by the frequencies and amplitudes of the foundation excitation. As the amplitudes of the base excitation increase, the amplitude of the axis trajectory tends to increase linearly, and the speed of growth is different at various base excitation frequencies. The shape of the axial trajectory is mainly affected by the foundation excitation frequencies. As the excitation frequency changes, the axis trajectory becomes complicated, and the combination resonance phenomenon occurs.

Introduction

Rotors are widely used in helicopter tail transmission systems. They are installed on the foundation through rolling bearings, damping rings and supports. In the working state, external excitation is often transmitted to the rotor through the foundation, which affects the normal operation of the rotor. The additional load caused by the foundation movement is more likely to cause damage to the rotor. Considering the dynamic characteristics of the rotor system of the foundation vibration is a key issue in the safety design of the helicopter transmission system; therefore, it is necessary to study it.

Cavalcante et al. [1] presented a methodology for the analysis of the foundation behaviour and its influence on the rotor-bearings-foundation system in which the foundation and rotor are discretized by the finite element method. Kang et al. [2] investigated the foundation effects on the dynamic characteristics of rotor-bearing systems in which three foundation types are considered. Dakel et al. [3, 4] studied the influence of eccentric mass and foundation motion coupling on the critical speed and axial trajectory of a single disk rotor system by finite element method. Duchemin et al. [5] theoretically and experimentally studied the influence of the base motion on the stability of the rotor system when it is running near the critical speed. Fawzi and Fred [6] analysed the dynamic response of the rotor system under the coupling action of eccentric mass and foundation motion when systems are subjected to linear support and nonlinear support, respectively. Edwards et al. [7] verified the dynamic characteristics of the flexible rotor-bearing-foundation system under foundation excitation through experiments and analysed the influence of foundation excitation parameters on the response. Yan et al. [8, 9] considered the displacement load of the foundation and, considering a Jeffcott rotor as the research object, analysed the dynamic response characteristics of the rotor system. Shaposhnikov et al. [10] talked about the methodology for the creation of a rotor-bearing-support system subjected to impact excitation, and the impact phenomenon was investigated further by way of the developed experimental test rig. Zhu et al. [11] studied the influence of transverse vibration of the foundation on the dynamic characteristics of an electromagnetic bearing rotor system through an experimental device with active electromagnetic bearing. Zhang [12] analysed the effect of base harmonic rotation, transverse simple harmonic motion, and base shock excitation on the dynamic response of the rotor system. Ni et al. [13] investigated the lateral bending vibration characteristics of the tail drive shaft of a helicopter in a non-inertial coordinate system. Wang et al. [14] studied the nonlinear response of horizontally placed rotors under foundation vibration. To sum up, although several studies related to the rotor vibration of the foundation excitation have been carried out and many new models considering variable parameters have been proposed, it should be noted that the models are relatively simple, and there are few studies on the influence of the foundation vibration of a complex rotor coupling system.

In this study, the two-point shafting with rubber damping rings supported by rolling bearings is taken as the research object. The coupling dynamic model of rotor-rolling bearings-supports with rubber damping rings is established using the finite element method and lumped mass method. The flexible thin-walled rotor, nonlinear effect of rolling bearing, rubber damping ring effect, coupling effect between the rotor and rolling bearings, and coupling effect between the rolling bearings and supports are fully considered. Beyond that, the Newmark numerical method is employed to calculate dynamic equations of motion. The dynamic model is verified through the analysis of the VC vibration effect of ball bearings, the influence of the rubber damping ring on rotor vibration and the unbalance response of the rotor. After that, the influence laws of different base excitation frequencies and amplitudes on the dynamic characteristics of the rotor coupling system are discussed in detail.

Mathematical Model

Physical Model

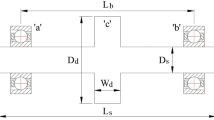
The complex rotor coupling system analysed in this study consists of a hollow rotor with rolling bearings supported at two ends, rubber damping rings outside the rolling bearings, and supports. The supports are fixed on the foundation by bolts. The three-dimensional model of the complex rotor coupling system is shown in Fig. 1. To simplify the model from the analytical perspective, a mechanical model of the rotor-rolling bearings-supports with rubber damping rings coupling system is constructed. Figure 2 shows the mechanical model discussed in this paper, and the symbols and their meanings are shown in “List of symbols”.

Fig. 1

Three-dimensional model of the rotor system

Fig. 2

Mechanical model of the rotor-rolling bearings-supports with rubber damping rings coupling system

Governing Differential Equations of the Coupling System

Rotor Dynamic Equations

As shown in Fig. 3, the rotor’s schematic diagram shows that the bearing inner ring is fixed on the rotor, thus taking the influence of the bearing inner ring mass and gravity into account, and the rotor is also affected by its own gravity and the ball bearing forces acting on its two ends. The method for determining the relative fixed reference system of any cross-section on the rotor is as follows: determine the position of the elastic centre line by the bending vibration displacement variable along the X and Y directions, respectively, namely, x_r(z, t) and y_r(z, t), and determine the cross-sectional orientation by the rotation angle $\phi(z,t)$ and $\psi (z,t)$, which turn around the X and Y directions, respectively, where the cross-section is around the centre line of the cross-section Z to rotate.

Fig. 3

Schematic diagram of the rotor

The finite element model of the rotor is established using Timoshenko beam elements considering shear deformation, gyroscopic moment and moment of inertia. The local coordinates of the beam elements are shown in Fig. 4. In this study, only lateral vibration is considered. Each node has four DOFs, which are translation along the X and Y directions and rotation around the X and Y axes. The displacement vector of the element node with eight DOFs, which can be expressed as

Fig. 4

Local coordinates of the beam elements

$$X_{e} = [\! \begin{array}{*{20}l} {x_{1} } & {y_{1} } &{\phi_{1} } & {\begin{array}{*{20}c} {\psi_{1} } & {x_{2} } &{y_{2} } &{\begin{array}{*{20}c} {\phi_{2} } & {\psi_{2} }\\ \end{array} } \\ \end{array} } \\ \end{array} \!]^{\text{T}} ,$$

$[\begin{array}{*{20}c} x & y & {\phi (z)} & {\psi (z)} \\ \end{array} ]^{\text{T} }$ is the displacement at any point in a beam element, which can be expressed by the product of the interpolation function and the displacement vector of the element node. According to Refs. [15,16,17], the mass, stiffness, gyroscopic and gravity matrix, M_e, K_e, G_e and Q_e, respectively, of each rotor beam element can be obtained.

Figure 5 is a schematic diagram of the ball bearing structure in which N is the number of balls, ω_φ represents the rotor angular velocity, R and r are the outer and inner race curvature radius, respectively. ω_cage represents the angular velocity of the rolling element, which can be given as follows:

Fig. 5

Schematic diagram of the rolling bearing structure

$$\omega_{\text{cage}} = \frac{{\omega_{\varphi } r}}{r + R}.$$

(1)

When the rolling bearing rotates, vibration can occur. Because the rolling bearing is subjected to radial load, the load of the ball is a function of the angular displacement of the bearing ring, and the total stiffness of the bearing changes continuously, resulting in the VC vibration phenomenon. Then, VC vibration frequency can be given by

$$\omega_{\text{vc}} = N\omega_{\text{cage}} = \omega_{\varphi } \left( {\frac{r}{R + r}N} \right) = \omega_{\varphi } B_{N} .$$

(2)

Here, B_N is the ratio of the VC vibration frequency to rotational frequency.

Supposing that the angular displacement of the ith ball is θ_i, which is given by $\theta_{i} = \omega_{\text{cage}} t + \frac{2\pi (i - 1)}{N}$, x and y represent the vibration displacements of the centre of the inner race in the X and Y directions, respectively, γ₀ is the ball bearing radial clearance, and the normal contact deformation between the ith ball and races can be described as

$$w_{{\theta_{i} }} = x\cos \theta_{j} + y\sin \theta_{j} - \gamma_{0} .$$

(3)

According to the conclusion of Ref. [18], the ball bearing’s nonlinear elastic forces acting on the rotor can be obtained as follows:

$$\left\{ {\begin{array}{*{20}c} {F_{kxb} = k_{p} \sum\limits_{i = 1}^{N} {(w_{{\theta_{i} }} )}^{3/2} H(w_{{\theta_{i} }} )\cos \theta_{i} } \\ {F_{kyb} = k_{p} \sum\limits_{i = 1}^{N} {(w_{{\theta_{i} }} )}^{3/2} H(w_{{\theta_{i} }} )\sin \theta_{i} } \\ \end{array} } \right..$$

(4)

Here, k_p is the contact stiffness, and $H(w_{{\theta_{i} }} ) = \left\{ {\begin{array}{*{20}c} {1,\begin{array}{*{20}c} {} & {w_{{\theta_{i} }} > 0} \\ \end{array} } \\ {0,\begin{array}{*{20}c} {} & {w_{{\theta_{i} }} \le 0} \\ \end{array} } \\ \end{array} } \right.$ represents a function of Haversian.

Suppose that x_wl(t) and y_wl(t) are the displacement variables of the left bearing outer ring in the X and Y directions, respectively, x_wr(t) and y_wr(t) represent the displacement variables of the right bearing outer ring in two directions, respectively, F_kxbl and F_kybl are the elastic forces of the left bearing acting on the rotor in the X and Y directions, respectively, F_kxbr and F_kybr represent the elastic forces of the right bearing acting on the rotor in X and Y directions, respectively. When z = 0, the relative displacement of the left bearing can be given by $\dot{x} = \dot{x}_{\text{l}} (0,t) - \dot{x}_{wl}$, ${\dot{\text{y}}} = \dot{y}_{\text{l}} (0,t) - \dot{y}_{wl}$, and the corresponding elastic bearing force can be obtained from Eq. (4), namely, F_kxbl = F_kxb, F_kybl = F_kyb. When z = L, then the relative displacement of the right bearing can be described as x = x_r(L, t) − x_wr, y = y_r(L, t) − y_wr, and the corresponding elastic bearing force can also be obtained from Eq. (4), namely, F_kxbr = F_kxb, F_kybr = F_kyb.

The damping force acting on the rotor by the rolling bearing is expressed by viscous damping commonly used in engineering, which can be given by

$$\left\{ {\begin{array}{*{20}c} {F_{cxb} = c\dot{x}} \\ {F_{cyb} = c\dot{y}} \\ \end{array} } \right..$$

(5)

According to Eq. (5), the damping force of the bearing outer ring can be expressed as follows:

$$\left\{ \begin{aligned} F_{cxbl} = {\text{c(}}\dot{x}_{\text{l}} (0,t) - \dot{x}_{wl} )\hfill \\ F_{cybl} = {\text{c}}(\dot{y}_{\text{l} } (0,t) - \dot{y}_{wl} )\hfill \\ F_{cxbr} = c(\dot{x}_{r} (L,t) - \dot{x}_{wr} ) \hfill \\ F_{cybr} = c(\dot{y}_{r} (L,t) - \dot{y}_{wr} ) \hfill \\ \end{aligned} \right..$$

(6)

The nonlinear force of rolling bearing applied to the rotor includes nonlinear elastic force and linear damping force, which can be given by

$$\left\{ {\begin{array}{*{20}c} {F_{xb} = F_{kxbl} + F_{cxbl} + F_{kxbr} + F_{cxbr} } \\ {F_{yb} = F_{{\text{k} ybl}} + F_{cybl} + F_{kybr} + F_{cybr} } \\ \end{array} } \right..$$

(7)

Combining all mass, stiffness, gyroscopic and gravity matrices M_e, K_e, G_e and Q_e of each rotor beam element can form the assembled matrices [M_r], [K_r], [G_r] and [Q_r]. Then, the mass of bearing inner rings is added to M_r, the bearing inner ring gravity and the rolling bearing force are added to Q_r, and the damping of the rolling bearings is added to [C_r]. The rotor system’s motion equation can be obtained as follows:

$$[{\mathbf{M}}_{{\mathbf{r}}} + {\mathbf{M}}_{{\mathbf{b}}} ]{\mathbf{\ddot{q}}} + ([{\mathbf{C}}_{{\mathbf{r}}} + {\mathbf{C}}_{{\mathbf{b}}} ] - \omega [{\mathbf{G}}_{{\mathbf{r}}} ]){\dot{\mathbf{q}}} + [{\mathbf{K}}_{{\mathbf{r}}} ]{\mathbf{q}} = [{\mathbf{Q}}_{{\mathbf{r}}} ] + [{\mathbf{Q}}_{{\mathbf{b}}} ]{ + }[{\mathbf{F}}_{{\mathbf{b}}} ].$$

(8)

Here, [M_r], [K_r], [C_r], [G_r] and [Q_r] represent the mass matrix, stiffness matrix, damping matrix, gyroscopic matrix, and gravity matrix of the rotor, respectively. [M_b] and [Q_b] are the mass matrix and gravity vector of the bearing inner ring, respectively. [C_b] and [F_b] denote the damping matrix and nonlinear elastic force vector of the bearing, respectively.

The rotor damping adopts Rayleigh damping, i.e. [C] = α[M] + β[K], where α and β represent the mass and stiffness damping coefficient, respectively, which could be obtained as

$$\alpha = 2\omega_{1} \omega_{2} (\xi_{1} \omega_{2} - \xi_{2} \omega_{1} )/(\omega_{{^{2} }}^{2} - \omega_{{^{1} }}^{2} ),$$

$$\beta = 2(\xi_{2} \omega_{2} - \xi_{1} \omega_{1} )/(\omega_{{^{2} }}^{2} - \omega_{{^{1} }}^{2} ).$$

Here, ξ₁ and ξ₂ represent the first and second modal damping ratio, respectively. ω₁ and ω₂ are the first- and second-order natural frequencies of the rotor system, respectively, which can be obtained through modal experiments.

Dynamic Equations of the Bearing Outer Ring

The outer ring of the bearing is subjected to the force of the rolling bearing and the force of the rubber damping ring. The rubber damping ring has the dynamic characteristics of viscoelastic materials, which is likely to experience structural damping. In this study, the Kelvin–Voigt linear mechanical model is employed to give the complex support stiffness [19]. Therefore, the complex supporting force of the rubber damping ring F_s can be expressed as

$$F_{\text{s}} = k^{ * } u = k_{1} (1 + i\eta ) \cdot u,$$

(9)

where k^*, u and η are the complex stiffness, relative displacement and loss factor of the rubber damping ring, respectively.

Regardless of the small angular displacement of the rubber damping ring, the relative displacement can be expressed as u = x^* + iy^*. Then, F_s can be written as

$$F_{\text{s}} = \left[ {\begin{array}{*{20}c} {F_{{x{\text{s}}}} } \\ {F_{{y{\text{s}}}} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {k1} & { - k1 \cdot \eta } \\ {k1 \cdot \eta } & {k1} \\ \end{array} } \right]\left( {\begin{array}{*{20}c} {x^{ * } } \\ {y^{ * } } \\ \end{array} } \right),$$

(10)

where x^* and y^* represent the relative displacement of the rubber damping ring in the horizontal and vertical directions, respectively.

Assuming that x_bl(t) and y_bl(t) are the displacement variables of the left support in the X and Y directions, respectively. x_br(t) and y_br(t) represent the corresponding displacement variables of the right support in two directions, respectively. F_xsl and F_ysl are the forces of the left rubber damping ring acting on the left bearing outer ring in the X and Y directions, respectively. F_xsr and F_ysr represent the forces of the right rubber damping ring acting on the right bearing outer ring in two directions, respectively, which can be obtained by solving Eq. (10). Then,

$$\left\{ {\begin{array}{*{20}c} {F_{xsl} = k_{1} (x_{wl} - x_{bl} ) - k_{1} \eta (y_{wl} - y_{bl} )} \\ {\begin{array}{*{20}c} {F_{ysl} = k_{1} \eta (x_{wl} - x_{bl} ) + k_{1} (y_{wl} - y_{bl} )} \\ {F_{{xs{\text{r}}}} = k_{1} (x_{wr} - x_{br} ) - k_{1} \eta (y_{wr} - y_{br} )} \\ {F_{ysr} = k_{1} \eta (x_{wr} - x_{br} ) + k_{1} (y_{wr} - y_{br} )} \\ \end{array} } \\ \end{array} } \right..$$

(11)

According to Newton’s second law, the differential equations for the bearing outer ring are written as follows:

$$\left\{ \begin{aligned} m_{bwl} \ddot{x}_{wl} + F_{xsl} - F_{cxbl} =& F_{kxbl} \hfill \\ m_{bwl} \ddot{y}_{wl} + F_{ysl} - F_{cybl} =& F_{kybl} - m_{bwl} g \hfill \\ m_{bwr} \ddot{x}_{wr} + F_{xsr} - F_{cxbr} =& F_{kxbr} \hfill \\ m_{bwr} \ddot{y}_{wr} + F_{ysr} - F_{cybr} =& F_{kybr} - m_{bwr} g \hfill \\ \end{aligned} \right..$$

(12)

Dynamic Equations of the Supports

The supports are subjected to the reaction force of the rubber damping ring, the linear elastic force and damping force between the supports and the foundation, and the foundation excitation. Suppose x_s(t) is the foundation displacement excitation in the X direction and y_s(t) is the foundation displacement excitation in the Y direction.

The differential equations of motion of the supports can be obtained as follows, by using Newton’s second law:

$$\left\{ \begin{aligned} m_{bsl} \ddot{x}_{bl} + k_{x1} (x_{bl} - x_{s} ) + c_{x1} (\dot{x}_{bl} - \dot{x}_{s} ) =& F_{xsl} \hfill \\ m_{bsl} \ddot{y}_{bl} + k_{y1} (y_{bl} - y_{s} ) + c_{x1} (\dot{y}_{bl} - \dot{y}_{s} ) =& F_{ysl} - m_{bsl} g \hfill \\ m_{bsr} \ddot{x}_{br} + k_{x1} (x_{br} - x_{s} ) + c_{x1} (\dot{x}_{br} - \dot{x}_{s} ) =& F_{xsr} \hfill \\ m_{bsr} \ddot{y}_{br} + k_{y1} (y_{br} - y_{s} ) + c_{x1} (\dot{y}_{\text{br}} - \dot{y}_{s} ) =& F_{ysr} - m_{bsr} g \hfill \\ \end{aligned} \right..$$

(13)

Rotor Coupling System Dynamics Equation

By combining Eqs. (8), (12), and (13), the coupling dynamic equations of rotor-rolling bearings-supports with rubber damping rings can be established as follows:

$$[{\bar{\mathbf{M}}}]{\mathbf{\ddot{X}}} + ([{\bar{\mathbf{C}}}] - \omega [{\bar{\mathbf{G}}}]){\dot{\mathbf{X}}} + [{\bar{\mathbf{K}}}]{\mathbf{X}} = [{\bar{\mathbf{Q}}}],$$

(14)

where ${\mathbf{[\bar{M}]}}$ is the coupling system mass matrix, including the rotor mass, bearing inner and outer ring mass, and support mass. ${\mathbf{[\bar{C}]}}$ is the coupling system damping matrix, including the rotor damping, bearing damping, and damping between supports and foundation. ${\mathbf{[\bar{G}]}}$ is the coupling system rotor gyroscopic matrix. $[{\bar{\mathbf{K}}}]$ is the stiffness matrix of the coupling system, including the rotor stiffness and stiffness between the support and foundation. $[{\bar{\mathbf{Q}}}]$ is a generalised force matrix of the coupling system, including the nonlinear bearing force, rubber damping ring force, rotor gravity, bearing inner and outer ring gravity, and support gravity.

Owing to the varying orders of magnitude for the value of each parameter, to guarantee the accuracy of calculation, the system should be modified to be dimensionless. Therefore, the non-dimensional parameters can be defined as

${\mathbf{X}} = \frac{{{\bar{\mathbf{X}}}}}{{\gamma_{0} }}$, τ = ωt, ${\dot{\mathbf{X}}} = \frac{{{\text{d}}{\mathbf{X}}}}{{{\text{d}}\tau }}\frac{{{\text{d}}\tau }}{{{\text{d}}t}} = {\mathbf{X^{\prime}}}\omega$, ${\mathbf{\ddot{X}}} = {\mathbf{X^{\prime\prime}}}\omega^{2} .$

Equation (14) can be converted into

$$[{\bar{\mathbf{M}}}]\gamma_{0} \omega^{2} {\mathbf{X^{\prime\prime}}} + ([{\bar{\mathbf{C}}}] - \omega [{\bar{\mathbf{G}}}])\gamma_{0} \omega {\mathbf{X^{\prime}}} + [{\bar{\mathbf{K}}}]\gamma_{0} {\mathbf{X}} = {\bar{\mathbf{Q}}}(x,\tau ).$$

(15)

Suppose $[{\mathbf{M}}] = [{\bar{\mathbf{M}}}]\gamma_{0} \omega^{2}$, $[{\mathbf{C}}] = ([{\bar{\mathbf{C}}}] - \omega [{\bar{\mathbf{G}}}])\gamma_{0} \omega$, and $[{\mathbf{K}}] = [{\bar{\mathbf{K}}}]\gamma_{0}$. Relatively, Eq. (15) can be rewritten as

$${\mathbf{[M]X^{\prime\prime}}} + {\mathbf{[C]X^{\prime}}} + {\mathbf{[K]X}} = [{\mathbf{Q}}].$$

(16)

Verification of the Dynamic Model of Rotor-Rolling Bearings-Supports with Rubber Damping Rings

Considering the complexity of the rotor coupling system, it is difficult to obtain satisfactory results using an analytical method. Therefore, the Newmark method is used to calculate the differential equations in which the integral step size takes 1/200 of the excitation period according to the input state aiming to obtain the responses of the rotor-rolling bearings-supports with rubber damping rings coupling system. For the sake of verifying the accuracy of the model, the main parameters of the coupling system are selected to be the same as those in Ref. [22]. The details are as follows:

$L = 1.4m$, E = 6.8 × 10¹⁰ Pa, μ = 0.3, $\rho = 2800kg/m^{{_{3} }}$,r₁ = 0.084 m, r₂ = 0.09 m, η = 0.12, k₁ = 1.5 × 10⁶ N/m, c = 300 N s/m, m_bsl = m_bsr = 10 kg, k_x1 = k_y1 = 5 × 10⁸ N/m, m_bwl = m_bwr = 0.05 kg, m_bsl = m_bsr = 0.08 kg, c_x1 = c_y1 = 1050 N s/m, N = 8, γ₀ = 20 μm, $k_{p} = 7.05 \times 10^{9} N/m^{3/2}$, r = 0.0401 m, R = 0.0639 m.

Influence of Rolling Bearing Stiffness on Rotor Vibration

As shown in Fig. 6, based on the rotor vibration waveform in the X direction at the rotating speed of 300 rpm, it can be seen that the waveform is a periodic motion and shows a plurality of small amplitude vibrations in each waveform period, which are generated when a plurality of balls of the rolling bearing pass through. From the spectrum analysis, it can be observed that there are many peaks in the spectrum diagram, including the VC vibration frequency of the rolling bearing and its harmonics. The research in Refs. [20, 21] also shows that when the rotor is far away from the critical speed, the frequency spectrum shows the rotational frequency and harmonic frequency of the ball when the motion is periodic.

Fig. 6

Vibration response in the X direction

Influence of the Rubber Damping Ring on Rotor Vibration

To study the effect of the rubber damping ring on the rotor bearing system, the dynamic response of the acceleration motion of the rotor system is calculated by applying an unbalance value, namely, 10 g mm, at the intermediate node of the rotor. The shaft is accelerated to 20,000 rpm by the angular acceleration α = 105 rad/s², and then the bending vibration response of the rotor system is calculated without and with the rubber damping ring, respectively. As shown in Fig. 7a, when the rotor system does not have a rubber damping ring, the system is in a subcritical speed transition state, and the vibration response amplitude increases with the increase in the rotational speed under the action of centrifugal force. As shown in Fig. 7b, when the rotor system has a rubber damping ring, the system is in a supercritical speed transition state, and a large amplitude occurs when the rotor accelerates to the natural frequency. Taking the rubber damping ring loss factor as η = 0.1, η = 0.2, η = 0.3, η = 0.4, it can be noted that the amplitude corresponding to the first-order critical speed gradually decreases as the rubber damping ring loss factor increases, and owing to the hysteresis effect of damping, the critical speed also becomes larger. It can be seen from the above analysis that by adjusting the support stiffness of the rubber damping ring, the critical speed of the system can be adjusted and controlled to meet the design requirements of the rotor. The deformation of the rubber damping ring itself causes an obvious damping effect at the support, thus absorbing the vibration energy of the rotor system. At the same time, it also shows that the modelling method in this study has high reliability.

Fig. 7

Influence of the rubber damping ring on rotor vibration

Analysis of Unbalanced Response

Applying the same unbalance value to the centre node of the rotor as given in Ref. [22], unbalance response analysis is performed. As can be seen from Fig. 8a, the resonance point in Ref. [22] is at the rotational speed of 5294 rpm, namely, 88.23 Hz. In this study, the excitation frequencies contain two aspects: one is the rotating frequency, and the other is the bearing’s VC vibration frequency. As shown in Fig. 8b, the rotor system peaks at 1593 rpm and 5100 rpm, which are caused by VC vibration and unbalanced force, respectively. The ratio of speeds corresponding to two peaks is equal to the bearing’s structural parameters, namely, B_N = 3.2. Therefore, the first-order natural frequency of the rotor system is 85 Hz.

Fig. 8

Speed–amplitude diagrams

Apparently, the results in this study are less than those in Ref. [22], and the main reason is that in Ref. [22], the hinges at two ends of the rotor as boundary conditions were used and the mode superposition method was employed to obtain the results. This study not only takes the flexible rotor effect into account but also considers the nonlinear bearing force and the rubber damping ring force, which is closer to the actual situation.

Influence of Foundation Excitation on the Dynamic Characteristics of Rotor-Rolling Bearings-Supports with Rubber Damping Rings

This study mainly investigates the influence of foundation excitation on the rotor dynamic characteristics at the working speed of 4200 rpm. Y_s(t) = A sin (2πf_base × t) is the displacement excitation, which is applied in the Y direction of the foundation. Here, A is the excitation amplitude, f_base is the foundation excitation frequency, and then the influence laws of different foundation excitation frequencies and amplitudes on rotor dynamics are studied. According to formula (3), the VC vibration frequency f_vc at this rotational speed can be solved, which is equal to 224 Hz. The other parameters of the rotor system are the same as the preceding part of the paper, which can be obtained from the third section.

Influence of Different Base Excitation Frequencies

Keep the base excitation amplitude A = 2 × 10⁻⁴ m constant, and take the base excitation frequencies as 0, 10 Hz, 20 Hz, 40 Hz, 80 Hz, 100 Hz, 128 Hz, and 224 Hz, and analyse the influence of the base excitation frequency on the rotor motion in detail by combining the axis locus diagram and spectrum diagram of the rotor vibration response.

As shown in Fig. 9a, the axis locus of the rotor under the action of the bearing force is a single ellipse when there is no foundation excitation. The frequency spectrum shows the VC vibration frequency of the bearing and its second harmonic at the operating speed.

Fig. 9

Orbits and spectrograms of the rotor vibration response

As shown in Fig. 9b–d, when the foundation excitation is applied in the Y direction, the displacement of the axis locus in the Y direction increases obviously while the displacement in the X direction does not change much, and the trajectory changes from single ellipse to complex elliptical orbit. Owing to the interaction between the foundation and the rotor system, the excitation frequency of the foundation also appears in the spectrum diagram. With the increase in the base excitation frequency, the shape of the axis locus tends to be complex, and its shape becomes a mesh structure. The corresponding amplitude of the VC vibration frequency and its second harmonic of the bearing in the spectrum diagram are unchanged, while the corresponding amplitude of the base excitation frequency increases slightly.

As shown in Fig. 9e–g, when the base excitation frequency is close to 85 Hz of the rotor’s first natural frequency, it has a greater influence on the motion of the rotor axis locus owing to the resonance effect. The displacement amplitude in the Y direction increases significantly, and the displacement amplitude in the X direction can also be influenced to some extent. As far away from the natural frequency, the effect of the base excitation frequency on the vibration amplitude of the rotor decreases. Meanwhile, the axis locus becomes chaotic, and the frequency of the rotor vibration response not only includes the base excitation frequency, the bearing’s VC vibration frequency and its second harmonic frequency but also contains the frequency generated by the combined resonance vibration. The component and corresponding relation of the combination resonance frequency is shown in Table 1. As shown, the combined resonant frequency meets a certain relationship, namely, | ± mf_base ± nf_vc| (m, n = 1, 2, 3…).

Table 1 Component and corresponding relation of the combination resonance frequency

As shown in Fig. 9h, the shape of the axis locus is a single ellipse when the foundation excitation frequency is equal to the VC vibration frequency of the bearing. The displacement amplitude in the Y direction of the rotor increases because of the effect of the foundation excitation, while the displacement amplitude in the X direction does not change. In the spectrum diagram, no combined resonance frequency appears, and the amplitude corresponding to the VC vibration frequency of the bearing increases obviously, while the amplitude corresponding to the second harmonic remains.

From the above analysis, it can be observed that the axis locus is a regular ellipse when the base excitation frequency is equal to the VC vibration frequency of bearing. Aiming to further study the influence of the relationship between the base excitation frequency and the bearing’s VC vibration frequency on the axis locus, the base excitation frequency is equal to 1/3, 1/2, 2 and 3 times the bearing’s VC vibration frequency, respectively. As shown in Fig. 10a–d, the axis locus becomes a 3-ring connected shape when the base excitation frequency is equal to 1/3 harmonic frequency of the VC vibration. The axis locus becomes a figure-eight track when the base excitation frequency is equal to 1/2 harmonic frequency of the VC vibration. The axis locus becomes an inverted figure-eight orbit when the foundation excitation frequency is equal to the second harmonic frequency of the VC vibration. The axis locus becomes the inverted 3-ring connected track when the base excitation frequency is equal to the third harmonic frequency of the VC vibration. According to the above research, the axis locus is a regular pattern when there are multiple relationships between the base excitation frequency and the bearing’s VC vibration frequency.

Fig. 10

Orbits of the rotor vibration response

The amplitude ratio indicates the ratio of the displacement amplitude of the rotor vibration response subjected to foundation excitation according to the amplitude when the foundation is fixed. According to the definition of the amplitude ratio, curves of the amplitude ratio with respect to the base excitation frequency are graphed under various base excitation amplitudes, as shown in Fig. 11.

Fig. 11

Change curve of the amplitude ratio with the base excitation frequency

It can be seen from the figure that no matter how large the amplitude of the base excitation is, when the base excitation frequency is less than 85 Hz of the resonance frequency, the amplitude ratio increases continuously with the increase in the excitation frequency and reaches the maximum value near the resonance point; however, the amplitude ratio gradually decreases when the foundation excitation frequency is greater than the resonance frequency. The main reason for this is that the rotor system has the rubber damping ring and the base movement is isolated by the damper. This phenomenon is likely given the description of the response of the damping system when the foundation is subjected to a simple harmonic motion in Ref. [23]. The influence of damping on the mass is indistinctive at high frequency subjected to the foundation excitation, and it is amplified and transmitted to the mass after passing through the spring and damping in the resonance region. At the same time, as can be seen from Fig. 11, in the entire process of changing with the base excitation frequency, the effect of the larger base excitation amplitude on the rotor movement amplitude is always outstanding.

To sum up, the base vibration frequency will bring about a complex change in the axial trajectory, which affects the stability of the rotor operation, and the rotor vibration will be too large near the natural frequency of the rotor system, and even the rub-impact fault of the rotor will occur. In the design of the dynamic characteristics of the tail rotor of the helicopter, we need to consider the components of the base excitation frequency that may occur in the working state and interact with the rotor system, which may cause resonant frequencies. The rotor system will generate a large vibration when these frequencies are equal to the operating speed; therefore, the foundation vibration frequency must be considered and effectively controlled to reduce the influence of the base excitation on the vibration response of the rotor system.

Influence of Different Base Excitation Amplitudes

Keeping the base excitation frequency f_base = 10 Hz unchanged, and the base excitation amplitudes A equal to 2 × 10⁻⁴ m, 4 × 10⁻⁴ m, and 8 × 10⁻⁴ m, the influence of different base excitation amplitudes on the rotor motion is studied, as shown in Fig. 12.

Fig. 12

Orbits and spectrograms of the rotor vibration response

The displacement of the rotor in the Y direction obviously increases when the base excitation is applied in the Y direction. With the increase in the base excitation amplitude, the amplitude of the axis track increases significantly, and the shape of the axis track changes a little bit. The amplitude corresponding to the base excitation frequency in the spectrum diagram increases obviously, which is proportional to the base excitation amplitude. Meanwhile, the amplitude corresponding to the bearing’s VC vibration frequency and its second harmonic are not changed.

The foundation excitation frequency is changed to be equal to the VC vibration frequency (242 Hz), 1/2 harmonic frequency (112 Hz) and third harmonic frequency (672 Hz), respectively, and the effect of the excitation amplitude on the rotor motion under different base excitation frequencies is studied. As shown in Fig. 13a–c, as the amplitude of the base excitation increases in the Y direction, the displacement amplitude in the Y direction increases significantly. The base movement in the Y direction has a certain influence on the displacement amplitude in the X direction when the excitation frequency is close to the natural frequency (e.g., f_base = 112 Hz); however, the shape of the axis locus is basically unchanged.

Fig. 13

Orbits of the rotor vibration response

Curves of the amplitude ratio with the base excitation amplitude at the excitation frequencies of 10 Hz, 40 Hz, 100 Hz, 112 Hz, 140 Hz and 224 Hz are graphed and shown in Fig. 14. It can be seen from Fig. 14 that the amplitude of the rotor vibration increases linearly with the increase in the foundation excitation amplitude at various foundation excitation frequencies. Meanwhile, the rotor vibration’s amplitude has different growth speeds at different foundation excitation frequencies. The amplitude ratio increases fast when the base excitation frequency is less than the natural frequency. When the base excitation frequency is greater than the natural frequency, owing to the damping effect of the rubber damping ring, the growth rate of the amplitude ratio decreases gradually, and as the base excitation frequency increases, the amplitude of the rotor vibration increases at a slower rate.

Fig. 14

Change curve of the amplitude ratio with the base excitation amplitude

In summary, as long as the amplitude of the base vibration exceeds a certain value, it will have a serious impact on the rotor system, causing the vibration of the rotor to increase sharply and even increasing the noise of the system. It is essential to consider the magnitude of the base vibration amplitude that appears under operational conditions and reasonably select the gap between the rotor and the stator to avoid the occurrence of rubbing and other faults.

Conclusions

The dynamic characteristics of rotor-rolling bearings-supports with rubber damping rings subjected to base vibration is studied. The Newmark method is utilised to solve the system differential equations. The main conclusions from this study are summarised as follows:

• 1. The base vibration in the horizontal or vertical direction has considerable influence on the rotor system in the corresponding direction, and it also has a certain effect on the movement in other directions near the natural frequency.

• 2. The base excitation frequency exerts an effect on the axis trajectory’s shape. As the base excitation frequency increases, the axis trajectory becomes more complicated and the combined resonance occurs when the excitation frequency exceeds a certain value. However, the axis locus presents a regular shape when multiple relationships exist between the base excitation frequency and the VC vibration frequency.

• 3. The base excitation frequency also shows a significant effect on the rotor motion’s amplitude. As the base excitation frequency increases, the rotor motion’s amplitude increases continuously, and the amplitude of the rotor movement reaches the maximum at the natural frequency. However, the influence of the base excitation on the rotor motion’s amplitude gradually deteriorated because of the damping effect of the system when the excitation frequency is greater than the natural frequency.

• 4. The base excitation amplitude has considerable influence on the rotor motion’s amplitude. As the base excitation amplitude increases, the rotor motion’s amplitude shows a linear growth trend, and the growth rate varies at different base excitation frequencies. The rotor motion’s amplitude increases rapidly when the foundation excitation frequency is lower than the natural frequency. Similarly, the rotor motion’s amplitude increases slowly due to the damping effect of the system when the excitation frequency is greater than the natural frequency, and as the base excitation frequency increases, the rotor motion’s amplitude increases at a slower rate.