1 Introduction

Axisymmetric base flow is a critical component in designing axisymmetric bodies such as missiles, projectiles and rockets. Despite a typical simple geometry, the base flow involves various flow phenomena mainly due to massive flow separation. As shown in Fig. 1, the turbulent boundary layer on the lateral side of the axisymmetric body separates at the base, entering into the wake region. The shear flow expands after the base and is mixed with the recirculating flow. These turbulent motions and flow interactions impose a challenge in modeling and computationally simulating an axisymmetric base flow.

Various computational efforts were reported in literature to investigate simulation methods for turbulent base flow. The Reynolds-averaged Navier–Stokes (RANS) approach suffers predicting such a separated flow [1,2,3,4]. Higher fidelity approaches including large-eddy simulation (LES) and direct-numerical simulation (DNS) would provide a better framework than RANS to predict the separated flow at the sharp corner of the base. Nonetheless, LES or DNS of axisymmetric base flow at a reasonably high Reynolds number is rare—e.g., Marrioti et al. [5] conducted the base flow at the diameter-based Reynolds number less than 2000. Upstream attached flow before the base increases a computational burden in an LES or DNS framework.

A hybrid RANS/LES approach is a reasonable choice for axisymmetric base flow because the upstream attached flow could be modeled adequately in the RANS mode, and the downstream separated flow is resolved in the LES mode. This hybrid approach including detached-eddy simulation (DES) has been used for axisymmetric base flow [6,7,8,9,10]. Forsythe et al. (2002) [6] suggested that a finer resolution would be required for DES computations to resolve a key flow feature in the separated flow, i.e., the shear layer instability. Later Simon et al. (2006) [7] and Shin et al. (2009) [8] explored the DES approach for axisymmetric base flows with modifying the DES model coefficient \(C_{DES}\). It should be emphasized that the model coefficient \(C_{DES}\) was calibrated in the homogeneous turbulence limit where the DES formula satisfies the homogeneous condition with the DES coefficient [11, 12]. Therefore, it is not recommended to modify the DES coefficient. In this study, the DES coefficient maintains the recommended value \(C_{DES}=0.65\). Since the delayed DES (DDES) model is less sensitive to grid resolution in switching between the RANS and LES modes [12], the DDES model is used in this study. The DDES model helps to mitigate well-known numerical issues including grid-induced separation and modeled-stress depletion occurring in the early version of DES [11]. The authors indeed noticed nonphysical separation in the boundary layer before the base with the early DES model.

Fig. 1
figure 1

Axisymmetric base flow at a subsonic speed in the current simulation. The flow is visualized with streamlines and two color contours, the density gradient magnitude \(\vert \nabla \rho \vert \) (top) and the pressure coefficient \(C_p\) (bottom)

Full size image

The current study takes into consideration the spatial resolution in the LES zone. Eddy-resolving simulation including DES relies on the grid quality to properly resolve turbulent flow. Nearly isotropic grids are recommended in the LES zone of the DES approach [13]. In addition to the grid isotropy, a fine resolution is required in the separated region, particularly near the RANS/LES transit region, to resolve the instability of the separated shear layer. A rapid transit to LES is preferred in order to reduce the modeled-stress depletion issue in hybrid RANS/LES methods [12]. Therefore, the level of the grid isotropy and resolution is systematically investigated in this study for well-conducted DES computations. It should be emphasized that the current approach is different to the model coefficient modification done in previous DDES studies [7, 8].

The paper is organized as follows. Numerical methods are presented in Sect. 2, including turbulence models and computational grids. Computational results are discussed in Sect. 3 with comparison to relevant literature data. Main findings of the current study are emphasized in Sect. 4 with a brief summary of this work.

2 Numerical Methodology

2.1 Simulation Overview

The experimental flow condition of Merz et al. [14] is selected for the current simulation. The flow conditions are set to the freestream Mach number \(M_\infty =0.54\) and the freestream temperature \(T_\infty =267.41K\). The Reynolds number based on the base diameter D is \(Re_D=\rho _\infty U_\infty D / \mu _\infty = 0.29 \times 10^6\) where the freestream velocity \(U_\infty \) and density \(\rho _\infty \) are used. The experiment is conducted with an axisymmetric cylinder located in a circular wind tunnel for axisymmetric base flow. Hybrid RANS/LES data of Kawai and Fujii [10] are also available for the current flow condition, which allows the authors to compare the current simulation with the relevant literature data.

The compressible Favre-averaged Navier–Stokes equations are numerically solved with the structured code CFL3D developed at NASA [15]. Two constitutive relations, i.e., the ideal gas law and Sutherland’s law, are used here. Variables are non-dimensionalized with the freestream density \(\rho _\infty \), sound speed \(a_\infty \), and the base diameter D. Convective and viscous terms in the governing equation are discretized with Roe’s flux-differencing with a third-order monotonic upstream-centered scheme for conservation laws (MUSCL) and second-order central differencing schemes, respectively. Note that the code CFL3D along with the aforementioned numerical schemes has been used in DDES computations [16]. Despite the subsonic nature of the flow, a smooth limiter which is specifically tuned to the upwind-biased spatial differencing scheme is utilized, as outlined by Krist et al. [15].

2.2 Turbulence Models

Two computational approaches, RANS and DDES, are used in this study. The standard version of the Spalart-Allmaras (SA) model is used for RANS computations. The SA equation is given as Eq. 1

$$\begin{aligned} \frac{D\hat{\nu }}{Dt}{} & {} = c_{b1}\left( 1 - f_{t2}\right) \hat{S}\hat{\nu } - \left[ c_{w1}f_w - \frac{c_{b1}}{\kappa ^2}f_{t2}\right] \left( \frac{\hat{\nu }}{d}\right) ^2 \nonumber \\{} & {} \quad +\frac{1}{\sigma }\left[ \frac{\partial }{\partial x_j}\left( (\nu + \hat{\nu })\frac{\partial \hat{\nu }}{\partial x_j}\right) + c_{b2}\frac{\partial \hat{\nu }}{\partial x_i}\frac{\partial \hat{\nu }}{\partial x_i}\right] . \end{aligned}$$
(1)

The turbulent eddy viscosity \(\mu _t\) is computed from Eq. 2,

$$\begin{aligned} \mu _t = \rho \hat{\nu }f_{v1}, \quad f_{v1} = \frac{\chi ^3}{\chi ^3+c^3_{v1}}, \quad \chi = \frac{\hat{\nu }}{\nu }, \end{aligned}$$
(2)

where the wall distance d is the RANS length scale. Other model coefficients and functions defined in the reference [17] are used in this study.

The delayed version of DES (called DDES) is chosen here. The DDES is based on the SA equation 1 with the length scale modification for LES-like computation in the region of flow separation [12]. The replacement of the RANS length scale d with an LES length scale proportional to the grid size \(\Delta \) allows the SA model to behave like the well-known Smagorinsky model, which is the main idea of the DES approach. The early DES version [11] uses the following comparison to replace d with the DES length \(\tilde{d}\) in Eq. 1: \(\tilde{d} = min(d,C_{DES}\Delta )\). The delayed DES (DDES) model was proposed to mitigate numerical issues associated with grid-induced separation and modeled-stress depletion [12]. In the current study, the DDES model is used to maintain the RANS mode in the attached flow even with fine resolution near the RANS/LES boundary. The length scale of DDES \(\tilde{d}\) is expressed in Eq. 3,

$$\begin{aligned} \tilde{d}= & {} d - f_d \max (0,d - C_{DES}\Delta ), \end{aligned}$$
(3)
$$\begin{aligned} f_d= & {} 1-\tanh ([8r_d]^3), \quad r_d = \frac{\nu _t + \nu }{\sqrt{\frac{\partial U_i}{\partial x_j}\frac{\partial U_i}{\partial x_j}}\kappa ^2d^2}, \end{aligned}$$
(4)

where \(\nu _t\) is the kinematic eddy viscosity, \(\nu \) the molecular viscosity, \(\partial U_i/\partial x_j\) the velocity gradient tensor, and \(\kappa \) the von Kármán constant.

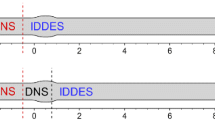
The LES length scale is determined by the grid cell volume, i.e., \(\Delta =(\Delta _x \Delta _y\Delta _z)^{1/3}\) in this study, following references [7, 18]. The current definition of the length scale \(\Delta =(\Delta _x \Delta _y\Delta _z)^{1/3}\) indicates that grids in the LES mode needs to be as isotropic as possible \(\Delta \simeq \Delta _x \simeq \Delta _y \simeq \Delta _z\). The standard DES coefficient \(C_{DES}=0.65\) is used here. The delayed function \(f_d\) indicates the RANS and LES zones in the current study as shown in Fig. 2. The attached boundary layer is treated in the RANS simulation, whereas the separated flow is well positioned in the LES zone. Note that the RANS zone outside the attached boundary layer does not deteriorate the current simulation because the flow is mostly uniform there.

Fig. 2
figure 2

The RANS and LES zones of the current DES computation of the axisymmetric base flow visualized with the delayed function \(f_d\)

Full size image
Fig. 3
figure 3

Computational domain of the G2 grids (left) and selected grids on the base surface (right). Every 8th grid line is visualized here

Full size image

2.3 Computational Domain

The computational domain is shown in Fig. 3. The uniform-inflow boundary is located 6.37D from the base in order to model the upstream boundary layer measured in the experiment. The outflow boundary is located 20D away from the base for sufficient wake development. The far-field boundary is located 10D from the axis of the body, which is sufficiently large because (1) the distance 10D is about 100 times of the upstream boundary layer thickness and (2) the wake area is only about 1% of the circular cross-section area of the domain. A small portion of the inviscid wall (here 1D in the streamwise direction) is included in the upstream of the no-slip cylinder for stable computation.

Table 1 Six grids in current DDES computations. The near wake region covers the range of \(0\le x \le 1.25D\) and \(0 \le r \le 0.5D\)
Full size table
Fig. 4
figure 4

Aspect ratio of the grids around the near wake region

Full size image

Current structured grids are listed in Table 1. Our initial grid (G1-Coarse) was generated, following the guideline provided in Kawai and Fujii (2007) [10]. Although computational data reported in [10] agree well with the relevant experiment of [14], current DDES computations on the G1-Coarse grid cause the LES mode to activate far downstream. As a result, the near wake region of \(0\le x \le 1.25D\) and \(0 \le r \le 0.5D\) is systematically refined. The resolution is almost doubled in the three directions x, r and \(\theta \) from a one-level coarser grid in the G1 series. Current computations indicate that the azimuthal direction is significant in generating nearly isotropic grids in the most of the near wake region. Therefore, G2 grids are designed to yield nearly isotropic grids in the near wake. The grid G2-Medium1 is finer than G1-Medium particularly in the azimuthal direction in the wake region. The azimuthal resolution is refined in the G2 series furthermore. The aspect ratio \(AR=\Delta _{max}/\Delta _{min}\) plotted in Fig. 4 clearly shows that the G2 grids reduce significantly the highly stretched region, which is in close proximity to the separating shear layer. Although the wall-normal grid size on the side of the cylinder increases in the G2 grids, this does not deteriorate the RANS mode for the attached boundary layer there.

The no-slip wall condition is set on the cylinder surface. The Riemann condition is applied at the far-field boundary. Inflow properties are fixed to the freestream, whereas outflow variables are obtained with the zero-gradient condition with the freestream static pressure. The inflow condition for the SA equation is \(\hat{\nu }_\infty =4\nu _\infty \), which is equivalent to \(\nu _{t,\infty } \approx 0.6\nu _\infty \). The recommended value is commonly utilized in SA-RANS computations to provide turbulent flow [19]. Here, the upstream boundary layer is turbulent, so the recommended turbulent inflow condition is still valid in the current DDES simulation.

Current unsteady computations require a small-enough time step to resolve the unsteady nature of the separating shear layer and the wake. A series of time steps \(\Delta _t U_\infty /D=0.0014, 0.0028\) and 0.0056 are tested in the current dual-time scheme, and \(\Delta _t U_\infty /D=0.0028\) is chosen for the most of the reported data here. Twenty sub-iterations with the sub-iteration CFL number of 3 are used per one physical time step for at least a three-order-of-the-magnitude drop in the residual. Turbulent statistics in the current base flow is obtained from the long enough time window of 2.5 flow-through times after the initial numerical transient of 1 flow-through time. About 10,000 time steps are required for the freestream to flow through the computational domain. Time-averaged computational data are further averaged in the azimuthal direction. Parallel computations with the Intel Xeon Gold Skylake processors are performed. G1-Fine and G2-Fine grids require 153,600 and 112,200 CPU hours for 1 flow-through time, respectively.

3 Results

3.1 Overview

The axisymmetric base flow at \(M_\infty = 0.54\) and \(Re_D=0.29\times 10^6\) is numerically simulated with the DDES model. Instantaneous base flow from the current DDES computation is shown in Fig. 5. The flow is fully attached before the base. Right after the base, the separated flow is rich in eddies. Since the attached upstream flow is modeled in the RANS mode, DDES provides steady mean flow for \(x<0\) even in the unsteady simulation. After the flow separation from the sharp base corner at \(x=0\), the LES mode is activated, which results in flow instabilities in the separating shear layer and turbulent eddies in the wake.

3.2 Grid Convergence Study

Appropriate spatial resolution for the base flow is investigated with the current four grids listed in Table 1. Three G1 grids (i.e., G1-Coarse, G1-Medium and G1-Fine) are generated, refining the spatial resolution in all the three direction in the near wake region for an one-level finer grid. Three other grids (G2) are designed for improved grid isotropy in the near wake region with three levels of the azimuthal resolution.

Fig. 5
figure 5

Vortical structures in the current DDES computation on the grid G2-Fine. The Q criterion colored by the vorticity magnitude \(|\omega |\times D / U_\infty \) is used for the flow visualization. The vorticity contour on the (x, r) plane is added to show the attached flow before the base

Full size image
Fig. 6
figure 6

Instantaneous vorticity (left) and eddy viscosity (right) fields on the (x, r) cross section in the current DDES simulation with (a) G1 grids and (b) G2 grids

Full size image

Instantaneous flow fields on the six grids are shown in Fig. 6. The eddy viscosity \(\mu _t\) (normalized with the molecular viscosity \(\mu \)) is plotted together to demonstrate how fine the grids are, except the G1-Coarse grid. Current grids (except the G1-Coarse grid) capture properly the Kelvin–Helmholtz instability, which is the two-dimensional motion, of the separating shear layer. The separating turbulent shear layer does not contain turbulent eddies at the beginning because of the upstream RANS mode. The switch to the LES mode in the current DDES computations allows the shear layer to be unstable because of the sudden drop of the eddy viscosity. A rapid shift to the LES mode is desirable in a typical DES simulation right after the separation because a shorter RANS-to-LES transition length provides a smaller region of modeled-stress depletion [12]. Except for the G1-Coarse grid, the current grids reduce the eddy viscosity in the level of the molecular viscosity or further more in the shear layer, allowing the proper development of the shear layer. The smaller eddies are resolved as the resolution is doubled in every direction with the G1 grids. The G2 grids offer both fine and isotropic resolution which help to capture small eddies as observed in the grid G1-Fine.

Fig. 7
figure 7

Instantaneous vorticity fields on the \((r,\theta )\) cross section at \(x=0.3D\) (upper half) and \(x=0.6D\) (bottom half) in the current DDES simulation with the (a) G1 and (b) G2 grids

Full size image

Vorticity fields in the recirculation region are shown in Fig. 7 at two selected axial locations \(x=0.3D\) and \(x=0.6D\). It has been recognized that three-dimensional vortical structures appear in an axisymmetric shear layer [20]. The Kelvin–Helmholtz instability generates an axisymmetric vortex ring in the vicinity of the base. The vortex ring is deformed by azimuthal perturbation. Such azimuthal undulation is well captured in the girds G1-Fine and the three G2 grids. The well-resolved azimuthal instability grows as it moves downstream and forms the 3D swirl in the shear layer, which is also observed in the experiment of the axisymmetric subsonic jet flow [20].

3.3 Upstream Boundary Layer

The current axisymmetric base flow includes attached turbulent boundary layer before the base as shown in Fig. 8. Both RANS and DDES computations provide the attached flow as observed in the experiment of [14]. The RANS mode is activated in all the DDES grids for the attached boundary layer, which is expected because of the delayed function in the DDES model regardless of the resolution variation. The current grid includes the upstream no-slip surface in the range of \(-6.37D \le \text {X}\le 0\) in order to reproduce the turbulent boundary layer of the experiment. The upstream length before the base is determined from the conventional correlation of turbulent boundary layer thickness on a flat plate [21] because the boundary layer on a cylinder becomes much like the boundary layer on a flat plate when the boundary layer thickness becomes smaller than the radius of curvature the wall (\(\delta /R<1\)) [22]. Since Mariotti et al. [5] studied the effect of the characteristics of the upstream boundary layer on the base flow, it is conjectured that the well-matched upstream flow is the first step towards well-resolved base flow downstream.

Fig. 8
figure 8

Comparison of the averaged velocity profiles of the boundary layer on the cylinder side at \(x=-2D\) with (a) the experimental data and (b) theoretical solution \((\kappa =0.41)\)

Full size image
Fig. 9
figure 9

Averaged DDES data with comparison to the steady RANS for (a) the mean velocity on the (x, r) cross section and (b) the time-averaged base pressure on the base surface

Full size image
Fig. 10
figure 10

Mean center-line velocity from the current DDES and RANS computations

Full size image

3.4 Wake Statistics

Turbulent statistics in the current base flow is obtained from the long enough time window of 2.5 flow-through times after the initial numerical transient of 1 flow-through time. About 10,000 time steps are required for the freestream to flow through the computational domain. Time-averaged computational data are further averaged in the azimuthal direction.

The mean velocity and pressure from the DDES simulation are shown in Fig. 9 with the comparison to the steady RANS. Current DDES computations provide an elongated recirculation bubble compared to the RANS. The rear stagnation point is located around \(x=1.4D\) in DDES whereas the stagnation point around \(x=D\) in RANS. The mean pressure on the base surface is almost uniform in DDES, which is expected due to the strong mixing in the wake. In contrast, the pressure varies erroneously in RANS.

Fig. 11
figure 11

Streamwise (top) and radial (bottom) velocity profiles at five streamwise locations in the wake region in current DDES on G1-Medium (\(\circ \), red), DDES on G1-Fine (—, red), DDES on G1-Medium2 (\(\circ \), blue), DDES on G2-Fine (—, blue) and RANS (- -, green)

Full size image

Current DDES computations on fine enough grids provide the mean center-line velocity as measured in the experiment of [14] (see Fig. 10)—note that the result with the previous hybrid RANS/LES is not documented in the paper. The agreement to the experimental data of the reversed flow is acceptable with the similar value of the negative peak velocity and the peak location. The length of the recirculation is slightly over-estimated in the current DDES computations. It should be noted that Merz [14] noticed that the velocity measurements by pitot-static tube is not accurate near the stagnation point because of the unsteady change of the flow direction. In contrast to the other grids, the G1-Coarse grid causes the qualitatively wrong flow field, mainly because of the significant delay of the LES switch in the wake region. The SA RANS simulation yields a smaller recirculation bubble ending around \(x=D\).

Streamwise U and radial \(U_r\) velocities in the wake are plotted in Fig. 11. Except G1-Coarse grid, the current grids provide almost identical mean velocity profiles, indicating that the averaged data reported here are not sensitive to a particular choice of the computational grid. It should be noted that the velocity range of two Figs. 10 and 11 are visually different, so a minor difference between computational grids are emphasized in Fig. 10. The streamwise velocity U profiles show that the separating shear layer spreads gradually, which leads to the appropriate simulation of the recirculation region shown in Fig. 10. The RANS simulation yields a rather rapid diffusion of the shear layer, resulting in the under-estimation of the recirculation size.

The mean pressure on the base is compared with relevant experiments [14, 23] and hybrid RANS/LES simulation [10] in Fig. 12. The hybrid RANS/LES data from Kawai and Fujii [10] is plotted as a constant line using the area-averaged value of [10]. The almost uniform distribution of the base pressure is expected because of strong mixing of the separated flow on the base. The current DDES computations predict the base pressure within the reported range \(-0.13 \le C_{p,base} \le 0.10\). The RANS simulation fails to predict not only the area-averaged base pressure but also the pressure distribution in the radial direction. It is interesting to notice that the coarse grid here provides the base pressure marginally although the center-line velocity in Fig. 10 is not well captured.

The current axisymmetric base flow resembles flow separation from a bluff body, resulting in the vortex shedding phenomena. The shedding frequency is investigated through the one-sided power-spectral density (PSD) of the radial velocity at a point (\(x=3R, r=1R\)) in the shear layer as shown in Fig. 13. The grid G2-Fine provides the shedding Strouhal number \(St_D=0.21\) which is similar to the relevant experimental measurements [23,24,25] as listed in Table 2. In contrast, the grid G1-Medium overestimates the major shedding frequency. A similar grid is used in the previous hybrid RANS/LES [10] which also overestimated \(St_D\). The improved grid isotropy in the G2 grid seems to help capture the shedding frequency. Also, the inertial subrange (denoted by the \(-5/3\) slope) is well captured.

Fig. 12
figure 12

Base pressure distribution along the radial direction

Full size image
Fig. 13
figure 13

(a) Power spectrum density (PSD) of the radial velocity fluctuation in two selected grids and (b) the full-range spectrum on the grid G2-Fine

Full size image
Table 2 The shedding frequency of the base flow in literature and current DDES on the G2-Fine grid
Full size table

4 Conclusions

Axisymmetric base flow in the subsonic condition is simulated with the DDES method. The eddy-resolving capability relies on the grid quality (including both the resolution and the isotropy) in the LES zone. The LES length scale is defined as the cubic root of the cell volume \(\Delta =(\Delta _x \Delta _y\Delta _z)^{1/3}\), as such more isotropic grids can represent the length scale better. Fine enough resolution is also critical in order to capture important flow features—here the instability of the separating shear layer and the consequent turbulent eddies in the near wake region. Therefore, the current study takes into consideration the spatial resolution in the LES zone, which has not been fully investigated in the literature. Six different grids are constructed as refining mainly the near-wake region to investigate the resolution requirement. This study differs from previous ones where the model coefficient \(C_{DES}\) varies to match relevant experimental data. The coefficient maintains the recommended value \(C_{DES}=0.65\) here.

The current grids except the grid G1-Coarse capture the shear layer instability properly. A rapid switch to the LES mode in the current simulation allows the shear layer to be unstable. The proper development of the shear layer generates turbulent eddies quickly which are required in LES computation. Furthermore, more refinement in the azimuthal direction on the G2 grids allows to capture the 3D nature of the shear layer instability. The refinement clearly improves the prediction of the wake statistics. The center-line velocity distribution on fine enough grids exhibits a good agreement with the experiment, including the similar maximum reverse velocity and its location. In contrast, the G1-Coarse grid brings a qualitatively wrong flow field. The shedding frequency of the base flow is investigated through the one-sided PSD of the radial velocity fluctuation. The G2-Fine grid, with its nearly isotropic layout and adequate resolution, accurately predicts the shedding frequency \(St_D\) as measured in experiments. Less isotropic grid such as G1-Medium overestimates \(St_D\) by about 30%, which was similarly reported in previous hybrid RANS/LES study [10] with the similar grid quality. The base pressure on the current simulation agrees well with the experimental measurement. The G1-Coarse grid here also provides the base pressure marginally, although the coarse grid failed to predict the mean center-line velocity.

Current eddy-resolving simulation with the DDES method suggests that the spatial resolution in the separated flow is critical in predicting the turbulent flow involving the shear layer and recirculation. Nearly isotropic grids with fine-enough resolution for major flow features (here, the separating shear layer and the recirculation) offer a well-designed setup for eddy-resolving simulation. It should be noted that some previous studies [7, 8] attempted to modify the suggested value of the DES coefficient \(C_{DES}=0.65\) which is well calibrated for the limit of isotropic turbulence. The current study indicates that the coefficient modification would not be required if a computational grid is properly generated for eddy-resolving simulation. Although the current study focuses on the axisymmetric base flow, a similar technique for grid generation could be used in other massively separated flows.