Introduction

With the consolidation of the development of algebraic reasoning in the early grades (i.e., early algebra) as a recent line of study (Cai & Howson, 2013), the relationship between the structure of arithmetic and algebraic reasoning at those ages continues to elicit research interest (Kieran et al., 2016; Warren et al., 2016). Within early algebra, generalized arithmetic approaches algebraic reasoning from arithmetic (Carraher & Schliemann, 2007) with the understanding that the properties of operations may facilitate arithmetic generalizations that contribute to students’ subsequent achievement in algebra (Blanton et al., 2011; Stephens et al., 2017, pp. 386–420).

According to several countries’ curricular guidelines (e.g., Ministerio de Educación y Formación Profesional, 2022; National Council of Teachers of Mathematics, 2006), students should recognize the generality of properties of operations from the early grades. Thus, there is a need to explore what kinds of problems could favour students’ understandings in the early grades. In addition, it is important to understand how different contexts are associated with the understandings students develop for different concepts (Di Martino, 2019; McGowen, 2017; Stephens et al., 2017, pp. 386–420). The purpose of this study is to describe the understandings of three arithmetic properties among kindergarten and first-grade students across different types of problems.

Arithmetic Properties in the Early Grades

In this study, we explored three arithmetic properties, as defined in Table 1 for the purposes of our work with kindergarten and first-grade students.

Table 1 Arithmetic properties (adapted from Blanton, 2008, p. 15)
Full size table

Carpenter et al. (2003) showed that elementary-grade students can verbally generalize arithmetic properties after working with specific cases. In addition, following instruction in the use of symbolic notation, second graders (Carpenter et al., 2003; Carpenter & Levi, 2000) and even first graders (Carpenter et al., 2005) were able to represent the additive identity and additive inverse properties algebraically. They identified properties using near and far numbers and subsequently represented them with expressions such as t + 0 = t and h − h = 0. Students nonetheless found it more difficult to recognize properties in equations such as a + b − b = a. In later research, Fujii and Stephens (2008) introduced problems using specific numbers, such as 78 − 49 + 49 = 78, and found that second graders were able to explain the property in general terms when using numbers in this way, as quasi-variables.

Some studies have found differences between students’ understandings of commutativity and of the other two properties (e.g., Bermejo & Rodríguez, 1993). Carpenter and Levi (2000) showed that first and second graders explained additive identity by attributing to zero the absence of transformation and for additive inverse they invoked the equality between the quantities when performing the operation. In contrast, while recognizing commutativity when represented symbolically, they were not able to explain the property in the same way that they were able to explain the two other properties. Regarding students’ understandings of the commutative property in the early grades, other studies have highlighted the importance of students’ thinking developing from specific quantities to more abstract symbols (Ching & Nunes, 2017), using near numbers (Bastable & Schifter 2017), and helping students understand the property by rearranging physical objects to show that quantities are conserved (Schifter, 2009).

Relatedly, research not specifically focused on arithmetic properties but related to other arithmetic and algebraic domains has highlighted the importance of how problems are formulated, finding that in a study of understandings of operations before being introduced to arithmetic, young children had greater difficulty working with numerical expressions (e.g., if 5 + 5 would be the same as 4 + 6) than with word problems with two boxes where the total quantity of candies would stay the same if a piece of candy was moved from one box to another (Britt & Irwin, 2011).

Further study is required to understand the effect of types of problems on students’ performance (McGowen, 2017; Stephens et al., 2017, pp. 386–420). Other studies with kindergarten and first-grade students who had received no formal instruction on symbolic representations revealed that identifying addition and subtraction number sentences was less demanding than producing these sentences, particularly for kindergarten students (Mark-Zigdon & Tirosh, 2017). Research on early algebra instruction in third grade (Blanton et al., 2015) has provided evidence regarding students’ ability to recognize the underlying structure of additive identity and commutativity and to express it symbolically after identifying these properties for specific numbers (such as a − a = 0 from 12 − 12 = 0).

Several studies have explored preschoolers’ conceptual understandings and their performance in problems that involve arithmetic properties. For example, regarding the commutative property, studies have found connections between conceptual understandings and the use of order-indifferent counting procedures to solve addition problems (Canobi et al., 2002; Cowan & Renton, 1996) among 4- to 6-year-old students. Patel and Canobi (2010) observed that 3- to 5-year-old children with strong understandings of unknown numbers were more accurate at solving word problems than those with poor conceptual understandings. In addition, in this age range, researchers have found performance differences among students across grades both in conceptual and procedural problems. However, studies in upper grades (fifth, sixth, and seventh grades) with both additive and multiplicative versions of six arithmetic concepts (identity, negation, commutativity, equivalence, inversion, and associativity) found no grade-related differences in conceptual knowledge, but older children were more accurate problem solvers (Robinson et al., 2018).

The research cited above reveals both early elementary students’ potential to recognize properties structurally and the effect of problem formulation on their arithmetic and algebraic performance. Prior research provides no specific information, however, on the relationship between types of understandings about properties and performance across different kinds of problems focused on properties, focusing instead on one kind of problem and one property at a time (Robinson et al., 2017). Understanding whether or not there are differences in children’s understandings across properties and different types of problems focused on properties in the early grades of elementary school could have instructional implications in the later grades of elementary school (Baroody et al., 2009).

As such, this study explores the types of understandings simultaneously across the three properties in the first grades of elementary school by focusing on the following research question: How are the types of understandings that kindergarten and first-grade students exhibit for the arithmetic properties of additive identity, additive inverse, and commutativity associated with different kinds of problems?

Theoretical Framework

In generalized arithmetic, students are encouraged to notice and represent the structures underlying arithmetic properties and justify and reason about the generalizations they observe (Kaput, 2008). Regarding this process related to arithmetic properties, Wittrock (1990) characterized understanding as the result of generating relations among concepts, new information and ideas, and our knowledge and experience base. To distinguish different kinds of understandings, Skemp (1987) differentiated between relational understandings, or simply “knowing both what to do and why” (p. 89), from instrumental understandings that imply that a student knows a rule or procedure and has the ability to use it, but “without reason” (p. 89). Students exhibit instrumental understandings when they use learned procedures without justifying the generality of the property and simply repeat mnemonically what they have heard. When students exhibit relational understandings, they formulate and justify the property describing the additive situation.

More recently, relational understandings have been approached from the perspective of conceptual knowledge (Star, 2005; Star & Stylianides, 2013). Among the different definitions for conceptual knowledge (Crooks & Alibali, 2014), one of them explicitly underscores justification as a key element of understanding the basis for procedures, or knowing why a procedure works. Molina and Mason (2009) highlight that students could justify their responses without carrying out specific calculations, instead referencing arithmetic properties. For example, students could say that the expression 27 + 48 − 48 = 26 is false, without carrying out any calculations, referencing the inverse property (a − a = 0) to justify their response. Besides understanding the components and structure of the expression that has to be justified, it is relevant for students to understand the structures of arithmetic they are working with. For this reason, to analyze relational understandings in this study, we will use Vergnaud’s (1996) framework of the three basic relationships in the conceptual field of additive structures (combination, transformation, and comparison, see Table 2) to describe students’ understandings of the arithmetic operations included in the expressions of the different properties of operations.

Table 2 Three basic relationships in additive situations (Vergnaud, 1996). Examples focus on the additive identity property for 6 + 0 = 6
Full size table

Using the tasks developed in prior studies as a starting point and to study their performance on different problems, in this study, we distinguish between four types of problems: operations (with both near and far numbers), open equations (with an unknown or missing value), word problems, and substitution problems. Three types of word problems were used: word problems with specific data (WPDs), word problems with indeterminate quantities (WPIs), and word problems with equations (WPEs). This classification is considered exhaustive using Anderson and Krathwohl’s (2001) taxonomy that characterizes learning objectives both from the knowledge dimension (factual, conceptual, procedural, and metacognitive) and cognitive process dimension (remember, understand, apply, analyze, evaluate, and create).

Table 3 includes information about the different types of problems we used.

Table 3 Examples of different types of problems used in this study
Full size table

Methodology

Participants

Two elementary schools in the Northeastern United States participated in the study. Each kindergarten and first-grade class selected (one each in each school) had around 22 students, for a total sample size of approximately 88 students. These two schools were selected because of their willingness to participate in the study and the differences between them. One of the two school districts had 20% low-income families and 6% English language learners and the other had 40% low-income students and 27% English language learners. Children and their parents provided their assent and consent, respectively, to participate in this research study. Their classroom teacher was present during the lessons and researchers received background criminal checks to be able to interview students in the school library, a public setting. The students had not engaged with these types of mathematical problems with their classroom teacher prior to the study.

Data Collection

Classroom Teaching Experiment

In each of the two schools, the study included a 7-week classroom teaching experiment (CTE) (Confrey & Lachance, 2000) that consisted of 30-min lessons implemented twice weekly taught by project researchers, for a total of 14 lessons and five individual interviews. The lessons were video-recorded and team meetings were held after each lesson to discuss the interim findings and redesign the subsequent lessons accordingly. All other teaching was carried out by the classroom teachers and did not include instruction about the arithmetic properties.

Lessons on Arithmetic Properties

Each of the three arithmetic properties was the focus of two lessons (for a total of six lessons), all of which followed the same pattern. In the first lesson for each property, the goal was to analyze information from which to formulate a conjecture about the arithmetic property and represent it in words, and to identify the values for which the conjecture was true. A word problem was used to model additive identity and inverse. For commutativity, students worked with manipulatives consisting of strips of unifix cubes of two different colours (see Fig. 1). The unifix cubes were used as a manipulative to represent the commutative property by showing how strips of cubes of the same length could be composed of different combinations of two different coloured cubes (e.g., both four red & three yellow cubes and three red & four yellow cubes composed strips of cubes of the same length: seven).

Fig. 1
figure 1

Sample problem from Lesson 1 for Commutative Property

Full size image

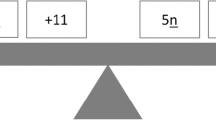
The goal of the second lesson for each property was to identify the generalization (e.g., arithmetic property) underlying the computational problems, and to represent the generalization using variables. For the three properties, the discussion was geared to the use of “any number” and the introduction of letters to represent the relationships between quantities (see Fig. 2).

Fig. 2
figure 2

Sample problem from Lesson 2 for Commutative Property

Full size image

The chronology of the CTE, along with the content of the lessons and interviews, is presented in Fig. 3.

Fig. 3
figure 3

Chronology of CTE and interviews

Full size image

Individual Interviews

Each of the four classroom teachers selected four students based on their ability to work with numbers, count, add, and subtract, ensuring that at least one low, one intermediate, and one high-performing student was chosen from each class. The selection was also based on students’ communication skills, which was important for participation in the interviews. Once the teachers had selected the interviewees, we tracked no additional data other than their school grade and performance on the CTE tasks. In this study, we analyze the understandings of arithmetic properties among these 16 students (8 kindergarteners and 8 first graders) from the data collected during the individual interviews.

We carried out a total of 80 individual interviews, five with each of the 16 students chosen. Two interviews (pre- and post-clinical) were clinical in nature and three interviews (pre-, mid-, and post-teaching experiment) followed the same structure as lessons in the CTE (diSessa, 2007; Ginsburg, 1997). During the pre- and post-clinical interviews, which included the same questions, the interviewer limited her role to assessing students’ initial and final understandings of arithmetic properties. In the other three interviews, the problems were similar to the ones included in the teaching experiment. The interviewer’s role in these interviews was similar to the teacher-researcher’s role in the teaching experiment: to probe students’ reasoning regarding the validity of arguments and their use of letters to represent quantities and relationships between quantities. The interviews, which lasted no longer than 30 min, were video-recorded. Both the interviews and the CTE lessons were carried out by a project researcher and observed by a second project team member whenever possible (interview problems can be found in Appendix A). Our focus in this study is exclusively on the researcher-led CTE, focused on generalized arithmetic and arithmetic properties. The rest of the instruction, delivered by the classroom teachers, was not focused on generalized arithmetic or arithmetic properties.

Data Selection and Analysis

In this paper, we specifically focus only on students’ responses to questions on arithmetic properties during the individual interviews. The data analyzed included the interview transcripts and any student work produced during these interviews. The full answer to each interview problem was our unit of analysis and was analyzed using the following categories (see Fig. 4), designed from Skemp’s (1987) and Vergnaud’s (1996) definitions. Categories are not mutually exclusive and each answer could be coded in more than one category.

Fig. 4
figure 4

Categories for analyzing understandings of properties

Full size image

We considered an understanding to be instrumental when the child simply repeated memorized facts (e.g., “The number jumps right through the zero”) or did not justify their response (without reason). We considered an understanding to be relational when the student could justify their response (knowing both what to do and why). In this case, we analyzed which of the three basic kinds of relationships in additive situations (i.e., combination, transformation, and comparison) the child used to justify the operation (an example of a relational understanding with transformation would be “Because if you have a certain number and then you take all of them away it is just zero”). For each one of the problems, we also analyzed whether the student’s response was correct or not. The first author of this paper coded all data and the code was confirmed by the second author. In cases of disagreements, the coding was discussed until agreement was reached. In order to visually present the differences in our findings across first grade and kindergarten, we use diagrams constructed with GeoGebra (see Figs. 5, 6, 7, 8, 9, and 10), where each axis shows the number of students who provided evidence of a relational understanding for each property.

Fig. 5
figure 5

Number of students who provide evidence of a relational understanding for each property for problems with near and far values at some moment during the CTE

Full size image
Fig. 6
figure 6

Number of students that provided evidence of relational understandings in each property for problems with open equations at some moment during the CTE

Full size image
Fig. 7
figure 7

Number of students who provided evidence of a relational understanding for each property for WPD problems at some moment during the CTE

Full size image
Fig. 8
figure 8

Number of students who provided evidence of a relational understanding for each property for the WPE problems at some moment during the CTE

Full size image
Fig. 9
figure 9

Number of students who provided evidence of a relational understanding for each property in WPI problems at some moment during the CTE

Full size image
Fig. 10
figure 10

Number of students who provided evidence of a relational understanding for each property for substitution problems at some moment during the CTE

Full size image

In this paper, we use codes to identify each of the 16 students. The first letter refers to the school (A or B), the second letter refers to the grade level (K for kindergarten and 1 for first grade), and the number refers to each one of the four students at each grade level in each school. So, for AK_2, this is a student from school A, in kindergarten, and coded as student “2” out of 4 in this grade at this school.

Results

This section describes students’ understandings of the three properties and analyzes their performance, in terms of number of correct responses, as well as progress in the different types of problems across the interviews carried out in the CTE. We also discuss the differences between kindergarten and first-grade students, followed by an overview of students’ overall performance.

Operations with Near and Far Numbers

Operations with near and far numbers for all three properties were included in the pre- and post-clinical interviews (see Table 3). Of the 16 students we interviewed (eight in kindergarten and eight in first grade) prior to the lessons, four kindergarten and seven first-grade students correctly answered the problems that involved both additive identity and inverse with near and far numbers. Figure 5 shows the number of students that provided evidence of a relational understanding of the corresponding properties during the CTE. We emphasize that the diagram is the same both for near and far numbers, which highlights that their answers are not just limited to computation but that they recognize the relationships between terms (Molina & Mason, 2009).

In the case of the inverse property, 13 students (all first-grade students and five kindergarten students) provided evidence of a relational understanding, pointing out the same quantity in the transformation or comparison of the terms (BK_3: because we take away all of them; A1_2: because if you have a certain number and then you take away all of them away its just zero). We observed difficulties among the three kindergarten students who did not provide evidence of a relational understanding (AK_1, AK_2, and BK_4) to work with problems with specific examples even with near values (AK_2: that means it equals again because you take away the same number equals the same number).

For the identity property, all students except 4 (two from kindergarten, AK_1 and BK_4, and two from first grade, A1_1 and A1_3) provided evidence of a relational understanding associated to a lack of transformation (AK_4: it is the same. They did not add anything. They did not put any). In the case of first-grade students that provided evidence of instrumental understandings, our observation is that their difficulties with justifying the properties had to do with the fact that they confused justifying the property with mnemonic rules they had learned (A1_1: The same number goes to the other side; A1_3: the number jumps right through the zero).

The commutative property is the one in which we observed the most differences between kindergarten and first-grade students. Prior to the CTE, we found commutativity with near and far numbers to be unfamiliar to one student in first grade (A1_3) and all of the kindergarteners except AK_1 and AK_3. However, throughout the CTE, we did not observe any kindergarten student who provided evidence of a relational understanding of the commutative property in problems with near or far numbers. In cases when kindergarten students were able to solve problems involving commutativity, the understanding they manifested was relational, through their verbalization of the property, without being able to justify it (BK_3: you are just flipping this part around, you are not flipping the whole thing around; AK_3: it is the same thing up here, but switched around). However, four first-grade students (A1_2, A1_3, B1_2, and B1_4) provided evidence of a relational understanding associated with the equality in the combination of quantities (A1_3: you are just adding the same numbers together; B1_2: even the numbers are switched around, and its the same, like four plus three equals seven if its flipped around like three plus four equals seven, its still the same).

In summary, we emphasize that, in problems that involved numbers, there was no difference between the use of near or far numbers and students’ relational understandings. We also did not observe differences between first-grade and kindergarten students’ relational understandings of the identity property. The properties where we did observe a difference were the inverse property, where first-grade students more frequently provided evidence of relational understandings and, especially, the commutative property, where no kindergarten student was able to justify the property.

Open Equations

Open equations were included during the interviews before and after the respective lesson on each property (pre- and mid-teaching experiment interviews for additive identity, mid- and post-teaching experiment interviews for additive inverse, and mid- and post-teaching experiment interviews for commutativity; see Table 3). Four kindergarten and seven first-grade students correctly answered the additive identity and inverse problems with open equations prior to the respective lessons for each property, perhaps because the children had had experience with open equations before the CTE. In the interviews that took place after the CTE lessons for each property, all the students correctly completed the problems for additive identity with open equations and all but one (BK_1) for additive inverse with open equations.

For the inverse and identity properties (see Fig. 6), all first-grade students provided evidence of relational understandings, justifying their answers through transformation or comparisons (A1_1: if you want to get zero, you had to subtract the same number from itself; A1_2: if you have zero, it says two minus signs, then you know that you should take away two, because nothing else would make zero). Similarly, four kindergarten students provided evidence of a relational understanding of these properties, but another four (AK_1, AK_4, BK_1, and BK_4 for inverse and AK_1, AK_4, BK_2, and BK_4 for identity) were not able to justify their answers. By the end of the CTE, we did not observe differences between kindergarten and first-grade students in the number of correct responses in additive inverse problems with open equations, but we did observe differences in their kinds of understandings.

We observed more difficulties around commutativity with open equations, particularly among kindergarteners. We observed a greater number of correct responses after the lessons on commutativity: in the mid-teaching experiment interviews, before the commutativity lessons, only three first graders (A1_1, B1_1, and B1_2) were able to correctly respond to all open-equation problems involving the commutative property. And, only four first-grade students (A1_2, B1_1, B1_2, and B1_4) provided evidence of a relational understanding of the commutative property associated with a justification of the equality due to the combination of quantities (B1_2: they just switched it around. They are both equal the same thing… s + r = a and r + s = a).

In summary, even though we did not observe differences in students’ solutions for identity and inverse problems, we did observe a greater difficulty among kindergarten students to justify their answers, and, therefore, to provide evidence of a relational understanding for open-equation problems. These differences were even starker for the commutative property, where no kindergarten student provided evidence of a relational understanding.

Word Problems with Data

Students were asked to solve WPD (see Table 3) in the pre- and mid-teaching experiment interviews for additive identity, one WPD in the mid-teaching experiment interviews for additive inverse, and none for commutativity. Even before the lessons started, 14 students (six kindergarten and eight first-grade students) correctly solved these kinds of word problems for both additive identity and inverse.

All first-grade students (see Fig. 7) provided evidence of a relational understanding for both properties (identity and inverse) and were able to justify their answers alluding to transformations and comparisons. However, only three kindergarten students (AK_2, AK3, and BK_3) were able to justify their answers for the inverse property and five did so for the identity property (AK_2, AK_3, AK_4, BK_1, and B_K3). The rest of the kindergarten students, even after the lessons in the CTE, had an instrumental understanding and had difficulty justifying their answers for these problems (BK_1: I just learned it. Thinking and counting; BK_4: because they’re the same thing. Because I saw the same numbers, the same numbers at each row).

Word Problems with Equations

These types of problems (see Table 3) were included in the interview prior to the lesson for each property (pre-teaching experiment interviews for additive identity and mid-teaching experiment interviews for additive inverse and commutativity). All first-grade and three kindergarten students correctly answered the additive identity and additive inverse problems that included these problems. The rest of the students answered correctly at least one WPE for at least one of these two properties at some point in the CTE.

In additive inverse and identity properties (see Fig. 8), seven first-grade children provided evidence of a relational understanding (all except A1_3 for additive identity and A1_1 for additive inverse), again associated with transformation and comparison problems (A1_2: zero is nothing. It’s a number that has anything to it… 13 + 0 = 13, 65 + 0 = 65, A + 0 = 0). However, only three kindergarten students (AK_2, AK_3, and BK_3) provided evidence of a relational understanding for additive identity and only two (AK_3 and BK_3) did so for additive inverse. Students who provided evidence of an instrumental understanding only showed particular situations and looked for answers without being systematic.

For the commutative property, the number of correct responses was lower than with the other two properties for WPE, especially in kindergarten, where none of the students completed these problems correctly in the mid-teaching experiment interviews prior to the respective lessons. In the mid-teaching experiment interviews, four students in first grade (A1_2, B1_1, B1_2, and B1_4) expressed a relational understanding of combination for WPE (B1_1: they are the same numbers, and if you add the same numbers together, like if you add the same numbers, like these kinds of equations, it’ll be equal the same).

We observed differences across properties for WPE problems, with less sophisticated responses for the commutative property compared to additive identity and inverse, as well as across groups, with no kindergarten students able to provide evidence of a relational understanding.

Word Problems with Indeterminate Quantities

For additive identity, the problems including WPI (see Table 3) were introduced before the lesson (pre-teaching experiment interview) and for additive inverse, before and after (mid- and post-teaching experiment interview). This type of problem was not used with commutativity. It is possible that this type of problem was too difficult for children to solve prior to the lessons on properties involving WPI given that only one first-grade student (B1_3), guided by the interviewer, managed to solve the problem correctly for additive identity with a relational understanding of transformation (see Fig. 9).

This difficulty for WPI was not observed for additive inverse in the mid-teaching experiment interviews, prior to the respective lessons. Additive inverse WPI in the mid-teaching experiment interviews were solved correctly by 14 of the students (six kindergarten and eight first-grade students). All of the first-grade students provided evidence of a relational understanding. In contrast, only three kindergarten students (AK_2, AK_3, and BK_3) provided evidence of a relational understanding, also associated to transformation and comparison (AK_3: cause there’s 15 people, and there’s 15 juice boxes, and there couldn’t be any more… gave all the juice boxes away to her friends).

The differences we observed between additive inverse and identity for WPI could be associated to the different moments in the CTE in which they were included. Students did not seem to be familiar with WPI problems prior to the CTE, and this was the only moment when additive identity problems with WPI were included. As with prior cases, kindergarten students had a lower frequency of relational understandings.

Substitution Problems

In the post-teaching experiment and post-clinical interviews, the substitution problems combined additive identity and inverse. Students were presented with an expression where they had to substitute and simplify using properties of arithmetic (e.g., presented with a + 0 − a + b and using the additive identity and inverse properties to simplify to b). For commutativity, substitution problems were presented to children prior to the respective lessons, during the mid-teaching experiment interviews. These problems involved using the property to substitute expressions (e.g., “What is 10 + 4? How can you use this to find 4 + 10 + 2?”).

Both in the post-teaching experiment and post-clinical interviews, after the lessons, the number of correct responses was small in substitution problems that combined additive identity and inverse in a single expression. Only four first graders (A1_4, B1_1, B1_2, and B1_4) provided evidence of a relational understanding in operations where they first had to substitute the additive inverse (a + b − b = a), but they found it difficult to transform quantities embedded in the expressions to produce an equivalent simplified equation. Three of them (A1_4, B1_1, and B1_4) also provided evidence of a relational understanding when they first had to substitute the additive identity (a + 0 – a + b). Substantial differences were observed between the two grades in these problems, for none of the kindergarteners (see Fig. 10) answered correctly any of these problems that involved both identity and inverse operations with substitutions, despite having exhibited relational understandings of additive identity and inverse when considered separately.

For the commutative property, in the mid-teaching experiment interviews, five first-grade students correctly answered the substitution problems. Even though three of them (A1_2, B1_1, and B1_2) expressed a relational understanding of combination, for the two other students an instrumental understanding was sufficient to correctly solve the problems. For the commutative property, no kindergarten student correctly answered these types of problems or expressed a relational understanding. The performance in terms of correct responses for substitution problems was the lowest compared to the other kinds of problems, with only one first grader (B1_1) correctly solving all the substitution problems.

Finally, Table 4 shows the number of properties for which each student reached relational understandings. The rows are ordered according to the last column to the right (i.e., “TOTAL”) which shows each child’s performance as the sum of the properties in which they provided evidence of relational understandings, with a sum of 16 being the maximum (three properties each for Operations, Open Equations, WPE, and Substitution Problems and two properties for WPD and WPI). In addition, we have highlighted in gray the instances in which children provided evidence of relational understandings for the maximum possible number of properties for that task.

Table 4 Number of properties in which children provided evidence of relational understandings
Full size table

From this perspective, we identify several interesting results. Two kindergarten students (DK_01 and MK_04) provide no evidence of relational understandings for any of the properties. Meanwhile, two other kindergarten students (DK_03 and MK_03) provided evidence of relational understandings and achieved greater global results than the two Grade 1 students (D1_01 and D1_03) with the fewest total number of relational understandings of properties. This result reflects both the challenges that some kindergarten students face in achieving relational understandings for properties and the potential of some other kindergarten students to achieve relational understandings for additive identity and additive inverse properties, though not for the commutative property.

As far as Grade 1 students’ potential, four students achieved the maximum possible performance in four of the six types of tasks. In addition, for all tasks, there was always at least one Grade 1 student who achieved the maximum possible performance for that task.

Conclusions

Throughout the CTE, 14 students (six kindergarten and eight first-grade students) exhibited a relational understanding based on additive transformation in both additive identity, generalizing the addition of zero as the absence of change (Carpenter & Levi, 2000; Carpenter et al., 2003), and additive inverse, as subtracting a quantity from itself. Although less frequently, a relational understanding with comparison of quantities was also observed in additive inverse and a relational understanding with combination in commutativity. Commutativity proved to be more difficult to understand relationally (Bastable & Schifter, 2017; Schifter, 2009), with nine students (six in kindergarten and three in first grade) tending to recognize the property simply as a learned procedure. The number of correct responses was the lowest and the gap between first graders and kindergarteners widest for this property, particularly where more complex problems such as word problems with equations and substitution were involved.

Two key ideas can be drawn from the observations regarding the different types of problems as they relate to children’s understandings of the properties. First, more students provided evidence of relational understandings with problems with near and far numbers, open equations, and word problems, while very few students (only four first-grade students) provided evidence of relational understandings for problems that included substitution and simplification of expressions that combined different properties. Second, regarding the differences found between kindergarten and Grade 1, our results are nuanced depending on the specific properties and tasks. The number of kindergarten students who provided evidence of relational understandings was lower than first-grade students for all types of problems and properties, but this difference was greater for the commutative property, where no kindergarten students provided evidence of a relational understanding for any of the problems. Having no more than an instrumental understanding of that property appears to have limited kindergarteners’ performance (Bastable & Schifter, 2017; Schifter, 2009). However, for the operations tasks, performance was similar among kindergarten and Grade 1 students for the identity property. Globally, after participating in the CTE, we found that some kindergarten students were unable to provide evidence of relational understandings for any of the properties. However, some other kindergarten students provided greater evidence for relational understandings than their Grade 1 peers. Furthermore, we have provided evidence of the kinds of the specific tasks and properties in which Grade 1 with stronger achievement had difficulties, helping to sketch out levels of complexity in cognitive processes (Anderson & Krathwohl, 2001).

The present findings have implications for teaching arithmetic properties. Commutativity must be broached differently from the other two properties, given the lower performance observed on this property compared with additive identity and inverse. The differences between the two grades suggest that instruction should focus on relational understandings from the outset by, for instance, stressing the validity of properties for large numbers (Schifter et al., 2008).

The most complex problems, judging from the number of correct responses and of relational understandings, were those that involved substitution and word problems with indeterminate quantities. The CTE revealed the importance of instruction for solving word problems with indeterminate quantities, in light of the progress observed in such problems after students learned to generalize specific cases and use letters to express indeterminate quantities. We also observed difficulties in word problems with equations involving commutativity but not the other two properties. This difference could be due to the number of variables involved, given that commutativity includes two variables while additive identity and inverse include only one. This suggests the need to design specific learning environments that could address the challenges that seem inherent to these types of problems.

We found that first graders were able to correctly answer problems with operations with near and far numbers, number sentences, and data-based word problems for the three properties. Even before the lesson on the respective property, these students correctly performed problems involving near and small numbers, number sentences, and open equations. In word problems with data focused on additive identity and inverse, both kindergarteners and first graders exhibited good performance prior to instruction, despite the attention required by such problems (Schliemann et al., 2003).

The differences between kindergarten and first-grade students highlight the importance of using different teaching approaches in these two grades. Overall performance was higher in first grade, where all the students performed well in the near and far numbers, open equations, and word problems with data problems. At least half of the kindergarten students also correctly performed those problems. This information is an indication that such problems are accessible and hence productive to explore the understandings of properties in these two grades. In contrast, word problems involving equations and indeterminate quantities were very difficult for kindergarteners, and problems dealing with substitution wholly inaccessible, for none of the kindergarten students performed them correctly for any of the properties. Our results highlight that some kinds of problems such as substitution and simplification in problems that combine properties are associated with relational understandings.

This study highlights the difference between correctly solving a problem and providing evidence of a relational understanding. In less complex problems, simply solving a problem correctly is not associated with relational understandings. Evidence of relational understandings requires asking students to justify, to explain their answers, and that students not be limited to learned rules (Molina & Mason, 2009). However, in more complex problems, correct responses and relational understandings are more aligned. Overall, more problems were correctly answered by first graders than by kindergarteners. WPI and substitution problems (ST) proved to be the most difficult problems. One first grader, B1_1, correctly solved all problems except for one, a WPI involving additive identity introduced prior to the lessons in the pre-teaching experiment interview. B1_3, another first-grade student, correctly answered all the problems except ST or problems that included WPE. The rest of the first graders correctly answered all the problems for additive identity, additive inverse, and commutativity with near and far numbers, open equations, and WPD. For every kindergarten student, there was always at least one of the properties for which they were unable to provide a single correct response for WPE, WPI, and ST. Their rate of correct responses was especially low for commutativity.

The design study reported here was an exploratory effort in our research to flesh out boundary points in young children’s thinking about generalizing arithmetic properties. In this, it was necessary to design problems that we viewed as likely accessible for students, as well as those that were intentionally more challenging. These results can help inform the design of classroom environments, given that curricular documents in different countries (e.g., Spain, Portugal, Australia, Canada, China, the United States, and Japan) have indicated the benefits of including algebraic thinking in the elementary school grades (Merino et al., 2013). Our results suggest how to design learning environments to support relational understandings of properties, including in kindergarten the additive identity and inverse properties for operations, open equations, and even WPD tasks. In Grade 1, our results indicate it would be appropriate to continue to work on the previous tasks and to also include the commutative property as well as the remaining kinds of tasks: WPE, WPI, and substitution.

The results portray an emerging picture of the constraints and affordances of the problem types we employed and provide insights into how to design future instruction for kindergarten and first-grade students that considers differences across arithmetic properties, especially commutativity (Bermejo & Rodríguez, 1993).