1 Introduction

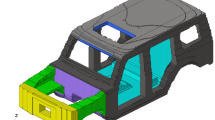
In the development of automotive bodies, the concept design stage is crucial because later design work may be impacted by earlier decisions. Generally, at concept design stage, the automotive structure in the BIW phase is simplified as a semi-rigid spatial frame structure, consisting of joints and beams (Fig. 1).

When the topology and joint properties are given, designing the cross sections of the BIW load-carrying frame is of great importance. Nevertheless, to date, there is no commercial software available. Several specialized software tools have been developed to aid the BIW development phase. Toyota Central R&D Labs proposed a first-order analysis concept for the BIW designers and developed finite-element-analysis software which can give static stiffness, NVH (Noise, vibration, and harshness) and crashworthiness analyses [1,2,3,4,5]. Hou et al. [6,7,8] developed an intelligent CAE system “ACD–ICAE” for auto-body concept design. Zuo et al. [9,10,11] developed the “Vehicle Body–FDO” software based on the NET framework, here, FDO stands for forward design and optimization. However, these studies are all based on the finite element method (FEM), which is an approximate method. In FEM, even a normal beam element may be divided into many segments to achieve higher accuracy, especially for dynamic analysis. Therefore, Qin et al. [12] proposed the TSMM to support exact static and dynamic analyses of a BIW structure. In this paper, a two-level cross-sectional optimization approach is proposed. An easy-to-use MATLAB toolbox was developed to assist in the concept design of automotive BIW structures. The optimization is solved using GA; a distributed parallel computing technique is used to speed up the computation.

Fig. 1
figure 1

The BIW concept model

Full size image

2 BIW Structural Analysis Using TSMM

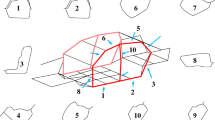
The TSMM is an exact approach both for static and dynamic analyses of any semi-rigid three-dimensional structure, which is modeled as an assemblage of prismatic members connected at their ends to joints. For the geometrical model of the automotive BIW concept structure (Fig. 2), each semi-rigid beam consists of a rigid beam and two semi-rigid connections. Each component is represented by three tensional and rotational springs around local x, y, and z axes. The springs are all massless and have zero length (Fig. 3); the symbols “b” and “e” denote the beginning and the ending joints, respectively. The model is constructed to simulate the actual flexibility of the auto-body joint.

Fig. 2
figure 2

Geometrical model of the concept structure in the BIW phase

Full size image
Fig. 3
figure 3

Semi-rigid beam element

Full size image

2.1 Introduction to TSMM

For the rigid beam (Fig. 3), the stiffness relation for each member is

$$\begin{aligned} \mathbf{Q}=\mathbf{ku} \end{aligned}$$
(1)

where Q is the end force vector, k the \(12\times 12\)-dimensional static or dynamic local stiffness matrix, and u the displacement vector. Exhaustive derivations for the static stiffness matrix are given in the monographs of Kassimali and McGuire [13, 14], and for dynamic stiffness in the literature [15, 16].

If the semi-rigid framed structure is large scale, a condensed model is needed to reduce the computational workload in modeling. Because of the convenient mutual transformation between transfer matrix and stiffness matrix, the TMM is employed to reduce the stiffness matrix for the semi-rigid beam (Fig. 3). Eventually, the condensed stiffness matrix \(\mathbf{k}_s\) for the semi-rigid beam which is also \(12\times 12\) dimensional can be derived [12], and the semi-rigid member in Fig. 3 can be analyzed as a common member. The DOFs of internal joints are discarded to dramatically reduce the structural stiffness matrix dimension for the large-scale engineering structure, e.g., the bus structure. Now it can be concluded that: (1) TSMM is derived from the governing differential equations, thus it is an exact structural analysis method; (2) TSMM is capable of condensing the stiffness matrices for the semi-rigid beam elements.

2.2 Solution for Equations

When the local stiffness matrices have been determined, the structural stiffness matrix S for the whole BIW concept structure is constructed by the direct stiffness method [13]. The structural stiffness relations of the whole structure under static equilibrium and free vibration conditions are written in the form

$$\begin{aligned} \mathbf{Sd}=\left\{ {\begin{array}{ll} \mathbf{P},&{}\hbox {static equilibrium} \\ \mathbf{0},&{}\hbox {free vibration} \\ \end{array}} \right. \end{aligned}$$
(2)

where d denotes the unknown joint displacement vector, and P is the joint load vector for the static condition. Then the joint displacements are stored using the skyline storage method [17] and computed using the substitution method [12, 13]; the eigenfrequencies are calculated by applying the Wittrick–Williams algorithm [18] in conjunction with the bisection method.

3 Two-Level Cross-Sectional Optimization

To increase energy efficiency and decrease emissions, the weight of auto-body must be as light as possible when performance targets (for instance, bending stiffness, torsional stiffness, and vibration) satisfy design requirements. The design of the cross sections for the BIW load-carrying frame in regard to weight is an intractable task, especially when there is no available detailed geometrical data of the auto-body. Therefore, a two-level cross-sectional optimization is performed.

3.1 Level 1: Cross-Sectional Size Optimization

In level-1 optimization, each of the cross-sectional shapes of the metal sheets is preliminarily simplified as a thin-walled rectangular section (Fig. 4) to find an intermediate solution with known topology and joints.

Fig. 4
figure 4

Simplified cross-sectional shape

Full size image
Fig. 5
figure 5

Static stiffness test conventions. a Bending test convention. b Torsion test convention

Full size image

Let \(\mathbf{x}\) denote the design variable vector,

$$\begin{aligned} \mathbf{x}=[\mathbf{w},\mathbf{h},\mathbf{t}] \end{aligned}$$
(3)

in which,

$$\begin{aligned} \left\{ \begin{array}{l} \mathbf{w}=[w_1 ,w_2 ,...,w_n ] \\ \mathbf{h}=[h_1 ,h_2 ,...,h_n ] \\ \mathbf{t}=[t_1 ,t_2 ,...,t_n ] \end{array}\right. \end{aligned}$$
(4)

where n denotes the number of members to be optimized. The mathematical form of size optimization problem can then be formulated as

$$\begin{aligned} \left\{ {{\begin{array}{l} {\mathop {\min }\limits _\mathbf{x} \quad m=f(\mathbf{x})} \\ {\mathrm{s.t.}\quad \left\{ {{\begin{array}{l} {\begin{array}{l} c_1 =\delta -\delta _\mathrm{allow} \\ c_2 =\phi -\phi _\mathrm{allow} \\ c_3 =\mathrm{freq}_\mathrm{allow} -\mathrm{freq} \\ \end{array}} \\ {\mathbf{LB}\le \mathbf{x}\le \mathbf{UB}} \\ \end{array} }} \right. } \\ \end{array} }} \right. \end{aligned}$$
(5)

where m is the BIW concept structure mass function; \(c_{i}\) (\(i=1,2,3)\) are the relevant constraints; \(\delta \) is the maximum vertical deflection under bending (Fig. 5a), where the constraints 1, 2, and 3 corresponding to the linear displacements in the global X, Y and Z axes, respectively, are restrained to zero; \(\phi \) is the angle of twist under torsion (Fig. 5b), where the definitions of the constraints are identical to those in Fig. 5a; \(\mathrm{freq}\) is the first-order eigenfrequency of the BIW concept structure undergoing free vibration; LB and UB are the lower and upper bound row vectors of \(\mathbf{x}\), respectively; \(\delta _\mathrm{allow} \), \(\phi _\mathrm{allow} \), and \(\mathrm{freq}_\mathrm{allow} \) are the allowable limit values for \(\delta \), \(\phi \), and \(\mathrm{freq}\), respectively.

The optimization problem described in Eq. (5) is one that is constrained and nonlinear. As GA is designed to solve such problems without gradient-based information [19], it is adopted here to find the global minimum of the BIW mass. The penalty method [20], introduced to handle constraints, introduces penalty functions defined as

$$\begin{aligned} p_i (\mathbf{x})=\left\{ {{\begin{array}{ll} r_i c_i ,&{}\quad \hbox {for}\,\,c_i >0 \\ 0,&{}\quad \hbox {otherwise} \\ \end{array} }} \right. \end{aligned}$$
(6)

where \(r_{i}\) (\(i=1,2,3)\) are the penalty coefficients of the relevant constraints. Hence, the fitness function of the GA is defined as

$$\begin{aligned} \mathrm{fitness}\,(\mathbf{x})=f(\mathbf{x})\hbox {+}\sum _{i=1}^3 {p_i (\mathbf{x})} \end{aligned}$$
(7)

3.2 Level 2: Cross-Sectional Shape and Thickness Optimization

Usually, the shape of a BIW frame is complex (Fig. 6). In level-2 optimization, shape and thickness optimization of a specified beam is performed when the engineer has determined the initial desired cross-sectional shape. Aside from the three constraints in Sect. 3.1, three manufacturing constraints are taken into consideration (Fig. 7). Considering that the sheet metal is formed using a stamping process, the draft angle must be larger than \(90{^{\circ }}\) (Fig. 7a). Also, intersecting metal sheets are not possible in assembly processing (Fig. 7b). In the practice, special instances were encountered, where flanges may be enclosed by a cell (Fig. 7c, point “A” is such a point, called an interior point). Such instances also should be avoided for they have no practical value. The three associated constraints must not be violated during the optimization process. Geometric properties of the completed shape can be reviewed in the study of Zuo [10].

Fig. 6
figure 6

Typical cross-sectional shape in an auto-body frame

Full size image
Fig. 7
figure 7

Disallowed manufacturing and assembly constraints. a Improper draft angle. b Intersection of sheets. c Invalid interior point

Full size image

To decrease the number of design variables, the scale vector method [21] is adopted (Fig. 8). The control points are classified as one of two types, i.e., the fixed point and movable point (Fig. 6). Fixed points, which are determined by geometric layout requirements or manufacture requirements, are constant during the optimization process. In contrast, the movable points can be successively changed by the scale vector method to obtain a better cross-sectional shape. For example, suppose the initial coordinate is a movable control point (e.g., No. 13 in Fig. 8) is (\(y_{13}\), \(z_{13})_\mathrm{ini}\). Firstly the yoz coordinate system is rotated with a counterclockwise angle \(\theta \) to get the y’oz’ coordinate system. Secondly the coordinates of this control point in the y’oz’ coordinate system are expressed as

$$\begin{aligned} \left[ {{\begin{array}{l} {y_{13}^{\prime } } \\ {z_{13}^{\prime } } \\ \end{array} }} \right] =\left[ {{\begin{array}{ll} {\cos \theta }&{} {\sin \theta } \\ {-\sin \theta }&{} {\cos \theta } \\ \end{array} }} \right] \left[ {{\begin{array}{l} {y_{13} } \\ {z_{13} } \\ \end{array} }} \right] _\mathrm{ini} \end{aligned}$$
(8)

Then the new coordinates of this control point in the yoz coordinate system in terms of a scale vector coefficient SV are expressed as

$$\begin{aligned} \left[ {{\begin{array}{l} {y_{13} } \\ {z_{13} } \\ \end{array} }} \right] _\mathrm{new} =\left[ {{\begin{array}{ll} {\cos \theta }&{} {-\sin \theta } \\ {\sin \theta }&{} {\cos \theta } \\ \end{array} }} \right] \left[ {{\begin{array}{ll} \mathrm{SV}&{} 0 \\ 0&{} 1 \\ \end{array} }} \right] \left[ {{\begin{array}{l} {y_{13}^{\prime } } \\ {z_{13}^{\prime } } \\ \end{array} }} \right] \end{aligned}$$
(9)

The design variable vector \(\mathbf{{x}'}\) is

$$\begin{aligned} \mathbf{{x}'}=[\theta ,\mathrm{SV},t] \end{aligned}$$
(10)

where \(\theta \) and SV are as given above, and t the thickness (Fig. 6). Thus, the scale vector method may be used to reduce the number of design variables and realize a cross-section optimization more efficiently.

The mathematical form of the level-2 shape optimization problem is

$$\begin{aligned} \left\{ {{\begin{array}{l} {\mathop {\min }\limits _{\mathbf{{x}'}} \quad {m}'={f}'(\mathbf{{x}'})} \\ {\mathrm{s.t.}\quad \left\{ {{\begin{array}{l} {\begin{array}{l} {c}'_1 ={\delta }'-{\delta }'_\mathrm{allow} \\ {c}'_2 ={\phi }'-\le {\phi }'_\mathrm{allow} \\ {c}'_3 =\mathrm{fre{q}}'_\mathrm{allow} -\mathrm{fre{q}}' \\ {c}'_4 ={n}'_\mathrm{aa} \\ {c}'_5 ={n}'_\mathrm{ip} \\ {c}'_6 ={n}'_\mathrm{ii} \\ \end{array}} \\ {\mathbf{L{B}'}\le \mathbf{{x}'}\le \mathbf{U{B}'}} \\ \end{array} }} \right. } \\ \end{array} }} \right. \end{aligned}$$
(11)

where the initial allowable values are outputs from the level-1 cross-sectional size optimization solution; \({m}'\) is the BIW conceptual structure mass function; \({c}'_i \) (\(i=1-6)\) are the relevant constraints; \({\delta }'\) is the maximum vertical deflection under bending condition; \({\phi }'\) is the angle of twist under torsional condition, as shown in Fig. 5b; \(\mathrm{fre{q}}'\) is the first-order eigenfrequency of the BIW conceptual structure undergoing free vibration; \(\mathbf{L{B}'}\) and \(\mathbf{U{B}'}\) are the lower and upper bound row vectors of \(\mathbf{{x}'}\), respectively; \({\delta }'_\mathrm{allow}\), \({\phi }'_\mathrm{allow}\), and \(\mathrm{fre{q}}'_\mathrm{allow} \) are the allowable limit values for \({\delta }'\), \({\phi }'\), and \(\mathrm{fre{q}}'\), respectively.

Fig. 8
figure 8

Coordinate transformation employed in the scale vector method

Full size image
Fig. 9
figure 9

Main architecture of the “ABCD” toolbox

Full size image
Fig. 10
figure 10

The GUI of “ABCD” toolbox

Full size image
Table 1 Bounds and optimized values of the design variables
Full size table

The penalty functions are

$$\begin{aligned} p_i (\mathbf{{x}'})=\left\{ {{\begin{array}{ll} {r}'_i {c}'_i ,&{}\quad \hbox {for}\,\,{c}'_i >0 \\ 0,&{}\quad \hbox {otherwise} \\ \end{array} }} \right. \end{aligned}$$
(12)

where \({r}'_i (i=1-6)\) are the penalty coefficients of the relevant constraints.

Hence, the fitness function of this GA is defined as

$$\begin{aligned} \mathrm{fitness}(\mathbf{x})=f(\mathbf{x}){+}\sum _{i=1}^6 {p_i (\mathbf{x})} \end{aligned}$$
(13)

4 Development of the Toolbox

MATLAB is an integrated, powerful, and user-friendly programming system, which is extensively used by scientists and engineers in many fields. Hence, there are many available open source codes, such as the GA toolbox developed by University of Sheffield [22] and is adopted for this study. Moreover, MATLAB provides high-level parallel computation techniques and enables users to parallelize the previous serial program just with a few modifications. For these reasons, the auto-body concept design toolbox (“ABCD” toolbox) was developed based on the MATLAB environment to assist in the concept design of the BIW structure. The toolbox makes use of object-oriented techniques as their virtues include encapsulation, polymorphism, inheritance, and code reusability.

The main architecture of the “ABCD” toolbox (Fig. 9) comprises three modules, such as the preprocessing, analysis (or optimization), and post-processing, similar to that in typical commercial CAE software. The graphical user interface of the toolbox is shown in Fig. 10. Furthermore, the program is parallelized using distributed parallel computing to remarkably speed up the optimization [12].

5 Numerical Examples

The validity of TSMM has been demonstrated by a detailed auto-body finite element model in the literature [12]. In this section, numerical examples of both level 1 and 2 optimization are carried out.

Fig. 11
figure 11

Convergence curve of the fitness function in level-1 optimization

Full size image

5.1 Level-1 Optimization

In level-1 optimization, the topology and joint properties for the geometrical model (Fig. 2) are given. Considering actual auto-body structures, symmetry, and the removal of unnecessary design variables, members 18, 19, and 20 are determined to share the same cross-section properties, as are member pairings (25, 26), (27, 28), (41, 42), (44, 45), and (47, 48). Therefore, the total number of variables is \(3\times 41=123\). All the design variables are defined as continuous variables in this study. Table 1 lists the cross-sectional size bounds and optimal values, where “LB” and “UB” signify lower and upper bounds, respectively, and “OPM” signify the optimum. The allowable limit values for the constraints, specifically, \(\delta \), \(\phi \), and \(\mathrm{freq}\), are set as 0.8000 mm, \(0.1800{^{\circ }}\), and 26.6000 Hz, respectively; penalty coefficients \(r_{i}\) (\(i=1,2,3)\) are assigned values of \(10^{2}\), \(3\times 10^{3}\), and 0.8, respectively. The convergence curve of the fitness function in level-1 optimization was plotted (Fig. 11). Table 2 lists the performance targets for the BIW structure after level-1 optimization.

5.2 Level-2 Optimization

Table 2 Performance targets after level-1 optimization
Full size table
Fig. 12
figure 12

Initial and optimized cross section of the upper B pillar

Full size image
Table 3 Bounds and optimized values of the design variables
Full size table
Fig. 13
figure 13

Convergence curve of the fitness function from level-2 optimization

Full size image
Table 4 Initial and optimized performance targets of the BIW conceptual structure in level 2 optimization
Full size table

In a level-2 optimization, a vertical support called the upper B pillar is optimized. The initial cross-section drawn by the engineer is shown in Fig. 12, where the units are in millimeters. Table 3 lists the cross-sectional size bounds. The allowable limit values for the constraints, i.e., \({\delta }'\), \({\phi }'\), and \(\text{ freq }'\), are set as 0.7067 mm, \(0.1538{^{\circ }}\) and 26.9705 Hz, respectively, and are outputs from the level-1 optimization (Sect. 5.1). The penalty coefficients \(r_{i}\) (\(i=1-6\)) are assigned values \(3.2\times 10^{2}\), \(8\times 10^{3}\), 10, 10, 10, and 10, respectively. The convergence curve of the fitness function for level-2 optimization is plotted in Fig. 13. From Table 4, the BIW mass decreases by 0.70%, whereas the three performance targets increase by various degrees. Hence, the two-level cross-sectional optimization method is efficient. Figure 12 presents the optimized cross section of the upper B pillar.

It should be noted that between level 1 and level 2 optimization, the cross-sectional shape change is large and abrupt. The cross-sectional dimensions should be preliminarily estimated before setting the cross-sectional size bounds in level 1 optimization, otherwise the feasible solution in level 2 optimization may not be solved properly. As an example, the cross-sectional dimensions of the upper B pillar drawn by the engineer in Fig. 12 are about \(90\times 100\). Thus the dimensions \(90\times 100\) in level 2 optimization should be contained in the size bounds of No. 25 cross section in level 1 optimization, and also the optimized sizes in level 1 optimization should be closed to \(90\times 100\). In Table 1, the final optimized sizes of No. 25 cross section are about \(93\times 111\), thus the two-level cross-sectional optimization can be solved properly.

6 Conclusions

This paper proposed a two-level cross-sectional optimization approach for auto-body forward concept design. The adopted TSMM is more exact than conventional FEM method and was used for the bending stiffness, torsional stiffness and free vibration analyses of BIW. Three manufacturing constraints were considered to promote the optimum solution more practice. Related numerical examples prove that the two-level cross-sectional optimization approach is effective and valid. Distributed parallel computing technique was employed to notably speed up the optimization with speedup ratio of 5.46 times. Consequently, the proposed method and the developed “ABCD” toolbox are able to promote the concept design of auto-body. However, the approach cannot be directly applied to the non-prismatic member. For a non-prismatic member, it should be divided into several prismatic members for structural analysis and optimization.