Neuro-fuzzy system development to estimate the compressive strength of improved high-performance concrete

Abstract

High-performance concrete (HPC) outperforms regular concrete due to incorporating additional components that go beyond the typical ingredients used in standard concrete. Various artificial analytical methods were employed to assess the compressive strength (CS) of high-performance concrete containing fly ash (FA) and blast furnace slag (BFS). The primary objective of this study was to present a practical approach for a comprehensive evaluation of machine learning algorithms in predicting the CS of HPC. The study focuses on utilizing the adaptive neuro-fuzzy inference system (ANFIS) to develop models for predicting HPC characteristics. To enhance the performance of ANFIS methods, the study incorporates the arithmetic optimization algorithm (AOA) and equilibrium optimizer (EO) (abbreviated as ANAO and ANEO, respectively). Notably, this research introduces novelty through the application of the AOA and EO, the evaluation of HPC with additional components, the comparison with prior literature, and the utilization of a large dataset with multiple input variables. The results indicate that the combined ANAO and ANEO systems demonstrated strong estimation capabilities, with R² values of 0.9941 and 0.9975 for the training and testing components of ANAO, and 0.9878 and 0.9929 for ANEO, respectively. The results comparison of this study presented the comprehensiveness and reliability of the created ANFIS model optimized with AOA for predicting the HPC’s CS improved with FA and BFS, which could be applicable for practical usages.

1 Introduction

High-performance concrete ($\mathrm{HPC}$) elements have found widespread application in structures such as large bridges, tall buildings, and dams, known for their exceptional performance (Esmaeili-Falak et al. 2018). Commonly included in the mixture are fly ash, blast furnace slag, and supplementary additives like super-plasticizers (Neville and Aitcin 1998; Leung 2001). The proportions of each ingredient can be adjusted to achieve desired efficiency and strength objectives (Pala et al. 2007). Due to the inherent non-homogeneity of concrete mixes, determining the appropriate mixing ratios and accurately predicting the compressive strength ($\mathrm{CS}$) of concrete poses a challenge. As a result, there has been considerable focus on employing machine learning ($\mathrm{ML}$) techniques to minimize the disparity between predicted and observed outcomes. In the past 20 years, a range of machine learning methodologies has been utilized to develop precise and efficient solutions for predicting the $\mathrm{CS}$ of $\mathrm{HPC}$ and other related fields. Artificial neural networks ($\mathrm{ANNs}$) with fuzzy style (Kasperkiewicz et al. 1995), and multi-layer (Sarıdemir 2009; Lee 2003; Esmaeili-Falak et al. 2019; Aghayari Hir et al. 2022) are the two most popular types, along $\mathrm{NN}$ with single layer (Lai and Serra 1997) and multi-layer (Najafzadeh and Azamathulla 2015; Najafzadeh et al. 2018; Najafzadeh and Saberi-Movahed 2019).

Yeh (1998a, 2006) provided a laboratory dataset of 1030/1133 individual tests conducted on $\mathrm{HPC}$. The dataset included eight dependent parameters and one independent parameter (i.e., $\mathrm{CS}$), representing the mixing percentages. Additional $\mathrm{ML}$ techniques that can be employed to forecast the properties of HPC encompass support vector machine ($\mathrm{SVM}$) (Rafiei et al. 2017; Yan and Shi 2010; Wu and Zhou 2022a), computational ensemble approaches such as random forest ($\mathrm{RF}$) (Han et al. 2019; Dawei et al. 2023), boosting smooth transition regression trees (Anyaoha et al. 2020; Zhu et al. 2022) or other methods (Wu and Zhou 2022b; Benemaran 2023). Some researchers have explored the combination of $\mathrm{ANNs}$ with fuzzy logic (Topcu and Sarıdemir 2008; Zarandi et al. 2008; Masoumi et al. 2020), regression analysis (Atici 2011), or a variety of algorithms including $\mathrm{SVM}$, $\mathrm{ANNs}$, and linear regression (Chou and Pham 2013; Chou and Tsai 2012). Young et al. (Young et al. 2019) employed $\mathrm{NN}$, gradient boosting ($\mathrm{GB}$), $\mathrm{RF}$, and $\mathrm{SVM}$ models to predict the $\mathrm{CS}$ of over 10,000 specimens. The study aimed to incorporate the actual mixtures and consider their industrial significance. Newer publications (Asteris et al. 2021; Nguyen et al. 2021a) provide insights into $\mathrm{ML}$ models that are often referred to as black box techniques. These models do not explicitly reveal the process of combining inputs to generate forecasts, yet they offer advantages such as high sensitivity, simplicity, and robustness. Due to the lack of a clear correlation between the $\mathrm{CS}$ and the input variables, utilizing them poses a significant challenge. To address this issue, various intricate mathematical theories have been developed to establish a connection. Yeh and Lien (2009) introduced a genetic operation tree approach that combined an operation tree with a genetic method to compute the $\mathrm{CS}$. Capitalizing on the advantages of $\mathrm{ANNs}$, researchers have integrated them with genetic programming ($\mathrm{GEP}$) (Chopra et al. 2016; Baykasoğlu et al. 2004) or fuzzy logic (Akkurt et al. 2004). However, it is worth mentioning that the detailed equations utilized in the mathematical formulations presented in these articles might be intricate and demanding to grasp. Linear, non-linear, and meta-heuristic regression approaches (Le-Duc et al. 2020; Chou et al. 2016) leverage the correlation coefficients of the factor percentages to predict the $\mathrm{CS}$. These diverse approaches offer various methods for estimating $\mathrm{CS}$. Bharatkumar et al. (2001) explored the impact of water content and mineral additions on the mixture design method of $\mathrm{HPC}$. Bhanja and Sengupta (2002) identified the correlation between water-to-cement ($W/C$) ratio, silica fume ($\mathrm{SF}$) substitution rates, and the $\mathrm{CS}$. Namyong et al. (2004) developed a regression method to predict the $\mathrm{CS}$ of conventional concrete. Zain and Abd (2009) aimed to forecast the strength of $\mathrm{HPC}$ using a multiple non-linear regression approach. Considering that laboratory samples may involve errors in the combination percentages and testing procedures, it becomes crucial to incorporate unknown factors into the classification algorithm (Young et al. 2019). The adaptive neuro-fuzzy inference system ($\mathrm{ANFIS}$) offers several advantages, including flexibility, universal approximation, and learning capability (Campo et al. 2011; Mittal et al. 2011; Chen et al. 2018). $\mathrm{ANFIS}$ enables the generation of flexible rules and the modeling of complex systems using linguistic variables and if–then rules. This makes it particularly suitable for domains where interpretability is crucial. $\mathrm{ANFIS}$ possesses the capability to approximate continuous functions with high precision. It employs a hybrid learning algorithm that merges gradient descent and least-squares estimation. This unique approach allows $\mathrm{ANFIS}$ to learn from data and optimize its parameters, rendering it suitable for a wide range of learning tasks, both supervised and unsupervised. Modern optimization algorithms utilize advanced search strategies and mechanisms to enhance both exploration and exploitation of the search space. Unlike older evolutionary optimizers, which may face difficulties in handling complex optimization problems characterized by high-dimensional search spaces, non-linear relationships, constraints, or multimodal landscapes, novel optimization algorithms are specifically designed to tackle such challenges. These new algorithms often incorporate mechanisms to improve robustness in the presence of noise or uncertainty in problem environments. Moreover, many novel optimization methods offer a high level of customization and flexibility, allowing them to be adapted to various problem domains (Sarkhani Benemaran et al. 2020; Esmaeili-Falak and Hajialilue-Bonab 2012; Moradi et al. 2020).

The primary objective of this study is to present a practical approach for a comprehensive evaluation of machine learning algorithms in predicting the $\mathrm{CS}$ of $\mathrm{HPC}$. The study focuses on utilizing the $\mathrm{ANFIS}$ to develop models for predicting $\mathrm{HPC}$ characteristics. To enhance the performance of $\mathrm{ANFIS}$ methods, the study incorporates the arithmetic optimization algorithm ($\mathrm{AOA}$) and Equilibrium optimizer ($\mathrm{EO}$), using a dataset of 1030 test samples, 8 input parameters, and $\mathrm{CS}$ as the target prediction variable. The obtained results are then compared with existing literature findings. Notably, this research introduces novelty through the application of the $\mathrm{AOA}$ and $\mathrm{EO}$, the evaluation of $\mathrm{HPC}$ with additional components, the comparison with prior literature, and the utilization of a large dataset with multiple input variables. These aspects contribute to advancing the understanding of predicting mechanical properties in $\mathrm{HPC}$ and provide a fresh approach for optimizing the performance of predictive models.

The innovativeness of this paper lies in several aspects:

• The researchers introduce and apply two optimization algorithms, namely the $\mathrm{AOA}$ and the $\mathrm{EO}$, to enhance the performance of the $\mathrm{ANFIS}$ for predicting the $\mathrm{CS}$ of $\mathrm{HPC}$. These algorithms may not have been widely used in this specific context before, and their incorporation demonstrates the potential for improving the accuracy of the predictive models.

• Evaluating the $\mathrm{CS}$ of $\mathrm{HPC}$ with these additional components adds novelty to the research, as it explores how different ingredients impact the concrete’s properties. This examination is crucial in understanding how to optimize $\mathrm{HPC}$ for specific applications.

• The primary objective of the research is to provide a practical approach for comprehensively evaluating machine learning algorithms for predicting the c $\mathrm{CS}$ of $\mathrm{HPC}$. While $\mathrm{ANFIS}$ is used as the main algorithm, the paper might explore and discuss the results obtained from other machine learning algorithms as well, contributing to a broader understanding of their effectiveness in this specific domain.

• The paper emphasizes the practical usages of the developed $\mathrm{ANFIS}$ models optimized with $\mathrm{AOA}$ and $\mathrm{EO}$ for predicting the $\mathrm{CS}$ of $\mathrm{HPC}$ improved with fly ash and blast furnace slag. By demonstrating the models’ effectiveness for real-world applications, the study provides actionable insights that can be directly implemented in the construction industry.

2 Methodology

2.1 Data

Larger than 1000 $\mathrm{HPC}$ specimens, which were applied in publications (Dawei et al. 2023; Anyaoha et al. 2020; Zhu et al. 2022; Wu and Zhou 2022b; Benemaran 2023), have been evaluated in this study (Yeh 2006, 1998a, b, 1999, 2003). All the instances were created using ordinary Portland cement ($\mathrm{OPC}$) and were then left to dry naturally. So far, the existing literature on $\mathrm{HPC}$ testing data has employed various types and sizes of samples. The compressive strength of $\mathrm{HPC}$ is determined based on eight variables: cement content (C), blast furnace slag to cement ratio ($\mathrm{BFS}/$C), fly ash to cement ratio ($\mathrm{FA}/$C), water-to-cement ratio ($\mathrm{W}/C$), superplasticizer to cement ratio ($\mathrm{SP}/$C), coarse aggregate to cement ratio ($\mathrm{CAG}/C$), fine aggregate to cement ratio ($\mathrm{FAG}/$C), and the curing time of HPC ($\mathrm{AC}$). In the database, Table 1 illustrates the ranges of these components, while Fig. 1 exhibits the distribution graphs for both the training and testing datasets.

Table 1 The value of statistical indices of inputs and goal

Fig. 1

The distribution of the variables

The dataset consisting of 1030 entries was divided into two sets: the training set accounted for 70% of the data, while the remaining 30% constituted the testing set. The selection of these subgroups from the source data was done randomly using a uniform distribution (Sarkhani Benemaran et al. 2022). Although previous publications (Leema et al. 2016; Khorsheed and Al-Thubaity 2013) suggested using various other train/test ratios, a 70/30 ratio for training/testing groups was employed in this investigation. The range of all input variables was found to be extensive. Through statistical analysis, it was demonstrated that the selection of these input variables was appropriate, as no significant overlap was observed in the eight-dimensional input space (Yeh 2006, 1998a, b, 1999, 2003). This is crucial for training $\mathrm{AI}$ systems with robust generalization capabilities.

Researchers utilized Eq. (1) to apply the Pearson correlation coefficient (${P}_{\mathrm{CC}}$):

$${\sigma }_{y, z}=\frac{\mu (y,z)}{{\delta }_{y}{\delta }_{z}}.$$

(1)

In Eq. (1), $\mu \left(y,z\right)$, ${\delta }_{y}$, and ${\delta }_{z}$ show the covariance between $y$ and $z$, the standard deviation of $y$, and the standard deviation of $z$. The ${P}_{\mathrm{CC}}$ values between the input and output parameters are depicted in Fig. 2. If there are significant positive or negative influences from ${P}_{\mathrm{CC}}$ that play a major role, the study’s failure to clarify the impact of these influences on the results might indicate a deficiency in the methodology employed. Several ${P}_{\mathrm{CC}}$ values were below 0.531, suggesting that these particular values are unlikely to be the primary source of the multicollinearity issues. The interplay between various variables is evident, with significant mutual influences observed (above a threshold of 0.641). The strongest correlation, at a value of 0.942, is observed between $\mathrm{CAG}/C$ and $\mathrm{FAG}/C$. In addition, there are notable negative correlations that may pose challenges during the prediction process. The most pronounced adverse associations are found between $C$ and $\mathrm{CAG}/C$, with a correlation of − 0.923.

Fig. 2

${P}_{\mathrm{CC}}$ matrix

2.2 Applied methods

2.2.1 Arithmetic optimization algorithm ($\mathrm{AOA}$)

A novel meta-heuristic approach called the $\mathrm{AOA}$ was put out in 2021 (Abualigah et al. 2021). As suggested by the name, the location updating formulas for finding the universal optimization answer represent four conventional arithmetic operators: multiplication operator ($M$), division operator ($D$), addition operator ($A$), and subtraction operator ($S$). The multiplication ($M$) and division ($D$) are employed for the exploratory search, providing enormous steps in the search area based on the various impacts of these four arithmetic operators. In addition, the exploitation search—which may produce tiny stage sizes in the search space—is executed using the addition ($A$) and subtraction ($S$) operations. Figure 3 displays the $\mathrm{AOA}$’s thorough optimization method.

Fig. 3

Location updating procedure of search agents in $\mathrm{AOA}$ and impacts of $\mathrm{MOA}$ on it (Abualigah et al. 2021)

The mathematical formulas for exploration and exploitation manners are given by the subsequent formulae, as shown in Fig. 3:

$$\begin{aligned} & {X}_{i}\left(t+1\right)=\left\{\begin{array}{l}{X}_{b}\left(t\right)\div \left(\mathrm{MOP}+\mathrm{eps}\right) \left(\left(\mathrm{UB}-\mathrm{LB}\right)\right.\\\quad\left.\times \mu +\mathrm{LB}\right), {\mathrm{rand}}<0.5\\ {X}_{b}\left(t\right)\times {\mathrm{MOP}}\times \left(\left(\mathrm{UB}-\mathrm{LB}\right)\times \mu +\mathrm{LB}\right), {\mathrm{rand}}\ge 0.5\end{array},\right.\end{aligned}$$

(2)

$$\begin{aligned}& {X}_{i}\left(t+1\right)=\left\{\begin{array}{l}{X}_{b}\left(t\right)-{\mathrm{MOP}}\times \\\left(\left(\mathrm{UB}-\mathrm{LB}\right)\times \mu \right.\\\left.+\mathrm{LB}\right), {\mathrm{rand}}<0.5\\ {X}_{b}\left(t\right)+{\mathrm{MOP}}\times \left(\left(\mathrm{UB}-\mathrm{LB}\right)\right.\\\left.\times \mu +\mathrm{LB}\right), {\mathrm{rand}}\ge 0.5\end{array}\right..\end{aligned}$$

(3)

Based on these equations, the recently produced location is denoted by ${X}_{i}\left(t+1\right)$. And in the ${t}$th iteration, search factors discovered the optimal spot at ${X}_{b}\left(t\right)$. To guarantee the dividend is positive, $\mathrm{eps}$ is a very modest positive value. A constant coefficient is $\mu$. The upper and lower border are denoted by $\mathrm{UB}$ and $\mathrm{LB}$. A random number evenly divided between 0 and 1 is called “$\mathrm{rand}$”. A crucial non-linear coefficient dropped from 1 to 0 simultaneously with the iterations is the math optimizer probability ($\mathrm{MOP}$). Moreover, here is the $\mathrm{MOP}$ computation expression:

$$\mathrm{MOP}=1-{\left(\frac{t}{T}\right)}^{\frac{1}{\alpha }}.$$

(4)

In Eq. (4), $\alpha$ stands for the constant that is fixed as 5 in $\mathrm{AOA}$, and $T$ denotes the iterations’ highest number.

The math optimizer accelerated ($\mathrm{MOA}$) used to balance exploration, and exploitation is also a crucial $\mathrm{AOA}$ parameter. The $\mathrm{MOA}$ is determined using the following equation:

$$\mathrm{MOP}\left(t\right)=\mathrm{Min}+t\times \left(\frac{\mathrm{Max}-\mathrm{Min}}{T}\right).$$

(5)

Based on this equation, $\mathrm{Max}$ and $\mathrm{Min}$ show the $\mathrm{MOA}$’s highest and lowest values. When the $\mathrm{AOA}$ begins to function, the exploration search—that is, multiplication ($M$) or division ($D$)—will be chosen and carried out if a random integer (among 0 and 1) is larger than the $\mathrm{MOA}$. If not, the addition ($A$) or subtraction ($S$) exploitation search will be carried out. The likelihood of local searches by search factors will rise as the number of iterations rises. In Algorithm 1, the pseudo-code for $\mathrm{AOA}$ is displayed.

2.2.2 Equilibrium optimizer ($\mathrm{EO}$)

As mentioned in Faramarzi et al. (2020), $\mathrm{EO}$ is a new and potential method since it produces outputs that are more precise than those of previous methods. In order to obtain the ideal hub heights for the wind turbines, it will be used here.

Control volume mass balance models are the foundation of $\mathrm{EO}$. It is used to calculate the equilibrium and dynamic states in that each particle’s concentration serves as a search factor. To achieve the optimal outcome (equilibrium state), the concentrations, as given in Eq. (6), are arbitrarily updated for every search agent about the optimal answers (equilibrium options):

$$\mathrm{CON}=\mathrm{COeq}+\left(\mathrm{CON}1-\mathrm{COeq}\right)\times f+\frac{g}{\lambda \times vo}\left(1-f\right).$$

(6)

Based on this equation, $f$ denotes an exponential term, $\mathrm{CON}1$ represents the beginning concentration, $g$ indicates the mass generation level, $\lambda$ stands for the turnover level, and $vo$ defines the control volume. $\mathrm{COeq}$ is the concentration in the equilibrium state.

The following three steps (Faramarzi et al. 2020) may be used to briefly summarize the $\mathrm{EO}$ method:

• Initializing and assessing the function which starts the population is the first stage. Equation (7), which describes the initialization in the observed area using a standard arbitrary initialization, depends on the dimensions and particle counts. ${C\mathrm{in}}_{j}$ stands for the particle $j$’s concentration vector, $C\mathrm{min}$ for the dimension’s lowest value and $C\mathrm{max}$ for its highest value, and ${\mathrm{rand}}_{j}$ for the particle $j$’s random vector, where $k$ is the particles count:

  $${C\mathrm{in}}_{j}=C\mathrm{min}+{\mathrm{rand}}_{j}\left(C\mathrm{max}-C\mathrm{min}\right) \quad \mathrm{for} \; j=\mathrm{1,2},\dots ,K.$$

  (7)

• The equilibrium pool and the options chosen from the population are covered in the second stage. In addition to the particle with the mean of the finest parts, the top four equilibrium options are also utilized. Using these five equilibrium possibilities, as shown in Eq. (8), the exploration and exploitation phases may be enhanced:

  $$C\mathrm{pool}=\left[\mathrm{COeq}1,\mathrm{COeq}2,\mathrm{COeq}3,\mathrm{COeq}4,\mathrm{COeq}(\mathrm{ave})\right].$$

  (8)

• The $\mathrm{EO}$ will adjust the concentration in the third stage to achieve an appropriate balance between exploration and exploitation. The following formula is a description of the procedure for updating the $\mathrm{EO}$ formula:

  $$\overrightarrow{\mathrm{CON}}=\overrightarrow{\mathrm{COeq}}+\left(\overrightarrow{\mathrm{CON}}-\overrightarrow{\mathrm{COeq}}\right)\times \overrightarrow{f}+\frac{\overrightarrow{g}}{\overrightarrow{\lambda }\times vo}\left(1-\overrightarrow{f}\right).$$

  (9)

Based on Eq. (9), $\overrightarrow{\mathrm{CON}}$ stands for the adjusted locations.

2.2.3 Adaptive neuro-fuzzy inference system ($\mathrm{ANFIS}$)

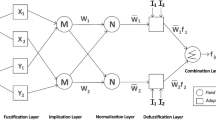
Fuzzy systems and neural networks are combined in the $\mathrm{ANFIS}$ model. Jang’s idea (Jang 1993) was used to address a variety of issues, notably forecasting and time series prediction. The “$\mathrm{IF}{-}\mathrm{THEN}$ rules” are used in the $\mathrm{ANFIS}$’s fundamental framework to produce the “Takagi–Sugeno inference model,” which generates input and output mappings.

Figure 4 depicts the fundamental organization of the $\mathrm{ANFIS}$, with $x$ and $y$ standing in for Layer 1 inputs and ${L}_{1i}$ for the node $i$’s output. One definition of this is

Fig. 4

Architecture schematics for $\mathrm{ANFIS}$

$${L}_{1i}={\mu }_{{A}_{i}}\left(x\right), i=\mathrm{1,2}, {L}_{1i}={\mu }_{{B}_{i-2}}\left(y\right), i=\mathrm{3,4},$$

(10)

$$\mu \left(x\right)={e}^{-{\left(\frac{x-{\rho }_{i}}{{\alpha }_{i}}\right)}^{2}}.$$

(11)

In these equations, ${A}_{i}$ and ${B}_{i}$ denote the membership values of the generalized Gaussian membership function, or $\mu$, furthermore ${\rho }_{i}$ and ${\alpha }_{i}$ stand for the premise variable set.

Layer 2’s result is calculated as follows:

$${L}_{2i}={\mu }_{{A}_{i}}\left(x\right)\times {\mu }_{{B}_{i-2}}\left(y\right).$$

(12)

Layer 3’s result is computed as follows:

$${L}_{3i}=\overline{{w }_{i}}=\frac{{\omega }_{i}}{\sum_{(i=1)}^{2}{\omega }_{i}}.$$

(13)

In this equation, ${w}_{i}$ stands for the ${i}$th result of layer number 2. Moreover, layer 4’s result is determined as follows:

$${L}_{4,i}=\overline{{w }_{i}}{f}_{i}=\overline{{w }_{i}}\left({p}_{i}x+{q}_{i}y+{r}_{i}\right).$$

(14)

In the abovementioned equation, a function denoted by the $f$ relies on the network’s input and variables. In addition, the terms ${p}_{i}$, ${r}_{i}$, and ${q}_{i}$ stand for the node I’s subsequent variables.

Eventually, $F$ and $\overline{{w }_{i}}$ (those stated in Eq. (13)), as described by Eq. (15), may be used to construct the result. Layer 5:

$${L}_{5}=\sum_{i}\overline{{w }_{i}}{f}_{i}.$$

(15)

In the $\mathrm{ANFIS}$ method, two essential factors are the steady and mean values of the input and output membership functions (Hussein 2016). Typically, gradient-based techniques are employed to adjust these parameters in $\mathrm{ANFIS}$. However, a major drawback of these methods is that they often get stuck in local optima, resulting in slow convergence rates (Bayat et al. 2019). To address this issue, optimization algorithms offer a valuable solution.

2.3 Performance indices

To evaluate the usefulness of $\mathrm{ANAO}$, and $\mathrm{ANEO}$ systems, six metrics were computed and compared (Wu and Zhou 2023; Esmaeili-Falak and Sarkhani Benemaran 2023). The following metrics were computed as appropriate metrics to gain this objective (Eqs. (16–21)):

• Coefficient of determination (${R}^{2}$)

  $${R}^{2}={\left(\frac{{\sum }_{p=1}^{P}\left({t}_{P}-\overline{t }\right)\left({y}_{P}-\overline{y }\right)}{\sqrt{\left[{\sum }_{p=1}^{P}{\left({t}_{P}-\overline{t }\right)}^{2}\right]\left[{\sum }_{p=1}^{P}{\left({y}_{P}-\overline{y }\right)}^{2}\right]}}\right).}^{2}$$

  (16)

• Root mean squared error ($\mathrm{RMSE}$)

  $$\mathrm{RMSE}=\sqrt{\frac{1}{P}\sum\limits_{p=1}^{P}{\left({y}_{p}-{t}_{p}\right)}^{2}.}$$

  (17)

• Mean absolute error ($\mathrm{MAE}$)

  $$\mathrm{MAE}=\frac{1}{P}\sum\limits_{p=1}^{P}\left|{y}_{p}-{t}_{p}\right|,$$

  (18)

• ${A}_{20-\mathrm{Index}}$

  $${A}_{20{\text{-Index}}}=\frac{{m}_{20}}{M}.$$

  (19)

• Relative absolute error ($\mathrm{RAE}$)

  $$\mathrm{RAE}=\frac{\sum_{p=1}^{P}\left|{y}_{p}-{t}_{p}\right|}{\sum_{p=1}^{P}\left|{y}_{p}-\overline{y }\right|}.$$

  (20)

• Root relative squared error ($\mathrm{RRSE}$)

  $$\mathrm{RRSE}=\sqrt{\frac{\sum_{p=1}^{P}{({y}_{p}-{t}_{p})}^{2}}{\sum_{p=1}^{P}{({y}_{p}-\overline{y })}^{2}},}$$

  (21)

  where, correspondingly, ${y}_{P}$, ${t}_{P}$, $\overline{t }$, and $\overline{y }$ are the goal, forecasted values, and the mean of the goal and forecasted of them. Here, $M$ is the sample count, and ${m}_{20}$ is the sample count with $\mathrm{Meas}./\mathrm{Est}.=0.8-1.2$.

3 Results and discussion

3.1 Development process

For modeling the $\mathrm{ANAO}$ and $\mathrm{ANEO}$, a beginning $\mathrm{ANFIS}$ model was proposed for the initial stage; then, the $\mathrm{AOA}$ and $\mathrm{EO}$ algorithms were introduced for optimizing the developed $\mathrm{ANFIS}$ model. In this task, the variables of membership functions of the produced $\mathrm{ANFIS}$ were trained (optimized) using the optimization algorithms. Herein, $\mathrm{RMSE}$ was utilized as a fitness function to evaluate the accuracy of the optimization procedure for the $\mathrm{ANAO}$ and $\mathrm{ANEO}$ models. Finally, the optimum $\mathrm{ANAO}$ and $\mathrm{ANEO}$ models were determined with the number of fuzzy terms and the highest iterations, as shown in Table 2.

Table 2 Control parameters of algorithms

3.2 Analysis

This paper presents the results of the single $\mathrm{ANFIS}$ and hybrid $\mathrm{ANAO}$ and $\mathrm{ANEO}$ designs in order to forecast the $\mathrm{CS}$ of the $\mathrm{HPC}$ system enhanced with $\mathrm{BFS}$ and $\mathrm{FA}$. By combining the crucial elements in the appropriate ratios, as mentioned earlier, the performance of $\mathrm{ANFIS}$ can be improved. The training and testing phases of the generated $\mathrm{ANAO}$ and $\mathrm{ANEO}$ systems are depicted in Fig. 5, illustrating the observed and calculated values of the $\mathrm{CS}$ of the $\mathrm{HPC}$. Furthermore, when the percentage error in $\mathrm{CS}$ concentration is plotted on a graph, a bell-shaped distribution of curves is observed, with the central point of the distribution aligning with the zero-error percentage line. The effectiveness of the single $\mathrm{ANFIS}$ and hybrid $\mathrm{ANAO}$ and $\mathrm{ANEO}$ in making accurate forecasts of $\mathrm{HPC}$’s $\mathrm{CS}$ was evaluated using various metrics, including ${R}^{2},$ $\mathrm{RMSE}$, $\mathrm{MAE},$ $\mathrm{RAE}$, $\mathrm{RRSE}$ and ${A}_{20{\text{-Index}}}$ (refer to Table 3). The results indicate that both $\mathrm{ANAO}$ and $\mathrm{ANEO}$ show great potential in delivering precise forecasts of $\mathrm{HPC}$’s $\mathrm{CS}$ compared to single $\mathrm{ANFIS}$.

Fig. 5

The conclusions of the $\mathrm{ANFIS}$ models, a $\mathrm{ANAO}$, b $\mathrm{ANEO}$

Table 3 Performance of the created models

One aspect of this study focuses on evaluating the efficacy of multiple iterations of the statistical identifiers ($\mathrm{ANFIS}$, $\mathrm{ANAO},$ and $\mathrm{ANEO}$) developed for the published studies. The findings of this inquiry were also subject to objective evaluation in comparison to other published studies. The results indicate that the combined $\mathrm{ANAO}$ and $\mathrm{ANEO}$ systems demonstrated strong estimation capabilities, with ${R}^{2}$ values of 0.9941 and 0.9975 for the training and testing components of $\mathrm{ANAO}$, and 0.9878 and 0.9929 for $\mathrm{ANEO}$, respectively. In order to identify the optimal approach, it is essential to examine and evaluate the generated signals thoroughly. When comparing the $\mathrm{ANEO}$, it was observed that the $\mathrm{ANAO}$ $\mathrm{RMSE}$ value decreased during training, decreasing from 1.9571 to 1.3588 $\mathrm{MPa}$. The testing results indicated a modest decline from 1.1351 to 0.6662 $\mathrm{MPa}$. Likewise, the $\mathrm{MAE}$, $\mathrm{RAE}$, and $\mathrm{RRSE}$ metrics yielded consistent results as the $\mathrm{RMSE}$, indicating that the $\mathrm{ANAO}$ exhibited greater proficiency in $\mathrm{CS}$ estimation. The $\mathrm{RRSE}$ values further supported this, with the $\mathrm{ANAO}$ achieving 0.0767 $\mathrm{MPa}$ for ${\mathrm{RRSE}}_{\mathrm{Train}}$ and 0.0496 $\mathrm{MPa}$ for ${\mathrm{RRSE}}_{\mathrm{Test}}$, which were lower compared to the $\mathrm{ANEO}$’s values of 0.1105 $\mathrm{MPa}$ for ${\mathrm{RRSE}}_{\mathrm{Train}}$ and 0.0845 $\mathrm{MPa}$ for ${\mathrm{RRSE}}_{\mathrm{Test}}$. Similar outcomes were observed for the ${A}_{20-\mathrm{Index}}$ signal, with a roughly 2% increase in both the training and testing sections for $\mathrm{ANAO}$. The analysis of $\mathrm{ANFIS}$ by itself as well depicts acceptable performance, where its effectiveness was improved by linking with optimization algorithms.

The estimates provided here were developed after comparing several different methods, including Gene Expression Programming ($\mathrm{GEP}$) (Mousavi et al. 2012), Semi-Empirical Method ($\mathrm{SEM}$) (Nguyen et al. 2021b), Gaussian Process Regression ($\mathrm{GPR}$) (Dao et al. 2020), artificial neural networks ($\mathrm{ANN}$) (Chou and Pham 2013), Multi-Gene Genetic Programming ($\mathrm{MGGP}$) (Gandomi and Alavi 2012), and Extreme Gradient Boosting ($\mathrm{XGB}$) (Lee et al. 2022). Upon examining the table, it becomes evident that our proposed $\mathrm{ANAO}$ outperformed the previous studies documented in the literature. $\mathrm{SEM}$ (Nguyen et al. 2021b) performed poorly when compared to $\mathrm{ANAO}$, with ${R}^{2}$ of 0.84 vs 0.9941, $\mathrm{RMSE}$ of 6.3 $MPa$ vs 1.3588 $MPa$, $MAE$ of 4.91 $MPa$ vs 0.4255 $MPa$, and ${A}_{20-\mathrm{Index}}$ of 0.68 vs 0.9958 $\mathrm{MPa}$. For example, $\mathrm{GEP}$ (Mousavi et al. 2012) demonstrated a much higher $\mathrm{MAE}$ and a slightly lower ${R}^{2}$ when compared to $\mathrm{ANAO}$ (by 0.8224 and 5.202, respectively). The newest technique, $\mathrm{XGB}$ (Lee et al. 2022), came close to overtaking $\mathrm{ANAO}$ but eventually fell short. Other techniques, such $\mathrm{MGGP}$ (Gandomi and Alavi 2012) and $\mathrm{ANN}$s (Chou and Pham 2013), performed worse than $\mathrm{ANAO}$, with ${R}^{2}$ values that are much lower than 0.9862, at 0.8046 and 0.8469, respectively. The $\mathrm{ANAO}$ also outperformed the $\mathrm{GPR}$ in terms of ${R}^{2}$, $\mathrm{RMSE}$, and $\mathrm{MAE}$ (Nguyen et al. 2021a). The $\mathrm{ANAO}$ structure, which was first created to represent $\mathrm{HPC}$’s $\mathrm{CS}$ and improved with $\mathrm{FA}$ and $\mathrm{BFS}$, is recommended for usage in this situation.

While the research described in the paper shows promising results in predicting the compressive strength of high-performance concrete (HPC) containing fly ash and blast furnace slag using machine learning techniques, there are several remaining issues that need to be addressed before its practical application.

The study used additional components such as fly ash and blast furnace slag, but the practical application may involve HPC mixtures with varying types and proportions of supplementary materials. The model needs to be validated for different combinations of ingredients and proportions to ascertain its effectiveness across a wide range of HPC mixtures. The model should be tested for its ability to predict compressive strength not only for the specific HPC mixtures used in the study but also for new and untested mixtures or conditions that may not be well-represented in the training dataset.

Practical implementation of the model requires assessing the cost–benefit trade-offs associated with using machine learning predictions compared to traditional testing methods. A thorough cost–benefit analysis can help justify the adoption of the proposed model in real-world scenarios.

HPC structures are often designed for long-term use, and their performance over time is critical. The research might have focused on predicting compressive strength at a particular point in time. However, the practical application of the model would require understanding how the HPC’s properties and strength evolve over extended periods, considering factors such as aging, environmental exposure, and durability.

4 Conclusions

The primary objective of this study is to present a practical approach for a comprehensive evaluation of machine learning algorithms in predicting the $\mathrm{CS}$ of $\mathrm{HPC}$. The study focuses on utilizing the single and hybrid $\mathrm{ANFIS}$ models to develop models for predicting $\mathrm{HPC}$ characteristics. Notably, this research introduces novelty through the application of the $\mathrm{AOA}$ and $\mathrm{EO}$, the evaluation of $\mathrm{HPC}$ with additional components, the comparison with prior literature, and the utilization of a large dataset with multiple input variables. These aspects contribute to advancing the understanding of predicting mechanical properties in $\mathrm{HPC}$ and provide a fresh approach for optimizing the performance of predictive models.

• The results indicate that the combined $\mathrm{ANAO}$ and $\mathrm{ANEO}$ systems demonstrated strong estimation capabilities, with ${R}^{2}$ values of 0.9941 and 0.9975 for the training and testing components of $\mathrm{ANAO}$, and 0.9878 and 0.9929 for $\mathrm{ANEO}$, respectively.

• When comparing the $\mathrm{ANEO}$, it was observed that the $\mathrm{ANAO}$ $\mathrm{RMSE}$ value decreased during training, decreasing from 1.9571 to 1.3588 $\mathrm{MPa}$. The testing results indicated a modest decline from 1.1351 to 0.6662 $\mathrm{MPa}$. Likewise, the $\mathrm{MAE}$, $\mathrm{RAE}$, and $\mathrm{RRSE}$ metrics yielded that the $\mathrm{ANAO}$ exhibited greater proficiency in $\mathrm{CS}$ estimation. The $\mathrm{RRSE}$ values further supported this, with the $\mathrm{ANAO}$ achieving 0.0767 $\mathrm{MPa}$ for ${\mathrm{RRSE}}_{\mathrm{Train}}$ and 0.0496 $\mathrm{MPa}$ for ${\mathrm{RRSE}}_{\mathrm{Test}}$, which were lower compared to the $\mathrm{ANEO}$’s values of 0.1105 $\mathrm{MPa}$ for ${\mathrm{RRSE}}_{\mathrm{Train}}$ and 0.0845 $\mathrm{MPa}$ for ${\mathrm{RRSE}}_{\mathrm{Test}}$. Similar outcomes were observed for the ${A}_{20-\mathrm{Index}}$ signal, with a roughly 2% increase in both the training and testing sections for $\mathrm{ANAO}$.

• The results comparison of this study with the literature presents the comprehensiveness and reliability of the created $\mathrm{ANFIS}$ model optimized with $\mathrm{AOA}$ for predicting the $\mathrm{HPC}$’s $\mathrm{CS}$ improved with $\mathrm{FA}$ and $\mathrm{BFS}$, which could be applicable for practical usages.

• The type and number of parameters play a crucial role in constructing algorithms frameworks. By gathering additional data from various initiatives, it becomes possible to reduce limitations on future studies and gain a clearer understanding of the adaptability of the models used to evaluate the $\mathrm{CS}$. The concept of employing innovative optimization approaches to improve the performance of computational models leads to the creation of a distinct generation of models that can be applied in diverse contexts. In this research, an $\mathrm{AOA}$ and $\mathrm{EO}$ techniques were employed to optimize the structure of the basic $\mathrm{ANFIS}$ model. Each optimization strategy contains unique and practical elements that require parametric analysis to achieve the optimal condition. Therefore, by utilizing different optimization methods, it becomes possible to eliminate this constraint.