Abstract
In this paper, a novel three-port Wilkinson power divider (WPD) with a compact size is designed and fabricated. New stepped impedance transmission lines, and two-part resonators between the input and output ports are used to suppress harmonics up to the ninth order and achieve a smaller size than a conventional power divider (75% size reduction) based on quarter-wavelength transmission lines. The characteristics of the transmission lines and resonators are obtained using an even and odd analysis. The results show that the S21 is about − 3.015 dB, the input return loss (S11) is better than − 24 dB, and at a central frequency of 2.6 GHz, harmonics are eliminated as far as the 9th order.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
One of the essential circuits in telecommunication systems is power dividers (PDs) used in many components such as antennas, phase shifters, power amplifiers, etc. Usually, three-port networks have loss-matching networks. To solve this problem, the resistance between output ports is used to increase isolation. Conventional Wilkinson power divider has drawbacks such as low fractional bandwidth (FBW), large size, and inability to eliminate high-frequency harmonics. Researchers have recently tried to improve performance and reduce PD size (Pozar 2011; Zonouri and Hayati 2021; Imani et al. 2020; Pouryavar et al. 2018; Imani et al. 2019; Zhang et al. 2021a; Hayati et al. 2023; Jamshidi et al. 2021; Sattari et al. 2023; Roshani et al. 2021; Zonouri et al. 2023; Jedkare et al. 2020; Zhang et al. 2013; Li et al. 2017; Zonouri and Hayati 2019; Gai et al. 2017; Lin et al. 2017; Hosseini Tabatabaee et al. 2021; Li et al. 2016; Hao et al. 2023; Zhang et al. 2021b; Roshani et al. 2022; Wilkinson 1960; Zhuang et al. 2018; Zhang et al. 2018; Vaziri et al. 2020; Zhan and Zhao 2017; Tian and Dong 2022; Xiao et al. 2020).
Different resonators and techniques are used in the PD structure, and different methods may be used to design these resonators, such as using a rectangular-shaped resonator (Pouryavar et al. 2018), triangular-shaped resonator (Imani et al. 2019), circular-shaped resonator (Zhang et al. 2021a) modified square resonator (Hayati et al. 2023), or a hybrid design technique (Jamshidi et al. 2021). The study of microstrip circuits has also attracted a lot of attention from academics in recent years, particularly with the use of intelligent approaches like GMDH neural networks (Sattari et al. 2023), multilayer perceptron network (Roshani et al. 2021) and the PSO optimization method (Zonouri et al. 2023).
Semicircular resonators in a symmetrical arrangement are utilized to provide small dimensions and a large pass-band in Jedkare et al. (2020). Nevertheless, the described structure uses spiral lines, making its implementation more difficult than it otherwise would be.
A small PD is introduced in Zhang et al. (2013). In this PD, the required transmission zeros are generated through the design of five resonators, but the high insertion losses and large size are the disadvantages of this design. A dual-band filtering WPD with multi-mode resonators is provided in Li et al. (2017), which can simultaneously divide the power and select the frequency, but suffers from a complex design structure. In (Zonouri and Hayati 2019), a low-pass WPD is provided with suppression of second to eighth-order harmonics with an attenuation level of 20 dB. The isolation at some points of the bandwidth is less than 10 dB.
In (Gai et al. 2017), the uneven distribution of power is clearly shown. The transmission lines' length determines this PD. Any modification to the transmission lines will cause an arbitrary power split between the terminals. The operating frequency of this circuit is 2 GHz. An adjustable WPD is designed and fabricated in Lin et al. (2017). Coupled lines are used in its design. But the large dimensions of the circuit and the disregard for high-frequency harmonics are its weaknesses. In (Hosseini Tabatabaee et al. 2021), the transmission lines of a quarter of the wavelength are replaced by oval and rectangular resonators. The size of the circuit is reduced by about 55% compared to the conventional structure. It also has low insertion loss and attenuates unwanted harmonics. In (Li et al. 2016), a dual-band microstrip Gysel power divider is presented, simultaneously dividing the signal at two frequency bands and two-phase shifts. Transmission line characteristics can control the frequency bands. Also, two isolated and separate areas can be created between the frequency bands with two transmission lines connected to the output ports. As a result, a wide and isolated frequency band is created, and finally, the PD is made from the two presented dual-band structures.
Branch loading was employed in the coupled line in Hao et al. (2023), and by adding a stepped impedance open circuit stub, the filtering performance and pass-band bandwidth were improved, as was the stopband rejection performance. Also, in this structure, bending the microstrip line between the input and output parts has resulted in physical access to the isolation resistance and increased isolation performance between the output ports.
In (Zhang et al. 2021b), a PD is provided that uses a cascaded pair of couple line segments, each loaded with a half-wavelength open-circuit stub. The filter's bandwidth, selectivity, and band stop may all be enhanced by using half-wavelength open-circuit stubs. However, it has a huge size and a complex design.
As an alternative to the original PD branches, in ref Roshani et al. (2022) LC parts are combined together. The proposed new branches have produced a PD scheme that is small and meets the target miniaturization percentage.
Designing a PD with a compact size, low losses, and broad bandwidth remains challenging. To our knowledge, the microstrip WPD design based on two-part resonators has not been reported. Most of them are single-part and, of course, have limited efficiency.
In this paper, a modified Wilkinson power divider using new stepped impedance transmission lines and two-part resonators is designed and presented. Due to the two-part resonator structure, this PD can suppress unwanted harmonics using its wide stopband. It can remove as many as nine unwanted harmonics. Furthermore, it has an operating band with an FBW of 73.3%, which indicates its wide working band. The main novelty of this article is the design of a PD in which two-part and stepped impedance resonators are used, in its layout, for the first time with this geometry. On the other hand, the dimensions of the proposed PD have been reduced by more than 75% compared to the conventional circuit. The rest of the article is structured as follows: the second section details the designed WPD and the associated even and odd mode analysis. The implementation of the microstrip and resonators used is described in Sect. 3. Finally, simulation results and comparisons with previously reported works are discussed. In summary, the WPD design method can be seen in Fig. 1
Flowchart of the WPD design method
2 Design of the stepped impedance WPD
2.1 Conventional WPD
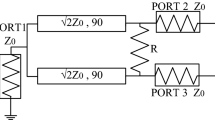
The conventional WPD consists of two transmission lines, shown in Fig. 2. In this structure, each transmission line's characteristic impedance (Z0) and the electrical length (Θ) must be calculated. The conventional WPD consists of two transmission lines in which the characteristic impedance equals \(\sqrt{2}\) Z0 (70.7 Ω), and the electrical length is 1/4 wavelength (90°) (Wilkinson 1960). The conventional WPD is a single frequency with relatively large dimensions, so it cannot be used in most radio frequency circuits today and must be modified.
Conventional WPD circuit diagram (Wilkinson 1960)
2.2 Stepped impedance circuit
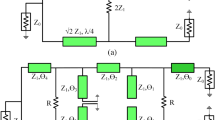
Figure 3a shows the physical 3D circuit of the stepped impedance WPD, and Fig. 3b demonstrates the equivalent stepped impedance WPD circuit. Z0 represents the impedance of the input and output ports, and R is the isolation resistance between the output ports (100 Ω). This design aims to calculate the optimal characteristic impedance of the odd and even mode for each section to reduce the return losses of all ports in the desired bandwidth.
a The physical 3D and b The equivalent circuit of the stepped impedance WPD
2.3 Odd-mode analysis
In the odd-mode sub-structure, Zodd is the equivalent impedance seen from the right, shown in Fig. 4. The odd-mode analysis is calculated step-by-step using the following equations:
Equivalent circuit for the odd mode
Next, the impedance equivalent to the left branch of the circuit is calculated as follows:
where Zodd is the output impedance and could be obtained from (18):
Based on (18), the derived reflection coefficient \({\Gamma }_{out}^{odd}\) in the output ports is calculated as follows:
In this design, like in the conventional WPD structure, the real part of Zo is equal to 50 Ω, and the imaginary part equals zero. Also, the isolation resistance is 100 Ω.
2.4 Even-mode analysis
In the even mode, as shown in Fig. 5, no current flows through resistors R or between the inputs of two transmission lines on port 1. Zeven is the equivalent impedance, which can be calculated as follow:
Equivalent circuit for the even mode
Next, the impedance equivalent to the right branch of the equivalent circuit is obtained as follows:
where Zeven is the input impedance on the left side of Fig. 5 and can be shown as:
According to (39), the reflection coefficient derived at the input port or parameter S11 can be obtained as follows:
So, due to the physical limitation in the implementation of the WPD, Z1, and Z6 are selected to be 168 and 160 Ω, respectively.
2.5 Parameters of the stepped impedance WPD
In the presented structure, the isolation between the output ports of the WPD is considered zero (S23 = 0) and is symmetric for simplicity as well. Therefore, Z1 = Z15, Z6 = Z10, Z2 = Z11, Z2 = Z11, Z3 = Z12, Z4 = Z13, and Z5 = Z14.
In the operating band of the stepped impedance WPD, the return loss is assumed to be greater than 15 dB. Furthermore, in the conventional structure, the characteristic impedance of each transmission line is 70.7Ω, so all the impedances and electrical lengths of the stepped impedance structure can be obtained according to Table 1 (Units are Z, Ω, θ°).
3 Microstrip WPD design
The proposed stepped impedance WPD design approach implements a microstrip waveguide. Microstrip technology is a good choice for implementing microwave filters, power dividers, and couplers. The advantages of using microstrip lines include compact size, low cost, easy fabrication, lightweight, and the ability to integrate them with other microwave circuit elements on a circuit board. Therefore, to implement the stepped impedance circuit, microstrip stubs and resonators are used, in which impedances two-part resonators replace Z2 to Z5 and Z11 to Z14. Stepped impedance resonators substitute the impedances Z7 to Z9.
3.1 Two-part resonators
According to Fig. 6a, two-part resonators have implemented symmetric impedances Z2 to Z5 and Z11 to Z14. In the presented design, the sizes of L2 and W2 are 7.4 and 0.1 mm, respectively, and the result of insertion losses (S21) for dimensions (a) L1 = 3.5 mm, W1 = 1.2 mm, (b) L1 = 3.7 mm, W1 = 1.2 mm, and (c) L1 = 3.7 mm, W1 = 1 mm is simulated in Fig. 6b. The simulation results show that the condition of mode (b) produces the best output response because it has produced two transmission zeros with the lowest level of attenuation and compared to mode (a) and (c), it has a better bandwidth.
a The layout, and b The simulated S12 of proposed two-part resonators in different dimensions
Figure 7a depicts the LC equivalent circuit of the two-part resonators. Following the method outlined in Refs. (Imani et al. 2020; Pouryavar et al. 2018), the inductor and capacitor values can be determined.
a L-C Equivalent. b The simulated S12 of proposed two-part resonators for the dimensions of mode (b)
Each microstrip line in the LC model can be thought of as a series inductor and a grounded capacitor. From this, the equivalent L-C circuit can be formed. The following set of equations can be used to accurately simulate transmission lines (Pozar 2011):
For \(w/h\le 1\):
For \(w/h\ge 1\):
where Z is the transmission line's characteristic impedance and Vp is its phase velocity. Light velocity is given by c, and is a constant quantity equal to 377 (120π) Ω; l is the length of the transmission line; w and h are the line width and substrate thickness, respectively. Table 2 lists the capacitor and inductor values used in the circuit seen in Figs. 7a and 9a.
Based on Fig. 7a, we may infer that the impedance seen from Va and Vb is Zb, Zc, and derive the transfer function as:
Both Eq. (45) and (46) assume a matched impedance of 50 O between the input and output ports in their calculations. Assuming Va and Vb are nodes, we now have:
where
From Eq. (46), (48) and Eq. (49), the transfer function of Vo and Vi can be written as:
Setting Eq. (52) to zero gives us the transmission zeros, thus we have:
As seen from the frequency simulation result of this structure with the dimensions of mode b in Fig. 7b, these resonators produce two transmission zeros (TZs) at a frequency of 7.9 GHz and 19.8 GHz, respectively. These novel resonators with long bases and two parts are designed to occupy a small space while creating TZ. Therefore, it can be concluded that the simulation results of the LC equivalent circuit with the layout are slightly different from each other.
3.2 Stepped impedance resonators
To increase the stopband bandwidth of the PD, another resonator is added to the microstrip circuit, as shown in Fig. 8a. Figure 3 shows this resonator consists of three different transmission lines whose impedances vary step by step. According to Fig. 8a, L3 and W4 are 1.3 and 0.4 mm, respectively. Also, the response of S12 for different W5/W3 ratios is simulated in Fig. 8b. The created transmission zeros can easily be moved by changing the dimensions of the resonator. For W5/W3 = 4.2, the most optimal result is obtained because two transmission zeros are obtained in the response, which has a better attenuation rate compared to others, and also reaches the highest level in the passband.
a The layout, and b The simulated S12 of stepped impedance resonators in different dimensions
The LC equivalent circuit of the stepped impedance resonator is shown in Fig. 9a. Based on Fig. 9a, we may infer that the impedance seen from Vx is Za, and derive the transfer function as:
a L-C Equivalent. b The simulated S12 of proposed stepped impedance resonators for W5/W3 = 4.2
Equation (53) assumes a matched impedance of 50 O between the input and output ports in their calculations. Assuming Vx is a node, we now have:
where
From Eq. (54) and Eq. (55), the transfer function of Vo and Vi can be written as:
Setting Eq. (57) to zero gives us the transmission zeros, thus we have:
Using the values of capacitors and inductors of Table 2, the cut-off frequencies in Eq. (58) and (59) are evaluated as:
According to Fig. 9b, this resonator also creates two TZs at a frequency of 11.2 GHz and 22.5 GHz, respectively. These frequencies are the resonance frequencies of the proposed resonator in Fig. 8a. As the layout simulation results show, the LC equivalent circuit analysis results are very close to each other compared to the simulation and have little difference, which shows the high validity of the calculated results.
3.3 Final structure
According to Fig. 10, the final structure of the proposed WPD is formed by combining the two-part with the stepped impedance resonators. This compact structure is symmetrical on the vertical axis, so it can be easily fabricated using microstrip technology. On the other hand, the equivalent impedance is equal to the impedance of each branch of the conventional WPD.
The layout of the final WPD structure
4 Simulation and fabrication results
The wide-band WPD is simulated on a Rogers RO4003 substrate with a thickness of 0.508 mm and a relative dielectric constant of 0.0022 using electromagnetic wave simulator software (ADS). The circuit's overall size equals 7.4 mm × 7.9 mm (0.106 λg × 0.114 λg). The photograph of the fabricated WPD is shown in Fig. 11. This circuit has an 75% reduction in dimensions compared to the conventional structure. Where λg is (Zonouri and Hayati 2019):
Fabricated WPD
where \({\varepsilon }_{re}\) is the microstrip line's effective dielectric constant.
Results of the measured and simulated return and insertion losses at the input port
Results of the measured and simulated return and insertion losses at the output port
Furthermore, the simulation and measurement results of S-parameters are shown in Figs. 12 and 13. As expected, there is a slight difference between the simulation result and the fabrication due to fabrication and soldering errors.
As can be seen, this single-band WPD at 2.6 GHz has an insertion loss of − 3.015 dB and fluctuates very little throughout the bandwidth.
According to Fig. 12, the proposed structure has a return loss of less than − 15 dB in the bandwidth, and S11 is equal to − 24 dB at the central frequency.
According to S11 = − 15 dB, the bandwidth is from 1.6 to 3.5 GHz, while the center frequency of 2.6 GHz. Since the bandwidth of the proposed power divider ranges from 1.6 GHz to 3.5 GHz and the center frequency is 2.6 GHz, FBW is calculated as follows (Zonouri and Hayati 2019):
The simulation results of return losses at the output port (S22–S33) and isolation between ports 2 and 3 (S23) are shown in Fig. 13. If we set the − 20 dB level as a comparison level, then this circuit has a wide stopband, in which it suppresses nine unwanted harmonics with the level of attenuation -20.5, 35.1, − 23.2, − 34.3, − 30.7, − 37.4, − 29.1, − 22.8, and − 31.1 dB, respectively.
In a PD, the input signal is divided into two output signals with the same amplitude. Still, there may be slight variations in the amplitude of the signals relative to each other, and the output signals have phase differences. Figure 14a, b depict the phase and amplitude variances between the output ports, respectively. The phase and amplitude differences are lower than 1.5° and less than 0.2 dB in the pass-band. Therefore, the proposed structure has an equal power division at the output ports and is symmetric.
a The phase and b the amplitude difference between output ports
Table 3 compares the proposed WPD's performance to that of comparable works. As can be seen, the simulated performance of the proposed structure outperforms other solutions in terms of insertion losses, FBW, return losses, technique and harmonic suppression. Also, the circuit size is smaller than most previous works and has a simpler structure. To put it simply, it excels at S-band uses. The presented circuit has the best FBW and insertion loss compared to other works, which makes its applications wider. Hence, the developed circuit has applications in airport radars for air traffic management, weather surveillance radar, and several telecommunication networks.
5 Conclusion
This article proposes a novel compact broadband WPD using microstrip lines at a central frequency of 2.6 GHz to improve the previous solutions using a novel two-part and stepped impedance resonator. The even and odd mode method has been used to analyze the designed circuit. The simulation results show that nine unwanted harmonics are suppressed. The FBW is 73.3%, and the circuit size is just 0.106 λg × 0.114 λg. The above properties make the designed WPD attractive for applications in microwave amplifiers for dividing or coupling power, antenna arrays, and mixers.
References
Gai C, Jiao YC, Weng ZB, Zhao G, Zhao YL (2017) Dual band gysel power divider with high power dividing ratio. Microw Opt Technol Lett 59(10):2428–2431
Hao H, Xu H, Ling Q, Wang Y (2023) Design of a planar filtering power divider with wide-stopband suppression. Electromagnetics:1–10.
Hayati M, Sattari MA, Zarghami S, Shah-ebrahimi SM (2023) Designing ultra-small Wilkinson power divider with multi-harmonics suppression. J Electromagn Waves Appl 37(4):575–591
Hosseini Tabatabaee A, Shama F, Sattari MA, Veysifard S (2021) A miniaturized Wilkinson power divider with 12th harmonics suppression. J Electromagn Waves Appl 35(3):371–388
Imani MA, Shama F, Alirezapoori M, Haghiri S, Ghadrdan A (2019) Ultra-miniaturized Wilkinson power divider with harmonics suppression for wireless applications. J Electromagn Waves Appl 33(14):1920–1932
Imani MA, Shama F, Roshani GH (2020) Miniaturized Wilkinson power divider with suppressed harmonics. Microw Opt Technol Lett 62(4):1526–1532
Jamshidi MB, Roshani S, Talla J, Roshani S, Peroutka Z (2021) Size reduction and performance improvement of a microstrip Wilkinson power divider using a hybrid design technique. Sci Rep 11(1):7773
Jedkare E, Shama F, Sattari MA (2020) Compact Wilkinson power divider with multi-harmonics suppression. AEU Int J Electron Commun 127:153436
Li J, Zhou H, Ma Q, Chai Y, Yan K (2016) Planar power divider with arbitrary power ratio for high power application and its miniaturization. In: 2016 IEEE International Conference on Microwave and Millimeter Wave Technology (ICMMT), vol. 1, pp. 238–240
Li Q, Zhang Y, Wu CTM (2017) High-selectivity and miniaturized filtering Wilkinson power dividers integrated with multi-mode resonators. IEEE Trans Compt, Packag Manufact Technol 7(12):1990–1997
Lin SC, Chen YM, Chiou PY, Chang SF (2017) Tunable Wilkinson power divider utilizing parallel-coupled-line-based phase shifters. IEEE Microw Wirel Compon Lett 27(4):335–337
Pouryavar R, Shama F, Imani MA (2018) A miniaturized microstrip Wilkinson power divider with harmonics suppression using radial/rectangular-shaped resonators. Electromagnetics 38(2):113–122
Pozar DM (2011) Microwave engineering. Wiley
Roshani S, Jamshidi MB, Mohebi F, Roshani S (2021) Design and modeling of a compact power divider with squared resonators using artificial intelligence. Wirel Pers Commun 117:2085–2096
Roshani S, Yahya SI, Alameri BM, Mezaal YS, Liu LW, Roshani S (2022) Filtering power divider design using resonant LC branches for 5G low-band applications. Sustainability 14(19):12291
Sattari MA, Hayati M, Shama F, Shah-Ebrahimi SM (2023) A miniaturized filter design approach using GMDH neural networks. Microw Opt Technol Lett. https://doi.org/10.1002/mop.33741
Tian H, Dong Y (2022) Packaged Filtering power divider with high selectivity, extended stopband and wide-band isolation. IEEE Trans Circ Syst II Express Briefs
Vaziri HS, Zarghami S, Shama F, Kazemi AH (2020) Compact bandpass Wilkinson power divider with harmonics suppression. AEU Int J Electron Commun 117:153107
Wilkinson EJ (1960) An N-way hybrid power divider. IRE Trans Microw Theory Tech 8(1):116–118
Xiao JK, Yang XY, Li XF (2020) A 3.9 GHz/63.6% FBW multi-mode filtering power divider using self-packaged SISL. IEEE Trans Circ Syst II Express Briefs 68(6):1842–1846
Zhan WL, Zhao XL (2017) Compact filtering power divider with harmonic suppression. J Electromagn Waves Appl 31(3):243–249
Zhang XY, Wang KX, Hu BJ (2013) Compact filtering power divider with enhanced second-harmonic suppression. IEEE Microw Wirel Compon Lett 23(9):483–485
Zhang G, Wang X, Hong JS, Yang J (2018) A high-performance dualmode filtering power divider with simple layout. IEEE Microw Wirel Compon Lett. 28(2):120–122
Zhang Q, Zhang G, Liu Z, Chen W, Tang W (2021a) Dual-band filtering power divider based on a single circular patch resonator with improved bandwidths and good isolation. IEEE Trans Circuits Syst II Express Briefs 68(11):3411–3415
Zhang Y, Wu Y, Yan J, Wang W (2021b) Wide-band high-selectivity filtering all-frequency absorptive power divider with deep out-of-band suppression. IEEE Trans Plasma Sci 49(7):2099–2106
Zhuang Z, Wu Y, Liu Y, Ghassemlooy Z (2018) Wide-band bandpass-to-all-stop reconfigurable filtering power divider with bandwidth control and all-passband isolation. IET Microw Anten Propag 12(11):1852–1858
Zonouri SA, Hayati M (2019) A compact ultra-wideband Wilkinson power divider based on trapezoidal and triangular-shaped resonators with harmonics suppression. Microelectron J 89:23–29
Zonouri SA, Hayati M (2021) A compact Gysel power divider with ultra-wide rejection band and high fractional bandwidth. Int J RF Microw Comput Aided Eng 31(6):e22643
Zonouri SA, Hayati M, Bahrambeigi M (2023) Design of dual-band Wilkinson power divider based on novel stubs using PSO algorithm. Int J Microw Wirel Technol:1–12.
Author information
Authors and Affiliations
Contributions
SD: writing-original draft preparation, conceptualization, supervision, project administration. JZ: software, validation, formal analysis, language review. ML: methodology, writing-original draft preparation, software, language review.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no competing of interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Duan, S., Zhang, J. & Liu, M. Design of an ultra-small Wilkinson power divider using two-part resonators for S-band applications. Multiscale and Multidiscip. Model. Exp. and Des. 6, 643–655 (2023). https://doi.org/10.1007/s41939-023-00166-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s41939-023-00166-9