1 Introduction

The benefits of composite materials, high strength/stiffness-to-weight ratio, superb thermos-mechanical properties and exceptional resistance to corrosion, have led engineers and scientists to continue to push their boundaries and find better material combinations, better manufacturing methods, and new design and analysis methods. However, modern engineering composites still present a challenge for analysis and design even after decades of research and use in manufacturing. Unlike metals which are homogenous and isotropic, composite materials are non-homogenous and anisotropic and thus their behavior under loading is much more complicated and more difficult to predict. Fatigue life is one area where continued research is needed to allow more efficient use of materials and safer designs.

Degrieck and Van Paepegem (2001) in their 2001 review of fiber-reinforced composite fatigue damage modeling generally classified the existing models into phenomenological models (later further classified into residual strength models and residual stiffness models in a 2015 review by Sevenois and Van Paepegem (2015) and progressive damage models (also known as mechanistic models). Fatigue life models are generally based on S–N curves that demand extensive experimental work. Additionally, as noted by Burham and Kim (2018), even with years of experiments, the models vary in their ability to predict stress ratios and are less flexible for applying to general scenarios. The phenomenological models use an evolution law to describe the residual strength and stiffness as it evolves often using a set of probability statistics that failure will occur after a given number of cycles (Degrieck and Paepegem 2001) and do not take into account the specific damage that can occur in composites. In a recent paper by D’Amore and Grassia (2019), they used a phenomenological model to look at constant amplitude loading and found their model to be accurate predictors for the constant loading but other types of loading it would not handle. The progressive damage models use a damage variable (such as crack growth or delamination) to quantitatively account for progression of damage. The drawback of progressive damage models is that the more variables a mode invokes, the more complicated the equations become and more time it takes to solve the simulations using finite element analysis codes. Yet progressive damage models are of interest because they offer the potential for more robust prediction model with fewer drawbacks of the other two model.

Although much research on progressive damage models has already been done, most of these models were case specific and were analytic or limited in scope due to the computational technology at the time (Degrieck and Paepegem 2001). Shorkrieh and Lessard (2000a, b) combined two models to propose a “generalized model” for unidirectional reinforced laminates. This analytic model has a reference point for a way to combine models or uses it as the base for their work such as Kennedy et al. who combined models in a similar way (Kennedy et al. 2013). Pasoce et al. just look at models for fatigue prediction due to delamination growth using both phenomenological and mechanistic models (Pascoe et al. 2013). Modified Shokrieh and Lassards empirical models are used in various studies such as those by Knight (2008) and more recently by Khan et al. where the authors implement user-defined material subroutine in (UMAT) ABAQUS to conduct fatigue analysis with good results (Khan et al. 2018). In the study by Babaei and Mostofi, they used singular value decomposition fatigue model to investigate fatigue in composites due to dynamic loading (Babaei and Mostofi 2016). Kaminski et al. presented a fatigue model for 3D interlock woven polymer matrix composites and ceramic matrix composites that they simulate in finite element code with results that show the monotonic and fatigue loading to cause similar damage (Kaminski et al. 2015). There are models that do not fit cleanly in a category such as the recent model by Dong et al. that uses a novel model of Puck’s Failure theory and non-linear models of residual stiffness and strength. Their model can be applied to multi-directional fiber-reinforce laminates with random stacking sequences with good results (Dong et al. 2016).

The majority of the papers above ended their conclusions with a statement that there is more work to be done. With modern computer technology providing faster computers and better software, there is still a need for efficient models that can handle larger structures to be accurately analyzed for residual and final fatigue failure. In light of furthering how various models can be applied, it is the objective of the present work to extend a progressive damage model to efficiently and accurately simulate fatigue failure in composite laminates subjected to dynamic loadings. A cycle-dependent material property degradation model was employed to account for fatigue damage due to arbitrary stress ratio without performing excessive quantities of testing. This generalized cycle-dependent material property degradation model is implemented into user subroutine USDFLD in ABAQUS for accurate stress analysis through which material degradation states are updated over the progressive fatigue loading. The present computational implementation is tested by comparing the simulated results with the existing experimental data. The comparison between the experimental and simulation results demonstrates the successful simulation capability of the present implementation.

2 Methods

2.1 Failure analysis for lamina

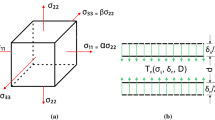
Failure criteria for laminated composites provide a means to determine the strength and the mode of failure of a unidirectional lamina under combined loading conditions. Numerous failure criteria have been proposed subjected to multiaxial loadings. Among the different failure criteria, the quadratic failure criterion such as Tsai and Wu is useful for predicting first ply failure, but cannot distinguish the mode of failure. Experimental evidence shows that the failure behavior of a unidirectional ply is different depending on the loading direction (tension or compression), failure location (matrix or fiber), and the loading condition (in-plane or out-of-plane shear loading conditions). In this study, the traditional failure criteria form for linear cases is modified for the nonlinear situation by considering the material nonlinearity parameter (Shokrieh and Lessard 2000a):

For tension failure:

$$\left( {\frac{{\sigma_{xx} }}{{X_{T} }}} \right)^{2} + \left( {\frac{{\frac{{\sigma_{xy}^{2} }}{{2E_{xy} }} + \frac{3}{4}\delta \sigma_{xy}^{4} }}{{\frac{{S_{xy}^{2} }}{{2E_{xy} }} + \frac{3}{4}\delta S_{xy}^{4} }}} \right) + \left( {\frac{{\frac{{\sigma_{xz}^{2} }}{{2E_{xz} }} + \frac{3}{4}\delta \sigma_{xz}^{4} }}{{\frac{{S_{xz}^{2} }}{{2E_{xz} }} + \frac{3}{4}\delta S_{xz}^{4} }}} \right) \ge 1,$$
(1)

where σxx, σxy, and σxz represent longitudinal stress, in-plane shear stress and out-of-plane shear stress, XT indicates the longitudinal tensile strength of a unidirectional lamina under static tensile stress in the fiber direction, δ is material nonlinearity parameter, which incorporates the shear nonlinearity (damage) prior to failure. In Eq. (1), Exy and Exz are in-plane shear stiffness and out-of-plane shear stiffness, Sxy and Sxz are in-plane shear strength and out-of-plane shear strength, respectively.

For compression failure:

$$\left( {\frac{{\sigma_{xx} }}{{X_{C} }}} \right)^{2} \ge 1,$$
(2)

where XC indicates the longitudinal compressive strength of a unidirectional lamina under static compressive stress.

Fiber-matrix shearing failure:

$$\left( {\frac{{\sigma_{xx} }}{{X_{C} }}} \right)^{2} + \left( {\frac{{\frac{{\sigma_{xy}^{2} }}{{2E_{xy} }} + \frac{3}{4}\delta \sigma_{xy}^{4} }}{{\frac{{S_{xy}^{2} }}{{2E_{xy} }} + \frac{3}{4}\delta S_{xy}^{4} }}} \right) + \left( {\frac{{\frac{{\sigma_{xz}^{2} }}{{2E_{xz} }} + \frac{3}{4}\delta \sigma_{xz}^{4} }}{{\frac{{S_{xz}^{2} }}{{2E_{xz} }} + \frac{3}{4}\delta S_{xz}^{4} }}} \right) \ge 1.$$
(3)

Matrix tension failure:

$$\left( {\frac{{\sigma_{yy} }}{{Y_{T} }}} \right)^{2} + \left( {\frac{{\frac{{\sigma_{xy}^{2} }}{{2E_{xy} }} + \frac{3}{4}\delta \sigma_{xy}^{4} }}{{\frac{{S_{xy}^{2} }}{{2E_{xy} }} + \frac{3}{4}\delta S_{xy}^{4} }}} \right) + \left( {\frac{{\sigma_{yz}^{2} }}{{S_{yz} }}} \right) \ge 1,$$
(4)

where σyy is the transverse stress, YT and Syz indicate static tensile strength and shear strength in the y–z plane, respectively.


Matrix compression failure:

$$\left( {\frac{{\sigma_{yy} }}{{Y_{C} }}} \right)^{2} + \left( {\frac{{\frac{{\sigma_{xy}^{2} }}{{2E_{xy} }} + \frac{3}{4}\delta \sigma_{xy}^{4} }}{{\frac{{S_{xy}^{2} }}{{2E_{xy} }} + \frac{3}{4}\delta S_{xy}^{4} }}} \right) + \left( {\frac{{\sigma_{yz}^{2} }}{{S_{yz} }}} \right) \ge 1,$$
(5)

where YC indicates the transverse compressive strength of a unidirectional static compressive stress in the transverse direction.

Normal tension failure:

$$\left( {\frac{{\sigma_{zz} }}{{Z_{T} }}} \right)^{2} + \left( {\frac{{\frac{{\sigma_{xz}^{2} }}{{2E_{xz} }} + \frac{3}{4}\delta \sigma_{xz}^{4} }}{{\frac{{S_{xz}^{2} }}{{2E_{xz} }} + \frac{3}{4}\delta S_{{xz\frac{{}}{{}}}}^{4} }}} \right) + \left( {\frac{{\sigma_{yz}^{2} }}{{S_{yz} }}} \right) \ge 1,$$
(6)

where σzz is normal stress and ZT is the normal tensile strength of a unidirectional static tensile stress.

Normal compression failure:

$$\left( {\frac{{\sigma_{zz} }}{{Z_{C} }}} \right)^{2} + \left( {\frac{{\frac{{\sigma_{xz}^{2} }}{{2E_{xz} }} + \frac{3}{4}\delta \sigma_{xz}^{4} }}{{\frac{{S_{xz}^{2} }}{{2E_{xz} }} + \frac{3}{4}\delta S_{{xz\frac{{}}{{}}}}^{4} }}} \right) + \left( {\frac{{\sigma_{yz}^{2} }}{{S_{yz} }}} \right) \ge 1,$$
(7)

where ZC is the normal compressive strength of a unidirectional tensile stress.

A stress state under fatigue loading is less than the maximum strength of the material, which causes no static mode of failure. However, as the number of loading cycles increases, the material properties and strengths degrade and eventually become lower than the applied stress state, causing catastrophic failure. Hence, to predict the fatigue failure subject to fatigue loading conditions, material properties under static loading conditions need to incorporate suitable material degradation rules subjected to fatigue loading conditions. The material strength R(n) is assumed to be a function of the number of cycles to failure (n) and its rate of change is described by a power-law equation:

$$\frac{dR(n)}{{dn}} = - A(\sigma )/m\left[ {R(n)} \right]^{m - 1} ,$$
(8)

where A(σ) is a function of the maximum cyclic stress and m is a constant. This model has been used by many authors (Sendeekyj 1981; Radhakrishnan 1984). By integrating Eq. (8) from 0 to n cycle and considering that R(n) is equal to the applied stress at the number of cycles to failure (Nf), the strength R(n) reduces to (Halpi et al. 1973):

$$\frac{{R^{m} (n) - \sigma^{m} }}{{R_{s}^{m} - \sigma^{m} }} = 1 - \frac{n}{{N_{f} }},$$
(9)

where Rs is the static material strength. Similar strength models have been proposed (Halpi et al. 1973; Broutman and Sahu 1972; Daniel and Charewiez 1986; Reifsnider and Stinchcomb 1986; Adam et al. 1986) to predict material degradation. In this study, we used the degradation model introduced by Adam et al. (1986) and modified by Shokrieh and Lessard (2000a):

$$\left( {\frac{R(n) - \sigma }{{R_{s} - \sigma }}} \right)^{\alpha } = 1 - \left( {\frac{\log (n) - \log (0.25)}{{\log (N_{f} ) - \log (0.25)}}} \right)^{\beta } ,$$
(10)

where α and β are fitting parameters that can be found experimentally. In Eq. (10), the equivalent number of fatigue cycle for a static loading is assumed to be a quarter of a cycle (0.25), which is a monotonically increasing part of a cycle (quarter if a cycle) in fatigue.

Similarly, the material stiffness E(n) also degrades as the number of cycles (n) increases under an alternating stress σ. Experiments shows, however, that the average strain to failure (εf) is constant and independent of the stress state and number of cycles (Hwang and Han 1986). The present study adopted the similar form of fatigue strength model given in Eq. (9) using the average strain to failure as

$$\left( {\frac{{E(n) - {\raise0.7ex\hbox{$\sigma $} \!\mathord{\left/ {\vphantom {\sigma {\varepsilon_{f} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\varepsilon_{f} }$}}}}{{E_{s} - {\raise0.7ex\hbox{$\sigma $} \!\mathord{\left/ {\vphantom {\sigma {\varepsilon_{f} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\varepsilon_{f} }$}}}}} \right)^{\gamma } = 1 - \left( {\frac{\log (n) - \log (0.25)}{{\log (N_{f} ) - \log (0.25)}}} \right)^{\lambda } ,$$
(11)

where Es indicates static stiffness, γ and λ are experimental curve fitting parameters.

Material strength and stiffness in Eqs. (1–7) will be degraded by Eqs. (9) and (10) under fatigue loading conditions.

2.2 Constant fatigue diagram

The number of cycles to failure (Nf) is a function of the applied stress (σ) and the stress ratio κ (σmin/σmax), requiring an infinite number of experiments to determine for every stress states and ratios. To avoid performing an infinite number of experiments, a constant fatigue diagram was used in the present study, which quantifies the interaction of alternating and mean stresses on the fatigue life of a material (Adam et al. 1986):

$$a = f\left( {1 - q} \right)^{u} \left( {c + q} \right)^{v} .$$
(12)

In Eq. (12), f, u, and v indicate curve fitting constants and a, q and c are defined by

$$a = \frac{{\sigma_{a} }}{{\sigma_{T} }}; \, q = \frac{{\sigma_{m} }}{{\sigma_{T} }}; \, c = \frac{{\sigma_{C} }}{{\sigma_{T} }},$$
(13)

where σT and σC indicate tensile and compressive stresses, σa alternation stress, and σm mean stress, defined by

$$\sigma_{a} = \frac{{\sigma_{\max } - \sigma_{{{\text{miin}}}} }}{2}\,and\,\sigma_{m} = \frac{{\sigma_{\max } + \sigma_{{{\text{miin}}}} }}{2}$$
(14)

Figure 1 depicts different constant fatigue life curves described by Eq. (12). Note that u and v are assumed to be linear function of fatigue life and be equal. This assumption is based on the observation that the curve-shape asymmetry of the constant life is not severe (Gathereole et al. 1994):

$$u\, = \,v\, = \,A\, + \,B{\log}N_{f} .$$
(15)
Fig. 1
figure 1

Constant fatigue diagram

Full size image

Equation (15) is changed to the following form to determine fitting parameters A and B:

$$u = \log \left( {\frac{\ln (a/f)}{{\ln \left[ {(1 - q)(1 + q)} \right]}}} \right) = A + B\log N_{f} .$$
(16)

Experiments would be conducted to create a σ-logNf curve for different stress ratios. Based on the data, u versus logNf curve is extracted from which A and B can be fitted.

2.3 Material degradation rule and progressive failure procedure

The present fatigue failure criteria and material degradation rules are implemented into the commercial finite element analysis code ABAQUS using user subroutine USDFLD (Hibbitt and Sorensen 1992). From Eq. (11), elastic property degradation can be expressed in terms of a degradation parameter η

$$E(n) = \eta E_{s} ,$$
(17)

where

$$\eta = \left[ {1 - \left( {\frac{\log n - \log 0.25}{{\log N_{f} - \log 0.25}}} \right)^{\lambda } } \right]^{{\frac{1}{\gamma }}} \left( {1 - \frac{\sigma }{{E_{s} \varepsilon_{f} }}} \right) + \frac{\sigma }{{E_{s} \varepsilon_{f} }}.$$
(18)

The value of ηi is assigned to a field variable (FV) in ABAQUS used for controlling the elastic properties. The material degradation parameters can be combined into failure criteria for multiaxial loading. The failure modes in Sect. 2.1 are considered in the model analyzed. A set of sudden material degradation rules are applied for each mode of failure during computation of ABAQUS as follows:

  1. (1)

    When the composite fails in fiber compression or fiber tensile modes, Ex, Ey, Ez, Exy, Eyz, Exz become zero.

  2. (2)

    When the composite fails in fiber-shearing modes, Exy becomes zero.

  3. (3)

    When the composite fails in matrix tensile and compression modes, Ey becomes zero.

  4. (4)

    When the composite fails in normal tensile or compression modes, Ez becomes zero

User subroutine USDFLD calculates the value of the failure indices in Eqs. (2–7). When the index exceeds a value of 1.0, the value of the filed variable is set to 1.0. This value is also stored as state variable (SD) that is passed into the next analysis iteration. The value assigned to a field variable (FV) is used to calculate elastic modus. ABAQUS uses linear interpolation between data points assigned to a field variable.

Parameters of material strength degradation \(\zeta\) are calculated in USDFLD and stored in the state variables:

$$R(n) = \zeta R_{s} ,$$
(19)

where

$$\zeta = \left[ {1 - \left( {\frac{\log n - \log 0.25}{{\log N_{f} - \log 0.25}}} \right)^{\beta } } \right]^{{\frac{1}{\alpha }}} \left( {1 - \frac{\sigma }{{R_{s} }}} \right) + \frac{\sigma }{{R_{s} }}.$$
(20)

The stiffness matrix of the finite element model is rebuilt and the stress analysis is performed in ABAQUS. Stresses are examined by the present fatigue failure criteria in user subroutine in each analysis step. If no sudden failure mode is indicated, the number of cycles (n) is updated. Figure 2 shows the computation process for the present progressive fatigue failure model. Parameter values in Eqs. (15–20) of the AS4 graphite/epoxy composite are listed in Table 1. They were obtained from experimental data available in the literature (Shokrieh and Lessard 2000b).

Fig. 2
figure 2

Computational flowchart of fatigue failure model

Full size image
Table 1 Parameters used in the present study
Full size table

3 Numerical results

We simulated the fatigue behavior of composite laminates made of AS4 graphite/epoxy under fatigue loading. Fatigue properties of AS4 graphite/epoxy composite have been characterized in the literature. We first examine fatigue behaviors of unidirectional plies subject to various uniaxial loading condition to ensure that the simulated degradation model is able to fit the decreasing material properties as the number of fatigue cycles increases. We then simulated the fatigue behavior of a unidirectional laminate subjected to biaxial stress state and compared the calculated results with experimental data.

3.1 Strength and stiffness under longitudinal tensile loading

The present method is utilized to study cycle-dependent strength and stiffness degradation of unidirectional lamia under tensile fatigue loading. The material properties and the failure strength of AS4 graphite/epoxy composite are listed in Tables 2 and 3.

Table 2 Elastic properties of AS4 graphite/epoxy composite (GPa) (Shokrieh and Lessard 2000b)
Full size table
Table 3 Strength of graphite composite (Shokrieh and Lessard 2000b)
Full size table

The unidirectional behavior and residual material properties of AS4 composite laminate under tension–tension fatigue loadings were experimentally characterized in the literature. Details of the experimental procedure are described in Shokrieh and Lessard (2000b). We performed finite element analysis (FEA) to predict strength and stiffness of unidirectional lamina deteriorated under tensile fatigue loading. Figure 3 shows the dimensions of a tensile fatigue test specimen used for FEA simulation. The composite specimen is meshed using ABAQUS eight-node brick elements (C3D8). A stress ratio of 0.1 was applied for cyclic loading.

Fig. 3
figure 3

Uniaxial fiber specimen under longitudinal fatigue loading

Full size image

Figure 4 shows experimental and simulated results of material strength vs the number of fatigue life results on the normalized scale of

$$\left( {\frac{{X_{{T/C}} (n) - \sigma }}{{X_{{T/C(s)}} - \sigma }}} \right)\,{\text{vs}}.\,\left( {\frac{{\log (n) - \log (0.25)}}{{\log (N_{f} ) - \log (0.25)}}} \right).$$
(21)
Fig. 4
figure 4

Normalized strength of a unidirectional lamina under a longitudinal tensile fatigue loading and b longitudinal compression fatigue loading (Shokrieh and Lessard 2000b)

Full size image

In the experimental work (Shokrieh and Lessard 2000b), to measure the residual strength and stiffness, two different stress states (80% and 60% of the longitudinal tensile static strength) were selected. A stress ratio of 0.1 was applied with a frequency below 10 Hz. In the simulation, stress states of 80% and 60% were also selected. Also a stress ratio of 0.1 was applied for load cycle. It is evident that although the load ratio is constant, the residual strength varies with the number of fatigue life cycles.

Next, degrading stiffnesses of a unidirectional lamina specimen under longitudinal tensile fatigue loading were calculated and plotted on the normalized scale of

$$\left( {\frac{{\log (n) - \log (0.25)}}{{\log (N_{f} ) - \log (0.25)}}} \right)\,{\text{vs}}.\,\left( {\frac{{E_{{xx}} (n) - {\raise0.7ex\hbox{$\sigma $} \!\mathord{\left/ {\vphantom {\sigma {\varepsilon _{{xxf}} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\varepsilon _{{xxf}} }$}}}}{{E_{{xxs}} - {\raise0.7ex\hbox{$\sigma $} \!\mathord{\left/ {\vphantom {\sigma {\varepsilon _{{xxf}} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\varepsilon _{{xxf}} }$}}}}} \right).$$
(22)

Again, the two different stress states (80% and 60% of the longitudinal tensile static strength) were chosen with the stress ratio of 0.1; high and low levels of stresses are considered by selecting these two states of stresses. It is clear from Fig. 5 that the FEA modeling simulated the decreasing part of the degradation trend well.

Fig. 5
figure 5

Normalized stiffness of a unidirectional lamina under longitudinal tensile fatigue loading (Shokrieh and Lessard 2000b)

Full size image

3.2 Strength and stiffness under loading in the matrix direction

Fatigue behavior of AS4 graphite/epoxy composite under matrix tensile and compressive loadings has also been studied. An FEA study is conducted to predict strength and stiffness of unidirectional lamia degraded under matrix tensile and compressive fatigue loadings. Figure 6 shows the dimensions of the specimen used for the FEA.

Fig. 6
figure 6

Uniaxial fiber specimen under transverse fatigue loading

Full size image

ABAQUS C3D8 elements were used to model the composite specimen. Tensile–tensile and compressive–compressive loading conditions were applied with the 0.1 load ratio. The results of experiments for measuring the residual strength (Shokrieh and Lessard 2000b) and FEA results are presented in Fig. 7 on the normalized scale of

$$\left( {\frac{{\log (n) - \log (0.25)}}{{\log (N_{f} ) - \log (0.25)}}} \right)\,{\text{vs}}.\,\,\left( {\frac{{Y_{{T/C}} (n) - \sigma }}{{Y_{{T/C(s)}} - \sigma }}} \right).$$
(23)
Fig. 7
figure 7

Normalized strength of a unidirectional lamina under a) transverse tensile fatigue loading and b) transverse compression fatigue loading (Shokrieh and Lessard 2000b)

Full size image

To measure the residual strength under tensile–tensile, two different states of stress (60% and 40% of the tensile transverse static strength) were selected. For compressive–compressive loadings, 70% and 50% of the transverse static strength were selected. ABAQUS results match well with experimental residual strength for both high and low stress levels.

Next, the results for the residual stiffness of a unidirectional 90° ply under tensile–tensile cyclic loading in the matrix direction is plotted on the normalized scale of

$$\left( {\frac{{\log (n) - \log (0.25)}}{{\log (N_{f} ) - \log (0.25)}}} \right)\,{\text{vs}}.\,\left( {\frac{{E_{{yy}} (n) - {\raise0.7ex\hbox{$\sigma $} \!\mathord{\left/ {\vphantom {\sigma {\varepsilon _{{yyf}} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\varepsilon _{{yyf}} }$}}}}{{E_{{yys}} - {\raise0.7ex\hbox{$\sigma $} \!\mathord{\left/ {\vphantom {\sigma {\varepsilon _{{yyf}} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\varepsilon _{{yyf}} }$}}}}} \right).$$
(24)

Figure 8 shows experimental data [27] and FEA simulation results of decreasing of the residual stiffness. It is evident that the degradation model is able to fit the decreasing stiffness as the number of fatigue cycles increases.

Fig. 8
figure 8

Normalized stiffness of a unidirectional lamina under transverse tensile fatigue loading [27]

Full size image

3.3 Strength and stiffness under in-plane loading

To study fatigue behavior of unidirectional lamia under in-plane shear loading, FEA of pure shear mode of deformation was conducted.

Figure 9 shows the dimensions of the FEA specimen model. Results of the shear strength of the specimen predicted by the present method were compared to the experimental result. The experimental result of a composite plate loaded with an in-plane load is presented in Reference [27]. In the experimental work, two different stress states (59% and 40% of static strength) were selected to measure the residual strength. The residual strength and the residual fatigue life of the composite specimen were plotted on the normalized scale of

$$\left( {\frac{{\log (n) - \log (0.25)}}{{\log (N_{f} ) - \log (0.25)}}} \right)\,{\text{vs}}.\,\left( {\frac{{S_{{xy}} (n) - \sigma }}{{S_{{xy(s)}} - \sigma }}} \right).$$
(25)
Fig. 9
figure 9

Uniaxial fiber specimen subjected to pure shear deformation

Full size image

The composite plate is meshed using C3D8R elements. In the simulation, stress states of 59% and 40% were also selected. Figure 10 shows the data characterizing the residual shear strength of the unidirectional composite plate experimentally and numerically.

Fig. 10
figure 10

Normalized shear strength of a unidirectional composite plate under in-plane shear loading [27]

Full size image

The degrading stiffness of the composite subjected to pure shear deformation was calculated and plotted on the normalized scale of

$$\left( {\frac{{\log (n) - \log (0.25)}}{{\log (N_{f} ) - \log (0.25)}}} \right)\,{\text{vs}}.\,\left( {\frac{{G_{{xy}} (n) - {\raise0.7ex\hbox{$\sigma $} \!\mathord{\left/ {\vphantom {\sigma {\varepsilon _{{xyf}} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\varepsilon _{{xyf}} }$}}}}{{E_{{xys}} - {\raise0.7ex\hbox{$\sigma $} \!\mathord{\left/ {\vphantom {\sigma {\varepsilon _{{xtf}} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\varepsilon _{{xtf}} }$}}}}} \right).$$
(26)

The experimental and numerical results of residual shear stiffness of the unidirectional composite plate are shown in Fig. 11. Simulated data well represented the degradation behavior of the strength and the stiffness for AS4 composite laminate subjected to in-plane shear loading.

Fig. 11
figure 11

Normalized shear stiffness of a unidirectional composite plate under in-plane shear loading

Full size image

3.4 Fatigue behavior of a unidirectional ply under biaxial state of stress

The cumulative fatigue damage method implemented into ABAQUS based on cycle-dependent material property degradation model is evaluated with an angle-ply laminate and validated by an experimental result. A set of static and fatigue experiments were reported in the literature with 30° off-axis specimens made from AS4 graphite/epoxy material (Shokrieh and Lessard 1997). The AS4 graphite/epoxy material is fully characterized and presented in Sect. 3. The off-axis unidirectional specimen under uniaxial tension loading is shown in Fig. 12. Applying a uniaxial loading on the off-axis specimen induces a biaxial state of stress in the on-axis direction. The experimental static strength of the specimen is 160.6 MPa. Tension–tension fatigue tests were conducted with the load ratio (Fmin/Fmax) of 0.1.

Fig. 12
figure 12

Off-axis unidirectional specimen under tensile loading

Full size image

ABAQUS predicted the number of cycles to failure under various applied stress conditions. A stress ratio of 0.1 was applied as cyclic loading. The composite specimen is meshed using C3D8 elements. The laminate stacking of the composite specimen model is [60/60/60/60]. The results obtained by the present method were compared with the experimental results (Fig. 12). The experimental S–N data [27] and simulated S–N values are shown by empty circles and filled circles, respectively. As shown in the figure, the present method reasonably simulated the behavior of the unidirectional ply under biaxial state of stress (Fig. 13).

Fig. 13
figure 13

Applied stress vs fatigue life (S–N) cure of the 30° off-axis specimen

Full size image

4 Conclusion

This study presented a numerical modeling approach to simulate the behavior of composite laminates subjected to fatigue loadings. The present approach is based on accurate stress analysis, material degradation rule, and failure analysis. The model is implemented into ABAQUS using USDFLD User Subroutine. Numerical tests of material characterization of the unidirectional composite lamina were performed for tension and compression for fiber and matrix direction and in-plane shear loadings and the results were compared to experimental data. Simulated data well represented the degradation behavior of the strength and the stiffness. The present model is able to predict the residual strength and stiffness and provide a final fatigue life of the composite laminates subjected to multiaxial fatigue loading conditions.