Particle swarm optimization technique for speed control and torque ripple minimization of switched reluctance motor using PID and FOPID controllers

Abstract

Switched Reluctance Motors has become one of the best solutions for EV applications because of its numerous benefits over other electric drive systems. Its excellent qualities are the robust design, double saliency, fault tolerance, and ability to withstand the heat of SRM drives. In order to minimize torque ripple and provide an exact speed response in SRM, this article mainly presents a speed and current control technique. The accurate speed control and torque ripple reduction of a SRM is controlled using the particle swarm optimization technique (PSO) with speed and current control mechanisms. The PID and FOPID speed controllers in the outer loop and current controller in the inner loop, respectively, are regulated, as are the 3-$\varnothing$, 6/4 SRM turn-on (${T}_{O}$), and turn-off (${T}_{F}$), angles. The results were compared with existing optimization methods such as the SHO, LUS, GA, Ant-Lion, NSGA-II, MOLGSA, GSA, Hybrid MOLGSA, and RGA-SBX algorithms, show that a cascaded Fractional order PID(FOPID) controller offers better speed, current, and torque responses, as well as smaller current and torque ripples, under numerous different load and speed conditions. Under all load conditions, it has been demonstrated that the PSO-FOPID controller has the best speed response and minimal torque ripples when compared to the PSO-PID controller.

1 Introduction

SRM is an effective competitor to BLDC, PMSM, and induction motors because of its inexpensive cost, simple construction, broad speed range, high torque when starting, flexible control, and fault tolerance [1]. In the last decade, researchers have carried out substantial studies on the SR Motor [2]. In Electric vehicle application SR Motors performance is good compared to induction motor, PMSM and BLDC motors [3]. SR Motor design has been greatly improved because of advanced development of power electronics converters and control techniques [4]. Due to their widespread usage in several applications including electric cars, robotic control applications, textile machines, and the aviation industries SR motors can run at high speeds [5]. Due to its double salient nature, continual switching action, and stator power supply, Nonlinear magnetic characteristics, undesirable torque ripples, and acoustic noise are typical problems with SR motors [6]. Because of these drawbacks, SR motors have a major influence on the system's reliability and safety. Researchers have also concentrated on developing novel control and design methodologies to enhance the performance of the SR Motor because standard regulation is challenging to implement properly [7]. The TSF, DTC, feedback control, and ATC techniques were described [8,9,10,11] to control torque ripples in SR Motor drives. The accurate speed response and torque ripple reduction of SRM utilizing LUS and SHO algorithms with PID and FOPID controllers were proposed in [12]. The author also discussed and compared with already existing optimization techniques with proposed techniques. Author mainly concentrated on torque ripples, speed response of SRM. Here main drawback of this study is constant T_O and T_F angles considered. utilizing current and speed control A method for reducing torque ripple was reported in [13] using a hybrid MOLGSA, MOL, and GSA with a PI controller and varying T_O and T_F angles.

For the purpose of controlling SRM drive speed and reducing torque ripple, [14] presented the Ant-Lion optimizer approach using a FOPID controller. The author also contrasted the recommended strategy with alternative optimisation techniques. In this scenario, it is assumed that the T_O and T_F are both constant. In [15], it was suggested to include a fuzzy logic controller to regulate an SRM's speed together with the accurate change of the T_O and T_F. in [16] focused on SRM torque ripple reduction utilizing a modified particle swarm optimization approach. in order to manage the speed of an SRM, [17] suggested using GA and an ant colony optimizer PID controller. The author focused mostly on PID speed control with optimization methods. The author did not examine the objective function in this case. The PSO technique is used to optimize a PID controller for SRM speed control [18]. The author mainly focused on speed control. The settling period of speed is lengthy here. The torque ripple reduction of SRM is described in [19] utilizing an artificial Bee colony optimization technique with a PID controller. The research's objective function is undefined. in [20] presents standard SRM motors and converter topologies, as well as various control approaches for minimizing torque ripples and SRM speed control. A unique objective function for double indicator optimisation is presented in [21]. In [22] offers a novel TSF implementation and an intelligent controller based on the flower pollination method for minimizing torque ripples in an SRM. The speed control of SRM using the ACO algorithm is described in [23]. In order to control PI, ACO is utilised. Here, a supply is provided by a photovoltaic system. A universal torque controller is described in [24] to eliminate torque ripple, increase the torque/current ratio, and enhance motor efficiency. The 8/6 SR motor is described in [25]. The toothed design of the rotor causes the SRM to vibrate and create acoustic noise. To overcome this problem, intelligent control systems such as ANN and FOPID have been created. [26] suggested a PEM fuel cell stack-feeding SRM using a multi-objective dragonfly optimizer. The author concentrated on three important performance indicators: torque per ampere ratio, torque smoothness factor, and average starting torque. [27] describes how to regulate SRM speed with torque ripple minimization using the NSGA-II algorithm. The PI controller is utilized here. In this method objective function is not clear. In SRM [28], turn-off angle variation using fuzzy logic is shown to reduce torque ripple. In [29], MOL techniques for controlling speed and reducing SRM torque ripple were introduced. in [30] presents a PID controller-based speed control of SRM with constant T_O and T_F. here, the settling time of speed response is very slow. Using Artificial neural network torque ripple and speed control of SRM with constant T_O and T_F presented in [31]. Speed control and performance indices of DC Motor is presented using PID controller [32, 33]. As seen in the previous literature, SRM speed control and torque ripple reduction are presented with specific speed and load torque, but in this proposed work, the performance of SRM is presented under different speed and loading conditions, and the results are analysed and compared with the proposed optimisation technique with already exciting optimisation techniques. Therefore, main contribution of this article.

• 1. Developing a cascaded PID and FOPID controller that improves the speed response of a 6/4 pole SR motor in addition to minimizing torque ripples and which enables accurate speed control.

• 2. Implementing the particle swarm optimization (PSO) technique, design the optimum gains of the two cascaded PID and FOPID controllers.

• 3. Comparing the speed response and load torque at different conditions using already existing optimization technique with proposed model.

• 4. Checking the outcomes of the proposed PSO-PID and PSO-FOPID controllers with those described in earlier literature.

The work is divided into five sections: Sect. 1 has an introduction, Sect. 2 contains the mathematical model of the SR Motor, and Sect. 3 contains a case study, the formulation of the objective function, and a description of the recommended optimization techniques. Sections 4 and 5 present the results and Discussions. Finally, Sect 6 discussed conclusions.

2 Mathematical modelling of SR Motor

Figure 1 illustrates the 1- $\phi$ equivalent circuit model of SRM drive.

Fig. 1

Single phase equivalent circuit of SRM

The resistive voltage drops and the rate of change of flux linkages are added together to form the applied voltage to a phase in SRM is given in below.

$$V={R}_{s}i+\frac{d\varphi (\theta ,i)}{dt}$$

(1)

where, ${R}_{s}$= per-phase resistance, $\varphi$= per-phase flux linkage

Equation of $\varphi$ given by:

$$\varphi =L\left(\theta ,i\right).i$$

(2)

where, L is the inductance depends upon on the rotor position as well as the phase current (${I}_{Phase})$.

Then, Phase voltage equation is

$$V={R}_{s}i+\frac{d\{L\left(\theta ,i\right)i\}}{dt}={R}_{s}i+L\left(\theta ,i\right)\frac{di}{dt}+i\frac{d\theta }{dt}.\frac{dL(\theta ,i)}{d\theta }$$

$$V={R}_{s}i+L\left(\theta ,i\right)\frac{di}{dt}+\frac{dL(\theta ,i)}{d\theta }{\omega }_{m}i$$

(3)

The induced Electromotive force(emf) equation is given below as:

$$e=\frac{dL(\theta ,i)}{d\theta }{\omega }_{m}i={K}_{b}{\omega }_{m}i$$

(4)

$${K}_{b}=\frac{dL\left(\theta ,i\right)}{d\theta }$$

(5)

The input power of SRM is given by

$${P}_{i}=V.i$$

$${P}_{i}={R}_{s}{i}^{2}+{i}^{2}\frac{dL}{dt}\left(\theta ,i\right)+L\left(\theta ,i\right)i\frac{di}{dt}$$

(6)

$$\frac{d}{dt}\left(\frac{1}{2}L(\theta ,i){i}^{2}\right)=L\left(\theta ,i\right)i\frac{di}{dt}+\frac{1}{2}{i}^{2}\frac{dL(\theta ,i)}{dt}$$

(7)

Equation (7) and (6) form an Eq. 8 shown below

$${P}_{i}={R}_{s}{i}^{2}+\frac{d}{dt}\left(\frac{1}{2}L(\theta ,i){i}^{2}\right)+\frac{1}{2}{i}^{2}\frac{dL(\theta ,i)}{dt}$$

(8)

$$time(t)=\frac{\theta }{{\omega }_{m}}$$

(9)

Air gap power equation is

$${P}_{a}=\frac{1}{2}{i}^{2}\frac{dL(\theta ,i)}{dt}=\frac{1}{2}{i}^{2}\frac{dL(\theta ,i)}{d\phi }.\frac{d\theta }{dt}=\frac{1}{2}{i}^{2}\frac{dL(\theta ,i)}{d\theta }{\omega }_{m}$$

(10)

$${P}_{a}={\omega }_{m}{T}_{e}$$

(11)

From Eq. 10 and 11 we will get Eq. 12 shown below

$${{T}_{e}=\frac{1}{2}i}^{2}\frac{dL(\theta ,i)}{d\theta }$$

(12)

3 Case study

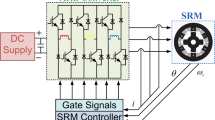
Figures 7 & 8 illustrates the simulation model, a 6/4, 3-$\varnothing$ SRM with a total output power of 60KW [12]. The SRM is powered by a 3-$\varnothing$ asymmetrical converter with a 240 V dc supply. A position sensor is attached to the rotor with optimized ${T}_{O}$ and ${T}_{F}$ values to regulate the switching frequency of phase currents. The SRM model is simulated in MATLAB/Simulink using the requirements stated in the appendix. A cascaded PID and FOPID controller with reference speeds of 1000 rpm, 1500 rpm, and 2000 rpm are incorporated to provide speed and current control in the outer & inner loops respectively.

3.1 Minimization of torque ripple in SRM drive

The Change in machine co-energy i.e., high torque ripple was caused by the position of a rotor, flux linkage of a stator, and excitation current. The inductance was affected by these factors were strongly reliant with nonlinear position of a rotor, which causes variation in phase current. By balancing the current profile and choosing suitable ${T}_{O}$ and ${T}_{F}$, the torque ripple may be reduced. In this work, ${T}_{O}$ and ${T}_{F}$ control is proposed together with torque ripple reduction for controlling current and speed. The speed controller and current controller employ standard PID and FOPID controller models. To improve the efficacy of the SRM drive, suitable combinations of eight optimal parameters for PID and twelve optimal parameters for FOPID have been identified, respectively. By using PSO optimization algorithm we will tune the PID and FOPID controller parameters these are Proportional, integral, derivative gains and Lambda(λ) and $\mu$ for both speed & current controllers and ${T}_{O}$ &  ${T}_{F}$ angles. The optimal combination of these gain values can enhance the performance of the SRM drive and torque ripples. In this situation, FOPID will perform better than a PID controller. The ISE Speed and ISE Current are two common forms of integral square errors which were used to assess the errors of speed & current respectively, as shown below Eqs. (14) and (15).

$$f=ISE=\underset{0}{\overset{\infty }{\int }}{e}_{\omega }^{2} dt$$

(13)

$${\text{ISE}}\_\mathrm{Speed }= \int ({{w}_{ref}-{w}_{m})}^{2}dt$$

(14)

$${\text{ISE}}\_\mathrm{Current }= \int ({{I}_{ref}-{I}_{m})}^{2}dt$$

(15)

Below Eq. 16 shown the torque ripple coefficient [27]

$${T}_{ripple}=\frac{{T}_{max}-{T}_{min}}{{T}_{mean}}$$

(16)

The following torque equation can be used to characterize the SRM performance [34].

$${T}_{Phase}\left(\theta ,i\right)= \frac{1}{2}{i}^{2}\frac{dL\left(\theta ,i\right)}{d\theta }$$

(17)

where [13] ${T}_{phase}$ is computed by the parameters using L, $\theta$, i, and ${T}_{total}\left(\theta ,i\right)$ (the total torque generated by 3-$\varnothing$ current) defined in the Eq. (18):

$${T}_{total}\left(\theta ,i\right)= \sum_{phase }\frac{1}{2}{i}^{2}\frac{dL(\theta ,i)}{d\theta }$$

(18)

The proposed optimization algorithm and objective function are described in the next section, and Fig. 2a, b, and c shows the variations in the 3-$\varnothing$ flux, current, & characteristics of magnetization.

Fig. 2

a Three phase flux b three phase current c characteristics of magnetization

3.2 Problem formulation

The inner current controller and outer speed controller are the two PID and two FOPID controllers that will be optimized in this scenario will enhance the response of speed & reduce the disturbances in the working functions of SRM. In order to make this efficient, Eqs. (19) and (20) are used to create the proposed FF, it is the summation of ISE current & speed [17].

The constraints considered in the formulation of the multi-objective problem are the ISE current of the inner loop and the ISE speed of the outer loop. The following two objectives are mentioned below.

As seen below, the minimization of the ISE current & speed is described by Eqs. (19) and (20).

$${f}_{1}={\text{min}}\left(IS{E}_{speed}\right)$$

(19)

$${f}_{2}={\text{min}}\left(IS{E}_{current}\right)$$

(20)

This is a method to formulate the optimization problem given below in Eq. (21)

$$Minf=\left({\int }_{0}^{{t}_{sim}}({{w}_{ref}-{w}_{m})}^{2}dt\right)+ \left({\int }_{0}^{{t}_{sim}}({{I}_{ref}-{I}_{m})}^{2}dt\right)$$

(21)

$$minf= {f}_{1}+ {f}_{2}$$

(22)

the following constraints are also subjected to the objective function:

$${K}_{p1,min}\le {K}_{p1}\le {K}_{p1,max}$$

$${K}_{i1,min}\le {K}_{i1}\le {K}_{i1,max}$$

$${K}_{d1,min}\le {K}_{d1}\le {K}_{d1,max}$$

$${K}_{p2,min}\le {K}_{p2}\le {K}_{p2,max}$$

$${K}_{i2,min}\le {K}_{i2}\le {K}_{i2,max}$$

$${K}_{d2,min}\le {K}_{d2}\le {K}_{d2,max}$$

$${K}_{p1,min}\le {K}_{p1}\le {K}_{p1,max}$$

$${K}_{i1,min}\le {K}_{i1}\le {K}_{i1,max}$$

$${\uplambda }_{min}\le {\uplambda }_{1}\le {\uplambda }_{max}$$

$${K}_{d1,min}\le {K}_{d1}\le {K}_{d1,max}$$

$${\upmu }_{min}\le {\upmu }_{1}\le {\upmu }_{max}$$

$${K}_{p2,min}\le {K}_{p2}\le {K}_{p2,max}$$

$${K}_{i2,min}\le {K}_{i2}\le {K}_{i2,max}$$

$${\uplambda }_{min}\le {\uplambda }_{2}\le {\uplambda }_{max}$$

$${K}_{d2,min}\le {K}_{d2}\le {K}_{d2,max}$$

$${\upmu }_{min}\le {\upmu }_{2}\le {\upmu }_{max}$$

where ${K}_{p1}$,${K}_{i1}$, ${K}_{d1}$ and ${K}_{p2}$,${K}_{i2}$, ${K}_{d2}$ are the PID speed and current controller gains and ${K}_{p1}$, ${K}_{i1}$,${\uplambda }_{1}$,${K}_{d1}$, ${\upmu }_{1}$ and${K}_{p2}$, ${K}_{i2}$,${\uplambda }_{2}$,${K}_{d2}$, ${\upmu }_{2}$ are the FOPID speed and current controller gains respectively.

The upper and lower limits for each PID, FOPID speed, and current parameter are provided in Eqs. (23) and (24), (25), and (26) respectively.

$${K}_{ps}\in \left[\mathrm{0,10}\right], {K}_{is}\in \left[\mathrm{0,10}\right] and {K}_{ds}\in \left[\mathrm{0,10}\right]$$

(23)

$${K}_{pi}\in \left[\mathrm{0,10}\right], {K}_{ii}\in \left[\mathrm{0,10}\right] and {K}_{di}\in \left[\mathrm{0,10}\right]$$

(24)

$${K}_{ps}\in \left[\mathrm{0,10}\right], {K}_{is}\in \left[\mathrm{0,10}\right], {\uplambda }_{is}\in \left[\mathrm{0,1}\right], {K}_{ds}\in \left[\mathrm{0,10}\right] and {\upmu }_{is}\in \left[\mathrm{0,1}\right]$$

(25)

$${K}_{pi}\in \left[\mathrm{0,10}\right], {K}_{ii}\in \left[\mathrm{0,10}\right], {\uplambda }_{ii}\in \left[\mathrm{0,1}\right], {K}_{di}\in \left[\mathrm{0,10}\right] and {\upmu }_{ii}\in \left[\mathrm{0,1}\right]$$

(26)

${\theta }_{on}$ and ${\theta }_{off}$ of lower and upper bounds are shown below equations,

$${\theta }_{on }\in \left[38.5, 51.5\right]$$

(27)

$${\theta }_{off }\in \left[60, 90\right]$$

(28)

3.3 Brief description of PID and FOPID controller

Due to its simple form and ease of parameter adjustment, a PID controller is the most extensively used controller in the industry for control applications. A traditional PID control approach does not deliver adequate performance when the process gets too complicated to define. As a result, it is incapable of capturing all design objectives and requirements over a wide variety of operating circumstances and disturbances [35].

$${G}_{c}\left(S\right)= {K}_{p}+{K}_{i}\frac{1}{S}+{K}_{D}S$$

(29)

For these reasons, FOPID controller configurations have been provided in multiple studies under various operating circumstances of the controlled systems to achieve the lowest steady-state error and enhance dynamic behaviour.

In recent years, academia and business have shown a strong interest in the FOPID controller [36]. actuality, because they have five parameters to choose from rather than three, they provide greater flexibility in controller design than a standard PID controller [37]. This, however, suggests that controller tuning may be far more complex. Figure 3 illustrates the PID, FOPID, and time domain of the FOPID controller block diagram. A fractional order PID controller's most popular design is the $P{I}^{\uplambda }{D}^{\mu }$ controller involving an integrator of order λ and a differentiator of order µ.

Fig. 3

Block diagram of PID, FOPID and time domain of FOPID controller

where λ and µ can be any real numbers. The transfer function of Such a controller has the form

$${G}_{c}\left(S\right)= {K}_{p}+{K}_{i}\frac{1}{{S}^{\uplambda }}+{K}_{D}{S}^{\upmu } , (\uplambda ,\upmu )>0$$

(30)

3.4 Turn-on and turn-off angle design

The ${T}_{O}$ and ${T}_{F}$ ultimately decide how well SRM performs. A number of variables which includes torque ripple, acoustic noise, torque-speed range and machine efficiency are influenced by ${T}_{O}$ and ${T}_{F}$. Figure 4 depicts the stator's per-phase inductance curve with rotor position advancement in Radians per second.

Fig. 4

Rotor position vs per phase inductance

${T}_{O}$: Rotor angle at the instant when respective phase is excited.

${T}_{F}$: Rotor angle at the instant when conducting phase turned off.

3.5 Methodology

Figure 5 shows the steps to find the Speed control and Torque ripple minimization of SRM drive.

Fig. 5

Flowchart for proposed system

3.6 Brief description of PSO algorithm

Numerous heuristic optimization techniques, including the genetic algorithm (GA), ant colony algorithm (ACO), PSO, and most recently, biogeography-based optimization (BBO), have been developed recently to solve a variety of complex engineering problems that are challenging to solve using conventional optimization techniques. Kennedy and Eberhart created PSO in 1995. Research revealed that PSO performs better than other algorithms. It is a population-based stochastic search technique. One of the finest qualities of this method is its extremely straightforward algorithm. It only uses two equations, which makes it easier to understand. It also has a simple convergence characteristic and an acceptable computational approach. Figure 6 illustrates the flowchart of PSO algorithm.

Fig. 6

Flowchart of PSO algorithm

Mathematically PSO can be explained as follows.

Velocity of particle (i) is adjusted as

$${V}_{j}^{k+1}= W{V}_{j}^{k}+{K}_{P}\times {R}_{p}\left({P}_{{best}_{j}}-{X}_{j}^{k}\right)+{K}_{G}\times {R}_{G}\times \left({G}_{best}t-{X}_{j}^{k}\right)$$

(31)

Position of particle (i) is adjusted as

$${X}_{i}^{k+1}= {X}_{t}^{i}+ {V}_{i}^{k+1}$$

(32)

where, the position and velocity of j^th particle at iteration k is represented by the variables ${V}_{j}^{k}$ and ${X}_{j}^{k}$ respectively. Shi and Eberhart described how to update the particle's velocity between iterations. The best position of swarm and agent j are ${G}_{best}$ and ${P}_{{best}_{j}}$ respectively. The cognitive and social parameters are predefined constants represented by ${K}_{P}$ and ${K}_{G}$.

The random numbers between 0 and 1 that were created are ${R}_{p}$ and ${R}_{G}$. In order for the PSO exploration process to find an optimal solution quickly and with fewer iterations, the inertia weight W keeps a balance between global and local search. The equation below shows that as the search process advances, the inertia weight W decreases linearly.

$$W= {W}_{max}-\left(\frac{{W}_{max}-{W}_{min}}{{K}_{max}}\right)K$$

(33)

Here, ${W}_{max}$ and ${W}_{min}$ respectively, represent the inertia weight's maximum and minimum values.

4 Results and discussions

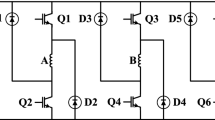
The proposed system for controlling speed and current consists of two controller loops. Figures 7 and 8 illustrates a three-phase SRM with a PID and FOPID speed controller in the outer loop and a PID and FOPID current controller in the inner loop, as well as an angle control for the ${T}_{O}$ and ${T}_{F}$ system. With the aim of simultaneously minimizing torque ripple and integral square error of speed and current, the multi-objective optimization problem statement is defined as searching the values of proportional, integral, and derivative gains, Lambda, and μ of PID and FOPID controllers for both current and speed controllers as well as ${T}_{O}$ and ${T}_{F}$ angle.

Fig. 7

Simulation model of SRM with PSO-PID Controller

Fig. 8

Simulation model of SRM with PSO-FOPID Controller

The particle swarm optimization (PSO) algorithm has been developed in. mfile and the model of the system under investigation has been developed in MATLAB/SIMULINK environment. Figure 9 shows the three-level asymmetric converter model to drive SRM.

Fig. 9

Three level asymmetric converter model to drive SRM motor

The analysis and simulation of three loading scenarios for 1000 rpm, 1500 rpm, 2000 rpm for various loading conditions these loading cases are: case 1: No load, case 2: 50N.m, case 3: 100N.m. load is simulated for 0.3 s interval.

Table 1 and 2 represent the current and speed controllers' PID and FOPID optimal gain values for the five loading conditions. Additionally, the results of various controllers developed in earlier literature and optimized using GA, Ant-lion, SHO, LUS, Ant colony, NSGA-II, MOL, RGA-SBX, GSA, and Hybrid MOLGSA are compared to the outcomes of the SRM time response with PID and FOPID coefficients optimized using PSO algorithms. Additionally, Table 3, 4, 5, 6, 7 and 8 provide the optimal FF values for the three loading scenarios while using various controllers with different speeds. The FF values for the PSO-FOPID controller are the lowest when compared to those of other optimization techniques.

Table 1 Output Results when ISE is optimized using PSO-FOPID

Table 2 Output Results when ISE is optimized using PSO-PID

Table 3 Optimal FF using PID controller and different algorithms at 1000 rpm

Table 4 Optimal FF using PID controller and different algorithms at 1500 rpm

Table 5 Optimal FF using PID controller and different algorithms at 2000 rpm

Table 6 Optimal FF using FOPID controller and different algorithms at 1000 rpm

Table 7 Optimal FF using FOPID controller and different algorithms at 1500 rpm

Table 8 Optimal FF using FOPID controller and different algorithms at 2000 rpm

Case 1: no-Load torque (T = 0N.m). Figure 10 and 11 illustrate the outcomes of the simulation for this case. In comparison to other techniques, the PSO-FOPID algorithm offers a better speed response when applying a reference speed of 1000, 1500, or 2000 rpm. As seen in Fig. 10a, b, c, Due to its quick response time and minimal study state error, the PSO technique offers the best transient and study-state performance. The PSO algorithm performs slightly better than other Techniques in terms of speed. Unfortunately, the high settling time of the GA Technique results in low-speed performance. Various speed ranges of the no load torque are presented in Fig. 11a, b, c. It can be observed through a comparison of the PSO and GA that the PSO can generate the lowest current ripples.

Fig. 10

PSO-FOPID No-Load Speed at a 1000 rpm, b 1500 rpm, c 2000 rpm

Fig. 11

PSO-FOPID No-Load torque at a 1000 rpm, b 1500 rpm, c 2000 rpm

Case 2 T = 50N.m. In this scenario, the SRM drive is subjected to a load torque of 50N.m at three different speeds (i.e., 1000, 1500, and 2000 rpm) at time t = 0.3 s shown in Fig. 12a, b, c. When compared to PSO-PID and GA, PSO-FOPID provides a faster speed response. Although the PSO-FOPID algorithm exhibits some allowable overshoot, it offers a quick response and is not impacted by disturbances. The Ant-colony, Ant-lion, and GA algorithms exhibit some study state error and slightly slower speed response compare to the PSO algorithm. The disturbance torque substantially affects the GA and has a worse off-speed response. The load torque under this case is shown in Fig. 13a, b, c from 0 to 0.3 s. The PSO technique produces the lowest torque ripples, whereas the GA algorithm produces larger torque ripples.

Fig. 12

PSO-FOPID (50 N.m. load) Speed at a 1000 rpm, b. 1500 rpm, c 2000 rpm

Fig. 13

PSO-FOPID 50N.m Load Torque at a 1000 rpm, b 1500 rpm, c 2000 rpm

Case 3 T = 100N.m. Figures 14 and 15 display the simulation results for this scenario. In this case, the SRM drive is applied a load torque of 100N.m at three distinct speeds (i.e., 1000, 1500, and 2000 rpm). The outcomes of this case simulation results are depicted in figure below. the PSO-FOPID simulation analysis conducted for various speed responses. the speed responses shown in Figs. 14a, b, c, 15a, b, c shows the PSO-FOPID load torque at 100N.m. at three distant speed ranges.

Fig. 14

PSO-FOPID (100 N.m. load) speed at a 1000 rpm, b 1500 rpm, c 2000 rpm

Fig. 15

PSO-FOPID (100 N.m. load) speed at a 1000 rpm, b 1500 rpm, c 2000 rpm

4.1 Comparison between PSO-FOPID controller with already existing algorithms

The effectiveness of the proposed PID and FOPID controllers using the PSO algorithm is compared in this section. As can be observed, PSO-FOPID has superior convergence and is more efficient than PSO-PID. Moreover, Tables 2 and 3 demonstrate optimal gains of PSO-PID, PSO-FOPID, and maximum, minimum, mean, and torque ripples for PSO-PID and PSO-FOPID controllers. When comparing the two techniques, PSO-FOPID produces less torque ripples than PSO-PID.

5 Discussions

Case 1: no load torque T = 0Nm. The PSO-FOPID's speed response setting time in Fig. 16c is considerably faster than Ant-lion-FOPID, SHO-FOPID, LUS-FOPID, GA-FOPID, respectively. As a result, The PSO-FOPID has the fastest speed response. In Fig. 16d shows the No-load torque at 2000 rpm speed, PSO-FOPID has very less torque ripples compare to Ant-lion-FOPID, SHO-FOPID, LUS-FOPID, GA-FOPID, respectively. In Fig. 16a the speed response settling time of PSO-PID is very less compare to Hybrid MOLSA-PID, MOL-PID, GSA-PID, SHO-PID, LUS-PID, RGA-SBX-PID, NSGA-II-PID, respectively. Figure 16b shows the No-load torque at 2000 rpm, here PSO-PID has very less torque ripples compare to MOLSA-PID, MOL-PID, GSA-PID, SHO-PID, LUS-PID, RGA-SBX-PID, NSGA-II-PID.

Fig. 16

a PSO-PID speed at 2000 rpm, b PPSO-PID No-load torque at 2000 rpm, c PSO-FOPID speed at 2000 rpm, d PSO-FOPID No-load torque at 2000 rpm

Case 2: load torque T = 50Nm. At a load of 50N.m, the speed response settling time of PSO-FOPID lower when compared to previous optimization techniques is shown in Fig. 17d. The speed response settling time of LUS-FOPID high compare to other optimization algorithms. Figure 17c shows the speed response at different optimization algorithms using FOPID controller, here PSO-FOPID. Figure 17a shows the speed response of different optimization techniques with PID controller. PSO-PID faster speed response then compare to other techniques. Figure 17b shows the 50N.m load torque of PID controller using Different optimization algorithms and torque ripples of PSO-PID has less compare to other Techniques. If we compare PSO-FOPID with PSO-PID, PSO-FOPID has less torque ripples and faster speed response.

Fig. 17

a PSO-PID speed at 2000 rpm, b PSO-PID 50 N.m load Torque at 2000 rpm, c PSO-FOPID Speed at 2000 rpm, d PSO-FOPID 50 N.m load Torque at 2000 rpm

Case 3: load torque T = 100Nm. The Simulation results for different optimization algorithm with FOPID and PID controller case are shown in Fig. 18. PSO-FOPID technique, as illustrated in Fig. 18c, significantly improves the speed response of SRM and speed settling time, compared to the PSO-PID controller shown in Fig. 18a and other optimization strategies in this study, the PSO-FOPID controller delivers a very quick speed response. Figure 18b, d shows the 100N.m load torque at different optimization techniques using PID and FOPID controllers, here PSO-FOPID gives less torque ripples compare to PSO- PID and other optimization techniques.

Fig. 18

a PSO-PID speed at 2000rpm, b PSO-PI D 100 N.m load torque at 2000 rpm, c PSO-FOPID speed at 2000 rpm, d PSO-FOPID 100 N.m load torque at 2000 rpm

The best FF for each of the three scenarios is shown in the Tables 3, 4, 5, 6, 7, 8 utilizing various optimization techniques with PID and FOPID controller methods. When compared to other optimization strategies, it can be seen that the PSO-PID and PSO-FOPID controllers have the lowest FF. PSO-FOPID controller is superior to PSO-PID in terms of optimal values, settling time, speed response time, and torque ripples.

6 Conclusions

To control the speed of an SRM motor and minimize the integral square error (ISE) of speed, current, and torque ripples, this work proposes a cascaded FOPID and PID controller with a particle swarm optimization technique. The optimal gain values for both the speed and current controllers are obtained along the turn-on (${T}_{O}$), and turn-off (${T}_{F}$) angles, and the maximum, minimum, mean torque, and torque ripples for various speed and load scenarios are identified. Comparisons with existing optimization methods based on cascaded PID and FOPID controllers, such as the SHO, LUS, GA, Ant-Lion, NSGA-II, MOLGSA, GSA, Hybrid MOLGSA, and RGA-SBX algorithms, show that a cascaded fractional order PID controller offers better speed, current, and torque responses, as well as smaller current and torque ripples, under numerous different types of load and speed conditions. Under all load conditions, it has been demonstrated that the PSO-FOPID controller has the best speed response and minimal torque ripples when compared to the PSO-PID controller. Based on the research results, it is possible to conclude that PSO-FOPID-based speed controllers increase SRM drive performance by minimizing torque ripple and settling time and giving a superior current profile due to their high exploitation capacity.

6.1 Future scope

Hardware Implementation of Switched reluctance motor can be done and compared simulation results with hardware results.

Appendix

SRM Drive Parameters	Ratings
Power	60KW
Voltage	240Volts
stator pole arc	30Deg
rotor pole arc	32Deg
stack length	51 mm
stator diameter	82.1 mm
rotor diameter	40 mm
number of windings per pole	72 turns
stator resistance	0.05Ω
inertia	0.05 kg.m2
friction	0.02 N.m.s
No of rotor poles	4
No of stator poles	6