1 Introduction

The economic strength of any country can be judged from the stock market growth in that country. To have a steady financial market the stability of stock market is very crucial. In the fields of finance, mathematics, economy, engineering the prediction of stock market price is a central issue [1]. The challenge is to predict what should be the right time for the investors to buy or sell. The risk associated with the stock market is high since investors invest huge amount of their money in it. This demand for the development of accurate methods that can aid in predicting the stock prices. The procedure to develop such methods is not straightforward since the indices associated with the stock market prices are highly nonlinear, time varying, dynamic, chaotic and nonparametric in nature [2]. These prices are also affected by some of the qualitative macro-economic factors such as political events, investor’s expectations, prices movement of other stocks, psychology of investors etc. [2]. The interest of the investor is to have some methods by which he can predict the stock trend, price or its index. They are dependent on it as these methods provide guard against the market risks. The government requires these methods for monitoring the fluctuations in the market. Considerable effort has been applied by the research community in building various algorithms and models and has achieved good results in predicting the prices of the stock. Basically, the stock market forecasting comes under two categories: in the first category the models are based in the theory of statistics. The second category involves the application of intelligent techniques such as artificial neural network (ANN) [3], particle swarm optimization (PSO) [4], and support vector machine (SVM) [5] etc. The results reported in the literature indicate that these intelligent techniques are much better than the conventional techniques especially in short term forecasting [6]. The stock price also shows dramatic variation in response to various complex factors, hence these intelligent techniques require continuous improvement in their part so that they can handle such variations [7]. Neural networks posses the ability to approximate the intrinsic mathematical relationship existing between the given set of input–output nonlinear data. In this paper we have used two variants of neural networks: RBFN and MLFFNN. Both are nonlinear in nature. The difference between the two is with respect to the functioning of hidden neurons. The other difference is that RBFN contains only one hidden layer whereas MLFFNN may contain more than one hidden layer. Also, the weights connecting the external inputs to the hidden neurons in RBFN are of unity value which is not the case in MLFFNN. Both these techniques along with other intelligent techniques such as fuzzy systems has been successfully applied in various areas [8,9,10,11].

1.1 Contributions of the paper

  1. 1.

    Proposed RBFN based stock price prediction model.

  2. 2.

    Compared the performance of RBFN based prediction model with that of the MLFFNN based model.

  3. 3.

    Recursive parameter optimization equations are obtained by implementing the Back-propagation algorithm.

The organization of the remaining paper is described as follows: Sect. 2 contains the discussion on the related research. Section 3 contains the mathematical description of the RBFN model and its defining equations. In Sect. 4 recursive update equations are obtained by implementing the back propagation algorithm. Section 5 contains the simulation results. Here, the performance of RBFN and MLFFNN based prediction models are tested and compared. In Sect. 6 the conclusion of the paper is given.

2 Related work

In Ref. [12], the authors have applied and compared the performances of the multi-layer perceptron (MLP), dynamic artificial neural network (DANN) and the hybrid neural networks for predicting the market values. The performance is evaluated using the two indicators: mean square error (MSE) and mean absolute deviate (MAD).

In Ref. [13], the authors have applied Probabilistic Neural Network (PNN) to model and predict the direction of return on market index of the Taiwan stock exchange. They have used the historical data to train the network. Furthermore, they have also compared the performance of the PNN with that of generalized methods of moments-Kalman filter and random walk forecasting models and found it superior.

In Ref. [14], the authors have considered both qualitative (political effect) and quantitative aspects in developing the prediction model. The model consists of genetic algorithm based fuzzy neural network (GAFNN) which is used to develop the inference rules for the knowledge based system. This system measures the qualitative factor. Further, the proposed method also integrates the ANN to handle the quantitative factors. The proposed method is the successfully applied on the Taiwan stock market.

In Ref. [15], the authors have proposed an improved model for C-fuzzy decision trees. The proposed model is based on the fuzzy time series. The improvements introduced in the proposed method involves the inclusion of new stopping criteria (which improved the computational time) and the use of fuzzy clustering with weight distance which is calculated using the information gain. The proposed method is also compared with the conventional models and its performance is found to be superior.

In Ref. [16], the authors have applied the adaptive neuro-fuzzy inference system (ANFIS) based controller to control the stock market process model. The proposed model involves the use of a membership function of the Gaussian shaped instead of bell and triangular since the Gaussian provided the better accuracy than the other two. Further, different combinations of 15 past stock prices are evaluated and the best set among them is then applied as the inputs to the ANFIS model. The proposed method is trained and validated using the well-developed stock markets-the Athens and the New York Stock Exchange (NYSE). The performance of the proposed model is found to be better than the other considered conventional methods.

In Ref. [17], the authors have used several ANN’s to forecast daily NASDAQ stock exchange rate. To train the networks, they have applied Back-Propagation algorithm. The training and testing data set consists of 70 and 29 days of samples respectively. The inputs applied to the networks consist of short-term historical stock prices as well as the day of week.

In Ref. [18], the authors have applied the ANN to predict the return price of the Japanese Nikkei 225 index. Initially they have applied back-propagation algorithm to tune the weights of the ANN. The proposed algorithm suffered from the local convergence problem. So to avoid it and to further improve the ANN prediction accuracy the authors have replaced Back-Propagation with the hybrid combination of GA and simulated annealing (SA).

In Ref. [19], the authors have explored the techniques of deep learning for the prediction of stock price. In particular, they have exploited the potential of deep learning method in extracting raw data (in large amount) features and do not require any previous knowledge regarding the predictors.

In Ref. [20], the authors have applied the combination of genetic network programming (GNP), MLP and time series models to predict the stock return. They have used evolutionary algorithms in parallel to ARMA in order to improve the accuracy of the daily return prediction. The MLP is used to classify the data and also the various time series models to forecast the stock return. The proposed method is tested on both turbulent markets and trending markets.

In Ref. [21], the authors have proposed a novel architecture of generative adversarial network (GAN) which consists of two components: MLP (used as a discriminator) and the long short-term memory (LSTM) (applied as an generator) for predicting the stock’s closing price. The proposed method has given much better performance than the other models based deep learning and machine learning in the prediction of closing price of stock.

3 Mathematical structure of RBFN model

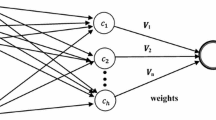
Figure 1 shows the structural view of the RBFN model. In this figure, vector X denotes an input vector containing m number of signals, that is \(X=(x_1,x_2, \ldots ,x_m)\). The neurons implementing the hidden layer are also known as radial centers and in this paper we have used Gaussian radial basis function as an activation for them [22]. There also exists few more choices for the activation function but among then the Gaussian function is more intuitive in a sense that it produces appreciable output if the input vector lies in its vicinity and vice-versa. Thus, each radial center represents one of the input vector and any ith radial center is denoted by \(C_i(k)\).

Fig. 1
figure 1

Structure of RBFN

Full size image

In case of RBFN, the input to hidden layer connections are non-adjustable and are kept constant to a unity value [23]. For the prediction of SISO and MISO type of time series the RBFN contains only single neuron in its output layer. Its induced field is nothing but the weighted sum of the Gaussian function outputs of the radial centers. The output layer weights connecting the radial centers to the output layer neuron is denoted by the vector \(W=[w_1,w_2,w_3,\ldots ,w_q)\). The total count of radial centers is denoted by q where the \(q \ll m\) to avoid over-fitting problem [24]. The RBFN output can be obtained as follows:

$$\begin{aligned} y_r(k)=\sum ^{q}_{i=1}{\psi _i(k)W_i(k)}. \end{aligned}$$
(1)

Symbol \(y_r(k)\) denotes the RBFN output at any kth time instant. The output of any \(C_{i}(k)\) radial center is given by the following mathematical equation

$$\begin{aligned} \psi _i(k)=\psi \left\| X(k)-C_i(k)\right\| , \end{aligned}$$
(2)

where the Gaussian function includes the calculation of Euclidean distance present between the input vector and the radial center \(C_{i}(k)\) and is denoted by the following notation \(\Vert X(k)-C_i(k)\Vert\). The Gaussian function, \(\psi (.)\), has the following definition [24]

$$\begin{aligned} \psi (t)=\exp \left( \frac{-t^2}{2\sigma ^2}\right) \end{aligned}$$
(3)

where \(t=\Vert X(k)-C_i(k)\Vert\) and the vector \(\sigma =(\sigma _1,\sigma _2,\ldots ,\sigma _q)\) is used to represent the width associated with each of the radial center.

4 Update rules for RBFN based prediction model

Figure 2 shown the implementation of RBFN based prediction model. The parameters associated with the RBFN will be sequentially updated during the application of learning algorithm. Their updation will be controlled by the recursive equations that are obtained using the BP method. In this method we first define a cost/objective function whose value needs to be minimized by adjusting the values of the RBFN parameters. Mean square error (MSE) is considered as an objective function. Let this objective function is denoted by \(E_{o}(k)\) and it is defined as follows:

Fig. 2
figure 2

General prediction model based on RBFN

Full size image
$$\begin{aligned} E_{o}(k)=\frac{1}{2}(y_d(k)-y_r(k))^2, \end{aligned}$$
(4)

where the actual stock price value is denoted by \(y_{d}(k)\) and the one predicted by RBFN is \(y_{r}(k)\). Now taking partial derivative of \(E_{o}(k)\) one by one with respect to each of the RBFN parameters we will obtain their corresponding update equations. Let us first find update equation for \(C_{ij}(k)\) where \(i=1\) to m, \(j= 1\) to q. Applying the chain rule we will get

$$\begin{aligned} \frac{\partial E_{o}(k)}{\partial C_{ij}(k)}= & {} \frac{\partial E_{o}(k)}{\partial y_r(k)} \times \frac{\partial y_r(k)}{\partial \psi _j(k)} \times \frac{\partial \psi _j(k)}{\partial C_{ij}(k)} \end{aligned}$$
(5)

or

$$\begin{aligned} \frac{\partial E_{o}(k)}{\partial C_{ij}(k)}= & {} \frac{\partial E_{o}(k)}{\partial y_r(k)} \times \frac{\partial y_r(k)}{\partial \psi _j(k)} \times \frac{\partial \psi _j(k)}{\partial t_j(k)} \times \frac{\partial t_j(k)}{\partial C_{ij}(k)}. \end{aligned}$$
(6)

After evaluating the expression for the individual partial derivatives in Eq. 6 and then adding momentum term (for expediting the learning of RBFN) we will get the following update equation for the radial centers

$$\begin{aligned} C_{ij}\left( k+1\right) =C_{ij}\left( k\right) +\varDelta C_{ij} + \alpha \varDelta C_{ij}(k-1), \end{aligned}$$
(7)

here \(\varDelta C_{ij}=\eta e_i(k)W_j(k)\frac{\psi _j(k)}{\sigma ^2_j(k)}(X_j(k)-C_{ij}(k))\) and \(\eta\) represents the learning rate parameter and its value is set anywhere in the interval (0, 1) and \(\alpha \varDelta C_{ij}(k-1)\) is the momentum term added in the update equation where, \(\alpha\), is known as a momentum constant. Its value is also selected from the 0 and 1 range. By doing the similar analysis we can obtain the update equations for the output layer weights as follows

$$\begin{aligned} \frac{\partial E_{o}(k)}{\partial W_{j}(k)} = \left( \frac{\partial E_{o}(k)}{\partial y_r(k)} \times \frac{\partial y_r(k)}{\partial W_j(k)} \right) . \end{aligned}$$
(8)

Hence each weight element present in the following vector \(W=[w_1,w_2,w_3,\ldots ,w_q]\) will be updated as follows

$$\begin{aligned} W_j (k+1)=W_j (k) +\varDelta W_j+ \alpha \varDelta W_j(k-1), \end{aligned}$$
(9)

where \(\varDelta w_j =\eta e_i(k)\psi _j(k)\). Finally, the update equations for the widths associated with the radial centers are computed as follows

$$\begin{aligned} \frac{\partial E_{o}(k)}{\partial \sigma _{j}(k)} = \left( \frac{\partial E_{o}(k)}{\partial y_r(k)} \times \frac{\partial y_r(k)}{\partial \psi _j(k)} \times \frac{\partial \psi _j(k)}{\partial \sigma _{j}(k)} \right) . \end{aligned}$$
(10)

So, every width element in the vector \(\sigma =(\sigma _1,\sigma _2,\ldots ,\sigma _q)\) will be updated as follows

$$\begin{aligned} \sigma _j(k+1)=\sigma _j(k)+\varDelta \sigma +\alpha \varDelta \sigma (k-1), \end{aligned}$$
(11)

where \(\varDelta \sigma =\eta e_i(k)W_j(k)\frac{\psi _j(k)t^2_j(k)}{\sigma ^3_j(k)}\). A flowchart is shown in Fig. 3 which describes the training steps involved in the RBFN prediction model.

Fig. 3
figure 3

Steps to train the RBFN prediction model

Full size image

5 Simulation results

In this section, performance of RBFN model is tested and compared with that of MLFFNN prediction model. In both these models, same number of hidden nodes is taken which is equal to 20. The value of \(\eta\) and \(\alpha\) are taken to be 0.025 and 0.067 respectively. Total number of inputs to prediction models are 10 and are denoted by input vector \(X= \{x_{1}(k), x_{2}(k),\ldots ,x_{10}(k)\}\). Total 100 input–output samples are used for training purpose [25]. To evaluate the performances of the models we have used average mean square error (AMSE) as a performance indicator and is defined as follows:

$$\begin{aligned} \textit{AMSE}=\frac{1}{N}\sum ^{N}_{i=1}{(y_{d}(k)-y_{r}(k))^2}, \end{aligned}$$
(12)

where N represents the total number of training samples. Further, to get effective results from the prediction models the experimental data requires some pre-processing. In our paper we have performed the normalization of the input–output data (in the \([0,\;1]\) range) using the following formula:

$$\begin{aligned} X_{{ Nor}}=\frac{X-X_{{ min}}}{X_{{ max}}-X_{{ min}}}, \end{aligned}$$
(13)

where \(X_{{ Nor}}\) represents the normalized value of any variable X and \(X_{{ max}}\) and \(X_{{ min}}\) represents its maximum and minimum value respectively. The data set is shown in the Table 1.

Table 1 Input–output data samples [25]
Full size table

The training was performed in an epoch type manner. In one epoch 100 training samples are presented and the average error obtained for the epoch is saved. Total of 2000 epochs are run for training the RBFN and MLFFNN based prediction models. At the end of the final epoch their prediction curves are plotted and compared. The description of 10 inputs given to the prediction models can be found in Ref. [25]. Figure 4 shows the initial stage of training response of prediction models. The response were plotted after the 450th epoch. Note that \(y_{d}(k)\) represents actual stock price and \(y_{n}(k)\) represents stock price predicted by the prediction models. It can be seen that RBFN output is closer to that of desired response as compared to the response obtained with MLFFNN. This shows the superior learning ability of RBFN over MLFFNN.

Fig. 4
figure 4

Prediction models response during initial phase of the training

Full size image

The corresponding average MSE obtained is shown in Fig. 5. From the plot it can be again seen that as the training progressed, the error reduces at a much faster rate in case of RBFN as compared to that obtained in MLFFNN model training phase.

Fig. 5
figure 5

Average MSE obtained during initial phase of training

Full size image

After a sufficient training was done which was continued till 2000 epochs, the responses of RBFN and MLFFNN prediction models after the last epoch is shown in Fig. 6.

Fig. 6
figure 6

Prediction models response after sufficient amount of training

Full size image

From the figure it can be seen that RBFN prediction model response is closer to the desired values as compared to prediction of stock price obtained with MLFFNN based model. This is further proved from the plot of AMSE which is shown in Fig. 7.

Fig. 7
figure 7

AMSE obtained during the training

Full size image

It can be seen easily from the MSE plot that error in case of RBFN decreases much rapidly as the training progressed when compared to error obtained with MLFFNN. This shows the superiority of RBFN model over the conventional MLFFNN model. The average MSE obtained when different values of learning rate are considered (keeping momentum constant to a fixed value) is shown in Fig. 8. From the bar graph it can be easily seen that we get lesser value of MSE in case of RBFN prediction model as compared to that obtained with MLFFNN model.

Fig. 8
figure 8

AMSE obtained during the training with different values of learning rate

Full size image

6 Conclusion

This paper presents the comparative analysis of prediction capabilities of two variants of neural networks: RBFN and MLFFNN. Simulation results indicate that the performance of RBFN based prediction model is found to be better than that obtained with MLFFNN model. A highly nonlinear stock market price data is used for the prediction purpose. The parameter update equations are derived using back-propagation algorithm. The prediction models and AMSE plots responses depicts that RBFN have performed much better than that of MLFFNN.