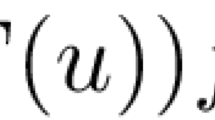Ground state solution for a critical Schrodinger equation involving the p-Laplacian operator and potential term

Abstract

In this article, our aim is to establish a generalized version of Berestycki–Lions theorem about the p-Laplacian operator. As an application of this theorem, we consider the existence and regularity of solution to the critical Schrödinger equation with potential term.

1 Introduction and main results

This paper is concerned with the following type of quasilinear elliptic equations:

$$\begin{aligned} -\Delta _p u+V(x) \vert u\vert ^{p-2}u=\vert u\vert ^{p-2} u+\vert u\vert ^{p^*-2} u, \quad x \in {\mathbb {R}}^N, \end{aligned}$$

(1.1)

where $1<p<N$, $p^*=\frac{Np}{N-p}$ is the Sobolev critical exponent, $\Delta _p u={\text {div}}\left( \vert \nabla u\vert ^{p-2} \nabla u\right)$ is the p-Laplacian operator and the potential term defined by $V(x)=\vert x\vert ^p$. Elliptic equations involving p-Laplacian has been extensively studied by many authors. See for example [2, 7, 8, 10] and the references therein. In recent years the problem (1.1) or the more general one

$$\begin{aligned} -\Delta _p u+V(x)\vert u\vert ^{p-2} u=f(x, u), \quad x \in {\mathbb {R}}^N, \end{aligned}$$

(1.2)

have been studied widely by many authors under variant conditions on the potential V and f. The case of $p = 2$, that is, the standard Laplace problem has been studied very well and has had a lot of results. Especially, in the pioneering work, Berestycki–Lions [3] studied the following equation

$$\begin{aligned} -\Delta u=g(u), \quad x \in {\mathbb {R}}^N, \end{aligned}$$

(1.3)

and obtained the existence result under some assumptions on g. Alves-Souto-Montenegro [1] who extended this result from sub-critical case to critical case by considering the equation

$$\begin{aligned} -\Delta u+u=f(u), \,\,\,\text {in}\,\, {\mathbb {R}}^N. \end{aligned}$$

(1.4)

Remark that if we set $g(s)=f(s)-s$, then the Eq. (1.4) goes back to the Eq. (1.3). Zhang and Zou [15] extended the results of [1] to the following general equation

$$\begin{aligned} -\Delta u=f(u)-V(x) u,\,\, x \in {\mathbb {R}}^N, \end{aligned}$$

(1.5)

where V satisfies, $V \in C\left( {\mathbb {R}}^N,{\mathbb {R}}\right)$, $0<V_0=\inf _{x \in {\mathbb {R}}^N} V(x)$, $V(x) \leqslant V_{\infty }=\lim _{\vert x\vert \rightarrow \infty } V(x)<\infty$, and there exists a function $\phi \in L^2\left( {\mathbb {R}}^N\right) \cap W^{1, \infty }\left( {\mathbb {R}}^N\right)$ such that $\vert x\vert \vert \nabla V(x)\vert \leqslant \phi ^2(x)$ for all $x \in {\mathbb {R}}^N$.

Recently, Yu Su [13] considered the existence result of Eq. (1.5) with $V(x)=\vert x\vert ^2$ and the nonlinearity satisfies $f(u)=u+\vert u\vert ^{2^*-2} u$. In [11], T. Saito extended the result obtained by H. Berestycki and P. L. Lions [3] to the p-Laplacian case. They consider the following equation:

$$\begin{aligned} -\Delta _p u=g(u), \quad x \in {\mathbb {R}}^N, \end{aligned}$$

(1.6)

and obtained the existence result under the assumptions:

$(g_0)$:

$g \in C({\mathbb {R}}, {\mathbb {R}}), g(s)$ is odd.

$(g_1)$:

$$\begin{aligned} -\infty<\liminf _{s \rightarrow 0} \frac{g(s)}{\vert s\vert ^{p-2} s} \le \limsup _{s \rightarrow 0} \frac{g(s)}{\vert s\vert ^{p-2} s}<0. \end{aligned}$$

$(g_2)$:

When $1<p<N$,

$$\begin{aligned} \lim _{s \rightarrow \infty } \frac{g(s)}{s^{p^*-1}}=0 \quad \text{ where } p^*=\frac{N p}{N-p}. \end{aligned}$$

When $p=N$,

$$\begin{aligned} \lim _{s \rightarrow \infty } \frac{g(s)}{\exp \left( \alpha s^{\frac{N}{N-1}}\right) }=0 \text{ for } \text{ any } \alpha >0. \end{aligned}$$

$(g_3)$:

There exists $\zeta _0>0$ such that $G\left( \zeta _0\right) >0$ where $G(s)=\int _0^s g(\tau ) d \tau$.

Zhaosheng Feng and Yu Su in [6] established a generalized version of Lions-type theorems for the p-Laplacian and applied them to show the existence result of Eq. (1.2) under some assumptions on the nonlinearity f with $V(x) = \frac{A}{\vert x\vert ^\alpha }$, where $\alpha$ and A are positive. In this paper, we extend the results of [13] from Laplacian operator to p-Laplacian operator. As far as we know, there is no result similar to that in [13] concerning problem (1.2) with $V(x)=\vert x\vert ^p$ and $f(u)=\vert u\vert ^{p-2} u+\vert u\vert ^{p^*-2} u$ in the p-Laplacian case. Before given our main result we recall the following definition

Definition 1.1

We say that a solution $u\in W_p^{1,p}\left( {\mathbb {R}}^N\right)$ is nontrivial when $u \ne 0$. A nontrivial solution is called a ground-state solution if its energy is minimal among the energy of all nontrivial solutions of (1.1).

Now we state our main result:

Theorem 1.2

Assume that $N> \max {\{2p^2-p,2p\}}$. Then Eq. (1.1) has a nonnegative ground state solution in $W_p^{1,p}\left( {\mathbb {R}}^N\right)$.

We also prove that any nonnegative weak solution of Eq. (1.1) has additional regularity properties.

Theorem 1.3

Assume that $N \geqslant 3$. If u is a nonnegative weak solution of Eq. (1.1), then $u \in L^{\infty }\left( {\mathbb {R}}^N\right)$.

The rest of this paper is organized as follows: Sect. 2 is dedicated to the continuous and compactness Sobolev embeddings. In Sect. 3, we present the proof of Lions-type Theorem. In Sect. 4, we prove Theorem 1.2. Finally in Sect. 5, we present the additional regularity properties, which is the proof of Theorem 1.3.

2 Embedding results

We introduce the following notations. Let

$$\begin{aligned} D^{1,p}\left( {\mathbb {R}}^N\right) :=\left\{ u \in L^{p^*}\left( {\mathbb {R}}^N\right) : \int _{{\mathbb {R}}^N}\vert \nabla u\vert ^p dx<\infty \right\} , \end{aligned}$$

with the semi-norm

$$\begin{aligned} \Vert u\Vert _{D^{1,p}\left( {\mathbb {R}}^N\right) }^p:=\int _{{\mathbb {R}}^N}\vert \nabla u\vert ^p \mathrm {~d} x. \end{aligned}$$

We need the following inequalities

$$\begin{aligned} S\left( \int _{{\mathbb {R}}^N}\vert u\vert ^{p^*} dx\right) ^{\frac{p}{p^*}} \leqslant \int _{{\mathbb {R}}^N}\vert \nabla u\vert ^p \mathrm {~d} x, \quad \forall u \in D^{1,p}\left( {\mathbb {R}}^N\right) , \end{aligned}$$

(2.1)

and

$$\begin{aligned} \bar{\mu } \int _{{\mathbb {R}}^N} \frac{\vert u\vert ^p}{\vert x\vert ^p} \mathrm {~d} x \leqslant \int _{{\mathbb {R}}^N}\vert \nabla u\vert ^p \mathrm {~d} x, \quad \forall u \in D^{1,p}\left( {\mathbb {R}}^N\right) , \end{aligned}$$

(2.2)

where S and $\bar{\mu } =\left( \frac{N-p}{p}\right) ^p$ are the best constants for Sobolev’s and Hardy’s inequalities, respectively. Let

$$\begin{aligned} W_p^{1,p}\left( {\mathbb {R}}^N\right) :=\left\{ u \in D^{1,p}\left( {\mathbb {R}}^N\right) \Bigg | \int _{{\mathbb {R}}^N}\vert x\vert ^p\vert u\vert ^p \mathrm {~d} x<\infty \right\} , \end{aligned}$$

with the norm

$$\begin{aligned} \Vert u\Vert _{W_p^{1,p}\left( {\mathbb {R}}^N\right) }^p:=\int _{{\mathbb {R}}^N}\vert \nabla u\vert ^p \mathrm {~d} x+\int _{{\mathbb {R}}^N}\vert x\vert ^p\vert u\vert ^p \mathrm {~d} x. \end{aligned}$$

Let

$$\begin{aligned} W_{p, \text{ rad } }^{1,p}\left( {\mathbb {R}}^N\right) :=\left\{ u \mid u \in W_p^{1,p}\left( {\mathbb {R}}^N\right) , u(x)=u(\vert x\vert )\right\} , \end{aligned}$$

be the set of radial functions in $W_p^{1,p}\left( {\mathbb {R}}^N\right)$. The first primary motivation of this paper is to establish the continuous and compactness embeddings results.

Proposition 2.1

Let $N \ge 3$. Then the following continuous and compactness embeddings hold:

$$\begin{aligned} \begin{aligned}&W_p^{1,p}\left( {\mathbb {R}}^N\right) \hookrightarrow L^r\left( {\mathbb {R}}^N\right) , \quad r \in \left[ p,p^*\right] , \\&W_p^{1,p}\left( {\mathbb {R}}^N\right) \hookrightarrow \hookrightarrow L^r\left( {\mathbb {R}}^N\right) , \quad r \in \left[ p,p^*\right) . \end{aligned} \end{aligned}$$

In Proposition 2.1, the following embedding is not compact:

$$\begin{aligned} W_p^{1,p}\left( {\mathbb {R}}^N\right) \hookrightarrow L^{p^*}\left( {\mathbb {R}}^N\right) . \end{aligned}$$

Proof of Proposition 2.1

The continuous embedding results: Using Hölder’s inequality and (2.2), we have

$$\begin{aligned} \begin{aligned} \int _{{\mathbb {R}}^N}\vert u\vert ^p \mathrm {~d} x =\int _{{\mathbb {R}}^N}\vert u\vert ^{\frac{p}{2}} \vert x\vert ^{-\frac{p}{2}} \vert u\vert ^{\frac{p}{2}} \vert x\vert ^{\frac{p}{2}} \textrm{d} x&\le \left( \int _{{\mathbb {R}}^N} \frac{\vert u\vert ^p}{\vert x\vert ^p} \mathrm {~d} x\right) ^{\frac{1}{2}}\left( \int _{{\mathbb {R}}^N}\vert x\vert ^p\vert u\vert ^p \mathrm {~d} x\right) ^{\frac{1}{2}}\\&\le \mu ^{-\frac{p}{2}} \Vert u\Vert _{W_p^{1,p}({\mathbb {R}}^N)}^{p} <\infty . \end{aligned} \end{aligned}$$

It follows from Hölder’s inequality that

$$\begin{aligned} \int _{{\mathbb {R}}^N}\vert u\vert ^q \mathrm {~d} x \le \left( \int _{{\mathbb {R}}^N}\vert u\vert ^p \mathrm {~d} x\right) ^{\frac{p^*-q}{p^*-p}}\left( \int _{{\mathbb {R}}^N}\vert u\vert ^{p^*} \mathrm {~d} x\right) ^{\frac{q-p}{p^*-p}}. \end{aligned}$$

This, implies that $W_p^{1,p}\left( {\mathbb {R}}^N\right) \hookrightarrow L^q\left( {\mathbb {R}}^N\right)$ for $q \in \left[ p,p^*\right]$.

The compact embedding result: Since $W_p^{1,p}\left( {\mathbb {R}}^N\right)$ is reflexive, for every sequence $\left\{ u_n\right\}$ that converges weakly to 0 in $W_p^{1,p}\left( {\mathbb {R}}^N\right)$, it has $\left\| u_n\right\| _{L^t\left( {\mathbb {R}}^N\right) } \rightarrow 0$ as $n\rightarrow \infty$, $t \in \left[ p,p^*\right)$.

Note that $\left\{ u_n\right\}$ is bounded, and weakly convergent in $W_p^{1,p}\left( {\mathbb {R}}^N\right)$. Given any $\varepsilon >0$, we divide the domain ${\mathbb {R}}^N$ into three parts:

$$\begin{aligned} \int _{{\mathbb {R}}^N}\vert u_n\vert ^p \mathrm {~d} x=\int _{\vert x\vert <\lambda }\vert u_n\vert ^p \mathrm {~d} x+\int _{\vert x\vert >\frac{1}{\lambda }}\vert u_n\vert ^p \mathrm {~d} x+\int _{\lambda \leqslant \vert x\vert \leqslant \frac{1}{\lambda }}\vert u_n\vert ^p \mathrm {~d} x, \end{aligned}$$

(2.3)

where $\lambda$ is to be determined.

For the first term on the right hand-side of (2.3), we deduce

$$\begin{aligned} \begin{aligned} \int _{\vert x\vert<\lambda }\vert u_n\vert ^p \mathrm {~d} x =\int _{\vert x\vert<\lambda }\vert x\vert ^p\vert x\vert ^{-p}\vert u_n\vert ^p \mathrm {~d} x&\leqslant \lambda ^p \int _{{\mathbb {R}}^N}\vert x\vert ^{-p}\vert u_n\vert ^p \mathrm {~d} x \\&\leqslant C \lambda ^p<\frac{\varepsilon }{3}, \end{aligned} \end{aligned}$$

for all $\lambda \leqslant \lambda _{1, \varepsilon }$. For the second term on the right hand-side of (2.3), We get

$$\begin{aligned} \begin{aligned} \int _{\vert x\vert>\frac{1}{\lambda }}\vert u_n\vert ^p \mathrm {~d} x&=\int _{\vert x\vert >\frac{1}{\lambda }}\vert x\vert ^p\vert x\vert ^{-p}\vert u_n\vert ^p \mathrm {~d} x \\&\leqslant C\vert \frac{1}{\lambda }\vert ^{-p} \int _{{\mathbb {R}}^N}\vert x\vert ^p\vert u_n\vert ^p \mathrm {~d} x \\&\leqslant C \lambda ^p<\frac{\varepsilon }{3}, \end{aligned} \end{aligned}$$

for all $\lambda \leqslant \lambda _{2, \varepsilon }$. For the third term on the right hand-side of (2.3), we choose $\lambda =\min \left\{ \lambda _{1, \varepsilon }, \lambda _{2, \varepsilon }\right\}$ and set

$$\begin{aligned} A_\lambda :=\left\{ x \in {\mathbb {R}}^N\vert \lambda \le \vert x \vert \le \frac{1}{\lambda }\right\} . \end{aligned}$$

According to the Arzela–Ascoli theorem, $\left\{ u_n\right\}$ admits a subsequence $u_{n_k}$ such that $u_{n_k}$ converges uniformly in $A_\lambda$. The sequence $u_n$ converges uniformly to 0 in $A_\lambda$, and hence for n large,

$$\begin{aligned} \int _{A_\lambda }\vert u_n\vert ^p \mathrm {~d} x<\frac{\varepsilon }{3}. \end{aligned}$$

Thus, $\left\| u_n\right\| _{L^p\left( {\mathbb {R}}^N\right) } \rightarrow 0$. By Hölder’s inequality, we have that

$$\begin{aligned} W_p^{1,p}\left( {\mathbb {R}}^N\right) \hookrightarrow \hookrightarrow L^t\left( {\mathbb {R}}^N\right) , \end{aligned}$$

for $t \in \left[ p,p^*\right)$. $\square$

3 Lions-type theorem

We recall a measurable function $u: {\mathbb {R}}^N \rightarrow {\mathbb {R}}$ belongs to the Morrey space with the norm $\Vert u\Vert _{{\mathcal {M}}^{q, \varpi }\left( {\mathbb {R}}^N\right) }$, where $q \in [1, \infty )$ and $\varpi \in (0, N]$, if and only if

$$\begin{aligned} \Vert u\Vert _{{\mathcal {M}}^q, \varpi \left( {\mathbb {R}}^N\right) }^q:=\sup _{R>0, x \in {\mathbb {R}}^N} R^{\varpi -N} \int _{B(x, R)}\vert u(y)\vert ^q \mathrm {~d} y<\infty . \end{aligned}$$

The following lemma is regarding the refined Sobolev inequality with the Morrey norm.

Lemma 3.1

[9] For $N \geqslant 3$, there exists $C>0$ such that for $\iota$ and $\vartheta$ satisfying $\frac{p}{p^*} \leqslant \iota <1$ and $1 \leqslant \vartheta <p^*$, we have

$$\begin{aligned} \left( \int _{{\mathbb {R}}^N}\vert u\vert ^{p^*} \mathrm {~d} x\right) ^{\frac{1}{p^*}} \leqslant C\Vert u\Vert _{D^{1, p}\left( {\mathbb {R}}^N\right) }^{\iota }\Vert u\Vert _{{\mathcal {M}}^{\vartheta ,}, \frac{\vartheta ({\mathbb {N}}-p)}{p}\left( {\mathbb {R}}^N\right) }^{1-\iota }, \end{aligned}$$

for any $u \in D^{1,p}\left( {\mathbb {R}}^N\right)$.

It follows from Lemma 3.1 and $W_p^{1,p}\left( {\mathbb {R}}^N\right) \subset D^{1,p}\left( {\mathbb {R}}^N\right)$, that

$$\begin{aligned} \left( \int _{{\mathbb {R}}^N}\vert u\vert ^{p^*} \mathrm {~d} x\right) ^{\frac{1}{p^*}} \leqslant C\Vert u\Vert _{W^{1, p}_p\left( {\mathbb {R}}^N\right) }^{\iota }\Vert u\Vert _{{\mathcal {M}}^{\vartheta ,}, \frac{\vartheta ({\mathbb {N}}-p)}{p}\left( {\mathbb {R}}^N\right) }^{1-\iota }. \end{aligned}$$

(3.1)

Proposition 3.2

Let $N \geqslant 3$ and $\left\{ u_n\right\} \subset W_p^{1,p}\left( {\mathbb {R}}^N\right)$ be any bounded sequence satisfies:

(Condition A) $\lim _{n \rightarrow \infty } \int _{{\mathbb {R}}^N}\vert u_n\vert ^p \mathrm {~d} x>0$ and $\lim _{n \rightarrow \infty } \int _{{\mathbb {R}}^N}\vert u_n\vert ^{p^*} \mathrm {~d} x>0$. Then the sequence $\left\{ u_n\right\}$ converges strongly to $u \not \equiv 0$ in $L_{\text{ loc } }^p\left( {\mathbb {R}}^N\right)$.

Due to (3.1), we can show the Proposition 3.2 as follows.

Proof of Proposition 3.2

We separate the proof into four steps.

Step 1. Let $\left\{ u_n\right\}$ be a bounded sequence in $W_p^{1,p}\left( {\mathbb {R}}^N\right)$. Up to a subsequence, we assume

$$\begin{aligned} u_n \rightharpoonup u \text { in } W_p^{1,p}\left( {\mathbb {R}}^N\right) , u_n \rightarrow u \text { a.e. in } {\mathbb {R}}^N, u_n \rightarrow u \text { in } L_{loc}^p\left( {\mathbb {R}}^N\right) . \end{aligned}$$

According to (3.1) and Condition A, for a large n, there exists $C_0>0$ such that

$$\begin{aligned} \left\| u_n\right\| _{{\mathcal {M}}^{p, N-p}\left( {\mathbb {R}}^N\right) } \ge C_0>0. \end{aligned}$$

On the other hand, from [9] we note that $\left\{ u_n\right\}$ is bounded in $W_p^{1,p}\left( {\mathbb {R}}^N\right)$ and

$$\begin{aligned} W_p^{1,p}\left( {\mathbb {R}}^N\right) \hookrightarrow L^{p^*}\left( {\mathbb {R}}^N\right) \hookrightarrow {\mathcal {M}}^{p, N-p}\left( {\mathbb {R}}^N\right) . \end{aligned}$$

Then, there exist $\bar{C}_0>0$ such that

$$\begin{aligned} \left\| u_n\right\| _{{\mathcal {M}}^{p, N-p}\left( {\mathbb {R}}^N\right) } \le \bar{C}_0. \end{aligned}$$

Hence,

$$\begin{aligned} C_0 \leqslant \left\| u_n\right\| _{{\mathcal {M}}^{p, N-p}\left( {\mathbb {R}}^N\right) } \leqslant \bar{C}_0. \end{aligned}$$

From the definition of Morrey space and above inequality, we deduce that there exist $\tau _n>0$ and $x_n \in {\mathbb {R}}^N$ such that

$$\begin{aligned} \tau _n^{-p} \int _{B\left( x_n, \tau _n\right) }\vert u_n(y)\vert ^p \mathrm {~d} y \geqslant \left\| u_n\right\| _{{\mathcal {M}}^{p, N-p}\left( {\mathbb {R}}^N\right) }^p-\frac{C_0}{2 n} \ge C_1>0 . \end{aligned}$$

(3.2)

Step 2. To show $\lim _{n \rightarrow \infty } \tau _n \ne \infty$ we first suppose on the contrary that $\lim _{n \rightarrow \infty } \tau _n=\infty$. In view of the boundedness of $\{u_n\}$ and Condition A, we get

$$\begin{aligned} 0<\lim _{n \rightarrow \infty } \int _{{\mathbb {R}}^N}\vert u_n\vert ^{p} \mathrm {~d} y \leqslant C. \end{aligned}$$

It follows from (3.2) that

$$\begin{aligned} \begin{aligned} 0<C_1&\le \tau _n^{-p} \int _{B\left( x_n,\tau _n\right) }\vert u_n\vert ^p \mathrm {~d} y \\&\le C \tau _n^{-p} \quad \rightarrow 0, \text{ as } n \rightarrow \infty . \end{aligned} \end{aligned}$$

Clearly, this is a contradiction.

We show that $\lim _{n \rightarrow \infty } \tau _n \ne 0$. Suppose on the contrary that $\lim _{n \rightarrow \infty } \tau _n=0$. By using the uniform boundedness of $\{u_n\}$ in $W_p^{1,p}\left( {\mathbb {R}}^N\right)$, we have

$$\begin{aligned} \lim _{n \rightarrow \infty }\left( \int _{{\mathbb {R}}^N}\vert u_n\vert ^{p^*} \mathrm {~d} y\right) ^{\frac{p}{p^*}} \leqslant C \lim _{n \rightarrow \infty }\left\| u_n\right\| _{W_p^{1,p}\left( {\mathbb {R}}^N\right) }^p \leqslant \bar{C}. \end{aligned}$$

Applying Hölder’s and Sobolev’s inequalities, for each $z \in {\mathbb {R}}^N$, we get

$$\begin{aligned} \begin{aligned} \int _{B\left( z, \tau _n\right) }\vert u_n\vert ^p \mathrm {~d} y&\le \left( \int _{B\left( z, \tau _n\right) } \textrm{d} y\right) ^{\frac{p^*-p}{p^*}}\left( \int _{B\left( z, \tau _n\right) }\vert u_n\vert ^{p^*} \mathrm {~d} y\right) ^{\frac{p}{p *}} \\&\le S^{-1}\left( \int _{B\left( 0, \tau _n\right) } \textrm{d} y\right) ^{\frac{p^*-p}{p^*}} \int _{B\left( z, \tau _n\right) }\vert \nabla u_n\vert ^p \mathrm {~d} y . \end{aligned} \end{aligned}$$

(3.3)

Covering ${\mathbb {R}}^N$ by balls of radius $\tau _n$ and center $z_m$, in such a way that each point of ${\mathbb {R}}^N$ is contained in at most $N+1$ balls, Using (3.3) and dominate convergent theorem, we find

$$\begin{aligned} \int _{{\mathbb {R}}^N}\vert u_n\vert ^p \mathrm {~d} y&\leqslant \sum _{m=1}^{\infty } \int _{B\left( z_m, \tau _n\right) }\vert u_n\vert ^p \mathrm {~d} y \\&\leqslant S^{-1}\left( \int _{B\left( 0, \tau _n\right) } \textrm{d} y\right) ^{\frac{p^*-p}{p^*}}\left( \sum _{m=1}^{\infty } \int _{B\left( z_m, \tau _n\right) }\vert \nabla u_n\vert ^p \mathrm {~d} y\right) \\&\leqslant (N+1) S^{-1}\left( \int _{B\left( 0, \tau _n\right) } \textrm{d} y\right) ^{\frac{p^*-p}{p^*}} \int _{{\mathbb {R}}^N}\vert \nabla u_n\vert ^p \mathrm {~d} y \\&\leqslant C(N+1) S^{-1}\left( \int _{B\left( 0, \tau _n\right) } \textrm{d} y\right) ^{\frac{p^*-p}{p^*}} \\&= C(N+1) S^{-1}\left( \frac{\omega _{N-1}}{N}\right) ^{1-\frac{p}{p^*}} \tau _n^{N(1-\frac{p}{p^*})}, \end{aligned}$$

where $\omega _{N-1}$ is the volume of the unit sphere in ${\mathbb {R}}^N$. Applying $\lim _{n \rightarrow \infty } \tau _n=0$, we get

$$\begin{aligned} \lim _{n \rightarrow \infty } \int _{{\mathbb {R}}^N}\vert u_n\vert ^p \mathrm {~d} y \leqslant C(N+1) S^{-1}\left( \frac{\omega _{N-1}}{N}\right) ^{1-\frac{p}{p^*}} \lim _{n \rightarrow \infty } \tau _n^{N(1-\frac{p}{p^*})}=0, \end{aligned}$$

which yields a contradiction to $\lim _{n \rightarrow \infty } \int _{{\mathbb {R}}^N}\vert u_n\vert ^p \mathrm {~d} x>0$ given in Condition A. Hence, applying the Bolzano-Weierstrass theorem, up to a subsequence, there exists $\bar{\tau } \in (0, \infty )$ such that $\lim _{n \rightarrow \infty } \tau _n=\bar{\tau } \ne 0$. Up to a subsequence, we have $\tau _n \in \left( \frac{\bar{\tau }}{2}, 2 \bar{\tau }\right)$. Its follows from (3.2) that

$$\begin{aligned} \frac{2^p}{\bar{\tau }^p} \int _{B\left( x_n, 2 \bar{\tau }\right) }\vert u_n(y)\vert ^p \mathrm {~d} y \ge C_1>0, \end{aligned}$$

which gives

$$\begin{aligned} \int _{B\left( x_n, 2 \bar{\tau }\right) }\vert u_n(y)\vert ^p \mathrm {~d} y \ge \frac{C_1 \bar{\tau }^p}{2^p}>0 . \end{aligned}$$

(3.4)

Step 3. We show that $\{x_n\}$ is a bounded sequence. By way of contradiction, we suppose that $\vert x_n\vert \rightarrow \infty$ as $n \rightarrow \infty$. Since $B\left( x_n, 2 \bar{\tau }\right) \subset B^c\left( 0,\vert \vert x_n\vert -2 \bar{\tau }\vert \right)$, we get

$$\begin{aligned} \begin{aligned} \int _{B\left( x_n, 2 \bar{\tau }\right) }\vert u_n(y)\vert ^p \mathrm {~d} y&\le \int _{B^c\left( 0,\vert \vert x_n\vert -2 \bar{\tau }\vert \right) }\vert u_n(y)\vert ^p \mathrm {~d} y \\&=\int _{B^c\left( 0,\vert \vert x_n\vert -2 \bar{\tau }\vert \right) }\vert y\vert ^{-p}\vert y\vert ^p\vert u_n(y)\vert ^p \mathrm {~d} y \\&\le \Vert x_n\vert -2 \bar{\tau }\vert ^{-p} \int _{B^c\left( 0,\vert \vert x_n\vert -2 \bar{\tau }\vert \right) }\vert y\vert ^p\vert u_n(y)\vert ^p \mathrm {~d} y \\&\le C\vert \vert x_n\vert -2 \bar{\tau }\vert ^{-p} \rightarrow 0, \text{ as } n \rightarrow \infty . \end{aligned} \end{aligned}$$

This contradicts (3.4). Hence, $\left\{ x_n\right\}$ is bounded.

Step 4. Note that $\left\{ x_n\right\}$ is bounded, so there exists $0<\tilde{C}<\infty$ such that

$$\begin{aligned} 0 \leqslant \vert x_n\vert <\tilde{C}. \end{aligned}$$

In view of $\lim _{n \rightarrow \infty } \tau _n=\bar{\tau } \ne 0$, up to a subsequence, we have

$$\begin{aligned} B\left( x_n, \tau _n\right) \subset B\left( 0,\vert x_n\vert +\tau _n\right) \subset B(0, \tilde{C}+2 \bar{\tau }). \end{aligned}$$

It follows from (3.2) that

$$\begin{aligned} \begin{aligned} 0<C_1 \bar{\tau }^p&=C_1 \lim _{n \rightarrow \infty } \tau _n^p \\&\le \lim _{n \rightarrow \infty } \tau _n^p \lim _{n \rightarrow \infty }\left( \tau _n^{-p} \int _{B\left( x_n, \tau _n\right) }\vert u_n\vert ^p \mathrm {~d} y\right) \\&=\lim _{n \rightarrow \infty } \int _{B\left( x_n, \tau _n\right) }\vert u_n\vert ^p \mathrm {~d} y \\&\le \lim _{n \rightarrow \infty } \int _{B(0, \tilde{C}+2 \bar{\tau })}\vert u_n\vert ^p \mathrm {~d} y. \end{aligned} \end{aligned}$$

In view of $W_p^{1,p}\left( {\mathbb {R}}^N\right) \hookrightarrow D^{1,p}\left( {\mathbb {R}}^N\right) \hookrightarrow L_{\text{ loc }}^p\left( {\mathbb {R}}^N\right)$, we obtain that

$$\begin{aligned} \int _{B(0, \tilde{C}+2 \bar{\tau })}\vert u\vert ^p \mathrm {~d} y >0, \end{aligned}$$

which implies that $u \not \equiv 0$. $\square$

Lemma 3.3

[12] Let $N \ge 3$ and $p \in (1, N)$. Then there exists $C>0$ such that the inequality

$$\begin{aligned} \vert u(x)\vert \leqslant \frac{C}{\vert x\vert ^\frac{N-p}{p}}\Vert u\Vert _{D^{1, p}\left( {\mathbb {R}}^N\right) },\quad a.e \,\,\text{ on }\,\,{\mathbb {R}}^N, \end{aligned}$$

holds for all $u \in D_{\text{ rad } }^{1,p}\left( {\mathbb {R}}^N\right)$.

Proposition 3.4

Let $N \geqslant 3$ and $\left\{ u_n\right\} \subset W_{p, \text{ rad } }^{1,p}\left( {\mathbb {R}}^N\right)$ be any bounded sequence satisfying: (Condition A). Then the sequence $\left\{ u_n\right\}$ converges strongly to $u \not \equiv 0$ in $L_{\text{ loc } }^p\left( {\mathbb {R}}^N\right)$.

Combining (3.1) with Lemma 3.3, we show Proposition 3.4.

Proof of Proposition 3.4

Let $\left\{ u_n\right\}$ be a bounded sequence in $W_{p, \text{ rad } }^{1,p}\left( {\mathbb {R}}^N\right)$. Similar to Step 1 of Proposition 3.2, we know that there exist $\tau _n>0$ and $x_n \in {\mathbb {R}}^N$ such that

$$\begin{aligned} \tau _n^{-p} \int _{B\left( x_n, \tau _n\right) }\vert u_n(y)\vert ^p \mathrm {~d} y \ge C_1>0. \end{aligned}$$

By an argument analogous to Step 2 of Proposition 3.2, we see that there exists $\bar{\tau } \in (0, \infty )$ such that

$$\begin{aligned} \lim _{n \rightarrow \infty } \tau _n=\bar{\tau }, \end{aligned}$$

and

$$\begin{aligned} \int _{B\left( x_n, 2 \bar{\tau }\right) }\vert u_n(y)\vert ^p \mathrm {~d} y \ge \frac{C_1 \bar{\tau }^p}{2^p}>0 . \end{aligned}$$

(3.5)

We now show $\left\{ x_n\right\}$ is bounded. Suppose by contradiction that $\vert x_n\vert \rightarrow \infty$ as $n \rightarrow \infty$. From Lemma 3.3, we get

$$\begin{aligned} \vert u_n(x)\vert \le \frac{C}{\vert x\vert ^{\frac{N-p}{p}}},\quad \text {a.e in}\,\,{\mathbb {R}}^N. \end{aligned}$$

For any $0< \varepsilon < \left( \frac{C_1 \bar{\tau }^p}{2^p\vert B(0,2 \bar{\tau })\vert }\right) ^{\frac{1}{p}}$, there exists an integer $M>0$ such that for any $n>M$, we have

$$\begin{aligned} \vert u_n(x)\vert \le \frac{C}{\vert \vert x_n\vert -2 \bar{\tau }\vert ^{\frac{N-p}{p}}} \leqslant \varepsilon ,\quad x \in B^c\left( 0,\vert \vert x_n\vert -2 \bar{\tau }\vert \right) . \end{aligned}$$

Since $B\left( x_n, \tau _n\right) \subset B^c\left( 0,\vert \vert x_n\vert -\tau _n\vert \right)$, it follows that

$$\begin{aligned} \int _{B\left( x_n, 2 \bar{\tau }\right) }\vert u_n(y)\vert ^p \mathrm {~d} y \leqslant \varepsilon ^p \int _{B\left( x_n, 2 \bar{\tau }\right) } \textrm{d} y=\varepsilon ^p\vert B(0,2 \bar{\tau })\vert <\frac{C_1 \bar{\tau }^p}{2^p}. \end{aligned}$$

This contradicts (3.5). Hence, $\left\{ x_n\right\}$ is bounded. Using the arguments similar to the step 4, we get

$$\begin{aligned} 0<C_1 \bar{\tau }^p \leqslant \lim _{n \rightarrow \infty } \int _{B(0, \tilde{C}+2 \bar{\tau })}\vert u_n\vert ^p \mathrm {~d} y. \end{aligned}$$

Applying the embedding $W_{p, \text{ rad } }^{1,p}\left( {\mathbb {R}}^N\right) \hookrightarrow D_{\text{ rad } }^{1,p}\left( {\mathbb {R}}^N\right) \hookrightarrow L_{\text{ loc } }^p\left( {\mathbb {R}}^N\right)$, we obtain $u \not \equiv 0$. $\square$

4 Existence of ground state solution of equation (1.1)

As we see, Eq. (1.1) is variational and its solutions are the critical points of the functional defined in $W_p^{1,p}\left( {\mathbb {R}}^N\right)$ by

$$\begin{aligned} J(u):=\frac{1}{p} \int _{{\mathbb {R}}^N}\left( \vert \nabla u\vert ^p+\vert x\vert ^p\vert u\vert ^p\right) \textrm{d} x-\frac{1}{p} \int _{{\mathbb {R}}^N}\vert u\vert ^p \mathrm {~d} x-\frac{1}{p^*} \int _{{\mathbb {R}}^N}\vert u\vert ^{p^*} \mathrm {~d} x. \end{aligned}$$

From Proposition 2.1, we know that the functional $J \in C^1\left( W_p^{1,p}\left( {\mathbb {R}}^N\right) , {\mathbb {R}}\right)$. It is easy to see that if $u \in W_p^{1,p}\left( {\mathbb {R}}^N\right)$ is a critical point of J, i.e.

$$\begin{aligned} \begin{aligned} 0=&\left\langle J^{\prime }(u), \varphi \right\rangle \\ =&\int _{{\mathbb {R}}^N}\left( \vert \nabla u\vert ^{p-2} \nabla u \nabla \varphi +\vert x\vert ^p \vert u\vert ^{p-2}u \varphi \right) \textrm{d} x-\int _{{\mathbb {R}}^N}\vert u\vert ^{p-2} u \varphi \textrm{d} x\\&\quad -\int _{{\mathbb {R}}^N}\vert u\vert ^{p^*-2} u \varphi \textrm{d} x \end{aligned} \end{aligned}$$

for all $\varphi \in W_p^{1,p}\left( {\mathbb {R}}^N\right)$, then u is a weak solution of Eq. (1.1). The Nehari manifold is

$$\begin{aligned} {\mathcal {N}}:=\left\{ u \in W_p^{1,p}\left( {\mathbb {R}}^N\right) \mid \left\langle J^{\prime }(u), u\right\rangle =0, u \ne 0\right\} , \end{aligned}$$

and

$$\begin{aligned} \bar{c}:=\inf _{u \in {\mathcal {N}}} J(u). \end{aligned}$$

We present an inequality, which plays an important role.

Lemma 4.1

For any $u \in W_p^{1,p}\left( {\mathbb {R}}^N\right)$ and $N \geqslant 3$, we have

$$\begin{aligned} \int _{{\mathbb {R}}^N}\vert u\vert ^p \mathrm {~d} x \leqslant \bar{\mu } ^{-\frac{1}{2}}\Vert u\Vert _{W_p^{1,p}\left( {\mathbb {R}}^N\right) }^p. \end{aligned}$$

Proof

Using Hölder’s inequality and (2.2), we get

$$\begin{aligned} \begin{aligned} \int _{{\mathbb {R}}^N}\vert u\vert ^p \mathrm {~d} x&\le \left( \int _{{\mathbb {R}}^N} \frac{\vert u\vert ^p}{\vert x\vert ^p} \mathrm {~d} x\right) ^{\frac{1}{2}}\left( \int _{{\mathbb {R}}^N}\vert x\vert ^p\vert u\vert ^p \mathrm {~d} x\right) ^{\frac{1}{2}} \\&\le \left( \frac{1}{\bar{\mu }}\int _{{\mathbb {R}}^N} \vert \nabla u\vert ^p \mathrm {~d} x\right) ^{\frac{1}{2}}\left( \int _{{\mathbb {R}}^N}\vert x\vert ^p\vert u\vert ^p \mathrm {~d}x+ \int _{{\mathbb {R}}^N} \vert \nabla u\vert ^p \mathrm {~d}x\right) ^{\frac{1}{2}} \\&\le \bar{\mu }^{-\frac{1}{2}}\Vert u\Vert _{D^{1,p}\left( {\mathbb {R}}^N\right) }^{\frac{p}{2}}\Vert u\Vert _{W_p^{1,p}\left( {\mathbb {R}}^N\right) }^{\frac{p}{2}} \\&\le \bar{\mu }^{-\frac{1}{2}}\Vert u\Vert _{W_p^{1,p}\left( {\mathbb {R}}^N\right) }^p, \end{aligned} \end{aligned}$$

where $\bar{\mu } =\left( \frac{N-p}{p}\right) ^p$. $\square$

We will use the version of the Mountain Pass Theorem given in Theorem 1.15 in [14].

Lemma 4.2

• (1) J verifies the hypotheses of the Mountain Pass Theorem. That is, there exists $\rho > 0$ and $w_0 \in W_p^{1,p}\left( {\mathbb {R}}^N\right)$ such that:

  $$\begin{aligned} \inf _{\Vert u\Vert _{W_p^{1,p}\left( {\mathbb {R}}^N\right) }=\rho } J(u)>0\ge J\left( w_0\right) . \end{aligned}$$

• (2) As a consequence of the Mountain Pass Theorem, there exists a bounded Palais-Smale sequence $\left\{ u_n\right\} \subset W_p^{1,p}\left( {\mathbb {R}}^N\right)$ such that

  $$\begin{aligned} J\left( u_n\right) \rightarrow c \text{ and } \left\| J^{\prime }\left( u_n\right) \right\| _{W_p^{-1,p}\left( {\mathbb {R}}^N\right) } \rightarrow 0 \text{, } \text{ as } n \rightarrow \infty , \end{aligned}$$

  where

  $$\begin{aligned} c:=\inf _{\gamma \in \Gamma } \sup _{t \in [0,1]} J(\gamma (t)), \end{aligned}$$

  and

  $$\begin{aligned} \Gamma :=\left\{ \gamma \in C\left( [0,1], W_p^{1,p}\left( {\mathbb {R}}^N\right) \right) \mid \gamma (0)=0, J(\gamma (1))<0\right\} . \end{aligned}$$

• (3) For each $u \in W_p^{1,p}\left( {\mathbb {R}}^N\right) \backslash \{0\}$, there exists a unique $t_u>0$ such that $t_u u \in {\mathcal {N}}$ and

  $$\begin{aligned} J\left( t_u u\right) =\max _{t>0} J(t u). \end{aligned}$$

• (4) We have

  $$\begin{aligned} c=\bar{c}=\overline{\bar{c}}:=\inf _{u \in W_p^{1,p}\left( {\mathbb {R}}^N\right) \backslash \{0\}} \sup _{t \geqslant 0} J(t u)>0. \end{aligned}$$

Proof

• (1) By using Proposition 2.1 and Lemma 4.1, we get

  $$\begin{aligned} \begin{aligned} J(u)&=\frac{1}{p} \int _{{\mathbb {R}}^N}\left( \vert \nabla u\vert ^p+\vert x\vert ^p\vert u\vert ^p\right) \textrm{d} x-\frac{1}{p} \int _{{\mathbb {R}}^N}\vert u\vert ^p \mathrm {~d} x-\frac{1}{p^*} \int _{{\mathbb {R}}^N}\vert u\vert ^{p^*} \mathrm {~d} x\\&\ge \frac{1}{p}\left( 1-\bar{\mu } ^{-\frac{1}{2}}\right) \Vert u\Vert _{W_p^{1,p}\left( {\mathbb {R}}^N\right) }^p-C\Vert u\Vert _{W_p^{1,p}\left( {\mathbb {R}}^N\right) }^{p^*}. \end{aligned} \end{aligned}$$

  Due that $p<\frac{N}{2}$, then $\bar{\mu } >1$ and this implies that

  $$\begin{aligned} 1>\bar{\mu } ^{-\frac{1}{2}}. \end{aligned}$$

  Since $p<p^*$, there exists a sufficiently small positive number $\rho$ such that

  $$\begin{aligned} \inf _{\Vert u\Vert _{W_p^{1,p}\left( {\mathbb {R}}^N\right) }=\rho } J(u)>0. \end{aligned}$$

  Let $u \in W_p^{1,p}\left( {\mathbb {R}}^N\right) \backslash \{0\}$, we have

  $$\begin{aligned} J(t u)&=\frac{t^p}{p}\Vert u\Vert _{D^{1,p}\left( {\mathbb {R}}^N\right) }^p+\frac{t^p}{p} \int _{{\mathbb {R}}^N}\vert x\vert ^p\vert u\vert ^p \mathrm {~d} x-\frac{t^p}{p} \int _{{\mathbb {R}}^N}\vert u\vert ^p \mathrm {~d}x\\&\quad -\frac{t^{p^*}}{p^*} \int _{{\mathbb {R}}^N}\vert u\vert ^{p^*} \mathrm {~d} x. \end{aligned}$$

  Since $p<p^*$, then $\lim _{t\rightarrow +\infty } J(t u)= -\infty$, which implies that there exists $t_u>0$ depend of u such that $J\left( t_u u\right) <0$ and $\left\| t_u u\right\| _{W_p^{1,p}\left( {\mathbb {R}}^N\right) }>\rho$. We take $w_0=t_u u$ and the proof of (1) is completed.

• (2) Applying the mountain pass theorem [14], there exists a Palais-Smale sequence $\left\{ u_n\right\} \subset$ $W_p^{1,p}\left( {\mathbb {R}}^N\right)$ such that

  $$\begin{aligned} J\left( u_n\right) \rightarrow c \text{ and } \left\| J^{\prime }\left( u_n\right) \right\| _{W_p^{-1,p}\left( {\mathbb {R}}^N\right) } \rightarrow 0 \text{, } \text{ as } n \rightarrow \infty . \end{aligned}$$

  Using Lemma 4.1, we get

  $$\begin{aligned} c+o(1)=J\left( u_n\right) =J\left( u_n\right) -\frac{1}{p^*}\left\langle J^{\prime }\left( u_n\right) , u_n\right\rangle \geqslant \frac{1}{N} \left( 1-\bar{\mu } ^{-\frac{1}{2}}\right) \left\| u_n\right\| _{W_p^{1,p}\left( {\mathbb {R}}^N\right) }^p. \end{aligned}$$

  We can deduce form this that $\left\{ u_n\right\}$ is bounded in $W_p^{1,p}\left( {\mathbb {R}}^N\right)$.

• (3) For each $u \in W_p^{1,p}\left( {\mathbb {R}}^N\right)$ with $u \not \equiv 0$, and $t \in (0, \infty )$, we set

  $$\begin{aligned} f_1(t)=J(t u)&=\frac{t^p}{p}\Vert u\Vert _{D^{1,p}\left( {\mathbb {R}}^N\right) }^p+\frac{t^p}{p} \int _{{\mathbb {R}}^N}\vert x\vert ^p\vert u\vert ^p \mathrm {~d} x\\ {}&\quad -\frac{t^p}{p} \int _{{\mathbb {R}}^N}\vert u\vert ^p \mathrm {~d} x-\frac{t^{p^*}}{p^*} \int _{{\mathbb {R}}^N}\vert u\vert ^{p^*} \mathrm {~d} x. \end{aligned}$$

  $f_1^{\prime }(t)=0$ if and only if

  $$\begin{aligned} \Vert u\Vert _{D^{1,p}\left( {\mathbb {R}}^N\right) }^p+\int _{{\mathbb {R}}^N}\vert x\vert ^p\vert u\vert ^p \mathrm {~d} x-\int _{{\mathbb {R}}^N}\vert u\vert ^p \mathrm {~d} x=t^{p^*-p} \int _{{\mathbb {R}}^N}\vert u\vert ^{p^*} \mathrm {~d} x. \end{aligned}$$

  By Lemma 4.1, the left hand of the above equality verifies

  $$\begin{aligned} \Vert u\Vert _{D^{1,p}\left( {\mathbb {R}}^N\right) }^p+\int _{{\mathbb {R}}^N}\vert x\vert ^p\vert u\vert ^p \mathrm {~d} x-\int _{{\mathbb {R}}^N}\vert u\vert ^p \mathrm {~d} x \ge \left( 1-\bar{\mu } ^{-\frac{1}{2}}\right) \Vert u\Vert _{W_p^{1,p}\left( {\mathbb {R}}^N\right) }^p>0. \end{aligned}$$

  We set

  $$\begin{aligned} f_2(t):=t^{p^*-p} \int _{{\mathbb {R}}^N}\vert u\vert ^{2^*} \mathrm {~d} x. \end{aligned}$$

  Since $\lim _{t \rightarrow 0} f_2(t) = 0$, $\lim _{t \rightarrow +\infty } f_2(t) = +\infty$ and $f_2$ is strictly increasing on $(0, +\infty )$, then there exists a unique $0<t_u<\infty$ such that $t_u u \in {\mathcal {N}}$, and $f_1$ takes the maximum at $t_u$.

• (4) For $u \in {\mathcal {N}}$, by the fact that $\left\langle J^{\prime }(u), u\right\rangle =0$ and Lemma 4.1, we have

  $$\begin{aligned} 0=\left\langle J^{\prime }(u), u\right\rangle \geqslant \left( 1-\bar{\mu } ^{-\frac{1}{2}}\right) \Vert u\Vert _{W_p^{1,p}\left( \textbf{R}^N\right) }^p-C\Vert u\Vert _{W_p^{1,p}\left( {\mathbb {R}}^N\right) }^{p^*}. \end{aligned}$$

  It follows that

  $$\begin{aligned} \Vert u\Vert _{W_p^{1, }\left( {\mathbb {R}}^N\right) }^{p^{*}-p} \geqslant C\left( 1-\bar{\mu } ^{-\frac{1}{2}}\right) , \end{aligned}$$

  which gives

  $$\begin{aligned} \Vert u\Vert _{W_p^{1,p}\left( {\mathbb {R}}^N\right) }>C. \end{aligned}$$

  We get

  $$\begin{aligned} J(u) \geqslant \left( \frac{1}{p}-\frac{1}{p^*}\right) \left( 1-\bar{\mu } ^{-\frac{1}{2}}\right) \Vert u\Vert _{W_p^{1,p}\left( {\mathbb {R}}^N\right) }^p>C. \end{aligned}$$

  This implies that J is bounded from below on ${\mathcal {N}}$ and $\bar{c}>0$. It is easy to see from (3) of Lemma 4.2 that $\bar{c}=\overline{\bar{c}}$. Notice that for any $u \in W_p^{1,p}\left( {\mathbb {R}}^N\right) \backslash \{0\}$, there exists a large $\tilde{t}>0$ such that $J(\tilde{t} u)<0$. Define a path $\gamma :[0,1] \rightarrow W_p^{1,p}\left( {\mathbb {R}}^N\right)$ by $\gamma (t)=t \tilde{t} u$. Clearly, $\gamma \in \Gamma$ and $c \leqslant \overline{\bar{c}}$. On the other hand, for each $\gamma \in \Gamma$ let $g(t):=\left\langle J^{\prime }(\gamma (t)), \gamma (t)\right\rangle$. Then $g(0)=0$ and $g(t)>0$ for the small $t>0$. From Lemma 4.1, it follows that

  $$\begin{aligned} \begin{aligned}&J(\gamma (1))-\frac{1}{p^*}\left\langle J^{\prime }(\gamma (1)), \gamma (1)\right\rangle \\&\quad \ge \frac{1}{N}\left( 1-\bar{\mu } ^{-\frac{1}{2}}\right) \Vert \gamma (1)\Vert _{W_p^{1,p}\left( \textbf{R}^N\right) }^p \\&\quad \ge 0. \end{aligned} \end{aligned}$$

  This implies that

  $$\begin{aligned} \left\langle J^{\prime }(\gamma (1)), \gamma (1)\right\rangle \leqslant p^* \cdot J(\gamma (1))<0. \end{aligned}$$

  Therefore, there exists $\tilde{\tilde{t}} \in (0,1)$ such that $g\left( \tilde{\tilde{t}}\right) =0$, that is, $\gamma \left( \tilde{\tilde{t}}\right) \in {\mathcal {N}}$ and $c \geqslant \bar{c}$.

$\square$

In the following Lemma, we estimate the mountain pass level.

Lemma 4.3

Assume that the assumptions of Theorem 3.2 hold. Then

$$\begin{aligned} 0<c<c^*:=\frac{1}{N} S^{\frac{p^*}{p^*-p}}. \end{aligned}$$

Proof

As we all know that the positive solutions of the following problem

$$\begin{aligned} -\Delta _p u=\vert u\vert ^{p^*-2} u, \quad \text{ in } {\mathbb {R}}^N, \end{aligned}$$

must be of the form

$$\begin{aligned} z_\sigma (x):=\frac{C \sigma ^{\frac{N-p}{p(p-1)}}}{\left( \sigma ^{\frac{p}{p-1}}+\vert x\vert ^{\frac{p}{p-1}}\right) ^{\frac{N-p}{p}}}. \end{aligned}$$

For more details, see the recent reference [5]. $z_\sigma$ is called the extremal function of (1.1). We have

$$\begin{aligned} \left\| z_\sigma \right\| _{D^{1,p}\left( {\mathbb {R}}^N\right) }^p=\left\| z_1\right\| _{D^{1,p}\left( {\mathbb {R}}^N\right) }^p=\int _{{\mathbb {R}}^N}\vert z_1\vert ^{p^*} \mathrm {~d} x=\int _{{\mathbb {R}}^N}\vert z_\sigma \vert ^{p^*} \mathrm {~d} x=S^{\frac{p^*}{p^*-p}}. \end{aligned}$$

A simple calculation gives,

$$\begin{aligned} \begin{aligned} \int _{{\mathbb {R}}^N}\vert x\vert ^p\vert z_\sigma \vert ^p \mathrm {~d} x&\le C \int _{{\mathbb {R}}^N}\vert x\vert ^p \left( \sigma ^{\frac{p}{p-1}}+\vert x\vert ^{\frac{p}{p-1}}\right) ^{-(N-p)} \textrm{d} x\\&\le C \int _0^{\infty }\rho ^p \left( \sigma ^{\frac{p}{p-1}}+\rho ^{\frac{p}{p-1}}\right) ^{-(N-p)}\rho ^{N-1} \textrm{d} \rho \\&= C \int _0^{\infty } \rho ^{N+p-1}\left( \sigma ^{\frac{p}{p-1}}+\rho ^{\frac{p}{p-1}}\right) ^{-(N-p)} \textrm{d} \rho \\&=C \int _0^1 \rho ^{N+p-1}\left( \sigma ^{\frac{p}{p-1}}+\rho ^{\frac{p}{p-1}}\right) ^{-(N-p)} \textrm{d} \rho \\&\quad +C \int _1^{\infty } \rho ^{N+p-1}\left( \sigma ^{\frac{p}{p-1}}+\rho ^{\frac{p}{p-1}}\right) ^{-(N-p)} \textrm{d} \rho . \end{aligned} \end{aligned}$$

It is not difficult to see that,

$$\begin{aligned} \int _0^1 \rho ^{N+p-1}\left( \sigma ^{\frac{p}{p-1}}+\rho ^{\frac{p}{p-1}}\right) ^{-(N-p)} \textrm{d} \rho \le \int _0^1 \rho ^{N+p-1}\left( \sigma ^{\frac{p}{p-1}}\right) ^{-(N-p)} \textrm{d} \rho <\infty . \end{aligned}$$

In view of $N>2p^2-p$, we have $N+p-1-\frac{p(N-p)}{p-1}<-1$ and then

$$\begin{aligned} \begin{aligned} \int _1^{\infty } \rho ^{N+p-1}\left( \sigma ^{\frac{p}{p-1}}+\rho ^{\frac{p}{p-1}}\right) ^{-(N-p)} \textrm{d} \rho&\le \int _1^{\infty } \rho ^{N+p-1} \rho ^{-\frac{p(N-p)}{p-1}} \textrm{d} \rho \\&=\int _1^{\infty } \rho ^{N+p-1-\frac{p(N-p)}{p-1}} \mathrm {~d} \rho <\infty . \end{aligned} \end{aligned}$$

This implies that $z_\sigma \in W_{p, \text{ rad } }^{1,p}\left( {\mathbb {R}}^N\right) \subset W_p^{1,p}\left( {\mathbb {R}}^N\right)$.

Note that,

$$\begin{aligned} \int _{{\mathbb {R}}^N}\vert z_\sigma \vert ^p \mathrm {~d} x=\sigma ^p \int _{{\mathbb {R}}^N}\vert z_1\vert ^p \mathrm {~d} x,\quad \int _{{\mathbb {R}}^N}\vert x\vert ^p \vert z_\sigma \vert ^p \mathrm {~d} x=\sigma ^{2p} \int _{{\mathbb {R}}^N}\vert x\vert ^p \vert z_1\vert ^p \mathrm {~d} x, \end{aligned}$$

and

$$\begin{aligned} \lim _{t \rightarrow \infty } J\left( t z_\sigma \right) =-\infty . \end{aligned}$$

Let $\bar{t}_\sigma>t_\sigma >0$ satisfy

$$\begin{aligned} \sup _{t \geqslant 0} J\left( t z_\sigma \right) =J\left( t_\sigma z_\sigma \right) \text{ and } J\left( \bar{t}_\sigma z_\sigma \right) <0 \text{. } \end{aligned}$$

Define $\gamma (t):=t \bar{t}_\sigma z_\sigma$, we get

$$\begin{aligned} c \leqslant \max _{t \in [0,1]} J(\gamma (t))=J\left( t_\sigma z_\sigma \right) . \end{aligned}$$

We have

$$\begin{aligned} \begin{aligned} 0&=\frac{d}{d t}\vert _{t=t_\sigma } J\left( t z_\sigma \right) \\&=\left( t_\sigma ^{p-1}-t_\sigma ^{p^*-1}\right) \left\| z_1\right\| _{D^{1,p}\left( {\mathbb {R}}^N\right) }^p+\sigma ^{2p} t_\sigma ^{p-1} \int _{{\mathbb {R}}^N}\vert x\vert ^p\vert z_1\vert ^p \mathrm {~d} x\\&\quad -\sigma ^{p} t_\sigma ^{p-1} \int _{{\mathbb {R}}^N}\vert z_1\vert ^p \mathrm {~d} x . \end{aligned} \end{aligned}$$

(4.1)

Let $t_0:=\limsup _{\sigma \rightarrow 0} t_\sigma$. We claim that $t_0<\infty$. Otherwise, we assume that $t_0=\infty$. Taking to supper limit as $\sigma \rightarrow 0$ in (4.1), we get

$$\begin{aligned} \begin{aligned}&\limsup _{\sigma \rightarrow 0} t_\sigma ^{p-1}\left( \left\| z_1\right\| _{D^{1,p}\left( {\mathbb {R}}^N\right) }^p+\sigma ^{2p} \int _{{\mathbb {R}}^N}\vert x\vert ^p\vert z_1\vert ^p \mathrm {~d} x\right) \\&\quad = \limsup _{\sigma \rightarrow 0}\left( t_\sigma ^{p^*-1}\left\| z_1\right\| _{D^{1,p}\left( {\mathbb {R}}^N\right) }^p+\sigma ^p t_\sigma ^{p-1} \int _{{\mathbb {R}}^N}\vert z_1\vert ^p \mathrm {~d} x\right) . \end{aligned} \end{aligned}$$

(4.2)

It follows from $p<p^*$ and $t_0=\infty$ that

$$\begin{aligned} \begin{aligned}&\underset{\sigma \rightarrow 0}{\limsup }\, t_\sigma ^{p-1}\left( \left\| z_1\right\| _{D^{1,p}\left( {\mathbb {R}}^N\right) }^p+\sigma ^{2p} \int _{{\mathbb {R}}^N}\vert x\vert ^p\vert z_1\vert ^p \mathrm {~d} x\right) \\&\quad < \underset{\sigma \rightarrow 0}{\limsup }\, t_\sigma ^{p^*-1}\left\| z_1\right\| _{D^{1,p}\left( {\mathbb {R}}^N\right) }^p \\&\quad \leqslant \limsup _{\sigma \rightarrow 0}\left( t_\sigma ^{p^*-1}\left\| z_1\right\| _{D^{1,p}\left( {\mathbb {R}}^N\right) }^2+\sigma ^{p} t_\sigma ^{p-1} \int _{{\mathbb {R}}^N}\vert z_1\vert ^p \mathrm {~d} x\right) . \end{aligned} \end{aligned}$$

This contradicts (4.2). That is, $t_0<\infty$.

We again pass to a limit as $\sigma \rightarrow 0$ in (4.1) to obtain

$$\begin{aligned} 0=\left( t_0^{p-1}-t_0^{p^*-1}\right) \left\| z_1\right\| _{D^{1,p}\left( {\mathbb {R}}^N\right) }^p, \end{aligned}$$

that is

$$\begin{aligned} t_0^{p-1}-t_0^{p^*-1}=0. \end{aligned}$$

Which implies

$$\begin{aligned} t_0=1. \end{aligned}$$

Let $\left\{ \sigma _n\right\}$ be a sequence such that $\sigma _n \rightarrow 0$ as $n \rightarrow \infty$. Up to a subsequence, still denoted by $\left\{ \sigma _n\right\}$, we have

$$\begin{aligned} \frac{t_0}{2}<t_{\sigma _n}. \end{aligned}$$

Hence, we can choose $\tilde{\sigma }>0$ small enough such that

$$\begin{aligned} \frac{t_0}{2}<t_{\tilde{\sigma }} \ne t_0. \end{aligned}$$

Set

$$\begin{aligned} g(t)=\frac{t^p}{p}-\frac{t^{p^*}}{p^*}. \end{aligned}$$

We have

$$\begin{aligned} g^{\prime }(t)=t^{p-1}-t^{p^*-1}. \end{aligned}$$

We get $g^{\prime }\left( t_0\right) =0$, $g^{\prime }(t)<0$ for $t>t_0$ and $g^{\prime }(t)>0$ for $t<t_0$. Hence, g(t) attains its maximum at $t_0$, which means

$$\begin{aligned} g(t)<g\left( t_0\right) =\frac{1}{N}, \end{aligned}$$

for any $t \ne t_0$. Then, from the above calculation and for sufficiently small $\tilde{\sigma }$, we have

$$\begin{aligned} J\left( t_{\tilde{\sigma }} z_{\tilde{\sigma }}\right)= & {} \left( \frac{t_{\tilde{\sigma }}^p}{p}-\frac{t_{\tilde{\sigma }}^{p^*}}{p^*}\right) \left\| z_1\right\| _{D^{1,p}\left( {\mathbb {R}}^N\right) }^p+\frac{\tilde{\sigma }^{2p} t_{\tilde{\sigma }}^p}{p} \int _{{\mathbb {R}}^N}\vert x\vert ^p\vert z_1\vert ^p \mathrm {~d} x-\frac{\tilde{\sigma }^p t_{\tilde{\sigma }}^p}{p} \int _{{\mathbb {R}}^N}\vert z_1\vert ^p \mathrm {~d} x \\\le & {} \left( \frac{t_{\tilde{\sigma }}^p}{p}-\frac{t_{\tilde{\sigma }}^{p^*}}{p^*}\right) \left\| z_1\right\| _{D^{1,p}\left( {\mathbb {R}}^N\right) }^p \\= & {} \left( \frac{t_{\tilde{\sigma }}^p}{p}-\frac{t_{\tilde{\sigma }}^{p^*}}{p^*}\right) S^{\frac{p^*}{p^*-p}} \\< & {} \frac{1}{N} S^{\frac{p^*}{p^*-p}}, \end{aligned}$$

This gives the desired result. $\square$

Lemma 4.4

Assume that the assumption of Theorem 1.2 hold. Let $\left\{ u_n\right\}$ be a $(P S)_c$ sequence of J with $0<c<c^*$. Then

$$\begin{aligned} \lim _{n \rightarrow \infty } \int _{{\mathbb {R}}^N}\vert u_n\vert ^p \mathrm {~d} x>0 \quad \text{ and } \quad \lim _{n \rightarrow \infty } \int _{{\mathbb {R}}^N}\vert u_n\vert ^{p^*} \mathrm {~d} x>0. \end{aligned}$$

Proof

Let $\left\{ u_n\right\}$ be the boundedness $(P S)_c$ sequence in $W_p^{1,p}\left( {\mathbb {R}}^N\right)$. We show $\lim _{n \rightarrow \infty } \int _{{\mathbb {R}}^N}\vert u_n\vert ^p \mathrm {~d} x>0$. Suppose on the contrary that $\lim _{n \rightarrow \infty } \int _{{\mathbb {R}}^N}\vert u_n\vert ^p \mathrm {~d} x=0$. By the definition of $(P S)_c$ sequence, we get

$$\begin{aligned} c+o_n(1)=\frac{1}{p}\left\| u_n\right\| _{W_p^{1,p}\left( {\mathbb {R}}^N\right) }^p-\frac{1}{p^*} \int _{{\mathbb {R}}^N}\vert u_n\vert ^{p^*} \mathrm {~d} x, \end{aligned}$$

and

$$\begin{aligned} o_n(1)=\left\| u_n\right\| _{W_p^{1,p}\left( {\mathbb {R}}^N\right) }^p-\int _{{\mathbb {R}}^N}\vert u_n\vert ^{p^*} \mathrm {~d} x, \end{aligned}$$

(4.3)

which imply

$$\begin{aligned} c+o_n(1)=\left( \frac{1}{p}-\frac{1}{p^*}\right) \left\| u_n\right\| _{W_p^{1,p}\left( {\mathbb {R}}^N\right) }^p . \end{aligned}$$

(4.4)

We deduct that $\lim _{n \rightarrow \infty }\left\| u_n\right\| _{W_p^{1,p}\left( {\mathbb {R}}^N\right) }>0$. Putting this into (4.3), we obtain that $\lim _{n \rightarrow \infty } \int _{{\mathbb {R}}^N}\vert u_n\vert ^{p^*} \mathrm {~d} x>0$. Applying (2.1) and (4.3), we have

$$\begin{aligned} \begin{aligned} \lim _{n \rightarrow \infty } \int _{{\mathbb {R}}^N}\vert \nabla u_n\vert ^p \mathrm {~d} x&\ge \lim _{n \rightarrow \infty } S\left( \int _{{\mathbb {R}}^N}\vert u_n\vert ^{p^*} \mathrm {~d} x\right) ^{\frac{p}{p^*}} \\&=\lim _{n \rightarrow \infty } S\left( \left\| u_n\right\| _{W_p^{1,p}\left( {\mathbb {R}}^N\right) }^p\right) ^{\frac{p}{p^*}} \\&\ge \lim _{n \rightarrow \infty } S\left( \int _{{\mathbb {R}}^N}\vert \nabla u_n\vert ^p \mathrm {~d} x\right) ^{\frac{p}{p^*}}, \end{aligned} \end{aligned}$$

which gives

$$\begin{aligned} S^{\frac{p^*}{p^*-p}} \leqslant \lim _{n \rightarrow \infty } \int _{{\mathbb {R}}^N}\vert \nabla u_n\vert ^p \mathrm {~d} x . \end{aligned}$$

(4.5)

From (4.4) and (4.5), we have

$$\begin{aligned} c \ge \left( \frac{1}{p}-\frac{1}{p^*}\right) S^{\frac{p^*}{p^*-p}}. \end{aligned}$$

This contradicts $c<c^*$, where $c^*$ is the critical level given in Lemma 4.3.

We now prove that $\lim _{n \rightarrow \infty } \int _{{\mathbb {R}}^N}\vert u_n\vert ^{p^*} \mathrm {~d} x>0$. Suppose on the contrary that

$$\begin{aligned} \lim _{n \rightarrow \infty } \int _{{\mathbb {R}}^N}\vert u_n\vert ^{p^*} \mathrm {~d} x=0. \end{aligned}$$

Using the definition of $(P S)_c$ sequence, we get

$$\begin{aligned} c+o_n(1)=\frac{1}{p}\left\| u_n\right\| _{W_p^{1,p}\left( {\mathbb {R}}^N\right) }^p-\frac{1}{p} \int _{{\mathbb {R}}^N}\vert u_n\vert ^p \mathrm {~d} x, \end{aligned}$$

and

$$\begin{aligned} o_n(1)=\left\| u_n\right\| _{W_p^{1,p}\left( {\mathbb {R}}^N\right) }^p-\int _{{\mathbb {R}}^N}\vert u_n\vert ^p \mathrm {~d} x, \end{aligned}$$

which shows $c=0$. This contradicts $c>0$. $\square$

4.1 Proof of Theorem 1.2

From Lemmas 4.2 and 4.3, there exists a bounded Palais-Smale sequence at level $c \in \left( 0, c^*\right)$. According to Lemma 4.4, we get

$$\begin{aligned} \lim _{n \rightarrow \infty } \int _{{\mathbb {R}}^N}\vert u_n\vert ^p \mathrm {~d} x>0 \text{ and } \lim _{n \rightarrow \infty } \int _{{\mathbb {R}}^N}\vert u_n\vert ^{p^*} \mathrm {~d} x>0. \end{aligned}$$

From Proposition 3.2, we have $\left\{ u_n\right\}$ converges weakly and a.e. to $u \not \equiv 0$ in $L_{l o c}^p\left( {\mathbb {R}}^N\right)$. Due to u is a weak solution and Brezis-Lieb Lemma [4], we have

$$\begin{aligned} \begin{aligned} \bar{c}&\le J(u)=J(u)-\frac{1}{p}\left\langle J^{\prime }(u), u\right\rangle =\left( \frac{1}{p}-\frac{1}{p^*}\right) \int _{{\mathbb {R}}^N}\vert u\vert ^{p^*} \mathrm {~d} x \\&\le \lim _{n \rightarrow \infty }\left( \frac{1}{p}-\frac{1}{p^*}\right) \int _{{\mathbb {R}}^N}\vert u_n\vert ^{p^*} \mathrm {~d} x \\&=\lim _{n \rightarrow \infty } J\left( u_n\right) -\frac{1}{p} \lim _{n \rightarrow \infty }\left\langle J^{\prime }\left( u_n\right) , u_n\right\rangle \\&=\lim _{n \rightarrow \infty } J\left( u_n\right) =c=\bar{c}, \end{aligned} \end{aligned}$$

which implies $J(u)=\bar{c}$. Moreover, we can choose $u \geqslant 0$. Therefore, $u \in W_p^{1,p}\left( {\mathbb {R}}^N\right)$ is a ground state solution of Eq. (1.1).

5 Regularity

In this section, we prove that any nonnegative weak solutions of Eq. (1.1) have additional regularity properties.

Lemma 5.1

Assume that all the conditions described in Theorem 1.3 hold. For each $L > 1$, define

$$\begin{aligned} u_L= {\left\{ \begin{array}{ll}u &{} \text{ if } u \le L, \\ L &{} \text{ if } u>L.\end{array}\right. } \end{aligned}$$

For $t>1$, set $\bar{u}_L=u\vert u_L\vert ^{p(t-1)}$ which is in $W_p^{1,p}\left( {\mathbb {R}}^N\right)$. Then we have

$$\begin{aligned} \left( \int _{{\mathbb {R}}^N}\vert u\vert u_L\vert ^{t-1}\vert ^{p^*} \mathrm {~d} x\right) ^{\frac{p}{p^*}} \le C t^p\left[ \int _{{\mathbb {R}}^N}\vert u u_L^{t-1}\vert ^p \mathrm {~d} x+\int _{{\mathbb {R}}^N}\vert u\vert ^{p^*-p}\vert u u_L^{t-1}\vert ^p \mathrm {~d} x\right] . \end{aligned}$$

Proof

Let $u \in W_p^{1,p}\left( {\mathbb {R}}^N\right)$ be a nonnegative weak solution of Eq. (1.1), then

$$\begin{aligned} \int _{{\mathbb {R}}^N} \vert \nabla u \vert ^{p-2}\nabla u \nabla \varphi \textrm{d} x+\int _{{\mathbb {R}}^N}\vert x\vert ^p\vert u \vert ^{p-2} u \varphi \textrm{d} x=\int _{{\mathbb {R}}^N} f(u) \varphi \textrm{d} x, \end{aligned}$$

for any $\varphi \in W_p^{1,p}\left( {\mathbb {R}}^N\right)$, where $f(u)=\vert u\vert ^{p-2} u+\vert u\vert ^{p^*-2} u$. Substituting ${\bar{u}_L}$ into the above equation, we get

$$\begin{aligned} \int _{{\mathbb {R}}^N} \vert \nabla u \vert ^{p-2}\nabla u \nabla {\bar{u}_L} \textrm{d} x+\int _{{\mathbb {R}}^N}\vert x\vert ^p\vert u \vert ^{p-2} u {\bar{u}_L} \textrm{d} x=\int _{{\mathbb {R}}^N} f(u) {\bar{u}_L} \textrm{d} x. \end{aligned}$$

(5.1)

Note that

$$\begin{aligned} \begin{aligned} \int _{{\mathbb {R}}^N}\vert \nabla (u \vert u_L\vert ^{t-1} )\vert ^p \mathrm {~d} x&\le \left[ 2^p+2 ^p(t-1)^p\right] \int _{{\mathbb {R}}^N} u_L^{p(t-1)}\vert \nabla u\vert ^p \mathrm {~d} x \\&\le C t^p \int _{{\mathbb {R}}^N} u_L^{p(t-1)}\vert \nabla u\vert ^p \mathrm {~d} x. \end{aligned} \end{aligned}$$

(5.2)

Since

$$\begin{aligned} \int _{{\mathbb {R}}^N} u u_L^{p(t-1)-1}\vert \nabla u\vert ^{p-2} \nabla u \nabla u_L \mathrm {~d} x=\int _{\{u \le L\}} u^{p(t-1)}\vert \nabla u\vert ^p \mathrm {~d} x \ge 0, \end{aligned}$$

it follows that

$$\begin{aligned} \begin{aligned}&\int _{{\mathbb {R}}^N}\vert \nabla u\vert ^{p-2} \nabla u \nabla \bar{u}_L \mathrm {~d} x \\ =&\int _{{\mathbb {R}}^N} u_L^{p(t-1)}\vert \nabla u\vert ^p \mathrm {~d} x+p(t-1) \int _{{\mathbb {R}}^N} u u_L^{p(t-1)-1}\vert \nabla u\vert ^{p-2} \nabla u \nabla u_L \mathrm {~d} x \\ \ge&\int _{{\mathbb {R}}^N} u_L^{p(t-1)}\vert \nabla u\vert ^p \mathrm {~d} x . \end{aligned} \end{aligned}$$

(5.3)

From (5.2) and (5.3), we deduce that

$$\begin{aligned} \int _{{\mathbb {R}}^N}\vert \nabla (u \vert u_L\vert ^{t-1} )\vert ^p \mathrm {~d} x \le C t^p \int _{{\mathbb {R}}^N} \vert \nabla u \vert ^{p-2}\nabla u \nabla {\bar{u}_L} \textrm{d} x. \end{aligned}$$

(5.4)

We have

$$\begin{aligned} \int _{{\mathbb {R}}^N}\vert x\vert ^p \vert u\vert ^{p-2}u \bar{u}_L \mathrm {~d} x=\int _{{\mathbb {R}}^N}\vert x\vert ^p \vert u\vert ^{p}\vert u_L\vert ^{p(t-1)} \mathrm {~d} x \ge 0. \end{aligned}$$

Using Sobolev’s inequality to get

$$\begin{aligned} \left( \int _{{\mathbb {R}}^N}\vert u\vert u_L\vert ^{t-1}\vert ^{p^*} \mathrm {~d} x\right) ^{\frac{p}{p^*}} \le C \int _{{\mathbb {R}}^N}\vert \nabla (u\vert u_L\vert ^{t-1})\vert ^p \mathrm {~d} x. \end{aligned}$$

(5.5)

It follows from (5.1), (5.4) and (5.5), that

$$\begin{aligned} \begin{aligned}&\left( \int _{{\mathbb {R}}^N}\vert u\vert u_L\vert ^{t-1}\vert ^{p^*} \mathrm {~d} x\right) ^{\frac{p}{p^*}}\\&\quad \le C\left[ \int _{{\mathbb {R}}^N}\vert \nabla (u\vert u_L\vert ^{t-1})\vert ^p \mathrm {~d} x+\int _{{\mathbb {R}}^N}\vert x\vert ^p\vert u \vert ^{p-2} u {\bar{u}_L} \mathrm {~d} x\right] \\&\quad \le C t^p\left[ \int _{{\mathbb {R}}^N} \vert \nabla u \vert ^{p-2}\nabla u \nabla {\bar{u}_L} \mathrm {~d} x+\int _{{\mathbb {R}}^N}\vert x\vert ^p\vert u \vert ^{p-2} u {\bar{u}_L} \mathrm {~d} x\right] \\&\quad \le C t^p\left[ \int _{{\mathbb {R}}^N}\vert u u_L^{t-1}\vert ^p \mathrm {~d} x+\int _{{\mathbb {R}}^N}\vert u\vert ^{p^*-p}\vert u u_L^{t-1}\vert ^p \mathrm {~d} x\right] . \end{aligned} \end{aligned}$$

The proof is completed. $\square$

Proof of Theorem 1.3

Let $\bar{d} \in {\mathbb {R}}^{+}$to be chosen later. Using Hölder’s inequality, we have

$$\begin{aligned} \begin{aligned}&\int _{{\mathbb {R}}^N}\vert u\vert ^{p^*-p}\vert u u_L^{t-1}\vert ^p \mathrm {~d} x \\&\quad = \int _{\{x \mid u \le \bar{d}\}}\vert u\vert ^{p^*-p}\vert u u_L^{t-1}\vert ^p \mathrm {~d} x+\int _{\{x \mid u>\bar{d}\}}\vert u\vert ^{p^*-p}\vert u u_L^{t-1}\vert ^p \mathrm {~d} x \\&\quad \le \bar{d}^{p^*-p} \int _{\{x \mid u \le \bar{d}\}}\vert u u_L^{t-1}\vert ^p \mathrm {~d} x\\&\qquad +\left( \int _{\{x \mid u>\bar{d}\}}\vert u\vert ^{p^*} \mathrm {~d} x\right) ^{\frac{p^*-p}{p^*}}\left( \int _{{\mathbb {R}}^N}\vert u u_L^{\mu -1}\vert ^{p^*} \mathrm {~d} x\right) ^{\frac{p}{p^*}} . \end{aligned} \end{aligned}$$

(5.6)

We choose $\bar{d}$ such that

$$\begin{aligned} \left( \int _{\{x \mid u>\bar{d}\}}\vert u\vert ^{p^*} \mathrm {~d} x\right) ^{\frac{p^*-p}{p^*}} \le \frac{1}{2C t^p}. \end{aligned}$$

So the inequality (5.6) become

$$\begin{aligned} \int _{{\mathbb {R}}^N}\vert u\vert ^{p^*-p}\vert u u_L^{t-1}\vert ^p \mathrm {~d} x&\le \bar{d}^{p^*-p} \int _{\{x \mid u \le \bar{d}\}}\vert u u_L^{t-1}\vert ^p \mathrm {~d} x \nonumber \\&\quad +\frac{1}{2C t^p} \left( \int _{{\mathbb {R}}^N}\vert u u_L^{t-1}\vert ^{p^*} \mathrm {~d} x\right) ^{\frac{p}{p^*}}. \end{aligned}$$

(5.7)

From inequality (5.7) and Lemma 5.1, we get

$$\begin{aligned} \left( \int _{{\mathbb {R}}^N}\vert u u_L^{t-1}\vert ^{p^*} \mathrm {~d} x\right) ^{\frac{p}{p^*}} \le 2 C t^p\left[ 1+\bar{d}^{p^*-p}\right] \int _{{\mathbb {R}}^N}\vert u u_L^{t-1}\vert ^p \mathrm {~d} x. \end{aligned}$$

Taking the limit as $L \rightarrow \infty$ in above inequality, we get

$$\begin{aligned} \left( \int _{{\mathbb {R}}^N}\vert u\vert ^{p^* t} \textrm{d} x\right) ^{\frac{p}{p^*}} \le 2 C t^p\left[ 1+\bar{d}^{p^*-p}\right] \int _{{\mathbb {R}}^N}\vert u\vert ^{p t} \textrm{d} x. \end{aligned}$$

That is

$$\begin{aligned} \Vert u\Vert _{L^{p^* t}\left( {\mathbb {R}}^N\right) } \le C^{\frac{1}{t}} t^{\frac{1}{t}}\Vert u\Vert _{L^{p t}\left( {\mathbb {R}}^N\right) }. \end{aligned}$$

(5.8)

Let $t=\frac{p^*}{p}$. Then

$$\begin{aligned} \Vert u\Vert _{L^{p^* t}\left( {\mathbb {R}}^N\right) } \le C^{\frac{1}{t}} t^{\frac{1}{t}}\Vert u\Vert _{L^{p^*}\left( {\mathbb {R}}^N\right) }. \end{aligned}$$

We can apply (5.8) with $t^2$ in place of t. Then

$$\begin{aligned} \Vert u\Vert _{L^{p^* t^2\left( {\mathbb {R}}^N\right) }} \le C^{\frac{1}{t^2}} t^{\frac{2}{t^2}}\Vert u\Vert _{L^{p^* t}\left( {\mathbb {R}}^N\right) } \le C^{\frac{1}{t}+\frac{1}{t^2}} \mu ^{\frac{1}{t}+\frac{2}{t^2}}\Vert u\Vert _{L^{p^*}\left( {\mathbb {R}}^N\right) }. \end{aligned}$$

Iterating the above process, for every integer n, we get

$$\begin{aligned} \Vert u\Vert _{L^{p^* t^n}\left( {\mathbb {R}}^N\right) } \le C^{\frac{1}{t}+\frac{1}{t^2}+\cdots +\frac{1}{t^n}} t^{\frac{1}{t}+\frac{2}{t^2}+\cdots +\frac{n}{t^n}}\Vert u\Vert _{L^{p^*}\left( {\mathbb {R}}^N\right) }. \end{aligned}$$

We have

$$\begin{aligned} \sum _{i=1}^{\infty } \frac{1}{t^i}=\frac{1}{t-1} \text{ and } \sum _{i=1}^{\infty } \frac{i}{t^i}=\frac{t}{(t-1)^2}. \end{aligned}$$

Passing $n \rightarrow \infty$, we obtain

$$\begin{aligned} \Vert u\Vert _{L^{\infty }\left( {\mathbb {R}}^N\right) } \le C^{\frac{1}{t-1}} t^{\frac{t}{(t-1)^2}}\Vert u\Vert _{L^{p^*}\left( {\mathbb {R}}^N\right) }<\infty . \end{aligned}$$

Consequently, the proof is completed. $\square$