Introduction

Structural reliability, which may greatly affect the generating electricity and endurance life of solid oxide fuel cells (SOFC), has significantly impeded the commercial applications of SOFC. The issues of electrochemical performance degradation of SOFC have been exposed due to the irreversible creep deformations that existed in the SOFC system [1, 2]. The creep deformations that changed the initial mechanical and electrochemical equilibrium could lead to a local electrochemical failure, contact resistance (CR) increasing, and the leakage of gasses [3, 4].

The deformation in a cell embedded in a stack originate from the sintering phase of the manufacturing process, the joining with the components of the single repeating units frame by sealing material, and the reduction of the nickel oxide in the anode [5, 6]. In addition, given that SOFCs are operated at high temperature, creep relieve stresses will bring a local and non-uniform irreversible deformation to a single cell and its connected component. Performance degradation or even failure will happen in the single cell when the creep deformation was accumulated [7], it is important to determine the creep parameters for studying the failure mechanism of SOFC. The data available compiled from the literature on the mechanical properties of SOFCs can meet the most stringent needs in mechanical characterizations [6], while the use of time or temperature-independent values may induce misleading predictions of the stress state. For instance, stress relief, the calculated result by finite element method (FEM) considering creep, will occur over SOFC operating timescales. The sealing area that relies on compression of the cells will tend to relax over time [8]. A finite element simulation on a bonded compliant seal structure of a planar SOFC was performed using a creep-damage model, the results showed that reasonably reducing the thickness of filler metal and foil can decrease the damage of the bonded compliant seal structure [9], the residual stress in the cell and the bonded compliant seal can be decreased by making use of the short-time creep relaxation effect [2]. However, the thickness reduction will lead to an increase of the risk of failures of the cell due to thermal buckling, loss of gas tightness or electrical contact [10]. No detailed analysis has been performed on the influence of creep on the stress evolution process of a single cell in planar SOFC stack.

The single cell of planar SOFC is a multilayer structure consisting of anode, electrolyte, and cathode. Most analyses of the stress in multilayer structure are based on linear elastic analysis. While the creep deformation in the single cell can result in stress relaxation and redistribution in the film/substrate system, very few investigations had been made for the creep analysis of layered structures. An analytical model was developed by Shen and Suresh [11] for steady-state creep deformations in multilayered materials during thermal cycling. The residual stresses, stress relaxation, and curvature during the monotonic temperature change can be predicted by this method, although the deviation of the method has not been explained clearly. An analytical model having closed-form solutions was developed by Zhang et al. [12] to estimate the effect of creep deformation on the stress relaxation and redistributions in the film/substrate bilayer system. Chen et al. [13] presented a model to elucidate either the film or the substrate subjected to creeping deformation. The results obtained by Chen’s model are consistent with the simulated results, Zhang’s creep solution [12] and Hsueh’s viscoelastic solution [14]. However, the creep both in substrate and film should be mentioned together in many cases.

In this paper, considering the creep behaviors of substrate and film synthetically, a model that is more convenient for SOFC is proposed to predict the evolutions of stresses and deformations. It is discussed that how the creep behaviors of anode, electrolyte, and cathode affect the stress and deformation evolution of YSZ with time increasing. A FEM is set up to verify the model.

Analytical model for creep analysis

The relation between strain and curvature of a multilayer structure

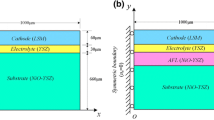
In the present analysis, a single anode-supported SOFC is modeled as an elastic multilayer thin-plate in which each individual component is assumed to be an isotropic and elastic material. As schematically shown in Fig. 1, for the multilayer structure, the thickness and top surface of layer i is ti and hi (i = 1, 2, ..., n), respectively. The corresponding thermoelastic properties are Ei, vi, αi, where E is the Young’s modulus, v is the Poisson’s ratio, and α is thermal expansion coefficient, respectively. Generally, layer 1 can be taken as a substrate, all other layers are films bonded to the layer 1. The coordinate axis x is located at the free surface of layer 1, and the axis y is aligned along the thickness direction of the plate pointing from the bottom surface to the top surface. Thus, the free surface of the uppermost film layer is located at y = hn. According to the Bernoulli-Euler assumption [13] that planar sections perpendicular to the axis remain planar after deformation due to the temperature fluctuation, the normal strain at the location y is

$$ \varepsilon \left(y,t\right)=\left[\left(\rho -{y}_{\mathrm{d}}+y\right)\mathrm{d}\theta -\rho \mathrm{d}\theta \right]/\rho \mathrm{d}\theta $$
(1)

where yd is the distance from the neutral axis for zero normal strain to the coordinate axis x, and ρ is the curvature radius of the neutral axis, dθ is the relative rotation angle of the two adjacent cross sections. Likewise, the normal strain at the coordinate axis x (i.e., y = 0) is

$$ {\varepsilon}_0(t)=\left[\left(\rho -{y}_{\mathrm{d}}\right)\mathrm{d}\theta -\rho \mathrm{d}\theta \right]/\rho \mathrm{d}\theta $$
(2)
Fig. 1
figure 1

Schematic of the multilayer structure and the coordinate system

Full size image

Substituting Eq. (2) into Eq. (1), the total strain in the multilayer system can be expressed as

$$ \varepsilon \left(y,t\right)={\varepsilon}_0(t)+k(t)y\ \left(0\le y\le {h}_n\right) $$
(3)

where k(t) = 1/ρ is the curvature of the neutral axis. It should be noted that the time-dependent deformation of the system is considered due to the introduction of creep deformation in the following section. Consequently, ε0(0) and k(0) denote the initial reference strain at the bottom surface of the substrate and initial curvature, respectively.

Creep deformation in the multilayer structure

When creep deformation is considered in the system, based on the generalized Hooke’s law, the constitutive relationship taking into account the thermal mismatch and creep deformation, simultaneously, can be expressed as

$$ {\sigma}_i\left(y,t\right)={E}_i^{\ast}\left[{\varepsilon}_i\left(y,t\right)-{\alpha}_i\varDelta T-{\varepsilon}_i^{cr}\left(y,t\right)\right]\kern0.5em \left(i=1,2,...n\right) $$
(4)

where Ei* is the biaxial modulus defined as Ei* = Ei /(1-νi), ΔT is the change of temperature, and εicr is the accumulated creep strain in layer i. For primary and the stationary creep regime, the inelastic stress-creep strain of the individual layer is governed by the classical power law model

$$ {\dot{\varepsilon}}_i^{cr}=A{\sigma}_i^n $$
(5)

in which the superscript dot denotes the derivative with respect to time t, A is the creep constant, and n is the stress exponent.

Without the action of external loading, the equilibrium equations for the axial force and bending moment of the multilayer system are given as

$$ \sum \limits_{i=1}^n{\int}_{h_{i-1}}^{h_i}{\sigma}_i\left(\varsigma, t\right) d\varsigma =0 $$
(6)
$$ \sum \limits_{i=1}^n{\int}_{h_{i-1}}^{h_i}{\sigma}_i\left(\varsigma, t\right)\varsigma d\varsigma =0 $$
(7)

It needs to point out that when i = 1, hi-1 (i.e. h0) is defined as zero. When t = 0, the creep strain is absent, by substituting Eqs. (3) and (4) into Eqs. (6) and (7), one can yield

$$ {\varepsilon}_0(0){C}_1+k(0){C}_2=N $$
(8)
$$ {\varepsilon}_0(0){C}_2+k(0){C}_3=M $$
(9)

in which

$$ {\displaystyle \begin{array}{l}{C}_1=\sum \limits_{i=1}^n{E}_i{t}_i\kern0.5em {C}_2=\frac{1}{2}\sum \limits_{i=1}^n{E}_i\left({h}_i^2-{h}_{i-1}^2\right)\\ {}N=\sum \limits_{i=1}^n{E}_i{\alpha}_i\varDelta T{t}_i\kern0.5em {C}_3=\frac{1}{3}\sum \limits_{i=1}^n{E}_i\left({h}_i^3-{h}_{i-1}^3\right)\\ {}M=\frac{1}{2}\sum \limits_{i=1}^n{E}_i{\alpha}_i\varDelta T\left({h}_i^2-{h}_{i-1}^2\right)\end{array}} $$

Thus, ε0(0) and k(0) can be by obtained by Eqs. (8) and (9)

$$ {\varepsilon}_0(0)=\left({C}_2M-{C}_3N\right)/\left({C}_2^2-{C}_1{C}_3\right) $$
(10)
$$ k(0)=\left({C}_2N-{C}_1M\right)/\left({C}_2^2-{C}_1{C}_3\right) $$
(11)

Then, the initial thermoelastic stresses responsible for ensuing creep response in layer i can be calculated from

$$ {\sigma}_i\left(y,0\right)={E}_i^{\ast}\left[{\varepsilon}_0(0)+k(0)y-{\alpha}_i\varDelta T\right]\kern0.5em \left(i=1,2,...n\right) $$
(12)

When t>0, the creep deformation occurs within the system. By differentiating Eqs. (6) and (7) with respect to t, along with some algebraic manipulation, the reference strain rate \( {\dot{\varepsilon}}_0(t) \) and curvature change rate \( \dot{k}(t) \) can be obtained by

$$ {\dot{\varepsilon}}_0(t)=\left({C}_2Q-{C}_3P\right)/\left({C}_2^2-{C}_1{C}_3\right) $$
(13)
$$ {\dot{k}}_0(t)=\left({C}_2P-{C}_1Q\right)/\left({C}_2^2-{C}_1{C}_3\right) $$
(14)

in which

$$ {\displaystyle \begin{array}{l}P=\sum \limits_{i=1}^n{\int}_{h_{i-1}}^{h_i}{E}_i^{\ast }{\dot{\varepsilon}}_i^{cr}\left(y,t\right) dy\\ {}Q=\sum \limits_{i=1}^n{\int}_{h_{i-1}}^{h_i}{E}_i^{\ast }{\dot{\varepsilon}}_i^{cr}\left(y,t\right) ydy\end{array}} $$

Again, making use of Eqs. (3) and (4), and carrying out the derivative with respect to time, the total strain rate and the stress rate in the system can be written as

$$ \dot{\varepsilon}\left(y,t\right)={\dot{\varepsilon}}_0(t)+\dot{k}(t)y $$
(15)
$$ {\dot{\sigma}}_i\left(y,t\right)={E}_i^{\ast}\left[{\dot{\varepsilon}}_0(t)+\dot{k}(t)y-{\dot{\varepsilon}}_i^{cr}\right] $$
(16)

It is evident that a combination of Eqs. (5), (14), (15), and (16) gives the partial differential governing equations for the development of stress and deformation with time in the system. Once the initial condition (i.e., Eq. (12)) is prescribed, the finite difference method is validated to be efficient for solving governing equations incrementally. For example, at any given time, the stress evolve with a time step can be calculated by

$$ {\sigma}_i\left(y,t+\varDelta t\right)={\sigma}_i\left(y,t\right)+{\dot{\sigma}}_i\left(y,t\right)\varDelta t $$
(17)

In this paper, all the iterative steps are implemented using Comsol Multiphysics.

Model geometry of the single cell of SOFC

The single cell of planar SOFC is a triple-layer structure consisting of anode, electrolyte, and cathode. Figure 2 illustrates the fabrication process of Ni-YSZ/YSZ/LSM single cells. First, the resultant NiO/YSZ powders were uniaxially pressed as a green substrate. Proper amount of YSZ powders and the substrate were then co-pressed to form a green bilayer and subsequently co-fired at 1400 °C in air for 4 h to densify the YSZ film. Cathode was prepared on the electrolyte with a screen-printing technique using slurry made of La0.5Sr0.4MnO3 (LSM). Single cells were achieved after calcinations at 1100°C for 2 h. Finally, NiO in anode have to be reduced to Ni at 850 °C in hydrogen.

Fig. 2
figure 2

Schematic protocol for preparing infiltrated electrodes

Full size image

Finite element model of the single cell of SOFC

An axisymmetric finite element model (FEM) was generated by the commercial code Abaqus following the geometry shown in Fig. 2d. The thickness of Ni-YSZ, YSZ, and LSM are 390 μm, 10 μm, and 20 μm, respectively. The length of the cell is 8.4 mm (4.2 mm in the axisymmetric model). The symmetric axis is located at the left side of the cell. The left node on the bottom face was fixed to make sure there is no large displacement during the simulation. Using the CAX4R bilinear axisymmetric quadrilateral element from the Abaqus element library, the solution was demonstrated to be mesh independent when the number of the elements is greater than 104,000.

Results and discussion

The available thermoelastic material properties in the literature for solid, fully dense material samples relevant to SOFCs, are summarized in Table 1 as a function of temperature. Where there is a variation of material properties such as E with temperature a linear interpolation is assumed between the data points quoted from the literature.

Table 1 Material properties of SOFC materials
Full size table

At high temperature, thermal stresses generate because of the mismatch CTE between layers of SOFC. Previous study indicates that stresses are relieved by plastic flow for temperature above 1200 °C [22]. Considering the behavior of plastic flow under high temperature, the fictitious zero-stress temperature for the half-cell composed of anode and electrolyte is supposed to be 1200 °C in the present study [22, 23]. When the half-cell is cooled to operation temperature of 800 °C from zero-stress temperature, both the cooling temperature difference ΔT1 and ΔT2 are − 400 °C. While ΔT3 for cathode is 300 °C due to the calcinations temperature is 1100 °C. After the initial thermal stress at 800 °C is calculated, the creep analysis of 10,000 h is carried out in the following step.

The evolutions of stress and strain in the single cell can be calculated by the analytical model and FEM described in “Analytical model for creep analysis” and “Finite element model of the single cell of SOFC” sections, respectively. Here we define the stress along X-direction as the axial stress (σ1). Correspondingly, the creep strains are defined as axial strain (ε1), if the effect of clamping load (a single cell in an SOFC stack have to endure a clamping load) on the stress and deformation is not taken into account.

Initial residual stress in the single cell

Assuming that there is no creep deformation occurred in the cell until anode (NiO-YSZ) has been reduced. That is, only elastic deformation occurred during the process of sintering, calcinations, and reduction. The initial residual stress in three layers is shown in Fig. 3. It can be seen that the results calculated by the proposed model are in excellent agreement with finite element simulation. The anode substrate undergoes a stress transition from − 6.38 MPa (for y = 0) to 13.06 MPa (for y = 0.390 mm) along the thickness direction. The initial zero stress axis of the cell is located at y = 0.126 mm. The stress in electrolyte film (YSZ) ranges from − 136.49 to − 135.43 MPa. In cathode film (LSM), the stress is changed from 4.97 to 5.77 MPa.

Fig. 3
figure 3

Residual stress in Ni-YSZ, YSZ, and LSM along Y direction

Full size image

Creep stress and deformation in the single cell

The initial equilibrium state, residual stress, and deformation, will change due to anode, electrolyte, and cathode tending to creep when they are subjected to stress at high temperatures. The variation of the stress and deformation in electrodes can be calculated according to the foregoing proposed model.

Anode

Figure 4a shows the evolution of stress in anode. For the legends in Fig. 4a, the σ1(y = 0) and σ1(y = 0.39) denote the equal bi-axial stress in the free surface of anode located at y = 0, and the surface of anode at the anode/electrolyte interface located at y = 0.39 mm, respectively. It can be seen that both of the stresses drop dramatically at the first time but decrease slowly with the time increasing. The stress in the free surface of anode decreases from − 6.38 MPa in the elastic step to − 0.16 MPa at t = 10,000 h during creep. Correspondingly, the change of stress in anode near the anode/electrolyte interface is from 13.06 to 0.28 MPa.

Fig. 4
figure 4

The evolutions of a stress and b accumulated creep strain in anode at the free surface (y = 0) and that near the anode/electrolyte interface (y = 0.39 mm)

Full size image

The evolutions of the accumulated creep strains with time in anode are given in Fig. 4b. Generally, a high stress will lead to a large creep strain rate according to Eq. (5). With the time increasing, the accumulated creep strain in anode increases dramatically and thus leads to the suddenly decreased stress.

Electrolyte and cathode

The evolution of stress in electrolyte is shown in Fig. 5. For electrolyte, the initial stress (at the center of the electrolyte) is − 135.96 MPa, while − 6.92 MPa after creep of 10,000 h. The stress relaxation rate of electrolyte can be obtained as 94.91%. In comparison, the evolution of the stress in cathode is remarkably different from that in anode and electrolyte, as shown in Fig. 6. In the one hand, the stress relaxation rate is only 57.36% compared with that of anode and electrolyte. On the other hand, the stress starts at the initial stress, increases quickly to a peak value (19.25 MPa at 424 h), and then decrease gradually to a minimum (2.29 MPa at 10000 h). This unexpected overshoot behavior in cathode during creep process in contrast to the case of anode and electrolyte can be attributed to the creep rate mismatch [24] between anode and cathode. In other word, as the anode dominates creep deformation of overall cell (shown in the next section), the cathode is forced to tension, resulting in an increase in stress for maintaining the displacement continuity. When the creep rate induced by stress in cathode is fast enough to pursue the overall deformation, sequentially, the onset of stress drooping in cathode can be observed. In this sense, the overshoot behavior of stress in cathode can regarded as the creep resistance during initial stage of creep.

Fig. 5
figure 5

The stress and accumulated creep strain in electrolyte

Full size image
Fig. 6
figure 6

The stress and accumulated creep strain in cathode

Full size image

The effect of the creep behaviors of electrodes on the stress evolution

After closer inspection in regard to those accumulated creep strains obtained above, we find that the creep deformation of electrolyte (− 6.23e-6 at 10000 h) is so small that it can be ignored. Consequently, the problem arising from the inspection is that which layer may play significant effect on the stress evolution of a single cell during creep. Therefore, three different situations that the absence of creep deformation in NiO-YSZ, YSZ and LSM are investigated, respectively.

The stresses in electrolyte YSZ for different cases calculated by the analytical model and FEM are shown in Fig. 7. Upon neglecting creep contribution from different component, one can observe various stress relaxation behavior. When the creep behavior of anode is not considered, the stress in YSZ displays the least stress shift relative to the initial stress at the operating temperature of 800 °C. Therefore, one can conclude that the creep contribution of anode plays the most important role in the evolution of stress in the triple-layer structure. While the creep deformation of cathode is neglected, as shown in Fig. 7, the moderate stress relaxation rate of about 51.15% can be obtained after 10,000 h, reflecting the secondary importance of creep deformation in cathode for the structure stress relaxation. In contrast, the creep behavior of electrolyte can be ignored, because it brought little change of the stress evolution compared with the normal case that the creep behavior of all the components are regarded.

Fig. 7
figure 7

Comparison of the stresses in electrolyte in different situations

Full size image

The role of creep contribution for respective layer can also confirmed by the changes of the curvature of the single cell. The effects of creep behavior for anode, electrolyte, and cathode, respectively, are reproduced from Fig. 8, which is similar with that of the residual stresses in Fig. 7. It can be seen that the curvatures are increased with time and both the creep behaviors of anode and cathode cannot be ignored.

Fig. 8
figure 8

Comparison of the curvatures of the single cell in different situations

Full size image

It should be noted that, although these obtained results are based on the particular geometry in terms of anode-supported SOFC, the methodology and the model incorporating creep deformation for multilayer system presented in this paper are general. In principle, the creep deformation and stress relaxation within a multilayered system are dependent on the thickness of individual layer and corresponding material parameter related to it, according to Eqs. (13) and (14). That is to say, it is possibility to study other types of planar SOFC, such as cathode-supported scenario, as long as we know the corresponding input parameter including the structure parameters and creep properties. In addition, during reduction process, several complicated chemical strain [25], plastic deformation [26], and novel accelerated creep [27] were introduced, which can actually modify the initial stresses, hence ensuing creep responds, whereas are not considered in our model. Given that SOFC is operated at high temperature, creep and stress relaxation of the multilayer structure will impact the contact resistance of SOFC [28], a more sophisticated model incorporating this phenomenon during reduction may be considered for further study for precise prediction of the creep responds.

Conclusions

The single cell of SOFC is a triple-layer structure operating at high temperature. The creep behaviors of anode, electrolyte, and cathode can result in a stress relaxation and redistribution, and then bring a local and non-uniform irreversible deformation to the single cell and its connected component. In this study, an analytical model was presented to study the stress evolution of the SOFC. The results obtained by this method are in agreement with that calculated by FEM. The stresses both in anode and electrolyte will drop dramatically at the first time but decrease slowly with the time increasing. While the stress in cathode is first increased and then decreased. The evolution of stress in the single cell is greatly affected by the creep behavior of anode and cathode but little by electrolyte.