Fifty Years with the Cox Proportional Hazards Regression Model

Abstract

The 1972 paper introducing the Cox proportional hazards regression model is one of the most widely cited statistical articles. In the present article, we give an account of the model, with a detailed description of its properties, and discuss the marked influence that the model has had on both statistical and medical research. We will also review points of criticism that have been raised against the model.

1 Introduction

Many biostatistical problems deal with the way in which aspects of the distribution of a certain outcome variable, Y is related to covariates (or explanatory variables), $\varvec{z}=(z_1,\dots ,z_p)$ (e.g., Andersen and Skovgaard5). Standard statistical models in this area include the linear regression model $Y=\varvec{\beta }^\mathsf{T}\varvec{z}+\varepsilon$ for a quantitative Y where the error terms $\varepsilon _1,\dots ,\varepsilon _n$ are i.i.d. mean-zero random variables, some times assumed to follow a normal distribution. A less restrictive model assumes $Y_1,\dots ,Y_n$ to be conditionally independent given $\varvec{z}_1,\dots ,\varvec{z}_n$ with conditional expectations $E(Y_i\mid \varvec{z}_i)=\varvec{\beta }^\mathsf{T}\varvec{z}_i$ that are linear in the covariates but with no further distributional assumptions. In either case, the $\beta _j$-coefficients have the interpretation of mean differences for Y for a one-unit difference in the associated covariate $z_j$. For a binary Y, a standard regression model is the logistic model $\log (P(Y=1\mid \varvec{z})/(1-P(Y=1\mid \varvec{z})))=\beta _0+\varvec{\beta }^\mathsf{T}\varvec{z}$ where the $\beta _j$-coefficients ($j=1,\dots ,p$) are log(odds ratios) for the event $\{Y=1\}$ for a one-unit difference in the associated covariate $z_j$.

In survival analysis, the outcome is the survival time, say T, measured from a well-defined time origin, such as time of disease diagnosis, time of treatment initiation, or time of randomization, to the occurrence of an event of interest, often death from any cause. Thus, in survival analysis, the outcome variable is quantitative and one may wonder if standard linear regression models, as just described, would be applicable? Similarly, if interest focuses on the survival status (dead or alive) at a certain time point, $\tau$ then one may wonder whether a logistic regression model for the binary outcome $Y=I(T\le \tau )$ (where I(A) is the indicator for the event A) would be applicable? In both cases, the answer is ‘not directly’ because, in survival analysis, one has to face the problem of incomplete observation of T caused by right-censoring. Thus, practical restrictions in data collection will typically have the consequence that, for some subjects i, only the information that the survival time $T_i$ exceeds a certain observed value, say $C_i$, is available. This would be the case if, at the time of analysis, subject i is still alive and it is not known when that subject will ultimately die. Alternatively, subject i may drop out of the study (at time $C_i$) before its planned termination. In both cases, the observation of $T_i$ is said to be right-censored at $C_i$ and the presence of censoring has the consequence that standard methods such as linear or logistic regression analysis are not directly applicable and alternative methods of inference are needed.

Before discussing such alternatives, it should be mentioned that a natural question that arises is whether the available, incompletely observed survival times allow valid inference for the distribution of T. This is the assumption of independent censoring meaning that the knowledge at time t that a subject is still alive and uncensored should carry no information on the survival time T over and above the fact that $T>t$. This is a crucial assumption for any survival analysis technique, an assumption that, unfortunately, is untestable based on the available incomplete data. Thus, in any study involving survival analysis, it should be considered whether the mechanisms causing censoring can be assumed to be ‘independent’.

Returning to the problem of doing regression analysis for survival data, an obvious approach would be to try to adapt the linear regression model, e.g. by letting $Y=\log (T)$ and assuming $Y=\varvec{\beta }^\mathsf{T}\varvec{z}+\varepsilon$ combined with a suitable parametric choice for the distribution of the error terms. Possible such choices would be a normal distribution or an extreme value distribution, the latter corresponding to an assumption of T following a Weibull or, more specially, an exponential distribution. However, since little information on the shape of the right-hand tail of the distribution of T is available due to censoring, one is typically reluctant to impose such parametric assumptions. This was the situation when the paper by Cox 13 was conceived. In this article, we will describe the Cox proportional hazards regression model with a focus on how inference is done in the model and on the statistical properties of the resulting estimators. We will also give an account of the influence that the model has had in the field of statistics over the past 50 years and discuss some points of criticism of the model that have been put forward. An example from liver cirrhosis is used as illustration.

2 The Cox Model

We let T be the survival time measured from the chosen time origin. For the moment we will assume that T is a proper random variable, i.e., the event of interest is all-cause death or another event which will eventually happen to all subjects under study. In later sections, we will also study events which do not necessarily occur for all subjects, such as death from a specific cause. Let $S(t)=P(T>t)$ be the survival distribution function which we assume to be absolutely continuous with density f. By the assumption for T, we will have that $S(t)\rightarrow 0$ as $t\rightarrow \infty$. The hazard function for T is then

$$\begin{aligned} \lambda (t)=\lim _{\Delta t\rightarrow 0}\frac{P(T\le t+\Delta t\mid T>t)}{\Delta t}=\frac{f(t)}{S(t)} \end{aligned}$$

and has the interpretation as the instantaneous risk per time unit of failing just after time t given survival till t, i.e. $\lambda (t)\approx P(T\le t+\Delta t\mid T>t)/\Delta t$ when $\Delta t>0$ is small. It follows that S(t) can be recovered from the hazard via the relation

$$\begin{aligned} S(t)=\exp \left( -\int _0^t\lambda (u)du\right) , \end{aligned}$$

so, the hazard provides a way of characterizing the distribution of T. This has for long been a well-established fact, but it was an important novel contribution of Cox 13 to use the hazard function as the basis for modeling the distribution of T in relation to covariates $\varvec{z}=(z_1,\dots ,z_p)$. This was done by letting

$$\begin{aligned} \lambda (t;\varvec{z})=\lambda _0(t)\exp \left( \varvec{\beta }^\mathsf{T}\varvec{z}\right) , \end{aligned}$$

(1)

where $\lambda _0(t)\ge 0$ is an unspecified function of time t. Note that, by modeling the hazard function that conditions on the past information at any time t, and by letting $\lambda _0(t)$ be completely unspecified, one avoids making strict assumptions about the right-hand tail of the distribution. Apart from modeling survival data via the hazard function, the Cox model was innovative by being semi-parametric. Thus, the combination of a linear predictor $\varvec{\beta }^\mathsf{T}\varvec{z}$ including a finite number, p of regression coefficients $\varvec{\beta }$ with an unspecified (‘non-parametric’) baseline hazard $\lambda _0(t)$ raised the question of how to do inference in the suggested model. The original argument13 was that if $\lambda _0(t)$ is arbitrary, then it could be zero between the observed event times $t_{(1)},\dots , t_{(k)}$ (assumed distinct) which, therefore, must carry all information on $\varvec{\beta }$. This argument led to conditioning on the observed event times and multiply the conditional probabilities

$$\begin{aligned} \frac{\exp \left( \varvec{\beta }^\mathsf{T}\varvec{z}_{(i)}\right) }{\sum _{j\in R(t_{(i)})}\exp \left( \varvec{\beta }^\mathsf{T}\varvec{z}_{(j)}\right) } \end{aligned}$$

that the ‘right’ subject fails at $t_{(i)}$ given a failure at that time. Here, R(t), the risk set at time t, contains all subjects still alive and uncensored at that time and $\varvec{z}_{(j)}$ is the covariate vector for the subject with observation time $t_{(j)}$. The resulting estimating equations for $\varvec{\beta }$ are then obtained in connection with maximizing

$$\begin{aligned} PL(\varvec{\beta })=\prod _{i=1}^k\frac{\exp \left( \varvec{\beta }^\mathsf{T}\varvec{z}_{(i)}\right) }{\sum _{j\in R(t_{(i)})}\exp \left( \varvec{\beta }^\mathsf{T}\varvec{z}_{(j)}\right) }. \end{aligned}$$

This unusual likelihood construction led to a detailed discussion in the literature. Thus, Kalbfleisch and Prentice 28 showed that, under some conditions, $PL(\varvec{\beta })$ is the marginal likelihood of the rank vector for the observed failure times while other approaches were discussed by, e.g. Bailey 6, Jacobsen 26, Johansen27, Kalbfleisch and Prentice 29. To shed further light on the properties of PL, Cox 14 introduced the concept of a ‘partial likelihood’ and showed that PL is, indeed, an example of this. Similarly, estimation of the (cumulative) baseline hazard $\Lambda _0(t)=\int _0^t\lambda _0(u)du$ as well as asymptotic properties of the resulting estimators were not obvious and a further discussion took place in the literature. Thus, results on asymptotic normality of $\widehat{\varvec{\beta }}$ were presented by, e.g. Andersen and Gill4 and Tsiatis46. The latter approach using counting processes will be summarized in the next section. Finally, discussions of the efficiency of the model appeared 16^,40, raising the question about how much statistical precision was lost by making no assumptions concerning the shape of the survival time distribution (unspecified baseline hazard) compared to assuming, e.g. a Weibull shape.

3 The ‘Modern’ Approach to Inference in the Cox Model

The observed survival data may be represented as counting processes, as follows (e.g., Andersen et al,2, Andersen and Gill 4). For independent subjects $i=1,\dots ,n$, we observe $(\widetilde{T}_i, D_i, \varvec{z}_i)$, where $\widetilde{T}_i=T_i\wedge C_i$ is the minimum of the true survival time $T_i$ and a time of right-censoring, $C_i$ and $D_i=I(\widetilde{T}_i=T_i)$ is the indicator of observing the true survival time $T_i$ for that subject. The counting process observed for subject i is then

$$\begin{aligned} N_i(t)=I(\widetilde{T}_i\le t, D_i=1) \end{aligned}$$

and under independent censoring (e.g., Andersen et al.2, Kalbfleisch and Prentice 29), $N_i(t)$, by the Doob-Meyer decomposition (e.g., Andersen et al.2), can be written as

$$\begin{aligned} N_i(t)=\int _0^t Y_i(u)\lambda _i(u)du+ M_i(t). \end{aligned}$$

(2)

In (2), $\lambda _i(t)$ is the hazard function for the distribution of $T_i$, $Y_i(t)=I(\widetilde{T}_i\ge t)$ is the at-risk indicator and $M_i(t)$ is a martingale. The integrand $Y_i(u)\lambda _i(u)$ is the intensity process for $N_i(t)$. The counting process approach to survival analysis has a number of advantages. First, via (2), a number of mathematical results on martingales may be applied when studying (large sample) properties of the inference methods. We will exemplify this shortly. Second, via Jacod’s formula (e.g., Andersen et al.2) it is possible to establish a likelihood on which inference may be based leading, in fact, to the Cox partial likelihood discussed in the previous section. Third, this formulation directly extends to situations where modeling the hazard of an event which will not necessarily occur to all subjects with probability 1 is considered.

According to Jacod’s formula, the conditional likelihood given $\varvec{z}$ based on observing $((N_i(t), Y_i(t), \varvec{z}_i), i=1,\dots ,n)$ for $0<t\le \tau$ is

$$\begin{aligned} L=\prod _{i=1}^n \exp \bigl (-\int _0^{\tau }Y_i(t)\lambda _i(t\mid \varvec{z}_i)dt\bigr )\prod _t \bigl (Y_i(t)\lambda _i(t\mid \varvec{z}_i)\bigr )^{dN_i(t)} \end{aligned}$$

where $dN_i(t)=N_i(t)-N_i(t-)$ is the jump in $N_i$ at time t (0 or 1). (In fact, the full conditional likelihood given $\varvec{z}$ also contains factors arising from observing some censoring times, however, under the assumption of non-informative censoring, i.e. the censoring times carry no information on the hazard model parameters, L is proportional to the full likelihood; e.g. Andersen et al. 2, Kalbfleisch and Prentice29)

If $T_i$ follows the Cox model (1), then L is a function of the baseline hazard $\lambda _0(\cdot )$ and of the regression coefficients $\varvec{\beta }$. Differentiating, formally, $\log (L)$ with respect to a single $\lambda _0(t)$ and solving the resulting score equation for given $\varvec{\beta }$ lead to

$$\begin{aligned} \widehat{\lambda _0(t)dt}=\frac{\sum _idN_i(t)}{\sum _iY_i(t)\exp (\varvec{\beta }^\mathsf{T}\varvec{z}_i)}, \end{aligned}$$

(3)

and inserting (3) into L yields the profile likelihood

$$\begin{aligned} PL(\varvec{\beta })\times \exp \left( -\int _0^{\tau }\sum _idN_i(t)\right) \prod _t\left( \sum _idN_i(t)\right) ^{\sum _idN_i(t)} \end{aligned}$$

where the first factor

$$\begin{aligned} PL(\varvec{\beta })=\prod _i\prod _t\left( \frac{Y_i(t)\exp (\varvec{\beta }^\mathsf{T}\varvec{z}_i)}{\sum _jY_j(t)\exp (\varvec{\beta }^\mathsf{T}\varvec{z}_j)}\right) ^{dN_i(t)} \end{aligned}$$

(4)

is Cox’s partial likelihood and the second factor does not depend on the $\varvec{\beta }$-parameters. To estimate $\varvec{\beta }$, $PL(\varvec{\beta })$ is maximized by computing the Cox score

$$\begin{aligned} \varvec{U}_{\tau }(\varvec{\beta })=\frac{\partial }{\partial \varvec{\beta }}\log (PL(\varvec{\beta }))=\sum _i\int _0^{\tau }Y_i(t)\left( \varvec{z}_i-\frac{\sum _j Y_j(t)\varvec{z}_j\exp (\varvec{\beta }^\mathsf{T}\varvec{z}_j)}{\sum _j Y_j(t)\exp (\varvec{\beta }^\mathsf{T}\varvec{z}_j)}\right) dN_i(t) \end{aligned}$$

(5)

and solving the resulting score equations. This leads to the Cox maximum partial likelihood estimator $\widehat{\varvec{\beta }}$ and inserting this into (3) yields the Breslow estimator (9) of the cumulative baseline hazard $\Lambda _0(t)$:

$$\begin{aligned} \widehat{\Lambda }_0(t)=\int _0^t\frac{\sum _idN_i(u)}{\sum _iY_i(u)\exp (\widehat{\varvec{\beta }}^\mathsf{T}\varvec{z}_i)}. \end{aligned}$$

(6)

It turns out that large-sample inference for $\widehat{\varvec{\beta }}$ may be based on standard likelihood results for $PL(\varvec{\beta })$. A crucial step is here to note that, evaluated at the true regression parameter, $\varvec{\beta }_0$ and considered as a process in t when based on the data from [0, t], (5) is a martingale 2^, 4. Thus, by (2), $N_i(t)=\int _0^tY_i(u)\lambda _0(u)\exp (\varvec{\beta }_0^\mathsf{T}\varvec{z}_i)du+M_i(t)$ and

$$\begin{aligned} \varvec{U}_t& (\varvec{\beta }_0)\\ = & {} \sum _i\int _0^{t}Y_i(u)\bigl (\varvec{z}_i\\ & \quad -\frac{\sum _j Y_j(u)\varvec{z}_j\exp (\varvec{\beta }_0^\mathsf{T}\varvec{z}_j)}{\sum _j Y_j(u)\exp (\varvec{\beta }_0^\mathsf{T}\varvec{z}_j)}\bigr )dN_i(u) \\= & {} \sum _i\int _0^{t}Y_i(u)\bigl (\varvec{z}_i\\ & \quad -\frac{\sum _j Y_j(u)\varvec{z}_j\exp (\varvec{\beta }_0^\mathsf{T}\varvec{z}_j)}{\sum _j Y_j(u)\exp (\varvec{\beta }_0^\mathsf{T}\varvec{z}_j)}\bigr )dM_i(u). \end{aligned}$$

Thereby, martingale central limit theorems (e.g., Andersen et al.2) may be applied to the score and, via fairly standard Taylor expansion arguments, asymptotic normality for $\widehat{\varvec{\beta }}$ may be obtained. Further, model-based standard deviations of $\widehat{\varvec{\beta }}$ may be obtained from the second derivative of $\log (PL(\varvec{\beta }))$ and, thereby, the resulting Wald tests (as well as score- and likelihood ratio tests) are also valid. Martingale results may also be applied when studying large-sample properties of the Breslow estimator $\widehat{\Lambda }_0(t)$ and the plug-in estimator

$$\begin{aligned} \widehat{S}(t\mid \varvec{z}_0)=\exp \left( -\widehat{\Lambda }_0(t)\exp (\widehat{\varvec{\beta }}^\mathsf{T}\varvec{z}_0)\right) \end{aligned}$$

(7)

of the estimated survival function for given covariates $\varvec{z}_0$.

This derivation only builds on properties of counting processes showing that a Cox-type model may also be studied for the intensity process of a counting process that counts events such as cause-specific deaths, or recurrent events such as repeated hospitalisations (though the conditions needed for applying the martingale central limit theorem will vary among these different situations). Thereby, Cox-type models have much wider applicability, going beyond the simple survival situation, as we will further discuss in Sect. 5.

4 An Example

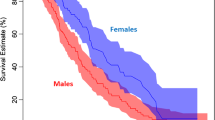
Lombard et al.37 reported on a randomized trial, PBC3, conducted at six European hospitals between 1983 and 1988. In brief, 349 patients with primary biliary cirrhosis (PBC) were randomized to the active drug CyA ($n=176$) or to placebo ($n=173$). Patients were followed until death from any cause or to liver transplantation, with 44 patients experiencing this composite end-point in the CyA group and 46 in the placebo group. Four patients dropped out of the trial before its planned termination on 1 January 1989 and the remaining (255) patients were alive without a liver transplantation on that date and these patients were all censored. The data are available from the web pages of Andersen and Skovgaard5.

Figure 1:

Kaplan–Meier estimates by treatment in the PBC3 trial.

Figure 1 shows the Kaplan and Meier30 curves by treatment and it is seen that they are quite close, a fact that is sustained by fitting a Cox model including only the treatment indicator $z_1=I(\text {CyA treatment})$. In this model, the estimated regression coefficient is $\widehat{\beta }_1=-0.059$ with an estimated standard deviation of 0.211, leading to an estimated hazard ratio of $\exp (-0.059)=0.94$ with 95% confidence limits from 0.62 to 1.43.

Even though PBC3 was a randomized study, it turned out that the CyA group had slightly less favorable average values of the important biochemical prognostic variables serum albumin (37.1 g/L for CyA, 39.3 g/L for placebo) and serum bilirubin (48.6 $\mu$mol/L for CyA, 42.3 $\mu$mol/L for placebo). Thus, the estimated treatment effect after adjustment for these two variables (bilirubin after a log-transformation) differs somewhat from the unadjusted coefficient cited above, see Table 1. The treatment groups now seem to differ significantly (95% confidence interval for the treatment hazard ratio ranges from 0.36 to 0.87). The log-transformation of serum bilirubin was determined after careful inspection of plots of cumulative martingale residuals (e.g., Lin et al.36).

Table 1: Estimated coefficients (and SD) from a Cox model for the PBC3 data with linear effects of albumin and $\log _2$(bilirubin).

Graphical illustration of the results from the multiple Cox regression model can be done by estimating survival curves for treated and control patients with some given value of the biochemical adjustment variables, see Eq. (7). However, since that would provide one set of curves for each chosen covariate pattern, it would be of interest to summarize the multiple regression model graphically by a single set of curves. This may be done using the g-formula (e.g., Hernan and Robins25), as follows. Two predictions are performed for each subject, i, one setting treatment to CyA and one setting treatment to placebo and in both predictions keeping the observed values $(z_{2i},z_{3i})$ for albumin and bilirubin. The predictions for each value of treatment are then averaged over $i=1,\dots ,n$:

$$\begin{aligned} \widehat{S}_j(t)=\frac{1}{n}\sum _i\widehat{S}(t\mid z_1=j, z_{2i}, z_{3i}),\quad j=0,1. \end{aligned}$$

(8)

The g-formula results in the curves shown in Fig. 2. Note that, if randomization in the PBC3 study had been more successful, then these curves would resemble the Kaplan–Meier estimates in Fig. 1. However, using the curves obtained based on the g-formula, it is possible to visualize the treatment effect on the probability scale after covariate-adjustment.

Figure 2:

Estimated survival curve in the two treatment groups in the PBC3 trial based on the g-formula.

5 Influence of the Cox Paper

The short-term influence of the paper was touched upon in Sect. 2. Thus, as mentioned there, it triggered a discussion dealing with the kind of likelihood on which inference should be based, with how to non-parametrically estimate the baseline hazard, with large sample properties of the estimators, and with their asymptotic efficiency.

But also on a long-term basis, the paper has been very influential, both within the field of survival analysis and more generally in theoretical statistics. In survival analysis, the multiplicative semi-parametric structure (1) soon became the primary choice when setting up regression models for various parameters. In Sect. 2, we described the model as a model for the hazard function $\lambda (t)=f(t)/S(t)$ of a proper random variable, T with density f and survival distribution function S. However, a similar model was proposed for the cause-specific hazard in competing risks 41. Here, a number of distinct causes of death $D\in \{1,\dots ,k\}$ are envisaged and the cause j-specific hazard

$$\begin{aligned} \lambda _j(t)=\lim _{\Delta t\rightarrow 0}\frac{P(T\le t+\Delta t, D=j\mid T>t)}{\Delta t} \end{aligned}$$

is assumed to have the form

$$\begin{aligned} \lambda _j(t;\varvec{z})=\lambda _{j0}(t)\exp (\varvec{\beta }_j^\mathsf{T}\varvec{z}). \end{aligned}$$

The competing risks model is a simple example of a multi-state model with one initial transient state ‘0: alive’ and k absorbing states $j=1,\dots ,k$ representing death from the different causes, and the cause-specific hazard, $\lambda _j(t)$ is then the $0\rightarrow j$ transition hazard. Andersen and Borgan1 studied general multi-state processes, say X(t), with transition probabilities $P_{hj}(s,t)=P(X(t)=j\mid X(s)=h), s<t$ (where h, j are states) and modeled the transition intensities

$$\begin{aligned} \lambda _{hj}(t)=\lim _{\Delta t\rightarrow 0}\frac{P_{hj}(t, t+\Delta t)}{\Delta t}, \quad j\ne h \end{aligned}$$

in the form (1). In both cases, inference and asymptotic properties follow the lines of Sect. 3.

In the competing risks model, the time of transition into state j is the improper random variable $T_j=\inf _{t>0}\{t:X(t)=j\}$ with hazard function

$$\begin{aligned} \lambda _j^*(t)=\lim _{\Delta t\rightarrow 0}\frac{P(T_j\le t+\Delta t\mid T_j>t)}{\Delta t}, \end{aligned}$$

the cause j sub-distribution hazard. Fine and Gray18 proposed a model for the sub-distribution hazard in the form (1), i.e. with an unspecified baseline function and with covariates entering multiplicatively via a linear predictor. Similar models were studied by Lin34 for expected medical costs in [0, t] and by Lin et al. 35 and by Ghosh and Lin 20 for the expected number of events in [0, t] in a recurrent events situation (without or with a terminal event). In all these cases, the parameter of interest was assumed to have the form

$$\begin{aligned} \mu (t;\varvec{z})=\mu _0(t)\exp (\varvec{\beta }^\mathsf{T}\varvec{z}) \end{aligned}$$

(with the baseline function $\mu _0(t)$ unspecified except from being non-decreasing). In these cases, the Cox-type model does not specify the entire probability distribution of the data under study and, hence, no likelihood is available. Instead, inference is based on estimating equations that are generalizations of the Cox score (5), now requiring inverse probability of censoring weighting to account for the incomplete observation. Derivation of asymptotic properties of the resulting estimators now needs the use of empirical process theory rather than martingale results.

These examples illustrate that the multiplicative ‘Cox structure’ is the default choice in survival analysis. Also in other special cases, such as random effects (‘frailty’) models (e.g., Clayton and Cuzick 12, Duchateau and Janssen 15) and covariate measurement error models (e.g., Carroll et al. 11), Cox type models are typically studied even though the mathematical properties of the resulting models may not be quite as attractive as when looking, e.g. at additive hazards models.

In the more general field of theoretical statistics (outside survival analysis), the Cox paper has also had a remarkable influence. Thus, entirely new areas of research on partial likelihood (e.g., Gill 21, Slud 43, 44, Wong 50) and semi-parametric inference (e.g., Begun et al. 7, Bickel et al. 8, Tsiatis 47) have emerged.

Studying the many citations to Cox 13, it appears that the vast majority comes from the medical world. This reflects that in clinical studies dealing with time-to-event problems, the Cox model (maybe in connection with the Kaplan–Meier estimator) has developed into the method of choice. This is likely related to the fact that in the 1970s, when the model was proposed, many clinical trials in cancer and other chronic diseases were launched worldwide where methods for survival data analysis were needed, and also that standard software packages soon made the Cox model generally available. And this is in spite of the fact that other models, such as accelerated failure time models, may provide parameters with a more intuitive interpretation than that of hazard ratios. We will return to this in the next section.

6 Some Criticism Raised Against the Cox Model

In this section, we will first focus on the two-sample situation corresponding to a single binary covariate $z\in \{0,1\}$. This could be the situation in a randomized clinical trial with a time-to-event outcome and with $z=1$ representing active treatment and $z=0$ control as exemplified in Sect. 4. Analyzing the data using the Cox model provides a nice and apparently simple one-number summary of the treatment effect, namely the hazard ratio $\exp (\beta )$. Nevertheless, several points of criticism against the model have been raised.

6.1 Hazard Ratio Interpretation-1

The hazard ratio does not have a simple clinical interpretation and it is some times confused with a ‘risk ratio’. However, in the two-sample model, the risk ratio at time t resulting from a Cox model in the absence of competing risks is

$$\begin{aligned} RR=\frac{1-S(t\mid z=1)}{1-S(t\mid z=0)}=\frac{1-\exp (-\Lambda _0(t)\exp (\beta ))}{1-\exp (-\Lambda _0(t))} \end{aligned}$$

and only in a ‘low risk’ situation (i.e., $\exp (-\Lambda (t))\approx 1-\Lambda (t)$) is $RR\approx \exp (\beta )$. Thus, the ‘risk ratio’ interpretation does not hold in general. Also, in the presence of competing risks, the cause-1 risk ratio is the ratio between cumulative incidences $P(T\le t, D=1\mid z)$ that also depend on the cause-specific hazards for the causes competing with cause 1. Thus, in this case, the risk ratio interpretation of $\exp (\beta )$ can be completely wrong, see e.g. Andersen et al.3 for an example of this.

6.2 Hazard Ratio Interpretation-2

The hazard ratio has also been criticized for not having a causal interpretation (e.g., Hernan24, Martinussen et al.39). To discuss this problem, a definition of causality is needed and we will define causality as in Martinussen et al.39 following the tradition of ‘potential outcomes’ (e.g., Hernan and Robins25). Thus, we let $T^0_i$ be the potential survival time that would be realized if subject i, possibly contrary to the fact, was given treatment 0 and define $T^1_i$ similarly. A causal contrast then compares the distributions of $T^0$ and $T^1$, i.e. addressing what would happen if all subjects were treated with control compared to what would happen if all subjects were given the active treatment. Examples include $E(T^0)-E(T^1)$ or $P(T^0\le t)/P(T^1\le t)$. The hazard ratio at time t can, for a two-sample Cox model for the potential outcomes, be written as

$$\begin{aligned} \exp (\beta )=\frac{\log (P(T^1>t))}{\log (P(T^0>t))} \end{aligned}$$

and it is estimable if treatment allocation is randomized as in the PBC3 study, Sect. 4. It does, therefore possesses a causal interpretation, albeit not a very attractive one. On the other hand, the standard interpretation of the hazard ratio is

$$\begin{aligned} \exp (\beta ) = \frac{\lim _{\Delta t\rightarrow 0}P(T^1\le t+\Delta t|T^1> t)/\Delta t}{\lim _{\Delta t\rightarrow 0}P(T^0\le t+\Delta t|T^0> t)/\Delta t} \end{aligned}$$

and it is seen to contrast the two sub-populations $\{T^0> t\}$ and $\{T^1> t\}$ that are different when treatment does have an impact on survival. This shows that, for a time-varying hazard ratio, e.g. with $\lambda (t\mid z=1)/\lambda (t\mid z=0)<1$ for $t<t_0$ and $\lambda (t\mid z=1)/\lambda (t\mid z=0)=1$ for $t\ge t_0$, it would be incorrect to infer that ‘treatment works for $t<t_0$’ but ‘treatment is inefficient for $t\ge t_0$’.

Leaving the two-sample situation and looking, more generally, at a multiple Cox regression model including covariates $\varvec{z}=(z_1,\dots ,z_p)$, some further points of criticism have been raised.

6.3 Accelerated Failure Time Models

As mentioned in the introduction, a very natural approach to regression modeling in survival analysis would be to extend the classical linear regression model

$$\begin{aligned} \log (T)=\varvec{\beta }^\mathsf{T}\varvec{z}+\varepsilon \end{aligned}$$

to allow for censored data. This model is known as the accelerated failure time model (AFT) as it provides parameters with an interpretation as acceleration factors. Thus, if subject 1 has $z=1$ and subject 2 has $z=0$ then $T_1\approx T_2\exp (\beta )$ and, thereby, the coefficient $\beta$ has a nice and simple interpretation. This ‘physical’ interpretation was, in fact, mentioned already by Cox13 who, on the other hand, discussed the proportional hazards model as ‘convenient, flexible and yet entirely empirical’. Inference in the AFT model can be based on Jacod’s likelihood (Sect. 2) if a parametric specification of the distribution of the i.i.d. error terms $(\varepsilon _i, i=1,\dots n)$ is given. However, as mentioned in the Introduction, this would entail specifying the shape of the tail of the distribution for which little information is available based on censored data and, therefore, also semi-parametric inference in the AFT model, i.e. without specifying the distribution of the error terms, has been discussed (e.g., Buckley and James10).

6.4 Over-Simplicity

It has been argued (e.g., van Houwelingen and Putter48) that proportional hazards is the exception rather than the rule and that more flexible hazard models should be applied (e.g., Martinussen et al.38, Schemper42). Also, Stensrud and Hernan45 in a JAMA letter made the claim that ‘in practice, a constant hazard ratio does not occur for most medical applications’.

6.5 Non-collapsibility

Consider a situation with two covariates: a binary treatment indicator $z_1$ as above and another variable $z_2$ and consider the two Cox models $\lambda _0(t)\exp (\beta _1z_1)$ and $\widetilde{\lambda }_0(t)\exp (\widetilde{\beta _1}z_2+\widetilde{\beta }_2z_2)$. Then, as noted, e.g. by Gail et al.19, if $\widetilde{\beta }_2\ne 0$, i.e. when $z_2$ is associated with survival, then $\beta _1\ne \widetilde{\beta }_1$ even in a randomized study where $z_1$ and $z_2$ are independent. This is known as non-collapsibility and has the consequence that when quoting a coefficient from a Cox model, it should always be emphasized which other covariates that the model included. In the PBC3 trial (Sect. 4), it was seen that the treatment effects with or without adjustment for two strong prognostic variables were very different (though, in that example, treatment was not quite independent of $(z_2,z_3)$ because of the unsuccessful randomization).

6.6 Inferiority Compared to Machine Learning for Prediction Purposes

A number of studies (e.g., Kim et al.31, Leger et al.33) have compared the performance of predictions based on multiple Cox regression models with that of different machine learning techniques, such as ‘deep learning’, and have found that the latter generally outperform the Cox model. In fact, machine learning methods for survival analysis, including methods for high-dimensional covariates, have been and continue to be a very active area of research. Important contributions to this field include Fang et al.17, Goeman22, Kvamme et al.32, Witten and Tibshirani49, Hao et al. 23.

7 Discussion

As summarized above, the current situation is that the Cox13 proportional hazards regression model is an extremely popular and influential statistical model for survival data analysis and it provides a one-number summary of the way in which a covariate is associated with the survival time outcome—the hazard ratio. Nevertheless, as discussed in Sect. 6, the model has been criticized in a number of ways.

However, difficulties in interpreting the hazard ratio (be it clinically or causally) may be circumvented by reporting predicted absolute risk curves, e.g. in the form of survival curves as shown in the example of Sect. 4. Similarly, if a proportional hazards model is too simple to adequately fit a data set at hand then flexible extensions of the model exist (e.g., van Houwelingen and Putter48s) from which, once more, absolute risk curves are estimable. Also, the problem with non-collapsibility may be approached by, as an alternative to presenting hazard ratios, estimating absolute risk curves, e.g., using the g-formula (again exemplified in the PBC3 example). Finally, the fact that alternative methods, such as machine learning techniques, may provide superior predictions compared to a Cox model does not seem to have had the consequence that the Cox model is being abandoned. Rather, the model will likely be included in ensemble methods used for survival prediction together with more recently developed techniques in this area.

In conclusion, we believe that the Cox model will remain an important statistical tool in survival analysis, perhaps however, with a shift of focus from exclusive use of hazard ratios to more emphasis on using the model to provide absolute risk estimates, likely in combination with machine learning techniques.