Introduction

In China, a two-phase large circular collider project was launched when the Higgs boson was discovered at the Large Hadron Collider (LHC) at CERN in 2012. In the first stage, the Circular Electron–Positron Collider (CEPC) will be built in a 100-km tunnel as a Higgs factory to study Higgs physics in great depth. In the next stage, the SPPC will be built in the same tunnel to explore new physics beyond the standard model [1,2,3,4]. In the world, a similar project called Future Circular Collider (FCC) has been studied at CERN since 2013 [5]. It also includes two major colliders, as one being FCC-ee which is a high-precision e+e− circular collider and the other one being FCC-hh which is a proton–proton collider. In 2020 June, the European Strategy for Particle Physics 2020 upgrade defines FCC-ee as the first stage and FCC-hh as the second, which makes FCC very similar to the CEPC-SPPC roadmap. The baseline parameters of SPPC and FCC-hh are summarized in Table 1 [4,5,6,7,8].

Table 1 Main parameters for SPPC and FCC-hh [4,5,6,7,8]
Full size table

The collision energy in center of mass and luminosity are the two major parameters for the performance of a collider. For physics runs, it is very important to accumulate sufficiently large data by detectors. Whereas the event rate is proportional to the luminosity, the integrated luminosity over an operation period is the design goal for a collider. For example, SPPC aims to obtain 30 ab−1 in 10–15 years. Thus, the luminosity optimization and leveling schemes to enhance the averaged luminosity are pursued in all the modern colliders, including SPPC where the luminosity design goal and the beam energy scale are unprecedented. In this article, the study results for the optimization and leveling of luminosity in SPPC are presented.

Luminosity optimization and leveling methods in SPPC

Motivation and methods for luminosity optimization and leveling

In this section, we mostly follow the approach of [7] to discuss the analytic model used to guide luminosity optimization and leveling. Compared with the nominal luminosity that is usually the initial luminosity when the physics data collection starts in a machine cycle, the averaged luminosity over a cycle is more meaningful to evaluate collision efficiency. The reason is that the luminosity does not keep the same in a cycle. On one hand, during a machine cycle, there will be always a length of time needed for the preparation of the beams for the next collision, for example, magnet ramping down, injection, acceleration and so on. This time period without collision is called the turnaround time, and a cycle period is the sum of physics run time and turnaround time. In SPPC, the applied turnaround time is 2.4 h that is about 3 times of the available one of 0.81 h. On the other hand, due to the burning-off of the protons and emittance change during the collision process, the instant luminosity may vary in the course. At the same time, there are also factors limiting the luminosity to go too higher, such as beam instabilities and event pileup.

Considering two round Gaussian beams colliding at the IP, the luminosity without taking into account the crossing angle and the hourglass effect is expressed as

$$L = \frac{{f_{{{\text{rev}}}} n_{{\text{b}}} N_{{\text{b}}}^{2} }}{{4\pi \beta^{*} \varepsilon }},$$
(1)

where frev is the revolution frequency, nb is the number of bunches, Nb is the bunch population, β* is the beta function at IP in the horizontal or vertical phase plane (β* =  βx* =  βy*), ε is the rms geometric emittance in the horizontal or vertical phase plane (ε = εx = εy). From Eq. (1), as frev is almost fixed for a given circumference, three parameters, bunch population (and its associated parameter nb), β* and emittance are responsible for the luminosity, but they may vary during a machine cycle. Different machine designs are to optimize these parameters to obtain high averaged luminosity.

The beam–beam parameter that is to describe the linear tune shift of small amplitude particles within a bunch can indicate the influence of the beam–beam effects, and it is expressed by

$$\xi = n_{IP} \frac{{r_{p} N_{b} }}{4\pi \gamma \varepsilon },$$
(2)

where nIP is the number of interaction points, γ is the Lorentz factor, rp is the classical proton radius. It is noted that the beam–beam parameter depends on the bunch population and emittance.

The pileup event per crossing is very important in the detector design. Higher the averaged event rate, higher physics run efficiency. However, it should be avoided to seek high averaged event rate by very high event per crossing, as this will lead to the saturation in the detector, even the future detector is expected to handle higher pileup event per crossing. The pileup event per bunch collision can be calculated by

$$\mu = \sigma_{{{\text{inel}}}} \frac{L}{{n_{{\text{b}}} f_{{{\text{rev}}}} }} = \sigma_{{{\text{inel}}}} \frac{{N_{{\text{b}}}^{2} }}{{4\pi \beta^{*} \varepsilon }},$$
(3)

where σinel is the inelastic p–p cross section. One can see that the event per crossing is proportional to the luminosity and can be reduced by using more number of less populated bunches. It is related dynamically with the evolution of bunch population, β* and emittance during a collision cycle.

The emittance in both the transverse and longitudinal phase planes is naturally damped due to synchrotron radiation at the collision energy at SPPC, if no emittance heating mechanism is applied. Its evolution follows an exponential decay as

$$\varepsilon \left( t \right) = \varepsilon \left( 0 \right){\text{e}}^{{ - \frac{t}{\tau }}} ,$$
(4)

where τ is the transverse emittance damping time. With the exponential decay of the transverse emittance, the luminosity, beam–beam parameter and pileup event may increase from the starting of collision. The original β* is defined by the IP insertion lattice with a limitation from the aperture of the inner triplet quadrupoles [3]. The shrinking of the emittance also provides a possibility to reduce the β* dynamically, since with the given apertures of the inner quadrupole triplets and a smaller transverse emittance, it will allow the IR optics optimization with a larger maximum βthat will lead to a smaller β*. The advantage of dynamic β* will be explored for luminosity leveling in Sect. 2.2.

In addition to the inevitable beam loss due to the so-called particle burning-off during the collisions at IPs, the beam loss is also caused by the beam–beam effects in hadron colliders [9,10,11,12]. And there are other less important loss mechanisms like intra-beam scattering, collision with residual gas and so on. When only the burning-off is considered, the bunch population will follow the expression:

$$\frac{{{\text{d}}N_{{\text{b}}} }}{{{\text{d}}t}} = - \sigma_{{{\text{tot}}}} n_{{{\text{IP}}}} \frac{L}{{n_{{\text{b}}} }},$$
(5)

where σtot is the total p–p cross section that decides the bunch population evolution. Then, the time-dependent bunch population can be calculated by combining Eqs. (1), (4) and (5) [7]:

$$N_{{\text{b}}} \left( t \right) = \frac{1}{{\frac{K\tau }{{\varepsilon \left( 0 \right)}}\left( {{\text{e}}^{t/\tau } - 1} \right) + \frac{1}{{N_{{\text{b}}} \left( 0 \right)}}}},$$
(6)
$$K = \frac{{\sigma_{{{\text{tot}}}} f_{{{\text{rev}}}} n_{{{\text{IP}}}} }}{{4\pi \beta^{*} }}.$$
(7)

If the instant luminosity is limited by the maximum allowable beam–beam parameter (ξmax), beam–beam parameter will reach to a flat top from a lower value from the beginning, since then the luminosity gradually decreases and the bunch population evolution can be expressed by [7]

$$\frac{{{\text{d}}N_{{\text{b}}} }}{{{\text{d}}t}} = - \frac{{\sigma_{{{\text{tot}}}} f_{{{\text{rev}}}} \gamma \xi_{\max } }}{{\beta^{*} r_{{\text{p}}} }}N_{{\text{b}}} ,$$
(8)
$$N_{{\text{b}}} \left( t \right) = N_{{\text{b}}} \left( 0 \right){\text{e}}^{{\left( { - Xt} \right)}} ,$$
(9)
$$X \equiv \frac{{\sigma_{{{\text{tot}}}} f_{{{\text{rev}}}} \gamma \xi_{\max } }}{{\beta^{*} r_{{\text{p}}} }}.$$
(10)

In this case, the emittance has to be controlled by some external noise instead of natural shrinking to keep the constant tune shift and is given [7]:

$$\varepsilon \left( t \right){ = }\varepsilon \left( 0 \right){\text{e}}^{{\left( { - Xt} \right)}} .$$
(11)

In SPPC, the nominal beam–beam parameter for two IPs is 0.015, but the LHC machine study and beam–beam simulation studies show that a much higher tune shift such as 0.03 is possible [13,14,15]. Here, both values (ξmax = 0.015, 0.03 for 2 IPs) are considered for comparison.

If the maximum event per crossing to avoid overlarge pileup in the detectors is used to restrain the instant luminosity to go too higher, the bunch population changing rate can be presented by

$$\frac{{{\text{d}}N_{{\text{b}}} }}{{{\text{d}}t}} = - \sigma_{{{\text{tot}}}} n_{{{\text{IP}}}} \frac{{f_{{{\text{rev}}}} \mu_{\max } }}{{\sigma_{{{\text{inel}}}} }},$$
(12)

where μmax is the maximum pileup event per bunch collision [7]. The whole measures to increase the averaged luminosity but avoid the over-loaded pileup event and keep it at an almost constant level are called the luminosity leveling, which is very important in the design and operation of future hadron colliders. As an example, three types of luminosity leveling have been suggested in the LHC [16,17,18], where the beam kinetic energy is much lower and there is almost no significant emittance shrinking due to synchrotron radiation. First, luminosity leveling can be carried out using a gradually decreasing crossing angle in the crossing plane to gradually reduce the luminosity reduction due to the crossing angle. Second, luminosity leveling can be helped with a gradually decreasing transverse offset orthogonal to the crossing plane, which controls the peak luminosity. Third, luminosity leveling can be assisted by a gradually β* squeezing. In Fig. 1, a sketch of these three luminosity leveling techniques is shown [16].

Fig. 1
figure 1

A sketch of three different luminosity leveling methods

Full size image

With the controlled maximum pileup event per crossing, according to Eq. (12), the bunch population decreases linearly with time:

$$N_{{\text{b}}} \left( t \right) = - W\left( {t - t_{\mu \max } } \right) + N_{{\text{b}}} \left( {t_{\mu \max } } \right),$$
(13)
$$W = \frac{{\sigma_{{{\text{tot}}}} f_{{{\text{rev}}}} n_{{{\text{IP}}}} }}{{\sigma_{{{\text{inel}}}} }}\mu_{\max } ,$$
(14)

where tμmax is the time when the maximum pileup event is reached [7]. If β* is maintained constant during the process, according to Eq. (3), the emittance should be controlled in the following way [7]:

$$\varepsilon \left( t \right){ = }\varepsilon \left( {t_{\mu \max } } \right)[1 - {{\left( {W\left( {t - t_{\mu \max } } \right)} \right)} \mathord{\left/ {\vphantom {{\left( {W\left( {t - t_{\mu \max } } \right)} \right)} {\left( {N_{{\text{b}}} \left( {t_{\mu \max } } \right)} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {N_{{\text{b}}} \left( {t_{\mu \max } } \right)} \right)}}]^{2} .$$
(15)

An efficient way to alleviate the limitations imposed by the beam–beam parameter and maximum event per crossing is that one fills the colliding rings with smaller bunch spacing, say from the nominal 25 to 10 ns or 5 ns, when keeping the beam current unchanged. The bunching structure is formed in the injector chain and some kind of bunch splitting method is under investigation at the MSS (Medium Stage Synchrotron, energy range 10–180 GeV) or the third stage of the injector chain [2]. This increases the number of bunches and reduces the bunch population. Certainly it will cause other problems, e.g., larger crossing angle is needed because the increasing number of long-range interactions might make the more serious beam–beam interactions. Limited by the apertures of the inner quadrupole triplets which the two beams share, one cannot increase the crossing angle beyond the natural limit. The luminosity loss due to the crossing angle will be discussed in Sect. 3.1.

The β* is assumed to be constant during collision in the above analysis, but dynamic β* can provide a possibility to further increase luminosity. Here we derive expressions for the change in the bunch population due to the burning-off, assume that β* is squeezed linearly to increase instant luminosity:

$$\frac{{{\text{d}}N_{{\text{b}}} }}{{{\text{d}}t}} = - \frac{{\sigma_{{{\text{tot}}}} f_{{{\text{rev}}}} n_{{{\text{IP}}}} }}{{4\pi \left( {\beta^{*} - rt} \right)}}\frac{{N_{{\text{b}}}^{2} }}{\varepsilon },$$
(16)

where r is the changing rate of β*, then the time-dependent bunch population can be calculated combining Eqs. (4) and (16):

$$N_{{\text{b}}} \left( t \right){ = }\frac{{4\pi N_{{\text{b}}} \left( 0 \right)\varepsilon \left( 0 \right)}}{{\left( {4\pi \varepsilon \left( 0 \right) - \frac{1}{r}N_{{\text{b}}} \left( 0 \right)f_{{{\text{rev}}}} n_{{{\text{IP}}}} \sigma_{{{\text{tot}}}} {\text{e}}^{{\left( {\frac{{\beta^{*} }}{r\tau }} \right)}} {\text{Ei}}\left( { - \frac{{\left( {\frac{1}{r}\beta^{*} - t} \right)}}{\tau }} \right) + \frac{1}{r}N_{{\text{b}}} \left( 0 \right)f_{{{\text{rev}}}} n_{{{\text{IP}}}} \sigma_{{{\text{tot}}}} {\text{e}}^{{\left( {\frac{{\beta^{*} }}{r\tau }} \right)}} {\text{Ei}}\left( { - \frac{{\beta^{*} }}{r\tau }} \right)} \right)}},$$
(17)

where Ei(x) is the exponential integral over t for the function et/t from negative infinity to x.

The annual integrated luminosity can be evaluated according to Eq. (18).

$$\sum \left( {1\;{\text{year}}} \right) = \int\limits_{{{\text{year}}}} {L\left( t \right)\;{\text{d}}t = T_{{{\text{tot}}}} AL_{{{\text{ave}}}} } ,$$
(18)

where Ttot is the total time planned in a year for physics operation, A is the machine availability that describes the machine efficiency taking into account hardware failures, Lave is the averaged luminosity over a machine cycle. In LHC, the availability is about 71% in 2012 [19]; Ttot is usually set 160 days; the averaged luminosity is 5.5 × 1033 cm−2 s−1; the annual integrated luminosity is estimated to 55 fb−1 [7]. The similar operation days per year (126–140 days) and machine availability (70%) are assumed for FCC-hh [20]. With the expected annual integrated luminosity, one can plan for how many years operation for a physics run period.

Different luminosity optimization and leveling schemes in SPPC

With the general design goal for the integrated luminosity as mentioned in the last paragraph of Sect. 1, different luminosity optimization and leveling schemes to enhance the averaged luminosity in SPPC have been studied, and they employ the methods described in Sect. 2.1 and different beam control techniques or combinations. Six promising scenarios or schemes are described here. For each scenario, the optimum physic run time is searched to maximize the averaged luminosity. The similar operation 160 days and machine availability of 70% are supposed for SPPC, which are similar to LHC and FCC-hh. Table 2 shows the summary of the key parameters and results, and some parameters as a function of time over two cycles are depicted in Fig. 2. The parameters in Table 1 are used for the study, except that crab cavities are assumed in place, which restore the luminosity loss due to the crossing angle.

Table 2 Relevant parameters are summarized for different cases
Full size table
Fig. 2
figure 2

Development of relevant parameters over two cycle periods is plotted for different cases. Cases from a to f are consistent with the explanation in Table 2. The (red/blue/magenta/green) solid line represents the (luminosity/emittance/bunch population/beam–beam parameter) evolution with the time. In Cases e and f, there is another black solid line for the β* evolution with the time

Full size image

Case A: Constant beam–beam parameter 0.015

In this case, it is based on the nominal parameters, assuming the beam–beam parameter will be kept constant at 0.015 during the physics run. The emittance is controlled to follow the expression in Eq. (11) by means of an emittance heating system. Comparing Eq. (11) with Eq. (4), the emittance decreases by different exponential factors, with X = 2.36 × 10–5 in Eq. (11) much smaller than 1/τ = 1.18 × 10–4 in Eq. (4). In this case, as shown in Fig. 2a the luminosity, emittance and bunch population decay in the same exponential factor during the physics run. The maximum pileup event per crossing is set to be 418 in this case, which is conservative as compared to 700 in FCC-hh [7] and a modest increase as compared to 140 in HL-LHC [21]. Then, the averaged luminosity of 0.68 × 1035 cm−2 s−1 is obtained, which is almost the half of the initial luminosity of 1.20 × 1035 cm−2 s−1.

Case B: Beam–beam parameter limitation of 0.03

In this case, it is still based on the nominal parameters but allows the beam–beam parameter to increase until the imposed limit of 0.03 during the physics run. The emittance decay will be slowed when the beam–beam parameter reaches the limit at the moment t1. The instant luminosity first increases and reaches the maximum at t1, and then starts to decrease. Thus, both the peak luminosity and the pileup event are quite larger than that in Case A, with the maximum pileup event of 624. Meanwhile, this case shows the averaged luminosity of 1.00 × 1035 cm−2 s−1 which is significantly larger than Case A and so is the integrated annual luminosity.

Case C: Pileup event control with the beam–beam parameter limitation of 0.03

This case is complementary to Case B in order to lower down the maximum pileup event to 418. During the luminosity leveling, the bunch population decrease linearly following Eq. (13) and the emittance decreases following Eq. (15). Comparing Eq. (1) with Eq. (2), if the luminosity keeps constant, the beam–beam parameter must keep increasing. Thus, when the beam–beam parameter reaches the limit of 0.03, the bunch population and emittance will start to evolve as in Case A. In this case, the emittance needs to be heated during the whole physics run. The peak luminosity and the maximum pileup event are same as in Case A, but the averaged luminosity of 0.88 × 1035 cm−2 s−1 is higher than the one in Case A and lower than in Case B.

Case D: Smaller bunch spacing of 10 ns

Cases D and E are designed to reduce the event pileup and beam–beam parameter with the bunch spacing of 10 ns. The number of bunches is increased by 2.5 times, and the initial bunch population will be proportionally decreased by 2.5 times to keep the initial circulation current constant. The crossing angles are increased accordingly to keep the beam separation at the parasitic collisions unchanged. Crab cavities are assumed to be used here; thus, the luminosity loss due to larger crossing angles can be ignored.

Case D is the similar as Case B with the major differences in bunch population and number of bunches, and the initial beam–beam parameter is only 0.006 for two IPs. Therefore, it takes a longer time (defined as t1′) than t1 in Case B to reach the beam–beam parameter limit of 0.03. Since the initial luminosity is reduced by a factor of 2.5 same as the bunch population, the peak luminosity is lower than that in Case B, and the averaged luminosity is also smaller. Certainly, the event pileup problem almost disappears as the maximum pileup event per crossing is only 217.

Case E: Smaller bunch spacing of 10 ns with dynamic β *

Compared with Case E, here β* is linearly squeezed from 0.75 to 0.25 m within 2.5 h to enhance the instant luminosity. In the first 2.5 h, the emittance drops exponentially as shown in Eq. (4) and the change rate of bunch population described by Eq. (16) will become

$$\frac{{{\text{d}}N_{b} }}{{{\text{d}}t}} = - \frac{{\sigma_{{{\text{tot}}}} f_{{{\text{rev}}}} n_{{{\text{IP}}}} }}{{4\pi \left( {\beta^{*} - 0.2t} \right)}}\frac{{N_{{\text{b}}}^{2} }}{\varepsilon }.$$
(19)

As shown in Fig. 2e, the luminosity and beam–beam parameter continuously increase when the β* decreases. The beam–beam parameter is only 0.014 at the end of β* reduction but will go up until reaching 0.03. The maximum pileup event is also at a lower level of 358 and the averaged luminosity is improved as expected by a factor of 1.6 compared with Case D.

Case F: Smaller bunch spacing of 5 ns with dynamic β *

In this case, the bunch spacing is further reduced to only 5 ns to explore the possibility of further reducing event pileup. Similarly, the initial bunch population will proportionally decrease by 5 times to keep the same circulation current and the initial beam–beam parameter is only 0.003 for 2 IPs. Different from Case E, no emittance heating and limitation are applied. Both the maximum event pileup and beam–beam parameter are in quite lower levels as shown in Fig. 2f. The maximum pileup event is the lowest among all the cases and the maximum beam–beam parameter of 0.021 is on the safe side. The averaged luminosity is higher than that in the other cases except Case E.

For all the above cases, the minimum turnaround time of 0.81 h has been studied. It can enhance the averaged luminosity in all the cases, and the results are shown in Table 2 in brackets. In summary, all the above cases can be applied at SPPC, and different schemes may be considered in different stages. For example, Case A being the simplest one can be considered for the initial operation stage, and Cases D, E and F requiring much manipulations including the bunching splitting in the injector chain can be considered in the later operation phase. The highest annual integrated luminosity with two IPs in Case E can reach 2.6 ab−1 that is close to the initial design goal of 3.0 ab−1, but the design goal can be met with a smaller turnaround time between the minimum 0.81 h and the nominal 2.4 h. Thus, it is reasonable to say that the physics operation goal of 30 ab−1 in integrated luminosity can be met in 10–15 years. The crab cavities are particularly important in Cases E and F because the reduction factor in luminosity due to the large crossing angles becomes smaller with a squeezing β*. The reduction factor Fx/y due to the crossing angle without crab cavities can be calculated by

$$F_{x/y} = \frac{1}{{\sqrt {1 + \left( {\frac{{\theta \sigma_{z} }}{{2\sigma_{x/y} }}} \right)^{2} } }},$$
(20)

where θ is the crossing angle, σz is the longitudinal bunch length and σx/y is the horizontal/vertical transverse bunch size. However, this luminosity loss can also be recovered with another method, which will be studied in the next section.

Flat beam optics as the backup plan in the case of no crab cavities

Introduction to the flat optics

Different cases in the last section are studied with the so-called round optics (βx* = βy*) and the use of crab cavities. As mentioned above, when β* drops to 0.25 m, the luminosity reduction factor due to a large crossing angle will decrease rapidly and it becomes 0.48 according to Eq. (20), which implies that the half luminosity will be lost. The flat optics was proposed to recover the luminosity loss caused by crossing angle when crab cavities are unavailable [22, 23]. In the flat optics, β* is preferred smaller in the parallel plane and larger in the crossing plane to mitigate the influence of crossing angle when keeping high luminosity. In LHC, the nominal β* of 0.55 m corresponds to a luminosity reduction factor of 0.82 and in the LHC Upgrade the β* of 0.15 m corresponds to a luminosity reduction factor of 0.37 [23]. Thus, an alternative flat optics βx/y* = 7.5/30 cm at IP1 (vertical crossing) and βx/y* = 30/7.5 cm at IP5 (horizontal crossing) was designed to improve the luminosity reduction factor to 0.62. Such a large change in β* in the round or flat optics can be achieved by a novel optics concept or achromatic telescopic squeezing (ATS) [22]. As it cannot fully compensate the luminosity loss due to the large crossing angle, the flat optics is regarded as a backup plan in the case of no crab cavities.

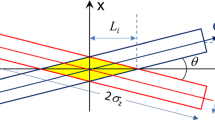
To obtain the smallest β* in the crossing plane is limited by two factors: the parasitic separations that denote the separations between the two colliding beams at the parasitic crossing locations close to the IP and the crossing angle. The parasitic separations before the triplet quadrupoles are approximately calculated in the following formula:

$$d = \frac{\theta s}{{\sqrt {\varepsilon \left( {\beta^{*} + \frac{{s^{2} }}{{\beta^{*} }}} \right)} }} \approx \frac{{\theta \sqrt {\beta^{*} } }}{\sqrt \varepsilon },$$
(21)

where s is the distance from the IP [24]. This expression just associates β* with the parasitic separation and the crossing angle. When β* gets smaller, the parasitic separations also become smaller if the crossing angle keeps the same, since the parasitic separations have important impact to beam–beam interactions and smaller separations may cause the beam instabilities [24]; thus, the parasitic separations should not be too small. On the other side, a larger crossing angle to maintain the original parasitic separation will reduce the luminosity reduction factor according to Eq. (20). This is the case with the round optics.

In the flat optics, βx* and βy* can be optimized independently to obtain a balance between the luminosity and parasitic crossing separations. The luminosity can be calculated by Eq. (22), assuming the crossing occurs in the horizontal plane [23].

$$L = \frac{{n_{{\text{b}}} N_{{\text{b}}}^{2} f_{{{\text{rev}}}} }}{{4\pi \varepsilon \sqrt {\beta_{x}^{*} \beta_{y}^{*} } }} \cdot F_{x} \cdot H_{A} \left( {\tilde{A}_{x} ,\tilde{A}_{y} ;F_{x} } \right)$$
(22)

where

$$H_{A} \left( {\tilde{A}_{x} ,\tilde{A}_{y} ;F_{x} } \right){ = }\frac{2}{\sqrt \pi }\int_{0}^{\infty } {{\text{d}}u} \frac{{\exp \left[ { - u^{2} \left( {\frac{{1 + F_{x}^{2} \tilde{A}_{x} \tilde{A}_{x} u^{2} }}{{1 + \tilde{A}_{x} \tilde{A}_{x} u^{2} }}} \right)} \right]}}{{\sqrt {\left( {1 + \tilde{A}_{x} \tilde{A}_{x} u^{2} } \right)\left( {1 + \tilde{A}_{y} \tilde{A}_{y} u^{2} } \right)} }},$$
(23)
$$\tilde{A}_{x} { = }\frac{{F_{x} \sigma_{z} }}{{\beta_{x}^{*} }},\quad \tilde{A}_{y} { = }\frac{{F_{x} \sigma_{z} }}{{\beta_{y}^{*} }},$$
(24)
$$\beta { = }\beta_{x/y}^{*} + \frac{{s^{2} }}{{\beta_{x/y}^{*} }}.$$
(25)

The first term in Eq. (22) is the ideal luminosity, and the third term (HA) is the luminosity reduction factor due to the hourglass effect as shown in Eq. (23). The hourglass effect due to the change in β along the bunch length as shown in Eq. (25) is more important when β* is very small.

Flat beam optics with constant first parasitic separation

The parasitic separations vary at different locations in the interaction area [24]. As the parasitic separations on the inner side of the inner quadrupole triplets have the same value, the first parasitic separation is taken in the following study. First, we search the best flat optics when keeping the first parasitic separation constant under the limitation of crossing angle.

The luminosity is calculated for different β* aspect ratios (βx*/βy*) with the same first parasitic separation of 12σx. Figure 3 shows the initial luminosity and the reduction factor due to the hourglass effect as a function of βx* with different fixed values of βy*. The crossing is on the horizontal plane. It is interesting to see that the reduction factor due to the hourglass effect drops rapidly with larger βx*, when βy* < 0.075 m. β* = 0.075 m means that the beam spot size is almost the same as the bunch length. Meanwhile, when both βx* and βy* are very small, the hourglass effect enhances the overlapping in the crossing plane so that the hourglass effect in the same plane is partially compensated [23]. Although the hourglass effect becomes severe with βy* < 0.075 m, the luminosity still benefits from a small βy* as shown in Fig. 3a. As a comparison, referring to the flat optics design of the LHC upgrade [23], βy* is also chosen at 0.075 m, though the two machines are at different energy scales.

Fig. 3
figure 3

Luminosity (top) and reduction factor due to the hourglass effect (bottom) as a function of βx* with different fixed values of βy*, and with the same first parasitic separation of 12σ. Red line is for round optics

Full size image

Figure 4 shows the reduction factor due to crossing angle with respect to βx*. It is independent from βy* as the crossing happens in the horizontal plane. The monotonously decreasing of the reduction factor with decreasing βx* indicates that the choice of βx* should be a compromise. The green line in Fig. 3a shows the luminosity reaches the maximum at βx* ≈ 0.4 m, when βy* = 0.075 m is chosen as mentioned above. For the design of βx* at 0.4 m, there is a significant luminosity increase compared with the round optics as the red line shows. Although small βx* is constrained by the apertures of the inner quadrupole triplets, further decreasing βy* is allowed, since the two beams are fully overlapped in the vertical plane.

Fig. 4
figure 4

Reduction factor due to the crossing angle as a function of βx*

Full size image

Flat beam optics with a constant crossing angle

In this subsection, the flat optics when keeping the crossing angle of 110 μrad under the limitation of the first parasitic separation is discussed. As in Sect. 3.2, the luminosity is calculated with different β* aspect ratios and the crossing is in the horizontal plane, as shown in Fig. 5a. Figure 5b shows how the reduction factor due to the hourglass effect is affected by βy*; thus, βy* is chosen as 0.075 m for the same reason in the last section. Meanwhile, the overlapping effect with the decreasing βx* becomes more obvious with βx* being very small due to the constant crossing angle and results in HA even slightly larger than 1 [23].

Fig. 5
figure 5

Luminosity (top) and reduction factor of the hourglass effect (bottom) as a function of βx* with different βy*. Red line is for round optics

Full size image

The first parasitic separation with different βx* and the constant crossing angle of 110 μrad is plotted in Fig. 6. Here βx* is constrained by the first parasitic separation of no less than 10σ, which indicates βx* > 0.5 m. The green line in Fig. 5a shows that the luminosity decreases gradually with the increasing βx*, when the latter is larger than 0.1 m. Thus, the optimal luminosity will be with βx* of 0.5 m, and it is considered very high compared with the baseline scheme.

Fig. 6
figure 6

First parasitic separation as a function of βx*

Full size image

The comparison of the luminosity, reduction factors due to the crossing angle and the hourglass effect for different schemes in the round optics and also the flat optics is shown in Table 3. Case 0 is the baseline parameters of SPPC and Case 1 is for smaller β*, both in the round optics. Cases 2, 3 and 4 are in the flat optics. One can see that the reduction factor Fx can be improved from 0.48 in Case 1 to 0.66 in Case 2 with the same first parasitic separation of 12σ. It can be further increased by keeping the crossing angle of 110 μrad, as in Cases 3 and 4, but the parasitic separations become smaller. The best case for the luminosity is with Case 3, which is almost two times of that in Case 1 where no crab cavities are applied.

Table 3 Comparison of the luminosity, reduction factors due to the crossing angle and the hourglass effect with Cases 0 being the nominal baseline design, Case 1 being small β* in the round optics and Cases 2, 3 and 4 in the flat optics
Full size table

Conclusion

The methods for the luminosity optimization and leveling in SPPC have been studied. They include two major parts: one is with different sets of the beam parameters at the collision to obtain higher possible averaged luminosity and at the same time with the effort to control the pileup event per crossing in the detectors; the other is with the so-called flat beam optics to provide a very small β* in the parallel plane and a relatively larger β* in the crossing plane, which is particularly useful when crab cavities are not available. The former includes the emittance managing and allowable beam–beam parameter during the physics run, different circulating bunch structure (population and spacing), dynamic β*, turnaround time, etc. In the optimum case, one can reach the annual integrated luminosity of 3.2 ab−1, which means that the integrated luminosity of 30 ab−1 as the physics operation goal might be achieved in 10–15 years, although crab cavities are mandatory to restore the luminosity reduction due to the crossing angle effect, when β* is very small. However, the study shows that with the flat beam optics the luminosity reduction can be well controlled without crab cavities.