Axiomatic Models of Rational Behavior and Interpretations

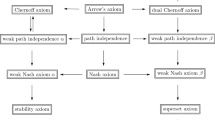
Abstract

In order to build a model of rational behavior in economics we can start with a function describing the agent’s behavior through reasonable properties from which preferences can be deduced. Conversely, the model can be based on a preference relation which is assumed to possess some properties implying the existence of a reasonable choice correspondence. Both approaches allow potent models of the individual’s behavior to be constructed. In this article it will be shown that the axioms of a model describing rational behavior by a real-valued function can be interpreted by the well-known income compensation function depending on a given preference relation. Accordingly, we will introduce a second model describing the individual behavior. As an interpretation the distance function, a widely used tool in economics, can be shown to fulfill the axioms of the second model. These different approaches make it possible to analyze choice behavior from different points of view. Hence, we may achieve a deeper insight into the economic problems lying behind these approaches.

1 Introduction

Instead of modeling consumer behavior on the basis of a utility function or preference relation, we can choose another approach by introducing a function that has an appropriate structure on a set of alternatives which will be interpreted as commodity bundles. The properties of this function characterize rational behavior in a certain context. By means of such a function the individual’s preference relation is recovered. Modeling consumer behavior on the basis of a given demand function combines observable variables, such as prices, income, and a demand for quantities of goods, with unobservable variables, such as consumer’s preferences or utility function. This is well known from the theory of revealed preference or integrability theory. Although both of these models are concerned with given demand functions, they differ considerably: the theory of revealed preference assumes the weak or strong axiom of revealed preference (Samuelson 1938; Houthakker 1950), whereas integrability theory is built on certain axioms concerning the differentiability of the given demand function (Samuelson 1950; Hurwicz and Uzawa 1971). In both theories the individual’s preferences can be recovered from the knowledge of the given demand function.

Revealed preference and integrability theory present conditions implying that the demand function is “derived” from a utility function, or—more generally—from a preference relation. By definition, saying that a demand function is derived (Chipman et al. 1971, p. 3) from some preference relation means that in any price p income situation M the individual chooses a preferred commodity bundle affordable in that situation. In accordance with the terminology used in Chipman et al. (1971, p. 3), it can be said that the preference relation “generates” the demand function.

The theory of revealed preference was created by Samuelson (1938), while integrability theory has been pioneered by Antonelli (1886), Georgescu-Roegen (1936) and Samuelson (1950). Both theories were originally developed in order to describe consumer behavior without the problematic and unobservable notion of utility. Samuelson introduced the theory of revealed preference in 1938 (Samuelson 1938, p. 62), writing: “I propose, therefore, that we start anew in direct attack upon the problem, dropping off the last vestiges of the utility analysis. This does not preclude the introduction of utility by any who may care to do so, nor will it contradict the results attained by use of related constructs. It is merely that the analysis can be carried on more directly, and from a different set of postulates”.

Later on, the works of Houthakker (1950), Hurwicz and Uzawa (1971), Richter (1971), and others considerably clarified and extended the theory of revealed preference and integrability theory. It was shown that different restrictions imposed on the demand function guarantee that this function is derived from a preference relation. This result relates consumer theory to utility theory from the point of view of a given demand function. Conversely, it is well known that a utility function, under certain restrictions, generates a demand function (Mas-Colell et al. 1995).

The present article is inspired by a work of L. McKenzie who also developed a model of consumer behavior without the notion of utility. In his article “Demand Theory Without a Utility Index” he writes (McKenzie 1957, p. 185): “It is my purpose here to describe an approach to the theory of demand which dispenses with the utility function entirely”. The basis of McKenzie’s demand theory is the function $M_x(p)$ defined as the minimum income needed, at prices p, to attain a commodity bundle viewed by the individual at least as good as x. This function is nowadays known as “income compensation function” (Hurwicz and Uzawa 1971, p. 116) or “McKenzie expenditure function” (Honkapohja 1987, p. 545). In this article we will also use the name “McKenzie income compensation function”. McKenzie showed in his article that by means of income compensation functions the basic theorems of demand theory can be obtained.

In the course of time, income compensation functions have proved to be an important tool in the theory of demand. Also in the theory of revealed preference and integrability theory, central questions, such as the existence of a preference relation generating a given demand function, were solved by means of income compensation functions (Chipman et al. 1971).

Inspired by the works of McKenzie (1957) and Honkapohja (1987), a former article of the author introduced a model of compensated consumer behavior based on a function having a structure which can be suitably interpreted in consumer theory. This model does not start with a utility function or, more generally, with a preference relation, but with conditions imposed on a real-valued function that describes rational consumer behavior. From properties of that function the individual’s preference relation can be recovered, and the McKenzie income compensation function based on that preference relation can be defined (Fuchs-Seliger 1990a). By means of that function important theorems of consumer theory can be deduced (Fuchs-Seliger 1990a, b).

The present paper extends the former article Fuchs-Seliger (1990a) by, conversely, starting with a McKenzie-type income compensation function depending on a given preference relation. It will be shown that the McKenzie-type income compensation function also fulfills the mathematical axioms, on which the model of compensated demand is based. Thus, we obtain another appropriate interpretation of that mathematical axiom system in consumer theory when the individual’s preference relation is given. It follows that compensated demand can be described by different approaches, depending on the information available about the consumer’s behavior or preference relation.

Accordingly, another model of individual behavior will be developed. This model is not based on a utility function, but on the individual’s observable choice behavior, described by properties of a function from which the individual’s preference relation can be recovered. If, conversely, the individual’s preference relation $\succeq$ is known, then it can be shown that the distance function $d(x,x^0)=max \{ \lambda \in \mathbb {R}_{++} | \frac{x}{\lambda } \succeq x^0 \}$, where $x^0$ is a reference commodity bundle, also satisfies the axioms on which that economic model is based. We thus obtain another reasonable interpretation of the formal axiom system in economics which is compatible with the former interpretation.

The distance function $d(x, x^0)$ was initially introduced to economic theory by Shephard (1953). The distance function $d(x,x^0)$ is not a classical distance function, since it does not satisfy the classical axioms of a mathematical distance function, such as $d(x,x)=0$ and $d(x,y)=d(y,x)$. It is an important tool in producer theory (Shephard 1953; Diewert 1982), consumer theory (Deaton 1979; Cornes 1992), welfare theory (Deaton and Muellbauer 1980), the theory of index numbers (Malmquist 1953; Deaton 1979), and other theories. Therefore, the application of the distance function is manifold in economics. Usually, it is defined on the basis of a given utility function or production function. However, in our context, we will define it, more generally, on the basis of a given preference relation.

We will show that the different models of rational behavior, presented in this article, are suitable to describe the individual’s behavior from different points of view.

The article is organized in the following way: in Sect. 2 the former model of compensated demand (Fuchs-Seliger 1990a) will be recalled where, by interpretation, price changes are compensated by income changes keeping the individual at a level of well-being not worse than before. In Sect. 3 some properties of the McKenzie income compensation function are provided that are important for the following analysis. In Sect. 4 it will be demonstrated that the McKenzie income compensation function also satisfies the mathematical structure of the model of compensated demand presented in Sect. 2. In Sect. 5 another model describing the economic behavior will be developed. This last model will be interpreted in Section 6 through the use of the distance function $d(x,x^0)$. In Sect. 7 we will establish relationships between the models of consumer behavior presented in Sects. 2 and 5.

2 A Formal Model of Compensated Demand

This section will start recalling the hypotheses of a former model of compensated demand presented in Fuchs-Seliger (1990a). A similar model precedingly was introduced by Honkapohja (1987). In both models important theorems about consumer behavior can be derived without using utility functions.

The former model introduced in Fuchs-Seliger (1990a) was constructed in the tradition of the theory of revealed preference or integrability theory which do not assume that the utility function or the preference relation of the agent is known. The preferences of the agent can be recovered from his behavior described by a mathematical function fulfilling certain axioms which can be appropriately interpreted in consumer theory. In this section we will reconsider compensated consumer behavior when the preferences of the individual are not known (Fuchs-Seliger 1990a) and the (observable) behavior of the individual is described by a function M(p, x) fulfilling the hypotheses of the axiom system (C I) to (C VI) to be introduced shortly.

In Sect. 4 it will be shown that the McKenzie income compensation function m(p, x), which assumes that the preferences of the individual are known, also satisfies these axioms under certain conditions.

M(p, x) and m(p, x) describe compensated consumer behavior from different starting points depending on the information available. Both functions use the same parameters.

We will consider a set $X \subseteq \mathbb {R}^n_+, X \ne \emptyset$, of alternatives which are interpreted as commodity bundles. Compensated consumer behavior will be described by a function M(p, x), where $p \in \mathbb {R}^n_{++}$ denotes a price vector and $x \in X$ a commodity bundle. M(p, x) is interpreted as the minimum money income needed to achieve a commodity bundle, say y, viewed by the consumer as at least as good as x, when he faces the money prices p.

The function M(p, x) is a mapping of $\mathbb {R}^n_{++} \times X$ into $\mathbb {R}_+$. It is supposed to satisfy the following basic axioms (Fuchs-Seliger 1990a, p. 112):

$$\begin{aligned} \begin{array}{lll} {\text {(C I)}} {} \quad \forall x \in X: {} [\forall p \in \mathbb {R}^n_{++}: px \ge M(p,x)].\\ {\text {(C II)}} {} \quad \forall x, y \in X: {} [(x \ne y \wedge \quad \forall p \in \mathbb {R}^n_{++}: px \ge M(p,y)) \Rightarrow \\ {} {} \exists p' \in \mathbb {R}^n_{++}: p'y \le M(p',x)]. \\ {\text {(C III) (i)}} {} \quad \forall x,y \in X: {} [\exists p^0 \in \mathbb {R}^n_{++}: M(p^0,x) = M(p^0,y) \Rightarrow \\ {} {} \forall p \in \mathbb {R}^n_{++}: M(p,x) = M(p,y)]. \\ {\text {(C III) (ii)}} {} \quad \forall x,y \in X: {} [\exists p^0 \in \mathbb {R}^n_{++}: M(p^0,x) > M(p^0,y) \Rightarrow \\ {} {} \forall p \in \mathbb {R}^n_{++}: M(p,x) > M(p,y)]. \\ \end{array} \end{aligned}$$

M(p, x) will be called income compensation function or minimum income function. By interpretation, (C I) means that at the prices p expenditure on the commodity bundle x is not less than the lowest spending M(p, x) that is needed in order to aquire a commodity bundle which is not worse than x in the eyes of the individual. (C II) can be interpreted accordingly. (C III) (i) and (ii) express the individual’s evaluation of the commodity bundles independently of the reference prices. Assuming that the consumer’s behavior satisfies the above hypotheses (C I) to (C III), it is possible to define consumer’s preferences in the following way (Honkapohja 1987, p. 554):

Definition 2.1

$\forall x,y \in X$:    $xRy \Longleftrightarrow \forall p \in \mathbb {R}^n_{++}$: $px \ge M(p,y)$.

It was shown in Fuchs-Seliger (1990a, Theorem 3, pp. 114–115) that the relation R possesses all those properties usually required in economic theory. It was also proved that for any $p^0 \in \mathbb {R}^n_{++}$, the function $M(p^0,x)$ represents the relation R (Fuchs-Seliger 1990a, Theorem 2, pp. 113–114), and therefore, for all $x,y \in X$ it follows, $xRy \Longleftrightarrow M(p^0,x) \ge M(p^0,y)$. These results will be summarized in our first theorem.

Theorem 1

The axioms (C I) to (C III) imply that

• (a) the relation R is complete ¹, transitive, upper semicontinuous ², strictly monotonic ³, and if X is convex, then the relation R is convex,

• (b) $M(p^0,x)$ represents the relation R for any fixed $p^0 \in \mathbb {R}^n_{++}$, i.e., $yRy' \Leftrightarrow M(p^0,y) \ge M(p^0,y'), \forall y,y' \in X$.

The relation R is recovered from the individual’s behavior described by the function M(p, x). In order to generate a convincing theory of consumer behavior, the following additional axioms were imposed on M(p, x) (Fuchs-Seliger 1990a, pp. 117–118):

• (C IV) $\forall p \in \mathbb {R}_{++}^n, \forall x \in X: [\exists z \in X: zRx \text{ and } pz=M(p,x)]$.

• For any fixed $p^0 \in \mathbb {R}^n_{++}$:

• (C V) $M(p^0,x)$ is continuous in x,

• (C VI) if X is convex, then $M(p^0,x)$ is strictly ${\mathrm{quasiconcave}}.$ ⁴

• As a special case, the following axiom is required:

• (C VII) $\lambda M(p^0,x)=M(p^0, \lambda x), \forall \lambda > 0$.

In accordance with traditional economic theory, the relation R should be continuous. Fortunately, this property is satisfied also by the relation R that we are defining.

Theorem 2

Assume (C I) to (C III) and (C V), then the relation R is continuous.

Proof

Since we already know that R is upper semicontinuous, we will show now that R is also lower semicontinuous. Therefore, consider $y\in X$ and a sequence $\langle x^k \rangle \subseteq X$ such that $yRx^k, \forall k$, and $x^k \rightarrow x^0 \in X$. Then by definition of R, for every $p \in \mathbb {R}_{++}^n, py \ge M(p,x^k), \forall k$, holds. The continuity of M(p, x) with respect to x immediately implies $py \ge M(p,x^0), \forall p \in \mathbb {R}_{++}^n$. And thus $yRx^0$. $\square$

Using the axioms (C I) to (C VI), a theory of compensated consumer behavior can be constructed step by step (Fuchs-Seliger 1990a).

We will build a bridge from the function M(p, x) to the McKenzie income compensation function m(p, x) so to show that the function m(p, x) also satisfies (C I) to (C VI), depending on the assumptions imposed on the given relation $\succeq$. This result is very important to our research, because it demonstrates that these two different approaches to the compensated demand by the functions M(p, x) and m(p, x) are not contradictory.

3 The Income Compensation Function m(p, x)

In the previous section we found that the function M(p, x) can be interpreted as an income compensation function describing the agent’s observable behavior. In this section we will turn to the McKenzie income compensation function m(p, x) which is defined by means of the individual’s preference relation. As already mentioned, the McKenzie income compensation function is an important tool in economic theory. It is defined on the basis of the preference relation $\succeq$ by

$$\begin{aligned} m(p,x) = min_{y\in X}\{py|y\succeq x\}, \end{aligned}$$

where $p \in \mathbb {R}_{++}^n$ is a price situation and $x,y \in X \subseteq \mathbb {R}_{+}^n$ are commodity bundles that can be achieved by an agent. By way of interpretation, m(p, x) is the minimum income the individual needs for aquiring a commodity bundle $y \in X \subseteq \mathbb {R}^n_+$ in the price situation p, making him at least as well-off as x. Suppose that in an initial price-income situation the agent could afford the commodity bundle x and that prices now have changed, so that the new prices are p. Then, m(p, x) is the minimum income which precisely compensates the consumer for the price change, in that it does not make his level of well-being worse than before, when he could afford commodity bundle x.

If instead of a preference relation a utility function $u: X \rightarrow \mathbb {R}$ is considered, then we obtain the function $e(p,s)=\min _{y \in X} \{ py|u(y) \ge s\}$, where $s \in \mathbb {R}$ denotes a utility level, instead of m(p, x). The function e(p, s) is called expenditure function in literature (Mas-Colell et al. 1995). Since m(p, x) is defined by means of a preference relation instead of a utility function, it is more general than e(p, s), because the relation $\succeq$ may not be transitive and complete, as the $\ge$ -relation is assumed to be and, hence, not representable by a utility function. Nevertheless, important results are obtained for consumer behavior such as, for instance, Shephard’s lemma or the existence of a demand function which is rational with respect to $\succeq$ (Fuchs-Seliger 1990b).

The following lemma presents assumptions guaranteeing that $min_{y \in X}\{py|y \succeq x\}$ exists (Fuchs-Seliger 2015, p. 1225). This result follows from the upper semicontinuity of $\succeq$ on the closed set X bounded from below and the continuity of $f_p(y)=py$ on X.

Lemma 1

Let $\succeq$ be a reflexive and upper semicontinuous relation on a closed set $X \subseteq \mathbb {R}_{+}^n$. Then, m(p, x) is well-defined for any $(p,x) \in \mathbb {R}_{++}^n \times X$.

It was shown that m(p, x) represents the given relation $\succeq$ continuously, which is an important tool for proving several assertions in this section. As a first step, I recall Theorem 1(a) in Fuchs-Seliger (2015, p. 1228). Therefore, we have:

Theorem 3

Let $X \subseteq \mathbb {R}_{+}^n$ be a closed cone, ⁵ and let $\succeq$ be a complete, transitive, and continuous relation on X. Then, for any $p^0 \in \mathbb {R}_{++}^n$, $x\succeq y \Leftrightarrow m(p^0,x) \ge m(p^0,y), \forall x,y \in X$.

If we additionally require that $\succeq$ is locally nonsatiated,⁶ then $m(p^0,x)$ is a continuous representation of $\succeq$ (Fuchs-Seliger 2015, Theorem 1(b), p. 1228). Therefore, we have:

Theorem 4

Let $\succeq$ be a transitive, complete, continuous, and locally nonsatiated relation on the closed cone $X \subseteq \mathbb {R}^n_+$. Then, for any fixed $p^0 \in \mathbb {R}_{++}^n, m(p^0, x)$ is a continuous representation of $\succeq$.

Since $m(p^0,x)$ represents the given relation $\succeq$ by money income, it is also called money-metric utility function (Samuelson 1974; Weymark 1985). In the following section it will be shown that $m(p^0,x)$ satisfies the axioms (C I) to (C VI).

4 An Interpretation of (C I) to (C VI) by m(p, x)

In accordance with McKenzie (1957), we will now consider an individual whose preference relation $\succeq$ on X is known. The individual’s compensated consumer behavior will be described by the McKenzie income compensation function m(p, x). We will prove that m(p, x) satisfies the axioms (C I) to (C VI) of the model presented in Sect. 2. This abstract mathematical model was interpreted by M(p, x), describing compensated consumer behavior without assuming that the preference relation of the individual is given. It was shown that the properties of M(p, x) allow to deduce the individual’s preference relation. In the present section we will proceed conversely, starting with the individual’s preference relation. Then, it will be shown that the McKenzie income compensation function m(p, x) also satisfies the axioms (C I) to (C VI) under appropriate conditions. Consequently, M(p, x) and m(p, x) describe compensated consumer behavior from different starting points, depending on the information available.

Theorem 5

Let $\succeq$ be a complete, transitive, and continuous relation on the closed cone $X \subseteq \mathbb {R}^n_+$. Then $m(p^0,x)$ satisfies (C I) and (C III) for any fixed $p^0 \in \mathbb {R}_{++}^n$.

Proof

(C I) follows immediately from the definition of $m(p^0,x)$ and the reflexivity and upper semicontinuity of $\succeq$.

Proof for (C III)(i): According to Theorem 3, $m(p^0,x)$ represents the relation $\succeq$ for any $p^0 \in \mathbb {R}_{++}^n$. Hence, defining indifference $\sim$ as usual by $x \sim y \Longleftrightarrow x \succeq y \wedge y \succeq x$, we have $m(p^0,x) = m(p^0,y)$ implying $x \sim y$ independently of $p^0 \in \mathbb {R}_{++}^n$, and thus we obtain $m(p,x) = m(p,y)$ for all $p \in \mathbb {R}_{++}^n$.

(C III)(ii) is similarly proved with the help of Theorem 3. $\square$

In order to demonstrate that (C II) holds as well, we preliminarily examine a property that will be central in the demonstration of (C II):

Property 4.1

For all $x \in X$, there exists $p \in \mathbb {R}_{++}^n: px = m(p,x)$.

This condition means that at least one price situation exists in which x itself is the cheapest commodity bundle which makes the individual as well-off as x. The proof of Property 4.1 also requires further preliminary results. Therefore, we will recall the notion of demand correspondences.

A demand correspondence $h: \mathbb {R}_{++}^n \times \mathbb {R}_+ \rightarrow 2^Y, Y \subseteq \mathbb {R}_+^n, Y \ne \emptyset$, $x \in h(p,M)$, is defined for prices p and income M. In every budget situation $B(p,M) = \{x\in Y | px \le M\}$, the consumer chooses a subset h(p, M) of B(p, M), so that $h(p,M) \ne \emptyset$.

Therefore, the agent chooses at least one commodity bundle in every budget situation.

h(p, M) is also called Walrasian demand correspondence (Mas-Colell et al. 1995, p. 23).

We will consider an individual who behaves rationally. Therefore, we introduce the following definition.

Definition 4.1

Given the relation $\succeq$ on Y, the demand correspondence h is called rational with respect to $\succeq$, if $h(p,M) = \{x \in Y | x \in B(p,M) \wedge \forall y \in B(p,M): x \succeq y\}$.

This means that the consumer chooses the best affordable commodity bundles in every budget situation. The following well-known lemma is important to our analysis. It is proved by the finite intersection property (Hildenbrand and Kirman 1988, proof of Proposition 2.1, p. 62).

Lemma 2

Let $\succeq$ be a complete, transitive, and continuous relation on a closed set $Y \subseteq \mathbb {R}_{+}^n$. Then there exists the demand correspondence $h: \mathbb {R}_{++}^n \times \mathbb {R}_+ \rightarrow 2^Y, x \in h(p,M)$, which is rational with respect to $\succeq$. If additionally $\succeq$ is locally nonsatiated, then, for all $x \in Y$:

$$\begin{aligned} x \in h(p,M) \Rightarrow px = M. \end{aligned}$$

From Lemma 1, we already know the conditions that imply the existence of $\min _{y\in X}\{py | y \succeq x\}$. The commodity bundles minimizing py for $y \succeq x$ and $y \in X$ define the compensated demand correspondence (Fuchs-Seliger 1990b; Cornes 1992) $g(p,x) = \arg \min _{y \in X} \{py | y \succeq x\}$.

If instead of the preference relation $\succeq$, the utility function $s=u(x)$ is given, then instead of g(p, x) we obtain the well-known correspondence $\tilde{g}(p,s)=arg \min _{y \in X}{ \{ py | u(y) \ge s\} }$, which is known as Hicksian demand correspondence (Deaton and Muellbauer 1980).

Between h(p, M) and g(p, x) the following relationship can be established:

Theorem 6

Assume the hypotheses of Theorem 4, then the following conditions hold:

• (a) for all $x \in h(p,M)$, where $(p,M) \in \mathbb {R}_{++}^n \times \mathbb {R}_+$, and for all $y\in g(p,x): y \sim x$,

• (b) for any $x \in X$ and $p \in \mathbb {R}^n_{++}$ and for all $z \in h(p,m(p,x))$ and $z'\in g(p,x): pz = m(p,x) = pz'$.

Proof

Proof for (a): For any $x \in h(p,M)$ and $y \in g(p,x)$ the definitions of g and h yield $y \succeq x$ and $py \le px \le M$. In view of the rationality of h with respect to $\succeq$, $x\succeq y$ follows. Hence, $x \sim y$.

Proof for (b): Let $z \in h(p,m(p,x))$ and $z' \in g(p,x)$. In view of the rationality of h with respect to $\succeq$, it follows that $z \succeq y$ for all $y \in B(p,m(p,x))$ and $pz \le m(p,x) = \min _{v \in X} \{pv | v \succeq x\}$. For $z' \in g(p,x)$, we obtain $z' \succeq x$ and $pz' \le pv$ for all $v \succeq x$. From this, $pz' \le px$ and $pz' = m(p,x)$ follows by the definition of g. Local nonsatiation of $\succeq$ yields $pz = m(p,x)$. Finally, this implies $pz = m(p,x) = pz'$. $\square$

Now, we are able to prove Property 4.1.

Theorem 7

Assume the hypotheses of Theorem 4 and, additionally, let a price-income situation (p, M) exist for every $x \in X$, such that for all $y \in B(p,M), x \succeq y$. Then Property 4.1 is satisfied.

Proof

Consider $x\in X$. According to Lemma 2, a demand correspondence that is rational with respect to $\succeq$ exists, and by assumption $x \in h(p,M)$, for some $(p,M) \in \mathbb {R}_{++}^n \times \mathbb {R}_+$. Since g(p, x) is well-defined, $y \succeq x$ follows for all $y \in g(p,x)$. By reflexivity of $\succeq$, $x \succeq x$, and thus $px \ge m(p,x)$. In view of Lemma 2, we know that $px = M$. Suppose, by way of contradiction, that $M > m(p,x) = py$. Since x is maximal with respect to $\succeq$ in B(p, M), then $x\succeq y$ must hold for $y \in B(p,M)$. Thus, in view of $y \succeq x$, $x \sim y$ follows. Since, in view of the above supposition $M > py$, local nonsatiation of $\succeq$ yields, there exists an $\epsilon$-neighborhood of y, $N_\epsilon (y)$, and $z \in N_\epsilon (y) \cap B(p,M)$, such that $z \succ y$. In view of $y \succeq x$ and $z \succ y$, transitivity of $\succeq$ and $\succ$ yields, $z \succ x$. However, since $pz \le M$, a contradiction to the rationality of h with respect to $\succeq$ results. As a consequence, $px = M = m(p,x)$, and Property (4.1) is fulfilled. $\square$

We are now able to demonstrate that m(p, x) satisfies (C II).

Theorem 8

Let the hypotheses of Theorem 7 hold. Then m(p, x) fulfills (C II).

Proof

Assume $x \ne y$ and $px \ge m(p,y), \forall p \in \mathbb {R}_{++}^n$. Let us first consider the case $x \succeq y$. Then we have $px \ge m(p,x) \ge m(p,y)$ by Theorem 3. Suppose, by way of contradiction, for all $p \in \mathbb {R}_{++}^n: py > m(p,x)$. From Property 4.1, we obtain $\exists p' \in \mathbb {R}_{++}^n: p'y = m(p',y)$ and thus, $m(p', y) > m(p', x)$. From Theorem 3, $y \succ x$ follows, in contradiction to $x \succeq y$. Hence, there exists $p' \in \mathbb {R}_{++}^n$, such that $p'y \le m(p',x)$.

Let us now suppose that $y \succ x$. From Theorem 3, $m(p,y) > m(p,x), \forall p \in \mathbb {R}^n_{++}$ follows. From assuming $px \ge m(p,y), \forall p \in \mathbb {R}_{++}^n$, we will obtain $px > m(p,x), \forall p \in \mathbb {R}^n_{++}$, in contradiction to Property 4.1, excluding the case $y \succ x$. $\square$

To prove (C IV), we go back to the definition of the relation R (Definition 2.1). Then (C IV) is formally equivalent to: $\forall p \in \mathbb {R}_{++}^n, \forall x \in X: [ \exists z \in X: \forall q \in \mathbb {R}_{++}^n: qz \ge M(q,x)$ and $pz = M(p,x)]$.

Using the above version, hypothesis (C IV) follows immediately, as is demonstrated by the following theorem.

Theorem 9

Assume the hypotheses of Theorem 4, then m(p, x) satisfies (C IV) and (C V).

Proof

In order to prove (C IV), consider $(p^0, x^0) \in \mathbb {R}_{++}^n \times X$. Then $m(p^0,x^0)$ is well-defined according to the above premises, and $z \in g(p^0,x^0)$ exists. Hence, $z \succeq x^0$, and by the definition of $m(\cdot , x^0)$: for all $q \in \mathbb {R}_{++}^n, qz \ge m(q,x^0)$. Moreover, since $z \in g(p^0,x^0), p^0z = m(p^0,x^0)$ follows.

(C V) follows immediately since we already know from Theorem 4 that the continuity of m(p, x) with respect to x follows as a consequence of the assumptions on $\succeq$. $\square$

We are now looking for conditions which imply that the axiom (CVI) is also satisfied by the function m(p, x).

This will be done in the next theorem.

Theorem 10

Assume the hypotheses of Theorem 3 and, additionally, let X be convex and $\succeq$ be strictly convex,⁷ then m(p, x) satisfies (C VI).

Proof

For any fixed $p^0 \in \mathbb {R}_{++}^n$ and any $x,y \in X$, and $x \ne y$, assume $m(p^0,x) \ge m(p^0,y)$. Hence, recalling that $\succeq$ is representable by $m(p^0, \cdot ), x \succeq y$ follows. Strict convexity and representability of $\succeq$ yield, $m(p^0, \lambda x + (1-\lambda ) y) > m(p^0,y), \forall \lambda \in (0,1)$. $\square$

Finally, in the case of homotheticity⁸ of $\succeq$, the axiom (C VII) is fulfilled by m(p, x).

Theorem 11

Let the hypotheses of Theorem 3 hold and, additionally, let $\succeq$ be homothetic, then $m(p^0, x)$ satisfies (C VII).

Proof

For all $\lambda > 0$,

$$\begin{aligned} m(p^0,\lambda x)&= \min _{z\in X}\{p^0z | z \succeq \lambda x\} = \min _{z\in X}\{p^0 \frac{\lambda z}{\lambda } | \frac{\lambda z}{\lambda } \succeq \lambda x\}\\&= \min _{z'\in X} \{ \lambda p^0 z'| \lambda z' \succeq \lambda x\} = \lambda \min _{z'\in X} \{p^0 z' | z' \succeq x \}\\&= \lambda m(p^0, x). \end{aligned}$$

$\square$

If $X=\mathbb {R}_{++}^n \cup \{ 0 \}$, $n>1$, then $\tilde{m} (p^0,x)=n \root n \of {\prod _{i=1}^n p^0_i x_i}$ satisfies (C VII). $\tilde{m} (p^0,x)$ is connected to the relation $\succeq ^0$, defined as: $x \succeq ^0 y \Longleftrightarrow \prod _{i=1}^n x_i \ge \prod _{i=1}^n y_i, \forall x,y \in X$, by $\min _{y \in X} \{ p^0y | y \succeq ^0 x \}$.

The preceding analysis revealed that the function $m(p^0,x)$ satisfies the axioms (C I) to (C VI) [or (C I) to (C VII)], depending on the assumptions imposed on $\succeq$. Therefore, $m(p^0,x)$ is a meaningful interpretation of that system of axioms. Moreover, it follows that M(p, x) and m(p, x) reasonably describe compensated consumer behavior, depending on the information available about the individual’s preference relation or behavior.

5 A Characterization of Distance Functions

Analogously to the preceding model with rational behavior, defined through axioms (C I) to (C V) and its application to compensated demand, we will now proceed by introducing another formal model that describes rational behavior. Afterwards, it will be shown that this model can be well interpreted in economics by the distance function

$$\begin{aligned} d(x,x^0)=\max \left\{ \lambda \in \mathbb {R}_{++} | \frac{x}{\lambda } \succeq x^0 \right\} , \end{aligned}$$

where $x^0$ is a reference commodity bundle. If instead of a preference relation a utility function u(x) is given, then, in consumer theory, the distance function is defined as

$$\begin{aligned} d'(x,x^0)=\max \{ \lambda \in \mathbb {R}_{++} | u( \frac{x}{\lambda } ) \ge s \} \text{ with } u(x^0)=s, \end{aligned}$$

where s is the utility level of $x^0$ (Cornes 1992, p. 76). By interpretation, $d'(x,x^0)$ is the maximum value by which x has to be scaled up or down in order to attain a utility level not worse than s.

It was Shephard (1953) who initially introduced distance functions into economic theory in the context of producer theory. Since then, the distance function has played an important role in various fields of economics (Deaton and Muellbauer 1980; Cornes 1992). The distance function used by Shephard is closely related to the Minkowski distance function $\Pi (x)=\inf \{ \tau | \tau > 0, \frac{x}{\tau } \in S\}$ known from mathematical literature (Valentine 1964).

The model we are going to introduce is also supposed to describe individual behavior without assuming that the individual’s preferences are known. The individual’s preferences can be recovered from the properties of the basic function of the axiom system (E I) to (E V).

We will consider a closed cone $X \subseteq \mathbb {R}_{+}^n$ as a set of alternatives. The individual’s behavior is described by a function $D: X\times X \rightarrow \mathbb {R}_+$ satisfying the following axioms:

• (E I) $D(x,x) = 1, \forall x \in X.$

• (E II) For any   $x', x'' \in$ X, and any fixed $y^0 \in$ X,

  • (i) $D(x', y^0) = D(x'',y^0) \Rightarrow \forall y \in X: D(x',y) = D(x'',y)$,

  • (ii) $D(x', y^0)> D(x'', y^0) \Rightarrow \forall y \in X: D(x',y) > D(x'',y)$.

    For any fixed   $y^0 \in X$:

• (E III) $D(x, y^0)$  is ${\mathrm{monotonic}}{\mathrm{{,}}}$ ⁹

• (E IV) $D(x, y^0)$  is continuous,

• (E V) if X is convex, then $D(x, {y}^0)$  is concave.

$D(x,y^0)$ may be interpreted as the desirability of the commodity bundle x in comparison with the reference commodity bundle $y^0$ or with any bundle y as in D(x, y). (E II) assumes that $D(x',y^0)=D(x'',y^0)$ and $D(x',y^0)>D(x'',y^0)$ must hold independently of the reference commodity bundle $y^0$. In Sect. 6 it will be shown that the distance function $d(x,x^0)$ fulfills the axioms of the model (E I) to (E V). It should be noted that (E V) implies (E IV) in the interior of X.

Assuming that the above axiom system describes the individual’s behavior, the relation $R_d$, revealing the individual’s preferences can be recovered, as it is shown by the following definition.

Definition 5.1

$x R_d x' \Longleftrightarrow D(x,y^0) \ge D(x', y^0)$, $\forall x,x' \in X$, $\forall$ fixed $y^0 \in X$.

In view of (E II), $xR_dy$ holds independently of the reference commodity bundle $y^0$. Based on the hypotheses (E I) to (E V), the relation $R_d$ possesses all the conventional properties that usually are imposed on the individual’s preferences.

Theorem 12

Assume axioms (E I) to (E IV), then the relation $R_d$ is complete, transitive, monotonic,¹⁰ and continuous. If, additionally, X is convex and (E V) holds, then $R_d$ is also convex.

Proof

Completeness, transitivity, and monotonicity follow immediately from the definition of $D(x,y^0)$ as a real value. In order to show the continuity of $R_d$ on X, we first demonstrate that $R_d$ is upper semicontinuous. Therefore, it has to be shown that $R(\tilde{x}) = \{x \in X| x R_d \tilde{x}\}$ is closed for any $\tilde{x} \in X$. Let us consider a sequence $<x^k> \subseteq X$, such that $x^k R_d \tilde{x}$ and $\lim _{k\rightarrow \infty } x^k = x^0 \in X$. By definition, $x^k R_d \tilde{x}$ means $D(x^k, y^0) \ge D(\tilde{x}, y^0)$ for any reference commodity bundle $y^0$. Since $D(\cdot , y^0)$ is assumed to be continuous, it follows that $D(x^0,y^0) \ge D(\tilde{x}, y^0)$ and, thus, $x^0 R_d \tilde{x}$. Lower semicontinuity of $R_d$ on X follows analogously. Hence, $R_d$ is continuous.

In order to show that $R_d$ is convex on the convex set X, consider $x, x', z \in X$, such that $x R_d z$ and $x' R_d z$. It has to be shown that $\lambda x + (1-\lambda ) x' R_d z, \forall \lambda \in [0,1]$ also holds. $x R_d z$ and $x' R_d z$ means that for any $y^0 \in X, D(x,y^0) \ge D(z,y^0)$ and $D(x',y^0) \ge D(z,y^0)$, respectively. From concavity of $D(\cdot , y^0)$, it follows that for all $\lambda \in [0,1]$,

$$\begin{aligned} D(\lambda x + (1- \lambda ) x', y^0)&\ge \lambda D(x,y^0) + (1-\lambda ) D(x',y^0),\\&\ge \lambda D(z,y^0) + (1-\lambda ) D(z,y^0) = D(z,y^0). \end{aligned}$$

Hence, by definition, $\lambda x+(1- \lambda )x' R_d z$. $\square$

If we assume that $D(x,y^0)$ is homogeneous of degree 1 in x, such that

$$\begin{aligned} (\mathrm{E VI}) \quad {\text {for any fixed}} \ y^0 \in X, D(\lambda x, y^0)=\lambda D(x,y^0), \quad \forall \lambda > 0, \end{aligned}$$

then the assumption of (E VI) immediately implies the homotheticity of $R_d$.

Theorem 13

Assume (E VI), then $R_d$ is homothetic.

In the following section we will show that the distance function $d(x,x')$ satisfies axioms (E I) to (E V) under appropriate conditions. Thus, $d(x,x')$ is a significant interpretation of the model represented by the axioms (EI) to (EV) so that $D(x,x')$ and $d(x,x')$ are equivalent descriptions of the agent’s economic behavior.

6 An Interpretation of (E I) to (E V) by $d(x,x')$

It will be shown now that the distance function

$$\begin{aligned} d(x,x^0) = \max \left\{ \lambda \in \mathbb {R_{++}} | \frac{x}{\lambda } \succeq x^0\right\} \end{aligned}$$

fulfills the axioms (E I) to (E V) depending on the properties of the given relation $\succeq$. As already mentioned, this distance function was introduced into economics by Shephard (1953). If $d(x,x^0)=\lambda >1$, then x has to be scaled down in order to attain the same level of well-being as $x^0$. Conversely, if x and $x^0$ are interchanged, then $d(x^0,x)=\delta <1$, and, therefore, $x^0$ must be scaled up to attain the same level of well-being as x. We will assume the following hypotheses (Fuchs-Seliger 2015):

• (D1) $X \subseteq \mathbb {R}^n_{+}$ is a closed cone.

• (D2) $\succeq$ is a complete, transitive, and continuous relation on X.

• (D3) $\succeq$ is monotonic.

• (D4) $\succeq$ is homothetic.

Assuming the above hypotheses (D1), (D2), and (D3), we obtain the following fundamental results (Fuchs-Seliger 2015, Lemma 5, p. 1230):

Lemma 3

Let $\succeq$ satisfy (D1) to (D3). Then for all $x,x' \in X \cap \mathbb {R}^n_{++}$, (a) $d(x,x') \in \mathbb {R}_{++}$, (b) $\frac{x}{d(x,x')} \sim x'$.

At this point, we are to prove that the distance function $d(x,y^0)$ is an interpretation of the axiom system (E I) to (E V) in economics. The proofs follow immediately as consequences of the representability of the relation $\succeq$ by the distance function $d(x,y^0)$ (Fuchs-Seliger 2015, Theorem 2, p. 1231).

Theorem 14

Assume the hypotheses (D1) to (D4), then $d(x,y^0)$ satisfies (E I) to (E IV) for $x,y^0 \in X \cap \mathbb {R}^n_{++}$. If additionally X is convex and $\succeq$ is also convex, then $d(x,y^0)$ satisfies (E V) on $X \cap \mathbb {R}^n_{++}$.

Remark

Note that the definition of $d(x,x^0)$ and the assumptions on $d(x,x^0)$ results in

$d(x',x'')>1 \Rightarrow d(x'',x')<1$.

Thus, as was obvious from previous analysis, the distance function $d(x,x')$ fulfills the axioms imposed on $D(x,x')$ and describes the agent’s economic behavior accordingly.

From this, it follows that if the individual’s preference relation is known and has the conventional properties required in Theorem 14, then the individual behaves according to the axioms (E I) to (E V). Conversely, if the individual’s behavior adapts to the axiom system (E I) to (E V), then an outside observer can conclude that the preferences of the individual meet the conditions usually imposed on the agent’s preference relation in traditional neoclassical consumer theory.

7 Relationships Between the Models

Previous analysis demonstrated that the distance function $d(x,x^0)$ fulfills the axioms (E I) to (E V), and therefore is an interpretation of that axiom system in the theory of consumer behavior. It is even possible to establish a bridge from the axiom system (C I) to (C VII) to the axiom system (E I) to (E V) showing that for any fixed $x^0$, $d^0(x,x^0)=max\{ \lambda \in \mathbb {R}_{++} | \frac{x}{\lambda } R x^0\}$, where R is defined in Definition 2.1, also satisfies (E I) to (E V).

Theorem 15

Let $X \subseteq \mathbb {R}^n_{+}$ be a closed cone and let the axioms (C I), (C II), (C III), (C V), and (C VII) hold. Then the distance function $d^0(x,x^0)=max\{ \lambda \in \mathbb {R}_{++} | \frac{x}{\lambda } R x^0\}$ is well-defined for $x,x^0\in X \cap \mathbb {R}^n_{++}$, and satisfies (E I) to (E IV). If additionally X is convex, then $d^0(x,x^0)$ also satisfies (E V).

Proof

According to Theorems 1 and 2, the axioms (C I), (C II), (C III), and (C V) yield that R is complete, transitive, strictly monotonic, continuous, and convex, if X is convex. Moreover, the axiom (C VII) implies that the relation R is homothetic for the following reasons: by definition, xRy implies $px \ge M(p,y), \forall p \in \mathbb {R}^n_{++}$, and therefore due to (C VII), also $\lambda px \ge M(p,\lambda y), \forall \lambda >0$, holds. The definition of R yields $\lambda xR \lambda y$, $\forall \lambda >0$. Thus, R satisfies the hypotheses (D1) to (D4), and we can apply Theorem 14 to find that $d^0(x,x^0)$ fulfills (E I) to (E IV) for $x,x^0\in X \cap \mathbb {R}^n_{++}$, and (E V), if X is convex. $\square$

Conversely, we can assume the axioms (E I) to (E IV) and find that $m^0(p^0,x)=\min \limits _{y \in X} \{p^0y|yR_dx\}$, where $R_d$ is defined in Definition 5.1, satisfies the axioms (C I), (C III), (C IV), and (C V).

Theorem 16

Let $X \subseteq \mathbb {R}^n_{+}$ be a closed cone and let the axioms (E I) to (E IV) hold, then $m^0(p^0,x)$ for any $p^0 \in \mathbb {R}^n_{++}$ satisfies (C I), (C III), (C IV), and (C V).

Proof

Assuming that the axioms from (E I) to (E IV) hold, then Theorem 12 yields that $R_d$ is complete, transitive, monotonic, and continuous. Hence, Theorem 5 yields that $m^0(p^0,x)$ satisfies (C I) and (C III). Since $R_d$ is monotonic and $X \subseteq \mathbb {R}^n_{+}$ is assumed to be a closed cone, $R_d$ also is locally nonsatiated. Hence, it follows from Theorem 9 that $m^0(p^0,x)$ satisfies (C IV) and (C V). $\square$

Remark

If the conditions of Theorem 16 hold and if additionally X is convex and (E V) holds, then $m^0(p^0,x)$ is quasiconcave with respect to x. This follows, from the fact that $R_d$ is convex due to Theorem 12, and $R_d$ is representable by $m^0(p^0,x)$ due to Theorem 1 in Fuchs-Seliger (2015). Hence, it immediately follows that $m^0(p^0,x)$ is quasiconcave.

The validity of (C II) follows accordingly to Theorems 7 and 8 by means of Property 4.1.

The preceding section revealed that the axiom systems presented in this article have close relationships to each other. In real life, it depends on the availability of information which of the models is used to start our analysis of economic behavior.

8 Conclusions

In this article we have developed two different formal models of rational behavior without assuming that the individual’s utility function is known. These models are concerned with functions describing the individual observable behavior. Thus, the use of the word “utility”, which “continues to worry students into thinking that economic theory has injected some unsatisfactorily metaphysical concept into the works” (Cornes 1992, p. 86), can be avoided.

The above models have been constructed in the tradition of the theory of revealed preference and integrability theory. Both theories start with functions describing the consumer’s observable behavior and not with a utility function. Based on the hypotheses of these theories, the individual’s preference relation can be recovered.

As we have seen, these abstract models constructed by axioms (C I) to (C VI) and (E I) to (E V), assuming functions of different mathematical structures, can be reasonably interpreted in economic theory. The first one can describe compensated consumer behavior and the second one the desirability of commodity bundles relative to a reference commodity bundle. It can be shown that the individual’s preference relation deduced within these models possesses all those properties usually required in economics.

If, conversely, the individual’s preference relation is known, then the McKenzie income compensation function fulfills axioms (C I) to (C VI) under appropriate conditions and, hence is a powerful interpretation of that axiom system.

Accordingly, based on a given preference relation, it can be shown that the distance function introduced by Shephard in economic theory satisfies the axioms (E I) to (E V).

Finally, relationships between the axiom systems (C I) to (C VII) and (E I) to (E V) have been established.

The different approaches to economic behavior presented in this article allow for modelling economic problems in different ways and, hence, to obtain deeper insights into the economic intuition and problems that lie behind the theoretical models.