Treatment of Dependency and Correlation in Multiunit PSA Considering Seismic as External Event

Abstract

In the wake of Fukushima accident, throughout the world there is a concern about the safety of the nuclear reactor sites from external events such as seismic, flood, tsunami etc. Nuclear reactor sites around the world are mostly twin units or multi units. Hence, these days the concept of Reactor Park is also widely discussed, which brings out the requirement for proper site safety goals. As per International Atomic Energy Agency (IAEA) safety guide lines, the safety goals for single unit Nuclear Power Plants (NPPs) are very well established, but when it comes to multiunit sites the concept of site safety goals is not matured enough, hence, it is very much needed to establish these goals at the site level.Unlike the single unit Probabilistic Safety Assessment (PSA), the procedure for performing the PSA for multi-unit sites is not yet established. However, efforts are being made to standardise the procedure considering the various plants and their releases in a given site under consideration. In the multi unit PSA, special attention should be given while modeling the multi-unit initiating events, multi-unit PSA model, shared resources, inter-unit correlations, Common Cause Failure (CCF), modeling of Human Reliability Analysis (HRA) in the multi-unit parlance and risk aggregation. Among these issues, in the present paper focus is given for treatment of dependency and correlation as seismic core damage frequency is highly dependent on the modelling of dependency among the components. Conservative approach of considering fully dependence will give highly conservative results which may not be realistic. Hence, the main objective of the present study is treatment of dependency and correlation among various components considering the internal and external events possible in the site. The site under consideration is Tarapur site (Maharashtra, India) having two hypothetical advanced reactors. Scope of the analysis includes full power, external event (Seismic), Level 1 PSA considering reactor core as radioactivity source.

Introduction

Seismic Probabilistic Safety Assessment (SPSA) is an external event PSA study that is different from an internal-event PSA. In seismic PSA, seismic event is the main initiator and can initiate other internal initiating events in the plant. In this study, earthquakes of various levels needs to be considered along with their corresponding frequency of occurrence which is generally obtained from seismic hazard analysis. Also the seismic events have the capability to damage simultaneously all the redundant components, which are located at same elevation or different elevations, either in the single unit or multi units in a given site. Hence, in the seismic risk quantification it is very important to consider dependency and correlations between various components.

There are several studies made in this domain starting from Seismic Safety Margins Research Program (SSMRP) at the Lawrence Livermore National Laboratory (Budnitz et al. 2017; Cummings 1986) which is based on the concept of multi variable correlation over response and capacity factors of a structure. Also this technique needs information about joint probability distributions among various parameters of components and sometimes it is difficult to obtain all the required information. Mankamo model (1977) for identical components based on the principle of geometric mean was developed, however, it can be applied up to a maximum of four components. Reed et al. (2017) developed a procedure based on common sources of variability to quantify dependency between the components. Pellissetti and Klapp (2011) have proposed a method similar to the traditional Common Cause Failure (CCF) model which is applied in internal events PSA employing beta factors. This model assumes that whenever a common cause event occurs, all components within that common cause component group are assumed to fail. Hence, in this model interaction of two or more components failures cannot be modeled. W.S. Jung et.al. (2020) have developed a new methodology for modeling dependency between various components using explicit seismic common cause failures in the context of seismic multi unit PSA. This method also utilizes the concepts from SSMRP approach (multi variable correlation) to evaluate the multi component failure probabilities. Later these probabilities are converted to common cause failure factors by solving 2ⁿ− 1 probability equations for ‘n’ component system. As the number of components increases this method can be computationally intensive as it evaluates multiple integration using Montecarlo integration of multivariate normal (MVN) distribution. In order to overcome limitations of existing methods, Alpha Factor Model along with a novel approach to estimate the inter unit seismic common cause failure factors using distance separation factor is proposed in the present study.

PSA for Multi Unit Site

Unlike the single unit PSA, the procedure for performing the PSA for multi-unit sites is not yet established. However, efforts are being made to standardise the procedure considering the various plants and their releases in a given site under consideration. A site can consist of not only Nuclear Power Plants (NPPs) but also other Non Reactor Nuclear Facilities (NRNFs). Hence, the multi-unit PSA procedures should account for the releases from various plants and the risk from all the facilities in the site. A general framework developed (Hari Prasad et al. 2022) for performing the multi-unit PSA is utilised to perform the analysis.

Plant Information

In this study, the site considered is Tarapur, which is situated in the west coast of Maharashtra, India. The site lies in the moderate seismic zone of India. Being a coastal site, seawater will be used on once through basis for condenser cooling and process water cooling. In the present study, source of radioactivity is considered to be from reactor cores of twin hypothetical advanced reactor.The reactor is a vertical pressure tube type boiling light water cooled and heavy water moderated reactor relying on natural circulation for core cooling during normal and shutdown conditions. The reactor incorporates various passive features for decay heat removal, containment cooling and isolation. One of the important passive design features of this reactor is that the heat removal is achieved through natural circulation of primary coolant at all allowed power levels with no primary coolant pump. The details of layout of the site are shown in Fig. 1.

Fig. 1

Multi-Unit site layout

Multi Unit PSA Model

Separate Level 1 PSA models have been developed for both the reactors. Attention is given for coding the components/systems which are common to both the units by adopting same identification code. Apart from this a separate multi-unit PSA model has been created.

Multi-Unit Initiating Events

In this step, the initiating events (IEs) that have been selected from single unit PSA study are analysed to check whether they affect multiple units or facilities concurrently. In the present study, the available initiating events analysis from single unit are considered as the starting point. Engineering analysis is used for screening of multiunit initiating events based on shared systems/ resources and the following classification of initiating events have been considered for this study:

• (1) Category 1: IEs affecting only individual units resulting in to core damage.

• (2) Category 2: IEs which can affect both reactor units (E.g. Common pipe line from pump house resulting in Service Water System failure in both units, Main steam line break outside the reactor building due to the damage of common Turbine building during seismic event).

Multi-Unit Event Trees

The event tree development in MUPSA is similar to that of single unit PSA. However, care must be taken to include the various functional events from multiple units when developing the event tree for multi-unit initiating events. In the present study the event trees are developed from multi-unit context in Level 1 PSA. Some of the multi-unit initiating events considered in the analysis from Level 1 PSA are:

• (1) Reactor 1 Structural Failure

• (2) Reactor 2 Structural Failure

• (3) Pump House Structural Failure leading to Service Water System (SWS) failure of Reactor 1 and Reactor 2

• (4) Turbine Building Structural Failure leading to Main Steam Line Break Outside reactor Building (MSLBOB) of Reactor 1 and Reactor 2

• (5) Loss of offsite power (LOOP) affecting Reactor 1 and Reactor 2.

The event trees representing the above mentioned IEs are developed as primary, secondary and tertiary event trees for the seismic event. The primary seismic event tree represents the logical connection between all the above mentioned IEs. The event tree starts with a seismic initiator that is associated with the several seismic hazard bins with varying frequencies for each bin. The various consequences that have been considered in the analysis are shown in Table 1. Figure 2 shows the primary event tree developed for MUPSA study. In developing the seismic event trees for MUPSA study, an integrated PSA model has been developed based on the inputs from single unit PSA model (Hari Prasad, et al. 2022). It should be noted that in the Fig. 2 two different conventions are used for consequence and the code. For example under consequence column R2IES-S represents secondary event tree for functional event S-R2IES. That means S-R2IES is further expanded in a separate event tree called secondary event tree. Whereas, under code column, S-R2IES represents seismically induced IEs of Reactor 2, which is directly taken as Id of the functional event of the corresponding event tree. This code is generated based on the failure events in the event tree, success events are not considered while generating this code. This depends on the software tool being used, in the present case Risk Spectrum software tool is used.

Table 1 Various primary consequences considered in MUPSA

Fig. 2

Seismic primary event tree of MUPSA study

Accident Sequences

Once the event trees are developed for each initiating event, the dominating accident sequences which lead to core damage consequence can be identified from the event trees. The dominating accident sequences so obtained from the present analysis are shown in Tables 2 and 3. From these dominating accident sequences Core Damage Frequency (CDF) can be evaluated by summing up CDF contributions from all the individual sequences.

Table 2 Dominant accident sequences for CD1 at PGA 0.8 g

Table 3 Dominant accident sequences and their frequencies for CD12 at PGA 0.8 g

Fragility Evaluation Considering Dependency

The seismic fragility of a structure or equipment component is defined as the conditional probability of its failure for a given level of seismic input parameter, typically the peak ground acceleration (PGA).Dependence arises because the responses of components may be dependent for a given earthquake. Similarly, the capacities of components may also be dependent.Traditionally, while evaluating the fragility of the structures, systems and components (SSC) the conservative approach, that is, the identical components with same geometry, same orientation located in same elevation are considered as fully correlated and if one component fails all the components are considered to be failed during the seismic event.However, this procedure leads to very conservative results and may not be realistic. Hence, it is very important to model the dependency among the components in a realistic manner. In this section various methods available to model the component dependency is discussed and a new method based on Alpha factor model is highlighted.

Dependency and Correlation

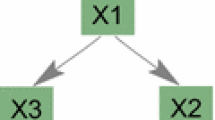
In the present study, dependency term is used in the context of component failures. If there exist two components and their failures are dependent, that means, probability of failure of one component has an effect on second component failure probability. In general, in the fragility evaluation of a structure two variables commonly used viz. response and capacity of a structure. Failure of a structure can be defined with these parameters such that failure can takes place, if the response of the structure exceeds its capacity. In a plant there can be several components which are identical or unidentical located at same or different elevations. There can dependency exist between these components from seismic input ground motion, response of the components and their capacities. The dependency between these components can be modeled using the concept of correlation (correlation coefficient). Figure 3 represents the various correlations that can be possible among various components in different units in a site.

Fig. 3

Representation of intra and inter unit correlations

Let X and Y denote the response and capacity vectors with means μ_X and μ_Y. The covariance matrices for the response and capacity are denoted as CoV (X_i,X_j)and CoV (Y_i,Y_j). The joint distributions of response and capacity are completely specified by these mean vectors and covariance matrices as given below.

Response vector, X and Capacity vector, Y

$$\left\{X\right\}=\left\{\begin{array}{c}\begin{array}{c}{X}_{1}\\ {X}_{2}\end{array}\\ \vdots \\ {X}_{n}\end{array}\right\}; \left\{Y\right\}=\left\{\begin{array}{c}\begin{array}{c}{Y}_{1}\\ {Y}_{2}\end{array}\\ \vdots \\ {Y}_{n}\end{array}\right\}$$

Mean and standard deviation vector of X and Y

$$\left\{{\mu }_{X}\right\}= \left\{\begin{array}{c}\begin{array}{c}{\mu }_{{X}_{1}}\\ {\mu }_{{X}_{2}}\end{array}\\ \vdots \\ {\mu }_{{X}_{n}}\end{array}\right\}; \left\{{\mu }_{Y}\right\}= \left\{\begin{array}{c}\begin{array}{c}{\mu }_{{Y}_{1}}\\ {\mu }_{{Y}_{2}}\end{array}\\ \vdots \\ {\mu }_{{Y}_{n}}\end{array}\right\}; \left\{{\sigma }_{X}\right\}= \left\{\begin{array}{c}\begin{array}{c}{\sigma }_{{X}_{1}}\\ {\sigma }_{{X}_{2}}\end{array}\\ \vdots \\ {\sigma }_{{X}_{n}}\end{array}\right\}; \left\{{\sigma }_{Y}\right\}= \left\{\begin{array}{c}\begin{array}{c}{\sigma }_{{Y}_{1}}\\ {\sigma }_{{Y}_{2}}\end{array}\\ \vdots \\ {\sigma }_{{Y}_{n}}\end{array}\right\}$$

(1)

Covariance matrix of X

$$\left[{C}_{X}\right]=\left[\begin{array}{ccc}\mathrm{CoV} \left({X}_{1},{X}_{1}\right)& \mathrm{CoV} \left({X}_{1},{X}_{2}\right)& \begin{array}{cc}\cdots & \mathrm{CoV} \left({X}_{1},{X}_{n}\right)\end{array}\\ \mathrm{CoV} \left({X}_{2},{X}_{1}\right)& \mathrm{CoV} \left({X}_{2},{X}_{2}\right)& \begin{array}{cc}\cdots & \mathrm{CoV} \left({X}_{2},{X}_{n}\right)\end{array}\\ \begin{array}{c}\vdots \\ \mathrm{CoV} \left({X}_{n},{X}_{1}\right)\end{array}& \begin{array}{c}\vdots \\ \mathrm{CoV} \left({X}_{n},{X}_{2}\right)\end{array}& \begin{array}{cc}\begin{array}{c}\vdots \\ \cdots \end{array}& \begin{array}{c}\vdots \\ \mathrm{CoV} \left({X}_{n},{X}_{n}\right)\end{array}\end{array}\end{array}\right]$$

$$\left[{C}_{X}\right]=\left[\begin{array}{ccc}{\sigma }_{{X}_{1}}^{2}& {\rho }_{X12}{\sigma }_{{X}_{1}}{\sigma }_{{X}_{2}}& \begin{array}{cc}\cdots & {\rho }_{X1n}{\sigma }_{{X}_{1}}{\sigma }_{{X}_{n}}\end{array}\\ {\rho }_{X21}{\sigma }_{{X}_{2}}{\sigma }_{{X}_{1}}& {\sigma }_{{X}_{2}}^{2}& \begin{array}{cc}\cdots & {\rho }_{X2n}{\sigma }_{{X}_{2}}{\sigma }_{{X}_{n}}\end{array}\\ \begin{array}{c}\vdots \\ {\rho }_{Xn1}{\sigma }_{{X}_{n}}{\sigma }_{{X}_{1}}\end{array}& \begin{array}{c}\vdots \\ {\rho }_{Xn2}{\sigma }_{{X}_{n}}{\sigma }_{{X}_{2}}\end{array}& \begin{array}{cc}\begin{array}{c}\vdots \\ \cdots \end{array}& \begin{array}{c}\vdots \\ {\sigma }_{{X}_{n}}^{2}\end{array}\end{array}\end{array}\right]$$

(2)

Correlation coefficient matrix of X

$$\left[ {\rho_{X} } \right] = \left[ {\begin{array}{*{20}c} {\rho_{X11} } & {\rho_{X12} } & {\begin{array}{*{20}c} \cdots & {\rho_{X1n} } \\ \end{array} } \\ {\rho_{X21} } & {\rho_{X22} } & {\begin{array}{*{20}c} \cdots & {\rho_{X2n} } \\ \end{array} } \\ {\begin{array}{*{20}c} \vdots \\ {\rho_{Xn1} } \\ \end{array} } & {\begin{array}{*{20}c} \vdots \\ {\rho_{Xn2} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} \vdots \\ \cdots \\ \end{array} } & {\begin{array}{*{20}c} \vdots \\ {\rho_{Xnn} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right] \Rightarrow \left[ {\rho_{X} } \right] = \left[ {\begin{array}{*{20}c} 1 & {\rho_{X12} } & {\begin{array}{*{20}c} \cdots & {\rho_{X1n} } \\ \end{array} } \\ {\rho_{X21} } & 1 & {\begin{array}{*{20}c} \cdots & {\rho_{X2n} } \\ \end{array} } \\ {\begin{array}{*{20}c} \vdots \\ {\rho_{Xn1} } \\ \end{array} } & {\begin{array}{*{20}c} \vdots \\ {\rho_{Xn2} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} \vdots \\ \cdots \\ \end{array} } & {\begin{array}{*{20}c} \vdots \\ 1 \\ \end{array} } \\ \end{array} } \\ \end{array} } \right]$$

(3)

Similar matrices can be defined for capacity factor Y also. Based on the failure criteria defined earlier, the limit state function can be defined as follows:

$$Z = \,X - Y$$

(4)

Probability of failure can be defined as

$$P \left(\mathrm{Failure}\right)=P\left(Z>0\right)$$

(5)

To estimate the failure probability of the components (considering the correlations) there are different methods available such as simulation methods (MonteCarlo, Latin Hyper Cube Sampling), analytical approximations such as First Order Reliability Method (FORM), Second Order Reliability Method (SORM) etc. (Budnitz et al. 2017).

Scale Factor Based Approach

In the fragility evaluation, the conditional probability of component failure is determined by considering the capacities of the components in various failure modes. The fragility curve for any component can be defined with the help of its median ground acceleration capacity, A_m, and the corresponding aleatory uncertainty ($\beta_{R}$) and epistemic uncertainty ($\beta_{U}$). Hence, the probability of failure (p_f) at a non exceedence probability (Q) can be expressed as (Allin Cornell 1968; Kennedy et al. 1980, 1988; Kennedy and Ravindra 1984):

$$p_{f} = \Phi \left[ {\frac{{\ln \left( {\frac{a}{{A_{m} }}} \right) + \beta_{u} \,\varphi^{ - 1} \left( Q \right)}}{{\beta_{R} }}} \right]$$

(6)

If both the uncertainties are combined together then the probability of failure can be given as follows:

$$\begin{gathered} p_{f\left( A \right)} = \Phi \left[ {\frac{{\ln \left( {\frac{a}{{A_{m} }}} \right)}}{{\beta_{C} }}} \right] \hfill \\ {\text{where}} \hfill \\ \beta_{C} = \sqrt {\beta_{R}^{2} + \beta_{U}^{2} } \hfill \\ \end{gathered}$$

(7)

in which Φ (^.) is the standard Gaussian cumulative function. The A_m value can be obtained from reference earthquake ground motion and median scale factor (Kennedy and Ravindra 1984).

Various Dependency Models

In this section various dependency models that were discussed previously are briefly explained highlighting their limitations.

Multiple Integration Method (SSMRP Method)

In this SSMRP (Budnitz et al. 2017; Cummings 1986) method, the response and capacity of various components located at different elevations were represented by a joint lognormal distribution.If a cut set contains more than one component, then cut set failure is defined as all responses exceeding their associated capacities.

$$\begin{aligned} P\left( {{\text{Failure}}} \right) & = P\left( {Z_{1} > 0 \cap Z_{2} > 0 \cap \ldots \cap Z_{n} > 0} \right) \\ &= P\left( {Z_{1} > 0,Z_{2} > 0, \ldots , Z_{n} > 0} \right) \\ \end{aligned}$$

$$P\left( {{\text{Failure}}} \right) = \int\limits_{0}^{\infty } {\int\limits_{o}^{\infty } { \cdot \cdot \cdot } } \int\limits_{o}^{\infty } f_{Z}{\left( {z_{1} ,z_{2} , \ldots ,z_{n} } \right)dz_{1} dz_{2} \ldots dz_{n} }$$

(8)

where $f_{Z} \left( {z_{1} , z_{2} , \ldots ,z_{n} } \right)$ is the joint probability density function of Z which is defined in terms of response (X) and capacity (Y) as in Eq. 4. The SSMRP method can be applied to various dependent components located at various locations in the plant. However, it needs the information regarding the joint probability density functions and covariance matrix between various components which is difficult to obtain for most of the components. However, depending on the contribution to the overall risk the fragility of the components can be evaluated by this procedure.

Mankamo Model

In Mankamo model (Budnitz et al. 2017; Mankamo 1977), the dependency between various identical components located at same elevation can be modeled as follows. Consider two events A and B, the lower and upper bounds on joint failure probability can be given by:

$$P\left[ A \right]. \, P\left[ B \right] \, < \, P\left[ {AB} \right] \, < {\text{ min }}\left\{ {P\left[ A \right], \, P\left[ B \right]} \right\}$$

(9)

The geometric mean of these bounds can be represented as

$$P\left[ {AB} \right] \, = \, \left( {P\left[ A \right]. \, P\left[ B \right]. \, \min \, \left\{ {P\left[ A \right], \, P\left[ B \right]} \right\}} \right)^{1/2}$$

(10)

In the case of two identical components, P = P [A] = P [B], this reduces to

$$P\left[ {AB} \right] \, = \, P^{1.5}$$

This model allows consideration of up to four identical components having arbitrary failure correlation coefficients.In the present study, wherever applicable,the above procedure has been used to develop the fragility curves for redundant components.

Beta Factor Model

Pellissetti and Klapp (2011) have proposed an approach that uses the traditional CCF models that are used in internal events PSA that uses beta factors. The beta factor model is a single parameter model,which uses one parameter in addition to the total component failure probability to calculate the CCF probabilities.

$${{\varvec{Q}}}_{{\varvec{I}}}=\left(1-{\varvec{\beta}}\right){{\varvec{Q}}}_{{\varvec{t}}}$$

$${{\varvec{Q}}}_{{\varvec{m}}}={\varvec{\beta}}{{\varvec{Q}}}_{{\varvec{t}}}$$

(11)

where Q_t is the total failure probability of one component (Q_t = Q_I + Q_m), Q_I is the independent failure probability of the single component, Q_m is the probability of basic event failure involving ‘m’ specific components, and ‘m’ is the maximum number of components in a common cause group.

This method assumes whenever a common cause event occurs, all components within that group are assumed to fail. Hence, in this model either single component failure or all component failure can be modeled but interaction (failure) of two or more components cannot be modeled. In order to overcome this difficulty, in the present study a new approach based on Alpha Factor Model is proposed.

Explicit Modeling of Seismic Dependency

Jung et.al. (2020) have proposed a new methodology for modeling dependency between various components using explicit seismic common cause failures by converting correlated seismic failures into seismic CCFs with which the seismic risk can be quantified similar to internal event PSA. Similar to SSMRP approach this method evaluates multiple integration using Montecarlo integration of multivariate normal distribution to evaluate the multi component failure probabilities. Equation (12) shows the combination probability of seismic failures such as P_12…n (a) = P (${\cap }_{i=1}^{n}{A}_{i}<a)$

$${P}_{12..n}\left(a\right)={\int }_{-\infty }^{\mathit{ln}\left(\frac{a}{{x}_{1m}}\right)}{\int }_{-\infty }^{\mathit{ln}\left(\frac{a}{{x}_{2m}}\right)}...{\int }_{-\infty }^{\mathit{ln}\left(\frac{a}{{x}_{nm}}\right)}\frac{1}{\sqrt{\left|\Sigma \right|{\left(2\pi \right)}^{n}}}\mathrm{exp}\left(-\frac{1}{2}{x}^{t}{\Sigma }^{-1}x\right)\mathrm{d}x$$

(12)

Where

$$\sum = \left[ {\begin{array}{*{20}c} {\beta_{1}^{2} } & {\beta_{12}^{2} } & {...} & {\beta_{1n}^{2} } \\ {\beta_{21}^{2} } & {\beta_{2}^{2} } & {...} & {\beta_{2n}^{2} } \\ {...} & {...} & {...} & {...} \\ {\beta_{n1}^{2} } & {\beta_{n2}^{2} } & {...} & {\beta_{n}^{2} } \\ \end{array} } \right],\,\,\,\beta_{ij}^{2} = {\text{CoV}} \left( {X_{i} ,X_{j} } \right),\,\,\,x^{t} = \left[ {x_{1} \,\,\,x_{2} \,\,\,...\,\,\,x_{n} } \right]$$

These combination probabilities of correlated seismic failures are calculated by using MVN integration. Later these probabilities are converted to common cause failure factors by solving 2ⁿ-1 probability equations which are usually in the form as shown in Eq. (13).

$$S = \bigcup\limits_{i} {S_{i} } = S_{1} + S_{2} + ...$$

$$P\left( S \right) = 1 - \prod\limits_{i} {\left( {1 - P\left( {S_{i} } \right)} \right)}$$

(13)

where S can be summation of seismic CCFs, P(S) can be combination probabilities (P1, P2, P12, etc.) and P (S_i) can be CCF probabilities (Q1, Q2, Q12 etc.).). In this approach one has to solve the MVN integration which needs covariance matrix between various components (difficult to obtain) as well as probability equations, as number of components increases the process may be computationally intensive.

Alpha Factor Model

In this model, the basic event probabilities can be expressed in terms of total component failure probability (Q_t) and the alpha factors as follows (NUREG 1988):

$${{\varvec{Q}}}_{{\varvec{k}}}^{\left({\varvec{m}}\right)}=\frac{{\boldsymbol{\alpha }}_{{\varvec{k}}}^{\left({\varvec{m}}\right)}}{\left(\begin{array}{c}{\varvec{m}}-1\\ {\varvec{k}}-1\end{array}\right)}{{\varvec{Q}}}_{{\varvec{t}}}$$

(14)

where α_k^(m) is ratio of the probability of failure events involving any k components over the total failure probability of all failure events in a group of m components, and ∑_k α_k^(m) = 1.With this approach it is possible to model interaction between 2 or more components apart from failure of all the components. for the case of 3 component system, the αfactors can be defined as follows:

$${Q}_{1}={\alpha }_{1}{Q}_{t};{Q}_{2}=\frac{1}{2}{\alpha }_{2}{Q}_{t};{Q}_{3}={{\alpha }_{3}Q}_{t}$$

$${\alpha }_{1}=\frac{{Q}_{1}}{{Q}_{t}};{\alpha }_{2}=\frac{{2Q}_{2}}{{Q}_{t}};{\alpha }_{3}=\frac{{Q}_{3}}{{Q}_{t}}$$

$$Q_{t} = Q_{1} + 2Q_{2} + Q_{3}; \sum\limits_{{i = 1}}^{3} {\alpha _{i} = 1}$$

where Q₁ is single component failure probability, Q₂ is probability of failure of two components simultaneously and Q₃ is probability of failure of three components simultaneously. These probabilities can be obtained based on the MVN integration technique as discussed in the previous sections.However, in this study main emphasis is given for reducing the efforts to derive these common cause factors among the components located in different plants which is termed as inter unit seismic CCF factors which is explained as below. In some literature (Jang 2020) these factors have been derived based on Swain dependency model (Swain and Guttmann 1990). However, they are derived from internal event MUPSA point of view. Hence, usage of these factors in the external event context needs to be verified.

An attempt is made to derive simple model based on the distance separation factor between various plants. It is assumed that when the seismic vibratory motion stuck the site the seismic energy attenuates from the site boundary till it reaches various plants in the site. Due to this attenuation, similar components located at same elevation in various plants may experience different loading conditions and because of which some components may fail simultaneously and some may not fail. Based on this principle inter seismic CCF factors have been derived. Consider the site boundary as shown in the Fig. 4 which consists of 3 NPPs such as NPP1, NPP2 and NPP3.

Fig. 4

Schematic of Site Boundary and Earthquake Source

The following information can be deduced from the Fig. 4.

$${R}_{1}=\sqrt{{h}^{2}+{d}^{2}}$$

$${R}_{2}=\sqrt{{R}_{1}^{2}+{d}_{1}^{2}}$$

$${R}_{3}=\sqrt{{R}_{1}^{2}+{\left({d}_{1}+{d}_{2}\right)}^{2}}$$

(15)

where R₁, R₂, R₃ are hypocentral distance from source to NPP1, NPP2 and NPP3 respectively. ‘h’ is the depth of source, ‘d’ is the epicentral distance from source to NPP1. ‘d₁’ and ‘d₂’ are distance between NPP1 & NPP2 and NPP2 & NPP3 respectively. Now consider the attenuation relationship to estimate the peak ground acceleration (PGA) at the various plants in the site. As an example, McGuire’s (1978) (Verma et al. 2015) attenuation relationship has been considered.

$$P\,{\text{gha}}\,(g) = 0.0306\,\exp \,(0.89M)\,(R)^{ - 1.17}$$

(16)

R = Hypocentral distance (in km). M = Magnitude.

Considering same magnitude and varying distances, various PGA values can be generated at various plants.

$${a}_{1}=0.0306\mathrm{exp} (0.89 M) ({R}_{1}{)}^{-1.17}$$

$${a}_{2}=0.0306\mathrm{exp} (0.89 M) ({R}_{2}{)}^{-1.17}$$

$${a}_{3}=0.0306\mathrm{exp} (0.89 M) ({R}_{3}{)}^{-1.17}$$

(17)

$$\frac{{a}_{2}}{{a}_{1}}={\left(\frac{{R}_{2}}{{R}_{1}}\right)}^{-1.17}, \frac{{a}_{3}}{{a}_{1}}={\left(\frac{{R}_{3}}{{R}_{1}}\right)}^{-1.17}, \frac{{a}_{3}}{{a}_{2}}={\left(\frac{{R}_{3}}{{R}_{2}}\right)}^{-1.17}$$

(18)

$${a}_{2}={f}_{12}{a}_{1}, {a}_{3}={f}_{13}{a}_{1}, {a}_{3}={f}_{23}{a}_{2}$$

where

$${f}_{12}={\left(\frac{{R}_{2}}{{R}_{1}}\right)}^{-1.17}{f}_{13}={\left(\frac{{R}_{3}}{{R}_{1}}\right)}^{-1.17}{f}_{23}={\left(\frac{{R}_{3}}{{R}_{2}}\right)}^{-1.17}$$

$${f}_{12}={\left(\frac{{{R}_{2}}^{2}}{{{R}_{1}}^{2}}\right)}^{-0.585}={\left(\frac{{{R}_{1}}^{2}+{{d}_{1}}^{2}}{{{R}_{1}}^{2}}\right)}^{-0.585}$$

$${f}_{13}={\left(\frac{{{R}_{3}}^{2}}{{{R}_{1}}^{2}}\right)}^{-0.585}={\left(\frac{{{R}_{1}}^{2}+{\left({d}_{1}+{d}_{2}\right)}^{2}}{{{R}_{1}}^{2}}\right)}^{-0.585}$$

$${f}_{23}={\left(\frac{{{R}_{3}}^{2}}{{{R}_{2}}^{2}}\right)}^{-0.585}={\left(\frac{{{R}_{1}}^{2}+{\left({d}_{1}+{d}_{2}\right)}^{2}}{{{R}_{1}}^{2}+{{d}_{1}}^{2}}\right)}^{-0.585}$$

f₁₂, f₁₃, f₂₃ are the PGA reduction factors between unit 1&2, 1&3 and 2&3 respectively. These factors can be related with common cause failure factors between various units with respect to input ground motion. Table 4 shows the various factors generated for various distances between the plants for a given R₁ value (in the present study it is considered as 10 km).

Table 4 Inter unit seismic common cause factors for various distances

The factors derived in the Table 4 shows not much deviation from one unit to another unit when there is not much distance between the two units. As the distance increases between 2nd and 3rd unit one can observe the decrease in the factors. It is true in the case of twin unit concept where the distance between two units will be minimal and hence, both the units can be considered as fully correlated. However, in the case of reactor park where apart from twin unit concept other reactors can exist but with a considerable distance separation factor. In the present study only two reactors (twin unit concept) have been considered and hence, both the reactors can be considered as fully correlated. However, for checking the bounds both uncorrelated and fully correlated cases have been considered. The procedure presented above is a novel approach to represent the inter unit seismic CCFs as a function of distance between the various plants in the site, however there is possibility of improving this technique.

Case Study

Consider the minimal cut set (MCS) of dominant accident sequences that were obtained for single unit core damage and two unit core damage as shown in Table 5. In the case of single unit, the first event is seismic initiator followed by grid failure, component A failure in PPIS, component B failure in SDS1 and component C failure in SDS2. In the present case when the seismic event occur the grid failure probability is considered as 1. Hence, to evaluate the accident sequence frequency it is required to evaluate fragilities of the component A, B and C.

Table 5 Dominating accident sequences

Single Unit

In the present study, component fragilities have been obtained based on the traditional scale factor approach as explained in “Scale Factor Based Approach” and the data for the same is shown in Table 6. As SSMRP procedure depends on joint probability distributions of response of the components  which is based on the time history analysis, due to unavailability of the data in the present study Mankamo model, Beta factor model and Alpha factor models have been utilised to obtain fragility curves of the minimal cut sets.

Table 6 Fragility parameters of various components

In PPIS system there are 2 components which are similar to R1-PPIS-A and are located in same elevation and hence the fragility of R1-PPIS-A gets modified based on the relation provided in Eq. 10 of Mankamo model. The original and modified fragility curves of the component R1-PPIS-A is shown in Fig. 5. At the system level all the components are considered independent to each other and the modified fragility curves have been utilised for obtaining the system level fragility curves which are shown in Fig. 6. Now consider the case of Beta Factor model, the fragility of R1-PPIS-A gets modified based on the relation provided in Eq. 11 and in the present case beta factor is considered as 0.1. Later these modified curves have been utilised for obtaining the system level fragility curves which are shown in Fig. 6. In the case of Alpha Factor model, individual component fragility curves get modified based on the number of similar components in that group based on the relation provided in Eq. 14. In the present study for the case of two component system, alpha factors are considered as α₁ = 0.95, α₂ = 0.05. The system level fragility curves so obtained are shown in Fig. 6.

Fig. 5

Fragility curves for PPIS components using Mankamo Method

Fig. 6

System fragility curve for Sequence 1 using Various Methods

Two Unit Case

In the two unit case, for the accident sequence to occur (or for the system failure) six components should be failed simultaneously. However some of the components are similar but existing in two different units as shown in Table 8.

Table 8 Component and Location data

As there is an ambiguity in application of Mankamo and Beta factor model to multi unit case, in the present study only Alpha factor model has been applied and the results are shown in Fig. 7.For the case of single unit following Alpha factors have been applied (for two component, α₁ = 0.95, α₂ = 0.05 and for four component α₁ = 0.95, α₂ = 0.0213, α₃ = 0.0101, α₄ = 0.0186). These factors are assumed from the internal events CCF analysis, however, these factors can be obtained based on the MVN integration method. Apart from this two cases one considering fully correlated and other one considering uncorrelated between two units also carried out to find the bounds on the calculations. In the case of fully correlated the results are same as single unit CDF.

Fig. 7

Fragility curves for Single unit and Two unit case using Alpha Factor Model

Results and Discussion

As described in “PSA for Multi Unit Site” in the present MUPSA study Site Core Damage Frequency (SCDF) has been considered as site risk metrics. The risk metrics has been evaluated based on the dominating accident sequences that arise from various initiating events. Following are the input required for the analysis:

• a. Frequency of occurrence of an earthquake of a particular PGA level which can be obtained from the seismic hazard curves.

• b. Conditional probability of occurrence of seismically induced structural failure as well as internal initiating event for a particular PGA level that can be obtained from the corresponding system fragility curves.

• c. Conditional failure probability of safety system for a particular PGA level, which can also be obtained from the corresponding system fragility curves.

The results obtained for the above mentioned risk metrics are discussed in detail in the following sub sections.

Results for Site CDF

In estimating the site core damage frequency (site CDF), initially single reactor CDF values have been estimated from the initiating events that are specific to the single reactor. Later, the Site CDF values have been estimated by considering the initiating events as outlined in “PSA for Multi Unit Site” from multi-unit perspective. In the present study, the consequence CD1, CD2 and CD12 have been considered as Site CDF. The results of single reactor as well as multi reactor CDF values are provided in Table 9.From this analysis the single unit CDF has been estimated as 4.324E− 07/yr, twin unit CDF has been estimated as 8.642E− 08/yr and Site CDF for Advanced Reactor due to seismic event has been estimated as 9.512E− 7/yr.

Table 9 Results for site CDF

Discussion on Site CDF

Based on the analysis the following observations have been made:

• 1. 99.4% of contribution towards Site CDF is coming from earthquake PGA level more than 0.5 g (as shown in the Fig. 8). This is due to the fact that at higher PGA levels the failure probability of most of the SSC are very high (nearly reaching 1) that means SSCs cannot withstand these levels of PGA and they are highly likely to fail.

• 2. The remaining 0.6% of contribution towards Site CDF is coming from earthquake PGA levels less than 0.5 g. It does not mean that SSCs would not fail at lower PGA levels, but the chance of failure is reduced. This is due to the fact that even though the SSCs are designed for SSE level (0.2 g in the present case) they can withstand higher levels of PGA due to the usage of higher factor of safety in the design.

• 3. The main contribution towards Site CDF is due to seismically induced failure of Class IV power supply. In this one, Grid failure is assumed during the seismic event that is failure probability is considered as 1 and Simultaneous failures of SDS 1, SDS 2 and PPIS.

Fig. 8

Contribution of various PGA bins towards Site CDF

Conclusion

In this study, treatment of dependency and correlations in the context of seismic PSA of multi units has been discussed. Several dependency models proposed in the literature have been studied and depending on the applicability of the models they have been utilised in the analysis. An approach based on Alpha factor model, which is being used in internal event PSA CCF analysis, has been proposed in this study along with a novel methodology to estimate the inter unit seismic CCF factors using distance separation factor among various units in the site.Unlike Beta factor model, this model has the capability of modelling simultaneous failure of two or more components. A case study on advanced reactor has been carried out to demonstrate the methodology. Seismically induced internal initiating events have been identified and seismic event trees have been developed for various initiating events. In finding out the system failure probabilities, seismic fragilities at component level and system level have been developed based on the corresponding seismic fault trees. Seismic CDF has been estimated from the dominating accident sequences. The Site CDF for the site (including simultaneous occurrence of core damage from Reactor 1 and Reactor 2) has been estimated as 9.512 × 10^–7/yr. This study has highlighted the importance of incorporating dependency modelling from inter-unit perspective in estimating risk from multi units in a reactor site.