1 Introduction

Liquid-fueled molten salt reactors (MSRs), first designed, constructed, and operated by the Oak Ridge National Laboratory (ORNL) in the United States during the 1940s, were selected by the Generation IV Nuclear Energy Systems International Forum as one of six Generation IV reactor systems [1]. Unlike traditional solid fuel nuclear reactors, liquid-fueled MSRs use high-temperature molten salt as the fuel and coolant. High-temperature fuel salt circulates in the primary loop, and a part of the delayed neutron precursors (DNPs) decays in the primary loop outside the core, which can cause delayed neutron loss. Therefore, the neutronics behavior of the liquid-fueled MSR is tightly coupled with the thermo-hydraulics of the system because the reactivity contribution of the DNP is strongly influenced by the fluid flow conditions. As the delayed neutron fraction (DNF) can significantly affect the dynamic characteristics of nuclear reactors, DNP effects are very important in reactor transient and safety analyses. Considering the unique flow characteristics of liquid fuel salt in liquid-fueled MSRs, the DNP flow effects have become a focus in contemporary liquid-fueled MSR research and development.

Owing to the introduction of liquid fuel, the delayed neutron precursors circulate in the primary loop with the carrier molten salt. The motion of the DNPs is one of the main challenges. Meanwhile, the fission heat directly released in the liquid fuel. Therefore, the thermal fluid with internal heat source is another key challenge. As a result, the physical model and corresponding codes for traditional solid-fueled nuclear reactors are not suitable for liquid-fueled MSRs, and it is necessary to re-derive the mathematical model and develop a new dynamic code for liquid-fueled MSRs. Currently, many researchers have developed new models and codes for liquid-fueled MSR and conducted flow effect analyses of the DNP.

Lapenta et al. [2] deduced a new point kinetics equation for liquid-fueled MSRs by considering a 1D imposed velocity field without temperature feedback. Shi and Li et al. [3, 4] successively extended the RELAP5/MOD4.0 code, added 0D and 1D DNP models with the primary loop, validated with the Molten Salt Reactor Experiment (MSRE) benchmarks, and simulated the different transient scenarios of the Molten Salt Breeder Reactor (MSBR) including the load demand change, primary flow, secondary flow, and reactivity transients. Diniz et al. [5] derived analytical solutions and a numerical method to analyze the influence of recirculation time through the external loop on the effective DNFs. Zhu et al. [6] added the DNP flow model to the Monte Carlo N-Particle Transport (MCNP) code and calculated the DNF of a small molten salt reactor under different steady-state flow conditions. Furthermore, Aufiero et al. [7] extended the SERPENT-2 Monte Carlo code to analyze the effective DNF at steady-state of the Molten Salt Fast Reactor (MSFR). Krepel et al. [8] developed a core dynamics code, DYN3D-MSR, based on the Forschungszentrum Rossendorf (FZR) in-house light water reactor code, DYN3D, which allows transient simulation by 3D neutronics and parallel channel thermal-hydraulics, and simulated the steady-state DNF loss and several transient scenarios of MSRE and MSBR. Zhuang et al. [9] developed a nodal expansion method (NEM) code, MOREL, and performed dynamic analyses on MSRE and the Thorium Molten Salt Reactor (TMSR) under perturbations of fuel pump start-up and coast-down, and by overheating and overcooling the inlet fuel temperature [10]. Zhang et al. [11] developed a coupled code, COUPLE, by solving the multi-group neutron diffusion equations and the incompressible Navier–Stokes equations with the standard k-\(\varepsilon\) model under 2D cylindrical geometry. This code was applied to the conceptual analysis of MSFR and the Molten Salt Actinide Recycler & Transmuter (MOSART) [12, 13]. Cammi et al. [14,15,16] developed a multi-physics simulation code based on the commercial software COMSOL Multiphysics, which was used to model and analyze the steady-state and transient characteristics of MSBR, MSRE, and MSFR. Cervi et al. [17] implemented an SP3 neutron transport solver and a neutron diffusion solver in OpenFOAM to analyze MSFR. A framework, named GeN-ROM [18], was developed using OpenFOAM and employs a proper orthogonal decomposition-aided reduced-basis technique (POD-RB). This framework was tested using a 2D multi-physics MSFR model with steady-state and transient scenarios. Tiberga et al. [19] from the Delft University of Technology developed a code coupling an incompressible Reynolds-averaged Navier–Stokes (RANS) model and an SN neutron transport solver and performed preliminary steady-state and transient simulations of MSFR. An open-source MSR simulation code, Moltres, was developed based on the Multi-physics Object-Oriented Simulation Environment (MOOSE) framework. In Moltres, the neutron diffusion, temperature, and precursor equations are fully coupled and solved with implicit time stepping. Moltres was utilized to study the steady-state and transient behavior of MSFR [20]. The PROTEUS-NODAL code was modified for MSR and coupled with the SAM system code under the MOOSE framework [21]. This coupled code system was verified and validated using the MSFR benchmark problem and MSRE experimental data.

With these developed codes, the unique phenomena of fuel flow in liquid-fueled MSRs have been well studied, especially in no-moderator fast-spectrum MSR concepts, such as MSFR [7, 12, 16, 17]. However, on the basis of the models and findings of the researchers mentioned above, the entire primary and secondary loop models need to be further considered and extended in channel-type liquid-fueled MSRs.

To more systematically analyze the flow field effect of the DNP in channel-type liquid-fueled MSRs, in this study, the ThorCORE3D code with coupled 3D core dynamics and 1D loop dynamics models of channel-type liquid-fueled MSRs was developed and validated with MSRE benchmarks. The DNF of MSRE under different flow conditions, including external loop recirculation time, fuel salt flow rate, and core flow field distribution, were modeled and simulated using the ThorCORE3D code. Subsequently, the flow field effects of DNPs in the reactivity insertion transient of MSRE under different flow field conditions were modeled and analyzed in detail.

2 Theory and method

2.1 Neutronics model

In liquid-fueled MSRs, liquid fuel salt circulates through the primary loop. The flow of the fuel salt has little effect on the neutron flux because the velocity is much lower than the neutron velocity [22]; however, the DNPs circulate with the liquid fuel salt and partially decay in the primary loop outside the reactor, which results in a reduction in the effective DNF and loss of reactivity. The multi-group diffusion theory is used to deduce the neutronics model of the liquid-fueled MSRs, which consists of 3D space-time multi-group neutron diffusion equations and DNP balance equations [23], given in Eqs. (1) and (2), for node n.

$$\begin{aligned}&\frac{\partial \Phi _{g}^{n}(r, t)}{v_{g}^{n} \partial t}-\nabla \cdot D_{g}^{n}(t) \nabla \Phi _{g}^{n}(r, t)+\Sigma _{\text {t}, g}^{n}(t) \Phi _{g}^{n}(r, t) \nonumber \\&\quad = \frac{\chi _{\text{p}, g}}{k_{\mathrm {eff}}} \sum _{g^{\prime }=1}^{G}\left( 1-\beta ^{n}\right) \left( \nu \Sigma _\text {f}\right) _{g^{\prime }}^{n}(t) \Phi _{g^{\prime }}^{n}(r,t)\nonumber \\&\quad + \sum _{g^{\prime }=1}^{G}\Sigma _{g^{\prime } \rightarrow g}^{n}(t) \Phi _{g^{\prime }}^{n}(r, t)+\sum _{j=1}^{M} \chi _{\text{d},j,g} \lambda _{j}^{n} C_{j}^{n}(r, t)\nonumber \\&\quad g=1,2,...,G \end{aligned}$$
(1)
$$\begin{aligned}&\frac{\partial C_{j}^{n}(r, t)}{\partial t}+\nabla \cdot \left( u^{n} C_{j}^{n}(r, t)\right) =-\lambda _{j}^{n} C_{j}^{n}(r, t)\nonumber \\&\quad +\nabla \cdot \left( \left( {{D_{\text {c},i}} + {D_\text {t}}} \right) \nabla C_{j}^{n}(r, t)\right) \nonumber \\&\quad +\frac{1}{k_\text {eff}} \sum _{g=1}^{G} \beta _{j}^{n}\left( \nu \Sigma _\text {f}\right) _{g^{\prime }}^{n}(t) \Phi _{g}^{n}(r, t), j=1,2,...,M \end{aligned}$$
(2)

where \(\Phi\) is the scalar flux; v is the neutron velocity; \(D_{g}\) is the neutron diffusion coefficient; \(\Sigma _\text {t}\), \(\Sigma _\text {f}\), and \(\Sigma _{g^{\prime } \rightarrow g}\) represent the macroscopic total, macroscopic fission, and macroscopic scattering cross-sections, respectively; \(k_{\mathrm {eff}}\) is the effective multiplication factor; C is the DNP concentration; \(\lambda\) is the DNP decay constant; \(\beta\) is the total fraction of delayed neutrons; \(\beta _{j}\) is the fraction of delayed neutrons in each group; \(\chi _\text {p}\) and \(\chi _{\text {d},j}\) represent the energy spectrum of prompt and delayed neutrons, respectively; u is the fuel salt velocity; \(D_{\text {c},i}\) and \(D_\text {t}\) are the DNP molecular and turbulent diffusion coefficients.

The time-dependent terms of the neutron multi-group diffusion equations are discretized using the backward Euler method together with an exponential transformation technique. These equations are then solved using NEM [24].

As the fuel flows through different separated channels in the core, the 3D DNP balance equations are simplified to a 1D form. Additionally, as molecular and turbulent diffusion are much smaller than convection transport in channel-type liquid-fueled MSRs, they can be neglected. These simplified 1D DNP balance equations are as follows:

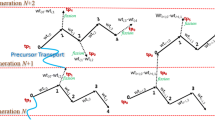
$$\begin{aligned}&\frac{\partial C_{j}^{n}(r, t)}{\partial t}+\frac{\partial \left( u^{n} C_{j}^{n}(r, t)\right) }{\partial z}=-\lambda _{j}^{n} C_{j}^{n}(r, t)\nonumber \\&\quad +\frac{1}{k_\text {eff}} \sum _{g=1}^{G} \beta _\text {j}^{n}\left( \nu \Sigma _\text {f}\right) _{g^{\prime }}^{n}(t) \Phi _{g}^{n}(r, t), j=1,2,...,M \end{aligned}$$
(3)

Applying the backward Euler method for temporal discretization and first-order upwind scheme for spatial discretization [25]:

$$\begin{aligned}&\frac{\partial C^n}{\partial t}\approx \frac{C^n_t-C^n_{t-\Delta t}}{\Delta t} \end{aligned}$$
(4)
$$\begin{aligned}&\frac{\partial }{\partial z}(u^nC^n)\approx \frac{u^nC^n-u^{n-1}C^{n-1}}{\Delta z} \end{aligned}$$
(5)

Then, Eq. (3) can be written as follows:

$$\begin{aligned}&\left( \frac{1}{\Delta t}+\frac{u^n}{\Delta z}+\lambda \right) C^n-\frac{u^{n-1}}{\Delta z}C^{n-1}=Q^n+\frac{1}{\Delta t}C^n_{t-\Delta t} \end{aligned}$$
(6)
$$\begin{aligned}&\quad Q^n={\left\{ \begin{array}{ll}\frac{1}{k_{\mathrm {eff}}}\sum ^G_{g =1}\beta ^n_{g}\nu \Sigma ^n_{\text {f},g}(t)\Phi ^n_g,\mathrm{core}\\ 0,\mathrm{external\quad loop} \end{array}\right. } \end{aligned}$$
(7)

The DNP of the different channels is homogenously mixed at the core outlet. At each time step, Eq. (6) is solved for each channel in the core and external loop using the Gauss–Seidel iteration method. The same space discretization mesh is adopted by the 3D neutron diffusion equations and 1D DNP balance equations, and the node average DNP concentration is transferred to the 3D neutron diffusion equations in the same node.

To calculate the reactor kinetics parameters and DNF loss, adjoint equations including adjoint DNP balance equations are proposed for liquid-fueled MSRs, as follows:

$$\begin{aligned}&-\nabla \cdot D_{g}^{n} \nabla \Phi _{g}^{\dagger n}(r)+\Sigma _{\text {t}, g}^{n} \Phi _{g}^{\dagger n}(r)\nonumber \\&\quad =\frac{\left( 1-\beta ^{n}\right) \left( \nu \Sigma _\text {f}\right) _{g}^{n}}{k_\text {eff}} \sum _{g^{\prime }=1}^{G} \chi _{\text{p}, g^{\prime }} \Phi _{g^{\prime }}^{\dagger n}(r)\nonumber \\&\quad +\sum _{g^{\prime }=1}^{G} \Sigma _{g \rightarrow g^{\prime }}^{n} \Phi _{g^{\prime }}^{\dagger n}(r)+\left( \nu \Sigma _\text {f}\right) _{g}^{n} \sum _{j=1}^{M} \beta _{j}^{n} C_{j}^{\dagger n}(r)\nonumber \\&\quad g=1,2,...,G \end{aligned}$$
(8)
$$\begin{aligned}&-\frac{\mathrm {d}\left( u^{n} C_{j}^{\dagger n}(r)\right) }{\mathrm {d}z}=\lambda _{j}^{n} \sum _{g=1}^{G} \chi _{\text{d}, j} \Phi _{g}^{\dagger n}(r)-\lambda _{j}^{n} C_{j}^{\dagger n}(r)\nonumber \\&\quad j=1,2,...,M \end{aligned}$$
(9)

where \(\Phi _{g}^{\dagger n}(r)\) and \(C_{j}^{\dagger n}(r)\) are the adjoint flux and adjoint DNP concentration, respectively. The adjoint equations are in the same form as the forward equations, and the same solver can be used to solve these equations, with several coefficients replaced. Then, the effective delayed neutron fractions \(\beta _{\mathrm {eff}}\) and effective DNP decay constants \(\lambda _{\mathrm {eff}}\) can be calculated as follows:

$$\begin{aligned}&\beta _{\mathrm {eff}, j}=\frac{\sum _{g=1}^{G} \langle \Phi _{g}^{\dagger n} \mid \chi _{\text{d}, j} \lambda _{j}^{n} C_{j}^{n}\rangle }{F} \end{aligned}$$
(10)
$$\begin{aligned}&\lambda _{\mathrm {eff}, j}=\frac{\sum _{g=1}^{G} \langle \Phi _{g}^{\dagger n} \mid \chi _{\text{d}, j} \lambda _{j}^{n} C_{j}^{n}\rangle }{\sum _{g=1}^{G} \langle \Phi _{g}^{\dagger n} \mid \chi _{\text{d}, j} C_{j}^{n}\rangle } \end{aligned}$$
(11)
$$\begin{aligned}F& = \sum \limits _{j = 1}^M \sum \limits _{g = 1}^G \left\langle {{\Phi }^{\dagger n}_g{|}{\chi _{\text{d},j}}\lambda _j^nC_j^n} \right\rangle \nonumber \\&\quad + {\left( {1 - \beta } \right) \sum \limits _{g = 1}^G \mathop \sum \limits _{g' = 1}^G \left\langle {{\Phi ^{\dagger n}_{g'}}|{\chi _{\text{p},g}}\left( {\nu {\Sigma _\text {f}}} \right) _{g'}^n\Phi _{g'}^n} \right\rangle } \end{aligned}$$
(12)

2.2 Homogenized few-group parameters

The homogenized few-group parameters required for neutronics calculation include few-group macroscopic cross-sections, neutron energy spectrum, delayed neutron parameters, etc. Considering the thermal feedback effect, the lattice code DRAGON [26] is used to generate few-group parameters at different fuel and graphite temperatures. During calculation, temperature-dependent few-group parameters are obtained using the bilinear interpolation method [27].

Fig. 1
figure 1

Channel geometry approximation in TH calculation

Full size image

2.3 Core thermal-hydraulics model

A parallel multi-channel core thermal-hydraulic model is implemented in the ThorCORE3D code to account for thermal feedback and fuel flow effects. In this model, the fuel channel and surrounding graphite components are approximated as cylindrical tubes, as shown in Fig. 1. Owing to the very high boiling point of molten salt, a single-phase flow model is adopted in the core thermal-hydraulics model. The 1D fluid momentum, energy, and mass balance equations can be written as follows:

$$\begin{aligned}&\frac{\partial (\rho u)}{\partial t}+\frac{\partial (\rho u^2)}{\partial z}+\frac{\partial p_\text {fric}}{\partial z}+g\rho +\frac{\partial p}{\partial z}=0 \end{aligned}$$
(13)
$$\begin{aligned}&\frac{\partial (\rho H)}{\partial t}+\frac{\partial (\rho uH)}{\partial z}=Q_\text {f}+Q_\text {w} \end{aligned}$$
(14)
$$\begin{aligned}&\frac{\partial \rho }{\partial t}+\frac{\partial (\rho u)}{\partial z}=0 \end{aligned}$$
(15)

where \(\rho\) is the density of the fuel salt; u is the fuel salt velocity; p is the pressure; H is the specific enthalpy of the fuel salt; g is the acceleration of gravity; \(p_\text {fric}\) is the frictional pressure drop; \(Q_\text {w}\) is the heat transfer between the fluid and graphite components; \(Q_\text {f}\) is the volumetric heat source in the fuel salt, which can be calculated as follows:

$$\begin{aligned} Q_\text {f}=\alpha _\text {f}\cdot \sum _{g=1}^G{\Sigma _{\text {kf},g} \Phi _g } \end{aligned}$$
(16)

where \(\Sigma _{\text {kf},g}\) is the macroscopic kappa-fission cross-section of group g, and \(\alpha _\text {f}\) is the proportion of fission energy released in the fuel salt.

The graphite components are approximated as hollow circular tubes with an inner radius of \(r_0\) and an outer radius of R. Similar to the heat transfer model of fuel rods in solid fuel nuclear reactors, the heat conduction equation of the graphite components in cylindrical geometry is defined as follows:

$$\begin{aligned} \rho_{\text{g}} c_{\text{p},\text{g}} \frac{\partial {T_{\text{g}}}}{\partial t}-\frac{\lambda _{\text{g}}}{r}\frac{\partial }{\partial r}\left( r\frac{\partial T_{\text{g}}}{\partial r}\right) ={Q}_{\text{g}}\end{aligned}$$
(17)

with the following boundary conditions:

$$\begin{aligned}&\left. \lambda _{\text{g}}\frac{\mathrm {d}T_{\text{g}}(r)}{\mathrm {d}r}\right| _{r=r_0} =h\left(T_{\text{g}}(r_0)-T_{\text {f}}\right) \end{aligned}$$
(18)
$$\begin{aligned}&\left. \lambda _{\text{g}}\frac{\mathrm {d}T_{\text{g}}(r)}{\mathrm {d}r}\right| _{r=R}=0 \end{aligned}$$
(19)

where \(T_{\text{g}}\) denotes the graphite temperature, \(\rho _{\text{g}}\) denotes the graphite density, \(c_{\text{p},{\text{g}}}\) denotes the graphite specific heat capacity, \(\lambda _{\text{g}}\) denotes the graphite thermal conductivity, r denotes the distance from the central line, h denotes the convective heat transfer coefficient, and \(Q_{\text{g}}\) denotes the volumetric heat source in the graphite.

The momentum and mass balance equations are solved using the backward Euler and finite difference methods. The energy balance equation is solved using the method of characteristics (MOC) [28], and the fuel temperature is used as the boundary condition for graphite heat conduction. It is assumed that the fuel salt flows separately in the lower and upper plenums, meaning that the fuel salt is distributed to each channel at the core inlet and mixed at the core outlet. The numerical models in the lower and upper plenums are the same as those in the channels.

For the heat conduction equation, the circular graphite component is divided into a series of concentric circular tubes of equal areas. The relationship between the average temperatures of neighboring tubes can be obtained analytically. Steady-state and transient equations can be transformed into the same form, which can then be solved using the tridiagonal matrix algorithm (TDMA).

Fig. 2
figure 2

Scheme of control volumes of the primary heat exchanger

Full size image

2.4 Molten salt loop model

Generally, liquid-fueled MSRs consist of two molten salt loops, that is, the fuel salt (primary) loop and the secondary coolant salt loop. Therefore, it is important to consider the molten salt loop model in the reactor system response. With the fuel salt in the liquid-fueled MSRs circulating in the primary loop, the DNP balance equations and the corresponding numerical methods in the primary loop are described in Sect. 2.1. In the loop model, the pipes and heat exchangers are approximately 1D and the heat loss in the pipes is ignored. As shown in Fig. 2, the fuel salt flows in the direction opposite to that of the cooling salt in the heat exchanger.

The energy balance equation in the fuel and coolant salts is defined as follows:

$$\begin{aligned} \rho {c_{\text {p},\text {f}}}\frac{{\partial T_\text {f}}}{{\partial t}} + \rho u{c_{\text {p},\text {f}}}\frac{{\partial T_\text {f}}}{{\partial z}} = {Q_\text {f}} + {Q_\text {w}} \end{aligned}$$
(20)

where \(c_{\text {p},\text {f}}\) denotes the fluid specific heat capacity. \(Q_\text {f}=0\) is always satisfied because the decay heat is ignored. \(Q_\text {w}\) is the heat transfer between the fluid and steel wall; in the pipes, \(Q_\text {w}=0\), while in the heat exchanger, \(Q_\text {w}\) was calculated as follows:

$$\begin{aligned} T_\text {f}(z)-T_\text {w}(z)=\frac{\varphi (z)}{h}=-\frac{Q_\text {w}(z)A}{\pi Dh} \end{aligned}$$
(21)

where \(\varphi (z)\) denotes the heat flux through the wall, A denotes the flow area, and D is the hydraulic diameter.

Using the fuel salt temperature and velocity from the core outlet as the inlet boundary conditions, the finite difference method is used to solve Eqs. (20) and (21) at steady-state, and the MOC method is used to solve the equations in the transient state. Next, the fuel salt temperature in the loop outlet is transferred as the inlet boundary condition of the core thermal-hydraulics model.

2.5 Coupling scheme

The calculation flow scheme of ThorCORE3D is shown in Fig. 3. Before steady-state or transient calculations, the few-group parameters must be generated at different operating temperatures. At the beginning of the calculation, a uniform power distribution is assumed, and the first thermal-hydraulic calculation of the entire system is performed. Subsequently, the few-group parameters are interpolated and updated according to the calculated thermal fluid parameters. The neutronics calculations, including the DNP balance equations, are conducted using the updated parameters, including cross-sections and flow velocity, and a new power distribution is obtained. The iteration is carried out until the parameters (e.g., \(k_\mathrm {eff}\) and temperatures) converge. The adjoint calculation is performed after the above iteration. The transient calculation can begin after a steady-state calculation. As in the steady-state calculation, the neutronics module and thermal-hydraulics module are also calculated iteratively until convergence, and then advanced to the next time step until the given time is reached.

Fig. 3
figure 3

Calculation flow scheme of the ThorCORE3D code

Full size image

2.6 Code validation

This section describes a preliminary validation of the ThorCORE3D code that was conducted based on MSRE benchmarks.

Fig. 4
figure 4

ThorCORE3D nodalization of the MSRE system

Full size image
Fig. 5
figure 5

MSRE axial nodalization

Full size image
Fig. 6
figure 6

MSRE radial nodalization

Full size image

2.6.1 Description and modeling of the MSRE

The MSRE is a molten salt experimental reactor designed, built, and operated by ORNL in the 1960s and is currently the only available source of experimental data for molten salt reactors with liquid fuel. The design power of the MSRE was 10 MWth, and the actual operating power was 8MWth. The U-235 and U-233 fuels were used in the early and later stages, respectively. The main design parameters and material properties are shown in Table 1.

A ThorCORE3D model of the MSRE system is shown in Fig. 4, and the two loops of the MSRE were modeled. The MSRE core model is shown in Figs. 5 and 6. The upper and lower plenums were equivalent to a cylinder with a height of 17.15 cm, and the height of the active core was 166.37 cm. The reactor was divided into 20 nodes along the axial direction, as shown in Fig. 5. Each fuel channel and the surrounding graphite were radially divided into a square segment, and each control rod channel and sample channel were equivalent to four channels, with a total of 1372 channels in the radial direction, as shown in Fig. 6. The lattice code DRAGON with the ENDF/B-VII.0 data library was used to generate the two-group parameters required by the ThorCORE3D code. Two-group parameters were generated at different fuel and graphite temperatures, and the expansion effects were also considered. The DNP parameters were obtained from the ORNL report, as listed in Table 2.

Table 1 Key parameters of MSRE [29,30,31]
Full size table
Table 2 Parameters of DNP
Full size table

2.6.2 Loss of DNF at steady-state operation

The effective DNF under the flow and static conditions of the fuel salt were calculated using Eq. (10), and the difference between the two states corresponds to the DNF loss caused by the molten fuel salt flow effect. As shown in Tables 3 and 4, a comparison of the ThorCORE3D numerical results, MSRE experimental values, ORNL numerical results, and other code numerical results with the loads of U-235 fuel and U-233 fuel are listed. The DNF losses calculated by the ThorCORE3D code agree well with the MSRE experimental values and are within the range of the values calculated by the other codes. The numerical results of the ThorCORE3D code using the DNP parameters from the ENDF/B-VII.0 library are close to the results obtained using parameters from the ORNL report. Hence, the DNP parameters from the ORNL report were directly applied in subsequent simulations.

Table 3 Loss in the delayed neutron fractions (\(10^{-5}\)) due to the fuel circulation for U-235 fuel [9, 33]
Full size table
Table 4 Loss in the delayed neutron fractions (\(10^{-5}\)) due to the fuel circulation for U-233 fuel [9, 33]
Full size table

2.6.3 Protected pump start-up and coast-down experiments

The protected pump start-up and coast-down experiments were part of the MSRE zero-power experiments in ORNL, and U-235 fuel was used during the experiment. During the pump start-up transient, the fuel pump of the primary loop was started at time zero, and the inlet flow rate started to change at 2 s and increased to the nominal value within 8 s. During the pump coast-down transient, the fuel flow rate decreased from the nominal values to zero in 20 s, as shown in Fig. 7. As the molten-fuel salt flowed out of the core, the distribution of DNP concentration changed, causing a loss of reactivity. A power of 1 kWth was maintained in the protected pump start-up and coast-down experiments using a control rod, and the change in the position of the control rod with time was recorded.

With the core power low and basically constant, the temperature feedback was ignored when the protected transients were simulated using the ThorCORE3D code. By searching for the position of the control rod to maintain the core power, the change in the control rod position was directly calculated, as shown in Fig. 8. Then, the rod position was converted into reactivity using the control rod value and compared with the experimental values and calculated values of other codes [8, 9], as shown in Figs. 9 and 10. As these figures show, the numerical results of the ThorCORE3D code are in good agreement with the experimental values.

Fig. 7
figure 7

Fuel flow curve during transient of protected fuel pump start up and coast down

Full size image
Fig. 8
figure 8

Change in control rod position during protected pump start-up and coast-down transients

Full size image
Fig. 9
figure 9

Compensated reactivity during protected pump start-up transient

Full size image
Fig. 10
figure 10

Compensated reactivity during protected pump coast-down transient

Full size image

2.6.4 Natural circulation experiment

During the natural circulation experiment, MSRE was operated using the U-233 fuel. The primary molten salt pump was kept closed and no control rod movement was considered. The fuel molten salt flow was driven only by natural circulation. At the beginning of the natural circulation transient, the reactor power was maintained at 4.1 kWth with a limited fuel mass flow rate. Subsequently, the cooling capacity of the secondary loop increased gradually; thus, the core inlet temperature decreased, and the core power increased owing to the reactivity negative feedback effect of temperature [30].

During the simulation, changes in the inlet temperature and fuel salt mass flow rate were used as inputs, as shown in Fig. 11. The variation in the core power was calculated and is shown in Fig. 12. There are a few different behaviors in the first 2000 s. This is because the experiment did not start from a steady state [33], whereas the ThorCORE3D code did. However, the numerical results at other times are in good agreement with the experimental values.

Fig. 11
figure 11

Changes in fuel mass flow rate and fuel inlet temperature in the natural circulation experiment

Full size image
Fig. 12
figure 12

Power history of the natural circulation experiment

Full size image

2.6.5 Reactivity insertion experiment

At ORNL, a series of experiments on MSRE with the U-233 fuel were performed to test the power response to reactivity insertion. In the 8 MWth case, a reactivity of \(1.39\times 10^{-4}\) was inserted in 1 s and the reactor power increased rapidly. Subsequently, the core temperature increased and caused a reactivity negative feedback effect, resulting in a slower increase in power and finally dropping to the initial level [34].

To fully consider the variation in the core inlet temperature with time, the MSRE molten salt loops were modeled with the ThorCORE3D code, and the temperature fields of the primary and secondary loops were solved. The numerical results were compared with the experimental values of MSRE, as shown in Fig. 13. The calculated results are in good agreement with the experimental values.

Fig. 13
figure 13

Power change in response to a step change in reactivity of \(1.39\times 10^{-4}\) at 8 MW

Full size image

3 Results and discussion

Table 5 Loss of DNF under different recirculation times
Full size table

3.1 Flow field effect on DNP at steady-state

In liquid-fueled MSRs, DNPs circulate with the fuel salt and partially decay in the primary loop outside the core. The DNF loss is directly affected by the flow field. In this section, the DNF loss of the MSRE with U-235 fuel under different flow conditions, including the external loop recirculation time, fuel salt flow rate, and core flow field distribution, is modeled and simulated using the ThorCORE3D code.

3.1.1 Effect of the recirculation time

In this scenario, the fuel molten salt flow rate and flow field distribution remain unchanged, and the loss of DNF on recirculation time from 0 to 20 s was simulated. As shown in Fig. 14, the DNF loss of each DNP group increases with recirculation time and gradually reaches saturation. The numerical results for recirculation times of 0 s, 5 s, 10 s, and 20 s are listed in Table 5, and the total loss increases from 162.2 pcm at 0 s to 239.8 pcm at 20 s. To obtain the DNF loss ratio of each DNP group and evaluate the effect of recirculation time on different DNP groups, the DNF loss value was normalized using the corresponding effective DNF of the non-flowing state, and the result is shown in Fig. 15. The losses of each DNP group are affected by the recirculation time differently. The first DNP group has a higher loss percentage, whereas the sixth group reaches saturation faster, which is because the sixth DNP group has a higher decay constant, most of which decay directly in the core, and an increase in the outer loop length has little effect on it.

Fig. 14
figure 14

Loss of DNF under different recirculation times

Full size image
Fig. 15
figure 15

Loss of DNF / \(\beta _\text {eff}\) static under different recirculation times

Full size image

Notably, at the limit situation of zero recirculation time, there should be no DNPs decay outside the core, but the results show that the DNF loss is not zero. This is because the flow of molten salt leads to the homogenization of the DNP in the core. The density distributions of the six DNP groups with zero recirculation time and static fuel are presented in Figs. 16 and 17. More delayed neutrons are released at the core edge as the molten salt flowed, where the neutron importance is lower, leading to reactivity loss.

Fig. 16
figure 16

Density distribution of DNPs in the MSRE with zero recirculation time

Full size image
Fig. 17
figure 17

Density distribution of DNPs in the MSRE with static fuel

Full size image
Table 6 Loss of DNF under different mass flow rates
Full size table

3.1.2 Effect of fuel flow rate

The DNF loss on the fuel salt mass flow rate from zero to twice the nominal mass flow rate (187.5 kg/s) was simulated with a recirculation time of 10 s. As Fig. 18 shows, the DNF loss of each DNP group increases with the fuel flow rate and gradually reaches saturation. When the flow rate is zero, there is no DNF loss in any DNP group, as in solid-fuel nuclear reactors. The results for 50%, 100%, and 200% of the nominal flow rate are listed in Table 6. The total loss reaches 286.6 pcm in the 200 % mass flow state. Then, the DNF loss is normalized using the corresponding effective DNF of the non-flowing state. As Fig. 19 shows, the DNF loss of each DNP group is affected differently by the fuel salt flow. The first DNP group has a higher percentage loss and reached saturation faster, but the last three DNP groups still do not reach saturation in the 200 % mass flow state. This is because the decay constant of the first DNP group is small and the decay is slower. When the fuel salt flow increases, the effect of the DNP returning to the core in the first DNP group is clearer, reaching the saturation state faster.

Fig. 18
figure 18

Loss of DNF under different mass flow rates

Full size image
Fig. 19
figure 19

Loss of DNF / \(\beta _\text {eff}\) static under different mass flow rates

Full size image
Table 7 Loss of DNF under different flow distributions
Full size table

3.1.3 Effect of the core flow field distribution

The mass flow distribution of the fuel salt in the radial direction of the core was linearly fitted as follows:

$$\begin{aligned} G_\text {m}=kr_\text {c}+0.149 \end{aligned}$$
(22)

where \(G_\text {m}\)(kg/s) denotes the mass flow rate of a single channel, \(r_{\text {c}}\)(cm) denotes the distance from the channel to the core central line, and k(\({\text {kg}}/({\text {cm}}\cdot {\text {s}})\)) denotes the slope. As Fig. 20 shows, the upper limit of the absolute value of k is \(2.04\times 10^{-3}\) \({\text {kg}}/({\text {cm}}\cdot {\text {s}})\) because the flow rate is zero in the center or edge channel at this time. \(k<0\) indicates that the flow rate in the central area of the reactor is relatively large, and \(k=0\) indicates a uniform mass flow rate for each channel. DNF loss was calculated using the flow distribution represented by the shaded area in Fig. 20.

Fig. 20
figure 20

Mass flow distribution along radial direction

Full size image

As Fig. 21 shows, DNF loss decreases approximately linearly as k increases. Owing to the higher neutron flux density in the central core area, the DNP concentration is also higher than that at the edge. When k increases, the flow rate in the central area of the core decreases, causing a decrease in the amount of DNP flowing out of the core, thereby decreasing DNF loss. The results of the three special cases are listed in Table 7, and the DNF losses differ by at most 68.2 pcm under different flow field distributions.

To accurately determine the influence of the flow field distribution, the DNF loss was normalized using the DNF loss under uniform flow conditions. As Fig. 22 shows, the DNP loss of the first DNP group is approximately \(10\%\) affected by the flow field distribution, whereas it reaches \(60\%\) for the sixth DNP group. This is because when the fuel flow rate is near the nominal flow rate, the DNF loss of the first DNP group that changes with the flow rate is not obvious, while the DNF loss of the sixth DNP group continues to rise. The change in the flow field distribution is reflected in the change in the flow rate of each channel; therefore, the sixth DNP group is more significantly affected by the flow distribution.

Fig. 21
figure 21

Loss of DNF under different flow distributions

Full size image
Fig. 22
figure 22

Loss of DNF / DNF loss at uniform flow condition under different flow distributions

Full size image

3.2 Flow field effect in reactivity insertion transient

In this section, the MSRE system responses with U-235 fuel under different initial conditions are calculated for the reactivity insertion transient. The transient starts with a nominal power of 8 MWth, and the reactivity of 26 pcm is inserted in 1 s so that the reactor power increases rapidly; however, the power increase caused by the reactivity jump is slowed down by the reactivity negative feedback caused by the temperature increase.

Fig. 23
figure 23

Power response under different recirculation times

Full size image
Fig. 24
figure 24

Temperature response under different recirculation times

Full size image

First, the influence of different external loop recirculation times of the fuel salt on the system response in reactivity insertion transient was simulated and analyzed. Three cases with recirculation times of 5 s, 10 s, and 20 s were selected for this study, whereas the other parameters were the same. These power responses are shown in Fig. 23. The peak value of the power curve at the recirculation time of 20 s is approximately 20% higher than that of the normal case of 10 s, whereas the power of the 5 s case is lower because the DNPs decay in the external loop increase when the recirculation time increases, resulting in a lower effective delayed neutron fraction of the reactor core, as discussed in Sect. 3.1.2. DNF is an important parameter in reactor control. When introducing the same reactivity, the peak value in the process of the power response of the reactor with a lower effective delayed neutron fraction is higher. In Fig. 24, the responses of the average fuel salt and graphite temperatures are shown. At the beginning of the transient, the average fuel salt temperature increases owing to the increase in the power. When the hot molten salt flows through the external loop and re-enters the core, the average molten salt temperature further increases and reaches its highest value at approximately 40 s. In the 20 s recirculation time case, the initial temperature increases faster because of the faster power increase; however, owing to the longer external loop, the hot molten salt re-enters the core later, and the average molten salt temperature of the \(\text{20 s}\) recirculation time case is overtaken by the other two cases. The curve fluctuates slightly because of the inflow and outflow of molten salt in the primary circuit. Finally, the average molten salt temperature and graphite temperature of the three cases are stable at the same level.

Fig. 25
figure 25

Power response under different mass flow rates

Full size image
Fig. 26
figure 26

Temperature response under different mass flow rates

Full size image

Next, the influence of the fuel salt flow rate on the system response in the transient state was simulated and analyzed. Keeping the other parameters constant, three cases with mass flow rates of 93.75 kg/s, 187.5 kg/s, and 375 kg/s were selected. As shown in Fig. 25, the peak of the power curve is higher when the fuel salt flow is larger; this higher peak is caused by two factors. The first reason is that when the flow rate increases, the effective DNF decreases, and thus, the system response is more sensitive to the reactivity jump. Another reason is that, when the fuel flow rate is high, the fuel temperature increases slowly, as shown in Fig. 26; thus, the reactivity negative feedback introduced is smaller. When the fuel flow rate is low, the heat could not be removed quickly, and the temperature of the molten salt increases extremely rapidly, which results in a rapid decrease in the core power, as shown by the red line in Figs. 25 and 26.

Fig. 27
figure 27

Power response under different flow distributions

Full size image
Fig. 28
figure 28

Temperature response under different flow distributions

Full size image

Finally, the influence of the core fuel salt flow field distribution on the system response in reactivity insertion transient was calculated. Three fuel flow distribution cases, with a flow rate higher in the central area, a uniform flow rate in the whole core, and a flow rate higher in the peripheral area, were selected for analysis, corresponding to \(k=-2.04\), 0, \(2.04\times 10^{-3}\)  \({\text {kg}}/({\text{cm}}\cdot {\text{s}})\) in Sect. 3.1.3. As shown in Fig. 27, the power peaks occur at approximately 20 s in all cases, and the peak value decreases with an increase in k. This is because when k is smaller, the DNP loss is larger, and the effective DNF of the reactor is lower, which leads to a higher power response, and the peak value of the molten salt temperature is also higher, as shown in Fig. 28. Finally, the temperature and power of the three transient conditions became stable basically at the same level.

4 Conclusion

The effective DNF is an important parameter in the safety analysis of liquid-fueled MSRs, and the DNF loss is closely related to the state of the molten salt flow field in the reactor core and the external primary loop. In this study, to model and analyze the flow field effect of the delayed neutron precursor in channel-type liquid-fueled MSRs more systematically, a 3D dynamics code, ThorCORE3D, was developed and validated with MSRE benchmarks.

Subsequently, the effects of external loop recirculation time, fuel flow rate, and core flow field distribution on DNF loss under steady-state conditions were simulated using the ThorCORE3D code. The results show that the external loop recirculation time, fuel salt flow rate, and distribution of the fuel salt flow field significantly affect the steady-state effective DNF loss of the liquid-fueled MSRs, and the effect on DNF of different DNP groups differ. Both the DNP out-of-core decay and the change in DNP core distribution could cause a loss of DNF in the core.

Ultimately, the reactivity insertion transients of the MSRE under different external loop recirculation times, fuel flow rates, and core molten salt flow field distributions were simulated using the ThorCORE3D code, and the power and temperature responses were observed and analyzed in detail. The results show that the reactor system has different and instantaneous responses owing to different steady-state DNFs. Generally, the peak values of the reactor power and average fuel and graphite temperatures reach higher values when the initial DNF is smaller. Owing to the reactivity negative feedback effect, the power and temperature are eventually stabilized at the same level in different external loop recirculation times and different flow field distribution cases. When the fuel flow rates differ, the final powers and temperatures significantly differ owing to the combined effect of different DNF losses and temperature feedback.