1 Introduction

The transport and slowing down process of particles in a nuclear system is described by the linear Boltzmann transport equation, and the discrete ordinates method is one of the widely used and highly efficient deterministic methods for solving it. The anisotropic scattering effect is of importance both for reactor physics and for the shielding calculation, as reactors’ heterogeneous effect cannot be neglected, and geometric structures become more complex. Appropriately handling scattering anisotropy has an important influence on accuracy and efficiency. Especially for shielding problems, highly anisotropic angular flux distribution strengthens the influence of anisotropic scattering. Considering the fact that the influence on computational accuracy of scalar flux is problem-dependent, systematic analyses of numerical algorithms and cross sections used in simulations are required.

The conventional treatment for scattering in discrete ordinates transport codes is to expand the scattering cross section with truncated Legendre polynomials [1], and the spherical harmonics expansion method is a usual option to calculate scattering source terms. The requirement for the Legendre expansion varies among diverse models, and significant experience shows that the P5 order is sufficient to obtain accurate integral quantities [2], such as detector responses and fast neutron fluence rates for some problems of RPV analyses and fusion installation shielding. For the light nuclei’s elastic scattering reactions, merely increasing the expansion order cannot eliminate oscillations of approximated angular distributions. Therefore, Odom proposed the exact-kernel method [3] and modified the scattering source calculation method in deterministic codes, which generated much more accurate angular fluxes, but involved a larger storage requirement and longer execution time. The finite Legendre expansion generates negatives for differential scattering cross sections. A constrained least-squares algorithm, which modified high-order scattering Legendre moments, and a maximum entropy method [4] to represent scattering cross sections were developed by Dahl to correct this deficiency, and his methods could create a nonnegative expansion. Another family of nonnegative scattering cross section generating methods, inspired by or based on the Monte Carlo theory, were applied in SN and multi-group MC codes, including the hybrid Monte Carlo-discrete elements method proposed by DelGrande [5] and the piecewise-average group cross section method proposed by Gerts [6]. Jong Woon Kim employed angular data of elastic scattering [7] from ENDF libraries as a complementary part for basic multi-group cross sections, if needed. Moreover, transport approximations/corrections [8, 9] and fix-up selections in the scattering source calculation [10] also play a significant role in flux results. Additionally, the Galerkin quadrature [11, 12] proposed by Morel is a powerful technique for a highly anisotropic scattering source, and its application mainly concentrates on charged particle transport. Some numerical analyses on anisotropic scattering have been performed for reactor critical calculation [13,14,15,16] and analytical transport problems [17, 18].

The purpose of this study is to quantitatively analyze the impact of scattering anisotropy on SN transport calculation using the conventional Legendre expansion method. The required Legendre expansion order depends on both materials’ physical properties and angular flux distributions. The analyses in this paper are beneficial for users to choose proper algorithms for realistic shielding problems. We produce multi-group cross sections with the P9 expansion in the LANL 30N12G and Vitamin-J 175N42G structures using NJOY2016 [19]. We studied the scattering cross section expansion convergence of actual materials. Effects of parameters on scattering for neutron and photon transport were investigated, including the expansion order, transport correction, scattering source fix-up, and other model features. The remainder of the paper is organized as follows. Section 2 briefly describes the methods regarding the scattering source calculation for SN codes. The convergence analyses for water, iron, and other materials under truncated Legendre expansions are given in Sect. 3. We simulated a number of fix-source problems with simple geometry and homogeneous media, and the numerical results are summarized in Sect. 4. We draw some conclusions in Sect. 5.

2 Review of theory

ARES [20,21,22] is a multi-dimensional neutral particle transport code based on the discrete ordinates method, which is capable of solving critical and shielding problems. The general procedure and methods for calculating the scattering source in SN codes are briefly reviewed below. For simplicity, the time-independent transport equation without the fission source term in 1D slab geometry is considered as:

$$\mu \frac{{\partial \psi (x,E,\vec{\varOmega })}}{\partial x} + \varSigma_\text{t} (x,E)\psi (x,E,\vec{\varOmega }) = \int_{0}^{\infty } {{\text{d}}E^{{\prime }} } \int_{{\varOmega^{\prime}}} {\varSigma_\text{s} (x,E^{{\prime }} \to E,\vec{\varOmega }^{{\prime }} \to \vec{\varOmega })\psi (x,E^{{\prime }} ,\vec{\varOmega }^{{\prime }} ){\text{d}}\vec{\varOmega }^{{\prime }} + Q_{\text{fixed}} (x,E,\vec{\varOmega })} ,$$
(1)

where \(\psi\) is the angular flux; \(\mu\) is the direction cosine of \(\vec{\varOmega }\); \(Q_{\text{fixed}}\) is the fixed-source term; \(\varSigma_\text{t}\) and \(\varSigma_\text{s}\) are macroscopic total and scattering cross sections, respectively; x, E, and \(\vec{\varOmega }\) are the spatial, energy, and direction variables, respectively.

To solve the scattering integral after the energy and angular discretization, the scattering cross section is a function of the scattering angle and can be expanded in the series of Legendre polynomials as Eq. (2). The angular flux can likewise be expanded in Legendre polynomials or the spherical harmonics functions. According to the addition theorem, the scattering source term for discrete direction m and group g is calculated as Eq. (3) using the L-order expansion:

$$\varSigma_{{{\text{s}},g^{{\prime }} \to g}} (x,\mu_{0} ) = \sum\limits_{0}^{\infty } {\frac{2l + 1}{2}\varSigma_{{{\text{s}},l,g^{{\prime }} \to g}} (x)P_{l} } (\mu_{0} ),$$
(2)
$$Q_{{{\text{s}},g}}^{m} = \sum\limits_{{g^{{\prime }} = 1}}^{G} {\sum\limits_{l = 0}^{L} {\frac{2l + 1}{4\pi }} \varSigma_{{{\text{s}},l,g^{{\prime }} \to g}} \sum\limits_{n = - l}^{l} {\phi_{l,n,g} Y_{l,n} (\vec{\varOmega }_{m} )} } ,$$
(3)

where \(\varSigma_{{{\text{s}},l}}\) is the lth scattering Legendre moment; \(P_{l}\) is the l-order Legendre polynomial; \(\phi_{l,n}^{{}}\) denotes the lth, nth flux moment; \(Y_{l,n}^{{}}\) denotes the lth, nth spherical harmonics function; and G denotes the total number of energy groups.

This spherical harmonics expansion method is easy to use because of its small data storage requirement. If the exact-kernel representation or the piecewise function representation for scattering cross sections is used, the formula for the scattering source is modified to Eq.(4). Hence, angular fluxes for each discrete angle and transfer cross sections for each possible scattering angle need to be stored.

$$Q_{{{\text{s}},g}}^{m} = \sum\limits_{{g^{{\prime }} = 1}}^{G} {\sum\limits_{{m^{{\prime }} = 1}}^{M} {w_{{m^{\prime}}} \varSigma_{{\text{s},g^{{\prime }} \to g}}^{{m^{{\prime }} \to m}} \psi_{{g^{{\prime }} ,m^{{\prime }} }} } } ,$$
(4)

where \(\varSigma_{{{\text{s,}}g^{{\prime }} \to g}}^{{m^{{\prime }} \to m}}\) denotes the group-to-group and direction-to-direction scattering cross section; \(w\) denotes the discrete direction weight; and M denotes the total direction number.

When the expansion order is not sufficiently high to adequately handle the anisotropy, the expanded cross section may exhibit non-physical negative values among part of the angular range, and this may bring about a negative scattering source for certain directions. The negative source is one of the reasons for negative angular flux besides spatial discretization and mesh size. In the iterations of transport sweep, treatments for the negative source include economic and conservative manners. The economic fix-up directly sets the negative total source to zero. The conservative method first sorts sources of all directions and then removes all negatives as well as some small positives until the 0th source moment \(Q_{0}\) in Eq.(5) is restored, which ensures particle conservation as far as possible:

$$Q_{0} = \int_{4\pi } {Q(\vec{\varOmega }){\text{d}}\varOmega } \cong \sum\limits_{m = 1}^{M} {w_{m} Q^{m} } .$$
(5)

To avoid the negative scattering cross section, increasing expansion orders, the Legendre moment adjustment, and piecewise constant function representation are all available methods. In addition, proper transport approximations [8, 9] could improve accuracy with less cost for the Legendre expansion method. Transport cross sections with isotropic scattering are usually used in core physics analyses as the treatment for scattering anisotropy [15]. Strictly speaking, multi-group total cross sections are angle-dependent to a certain extent in theory, as presented in the multi-group 1D PN equation as Eq. (6):

$$\mu \frac{{\partial \psi_{g} (x,\mu )}}{\partial x} + \sum\limits_{l = 0}^{L} {\frac{2l + 1}{2}P_{l} (\mu )} \varSigma_{{{\text{t}},l,g}}^{{P_{N} }} (x)\phi_{g,l} (x) = \sum\limits_{l = 0}^{L} {\frac{2l + 1}{2}P_{l} (\mu )\sum\limits_{{g^{\prime}}}^{G} {\varSigma_{{{\text{s}},l,g^{{\prime }} \to g}}^{{P_{N} }} (x)\phi_{{g^{\prime},l}} (x)} + Q_{{{\text{fixed}},g}} (x,\mu )} .$$
(6)

Equation (6) can be transferred to the SN equation by moving the second term to the right side and then adding \(\varSigma_{\text{t},g}^{{S_{\text{N}} }} \psi_{g}\) term to both sides of the equation. However, angular-dependent total cross sections or the high-order Legendre moment of total cross sections are not used in the actual SN calculation, and this relationship is simplified by various transport approximations [19] by choosing total cross sections and scattering moments as Eq. (7):

$$\begin{aligned} & \varSigma_{{{\text{s}},l,g^{\prime} \to g}}^{{S_{{N}} }} = \varSigma_{{{\text{s}},l,g^{\prime} \to g}}^{{P_{N} }} ,\quad g^{{\prime }} \ne g \\ & \varSigma_{{{\text{s}},l,g \to g}}^{{S_{\text{N}} }} = \varSigma_{{{\text{s}},l,g \to g}}^{{P_{N} }} - \varSigma_{\text{t},l,g}^{{P_{N} }} + \varSigma_{\text{t},g}^{{S_{\text{N}} }} \\ & \begin{array}{*{20}l} {{\text{Consistent P: }}\varSigma_{\text{t},g}^{{S_{\text{N}} }} = \varSigma_{\text{t},0,g}^{{P_{N} }} } \hfill \\ {\quad {\text{Diagonal: }}\varSigma_{\text{t},g}^{{S_{\text{N}} }} = \varSigma_{\text{t},L + 1,g}^{{P_{N} }} - \varSigma_{{{\text{s}},L + 1,g \to g}}^{{P_{N} }} } \hfill \\ {\quad \quad {\text{Extend: }}\varSigma_{\text{t},g}^{{S_{\text{N}} }} = \varSigma_{\text{t},L + 1,g}^{{P_{N} }} - \sum\limits_{{g^{{\prime }} }} {\varSigma_{{{\text{s}},L + 1,g \to g^{{\prime }} }}^{{P_{N} }} } .} \hfill \\ \end{array} \\ \end{aligned}$$
(7)

The consistent P approximation directly adopts the scalar flux-weighted total cross sections and the L-order truncated Legendre moments of scattering cross sections. Other approximations modify total cross sections and within-group components of the scattering matrix using high-order information. The diagonal transport approximation considers within-group components in the (L + 1)-order scattering matrix and uses them to correct total cross sections. The extended transport approximation assumes the (L + 1)-order term of a scattering source for a given group equal to the scattering out of this group. These approximations reduce errors caused by disregarding high-order expansion terms. The cross section data needed for transport corrections are generated by the GROUPR module of NJOY and stored in MATXS-format libraries for the processing code TRANSX [23].

3 Convergence analyses of Legendre expansion

To date, the Legendre expansion has been the most widely used method in deterministic codes because of its stability and usability for the majority of neutron shielding problems. Here, a simple method is presented to compare the anisotropy of different materials. Results of convergence analyses could serve as auxiliaries and supplements for evaluating the relative strength of anisotropic scattering. For analyses of water and iron, multi-group cross sections were generated based on the ENDF/B-VII.1 data by NJOY2016 with the P9 expansion in LANL 30N12G and Vitamin-J 175N42G structures. Subsequently, TRANSX was used to produce materials’ macroscopic cross sections, where the density of water and iron were set to 1.0 g cm−3 and 7.87 g cm−3, respectively.

Elastic neutron scattering of light nuclei for high energy and Compton scattering caused by photons exhibit a highly forward peak. We mainly focus on the anisotropy of macroscopic cross sections of common shielding and structure materials. First, the normalized expansions for differential scattering cross sections are adopted as Eq. (8) to investigate the relative angular distribution:

$$F_{L} (\mu ) = \sum\limits_{l = 0}^{L} {\frac{2l + 1}{2}\frac{{\varSigma_{{{\text{s}},l}} (x)}}{{\varSigma_{{{\text{s}},0}} (x)}}P_{l} } (\mu ).$$
(8)

Functions in Eq. (8) can be drawn directly to observe the distribution, and analyses were performed based on the differential scattering cross section functions. Figure 1 shows some normalized differential neutron scattering cross sections of water under the consistent P approximation in the LANL group structure.

Fig. 1
figure 1

(Color online) Normalized differential neutron scattering cross section distributions of water

Full size image

Results and experiences show that within-group scattering is generally forward-peaky, the peak place of group differential scattering cross sections moves toward \(\mu_{0} = 0\) as the energy loss increases, and scattering in the high-energy range is more anisotropic. Additionally, there is a relationship between self-shielding treatment and anisotropic scattering. The self-shielding effect affects not only total cross sections in the resonance energy range, but also scattering cross sections as well as the corresponding angular distribution. The Bondarenko method [23] was adopted as the treatment for the resonance self-shielding effect. Comparison of infinite-dilute and self-shielded cross sections was performed based on the LANL structure library for iron material, as shown in Fig. 2. According to the normalized within-group scattering functions of the 17th group (2.48 × 10−2 to 6.76 × 10−2 MeV), anisotropy of within-group scattering is weakened with self-shielding treatment. Photon production cross sections are also modified by the self-shielding effect, which is disregarded in this study because of its almost isotropic scattering property.

Fig. 2
figure 2

(Color online) Comparison of infinite-dilute and self-shielded cross sections of iron

Full size image

Considering the investigation based on drawing scattering angular distributions is unrealistic for larger datasets, inspired by the scattering sampling functions of multi-group MC, we integrate normalized functions in the entire scattering angle interval and analyze anisotropy by the convergence of integrals. Factors \(f_{L}\) are defined to describe the gap between L-order truncated and (L − 2)-order truncated expansions, as indicated by Eq.(9):

$$f_{L}^{{}} = \int_{ - 1}^{1} {\left| {F_{L} (\mu ) - F_{L - 2} (\mu )} \right|{\text{d}}\mu } .$$
(9)

Factors \(f_{L}\) are integrals that measure the area of difference between normalized expansion functions, and the Legendre expansion is converged if this integral factor is small enough for L-order. A more anisotropic scattering of materials leads to a larger integral \(f_{L}\) for a given order. Considering that the true multi-group scattering angular distribution is unknown, these integrals evaluate the closeness of expanded functions of adjacent orders, and the intensity of anisotropy could be estimated. Integrals are computed including \(f_{3}^{{}}\), \(f_{5}^{{}}\), \(f_{7}^{{}}\), and \(f_{9}^{{}}\) with the Gauss quadrature based on the library of LANL structure under the consistent P approximation, and factors for the within-group neutron and gamma scatters of water and iron are shown in Fig. 3.

Fig. 3
figure 3

(Color online) Anisotropic factors for within-group neutron and gamma scattering of water and iron

Full size image

For neutron scattering of a given group, the factor value decreases as the order increases, which means that the Legendre expansion functions converge and negative ranges of cross sections are gradually reduced. Within-group neutron scattering of water is more anisotropic than that of iron because of H elastic scattering. On the contrary to neutron cases, factors of gamma scattering increase slightly, which represents intensive oscillations and inevitable negatives in the differential cross sections distribution. Negatives of expanded cross sections could be neglected when factors have small values. Factors of scattering between different groups are difficult to converge, because the peak of differential cross sections is close to the middle. The impact of group structures on the anisotropy was also investigated in this way. Factors of water’s neutron and gamma within-group scattering are listed in Table 1 based on libraries with different group structures. As energy groups are refined, within-group scattering becomes more anisotropic, which is proved by the fact that larger \(f_{L}\) factors of the same order are obtained for a finer group structure.

Table 1 Factors of water within-group scattering
Full size table

The anisotropy of several materials was likewise investigated in this manner including water, polyethylene, concrete, graphite, iron, SS304, and lead based on the Fendl3.0MG libraries. For neutron scattering of materials, the scattering anisotropy is relatively strong for all materials from 13 to 50 MeV, whose f5 factors range from 1.0 to 2.6. Because of the hydrogen element and its elastic scattering, within-group scattering of water and polyethylene is remarkably more anisotropic than other materials’ scattering below 0.1 MeV, where their f5 factors are greater than 1.0, whereas others are less than 0.1. Gamma scattering shows strong anisotropy similar to water and iron data above, and f5 factors of these materials become 2.8–3.6 from 1.3 to 50 MeV. Further analyses could be performed to predict accuracy and negatives of expanded scattering functions, and these comparisons may be helpful for users to pick key materials with strong anisotropy within a certain energy range.

4 Numerical results

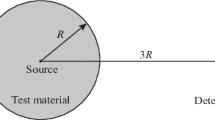
The generation of multi-group cross sections, algorithms of calculating the scattering source, and model features determine the effects of scattering anisotropy and simulation accuracy together. To investigate these effects, a series of 2D fixed-source problems with simple geometry were simulated with the ARES code. Models of test problems 1 and 2 have similar structures as shown in Fig. 4, where the two side lengths of the source region are 5 cm and 0.5 cm. Particles move more than 10 mean-free-paths from the source region to the system boundaries. The isotropic source only exists in the first group, because of the high-energy scattering’s strong anisotropy. Mesh sizes are set to 0.5 cm using weighted differencing spatial discretization, owing to the good resistance to negative fluxes. The Legendre Chebyshev quadrature sets of S32 order are adopted to minimize the angular discretization error. The iteration convergence criterion for group flux is equal to 5E−5, and no iteration acceleration technique is employed. The behaviors of different self-shielding treatments are out of the scope of this paper.

Fig. 4
figure 4

Sketch of test model 1 and 2

Full size image

The scalar flux results of the P9 expansion under consistent P approximation with the negative source conservative fix-up serve as references. To evaluate the integral errors of group fluxes, dose rates are computed based on the ANSI/ANS-6.1.1-1977 conversion factors, and the output comprises root-mean-square errors in Eq. (10) and maximum errors in Eq. (11) for mesh dose rates:

$$E_{\text{RMS}} = \sqrt {\frac{1}{N}\sum\limits_{ijk = 1}^{N} {\left( {\frac{{\sum\nolimits_{g}^{G} {C_{g} \phi_{{{\text{calc}},ijk,g}} } - \sum\nolimits_{g}^{G} {C_{g} \phi_{{{\text{ref}},ijk,g}} } }}{{\sum\nolimits_{g}^{G} {C_{g} \phi_{{{\text{ref}},ijk,g}} } }}} \right)^{2} } }$$
(10)
$$E_{\text{MAX}} = \mathop {\hbox{max} }\limits_{1 \le ijk \le N} \left| {\frac{{\sum\nolimits_{g}^{G} {C_{g} \phi_{{{\text{calc}},ijk,g}} } - \sum\nolimits_{g}^{G} {C_{g} \phi_{{{\text{ref}},ijk,g}} } }}{{\sum\nolimits_{g}^{G} {C_{g} \phi_{{{\text{ref}},ijk,g}} } }}} \right|$$
(11)

where \(\phi_{ijk,g}\) denotes the scalar flux of ijkth mesh of g group, \(C_{g}\) denotes the flux-dose conversion factor of g group, and N denotes the total number of meshes.

For neutron transport in water, the resulting errors obtained from model 1 and the computational time normalized by the shortest time are listed in Table 2. Generally, errors of mesh dose rates are quite small with P3 or higher expansions. With expansions of the same order and economic fix-up, extended and diagonal approximations obtain better results compared to the consistent P method, because these two corrections implicitly contain high-order scattering moment information, which ameliorates the negatives of the within-group scattering angular distribution. Better results are acquired with no fix-up or conservative fix-up for the negative source compared to results obtained by the economic fix-up. The economic fix-up ignores the 0th source moment conservation and damages particle balance. It exaggerates total scattering and leads to larger flux results. This effect may not be significant when negatives of scattering angular distribution are not severe, as given in Table 2. Although good scalar quantities could be gained without the fix-up, the angular flux distribution would be disturbed at the permission of a negative source, which is discussed below. The situation for neutron transport in iron is similar, and the errors are smaller. From the error distribution of dose rates, relative errors of results with the economic fix-up retain positive signs, and error values rise gradually as neutron transport distance increases. No clear pattern is observed in the error distributions of the other two algorithms. The relative errors of dose rates are similar to those of high-energy group fluxes and slightly larger than those at low energy. The \(E_{\text{RMS}}\) of dose rates could represent the average level of flux accuracy.

Table 2 Error norms and normalized computational time for neutron transport in water of model 1
Full size table

When low expansions are employed for neutron transport, relative errors of group fluxes and dose rates increase using the 175N42G library compared to the corresponding results using 30N12G library with the economic fix-up, while errors remain similar when using these two libraries with the conservative fix-up. Root-mean-square errors of flux for each group under the diagonal approximation are shown in Fig. 5, and the effect of group refinement is observed. The conservative fix-up method reduces differences of relative errors between fine and coarse libraries with the same expansion, which could compensate the effect of group refinement to a certain extent.

Fig. 5
figure 5

(Color online) Root-mean-square errors of group flux for neutron transport in water of model 1

Full size image

Errors obtained for the gamma transport of iron are listed in Table 3. The extended approximation produces negative 0th scattering moments for several groups at all expansion orders. The behavior of the economic fix-up becomes worse, as the negative situation becomes more severe for gamma scattering, which is indicated from the analyses in Sect. 3. The diagonal approximation and conservative fix-up are more proper for gamma transport problems. Errors in the gamma transport of water are smaller than those in iron owing to the longer mean-free-path of photons in water, despite similar anisotropy.

Table 3 Error norms and normalized computational time for gamma transport in iron of model 1
Full size table

The particle balance for the entire system is evaluated by comparing the sum of the total leakage and total collision, which are calculated based on fluxes of the ith iteration, and total source, which is calculated based on fluxes of (i − 1)th iteration without any fix-ups. The balance ratio is defined as Eq. (12), and particles are conserved if its value approaches zero:

$$R_{\text{balance}} = \frac{{\left| {{\text{Leakage}} + {\text{Collision}} - {\text{Source}}} \right|}}{\text{Source}}.$$
(12)

This ratio for simulations with no fix-up should be zero in theory; however, its magnitude is approximately 1E−15 to 1E−14 because of round-off errors. For neutron transport problems, the imbalance caused by economic fix-up mainly happens in the first few groups and attenuates with increasing expansion order. Ratios of gamma transport in iron under the diagonal approximation are shown in Fig. 6, and ratios for 10th, 11th, and 12th groups are below 1E−14. The conservative method could improve the global balance by about four magnitudes compared to the economic fix-up.

Fig. 6
figure 6

(Color online) Balance ratios of gamma transport in iron with negative source fix-up

Full size image

Besides monoenergetic source problems, continuous energy source problems were calculated using the Watt fission spectrum of 235U in model 1 involving neutron and photon coupled transport. The maximum ERMS of neutron dose rates is less than 0.1% among all cases for water and iron from P3 to P7 orders. The magnitude of error in the gamma dose rates is similar to that of neutron dose rates, considering that the accuracy of photon fluxes mainly depends on the local neutrons than on photons transporting from a distance. The differences among negative source fix-up methods can be disregarded, such that the economic fix-up is always recommended for shielding problems of RPV analyses [24]. For problems with a continuous energy source, the fixed source in each group weakens the effect of anisotropic scattering because of a larger proportion of uncollided flux in the scalar flux. More complicated scattering between groups may overshadow some effects observed in monoenergetic source problems.

The computational time of cases above was compared to evaluate the algorithm efficiency. With the P3 or P5 expansion, the diagonal approximation saves about 1–15% of the time in comparison with other approximations because of the smaller scattering ratio, which leads to fewer inner iterations to achieve convergence criteria. For negative source fix-ups, the conservative method would increase the computational time owing to its cost on sorting and source moment calculation. This influence on the computing time is related to the material property, expansion order, and group structure. When the LANL 30N12G or Vitamin-J 42G library is used, the conservative fix-up would increase the time by about 40% with the P3 expansion and by about 20% with the P5 expansion. For the Vitamin-J 175N library, this ratio decreases to about 10%, probably because the fix-up subroutine does not take effect in many low-energy groups. In general, the percentage of the conservative fix-up to the overall computational time would decrease with the expansion and group number increase. No fix-up may cause unacceptable disturbance for the iteration in some cases, preventing the iteration error to decrease stably and continuously.

Model features likewise play an important role in the magnitude of anisotropic scattering effects. The size of the source region, angular dependence of source particles, geometric model, material composition, and other problem-related quantities determine the angular flux distribution. A more anisotropic angular flux leads to a stronger scattering influence. Monoenergetic point source problems in model 2 were simulated. Compared to the model 1’s results, errors of model 2 are larger and the superiority of the conservative fix-up is more notable than the economic way. Error norms for photon transport in iron are shown in Table 4. To investigate the accuracy in the deep-penetration region, root-mean-square errors of mesh dose rates \(E_{\text{RMS}}^{\text{VB}}\) along the right vacuum boundary are likewise given. The angular flux is more forward-peaky for point source problems, and this makes the anisotropic scattering impact stronger. The small mean-free-path of photons encourages the accumulation of errors in spite of the small scattering ratio.

Table 4 Error norms for gamma transport in iron of model 2
Full size table

The effect of source particles’ angular dependence is analyzed qualitatively by monoenergetic surface incident source problems, whose model is shown in Fig. 7. A model with the isotropic incident (\(\psi_{\text{in}} (\mu ) = 1.0\)) and the other with exponential incident (\(\psi_{\text{in}} (\mu ) = {{\exp (3.0 \times \mu )} \mathord{\left/ {\vphantom {{\exp (3.0 \times \mu )} {\int {\exp (3.0 \times \mu ){\text{d}}\mu } }}} \right. \kern-0pt} {\int {\exp (3.0 \times \mu ){\text{d}}\mu } }}\)) about the direction cosine of discrete directions are adopted.

Fig. 7
figure 7

Sketch of test model 3

Full size image

The results of gamma transport in iron of model 3 are given in Table 5, where only the consistent P approximation is used, and results with the P9 expansion for respective problems serve as references. The effect of anisotropic scattering is stronger for the exponential incident problem, because the angular flux of this problem is more anisotropic by our modification for the angular dependence of the incident source.

Table 5 Error norms for gamma transport in iron of model 3
Full size table

To further evaluate the conservative fix-up and no fix-up methods, approximated slab problems with the isotropic incident from left side were solved, as shown in Fig. 8. A row of meshes is constructed with the side length equal to 1 cm. Although scalar flux results may converge quickly as the expansion order increases, it is extremely difficult to obtain accurate angular flux as references for each angle under the disturbance of spatial and angular discretization.

Fig. 8
figure 8

Sketch of test model 4

Full size image

Positivity is one of the desirable qualities for the SN calculation, and the ratios of the number of directions with negative angular fluxes to the total number of discrete directions in the quadrature sets were computed for each mesh and each group. The incident source only exists in the first group, and the P3 expansion is adopted under consistent P approximation. The differences between the two methods are not large for the neutron transport in water. However, the behaviors of these methods differ greatly for gamma transport in iron, and their results of negative angular flux ratios are shown in Fig. 9. The economic fix-up has the best ability to reduce occurrences of negative angular fluxes. This is not satisfactory for the economic fix-up for problems with highly anisotropic angular flux distributions, because it overestimates fluxes despite its elimination of the negative source. Almost all angular fluxes of backward directions are negative with no source fix-up, although good integral quantities could always be gained. Owing to discretization properties and improper mesh size, many spatial discretization schemes, such as diamond differencing and the linear finite element method, would produce non-physical negative angular flux despite the positive incident and source term. There is no doubt that the negative source aggravates the appearance of negative angular fluxes, and it may cause iteration divergence for some spatial treatments based on the exponential assumption. Therefore, source fix-ups are recommended to obtain as few as possible disturbances on transport solving.

Fig. 9
figure 9

(Color online) Negative angular flux ratio for each mesh and group

Full size image

Finally, monoenergetic directional point source problems were simulated to analyze the most severe case of anisotropy. Unfortunately, no reliable results could be obtained with the existing algorithms in ARES. The differences between results with P7 and P9 expansions remain fairly large. The Galerkin quadrature and strictly nonnegative scattering cross section may be required. The conventional Legendre expansion method cannot deal with this high degree of anisotropic problems. The algorithms used to describe anisotropic scattering affects the flux results more significantly as the proportion of collided flux within the scalar flux increases.

5 Conclusion

The methodology employed to handle anisotropic scattering is reviewed for deterministic transport codes. Due to the insufficiency of the Legendre expansion, non-physical negatives of scattering functions may result in a negative source of transport solving for highly anisotropic scattering media. This affects computational accuracy and exacerbates negative angular fluxes, as well as the process of iteration calculation. Convergence analyses of scattering Legendre moments and a series of numerical tests were performed in this study. An integral factor method was proposed to evaluate the precision of expanded scattering angular distributions by integrating functions of scattering moments. By checking the convergence of integral factors, the severity of negatives could be predicted. Gamma scattering exhibits much stronger anisotropy than neutron scattering, considering normalized within-group scattering functions.

Numerous 2D problems were simulated using the ARES transport code, and integral errors of dose rates were compared to analyze computational accuracy. The extended and diagonal transport approximations show better efficiency than the consistent P method for a given expansion order, which uses high-order information to reduce the negatives of scattering functions. However, the extended approximation may produce negative 0th scattering moments in some cases. Different algorithms have stronger effects on the gamma transport than on the neutron transport. The economic fix-up overestimates total scattering and scalar fluxes, especially for monoenergetic photon transport problems, and errors would accumulate and rise as the penetration distance increases. No fix-up and conservative fix-up show similar integral results; however, a serious situation exists with regard to negative angular fluxes if no fix-up is adopted. Few differences are detected among results using various algorithms for problems with the fission source, because the existence of a fixed source in every group increases the ratio of uncollided flux and weakens the scattering effect. The refinement of groups certainly makes within-group scattering more forward-peaky; however, this effect may not be important for integral quantities of common problems. Simulations of beam point source problems are sensitive to the anisotropic scattering and require a nonnegative cross section to handle anisotropy more accurately.

The proper treatments of scattering are important for computational accuracy, especially when angular flux is highly anisotropic or scattering is of strong anisotropy. This effect strengthens as the proportion of collided flux in the scalar flux increases. The analyses in this study assist to evaluate and determine options in SN codes. The Galerkin quadrature with the nonnegative cross section will be studied and implemented in the ARES code for beam source shielding problems in the future. Further comparisons will be performed for realistic engineering problems.